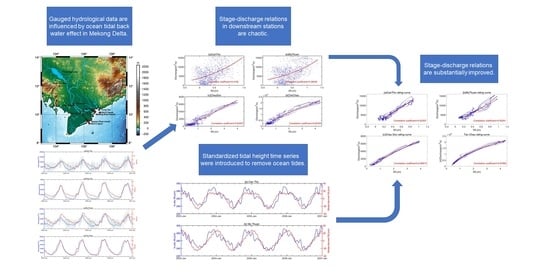
Improving Stage–Discharge Relation in The Mekong River Estuary by Remotely Sensed Long-Period Ocean Tides
Abstract
1. Introduction
2. Datasets and Assessment Metrics
2.1. In-Situ Hydrological Data
2.2. Sea Level Data from Tide Gauge Station
2.3. Global Ocean Tide Model Data
2.4. Assessment Metrics
3. Data Analysis and Methodology
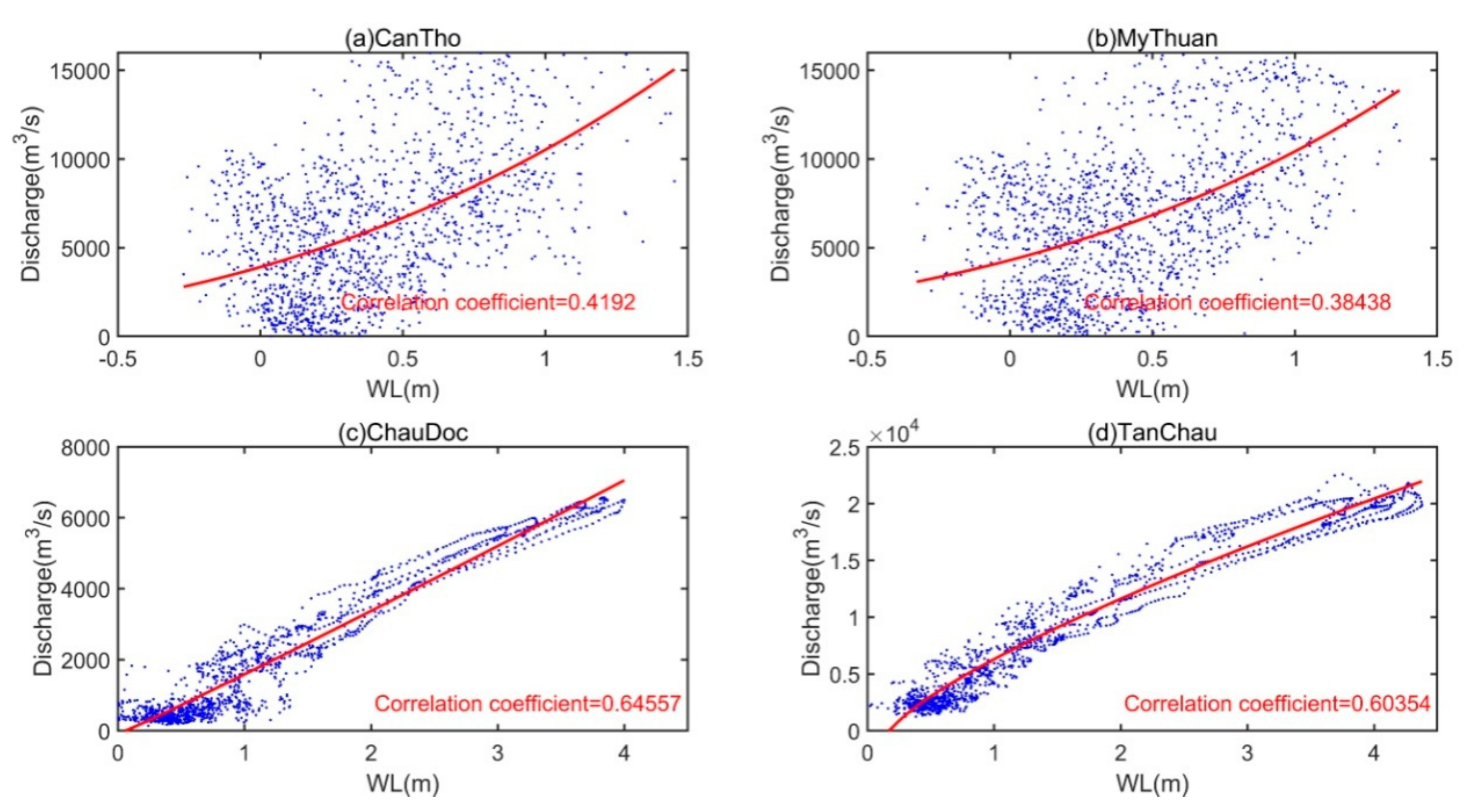
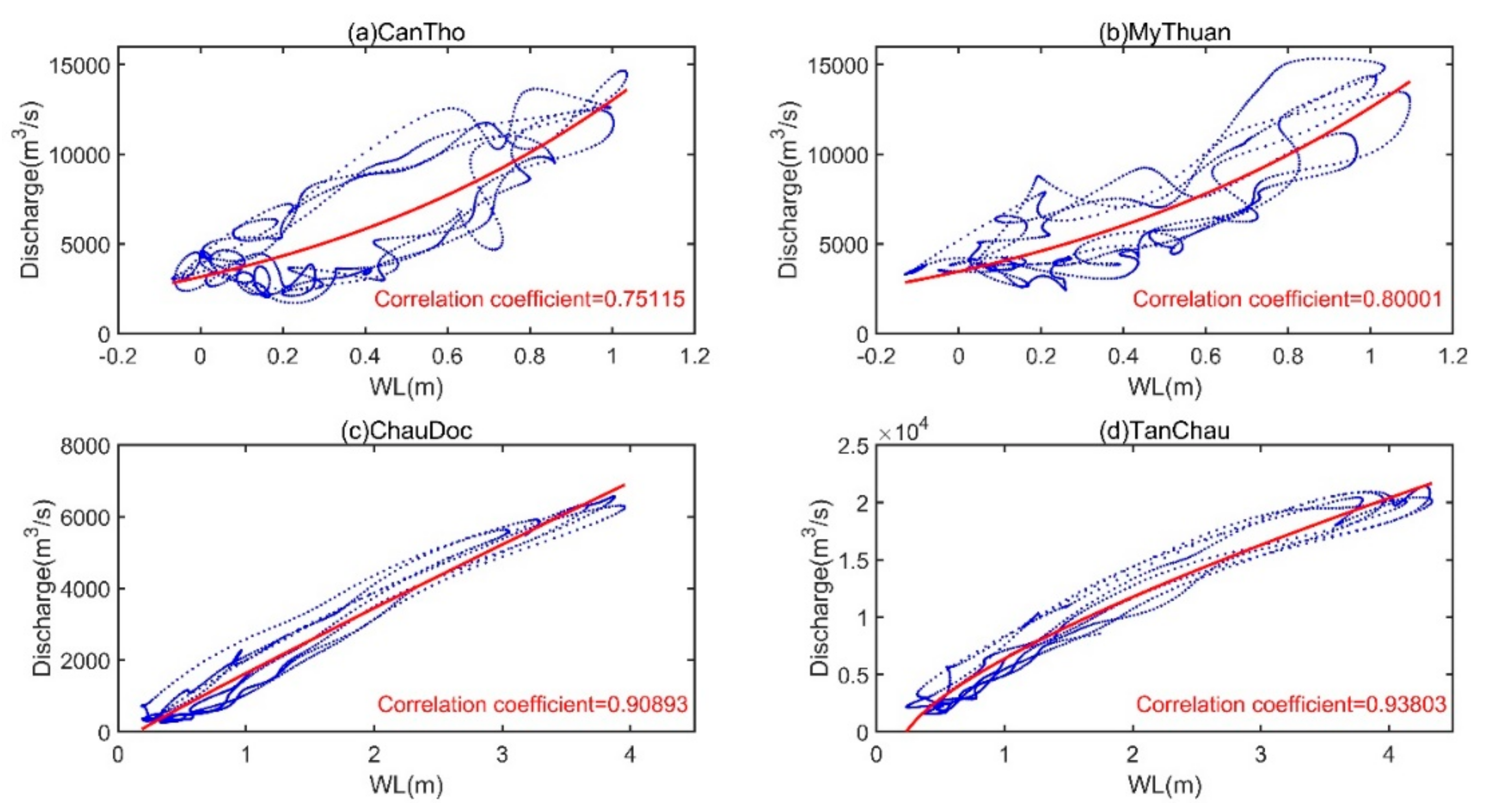
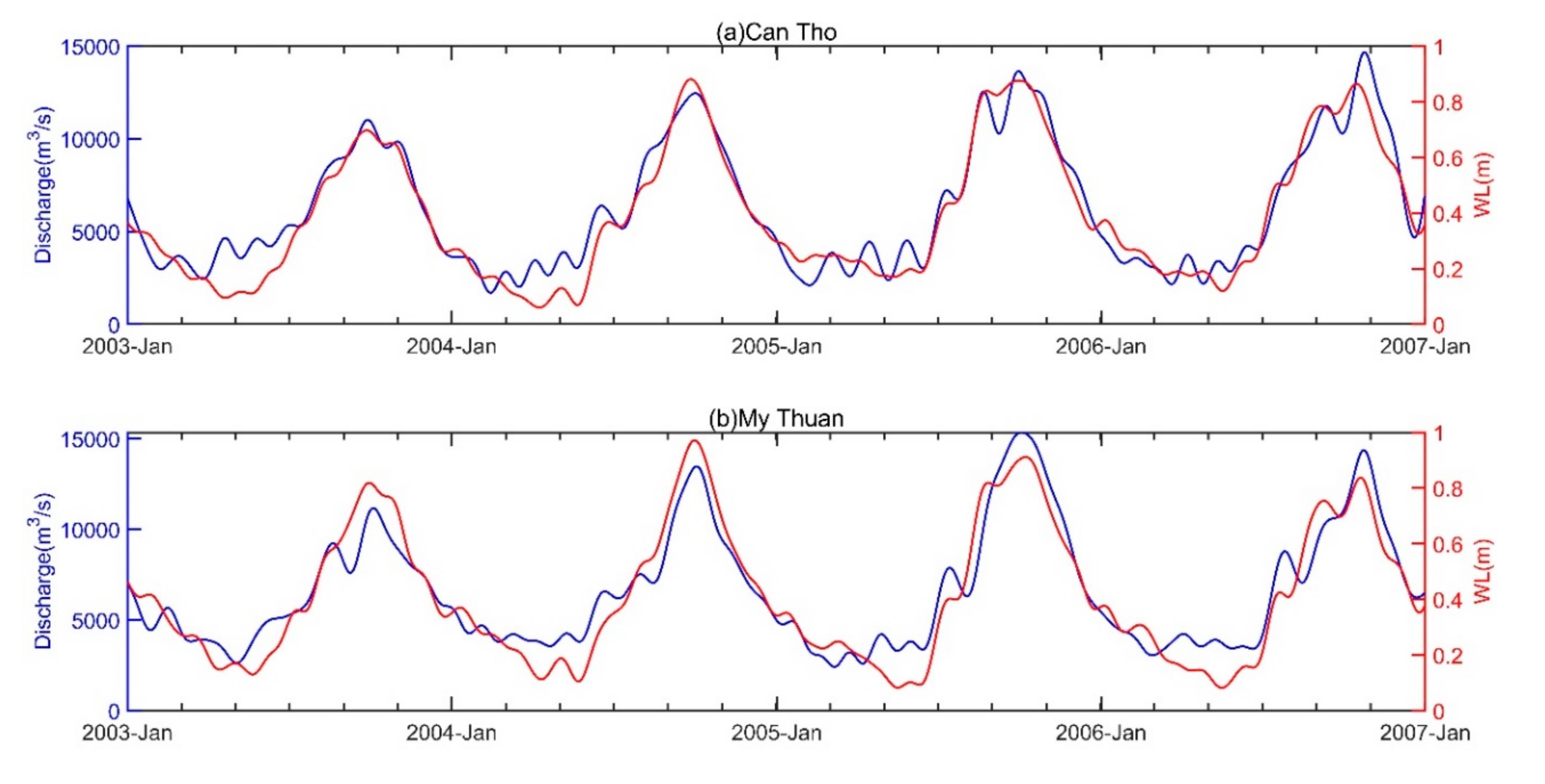
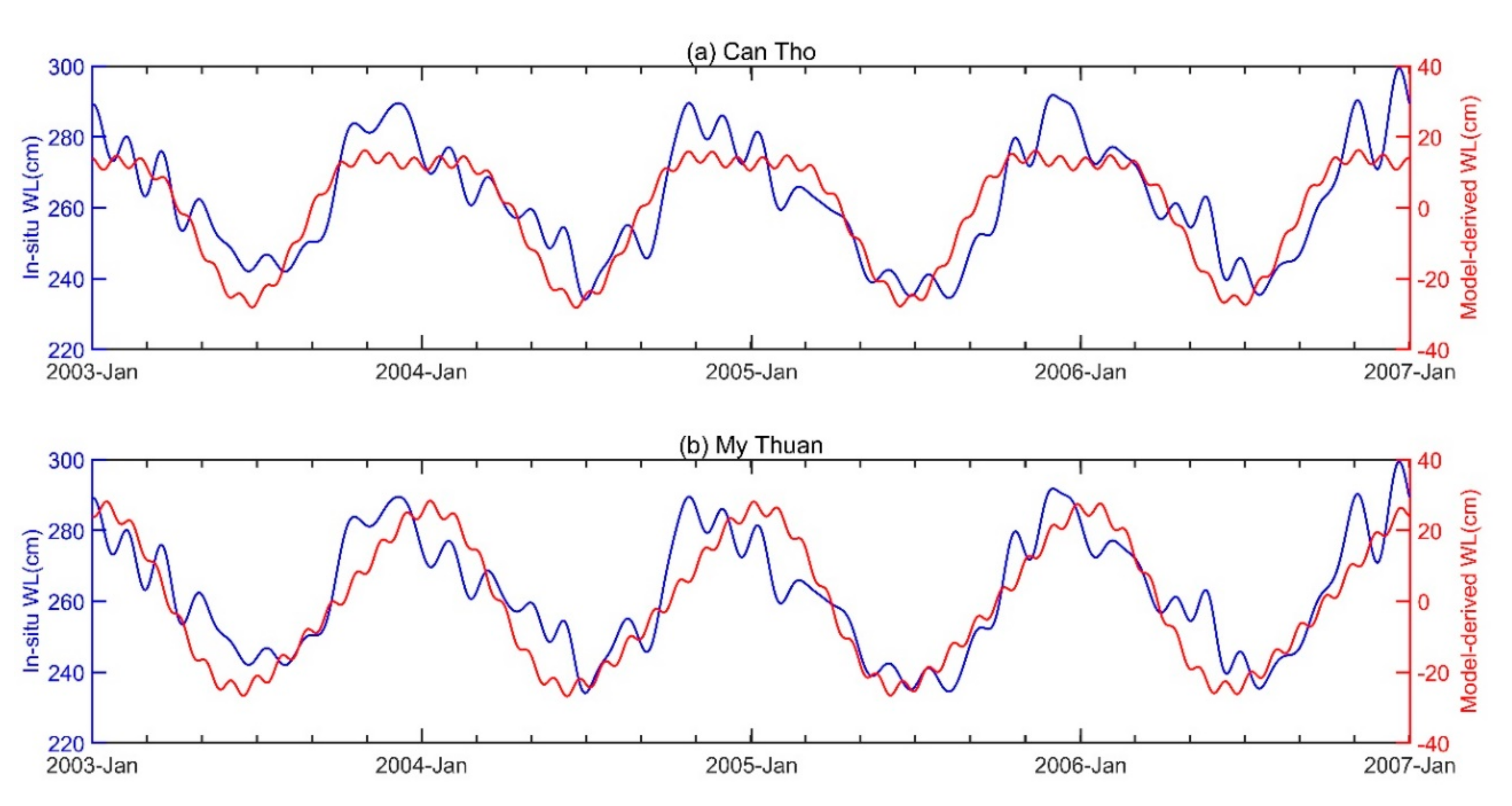
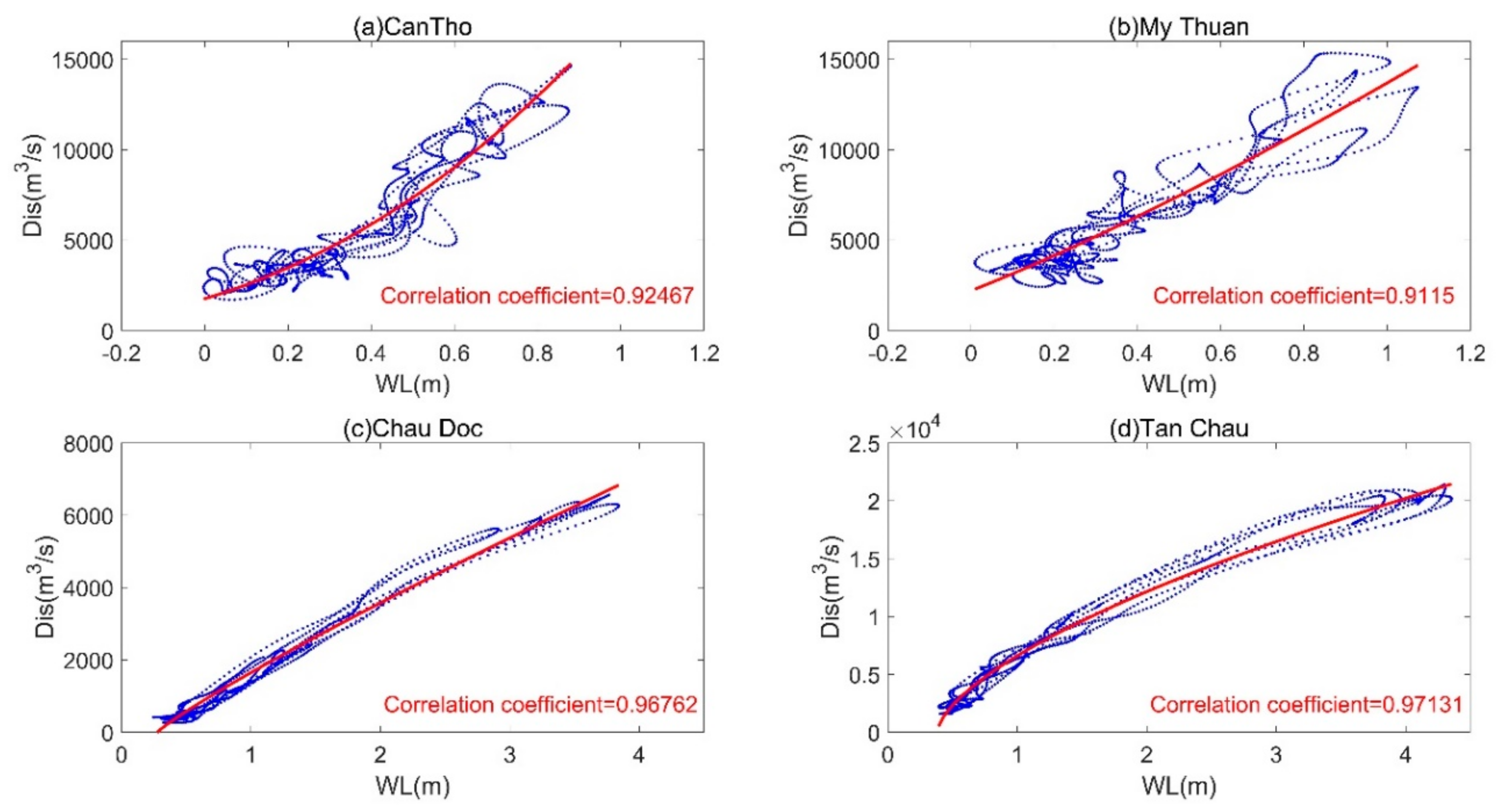
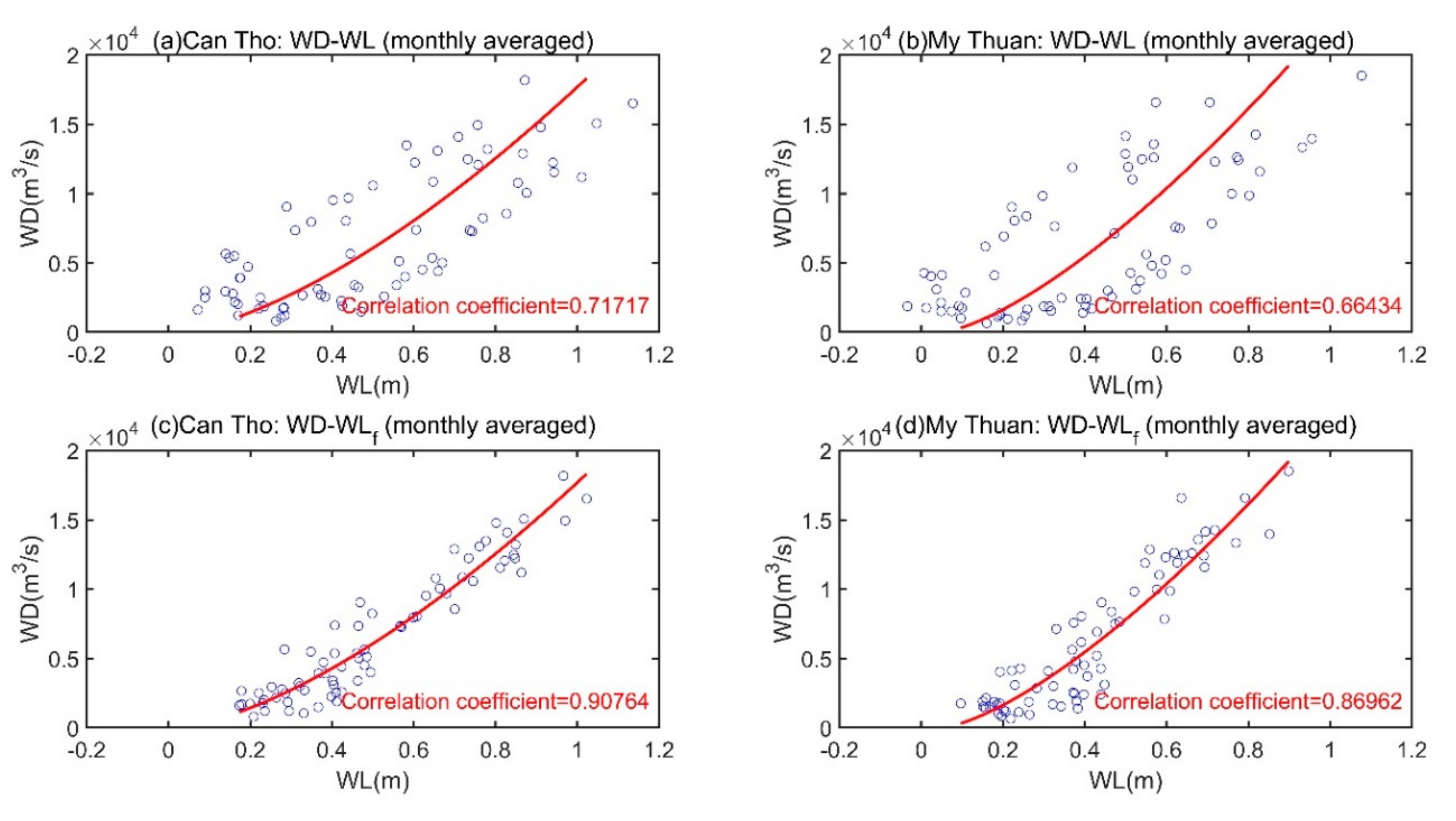
3.1. Data Analysis of Backwater Influence on Water Discharge (WD) and Water Level (WL)
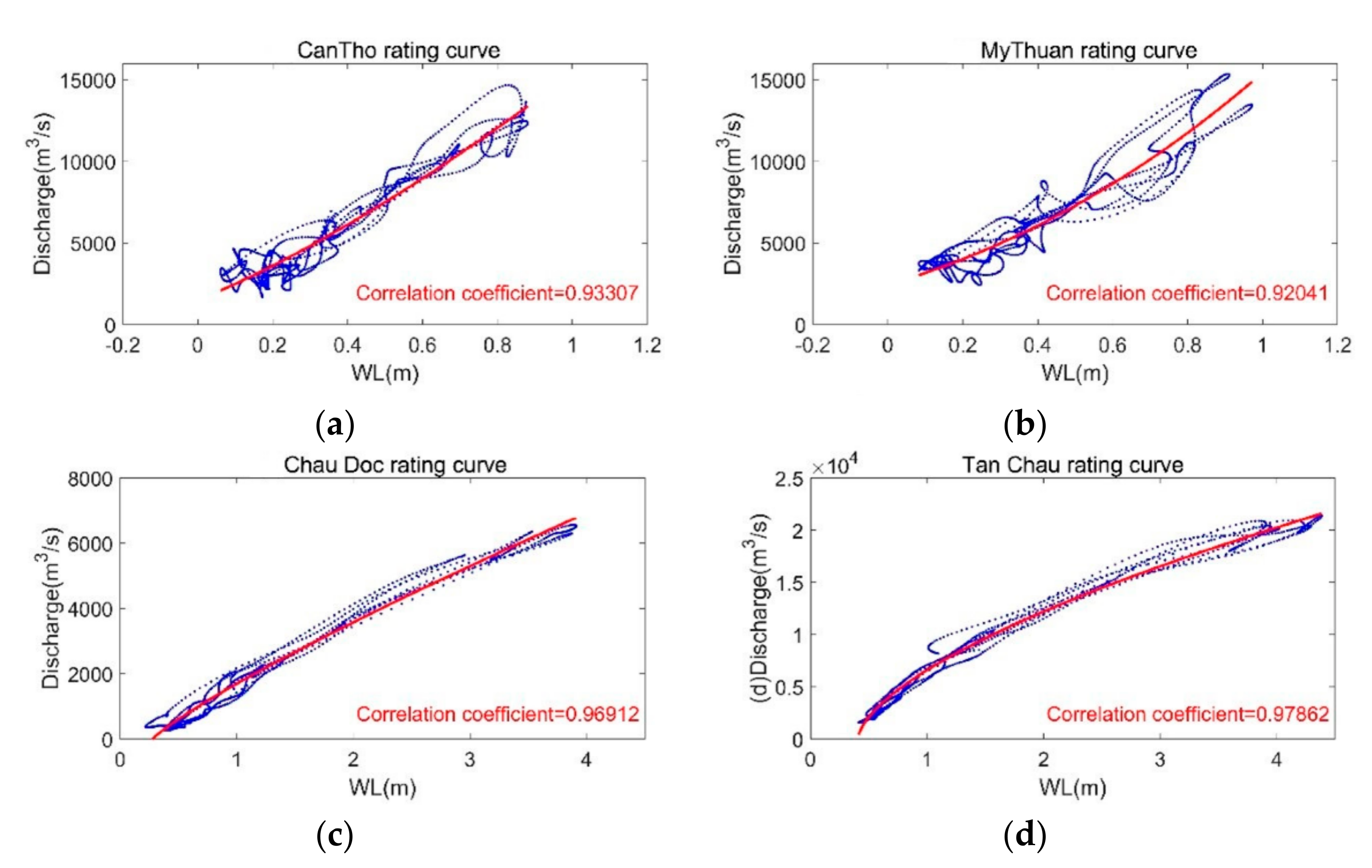
3.2. Incorporating Long-Period Ocean Tidal Components into Rating Curve
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zhang, H. The Analysis of the Reasonable Structure of Water Conservancy Investment of Capital Construction in China by AHP Method. Water Resour. Manag. 2008, 23, 1–18. [Google Scholar] [CrossRef]
- Cloke, H.L.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar] [CrossRef]
- Jarihani, A.A.; Callow, J.N.; Johansen, K.; Gouweleeuw, B. Evaluation of multiple satellite altimetry data for studying inland water bodies and river floods. J. Hydrol. 2013, 505, 78–90. [Google Scholar] [CrossRef]
- Lv, M.; Lu, H.; Yang, K.; Xu, Z.; Huang, X. Assessment of Runoff Components Simulated by GLDAS against UNH–GRDC Dataset at Global and Hemispheric Scales. Water 2018, 10, 969. [Google Scholar] [CrossRef]
- Fread, D.L. A Dynamic Model of Stage-Discharge Relations Affected by Changing Discharge; NOAA Technical Memorandum NWS HYDRO-16; National Weather Service: Silver Spring, MD, USA, 1973. [Google Scholar]
- Fread, D.L. Computation of stage-discharge relationships affected by unsteady flow. Water Resour. Bull. 1975, 11, 213–228. [Google Scholar] [CrossRef]
- Schmidt, A.R.; Yen, B.C. Stage-discharge ratings revisited. In Hydraulic Measurements and Experimental Methods, Proceedings of the EWRI and IAHR Joint Conference, Estes Park, CO, USA, 28 July–1 August 2002; American Society of Civil Engineers: Reston, VA, USA, 2002. [Google Scholar]
- Habib, E.H.; Meselhe, E.A. Stage-Discharge Relation for Low Gradient Tidal Streams Using Data Driven Models. J. Hydraul. Eng. 2006, 132, 482–493. [Google Scholar] [CrossRef]
- Chau, K.W.; Wu, C.L.; Li, Y.S. Comparison of several Flood Forecasting Models in Yangtze River. J. Hydrol. Eng. 2005, 10, 485–491. [Google Scholar] [CrossRef]
- Jain, S.K. Modelling river stage-discharge-sediment rating relation using support vector regression. Hydrol. Res. 2012, 43, 851–861. [Google Scholar] [CrossRef]
- Jain, S.K.; Chalisgaonkar, D. Setting up stage-discharge relations using ANN. J. Hydrol. Eng. 2000, 5, 428–433. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Jain, S.K. Radial basis function neural network for modeling rating curves. J. Hydrol. Eng. 2003, 8, 161–164. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R.L. Hydrological modelling using artificial neural networks. Prog. Phys. Geog. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Solomatine, D.P. Application of artificial neural network in stage-discharge relationship. In Proceedings of the 4th International Conference on Hydroinformatics, Iowa City, IA, USA, 23–27 August 2000. [Google Scholar]
- Simons, D.B.; Stevens, M.A.; Duke, J.H. Predicting stages on sand-bed rivers. Harb. Coast. Eng. Div. 1973, 99, 231–243. [Google Scholar]
- Dawdy, D.R. Depth-Discharge Relations of Alluvial Stream-Discontinuous Rating Curves. U.S. Geological Survey 1961; Report No. WSP 1498-C; U.S.G.P.O.: Washington, DC, USA, 1961. [Google Scholar]
- Hortle, K.G. Fisheries of the Mekong River Basin. In The Mekong Biophysical Environment of an International River Basin; Ian, C.C., Ed.; Academic Press: New York, NY, USA, 2009; pp. 197–239. [Google Scholar]
- Sassi, M.G.; Hoitink, A.J.F.; de Brye, B.; Deleersnijder, E. Downstream hydraulic geometry of a tidally influenced river delta. J. Geophys. Res. 2012, 117, F04022. [Google Scholar] [CrossRef]
- Gugliotta, M.; Saito, Y.; Nguyen, V.; Ta, T.K.O.; Nakashima, R.; Tamura, T.; Uehara, K.; Katsuki, K.; Yamamoto, S. Process regime, salinity, morphological, and sedimentary trends along the fluvial to marine transition zone of the mixed-energy Mekong River delta, Vietnam. Cont. Shelf Res. 2017, 147, 7–26. [Google Scholar] [CrossRef]
- Arias, M.E.; Cochrane, T.A.; Norton, D.; Killeen, T.J.; Khon, P. The Flood Pulse as the Underlying Driver of Vegetation in the Largest Wetland and Fishery of the Mekong Basin. AMBIO 2013, 42, 864–876. [Google Scholar] [CrossRef]
- Hecht, J.S.; Lacombe, G.; Arias, M.E.; Dang, T.D.; Piman, T. Hydropower dams of the Mekong River basin: A review of their hydrological impacts. J. Hydrol. 2019, 568, 285–300. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.P.; Saito, Y.; Nguyen, V.L. Recent evolution of the Mekong Delta and the impacts of dams. Earth Sci. Rev. 2017, 175, 1–17. [Google Scholar] [CrossRef]
- Brunier, G.; Anthony, E.J.; Goichot, M.; Provansal, M.; Dussoillez, P. Recent morphological changes in the Mekong and Bassac river channels, Mekong delta: The marked impact of river-bed mining and implications for delta destabilization. Geomorphology 2014, 224, 177–191. [Google Scholar] [CrossRef]
- Xue, Z.; Liu, J.P.; DeMaster, D.; Van, N.L.; Ta, T.K.O. Late Holocene Evolution of the Mekong Subaqueous Delta. Mar. Geol. 2010, 269, 46–60. [Google Scholar] [CrossRef]
- Paul, A.C. The Geology of the Lower Mekong River. In The Mekong Biophysical Environment of an International River Basin; Ian, C.C., Ed.; Academic Press: New York, NY, USA, 2009; pp. 13–28. [Google Scholar]
- Dang, T.D.; Cochrane, T.A.; Arias, M.E. Future hydrological alterations in the Mekong Delta under the impact of water resources development, land subsidence and sea level rise. J. Hydrol. Reg. Stud. 2018, 15, 119–133. [Google Scholar] [CrossRef]
- Gugliotta, M.; Saito, Y.; Nguyen, V.L.; Ta, T.K.O.; Tamura, T. Sediment distribution and depositional processes along the fluvial to marine transition zone of the Mekong River delta, Vietnam. Sedimentology 2019, 66, 146–164. [Google Scholar]
- Hoa, L.T.V.; Nhan, N.H.; Wolanski, E.; Cong, T.T.; Shigeko, H. The combined impact on the flooding in Vietnam’s Mekong River delta of local man-made structures, sea level rise, and dams upstream in the river catchment. Estuar. Coast. Shelf Sci. 2007, 71, 110–116. [Google Scholar]
- Woodruff, J.D.; Irish, J.L.; Camargo, S.J. Costal flooding by tropical cyclones and sea-level rise. Nature 2013, 504, 44–52. [Google Scholar] [CrossRef]
- Werner, A.D.; Bakker, M.; Post, V.E.A.; Vandenbohede, A.; Lu, C.; Ataie-Ashtiani, B.; Barry, D.A. Seawater intrusion processes, investigation and management: Recent advances and future challenges. Adv. Water Resour. 2013, 51, 3–26. [Google Scholar] [CrossRef]
- Minderhoud, P.S.J.; Coumou, L.; Erkens, G.; Middelkoop, H.; Stouthamer, E. Mekong delta much lower than previously assumed in sea-level rise impact assessments. Nature Comm. 2019, 10, 1–13. [Google Scholar]
- Wassmann, R.; Nguyen, X.H.; Chu, T.H.; To, P.T. Sea level rise affecting the Vietnamese Mekong Delta: Water elevation in the flood season and implications for rice production. Clim. Chang. 2004, 66, 89–107. [Google Scholar] [CrossRef]
- Kummu, M.; Tes, S.; Yin, S.; Adamson, P.; Józsa, J.; Koponen, J.; Richey, J.; Sarkkula, J. Water balance analysis for the Tonle Sap Lake–floodplain system. Hydrol. Process. 2014, 28, 1722–1733. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Ditmar, P.G.; Steele-Dunne, S.C.; Gunter, B.C.; Sutanudjaja, E.H. Assessing total water storage and identifying flood events over Tonlé Sap basin in Cambodia using GRACE and MODIS satellite observations combined with hydrological models. Remote Sens. Environ. 2016, 181, 162–173. [Google Scholar] [CrossRef]
- Frappart, F.; Biancamaria, S.; Normandin, C.; Blarel, F.; Bourrel, L.; Aumont, M.; Azemar, P.; Vu, P.L.; Le Toan, T.; Lubac, B.; et al. Influence of recent climatic events on the surface water storage of the Tonle Sap Lake. Sci. Total Environ. 2018, 636, 1520–1533. [Google Scholar] [CrossRef]
- Zhou, L.H.; Fok, H.S.; Ma, Z.T.; Chen, Q. Upstream Remotely-Sensed Hydrological Variables and Their Standardization for Surface Runoff Reconstruction and Estimation of the Entire Mekong River Basin. Remote Sens. 2019, 11, 1064. [Google Scholar]
- El-Jabi, N.; Wakin, G.; Sarraf, S. Stage-Discharge Relationship in Tidal Rivers. Ocean Eng. 1992, 118, 166–174. [Google Scholar] [CrossRef]
- Tozer, B.; Sandwell, D.T.; Smith, W.H.F.; Olson, C.; Beale, J.R.; Wessel, P. Global bathymetry and topography at 15 arc seconds: SRTM15+. Earth Space Sci. 2019, 1847–1864. [Google Scholar] [CrossRef]
- Koehnken, L. IKMP Discharge and Sediment Monitoring Program Review, Recommendations and Data Analysis. Part 1 and 2. Tech. Advice Water 2012, 2–36. [Google Scholar]
- Merrifield, M.; Aarup, T.; Allen, A.; Aman, B.; Caldwel, P.; Fernandes, R.; Hayashibara, H.; Hernandez, F.; Kilonsky, B.; Martin Miguez, B.; et al. The Global Sea Level Observing System (GLOSS). In Proceedings of the Ocean Obs. 09, Ocean information for Society: Sustaining the Benefits, Realizing the Potential, Venice–Lido, Italy, 21–25 September 2009. [Google Scholar]
- Godin, G. The daily mean level and short period seiches. IHR 1966, 43, 75–89. [Google Scholar]
- Godin, G. The Propagation of Tides up Rivers with Special Considerations on the Upper Saint Lawrence River. Estuarine Coas. Shelf Sci. 1999, 48, 307–324. [Google Scholar] [CrossRef]
- Godin, G. The Analysis of Tides; University of Toronto Press: Toronto, ON, Canada; Liverpool University Press: Buffalo, NY, USA, 1972. [Google Scholar]
- Brooks, B.A.; Merrifield, M.A.; Foster, J.; Werner, C.L.; Gomez, F.; Bevis, M.; Gill, S. Space geodetic determination of spatial variability in relative sea level change. Geophys. Res. Lett. 2007, 34, L01611. [Google Scholar] [CrossRef]
- Stammer, D.; Ray, R.D.; Andersen, O.B.; Arbic, B.K.; Bosch, W.; Carrère, L.; Cheng, Y.; Chin, D.S.; Dushaw, B.D.; Egbert, G.D.; et al. Accuracy assessment of global barotropic ocean tide models. Rev. Geophys. 2014, 52, 243–282. [Google Scholar] [CrossRef]
- Fok, H.S.; Iz, H.B.; Shum, C.K.; Yi, Y.; Andersen, O.; Braun, A.; Chao, Y.; Han, G.; Kuo, C.Y.; Matsumoto, K.; et al. Evaluation of Ocean Tide Models Used for Jason-2 Altimetry Corrections. Mar. Geod. 2010, 33 (Suppl. S1), 285–303. [Google Scholar] [CrossRef]
- Fok, H.S. Ocean Tides Modeling Using Satellite Altimetry. Ph.D. Thesis, School of Earth Sciences, State University, Columbus, OH, USA, 2012. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Mansanarez, V.; Renard, B.; Coz, J.L.; Lang, M.; Darienzo, M. Shift Happens! Adjusting stage-discharge rating curves to morphological changes at known times. Water Resour. Res. 2019, 55, 2876–2899. [Google Scholar] [CrossRef]
- Guo, L.C.; Zhu, C.Y.; Wu, X.; Wan, Y.; Jay, D.A.; Townend, I.; Wang, Z.B.; He, Q. Strong Inland Propagation of Low-Frequency Long Waves in River Estuaries. Geophys. Res. Lett. 2020. [Google Scholar] [CrossRef]
- Jay, D.A. Green’s Law Revisited: Tidal Long-Wave Propagation in Channels With Strong Topography. J. Geophys. Res. 1991, 96, 586–598. [Google Scholar] [CrossRef]
- Miller, J.L.; Gardner, L.R. Sheet flow in a salt-marsh basin, North Inlet, South Carolina. Estuaries 1981, 4, 234–237. [Google Scholar] [CrossRef]
- Gavin, H.P. The Levenberg-Marquardt Method for Non-Linear Least Squares Curve-Fitting Problems. Department of Civil and Environmental Engineering, Duke University: Durham, NC, USA, 2013; pp. 1–17. [Google Scholar]
- Seber, G.A.F.; Wild, C.J. Non-Linear Regression; Wiley-Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Möller, I.; Kudella, M.; Rupprecht, F.; Spencer, T.; Paul, M.; van Wesenbeeck, B.K.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-Lange, M.; et al. Wave attenuation over coastal salt marshes under storm surge conditions. Nature Geosci. 2014, 7, 727–731. [Google Scholar] [CrossRef]
- Arias, M.E. Impacts of Hydrological Alterations in the Mekong Basin to Tonle Sap Ecosystem. Ph.D. Thesis, Department of Civil and Natural Resources Engineering, University of Canterbury, Christchurch, New Zealand, 2003. [Google Scholar]
- Cochrane, T.A.; Arias, M.E.; Piman, T. Historical impact of water infrastructure on water levels of the Mekong River and Tonle Sap system. Hydrol. Earth Syst. Sc. 2014, 18, 4529–4541. [Google Scholar] [CrossRef]
- Running, S.; Mu, Q.; Zhao, M. MYD16A2 MODIS/Aqua Net Evapotranspiration 8-Day L4 Global 500m SIN Grid V006 [Data Set]. NASA EOSDIS Land Processes DAAC. 2017. Available online: https://lpdaac.usgs.gov/products/myd16a2v006/ (accessed on 25 October 2020).
- Huffman, G.J.; Bolvin, D.T. Real-Time TRMM Multi-Satellite Precipitation Analysis Data Set Documentation; NASA Goddard Space Flight Center location: Greenbelt, MD, USA; Science Systems and Applications, Inc.: Hampton, VA, USA, 2015. [Google Scholar]
- Gouweleeuw, B.T.; Kvas, A.; Gruber, C.; Gain, A.K.; Mayer-Gürr, T.; Flechtner, F.; Güntner, A. Daily GRACE gravity field solutions track major flood events in the Ganges–Brahmaputra Delta. Hydrol. Earth Syst. Sc. 2018, 22, 2867–2880. [Google Scholar] [CrossRef]
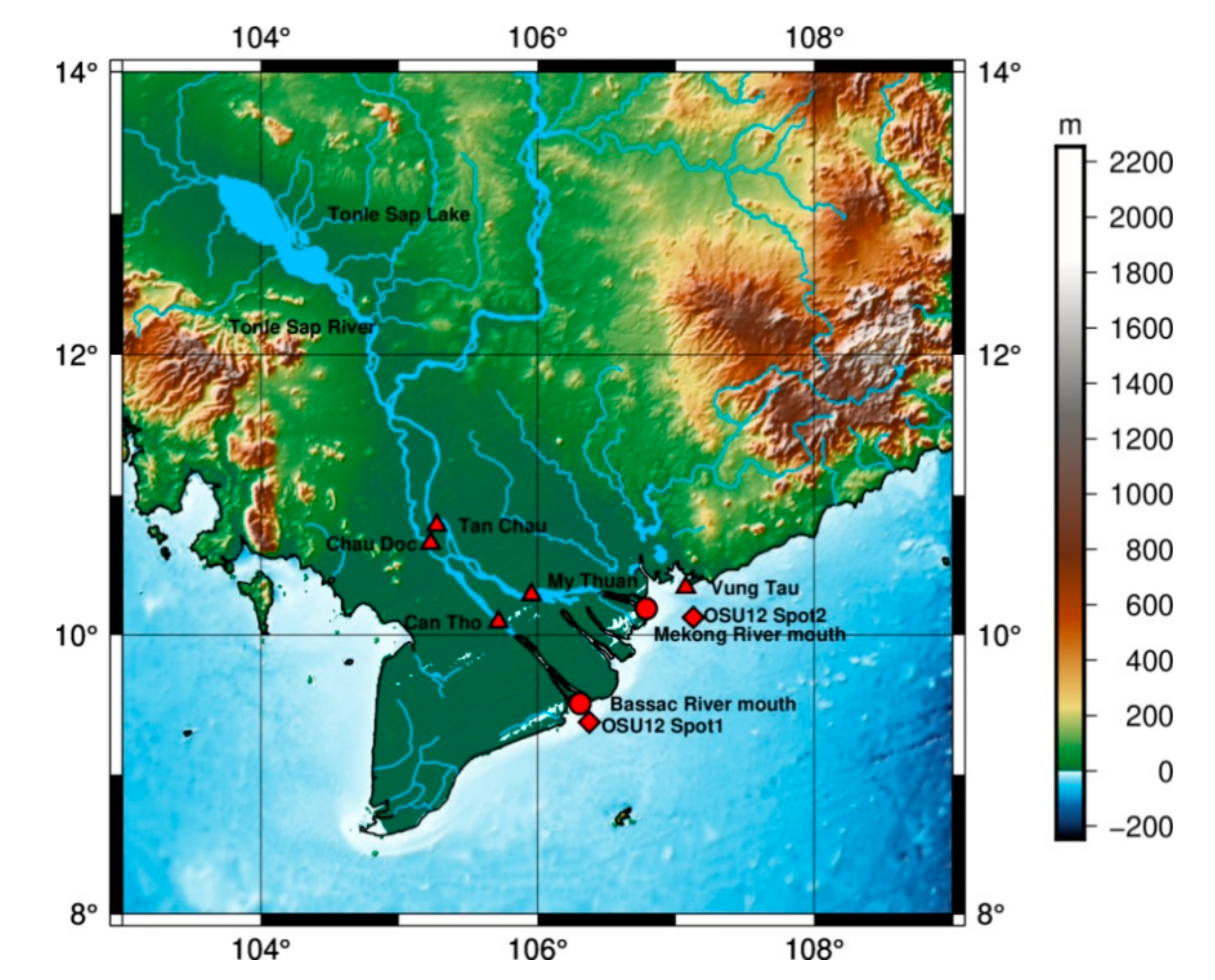
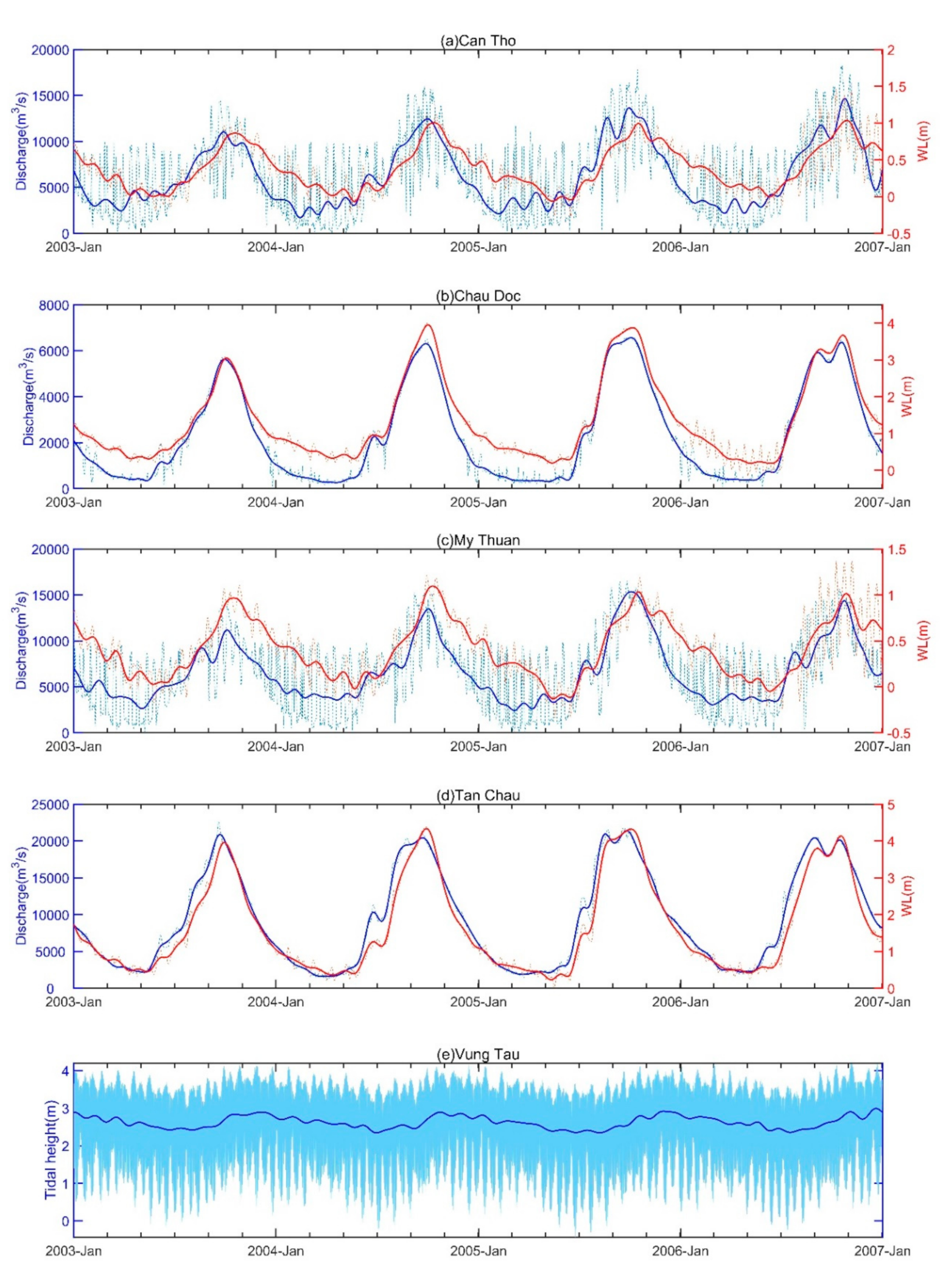
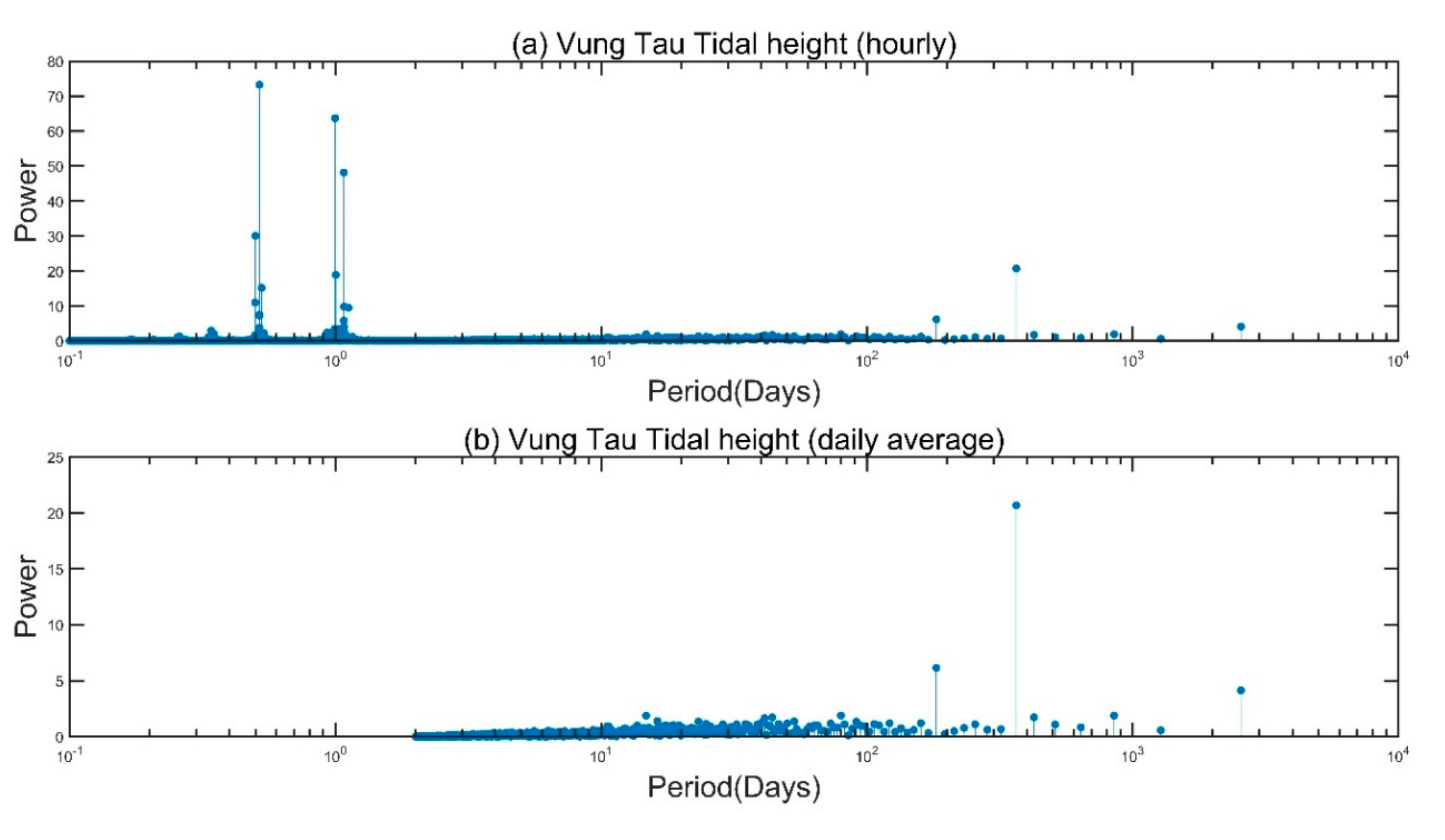

| Products | Location | Time Span | Temporal Resolution |
|---|---|---|---|
| In Situ Stations’ Water Level Data | Can Tho | 2003–2006 2009–2014 | Daily average |
| My Thuan | 2003–2006 2009–2014 | ||
| Chau Doc | 2003–2006 | ||
| Tan Chau | 2003–2006 | ||
| In Situ Stations’ Discharge Data | Can Tho | 2003–2006 2009–2014 | Daily (before 2006) Monthly (after 2009) |
| My Thuan | 2003–2006 2009–2014 | ||
| Chau Doc | 2003–2006 | ||
| Tan Chau | 2003–2006 | ||
| Tidal Gauge Data | Vung Tau | 2003–2014 | Hourly |
| OSU12 Global Ocean Tide Model Data | 9.375N, 106.375E | Tidal constituents (Sa, Ssa, Mm) | |
| 10.125N, 107.125E |
| Variable | Station | Maximum | Minimum | Mean | Standard Deviation |
|---|---|---|---|---|---|
| Original Water Discharge (1 × 104 m3/s) | My Thuan | 1.6500 | 0.0029 | 0.7263 | 0.4036 |
| Can Tho | 1.8400 | 0.0025 | 0.7206 | 0.4416 | |
| Tan Chau | 2.2597 | 0.1190 | 0.9359 | 0.6490 | |
| Chau Doc | 0.7120 | 0.0045 | 0.2625 | 0.2059 | |
| Processed Water Discharge (1 × 104 m3/s) | My Thuan | 1.5345 | 0.2423 | 0.7262 | 0.3109 |
| Can Tho | 1.4666 | 0.1704 | 0.7209 | 0.3236 | |
| Tan Chau | 2.1400 | 0.1600 | 0.9360 | 0.6470 | |
| Chau Doc | 0.7121 | 0.0266 | 0.2626 | 0.2043 | |
| Original Water Level (m) | My Thuan | 1.4225 | −0.3355 | 0.4619 | 0.3522 |
| Can Tho | 1.4591 | −0.2707 | 0.4168 | 0.3231 | |
| Tan Chau | 4.3831 | 0.0222 | 1.6820 | 1.2544 | |
| Chau Doc | 4.0036 | −0.1486 | 1.5017 | 1.1443 | |
| Processed Water Level (m) | My Thuan | 1.2165 | −0.1304 | 0.4620 | 0.3267 |
| Can Tho | 1.0358 | −0.0685 | 0.4171 | 0.2976 | |
| Tan Chau | 4.3361 | 0.2326 | 1.6825 | 1.2498 | |
| Chau Doc | 3.9558 | 0.1863 | 1.5019 | 1.1396 | |
| Original Tide height (m) | Vung Tau | 4.3300 | −0.4400 | 2.6433 | 0.8566 |
| Processed Tide height (m) | Vung Tau | 2.9984 | 2.3413 | 2.6436 | 0.1648 |
| Tide Components | Point1 (9.35°N,106.375°E) (in cm) | Point2 (10.125°N, 107.125°E) (in cm) | |
|---|---|---|---|
| Sa (365.25 days) | H1 | 24.41570 | 19.06151 |
| H2 | −1.56798 | −3.91959 | |
| Ssa (182.62 days) | H1 | 1.36968 | −6.76170 |
| H2 | 3.52620 | 2.07534 | |
| Mm (27.55 days) | H1 | 1.30950 | 0.32715 |
| H2 | −1.63984 | 1.72923 | |
| Station | Period: 365 Days | Period: 182.5 Days | Period: 14.7475 Days | ||||
|---|---|---|---|---|---|---|---|
| Relative Power | Initial Phase | Relative Power | Initial Phase | Relative Power | Initial Phase | ||
| Can Tho | WD | 1 | 95.2311° | 0.3060 | 173.5607° | 0.4727 | 25.1628° |
| WL | 1 | 58.5725° | 0.2535 | 168.3582° | 0.2997 | 244.1391° | |
| My Thuan | WD | 1 | 87.1219° | 0.3093 | 170.8565° | 0.5671 | 25.8326° |
| WL | 1 | 55.0654° | 0.2664 | 175.4839° | 0.3152 | 244.2108° | |
| Chau Doc | WD | 1 | 93.8689° | 0.3392 | 196.6511° | 0.0324 | 111.2065° |
| WL | 1 | 84.7393° | 0.3963 | 193.8528° | 0.0414 | 274.7407° | |
| Tan Chau | WD | 1 | 97.4019° | 0.2385 | 222.2999° | 0.0046 | 99.6860° |
| WL | 1 | 90.3988° | 0.3705 | 202.5387° | 0.0336 | 260.8400° | |
| Tidal Height Data | Station | a | b | c | R-Square | PCC | NSE | |
|---|---|---|---|---|---|---|---|---|
| In-situ measured | Can Tho | −0.2230 | 1.3661 | 0.1619 | 0.9291 | 0.9626 | 0.9266 | |
| My Thuan | −0.8665 | 2.4063 | 0.1480 | 0.8974 | 0.9468 | 0.8964 | ||
| Chau Doc | 0.2756 | 0.8592 | 0.1577 | 0.9790 | 0.9922 | 0.9843 | ||
| Tan Chau | 0.4052 | 0.6229 | 0.1819 | 0.9809 | 0.9946 | 0.9891 | ||
| OSU12 | Can Tho | −0.5949 | 2.3417 | 0.1722 | 0.8871 | 0.9383 | 0.8804 | |
| My Thuan | −0.3079 | 1.2619 | 0.1520 | 0.8631 | 0.9285 | 0.8621 | ||
| Chau Doc | 0.2762 | 0.8911 | 0.1582 | 0.9828 | 0.9934 | 0.9868 | ||
| Tan Chau | 0.3809 | 0.6335 | 0.1314 | 0.9750 | 0.9910 | 0.9820 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, H.; Fok, H.S.; Gong, J.; Wang, L. Improving Stage–Discharge Relation in The Mekong River Estuary by Remotely Sensed Long-Period Ocean Tides. Remote Sens. 2020, 12, 3648. https://doi.org/10.3390/rs12213648
Peng H, Fok HS, Gong J, Wang L. Improving Stage–Discharge Relation in The Mekong River Estuary by Remotely Sensed Long-Period Ocean Tides. Remote Sensing. 2020; 12(21):3648. https://doi.org/10.3390/rs12213648
Chicago/Turabian StylePeng, Hongrui, Hok Sum Fok, Junyi Gong, and Lei Wang. 2020. "Improving Stage–Discharge Relation in The Mekong River Estuary by Remotely Sensed Long-Period Ocean Tides" Remote Sensing 12, no. 21: 3648. https://doi.org/10.3390/rs12213648
APA StylePeng, H., Fok, H. S., Gong, J., & Wang, L. (2020). Improving Stage–Discharge Relation in The Mekong River Estuary by Remotely Sensed Long-Period Ocean Tides. Remote Sensing, 12(21), 3648. https://doi.org/10.3390/rs12213648