Multipath Exploitation with Time Reversal Waveform Covariance Matrix for SNR Maximization
Abstract
1. Introduction
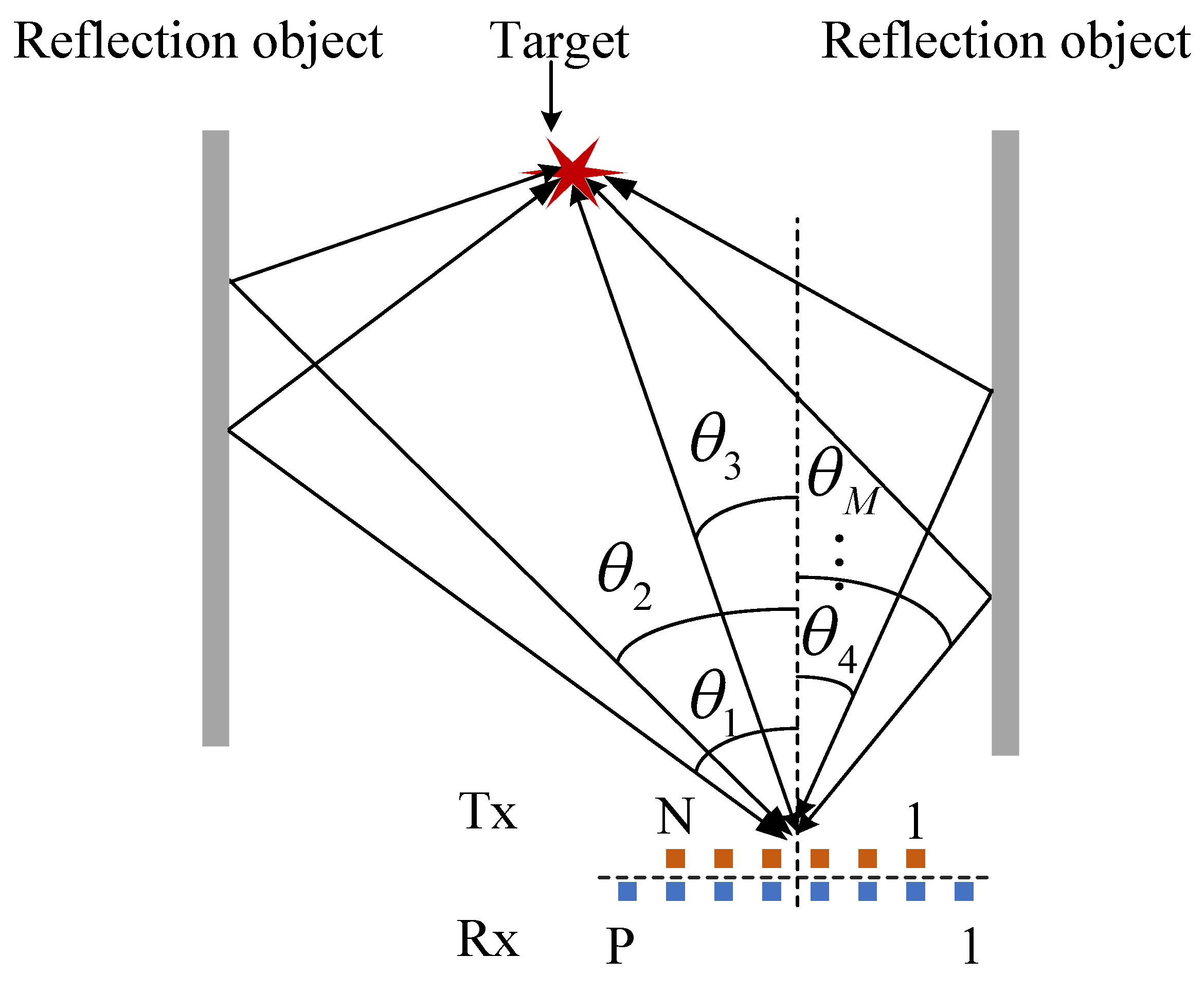
2. Multipath System Model
2.1. MIMO Radar
2.2. TR MIMO Radar
3. The Proposed Two-Stage Algorithm
3.1. Hermitian Multipath Information Matrix Reconstruction
3.2. Waveform Covariance Matrix Design
4. Simulation Results
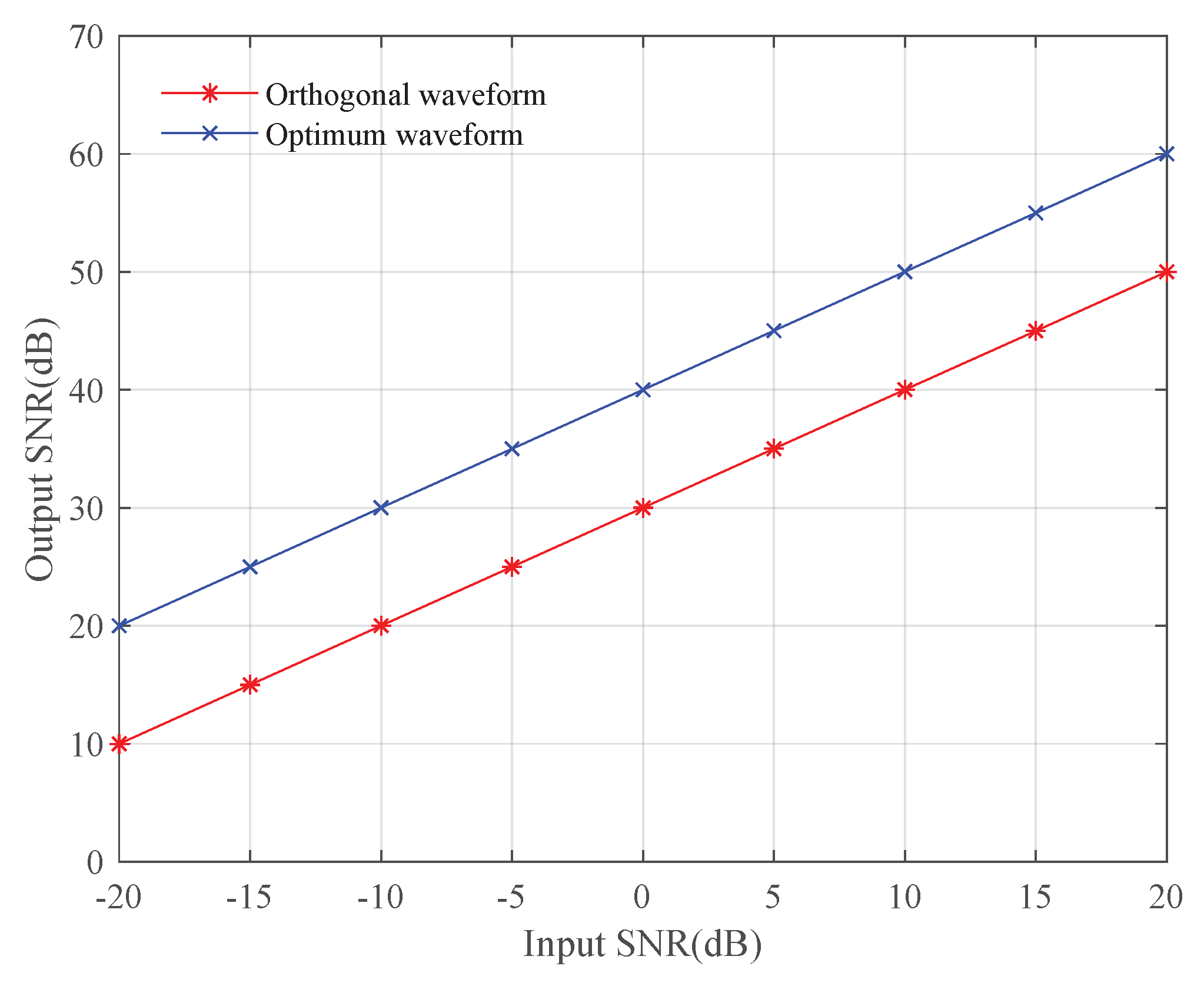
4.1. Output SNR Versus Input SNR
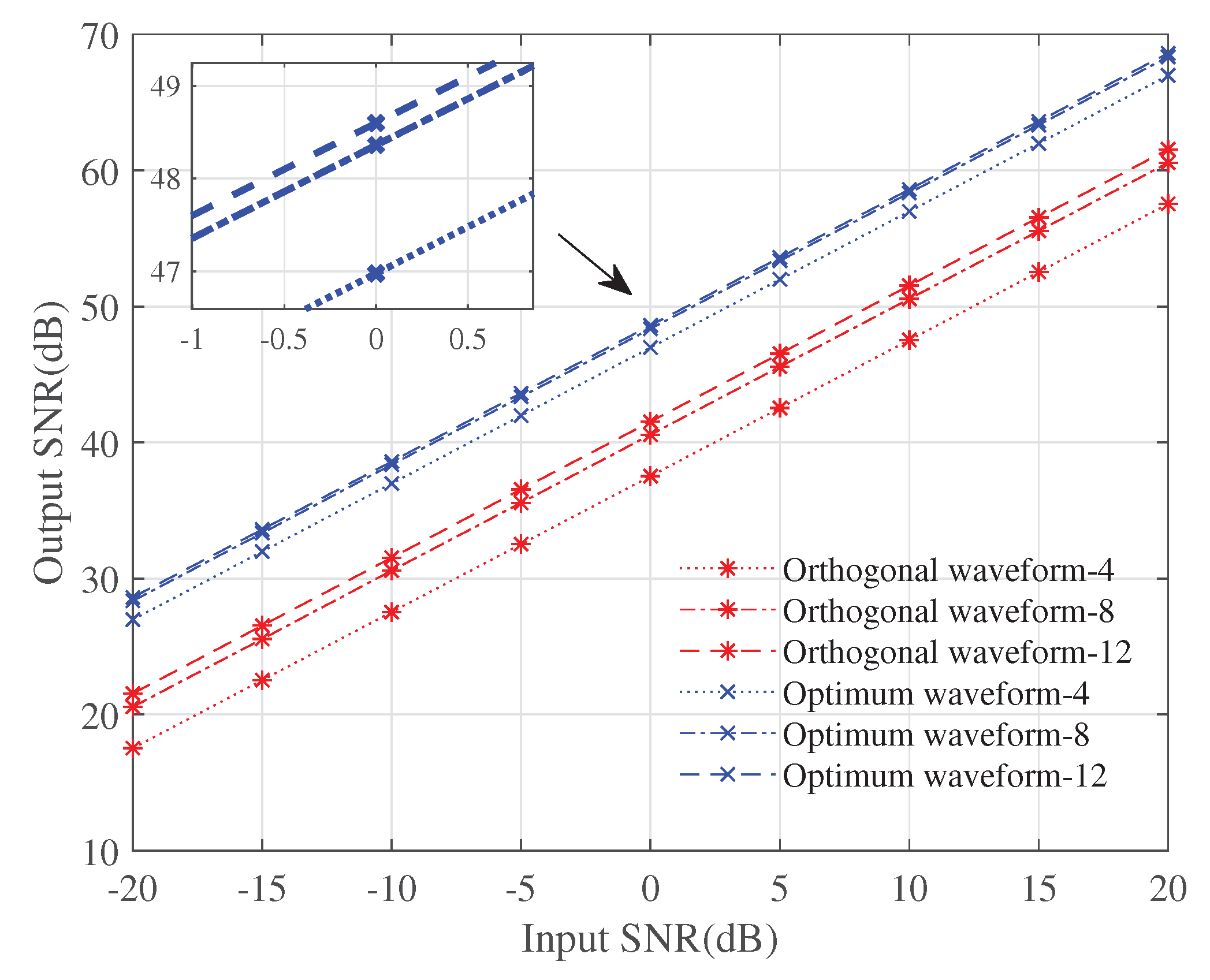
4.2. Output SNR with Different Numbers of Multipath
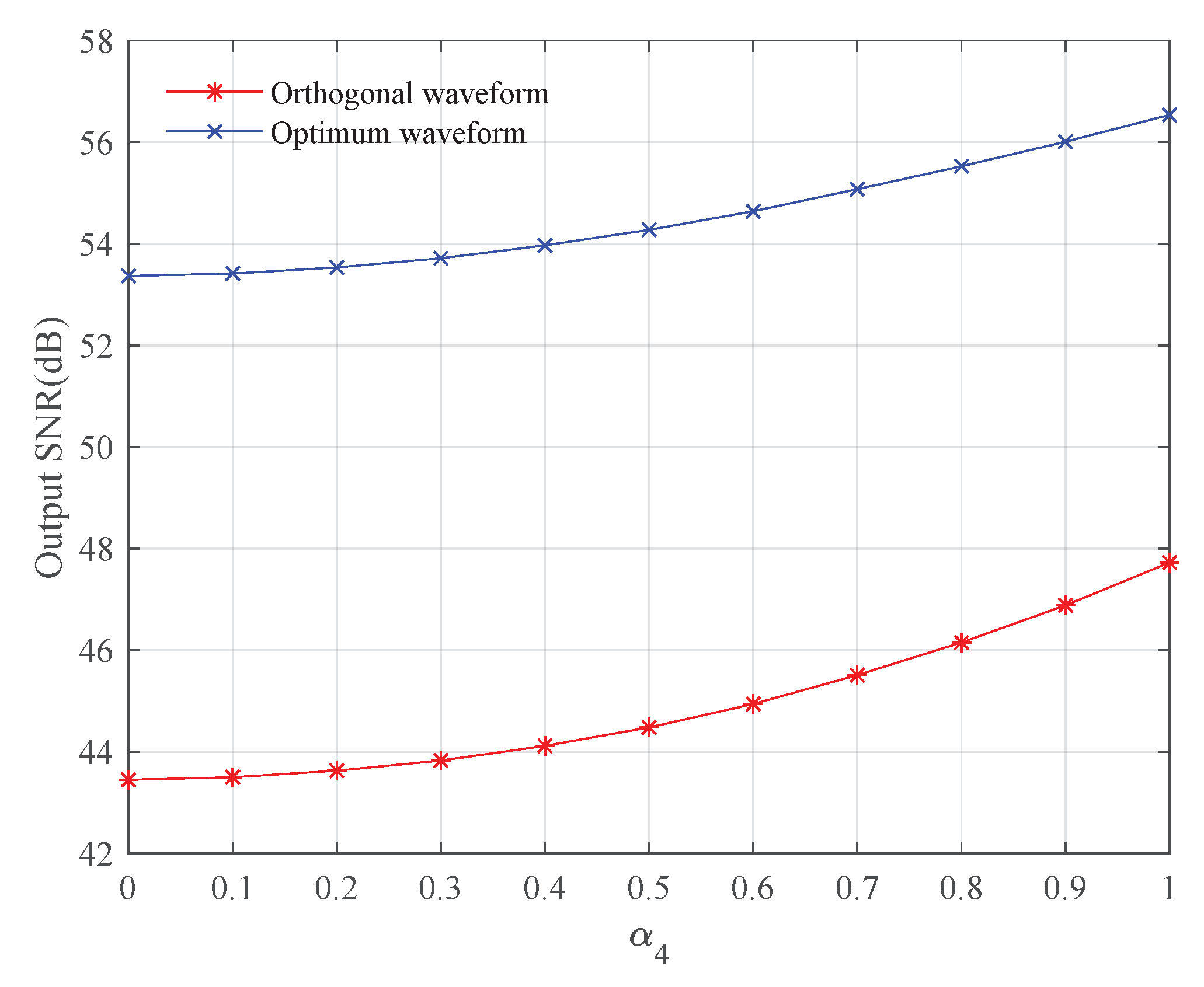
4.3. Output SNR with Different Amplitude Modulus Values
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Burkholder, R.J.; Pino, M.R.; Obelleiro, F. Low angle scattering from 2-D targets on a time-evolving sea surface. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1185–1190. [Google Scholar] [CrossRef]
- Feng, S.; Chen, J. Low-angle reflectivity modeling of land clutter. IEEE Geosci. Remote Sens. Lett. 2006, 3, 254–258. [Google Scholar] [CrossRef]
- Niu, C.; Zhang, Y.; Guo, J. Low angle estimation in diffuse multipath environment by time-reversal minimum-norm-like technique. IET Radar Sonar Navig. 2017, 11, 1483–1487. [Google Scholar] [CrossRef]
- Foroozan, F.; Asif, A.; Boyer, R. Time Reversal MIMO Radar: Improved CRB and Angular Resolution Limit. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Hossain, M.D.; Mohan, A.S. Eigenspace Time-Reversal Robust Capon Beamforming for Target Localization in Continuous Random Media. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1605–1608. [Google Scholar] [CrossRef]
- Sajjadieh, M.H.; Asif, A. Compressive sensing time reversal mimo radar: Joint direction and doppler frequency estimation. IEEE Signal Process. Lett. 2015, 22, 1283–1287. [Google Scholar] [CrossRef]
- Foroozan, F.; Asif, A.; Jin, Y.; Moura, J.M. Direction finding algorithms for time reversal MIMO radars. In Proceedings of the 2011 IEEE Statistical Signal Processing Workshop (SSP), Nice, France, 28–30 June 2011. [Google Scholar]
- Cui, G.; Li, H.; Rangaswamy, M. MIMO Radar Waveform Design With Constant Modulus and Similarity Constraints. IEEE Trans. Signal Process. 2014, 62, 343–353. [Google Scholar] [CrossRef]
- Du, X.; Aubry, A.; Maio, A.D.; Cui, G. Hidden Convexity in Robust Waveform and Receive Filter Bank Optimization Under Range Unambiguous Clutter. IEEE Signal Process. Lett. 2020, 27, 885–889. [Google Scholar] [CrossRef]
- Imani, S.; Ghorashi, S.A.; Bolhasani, M. SINR maximization in colocated MIMO radars using transmit covariance matrix. Signal Process. 2016, 119, 128–135. [Google Scholar] [CrossRef]
- Haghnegahdar, M.; Imani, S.; Ghorashi, S.A.; Mehrshahi, E. SINR Enhancement in Colocated MIMO Radar Using Transmit Covariance Matrix Optimization. IEEE Signal Process. Lett. 2017, 24, 339–343. [Google Scholar] [CrossRef]
- Chen, C.; Vaidyanathan, P.P. MIMO Radar Waveform Optimization With Prior Information of the Extended Target and Clutter. IEEE Trans. Signal Process. 2009, 57, 3533–3544. [Google Scholar] [CrossRef]
- Sharma, A.; Ram, S.S. MIMO waveform design for minimizing multipath from ground and ceiling reflections. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation and USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–24 July 2015. [Google Scholar]
- Chakraborty, B.; Li, Y.; Zhang, J.J.; Trueblood, T.; Papandreousuppappola, A.; Morrell, D. Multipath exploitationwith adaptivewaveform design for tracking in urban terrain. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010. [Google Scholar]
- Foroozan, F.; Asif, A. Time reversal MIMO radar for angle-Doppler estimation. In Proceedings of the 2012 IEEE Statistical Signal Processing Workshop (SSP), Ann Arbor, MI, USA, 5–8 August 2012; pp. 860–863. [Google Scholar]
- Foroozan, F.; Asif, A.; Jin, Y. Cramer-Rao bounds for time reversal mimo radars with multipath. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 137–154. [Google Scholar] [CrossRef]
- Jin, Y.; Moura, J.M.; O’Donoughue, N.; Harley, J. Single antenna time reversal detection of moving target. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 3558–3561. [Google Scholar]
- He, H.; Li, J.; Stoica, P. Waveform Design for Active Sensing Systems: Narrowband Beampattern to Covariance Matrix; Cambridge University Press: New York, NY, USA, 2012; pp. 187–212. [Google Scholar]
| Path Number | DOA (°) | Amplitude Factor | Delay Time (ns) |
|---|---|---|---|
| 1 | 2 | 1.0000 + 0.0000i | 0 |
| 2 | −2 | 0.8438 − 0.0753i | 2.0 |
| 3 | −5.4 | 0.6119 − 0.5846i | 6.1 |
| 4 | 5.5 | 0.8213 + 0.0168i | 10.3 |
| 5 | −6.8 | 0.7945 − 0.0884i | 17.5 |
| 6 | 9.4 | 0.4334 − 0.6536i | 20.4 |
| 7 | −10.2 | 0.7189 − 0.1566i | 31.2 |
| 8 | 11.2 | 0.5467 − 0.4211i | 34.7 |
| 9 | −11.6 | 0.5111 − 0.3501i | 35.4 |
| 10 | 12.8 | 0.5661 + 0.1740i | 39.0 |
| 11 | −14 | 0.4288 − 0.3190i | 40.6 |
| 12 | 19.5 | 0.4773 − 0.1480i | 45.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, C.; Fan, C.; Huang, X. Multipath Exploitation with Time Reversal Waveform Covariance Matrix for SNR Maximization. Remote Sens. 2020, 12, 3565. https://doi.org/10.3390/rs12213565
Xiong C, Fan C, Huang X. Multipath Exploitation with Time Reversal Waveform Covariance Matrix for SNR Maximization. Remote Sensing. 2020; 12(21):3565. https://doi.org/10.3390/rs12213565
Chicago/Turabian StyleXiong, Chao, Chongyi Fan, and Xiaotao Huang. 2020. "Multipath Exploitation with Time Reversal Waveform Covariance Matrix for SNR Maximization" Remote Sensing 12, no. 21: 3565. https://doi.org/10.3390/rs12213565
APA StyleXiong, C., Fan, C., & Huang, X. (2020). Multipath Exploitation with Time Reversal Waveform Covariance Matrix for SNR Maximization. Remote Sensing, 12(21), 3565. https://doi.org/10.3390/rs12213565






