A Hyperspectral Anomaly Detection Algorithm Based on Morphological Profile and Attribute Filter with Band Selection and Automatic Determination of Maximum Area
Abstract
1. Introduction
2. Materials and Methods
2.1. Morphological Profile
2.2. Attribute Filter
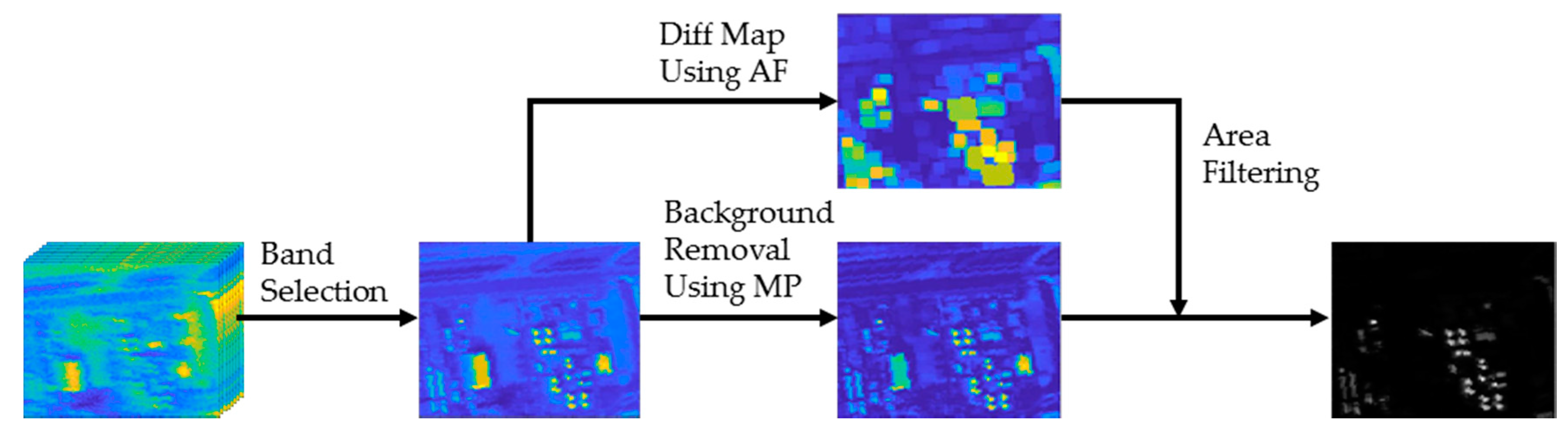
2.3. Proposed Algorithm
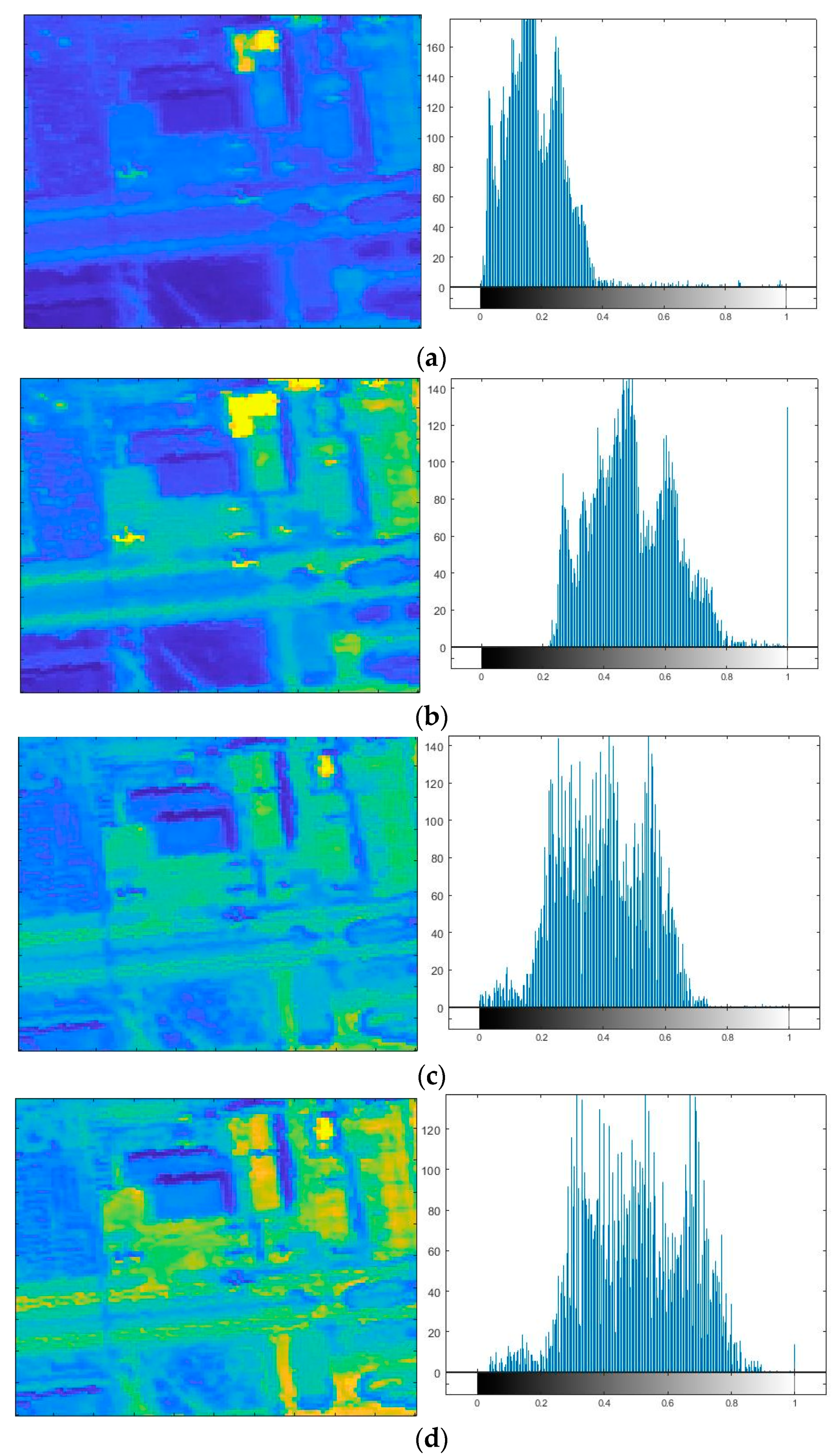
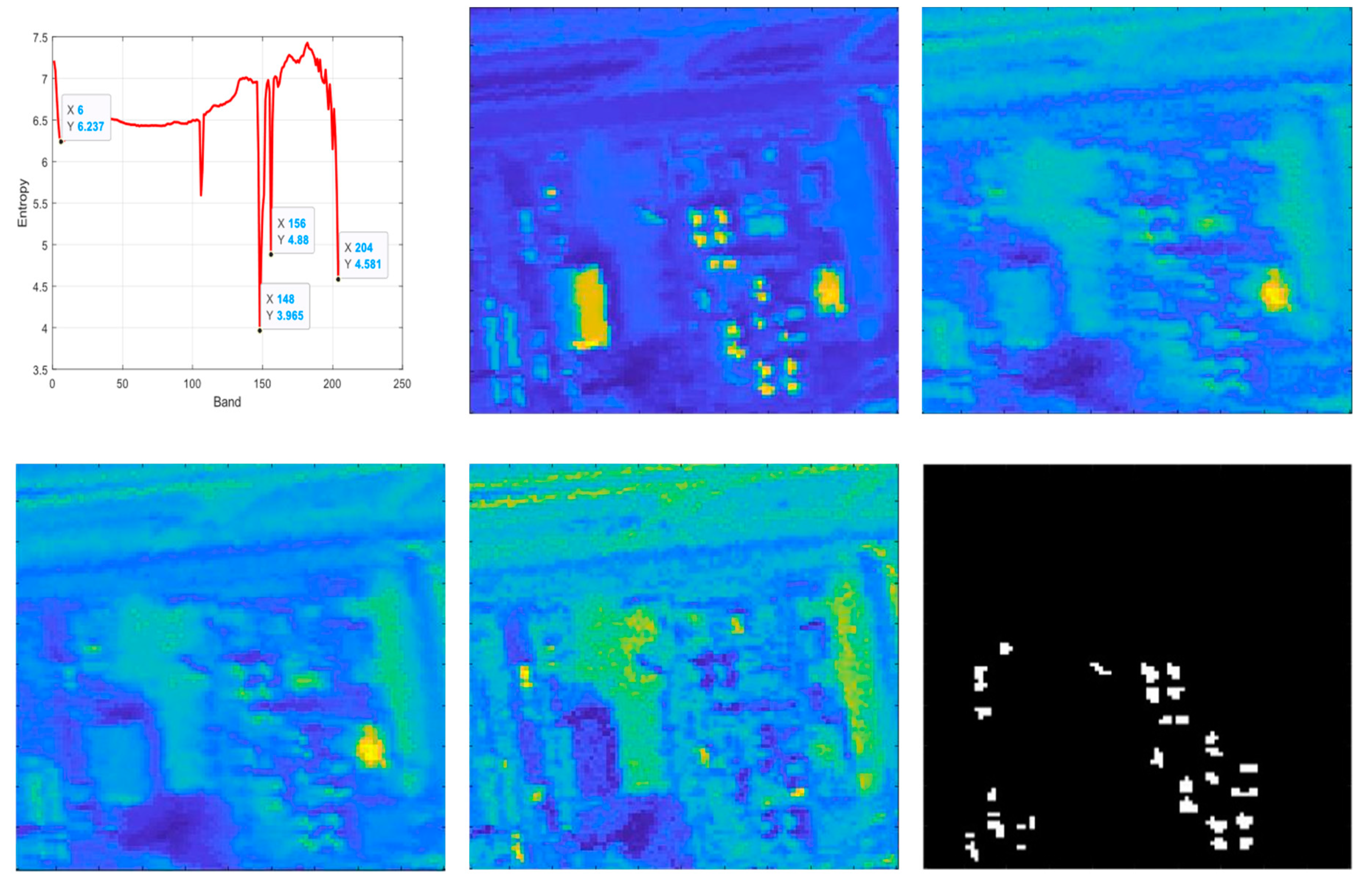
2.3.1. Entropy- and Histogram-Based Band Selection
2.3.2. Background Removal
2.3.3. Area Filtering
2.3.4. Area of Anomaly
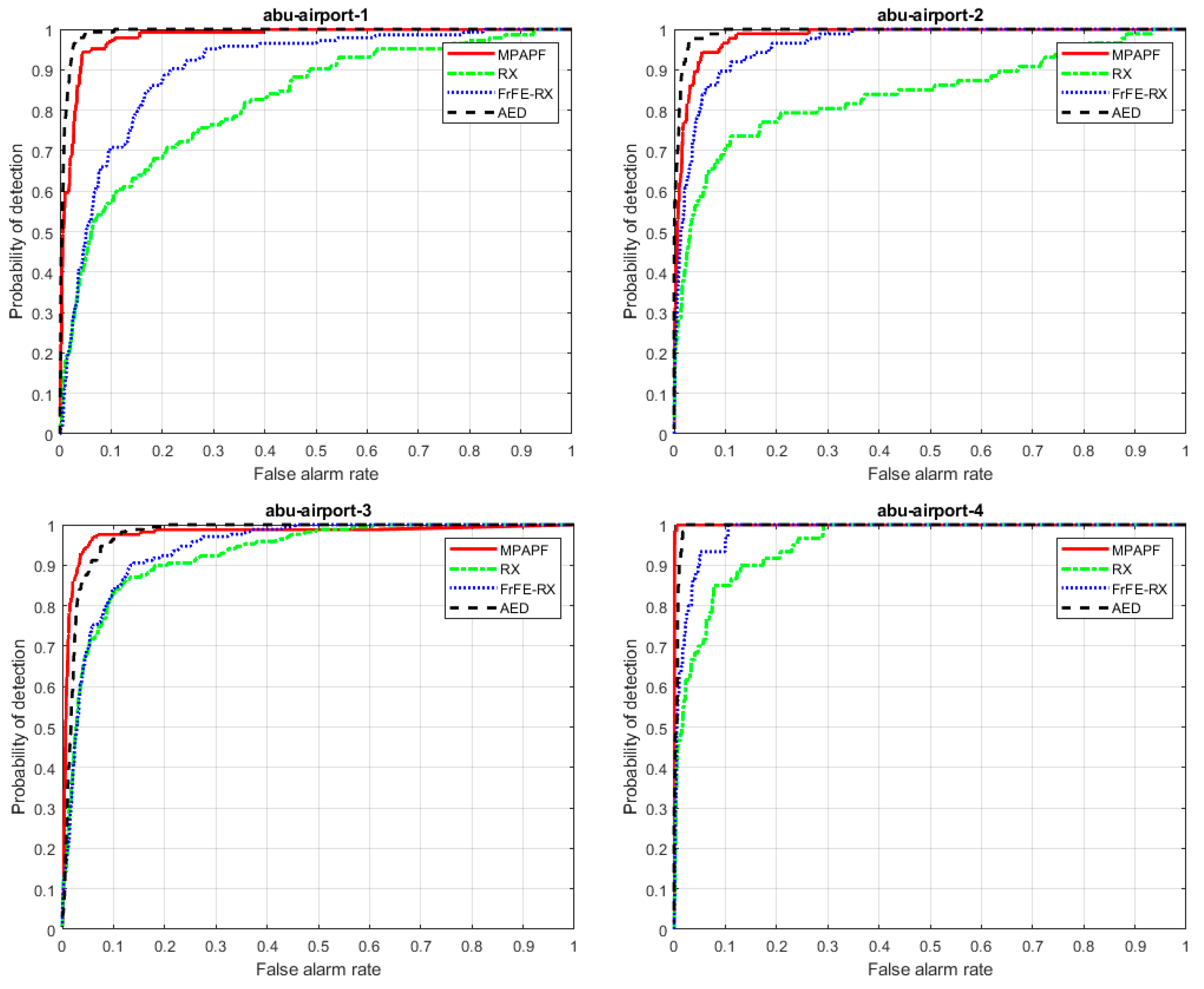
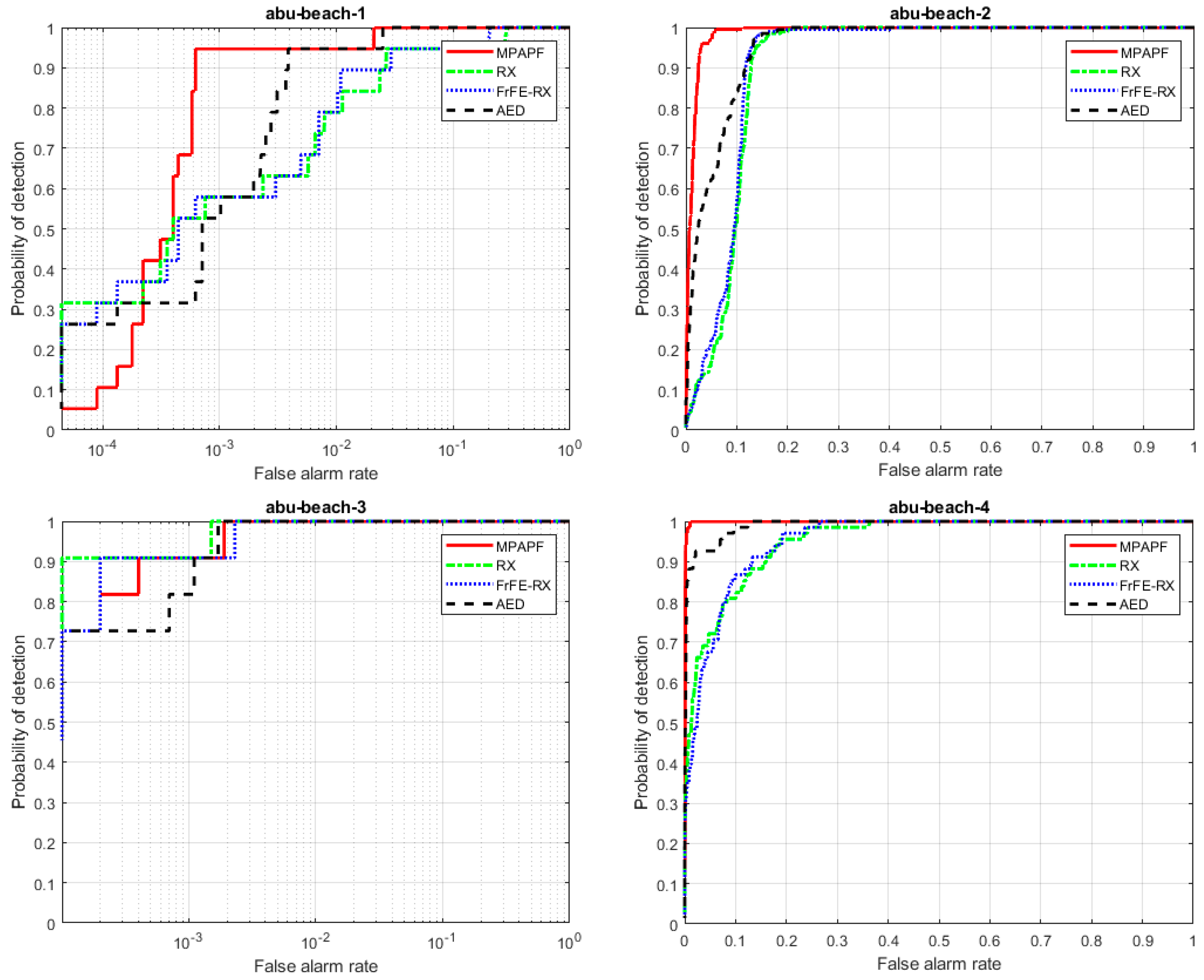
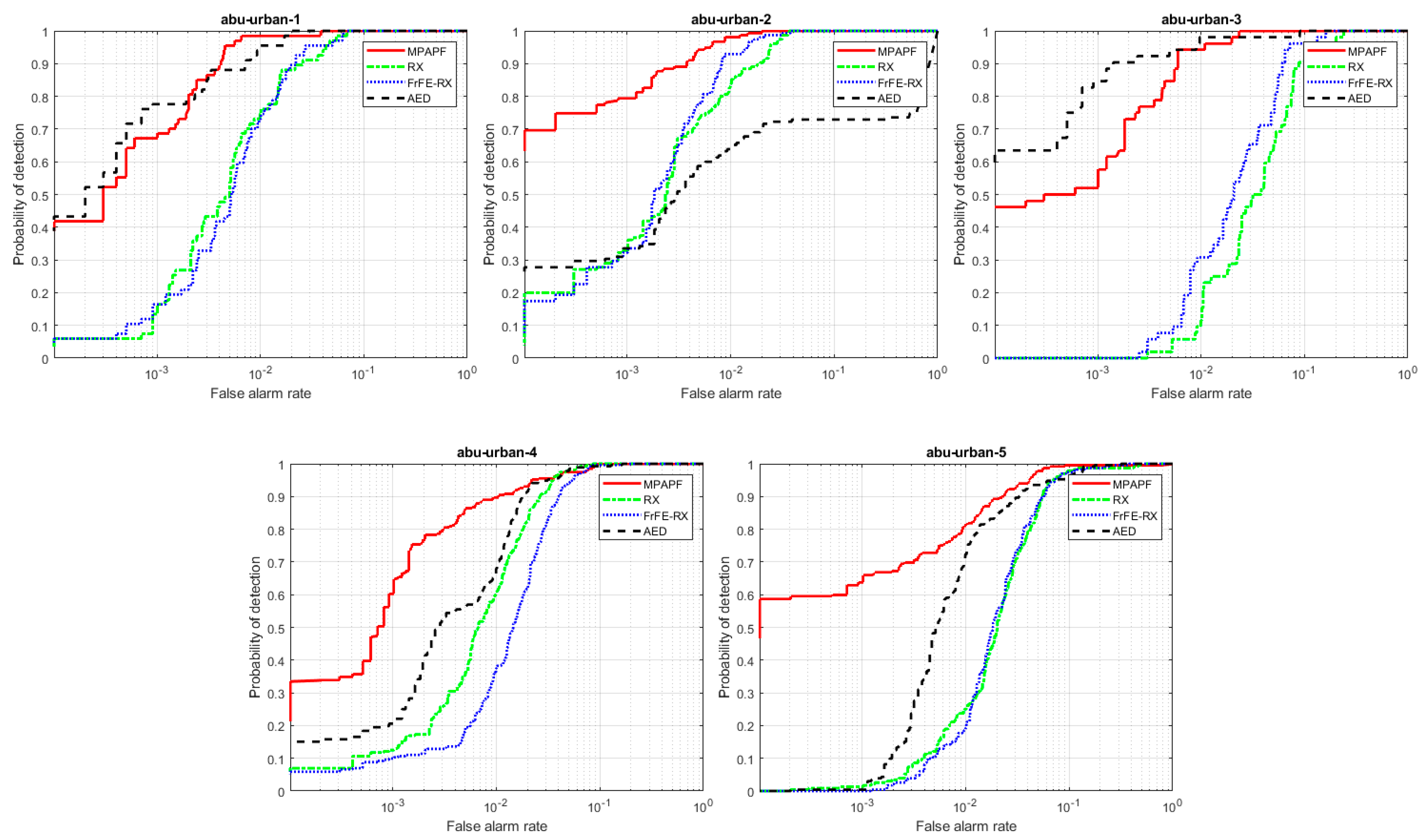
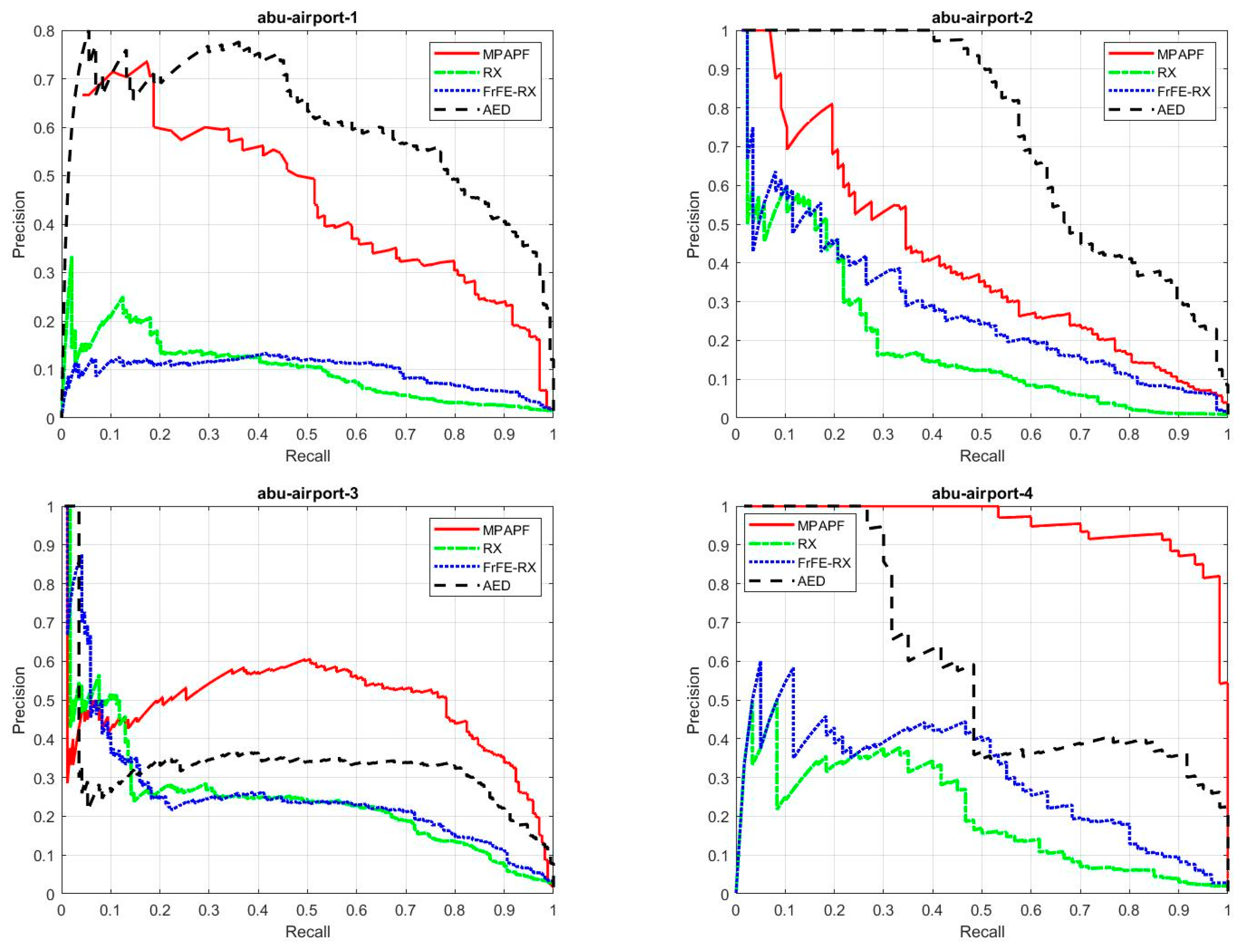
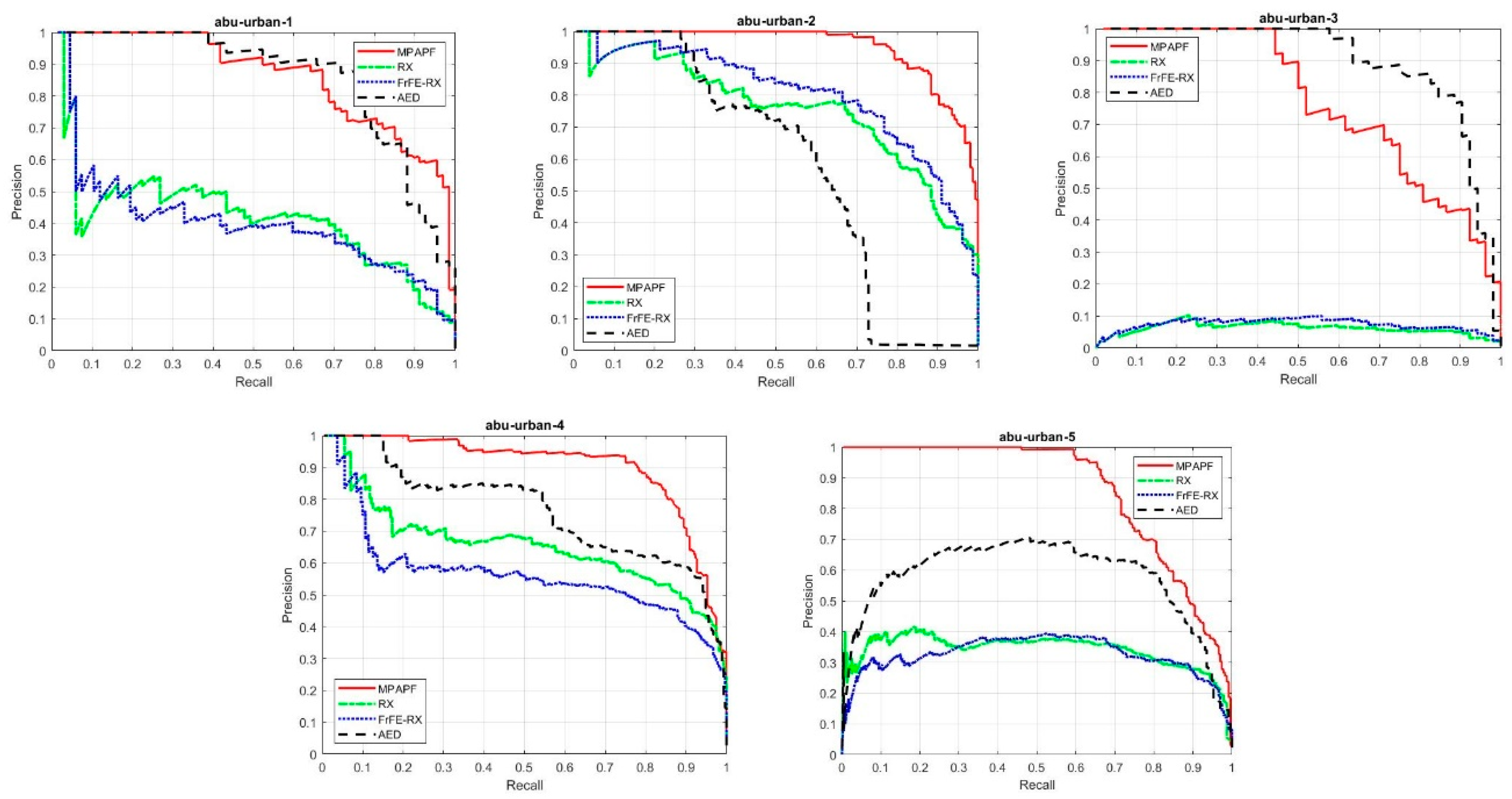
3. Experimental Results and Analysis
3.1. Data
3.2. Results
4. Discussion
4.1. Computing Time
4.2. Component Analysis
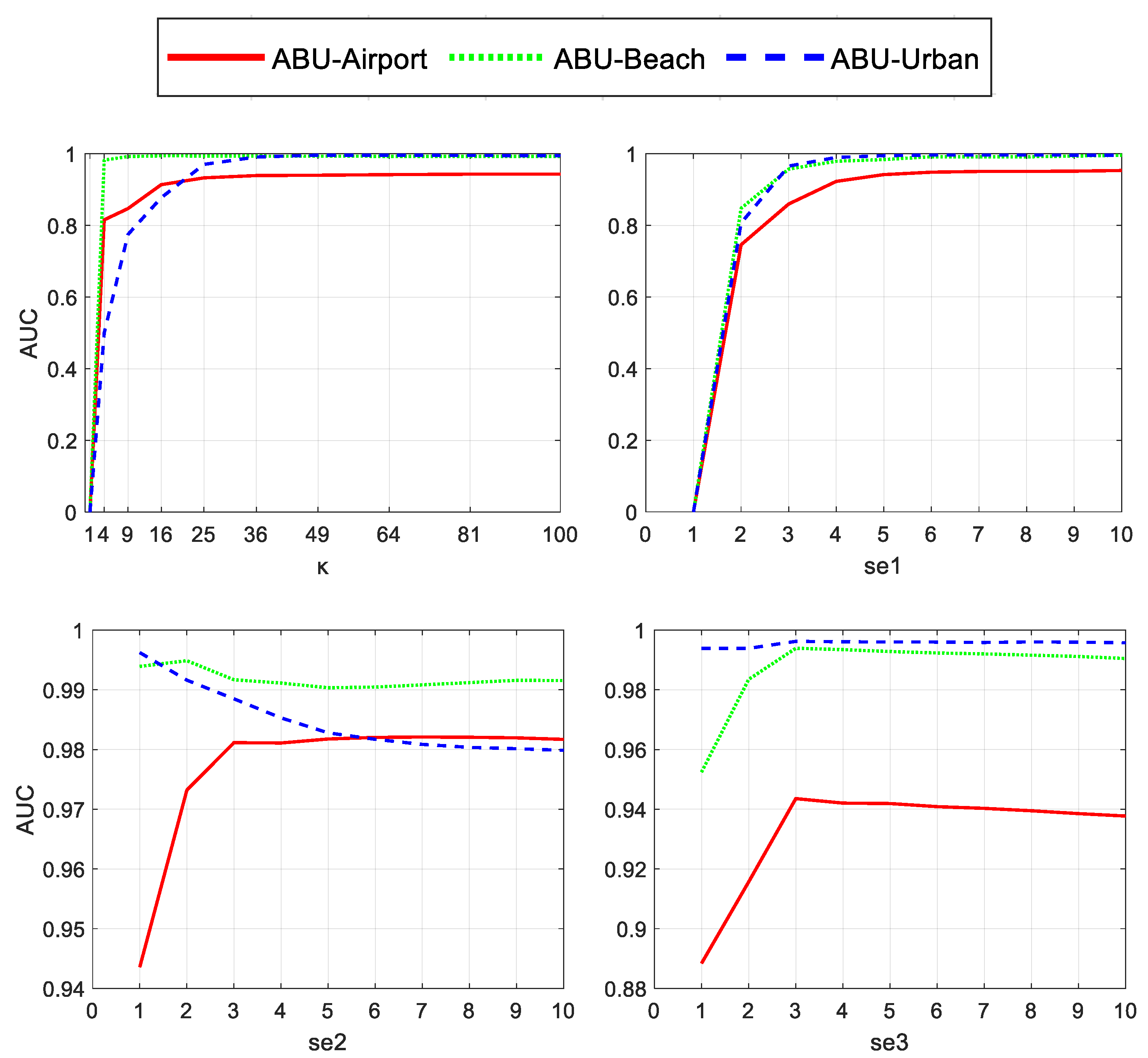
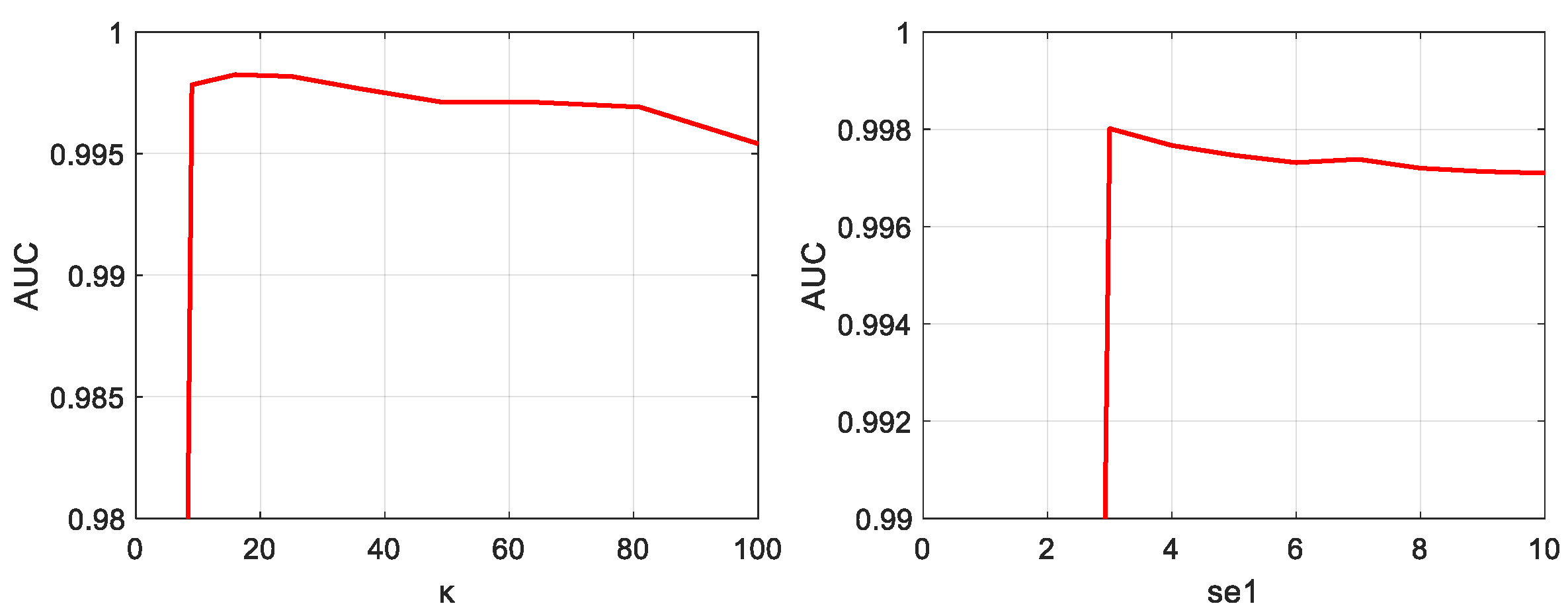
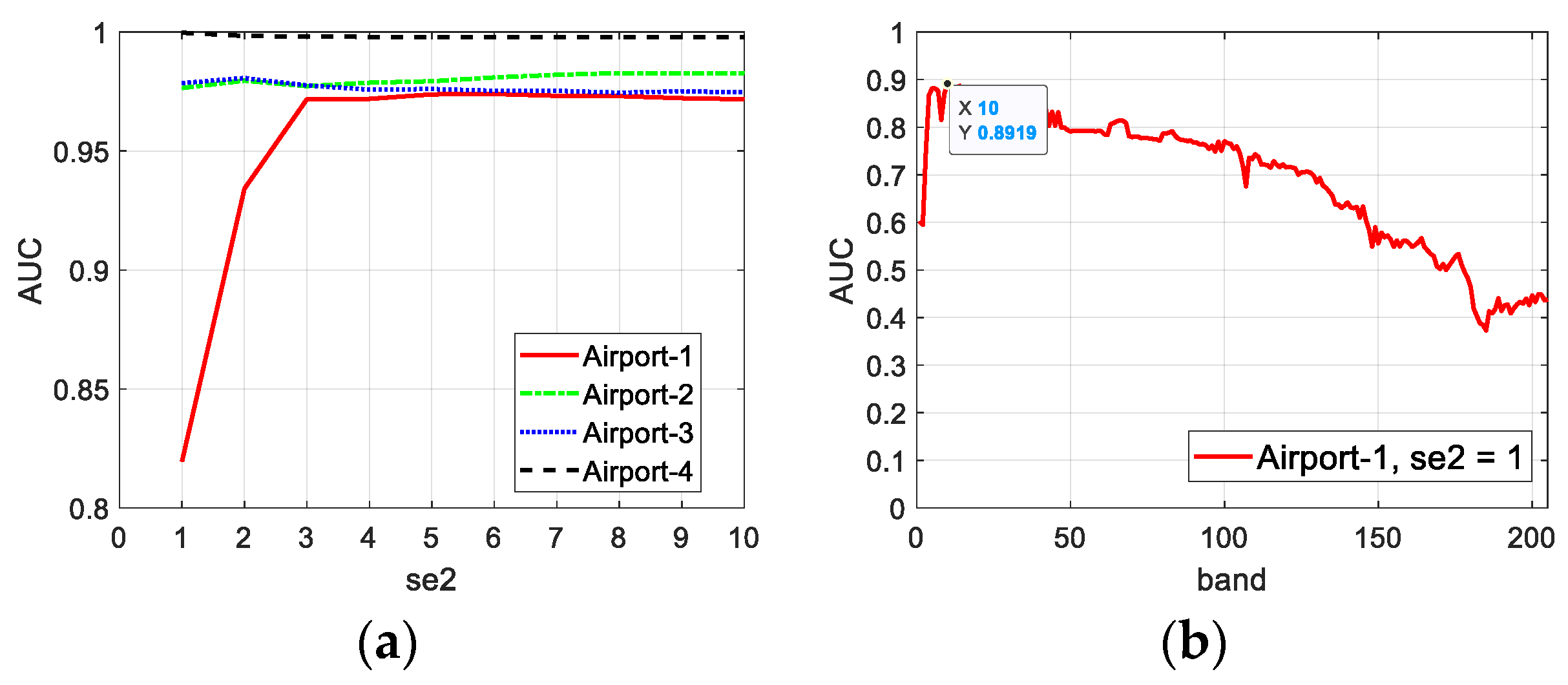
4.2.1. Parameter Sensitivity Analysis
4.2.2. Band Selection Effectiveness
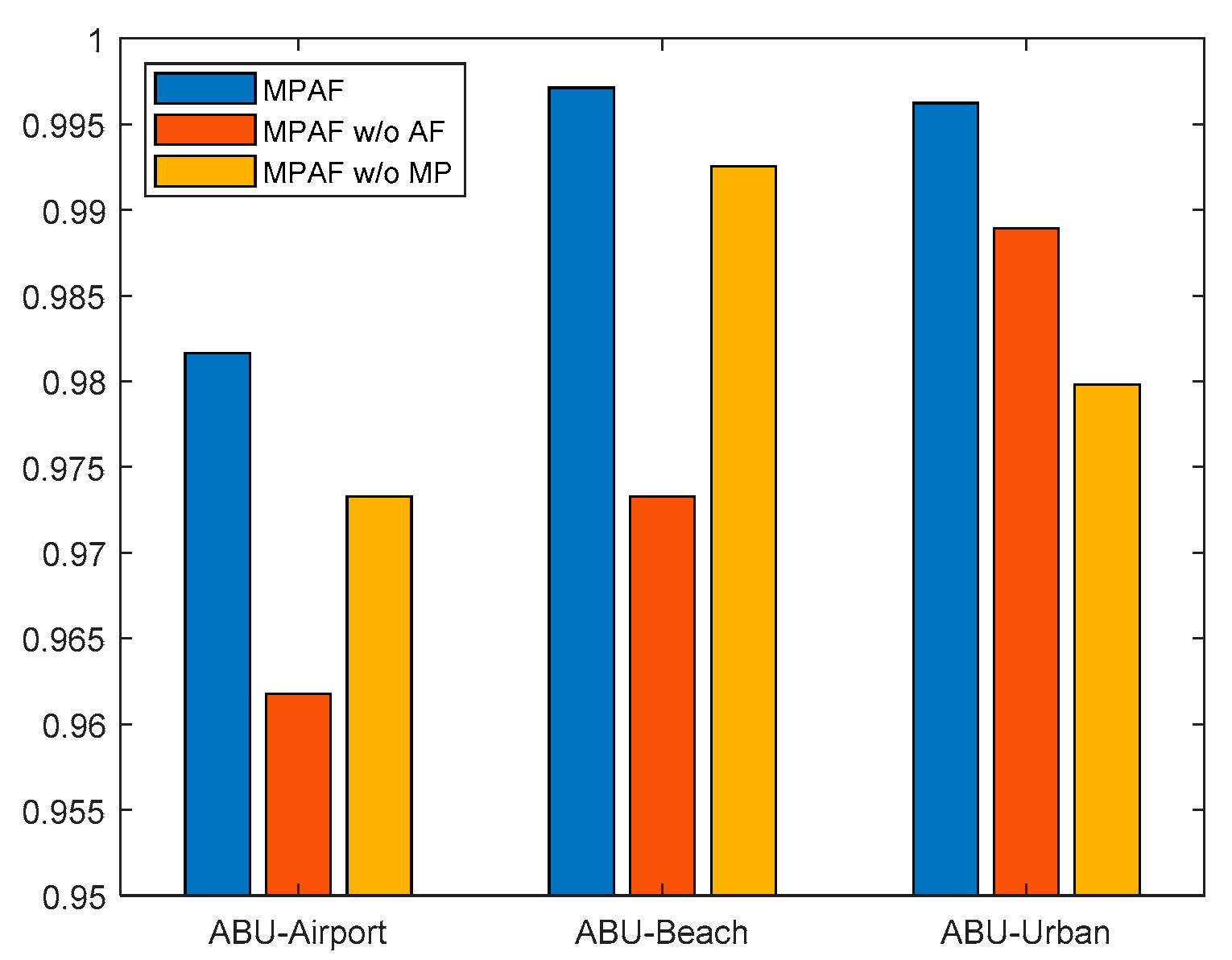
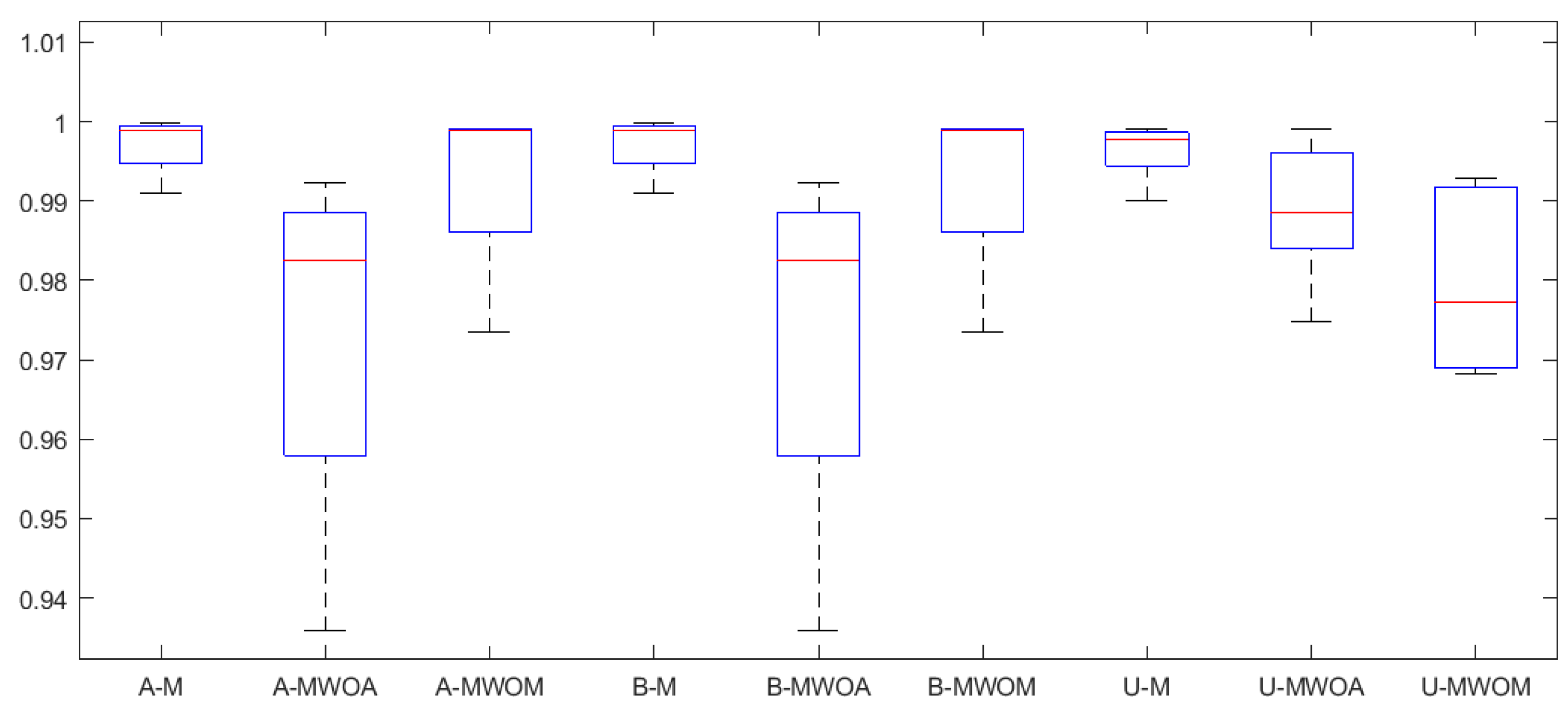
4.2.3. MP and AP Effectiveness
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rizkinia, M.; Okuda, M. Local abundance regularization for hyperspectral sparse unmixing. In Proceedings of the 2016 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA), Jeju, Korea, 13–16 December 2016; pp. 1–6. [Google Scholar]
- Rizkinia, M.; Okuda, M. Joint Local Abundance Sparse Unmixing for Hyperspectral Images. Remote Sens. 2017, 9, 1224. [Google Scholar] [CrossRef]
- Kizel, F.; Benediktsson, J.A. Spatially Enhanced Spectral Unmixing through Data Fusion of Spectral and Visible Images from Different Sensors. Remote Sens. 2020, 12, 1255. [Google Scholar] [CrossRef]
- Zeng, Y.; Ritz, C.; Zhao, J.; Lan, J. Attention-Based Residual Network with Scattering Transform Features for Hyperspectral Unmixing with Limited Training Samples. Remote Sens. 2020, 12, 400. [Google Scholar] [CrossRef]
- Fu, X.; Shang, X.; Sun, X.; Yu, H.; Song, M.; Chang, C.-I. Underwater Hyperspectral Target Detection with Band Selection. Remote Sens. 2020, 12, 1056. [Google Scholar] [CrossRef]
- Moeini Rad, A.; Abkar, A.A.; Mojaradi, B. Supervised Distance-Based Feature Selection for Hyperspectral Target Detection. Remote Sens. 2019, 11, 2049. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, X.; Wang, N.; Cen, Y. Joint Sparse and Low-Rank Multi-Task Learning with Extended Multi-Attribute Profile for Hyperspectral Target Detection. Remote Sens. 2019, 11, 150. [Google Scholar] [CrossRef]
- Fang, B.; Bai, Y.; Li, Y. Combining Spectral Unmixing and 3D/2D Dense Networks with Early-Exiting Strategy for Hyperspectral Image Classification. Remote Sens. 2020, 12, 779. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, L.; Xiao, C.; Qu, Y.; Zheng, K.; Marinoni, A. Hyperspectral Image Classification Based on a Shuffled Group Convolutional Neural Network with Transfer Learning. Remote Sens. 2020, 12, 1780. [Google Scholar] [CrossRef]
- He, Z.; He, D. Spatial-Adaptive Siamese Residual Network for Multi-/Hyperspectral Classification. Remote Sens. 2020, 12, 1640. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Song, S.; Liu, D. Hyperspectral Anomaly Detection via Dictionary Construction-Based Low-Rank Representation and Adaptive Weighting. Remote Sens. 2019, 11, 192. [Google Scholar] [CrossRef]
- Tan, K.; Hou, Z.; Ma, D.; Chen, Y.; Du, Q. Anomaly Detection in Hyperspectral Imagery Based on Low-Rank Representation Incorporating a Spatial Constraint. Remote Sens. 2019, 11, 1578. [Google Scholar] [CrossRef]
- Ma, D.; Yuan, Y.; Wang, Q. Hyperspectral Anomaly Detection Based on Separability-Aware Sample Cascade. Remote Sens. 2019, 11, 2537. [Google Scholar] [CrossRef]
- Rodríguez-Cuenca, B.; García-Cortés, S.; Ordóñez, C.; Alonso, M.C. Automatic Detection and Classification of Pole-Like Objects in Urban Point Cloud Data Using an Anomaly Detection Algorithm. Remote Sens. 2015, 7, 12680–12703. [Google Scholar] [CrossRef]
- Horstrand, P.; Díaz, M.; Guerra, R.; López, S.; López, J.F. A Novel Hyperspectral Anomaly Detection Algorithm for Real-Time Applications with Push-Broom Sensors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4787–4797. [Google Scholar] [CrossRef]
- Manolakis, D.; Truslow, E.; Pieper, M.; Cooley, T.; Brueggeman, M. Detection algorithms in hyperspectral imaging systems: An overview of practical algorithms. IEEE Signal Proc. Mag. 2014, 31, 24–33. [Google Scholar] [CrossRef]
- Chen, F.; Ren, R.; Van de Voorde, T.; Xu, W.; Zhou, G.; Zhou, Y. Fast Automatic Airport Detection in Remote Sensing Images Using Convolutional Neural Networks. Remote Sens. 2018, 10, 443. [Google Scholar] [CrossRef]
- Makki, I.; Younes, R.; Francis, C.; Bianchi, T.; Zucchetti, M. A Survey of Landmine Detection using Hyperspectral Imaging. ISPRS J. Photogramm. Remote Sens. 2017, 124, 40–53. [Google Scholar] [CrossRef]
- Taghipour, A.; Ghassemian, H. Hyperspectral Anomaly Detection Using Spectral–Spatial Features Based On the Human Visual System. Int. J. Remote Sens. 2019, 40, 8683–8704. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive Multiple-Band CFAR Detection of an Optical Pattern with Unknown Spectral Distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Zhou, J.; Kwan, C.; Ayhan, B.; Eismann, M.T. A Novel Cluster Kernel RX Algorithm for Anomaly and Change Detection Using Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6497–6504. [Google Scholar] [CrossRef]
- Imani, M. RX Anomaly Detector with Rectified Background. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1313–1317. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, B.; Feng, F.; Nan, J.; Li, C. Hierarchical Sub-Pixel Anomaly Detection Framework for Hyperspectral Imagery. Sensors 2018, 18, 3662. [Google Scholar] [CrossRef] [PubMed]
- Tao, R.; Zhao, X.; Li, W.; Li, H.; Du, Q. Hyperspectral Anomaly Detection by Fractional Fourier Entropy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4920–4929. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative Representation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1463–1474. [Google Scholar] [CrossRef]
- Vafadar, M.; Ghassemian, H. Hyperspectral Anomaly Detection Using Outlier Removal from Collaborative Representation. In Proceedings of the International Conference on Pattern Recognition and Image Analysis, Shahrekord, Iran, 19–20 April 2017; pp. 13–19. [Google Scholar]
- Su, H.; Wu, Z.; Du, Q.; Du, P. Hyperspectral Anomaly Detection Using Collaborative Representation With Outlier Removal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 5029–5038. [Google Scholar] [CrossRef]
- Tan, K.; Hou, Z.; Wu, F.; Du, Q.; Chen, Y. Anomaly Detection for Hyperspectral Imagery Based on the Regularized Subspace Method and Collaborative Representation. Remote Sens. 2019, 11, 1318. [Google Scholar] [CrossRef]
- Tu, B.; Li, N.; Liao, Z.; Ou, X.; Zhang, G. Hyperspectral Anomaly Detection via Spatial Density Background Purification. Remote Sens. 2019, 11, 2618. [Google Scholar] [CrossRef]
- Xie, W.; Jiang, T.; Li, Y.; Jia, X.; Lei, J. Structure Tensor and Guided Filtering-Based Algorithm for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4218–4230. [Google Scholar] [CrossRef]
- Lei, J.; Xie, W.; Yang, J.; Li, Y.; Chang, C. Spectral–Spatial Feature Extraction for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8131–8143. [Google Scholar] [CrossRef]
- Taghipour, A.; Ghassemian, H. Hyperspectral anomaly detection using attribute profiles. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1136–1140. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, X.; Li, S.; Li, K.; Li, J.; Benediktsson, J.A. Hyperspectral Anomaly Detection with Attribute and Edge-Preserving Filters. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5600–5611. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of Hyperspectral Data from Urban Areas Based on Extended Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Mura, M.D.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Morphological Attribute Profiles for the Analysis of Very High Resolution Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3747–3762. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y.; Lei, J.; Yang, J.; Chang, C.; Li, Z. Hyperspectral Band Selection for Spectral–Spatial Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3426–3436. [Google Scholar] [CrossRef]
- Wang, L.; Chang, C.I.; Lee, L.C.; Wang, Y.; Xue, B.; Song, M.; Yu, C.; Li, S. Band Subset Selection for Anomaly Detection in Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4887–4898. [Google Scholar] [CrossRef]
- Prasad, S.; Bruce, L.M. Limitations of Principal Components Analysis for Hyperspectral Target Recognition. IEEE Geosci. Remote Sens. Lett. 2008, 5, 625–629. [Google Scholar] [CrossRef]
- Ghamisi, P.; Mura, M.D.; Benediktsson, J.A. A Survey on Spectral–Spatial Classification Techniques Based on Attribute Profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image Analysis Using Mathematical Morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, PAMI-9, 532–550. [Google Scholar] [CrossRef]
- Breen, E.J.; Jones, R. Attribute Openings, Thinnings, and Granulometries. Comput. Vis. Image Underst. 1996, 64, 377–389. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Airport–Beach–Urban (ABU) Dataset. Available online: http://xudongkang.weebly.com/data-sets.html (accessed on 23 November 2019).
- Ferri, C.; Hernández-Orallo, J.; Flach, P. A Coherent Interpretation of AUC as a Measure of Aggregated Classification Performance. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Washington, DC, USA, 28 June–2 July 2011; pp. 657–664. [Google Scholar]

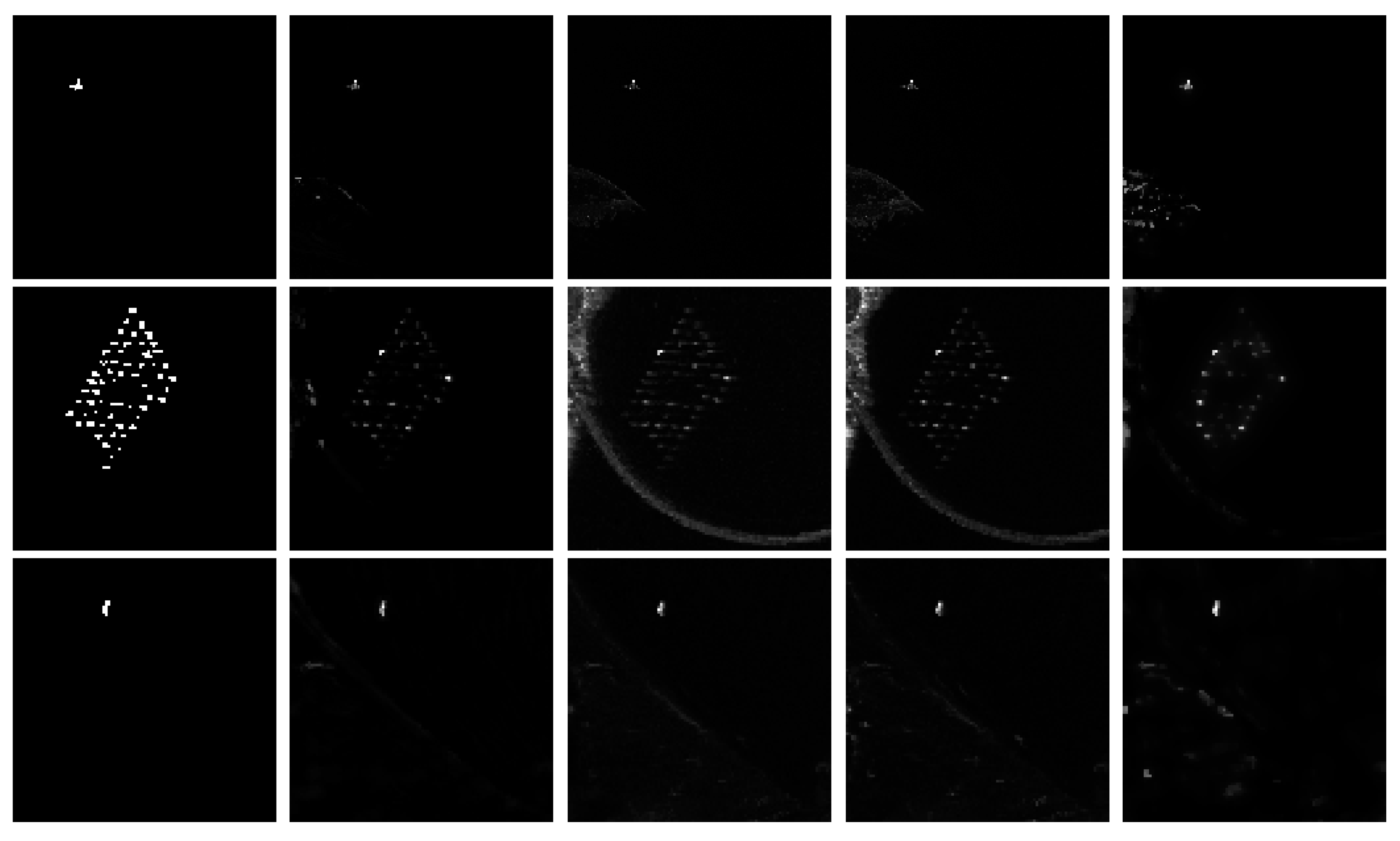



| Airport Scene | Captured Place | Resolution (pixel) | Band |
| 1 | Los Angeles | 100 × 100 | 205 |
| 2 | Los Angeles | 100 × 100 | 205 |
| 3 | Los Angeles | 100 × 100 | 205 |
| 4 | Gulfport | 100 × 100 | 191 |
| Beach Scene | Captured Place | Resolution (pixel) | Band |
| 1 | Cat Island | 150 × 150 | 188 |
| 2 | San Diego | 100 × 100 | 193 |
| 3 | Bay Champagne | 100 × 100 | 188 |
| 4 | Pavia | 150 × 150 | 102 |
| Urban Scene | Captured Place | Resolution (pixel) | Band |
| 1 | Texas Coast | 100 × 100 | 204 |
| 2 | Texas Coast | 100 × 100 | 207 |
| 3 | Gainesville | 100 × 100 | 191 |
| 4 | Los Angeles | 100 × 100 | 205 |
| 5 | Los Angeles | 100 × 100 | 205 |
| Airport Scene | |||||
| Hyperspectral Image (HSI) | MPAF | RX | FrFE-RX | AED | SDBP-D |
| Airport–1 | 0.9718 | 0.8221 | 0.9081 | 0.9923 | 0.9615 |
| Airport–2 | 0.9765 | 0.8404 | 0.969 | 0.9936 | 0.9842 |
| Airport–3 | 0.9785 | 0.9287 | 0.9424 | 0.9756 | 0.9662 |
| Airport–4 | 0.9997 | 0.9526 | 0.9854 | 0.9953 | 0.9930 |
| Average | 0.9816 | 0.8859 | 0.9512 | 0.9892 | 0.9762 |
| Beach Scene | |||||
| HSI | MPAF | RX | FrFE-RX | AED | SDBP-D |
| Beach–1 | 0.9992 | 0.9807 | 0.9862 | 0.9974 | 0.9959 |
| Beach–2 | 0.9910 | 0.9106 | 0.9161 | 0.9550 | 0.9876 |
| Beach–3 | 0.9998 | 0.9998 | 0.9997 | 0.9997 | 0.9999 |
| Beach–4 | 0.9985 | 0.9538 | 0.9541 | 0.9916 | 0.9763 |
| Average | 0.9971 | 0.9612 | 0.9640 | 0.9859 | 0.9899 |
| Urban Scene | |||||
| HSI | MPAF | RX | FrFE-RX | AED | SDBP-D |
| Urban–1 | 0.9986 | 0.9907 | 0.9918 | 0.9981 | 0.9989 |
| Urban–2 | 0.9990 | 0.9946 | 0.9962 | 0.789 | 0.9984 |
| Urban–3 | 0.9977 | 0.9513 | 0.9684 | 0.9976 | 0.9946 |
| Urban–4 | 0.9959 | 0.9887 | 0.9809 | 0.9912 | 0.9972 |
| Urban–5 | 0.9900 | 0.9692 | 0.9719 | 0.9845 | 0.9877 |
| Average | 0.9962 | 0.9789 | 0.9818 | 0.9521 | 0.9954 |
| Average (all scenes) | 0.9916 | 0.9420 | 0.9657 | 0.9757 | 0.9872 |
| Airport Scene | ||||
| HSI | MPAF | RX | FrFE-RX | AED |
| Airport–1 | 0.4284 | 0.0980 | 0.0966 | 0.6061 |
| Airport–2 | 0.3995 | 0.1876 | 0.2720 | 0.7247 |
| Airport–3 | 0.4746 | 0.2391 | 0.2486 | 0.3266 |
| Airport–4 | 0.9399 | 0.2000 | 0.2980 | 0.5828 |
| Average | 0.5606 | 0.1812 | 0.2288 | 0.5601 |
| Beach Scene | ||||
| HSI | MPAF | RX | FrFE-RX | AED |
| Beach–1 | 0.7204 | 0.3780 | 0.3756 | 0.3438 |
| Beach–2 | 0.6454 | 0.1127 | 0.1105 | 0.3362 |
| Beach–3 | 0.8272 | 0.8373 | 0.7763 | 0.7630 |
| Beach–4 | 0.5915 | 0.3118 | 0.2608 | 0.5850 |
| Average | 0.6961 | 0.4100 | 0.3808 | 0.5070 |
| Urban Scene | ||||
| HSI | MPAF | RX | FrFE-RX | AED |
| Urban–1 | 0.8448 | 0.4030 | 0.3877 | 0.8435 |
| Urban–2 | 0.9454 | 0.7464 | 0.7942 | 0.5764 |
| Urban–3 | 0.7545 | 0.0609 | 0.0731 | 0.8796 |
| Urban–4 | 0.8989 | 0.6510 | 0.5598 | 0.7580 |
| Urban–5 | 0.8552 | 0.3388 | 0.3199 | 0.5699 |
| Average | 0.8598 | 0.4400 | 0.4269 | 0.7255 |
| Average (all scenes) | 0.7055 | 0.3437 | 0.3455 | 0.5975 |
| Scene | MPAF | RX | FrFE-RX | AED |
|---|---|---|---|---|
| Airport | 0.26 | 0.15 | 31.08 | 0.55 |
| Beach | 0.32 | 0.22 | 40.13 | 0.69 |
| Urban | 0.17 | 0.14 | 22.89 | 0.41 |
| Average | 0.25 | 0.17 | 31.37 | 0.55 |
| Best Band | Band Selection | Difference | ||
|---|---|---|---|---|
| Airport Scene | Airport-1 | 0.9788 | 0.9718 | 0.007 |
| Airport-2 | 0.9857 | 0.9765 | 0.0092 | |
| Airport-3 | 0.9827 | 0.9785 | 0.0042 | |
| Airport-4 | 0.9998 | 0.9997 | 0.0001 | |
| Beach Scene | Beach-1 | 0.9996 | 0.9992 | 0.0004 |
| Beach-2 | 0.9921 | 0.991 | 0.0011 | |
| Beach-3 | 0.99996 | 0.9998 | 0.00016 | |
| Beach-4 | 0.9993 | 0.9985 | 0.0008 | |
| Urban Scene | Urban-1 | 0.9994 | 0.9986 | 0.0008 |
| Urban-2 | 0.9993 | 0.999 | 0.0003 | |
| Urban-3 | 0.9983 | 0.9977 | 0.0006 | |
| Urban-4 | 0.9974 | 0.9959 | 0.0015 | |
| Urban-5 | 0.9902 | 0.99 | 0.0002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andika, F.; Rizkinia, M.; Okuda, M. A Hyperspectral Anomaly Detection Algorithm Based on Morphological Profile and Attribute Filter with Band Selection and Automatic Determination of Maximum Area. Remote Sens. 2020, 12, 3387. https://doi.org/10.3390/rs12203387
Andika F, Rizkinia M, Okuda M. A Hyperspectral Anomaly Detection Algorithm Based on Morphological Profile and Attribute Filter with Band Selection and Automatic Determination of Maximum Area. Remote Sensing. 2020; 12(20):3387. https://doi.org/10.3390/rs12203387
Chicago/Turabian StyleAndika, Ferdi, Mia Rizkinia, and Masahiro Okuda. 2020. "A Hyperspectral Anomaly Detection Algorithm Based on Morphological Profile and Attribute Filter with Band Selection and Automatic Determination of Maximum Area" Remote Sensing 12, no. 20: 3387. https://doi.org/10.3390/rs12203387
APA StyleAndika, F., Rizkinia, M., & Okuda, M. (2020). A Hyperspectral Anomaly Detection Algorithm Based on Morphological Profile and Attribute Filter with Band Selection and Automatic Determination of Maximum Area. Remote Sensing, 12(20), 3387. https://doi.org/10.3390/rs12203387






