Probabilistic Mapping and Spatial Pattern Analysis of Grazing Lawns in Southern African Savannahs Using WorldView-3 Imagery and Machine Learning Techniques
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Land Cover and Classification Scheme
2.3. Data
2.3.1. Satellite Imagery
2.3.2. Reference Data
2.3.3. Auxiliary Data
2.4. Preparation of Image Features
2.5. Feature Selection
2.6. Machine Learning Algorithms
2.6.1. RF
2.6.2. SVM
2.6.3. CART
2.6.4. MLP
2.7. Algorithm Calibration and Evaluation
2.7.1. Data Preparation
2.7.2. Parameterisation, Training and Classification
2.7.3. Accuracy Assessment and Comparison
2.8. Spatial Analysis of Grazing Lawn Distribution
3. Results
3.1. Model Quality for Land Cover Classification
3.2. Grazing Lawn Occurrence Probability Prediction and Classification
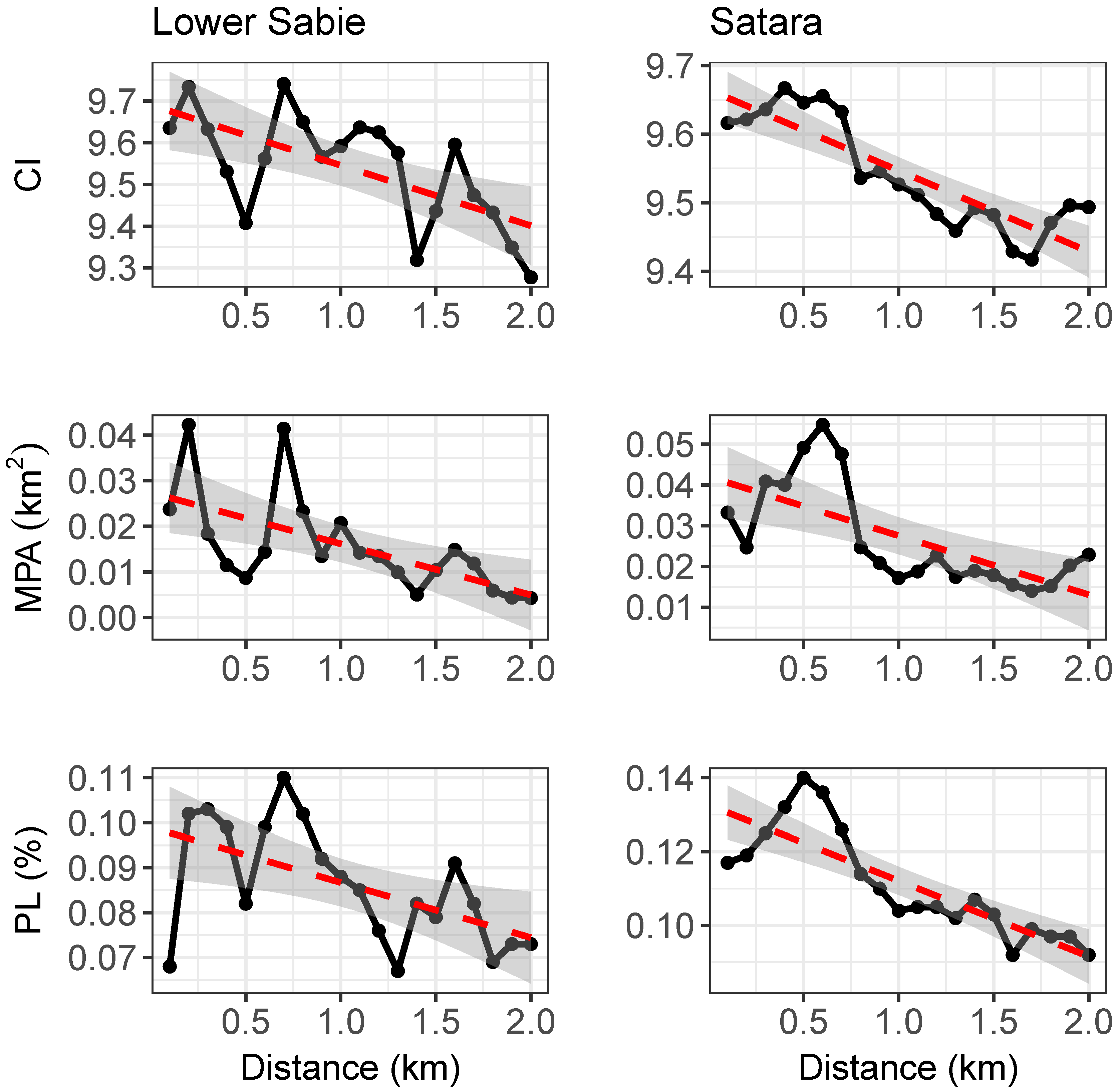
3.3. Spatial Patterns in Grazing Lawn Cover
4. Discussion
4.1. Model Quality for Savannah Land Cover Classification
4.2. Grazing Lawn Detection and Model Comparison
4.3. Spatial Patterns in Grazing Lawn Distribution
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Supplementary Data
Appendix A.1. Multicollinearity and Feature Selection

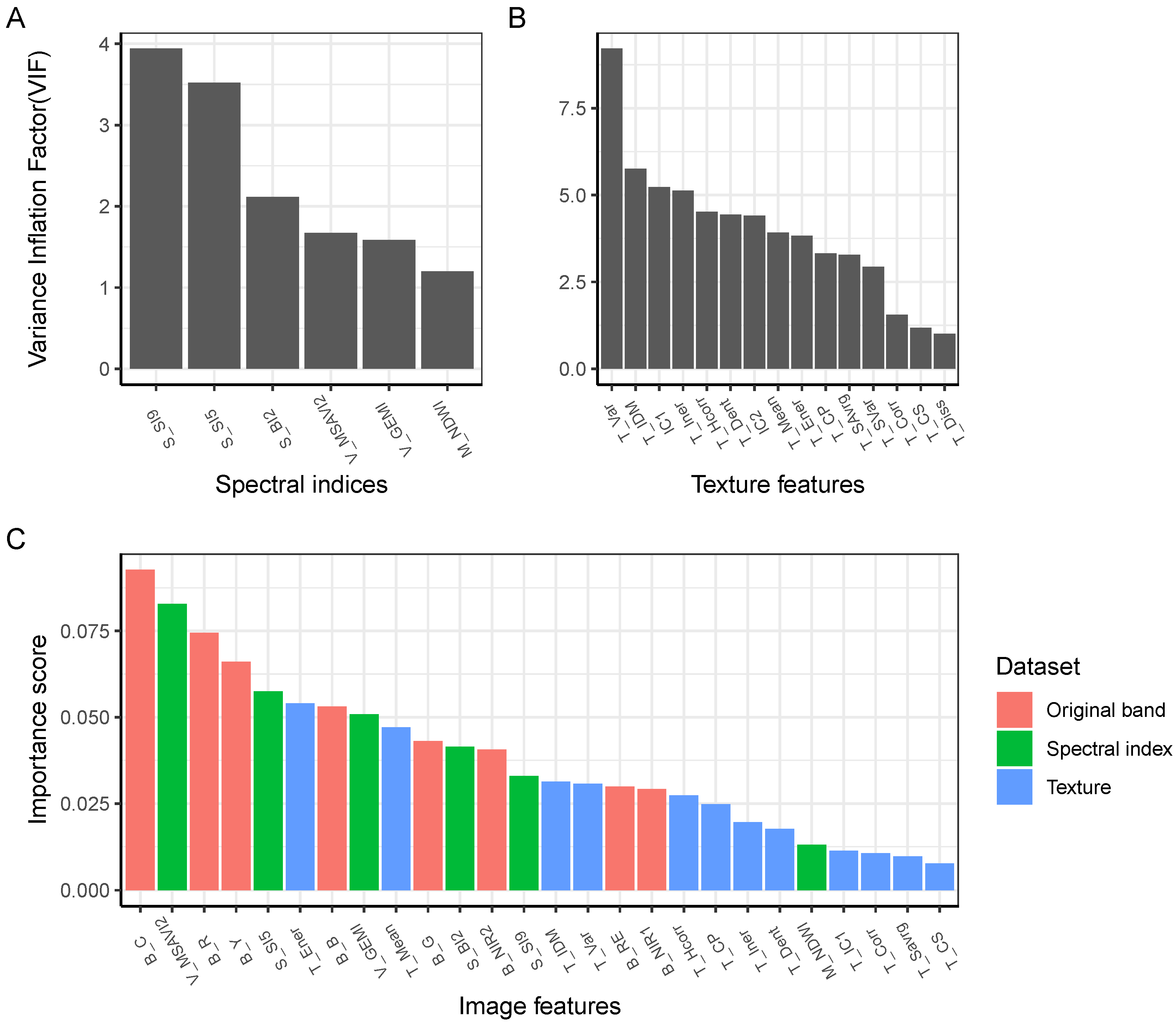
Appendix A.2. Comparison of Grazing Lawn Area Estimates across Models in Each Landscape
| Lower Sabie | Satara | ||
|---|---|---|---|
| Model Pair | -test | Model Pair | -test |
| CART v MLP | 0.000(1.00) | CART v MLP | 5.017(0.025) |
| CART v RF | 0.000(1.00) | CART v RF | 8.328(0.003) |
| CART v SVM | 0.000(1.00) | CART v SVM | 7.225(0.007) |
| MLP v RF | 0.000(1.00) | MLP v RF | 13.146(0.000) |
| MLP v SVM | 0.000(1.00) | MLP v SVM | 11.657(0.000) |
| RF v SVM | 0.000(1.00) | RF v SVM | 10.083(0.001) |
Appendix A.3. Confusion Matrices for the Lower Sabie Landscape
| RF | ||||
|---|---|---|---|---|
| Reference Class | Commission Error (%) | |||
| Grazing lawn | Other | |||
| Predicted Class | Grazing lawn | 84 | 16 | 16.00 |
| Other | 4 | 693 | 0.57 | |
| Omission Error (%) | 4.55 | 2.26 | ||
| SVM | ||||
|---|---|---|---|---|
| Reference Class | Commission Error (%) | |||
| Grazing lawn | Other | |||
| Predicted Class | Grazing lawn | 93 | 7 | 7.00 |
| Other | 7 | 690 | 1.00 | |
| Omission Error (%) | 7.00 | 1.00 | ||
| CART | ||||
|---|---|---|---|---|
| Reference Class | Commission Error (%) | |||
| Grazing lawn | Other | |||
| Predicted Class | Grazing lawn | 77 | 23 | 23.00 |
| Other | 12 | 685 | 1.72 | |
| Omission Error (%) | 13.48 | 3.25 | ||
| MLP | ||||
|---|---|---|---|---|
| Reference Class | Commission Error (%) | |||
| Grazing lawn | Other | |||
| Predicted Class | Grazing lawn | 97 | 3 | 3.00 |
| Other | 9 | 688 | 1.29 | |
| Omission Error (%) | 8.49 | 0.43 | ||
Appendix A.4. Confusion Matrices for the Satara Landscape
| RF | ||||
|---|---|---|---|---|
| Reference Class | Commission Error (%) | |||
| Grazing lawn | Other | |||
| Predicted Class | Grazing lawn | 90 | 13 | 12.62 |
| Other | 12 | 511 | 2.29 | |
| Omission Error (%) | 11.76 | 2.48 | ||
| SVM | ||||
|---|---|---|---|---|
| Reference Class | Commission Error (%) | |||
| Grazing lawn | Other | |||
| Predicted Class | Grazing lawn | 93 | 10 | 9.71 |
| Other | 14 | 509 | 2.68 | |
| Omission Error (%) | 13.08 | 1.93 | ||
| CART | ||||
|---|---|---|---|---|
| Reference Class | Commission Error (%) | |||
| Grazing lawn | Other | |||
| Predicted Class | Grazing lawn | 78 | 25 | 24.27 |
| Other | 25 | 498 | 4.78 | |
| Omission Error (%) | 24.27 | 4.78 | ||
| MLP | ||||
|---|---|---|---|---|
| Reference Class | Commission Error (%) | |||
| Grazing lawn | Other | |||
| Predicted Class | Grazing lawn | 88 | 15 | 14.56 |
| Other | 16 | 507 | 3.06 | |
| Omission Error (%) | 15.38 | 2.87 | ||
Appendix A.5. Final Model Hyperparameters
| Model | Optimal Hyper-Parameter Value | Description |
|---|---|---|
| RF | n_estimators = 2000, max_features = ‘auto’, max_depth = 20, min_samples_split = 2, min_samples_leaf = 1 | n_estimators = number of trees in the forest. max_features = number of features to consider for the split, ‘auto’ takes . max_depth = maximum depth of the tree. min_samples_split = minimum number of samples required to split an internal node. min_samples_leaf = minimum number of samples required to be at a leaf node. |
| MLP | hidden_layer_sizes = (150,100,50), activation = ‘logistic’, solver = ‘adam’, max_iter = 100, alpha = 0.0000001 | hidden_layer_sizes = number of neurons in each hidden layer (three layers in this case). activation = activation function of the hidden layer. solver = solver for weight optimization, ‘adam’ is based on the stochastic gradient optimizer. max_iter = maximum number of iterations. alpha = regularization parameter. |
| CART | criterion = ‘gini’, max_depth = 80, min_samples_split = 20, min_samples_leaf = 5 | criterion = function to measure quality of split. max_depth = maximum depth of tree. min_samples_split = minimum number of samples required to split an internal node. min_samples_leaf = minimum number of samples required to be at a leaf node. |
| SVM | C = 1000, gamma = 0.001, kernel = ‘rbf’ | C = regularization parameter. gamma = kernel coefficient. kernel = kernel type used, ‘rbf’ represents radial basis function. |
Appendix B. Analysis Script
References
- Sankaran, M.; Ratnam, J.; Hanan, N. Woody cover in African savannas: The role of resources, fire and herbivory. Glob. Ecol. Biogeogr. 2008, 17, 236–245. [Google Scholar] [CrossRef]
- Shorrocks, B.; Bates, W. The Biology of African Savannahs; Oxford University Press: Oxford, MS, USA, 2015. [Google Scholar]
- Cromsigt, J.P.; Kuijper, D.P. Revisiting the browsing lawn concept: Evolutionary Interactions or pruning herbivores? Perspect. Plant Ecol. Evol. Syst. 2011, 13, 207–215. [Google Scholar] [CrossRef]
- Cromsigt, J.P.; Olff, H. Dynamics of grazing lawn formation: An experimental test of the role of scale-dependent processes. Oikos 2008, 117, 1444–1452. [Google Scholar] [CrossRef]
- Owen-Smith, N. Pleistocene extinctions: The pivotal role of megaherbivores. Paleobiology 1987, 13, 351–362. [Google Scholar] [CrossRef]
- Cromsigt, J.P.; te Beest, M. Restoration of a megaherbivore: Landscape-level impacts of white rhinoceros in Kruger National Park, South Africa. J. Ecol. 2014, 102, 566–575. [Google Scholar] [CrossRef]
- Waldram, M.S.; Bond, W.J.; Stock, W.D. Ecological engineering by a mega-grazer: White rhino impacts on a South African savanna. Ecosystems 2008, 11, 101–112. [Google Scholar] [CrossRef]
- Gill, J.L.; Williams, J.W.; Jackson, S.T.; Lininger, K.B.; Robinson, G.S. Pleistocene megafaunal collapse, novel plant communities, and enhanced fire regimes in North America. Science 2009, 326, 1100–1103. [Google Scholar] [CrossRef]
- Owen-Smith, R.N. Megaherbivores. The influence of very large body size on ecology. In Megaherbivores: The Influence of Very Large Body Size on Ecology; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Hempson, G.P.; Archibald, S.; Bond, W.J.; Ellis, R.P.; Grant, C.C.; Kruger, F.J.; Kruger, L.M.; Moxley, C.; Owen-Smith, N.; Peel, M.J.; et al. Ecology of grazing lawns in Africa. Biol. Rev. 2015, 90, 979–994. [Google Scholar] [CrossRef]
- Donaldson, J.E.; Archibald, S.; Govender, N.; Pollard, D.; Luhdo, Z.; Parr, C.L. Ecological engineering through fire-herbivory feedbacks drives the formation of savanna grazing lawns. J. Appl. Ecol. 2018, 55, 225–235. [Google Scholar] [CrossRef]
- Archibald, S.; Bond, W.; Stock, W.; Fairbanks, D. Shaping the landscape: Fire–grazer interactions in an African savanna. Ecol. Appl. 2005, 15, 96–109. [Google Scholar] [CrossRef]
- Archibald, S. African grazing lawns—How fire, rainfall, and grazer numbers interact to affect grass community states. J. Wildl. Manag. 2008, 72, 492–501. [Google Scholar] [CrossRef]
- Veldhuis, M.P.; Fakkert, H.F.; Berg, M.P.; Olff, H. Grassland structural heterogeneity in a savanna is driven more by productivity differences than by consumption differences between lawn and bunch grasses. Oecologia 2016, 182, 841–853. [Google Scholar] [CrossRef] [PubMed]
- Leonard, S.; Kirkpatrick, J.; Marsden-Smedley, J. Variation in the effects of vertebrate grazing on fire potential between grassland structural types. J. Appl. Ecol. 2010, 47, 876–883. [Google Scholar] [CrossRef]
- Helman, D.; Lensky, I.M.; Tessler, N.; Osem, Y. A phenology-based method for monitoring woody and herbaceous vegetation in Mediterranean forests from NDVI time series. Remote Sens. 2015, 7, 12314–12335. [Google Scholar] [CrossRef]
- Marston, C.G.; Aplin, P.; Wilkinson, D.M.; Field, R.; O’Regan, H.J. Scrubbing up: Multi-scale investigation of woody encroachment in a southern African savannah. Remote Sens. 2017, 9, 419. [Google Scholar] [CrossRef]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective, 4th ed.; Prentice Hall Press: Boston, MA, USA, 2015; p. 544. [Google Scholar]
- Khorram, S.; van der Wiele, C.F.; Koch, F.H.; Nelson, S.A.; Potts, M.D. Future trends in remote sensing. In Principles of Applied Remote Sensing; Springer: Cham, Switzerland, 2016; pp. 277–285. [Google Scholar]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Vajsova, B.; Walczynska, A.; Bärisch, S.; Åstrand, P.J.; Hain, S. New Sensors Benchmark Report on WorldView-4: Geometric Benchmarking over Maussane Test Site for CAP Purposes. 2017. Available online: https://core.ac.uk/download/pdf/93512541.pdf (accessed on 27 October 2019).
- Kaszta, Ż.; Van De Kerchove, R.; Ramoelo, A.; Cho, M.; Madonsela, S.; Mathieu, R.; Wolff, E. Seasonal separation of African savanna components using worldview-2 imagery: A comparison of pixel-and object-based approaches and selected classification algorithms. Remote Sens. 2016, 8, 763. [Google Scholar] [CrossRef]
- Schuster, C.; Schmidt, T.; Conrad, C.; Kleinschmit, B.; Förster, M. Grassland habitat mapping by intra-annual time series analysis—Comparison of RapidEye and TerraSAR-X satellite data. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 25–34. [Google Scholar] [CrossRef]
- Whiteside, T.G.; Boggs, G.S.; Maier, S.W. Comparing object-based and pixel-based classifications for mapping savannas. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 884–893. [Google Scholar] [CrossRef]
- Abdi, A.M. Land cover and land use classification performance of machine learning algorithms in a boreal landscape using Sentinel-2 data. GISci. Remote Sens. 2020, 57, 1–20. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and regression trees. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Del Frate, F.; Pacifici, F.; Schiavon, G.; Solimini, C. Use of neural networks for automatic classification from high-resolution images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 800–809. [Google Scholar] [CrossRef]
- Camargo, F.F.; Sano, E.E.; Almeida, C.M.; Mura, J.C.; Almeida, T. A comparative assessment of machine-learning techniques for land use and land cover classification of the Brazilian tropical savanna using ALOS-2/PALSAR-2 polarimetric images. Remote Sens. 2019, 11, 1600. [Google Scholar] [CrossRef]
- Symeonakis, E.; Higginbottom, T.P.; Petroulaki, K.; Rabe, A. Optimisation of savannah land cover characterisation with optical and SAR data. Remote Sens. 2018, 10, 499. [Google Scholar] [CrossRef]
- Otukei, J.R.; Blaschke, T. Land cover change assessment using decision trees, support vector machines and maximum likelihood classification algorithms. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S27–S31. [Google Scholar] [CrossRef]
- Omer, G.; Mutanga, O.; Abdel-Rahman, E.M.; Adam, E. Performance of support vector machines and artificial neural network for mapping endangered tree species using WorldView-2 data in Dukuduku forest, South Africa. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4825–4840. [Google Scholar] [CrossRef]
- E Silva, L.P.; Xavier, A.P.C.; da Silva, R.M.; Santos, C.A.G. Modeling land cover change based on an artificial neural network for a semiarid river basin in northeastern Brazil. Glob. Ecol. Conserv. 2020, 21, e00811. [Google Scholar] [CrossRef]
- Smit, I.P.; Archibald, S. Herbivore culling influences spatio-temporal patterns of fire in a semiarid savanna. J. Appl. Ecol. 2019, 56, 711–721. [Google Scholar] [CrossRef]
- Venter, F.J.; Scholes, R.J.; Eckhardt, H.C. The abiotic template and its associated vegetation pattern. Kruger Exp. Ecol. Manag. Savanna Heterog. 2003, 83, 129. [Google Scholar]
- Van Wilgen, B.W.; Govender, N.; Smit, I.P.; MacFadyen, S. The ongoing development of a pragmatic and adaptive fire management policy in a large African savanna protected area. J. Environ. Manag. 2014, 132, 358–368. [Google Scholar] [CrossRef] [PubMed]
- Venter, F. A Classification of Land for Management Planning in the Kruger National Park. Unpublish. Ph.D. Thesis, University of South Africa, Pretoria, ZA, South Africa, 1990. [Google Scholar]
- Munyati, C.; Sinthumule, N. Change in woody cover at representative sites in the Kruger National Park, South Africa, based on historical imagery. SpringerPlus 2016, 5, 1417. [Google Scholar] [CrossRef] [PubMed]
- Kleynhans, E.J.; Jolles, A.E.; Bos, M.R.; Olff, H. Resource partitioning along multiple niche dimensions in differently sized African savanna grazers. Oikos 2011, 120, 591–600. [Google Scholar] [CrossRef]
- Govender, N.; Trollope, W.S.; Van Wilgen, B.W. The effect of fire season, fire frequency, rainfall and management on fire intensity in savanna vegetation in South Africa. J. Appl. Ecol. 2006, 43, 748–758. [Google Scholar] [CrossRef]
- Zizka, A.; Govender, N.; Higgins, S.I. How to tell a shrub from a tree: A life-history perspective from a S outh A frican savanna. Austral Ecol. 2014, 39, 767–778. [Google Scholar] [CrossRef]
- Brandt, M.; Tappan, G.; Diouf, A.A.; Beye, G.; Mbow, C.; Fensholt, R. Woody vegetation die off and regeneration in response to rainfall variability in the West African Sahel. Remote Sens. 2017, 9, 39. [Google Scholar] [CrossRef]
- Bucini, G.; Saatchi, S.; Hanan, N.; Boone, R.B.; Smit, I. Woody cover and heterogeneity in the savannas of the Kruger National Park, South Africa. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 4, p. 334. [Google Scholar]
- Corcoran, J.; Knight, J.; Pelletier, K.; Rampi, L.; Wang, Y. The effects of point or polygon based training data on RandomForest classification accuracy of wetlands. Remote Sens. 2015, 7, 4002–4025. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Van Niel, T.G.; McVicar, T.R.; Datt, B. On the relationship between training sample size and data dimensionality: Monte Carlo analysis of broadband multi-temporal classification. Remote Sens. Environ. 2005, 98, 468–480. [Google Scholar] [CrossRef]
- Smit, I.P.; Grant, C.C.; Devereux, B.J. Do artificial waterholes influence the way herbivores use the landscape? Herbivore distribution patterns around rivers and artificial surface water sources in a large African savanna park. Biol. Conserv. 2007, 136, 85–99. [Google Scholar] [CrossRef]
- Marston, C.G.; Wilkinson, D.M.; Reynolds, S.C.; Louys, J.; O’Regan, H.J. Water availability is a principal driver of large-scale land cover spatial heterogeneity in sub-Saharan savannahs. Landsc. Ecol. 2019, 34, 131–145. [Google Scholar] [CrossRef]
- Haklay, M.; Weber, P. Openstreetmap: User-generated street maps. IEEE Pervasive Comput. 2008, 7, 12–18. [Google Scholar] [CrossRef]
- Balzarolo, M.; Vicca, S.; Nguy-Robertson, A.; Bonal, D.; Elbers, J.; Fu, Y.; Grünwald, T.; Horemans, J.; Papale, D.; Peñuelas, J.; et al. Matching the phenology of Net Ecosystem Exchange and vegetation indices estimated with MODIS and FLUXNET in-situ observations. Remote Sens. Environ. 2016, 174, 290–300. [Google Scholar] [CrossRef]
- Liu, Y.; Hill, M.J.; Zhang, X.; Wang, Z.; Richardson, A.D.; Hufkens, K.; Filippa, G.; Baldocchi, D.D.; Ma, S.; Verfaillie, J.; et al. Using data from Landsat, MODIS, VIIRS and PhenoCams to monitor the phenology of California oak/grass savanna and open grassland across spatial scales. Agric. For. Meteorol. 2017, 237, 311–325. [Google Scholar] [CrossRef]
- Munyati, C.; Balzter, H.; Economon, E. Correlating Sentinel-2 MSI-derived vegetation indices with in-situ reflectance and tissue macronutrients in savannah grass. Int. J. Remote Sens. 2020, 41, 3820–3844. [Google Scholar] [CrossRef]
- Fajji, N.G.; Palamuleni, L.G.; Mlambo, V. Evaluating derived vegetation indices and cover fraction to estimate rangeland aboveground biomass in semi-arid environments. South Afr. J. Geomat. 2017, 6, 333–348. [Google Scholar] [CrossRef]
- Yin, X.; Wang, C.; Zong, Z.; Wang, H.; Zhang, H.; Zhang, W. Biomass estimation of desert steppe based on spectral indices along a precipitation gradient. Spectrosc. Lett. 2018, 51, 324–331. [Google Scholar] [CrossRef]
- Guerini Filho, M.; Kuplich, T.M.; Quadros, F.L.D. Estimating natural grassland biomass by vegetation indices using Sentinel 2 remote sensing data. Int. J. Remote Sens. 2020, 41, 2861–2876. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Daughtry, C.S.; Li, L. Feasibility of estimating leaf water content using spectral indices from WorldView-3’s near-infrared and shortwave infrared bands. Int. J. Remote Sens. 2016, 37, 388–402. [Google Scholar] [CrossRef]
- Roberto, C.; Lorenzo, B.; Michele, M.; Micol, R.; Cinzia, P. 10 Optical Remote Sensing of Vegetation Water Content. In Hyperspectral Remote Sensing of Vegetation; CRC Press: Boca Raton, FL, USA, 2016; p. 227. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Pratt, W.K. Introduction to Digital Image Processing, 1st ed.; CRC Press: Boca Ranton, FL, USA, 2013; p. 756. [Google Scholar]
- Inglada, J.; Christophe, E. The Orfeo Toolbox remote sensing image processing software. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 4. [Google Scholar]
- Johansen, K.; Phinn, S. Mapping indicators of riparian vegetation health using IKONOS and Landsat-7 ETM+ image data in Australian tropical savannas. In Proceedings of the IGARSS 2004—2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1559–1562. [Google Scholar]
- Paneque-Gálvez, J.; Mas, J.F.; Moré, G.; Cristóbal, J.; Orta-Martínez, M.; Luz, A.C.; Guèze, M.; Macía, M.J.; Reyes-García, V. Enhanced land use/cover classification of heterogeneous tropical landscapes using support vector machines and textural homogeneity. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 372–383. [Google Scholar] [CrossRef]
- Elhag, M. Evaluation of different soil salinity mapping using remote sensing techniques in arid ecosystems, Saudi Arabia. J. Sens. 2016, 2016, 7596175. [Google Scholar] [CrossRef]
- Alonso, M.C.; Malpica, J.A.; de Agirre, A.M. Consequences of the Hughes phenomenon on some classification techniques. In Proceedings of the ASPRS 2001 Annual Conference, Milwuakee, WI, USA, 1–5 May 2011; pp. 1–5. [Google Scholar]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Pal, M.; Foody, G.M. Feature selection for classification of hyperspectral data by SVM. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2297–2307. [Google Scholar] [CrossRef]
- Naimi, B.; Hamm, N.A.; Groen, T.A.; Skidmore, A.K.; Toxopeus, A.G. Where is positional uncertainty a problem for species distribution modelling? Ecography 2014, 37, 191–203. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Granitto, P.M.; Furlanello, C.; Biasioli, F.; Gasperi, F. Recursive feature elimination with random forest for PTR-MS analysis of agroindustrial products. Chemom. Intell. Lab. Syst. 2006, 83, 83–90. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Lawrence, R.L.; Moran, C.J. The AmericaView classification methods accuracy comparison project: A rigorous approach for model selection. Remote Sens. Environ. 2015, 170, 115–120. [Google Scholar] [CrossRef]
- Huang, C.; Davis, L.; Townshend, J. An assessment of support vector machines for land cover classification. Int. J. Remote. Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Shi, D.; Yang, X. An assessment of algorithmic parameters affecting image classification accuracy by random forests. Photogramm. Eng. Remote Sens. 2016, 82, 407–417. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Galiano, V.R.; Panday, P.; Neeti, N. An evaluation of bagging, boosting, and random forests for land-cover classification in Cape Cod, Massachusetts, USA. GISci. Remote Sens. 2012, 49, 623–643. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Wang, L.; Hu, L.; Gong, P. Comparison of classification algorithms and training sample sizes in urban land classification with Landsat thematic mapper imagery. Remote Sens. 2014, 6, 964–983. [Google Scholar] [CrossRef]
- Foody, G.; Pal, M.; Rocchini, D.; Garzon-Lopez, C.; Bastin, L. The sensitivity of mapping methods to reference data quality: Training supervised image classifications with imperfect reference data. ISPRS Int. J. Geo-Inf. 2016, 5, 199. [Google Scholar] [CrossRef]
- Maxwell, A.; Warner, T.; Strager, M.; Conley, J.; Sharp, A. Assessing machine-learning algorithms and image-and lidar-derived variables for GEOBIA classification of mining and mine reclamation. Int. J. Remote Sens. 2015, 36, 954–978. [Google Scholar] [CrossRef]
- Eisavi, V.; Homayouni, S.; Yazdi, A.M.; Alimohammadi, A. Land cover mapping based on random forest classification of multitemporal spectral and thermal images. Environ. Monit. Assess. 2015, 187, 291. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees, 1st ed.; Routledge: New York, NY, USA, 2017; p. 368. [Google Scholar]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, Y. Statistical learning theory and state of the art in SVM. In Proceedings of the Second IEEE International Conference on Cognitive Informatics, London, UK, 20 August 2003; pp. 55–59. [Google Scholar]
- Camps-Valls, G.; Bruzzone, L. Kernel Methods for Remote Sensing Data Analysis, 1st ed.; John Wiley & Sons: Chichester, UK, 2009; p. 434. [Google Scholar]
- Xie, Z.; Chen, Y.; Lu, D.; Li, G.; Chen, E. Classification of land cover, forest, and tree species classes with ZiYuan-3 multispectral and stereo data. Remote Sens. 2019, 11, 164. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P.M. An assessment of the effectiveness of decision tree methods for land cover classification. Remote Sens. Environ. 2003, 86, 554–565. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Morgan Kaufmann Publishers, Inc.: San Mateo, CA, USA, 2014. [Google Scholar]
- Bittencourt, H.R.; Clarke, R.T. Use of classification and regression trees (CART) to classify remotely-sensed digital images. In Proceedings of the IGARSS 2003—2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 6, pp. 3751–3753. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 29 October 2019).
- Bischof, H.; Schneider, W.; Pinz, A.J. Multispectral Classification of Landsat-Images Using Neural Networks. IEEE Trans. Geosci. Remote Sens. 1992, 30, 482–490. [Google Scholar] [CrossRef]
- Kanellopoulos, I.; Varfis, A.; Wilkinson, G.; Megier, J. Land-cover discrimination in SPOT HRV imagery using an artificial neural network—A 20-class experiment. Int. J. Remote. Sens. 1992, 13, 917–924. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2019, 105524. [Google Scholar] [CrossRef]
- Singh, B.K.; Verma, K.; Thoke, A. Investigations on impact of feature normalization techniques on classifier’s performance in breast tumor classification. Int. J. Comput. Appl. 2015, 116, 11–15. [Google Scholar]
- Wainer, J.; Cawley, G. Nested cross-validation when selecting classifiers is overzealous for most practical applications. arXiv 2018, arXiv:1809.09446. [Google Scholar]
- Cawley, G.C.; Talbot, N.L. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Hird, J.N.; DeLancey, E.R.; McDermid, G.J.; Kariyeva, J. Google Earth Engine, open-access satellite data, and machine learning in support of large-area probabilistic wetland mapping. Remote Sens. 2017, 9, 1315. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 3rd ed.; CRC Press: Boca Ranton, FL, USA, 2019; p. 346. [Google Scholar]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- McNemar, Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157. [Google Scholar] [CrossRef]
- Roggo, Y.; Duponchel, L.; Huvenne, J.P. Comparison of supervised pattern recognition methods with McNemar’s statistical test: Application to qualitative analysis of sugar beet by near-infrared spectroscopy. Anal. Chim. Acta 2003, 477, 187–200. [Google Scholar] [CrossRef]
- Herold, A. Remote sensing and spatial metrics-a new approach for the description of structures and changes in urban areas. In Proceedings of the IGARSS 2001—Scanning the Present and Resolving the Future, IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, NSW, Australia, 9–13 July 2001; Volume 1, pp. 366–368. [Google Scholar]
- Mcgarigal, K.; Marks, B.J. Spatial Pattern Analysis Program for Quantifying Landscape Structure; Gen. Tech. Rep. PNW-GTR-351; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Gaithersburg, MD, USA, 1995; pp. 1–122. [Google Scholar]
- Evans, J.S.; Ram, K. Package ‘spatialEco’. 2019. Available online: https://github.com/jeffreyevans/spatialEco (accessed on 27 October 2019).
- Kukunda, C.B.; Duque-Lazo, J.; González-Ferreiro, E.; Thaden, H.; Kleinn, C. Ensemble classification of individual Pinus crowns from multispectral satellite imagery and airborne LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 12–23. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Rivas, M. Evaluation of different machine learning methods for land cover mapping of a Mediterranean area using multi-seasonal Landsat images and Digital Terrain Models. Int. J. Digit. Earth 2014, 7, 492–509. [Google Scholar] [CrossRef]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree species classification with random forest using very high spatial resolution 8-band WorldView-2 satellite data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Ghosh, A.; Joshi, P.K. A comparison of selected classification algorithms for mapping bamboo patches in lower Gangetic plains using very high resolution WorldView 2 imagery. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 298–311. [Google Scholar] [CrossRef]
- Schulp, C.J.; Burkhard, B.; Maes, J.; Van Vliet, J.; Verburg, P.H. Uncertainties in ecosystem service maps: A comparison on the European scale. PLoS ONE 2014, 9, e0109643. [Google Scholar] [CrossRef]
- Ferchichi, A.; Boulila, W.; Farah, I.R. Reducing uncertainties in land cover change models using sensitivity analysis. Knowl. Inf. Syst. 2018, 55, 719–740. [Google Scholar] [CrossRef]
- Janssen, L.L.; Vanderwel, F.J. Accuracy assessment of satellite derived land-cover data: A review. Photogramm. Eng. Remote Sens. 1994, 60, 6448244. [Google Scholar]
- Foody, G.M. Thematic map comparison. Photogramm. Eng. Remote Sens. 2004, 70, 627–633. [Google Scholar] [CrossRef]
- Momeni, R.; Aplin, P.; Boyd, D.S. Mapping complex urban land cover from spaceborne imagery: The influence of spatial resolution, spectral band set and classification approach. Remote Sens. 2016, 8, 88. [Google Scholar] [CrossRef]
- Grant, C.; Scholes, M. The importance of nutrient hot-spots in the conservation and management of large wild mammalian herbivores in semi-arid savannas. Biol. Conserv. 2006, 130, 426–437. [Google Scholar] [CrossRef]
- Smit, I.P. Resources driving landscape-scale distribution patterns of grazers in an African savanna. Ecography 2011, 34, 67–74. [Google Scholar] [CrossRef]
- Redfern, J.V.; Grant, R.; Biggs, H.; Getz, W.M. Surface-water constraints on herbivore foraging in the Kruger National Park, South Africa. Ecology 2003, 84, 2092–2107. [Google Scholar] [CrossRef]
- Berry, H.; Louw, G. Nutritional measurements in a population of free-ranging wildebeest in the Etosha National Park. Madoqua 1982, 13, 101–125. [Google Scholar]
- Burkepile, D.E.; Burns, C.E.; Tambling, C.J.; Amendola, E.; Buis, G.M.; Govender, N.; Nelson, V.; Thompson, D.I.; Zinn, A.D.; Smith, M.D. Habitat selection by large herbivores in a southern African savanna: The relative roles of bottom-up and top-down forces. Ecosphere 2013, 4, 1–19. [Google Scholar] [CrossRef]




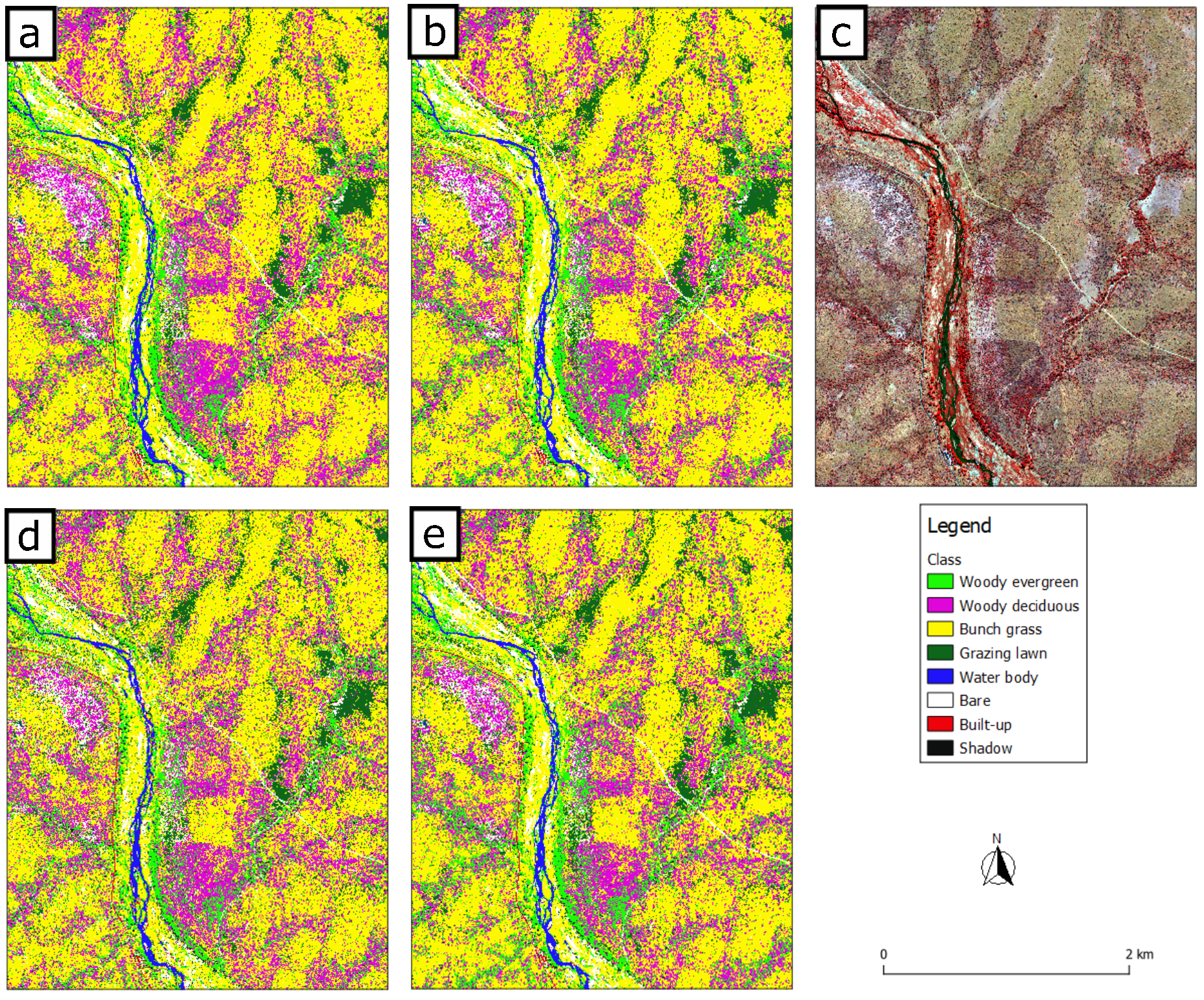
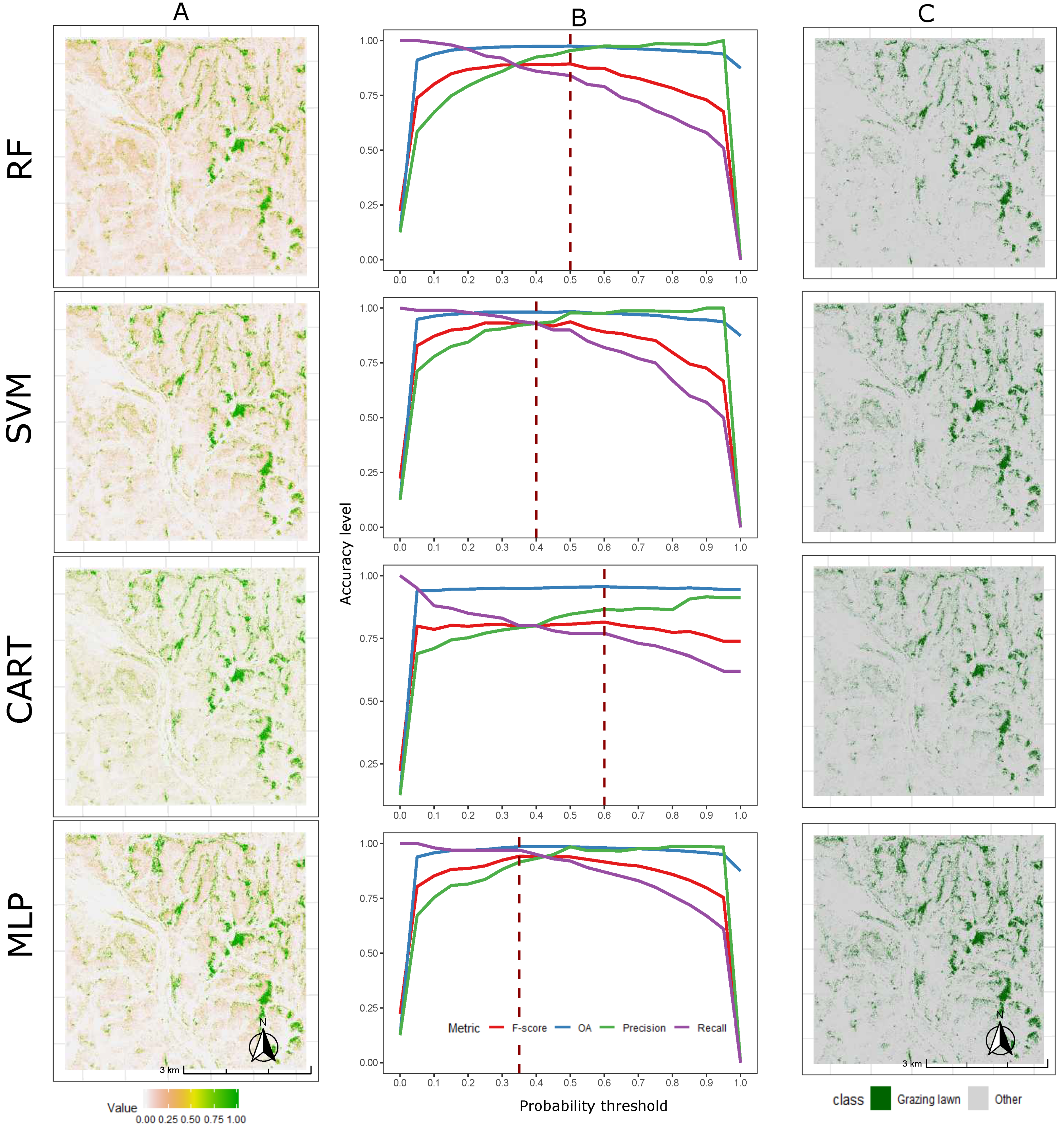


| Land Cover | Reference Samples | |||
|---|---|---|---|---|
| ID | Name | Description | Model Training | Map Validation |
| 1 | Woody evergreen | Woody vegetation components that are adapted to retain their leaves all year round. Classified based on dry season field observations. | 863 (3.94) | 100/80 |
| 2 | Woody deciduous | Woody vegetation components that are adapted to retain their leaves in the wet season and shed them in the dry season. Classified based on dry season field observations. | 1047 (3.26) | 100/65 |
| 3 | Bunch grass | Tall grass patches with height >20 cm, and often occur as dense patches with upright growth form. | 680 (10.12) | 100/114 |
| 4 | Grazing lawn | Short grass patches with height <20 cm, and often occur in sparse distribution with stoloniferous growth form. | 465 (7.99) | 100/103 |
| 5 | Water body | Water bodies occurring within the landscapes including rivers, streams and reservoirs. | 58 (3.18) | 100/38 |
| 6 | Bare | Bare surfaces occurring as patches of exposed soil and includes dusty trails and rocky outcrops. | 464 (4.29) | 100/74 |
| 7 | Built-up | Built artificial structures within the landscape as well as asphalt and concrete coated surfaces such as roads and bridges. | 37 (0.75) | 100/64 |
| 8 | Shadow | Shadows of trees and other tall structures falling on adjacent surfaces which results in very dark or low brightness values. | 193 (0.63) | 100/88 |
| Dataset | Description | Temporal Coverage | Source |
|---|---|---|---|
| WorldView-3 imagery | Multi-spectral 8-band satellite imagery with 1.24 m spatial resolution. Bands include: Coastal (C: 400–450 nm), Blue (B: 450–510 nm), Green (G: 510–580 nm), Yellow (Y: 585–625 nm), Red (R: 630–690 nm), Red Edge (RE: 705–745 nm), Near Infrared 1 (NIR1: 770–895 nm), Near Infrared 2 (NIR2: 860–1040 nm). | July 2019 | European Space Imaging |
| Reference data | Input image pixels labeled according to land cover classification nomenclature. Pixels were extracted from reference polygon and point features. | June 2019–July 2019 | Georeferenced field survey locations; Field photos; and Google Earth and VHR scenes |
| Auxiliary data | OpenStreetMaps watercourses data sourced as line vector layer for streams and rivers, and polygon vector layer for reservoirs. | November 2019 | www.openstreetmap.org |
| Data (abbreviation) | Description |
|---|---|
| Spectral features from individual bands (B): B_C, B_B, B_G, B_Y, B_R, B_RE, B_NIR1, B_NIR2 | Coastal, Blue, Green, Yellow, Red, Red Edge, Near Infrared-1, Near Infrared-2 |
| Spectral features from vegetation (V), moisture (M) and soil (S) indices: V_NDVI, V_TNDVI, V_RVI, V_SAVI, V_TSAVI, V_MSAVI, V_MSAVI2, V_GEMI, V_IPVI, V_LAI, M_NDWI, M_NDWI2, M_MNDWI, S_BI2, S_BI, S_CI, S_RI, S_NDSI, S_SI1, S_SI2, S_SI3, S_SI4, S_SI5, S_SI6, S_SI7, S_SI8, S_SI9 | Normalized Difference Vegetation Index, Transformed Normalized Vegetation Index, Ratio Vegetation Index, Soil Adjusted Vegetation Index, Transformed Soil Adjusted Vegetation Index, Modified Soil Adjusted Vegetation Index, Modified Soil Adjusted Vegetation Index-2, Global Environment Monitoring Index, Infrared Percentage Vegetation Index, Leaf Area Index, Normalized Difference Water Index, Normalized Difference Water Index-2, Modified Normalized Difference Water Index, Brightness Index-2, Brightness Index, Color Index, Redness Index [62], Normalized Difference Salinity Index, Salinity Index-1, Salinity Index-2, Salinity Index-3, Salinity Index-4, Salinity Index-5, Salinity Index-6, Salinity Index-7, Salinity Index-8, Salinity Index-9 [65] |
| Haralick texture features (T): T_Ener, T_Ent, T_Corr, T_IDM, T_Iner, T_CS, T_CP, T_HCorr, T_Mean, T_Var, T_Diss, T_SAvrg, T_SVar, T_SEnt, T_Dent, T_DVar, T_IC1, T_IC2 | Energy, Entropy, Correlation, Inverse Distance Moment, Inertia, Cluster shade, Cluster prominence, Haralick correlation, Mean, Variance, Dissimilarity, Sum average, Sum variance, Sum entropy, Difference of Entropies, Difference of variances, Information correlation-1, Information correlation-2 [62] |
| Model | Accuracy Metric | |
|---|---|---|
| F-Score | Overall Accuracy | |
| RF | ||
| SVM | ||
| CART | ||
| MLP | ||
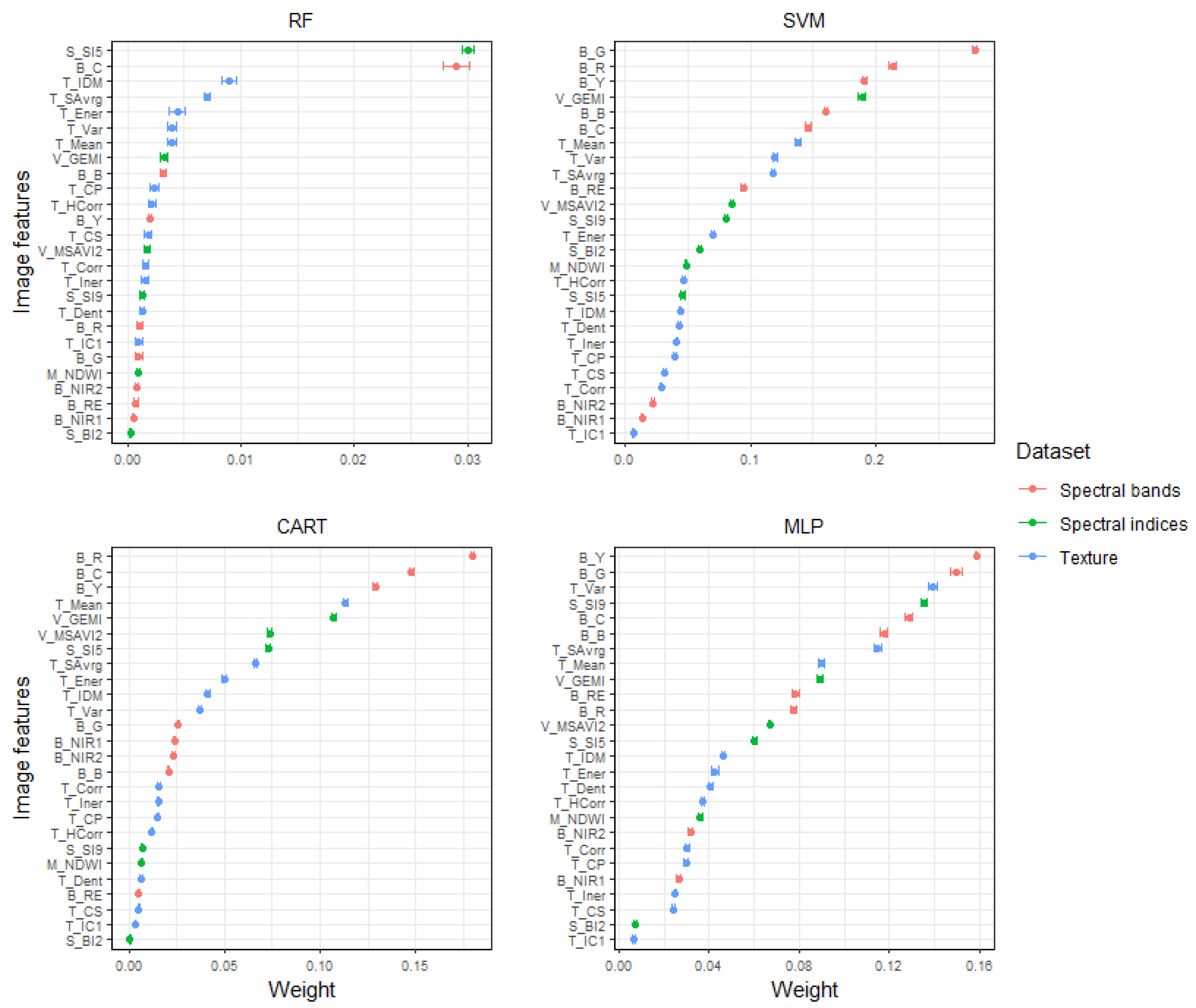
| Dataset | Image Feature | Model | |||
|---|---|---|---|---|---|
| RF | SVM | CART | MLP | ||
| Spectral band | B_C | ⊠ | ⊠ | ⊠ | |
| B_B | ⊠ | ||||
| B_G | ⊠ | ⊠ | |||
| B_Y | ⊠ | ⊠ | ⊠ | ⊠ | |
| B_R | ⊠ | ⊠ | |||
| B_RE | |||||
| B_NIR1 | |||||
| B_NIR2 | |||||
| Spectral index | V_GEMI | ⊠ | ⊠ | ⊠ | ⊠ |
| V_MSAVI2 | ⊠ | ⊠ | ⊠ | ⊠ | |
| M_NDWI | |||||
| S_SI5 | ⊠ | ⊠ | |||
| S_SI9 | ⊠ | ⊠ | |||
| S_BI2 | |||||
| Texture | T_Ener | ⊠ | ⊠ | ||
| T_Corr | |||||
| T_IDM | ⊠ | ||||
| T_Iner | |||||
| T_CS | |||||
| T_CP | |||||
| T_HCorr | |||||
| T_Mean | ⊠ | ⊠ | ⊠ | ||
| T_Var | ⊠ | ⊠ | |||
| T_SAvrg | ⊠ | ⊠ | ⊠ | ⊠ | |
| T_Dent | |||||
| T_IC1 | |||||
| Landscape | Accuracy Metric | Model Score | |||
|---|---|---|---|---|---|
| RF | SVM | CART | MLP | ||
| Lower Sabie | Precision | 0.95 | 0.93 | 0.87 | 0.92 |
| Recall | 0.84 | 0.93 | 0.77 | 0.97 | |
| F-score | 0.89 | 0.93 | 0.81 | 0.94 | |
| Satara | Precision | 0.88 | 0.87 | 0.76 | 0.85 |
| Recall | 0.87 | 0.90 | 0.76 | 0.85 | |
| F-score | 0.87 | 0.89 | 0.76 | 0.85 | |
| Landscape | Area Estimate (km2) | |||
|---|---|---|---|---|
| RF | SVM | CART | MLP | |
| Lower Sabie | 2.46 | |||
| Satara | ||||
| Lower Sabie | Satara | ||
|---|---|---|---|
| Model Pair | -test | Model Pair | -test |
| CART v MLP | 14.667(0.000) | CART v MLP | 5.891(0.015) |
| CART v RF | 10.316(0.001) | CART v RF | 13.395(0.000) |
| CART v SVM | 16.000(0.000) | CART v SVM | 11.574(0.000) |
| MLP v RF | 2.450(0.117) | MLP v RF | 1.250(0.264) |
| MLP v SVM | 0.100(0.752) | MLP v SVM | 1.565(0.211) |
| RF v SVM | 2.083(0.149) | RF v SVM | 0.000(1.000) |
| Landscape Metric | Lower Sabie | Satara | ||
|---|---|---|---|---|
| r | r2 | r | r2 | |
| PL | −0.55 | 0.30 * | −0.84 | 0.70 *** |
| MPA | −0.62 | 0.39 ** | −0.68 | 0.46 ** |
| CI | −0.65 | 0.42 ** | −0.87 | 0.75 *** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awuah, K.T.; Aplin, P.; Marston, C.G.; Powell, I.; Smit, I.P.J. Probabilistic Mapping and Spatial Pattern Analysis of Grazing Lawns in Southern African Savannahs Using WorldView-3 Imagery and Machine Learning Techniques. Remote Sens. 2020, 12, 3357. https://doi.org/10.3390/rs12203357
Awuah KT, Aplin P, Marston CG, Powell I, Smit IPJ. Probabilistic Mapping and Spatial Pattern Analysis of Grazing Lawns in Southern African Savannahs Using WorldView-3 Imagery and Machine Learning Techniques. Remote Sensing. 2020; 12(20):3357. https://doi.org/10.3390/rs12203357
Chicago/Turabian StyleAwuah, Kwame T., Paul Aplin, Christopher G. Marston, Ian Powell, and Izak P. J. Smit. 2020. "Probabilistic Mapping and Spatial Pattern Analysis of Grazing Lawns in Southern African Savannahs Using WorldView-3 Imagery and Machine Learning Techniques" Remote Sensing 12, no. 20: 3357. https://doi.org/10.3390/rs12203357
APA StyleAwuah, K. T., Aplin, P., Marston, C. G., Powell, I., & Smit, I. P. J. (2020). Probabilistic Mapping and Spatial Pattern Analysis of Grazing Lawns in Southern African Savannahs Using WorldView-3 Imagery and Machine Learning Techniques. Remote Sensing, 12(20), 3357. https://doi.org/10.3390/rs12203357






