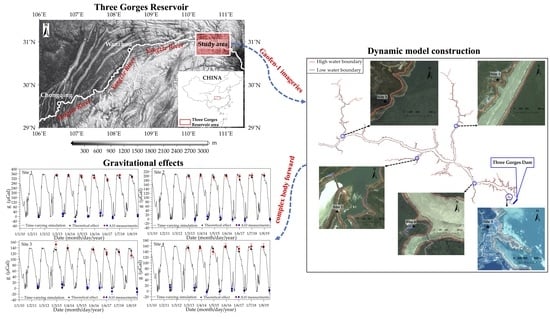
Simulation of the Dynamic Water Storage and Its Gravitational Effect in the Head Region of Three Gorges Reservoir Using Imageries of Gaofen-1
Abstract
1. Introduction
2. Data and Methods
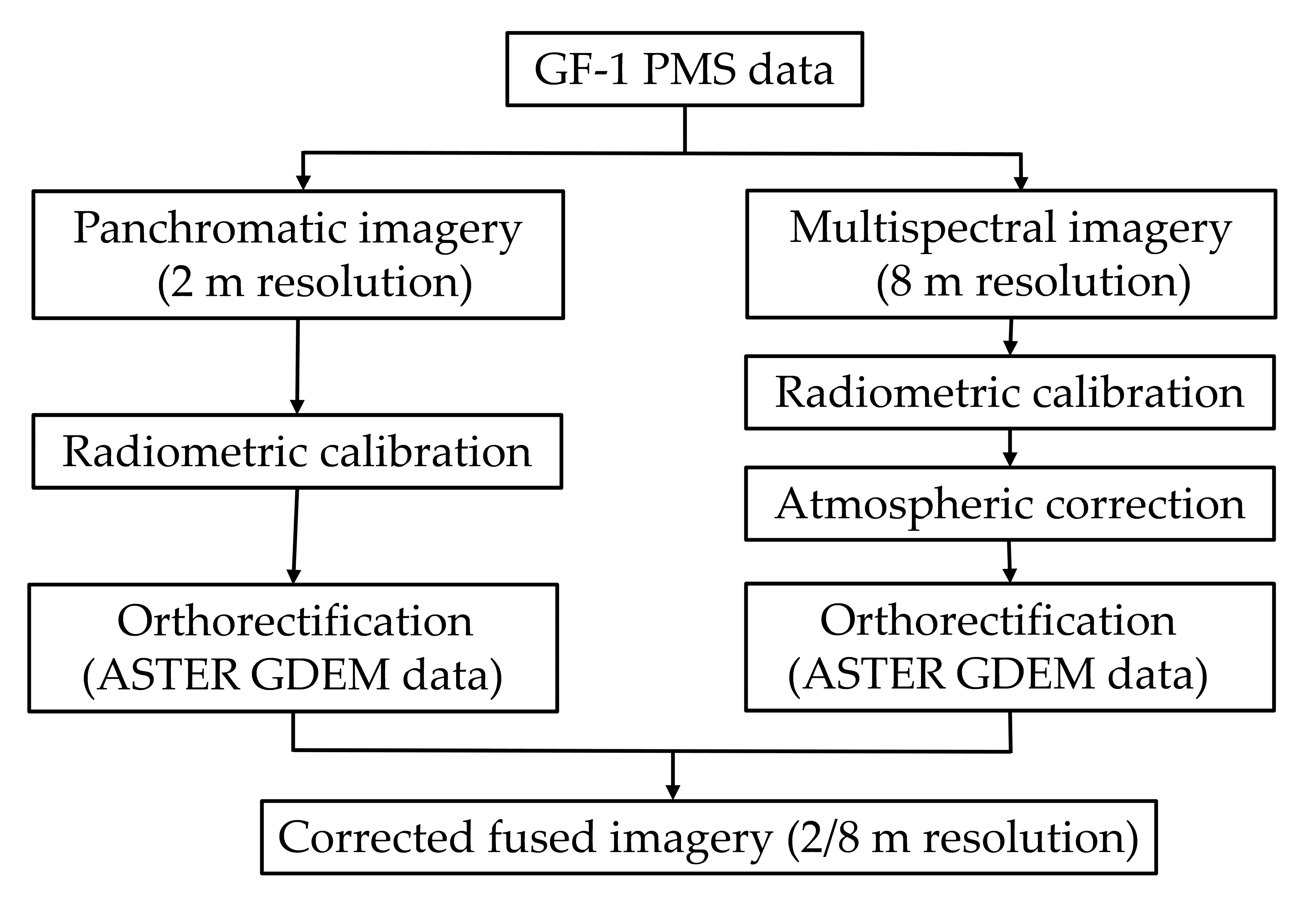
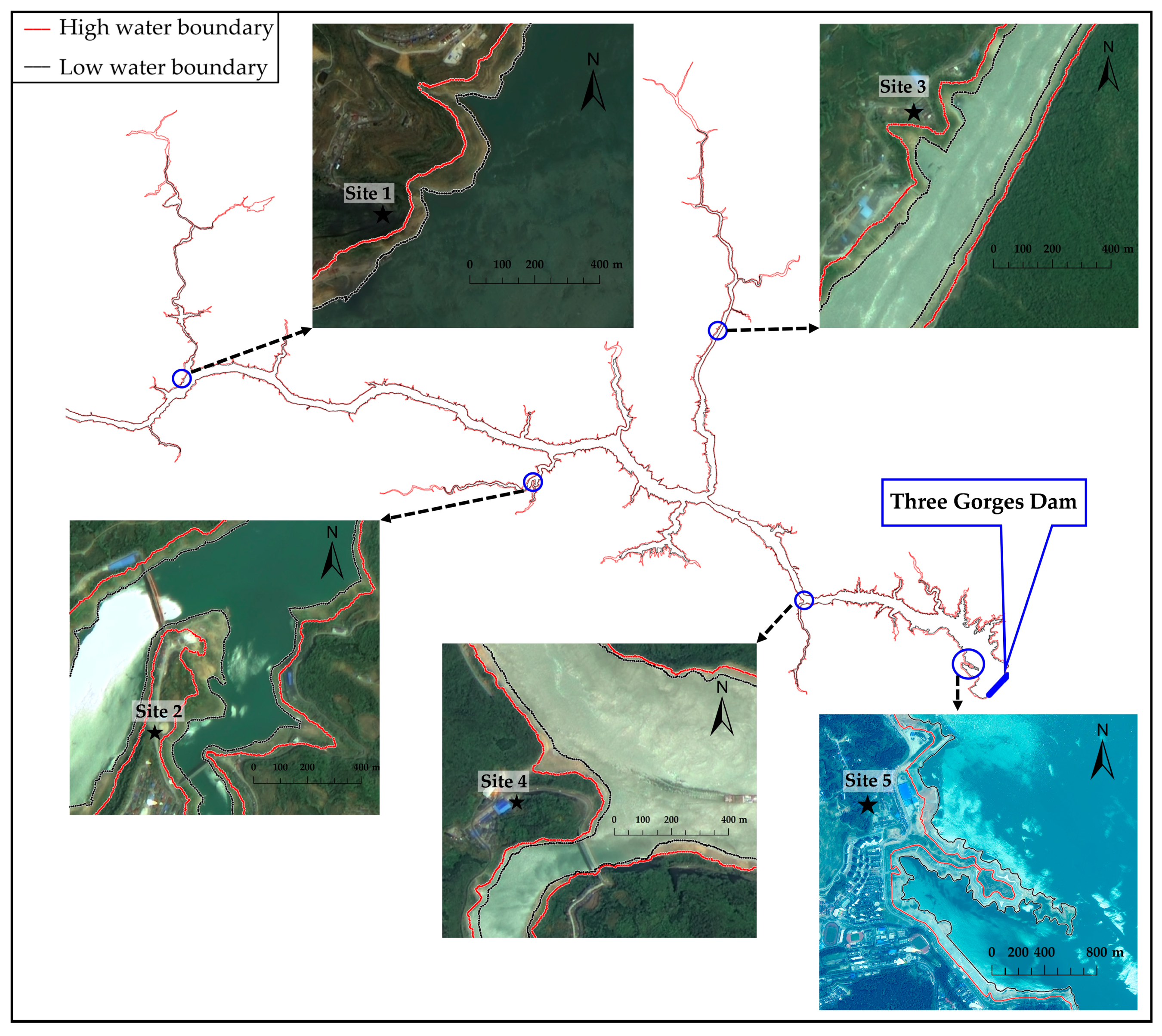
2.1. GF-1 Imageries and Data Preprocessing
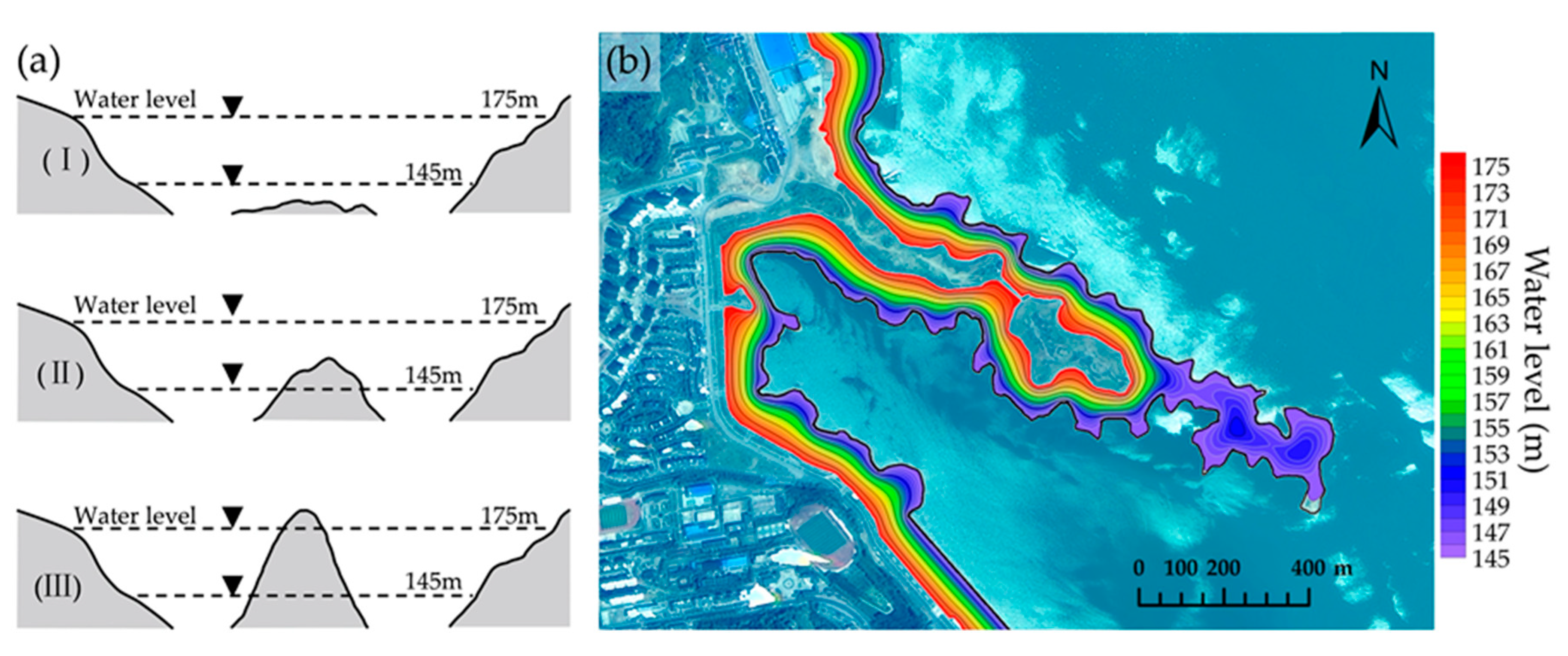
2.2. Extraction of Water Boundaries
2.3. Dynamic Model Construction
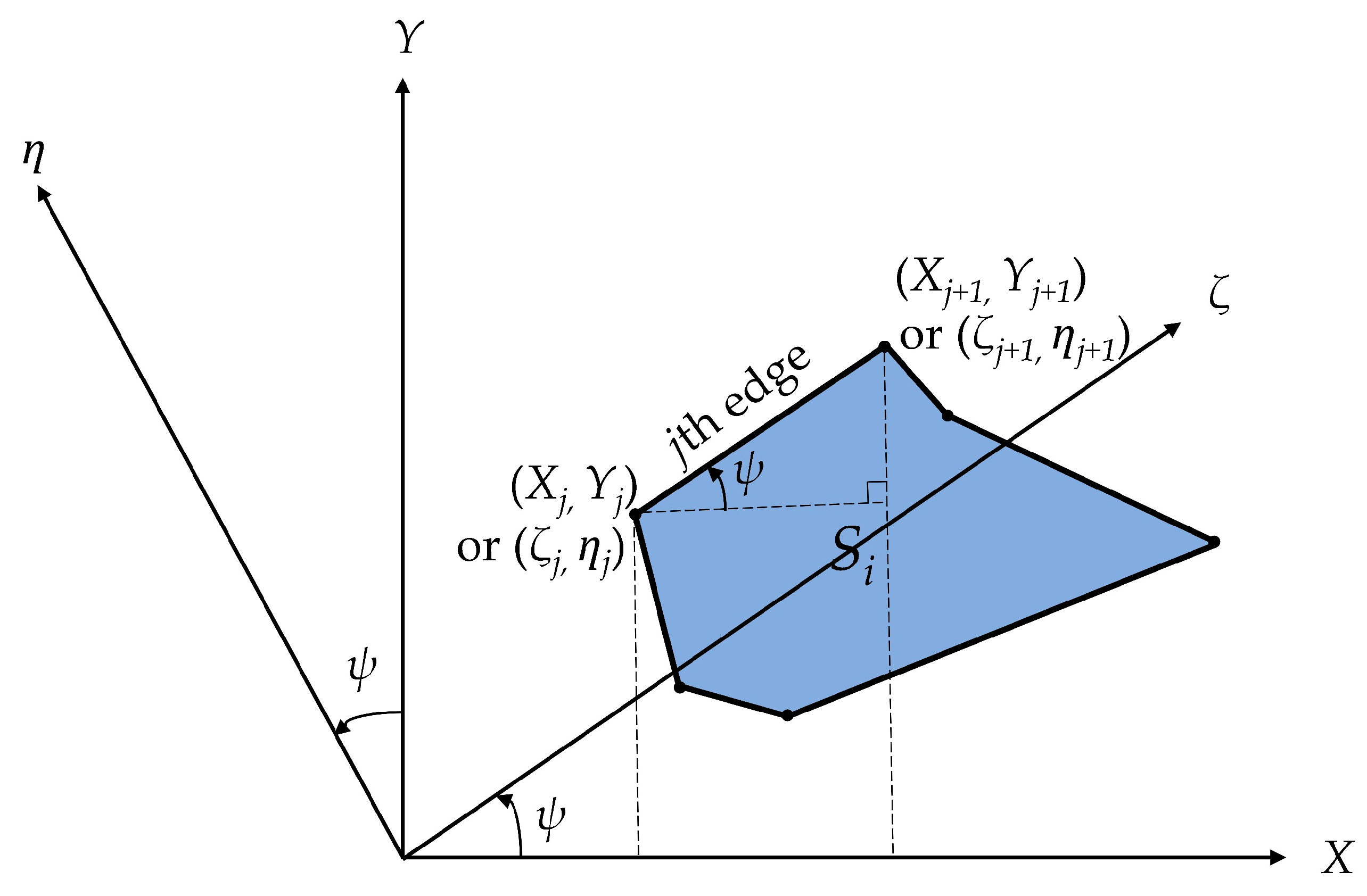
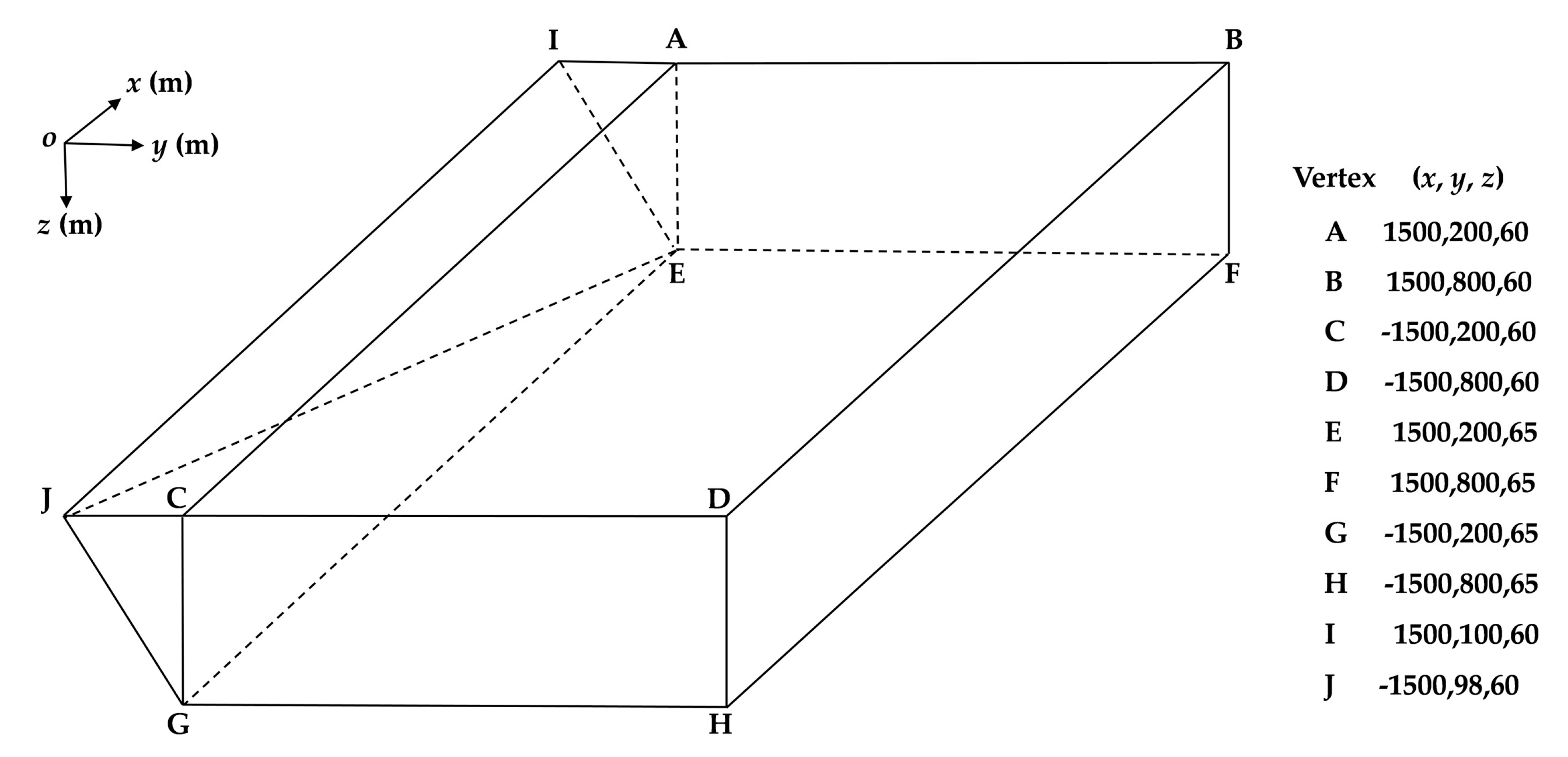
2.4. Principle of Gravitational Effect Computation
3. Results
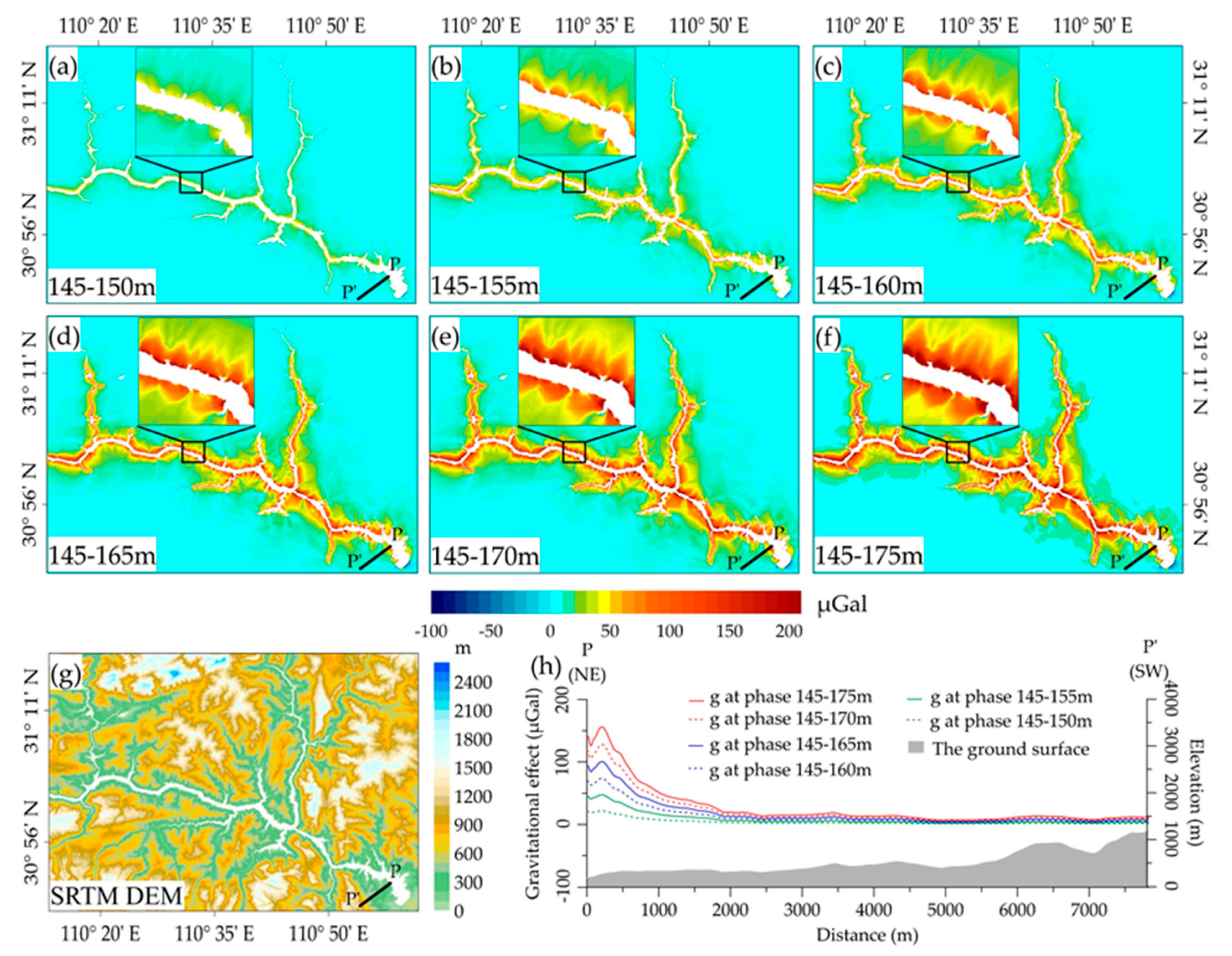
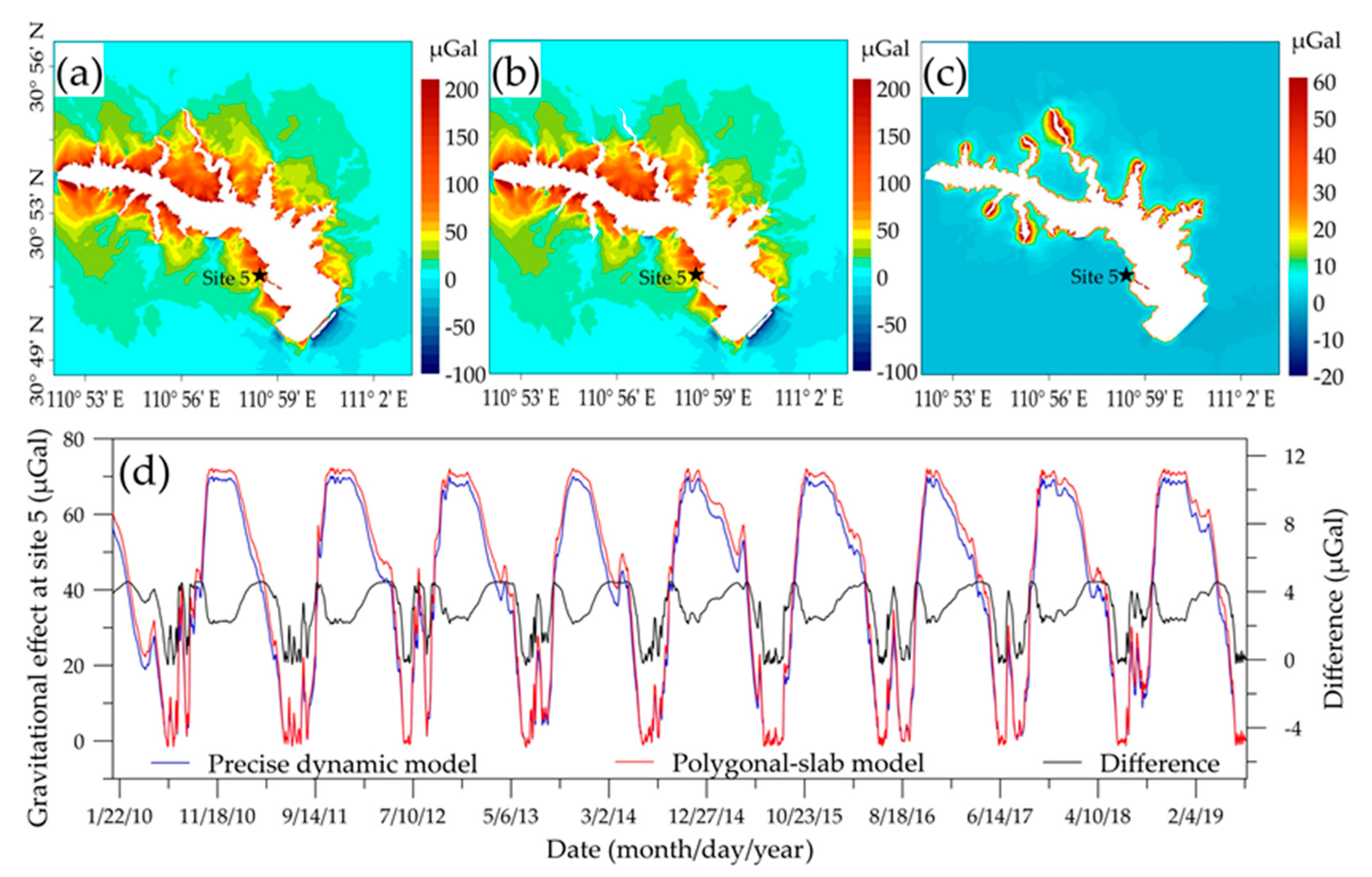
3.1. Gravitational Effects of Dynamic Water Storage in Head Region of TGR
3.2. Comparison with the Measurement of Absolute Gravimeter
4. Discussion
4.1. The Capacity of the Dynamic Water Storage Model
4.2. Simulation Accuracy
4.3. Other Influences
5. Conclusions
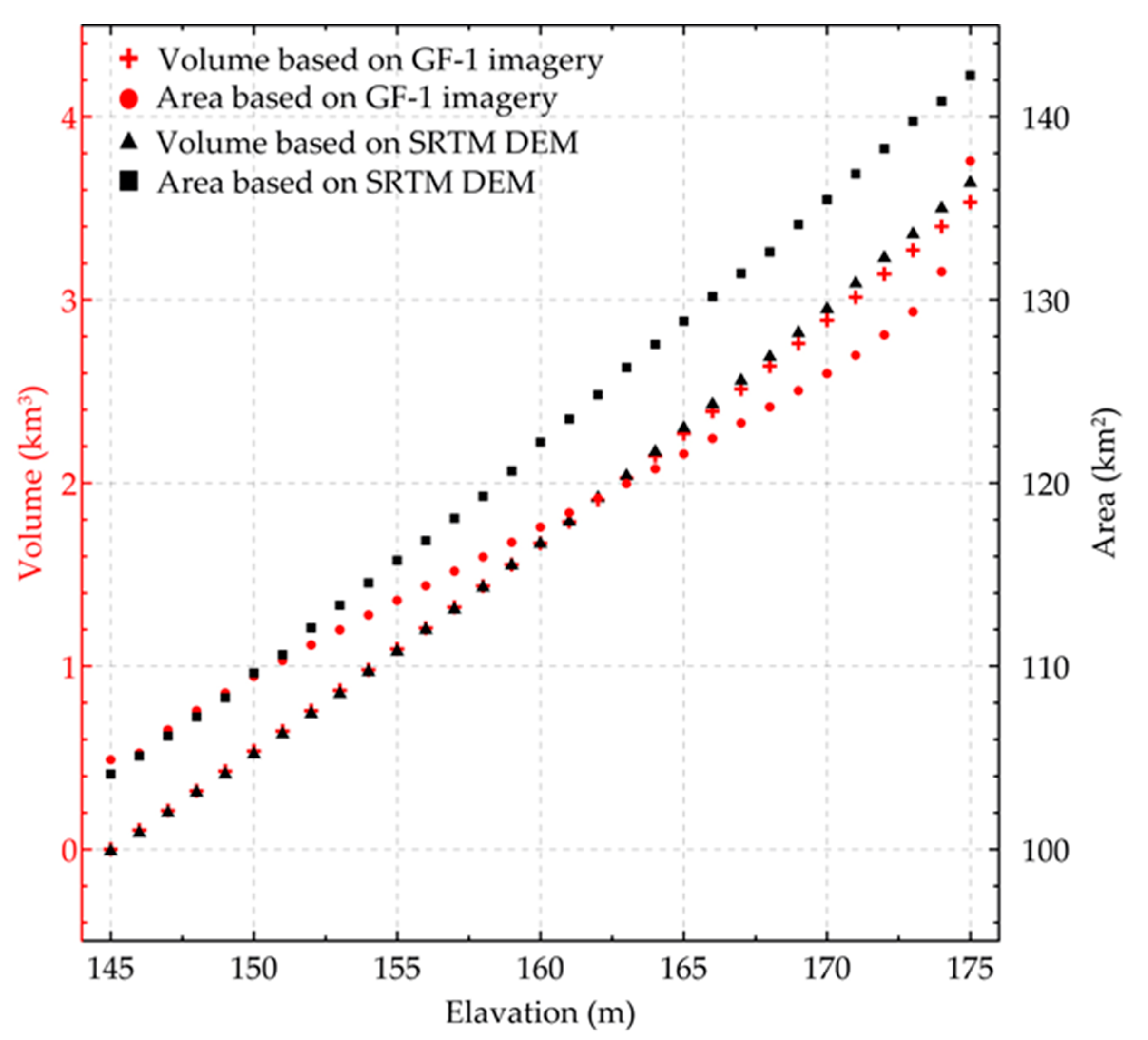
- In front of the dam (Zigui area), the annual water boundary change can be up to 100 m in horizontal direction. In the tributary area of the TGR, the changes of the water boundary are more obvious, especially in the north of Badong area. The dynamic water storage model constructed in this study consists of water boundaries (31 in total) at different impoundment periods, i.e., from 145 m to 175 m. The resolution of the model is approximately 8 m in horizontal direction and approximately 1 m in vertical direction, which is an important way to describe the local dynamic characteristics in the impounding and releasing water process.
- The high-precision forward modeling method of gravitational effect can avoid the error caused by model approximation. The gravitational effect of TGR water storage is obvious within 1000 m of the reservoir bank, and the maximum gravity change caused by the 30-m water level change (from 145 m to 175 m) can reach nearly 600 μGal. The ground multiyear gravity observation data from A10 absolute gravimeters verified the simulations. Our results confirm that the gravitational effects change caused by TGR impoundment is the main contribution of the gravity field changes in the study area. The differences between in situ observations and simulation results can help in further tracking of the effects of geological disasters, such as earthquakes and landslides.
- The comparison results show that the dynamic water storage model has more advantages in identifying changes in water storage in local areas and is statistically more accurate in obtaining TGR capacity information when compared to the previous model. However, the potential users should consider the spatial position and coordinate accuracy of the calculated point when applying the dynamic water storage model.
- The accuracy of the dynamic water storage model is related to factors such as satellite imagery preprocessing (e.g., data calibration), imagery quality, cloud cover, and extraction method for water boundaries. In addition, manual visual interpretation can solve the influence of interference factors (e.g., river vessels, mountain shadows, water pollutants, etc.) With the continuous accumulation and update of the remote sensing data and the development of water boundary extraction technology, it can be expected that the accuracy of the water storage model will be improved in the future.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wang, J.; Sheng, Y.; Gleason, C.J.; Wada, Y. Downstream Yangtze River levels impacted by Three Gorges Dam. Environ. Res. Lett. 2013, 8, 044012. [Google Scholar] [CrossRef]
- Long, D.; Yang, Y.; Wada, Y.; Hong, Y.; Liang, W.; Yaning, C.; Yong, B.; Hou, A.; Wei, J.; Chen, L. Deriving scaling factors using a global hydrological model to restore GRACE total water storage changes for China’s Yangtze River Basin. Remote Sens. Environ. 2015, 168, 177–193. [Google Scholar] [CrossRef]
- Boy, J.P.; Chao, B.F. Time-variable gravity signal during the water impoundment of China’s Three-Gorges Reservoir. Geophys. Res. Lett. 2002, 29, 2200. [Google Scholar] [CrossRef]
- Wang, X.W.; Linage, C.; Famiglietti, J.; Zender, C.S. Gravity Recovery and Climate Experiment (GRACE) detection of water storage changes in the Three Gorges Reservoir of China and comparison with in situ measurements. Water Resour. Res. 2011, 47, W12502. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, C.Y.; Liang, S.M.; Yang, Q.; Hu, M.Z.; Feng, W. Monitoring of the temporal and spatial variation of groundwater storage in the Three Gorges area based on the CORS network. J. Appl. Geophys. 2017, 146, 160–166. [Google Scholar] [CrossRef]
- Li, F.P.; Wang, Z.T.; Chao, N.F.; Song, Q.Y. Assessing the Influence of the Three Gorges Dam on Hydrological Drought Using GRACE Data. Water. 2018, 10, 669. [Google Scholar] [CrossRef]
- Tang, H.M.; Wasowski, J.; Juang, C.H. Geohazards in the three Gorges Reservoir Area, China–Lessons learned from decades of research. Eng. Geol. 2019, 261, 105267. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, C.Y.; Hu, M.Z.; Yang, Q.; Liang, S.M.; Kang, S.J. Monitoring and analysis of geological hazards in Three Gorges area based on load impact change. Nat. Hazards 2019, 97, 611–622. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, M.; Sun, G.; Gong, J. Analysis of the water volume, length, total area and inundated area of the Three Gorges Reservoir, China using the SRTM DEM data. Int. J. Remote Sens. 2005, 26, 4001–4012. [Google Scholar] [CrossRef]
- Wang, X.W.; Chen, Y.; Song, L.C.; Chen, X.Y.; Xie, H.J.; Liu, L. Analysis of lengths, water areas and volumes of the Three Gorges Reservoir at different water levels using Landsat images and SRTM DEM data. Quat. Int. 2013, 304, 115–125. [Google Scholar] [CrossRef]
- Wang, L.S.; Chen, C.; Zou, R.; Du, J.S. Surface gravity and deformation effects of water storage changes in China’s Three Gorges Reservoir constrained by modeled results and in situ measurements. J. Appl. Geophys. 2014, 108, 25–34. [Google Scholar] [CrossRef]
- Wang, L.S.; Chen, C.; Ma, X.; Du, J.S. A Water Storage Loading Model by SRTM-DEM Data and Surface Response Simulation of Gravity and Deformation in the Three Gorges Reservoir of China. Acta Geod. Cartogr. Sin. 2016, 45, 1148–1156, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Yao, Y.S.; Wang, Q.L.; Liao, W.L.; Zhang, L.F.; Chen, J.H.; Li, J.G.; Yuan, L.; Zhao, Y.N. Influences of the Three Gorges Project on seismic activities in the reservoir area. Sci. Bull. 2017, 62, 1089–1098. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, D.X.; Liu, Y.W.; Che, Y.T.; Qin, D.J. Impact of impoundment on groundwater seepage in the Three Gorges Dam in China based on CFCs and stable isotopes. Environ. Earth Sci. 2014, 72, 4491–4500. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Yao, T.D.; Chen, W.F.; Zheng, G.X.; Shum, C.K.; Yang, K.; Piao, S.L.; Sheng, Y.W.; Yi, S.; Li, J.L.; et al. Regional differences of lake evolution across China during 1960s–2015 and its natural and anthropogenic causes. Remote Sens. Environ. 2019, 221, 386–404. [Google Scholar] [CrossRef]
- Wang, M.L.; Du, L.J.; Ke, Y.H.; Huang, M.Y.; Zhang, J.; Zhao, Y.; Li, X.J.; Gong, H.L. Impact of Climate Variabilities and Human Activities on Surface Water Extents in Reservoirs of Yong ding River Basin, China, from 1985 to 2016 Based on Landsat Observations and Time Series Analysis. Remote Sens. 2019, 11, 560. [Google Scholar] [CrossRef]
- Entwistle, N.; Heritage, G.; Milan, D. Recent remote sensing applications for hydro and morpho dynamic monitoring and modelling. Earth Surf. Process. Landf. 2018, 43, 2283–2291. [Google Scholar] [CrossRef]
- Wang, C.; Jia, M.M.; Chen, N.C.; Wang, W. Long-Term Surface Water Dynamics Analysis Based on Landsat Imagery and the Google Earth Engine Platform: A Case Study in the Middle Yangtze River Basin. Remote Sens. 2018, 10, 1635. [Google Scholar] [CrossRef]
- Rokni, K.; Ahmad, A.; Selamat, A.; Hazini, S. Water Feature Extraction and Change Detection Using Multitemporal Landsat Imagery. Remote Sens. 2014, 6, 4173–4189. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Zheng, G.X.; Gao, Y.; Xiang, Y.; Lei, Y.B.; Li, J.L. Automated Water Classification in the Tibetan Plateau Using Chinese GF-1 WFV Data. Photogramm. Eng. Remote Sens. 2017, 83, 509–519. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; He, H.X.; Yu, C.H.; Zhang, W.; Li, L.Y.; Meng, L.K. Using the modified two-mode method to identify surface water in Gaofen-1 images. J. Appl. Remote Sens. 2018, 13, 022003. [Google Scholar] [CrossRef]
- Du, W.Y.; Chen, N.C.; Liu, D.N. Automatic Balloon Snake Method for Topology Adaptive Water Boundary Extraction: Using GF-1 Satellite Imagery as an Example. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 5381–5394. [Google Scholar] [CrossRef]
- Du, W.Y.; Chen, N.C.; Liu, D.N. Topology adaptive water boundary extraction based on a modified balloon snake: Using GF-1 satellite images as an example. Remote Sens. 2017, 9, 140. [Google Scholar] [CrossRef]
- Zhu, S.Y.; Wan, W.; Xie, H.J.; Liu, B.J.; Li, H.; Hong, Y. An efficient and effective approach for georeferencing AVHRR and GaoFen-1 imageries using inland water bodies. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 2491–2500. [Google Scholar] [CrossRef]
- David, C.; Caroline, D.L.; Jacques, H.; Boy, J.P.; Famiglietti, J. A comparison of the gravity field over Central Europe from superconducting gravimeters, GRACE and global hydrological models, using EOF analysis. Geophys. J. Int. 2012, 189, 877–897. [Google Scholar] [CrossRef]
- Crossley, D.; Hinderer, J.; Riccardi, U. The measurement of surface gravity. Rep. Prog. Phys. 2013, 76, 046101. [Google Scholar] [CrossRef]
- Wang, H.; Hsu, H.T.; Zhu, Y.Z. Prediction of surface horizontal displacements, and gravity and tilt changes caused by filling the Three Gorges Reservoir. J. Geod. 2002, 76, 105–114. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- McFeeters, S.K. Using the normalized difference water index (NDWI) within a geographic information system to detect swimming pools for mosquito abatement: A practical approach. Remote Sens. 2013, 5, 3544–3561. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Rroud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Ma, R.F.; Duan, H.T.; Hu, C.M.; Feng, X.Z.; Li, A.N.; Ju, W.M.; Jiang, J.H.; Yang, G.S. A half-century of changes in China’s lakes: Global warming or human influence? Geophys. Res. Lett. 2010, 37, L24106. [Google Scholar] [CrossRef]
- Ma, R.F.; Yang, G.S.; Duan, H.T.; Jiang, J.H.; Wang, S.M.; Feng, X.Z.; Li, A.N.; Kong, F.X.; Xue, B.; Wu, J.L.; et al. China’s lakes at present: Number, area and spatial distribution. Sci. China Earth Sci. 2011, 54, 283–289. [Google Scholar] [CrossRef]
- Wan, W.; Long, D.; Hong, Y.; Ma, Y.Z.; Yuan, Y.; Xiao, P.F.; Duan, H.T.; Han, Z.Y.; Gu, X.F. A lake data set for the Tibetan Plateau from the 1960s, 2005, and 2014. Sci. Data 2016, 3, 160039. [Google Scholar] [CrossRef]
- Barnett, C.T. Theoretical modeling of the magnetic and gravitational fields of an arbitrary shaped three-dimensional body. Geophysics 1976, 41, 1353–1364. [Google Scholar] [CrossRef]
- Okabe, M. Analytical expressions for gravity anomalies due to homogeneous polyhedral bodies and translations into magnetic anomalies. Geophysics 1979, 44, 730–741. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |




| Sensor | Band No. | Spectral Range (μm) | Spatial Resolution (m) | Swath Width (km) | Repeat Cycle (Days) | Regression Cycle (Days) |
|---|---|---|---|---|---|---|
| Panchromatic camera | 0.45–0.89 | 2 | 60 (2 cameras combined) | 3–5 | 41 | |
| Multispectral camera | B1 | 0.45–0.52 | 8 | |||
| B2 | 0.52–0.59 | |||||
| B3 | 0.63–0.69 | |||||
| B4 | 0.77–0.89 |
| Impoundment Period | Imagery No | Product ID | Center Coordinate (WGS84) | Acquired Date | Cloud Cover (%) | Water Level (m) |
|---|---|---|---|---|---|---|
| Low water level (June to August) | 1 | 2446123 | 30°43′, 110°58′ | 27 June 2017 | 7 | 145.66 |
| 2 | 2446067 | 31°04′, 110°40′ | 14 | |||
| 3 | 96759 | 31°17′, 110°28′ | 8 August 2015 | 8 | 145.48 | |
| 4 | 96760 | 31°00′, 110°24′ | 13 | |||
| High water level (November to February) | 5 | 177856 | 30°51′, 110°16′ | 6 December 2013 | 0 | 174.40 |
| 6 | 126992 | 30°47′, 110°38′ | 0 | |||
| 7 | 127087 | 31°08′, 110°21′ | 0 | |||
| 8 | 1939558 | 31°00′, 111°01′ | 5 November 2016 | 0 | 174.40 | |
| 9 | 1939560 | 30°43′, 110°57′ | 0 | |||
| 10 | 1939455 | 31°04′, 110°40′ | 0 | |||
| 11 | 1939462 | 31°20′, 110°44′ | 0 |
| Imagery No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimal threshold | 0.23 | 0.47 | 0.48 | 0.47 | 0.31 | 0.20 | 0.34 | 0.13 | 0.14 | 0.07 | 0.01 |
| Simulating Approach | Gravitational Effect (μGal or 10−8 m/s2). at Observation Point | ||
|---|---|---|---|
| P1 | P2 | P3 | |
| Cuboid | 14.5003 | 181.7064 | 14.5003 |
| Asymmetry heptahedron | 21.3529 | 183.4860 | 14.7599 |
| Asymmetry hexahedron (i.e., left part) | 6.8526 | 1.7796 | 0.2596 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Wang, L.; Chen, C.; Du, J.; Sun, S. Simulation of the Dynamic Water Storage and Its Gravitational Effect in the Head Region of Three Gorges Reservoir Using Imageries of Gaofen-1. Remote Sens. 2020, 12, 3353. https://doi.org/10.3390/rs12203353
Ma X, Wang L, Chen C, Du J, Sun S. Simulation of the Dynamic Water Storage and Its Gravitational Effect in the Head Region of Three Gorges Reservoir Using Imageries of Gaofen-1. Remote Sensing. 2020; 12(20):3353. https://doi.org/10.3390/rs12203353
Chicago/Turabian StyleMa, Xian, Linsong Wang, Chao Chen, Jinsong Du, and Shida Sun. 2020. "Simulation of the Dynamic Water Storage and Its Gravitational Effect in the Head Region of Three Gorges Reservoir Using Imageries of Gaofen-1" Remote Sensing 12, no. 20: 3353. https://doi.org/10.3390/rs12203353
APA StyleMa, X., Wang, L., Chen, C., Du, J., & Sun, S. (2020). Simulation of the Dynamic Water Storage and Its Gravitational Effect in the Head Region of Three Gorges Reservoir Using Imageries of Gaofen-1. Remote Sensing, 12(20), 3353. https://doi.org/10.3390/rs12203353