Recent Climate Change Feedbacks to Greenland Ice Sheet Mass Changes from GRACE
Abstract
1. Introduction
2. Data
2.1. GRACE Data
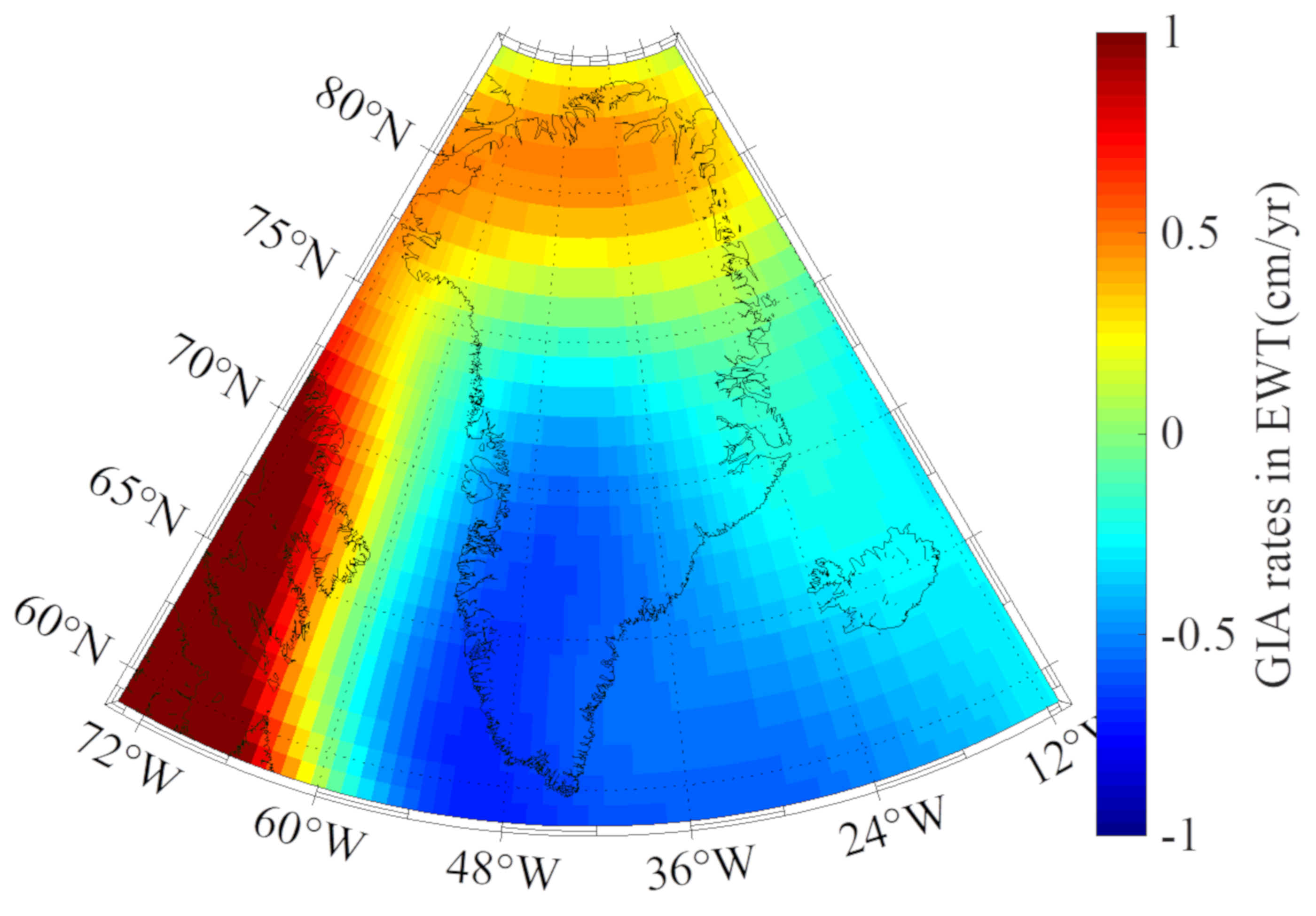
2.2. GIA Model
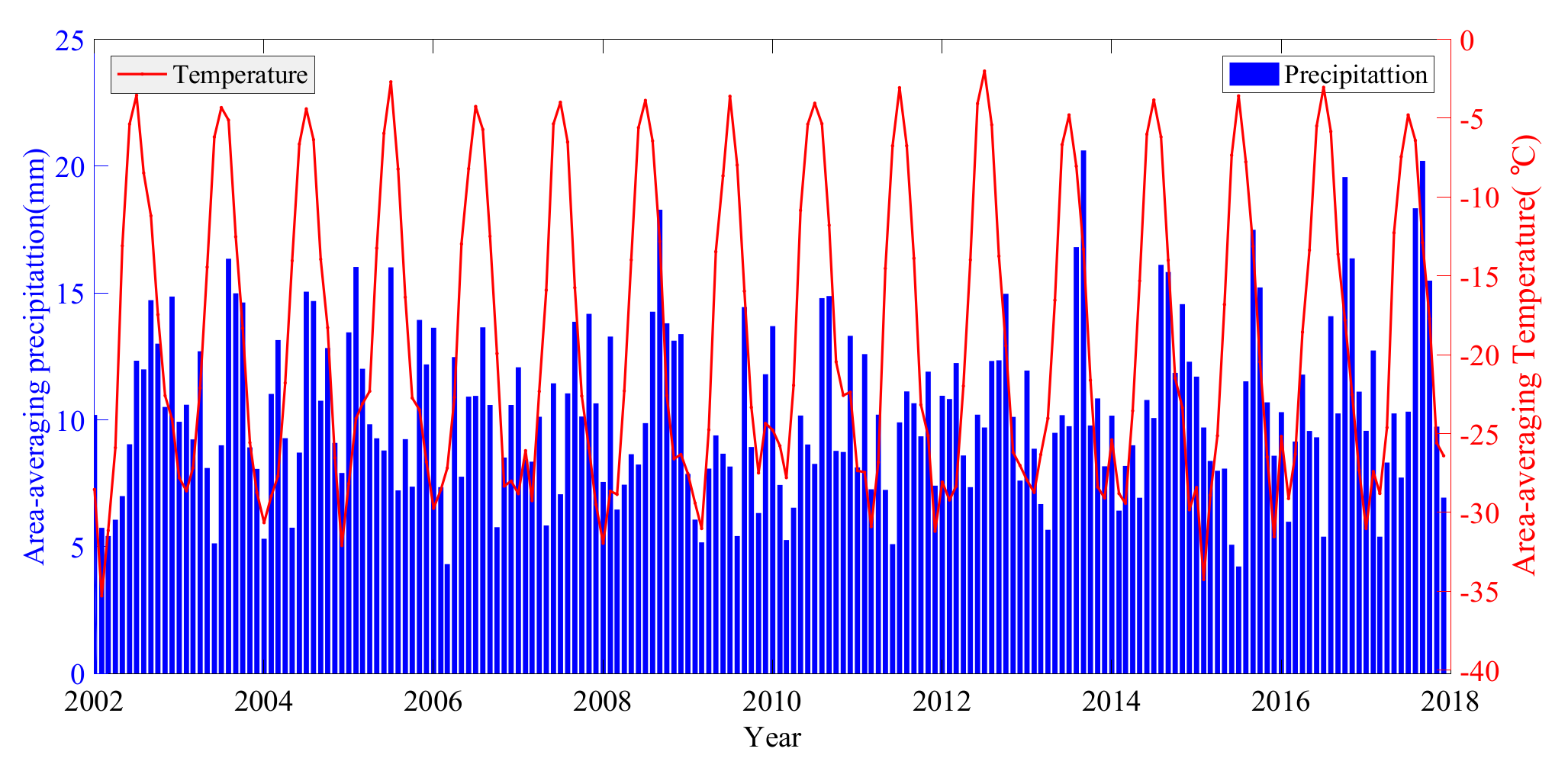
2.3. Climate Data
3. Methodology
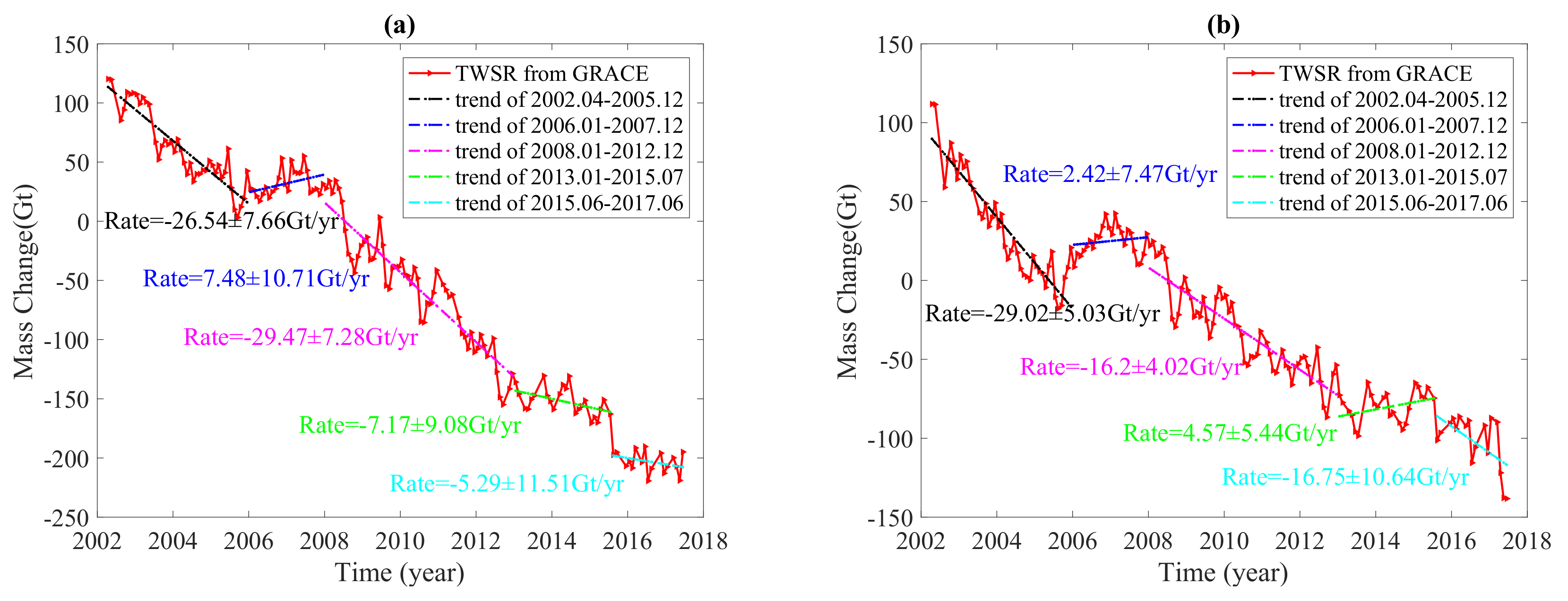
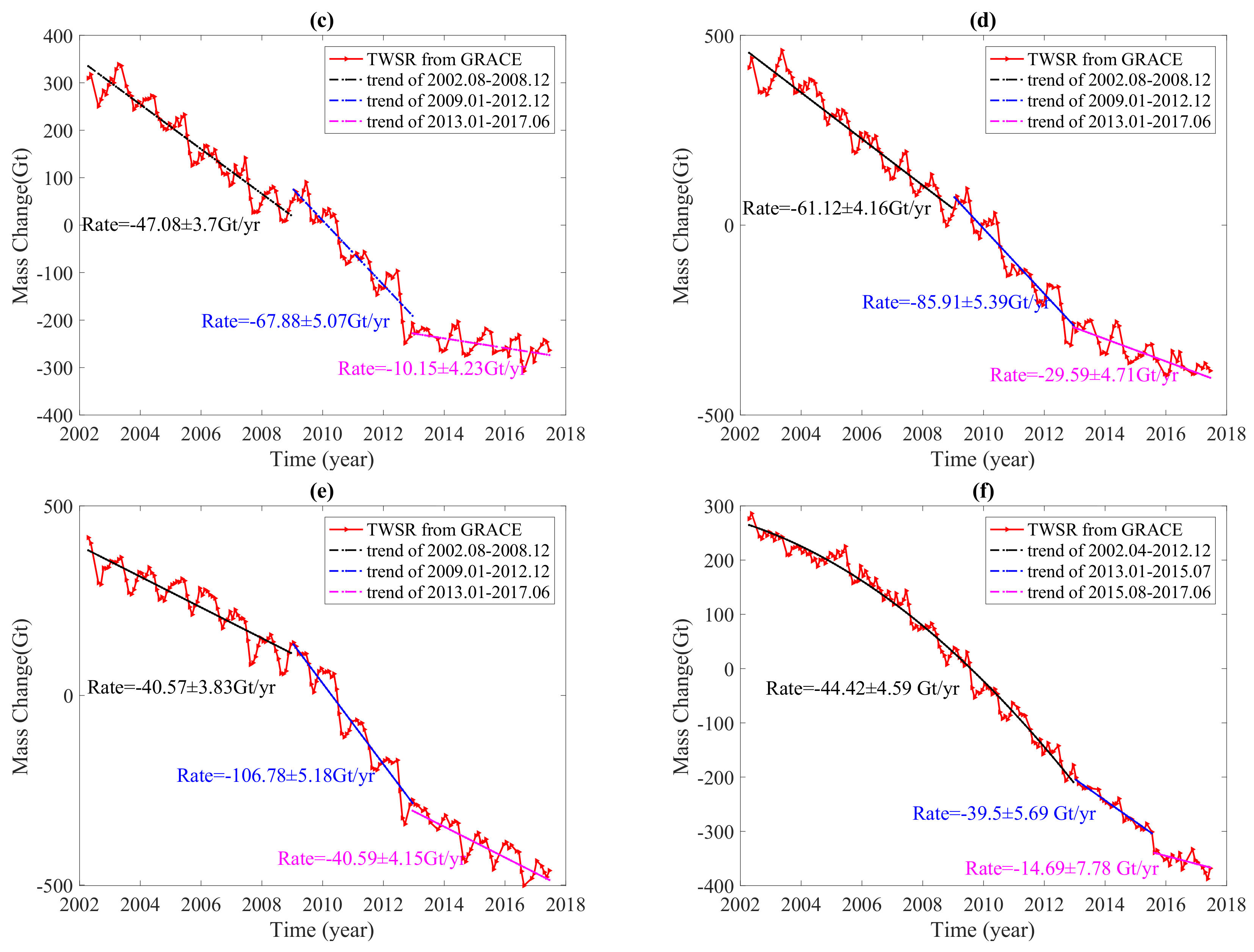
3.1. Time Series Analysis of Mass Changes from GRACE
3.2. Spearman Rank Correlation Coefficient
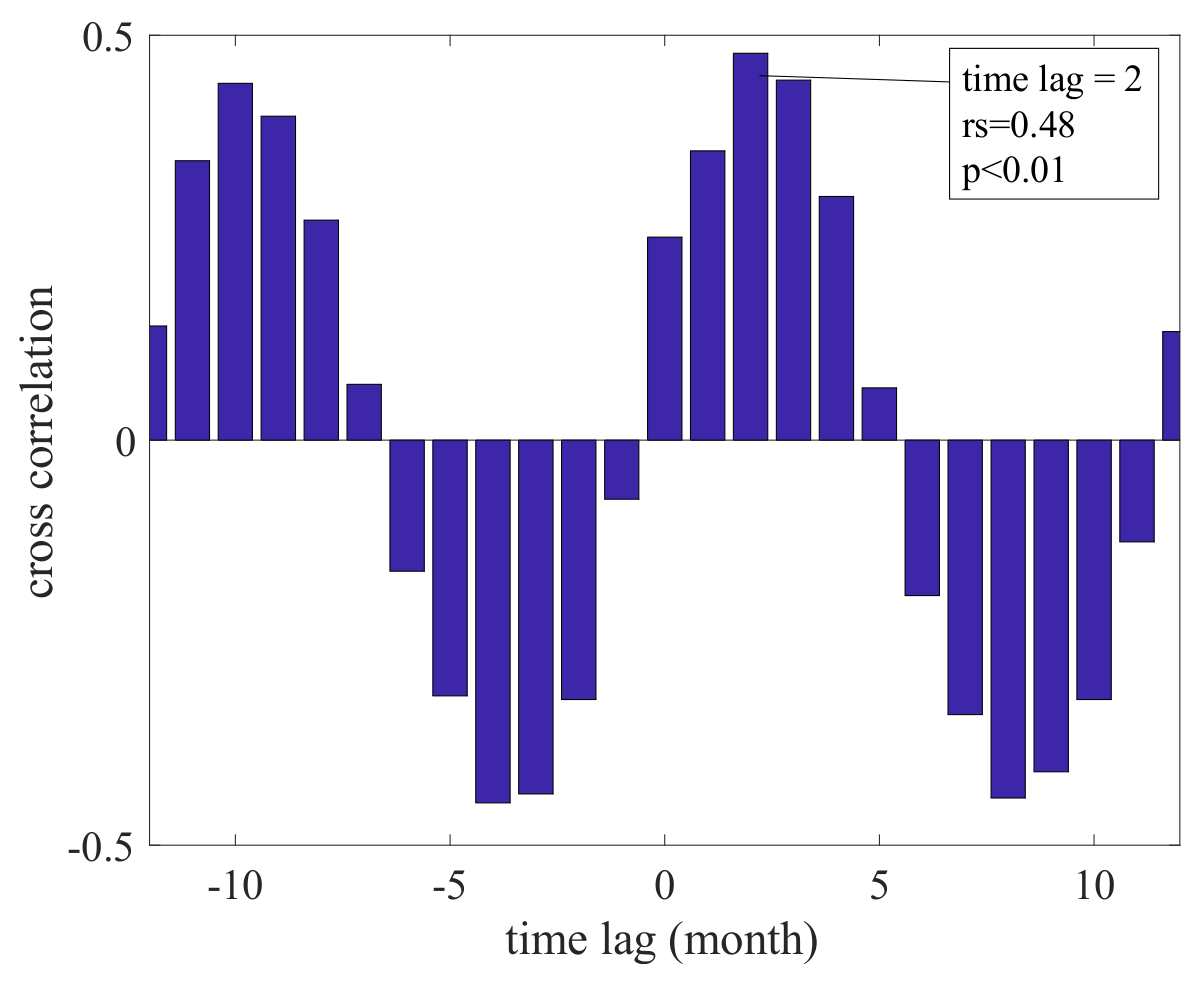
3.3. Cross-Correlation and Time Lag
3.4. Ridge Regression
4. Results and Analysis
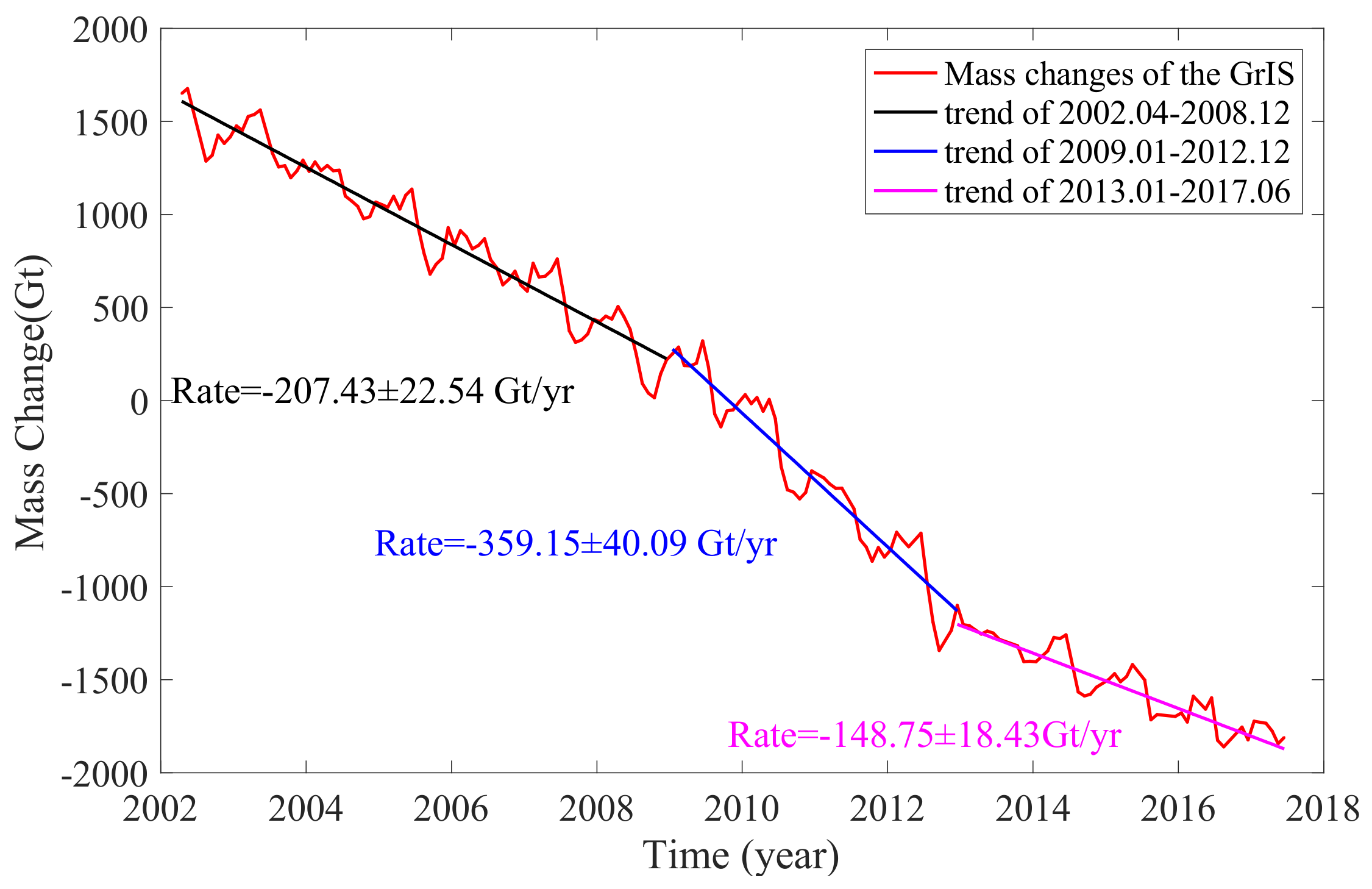
4.1. Mass Change from GRACE
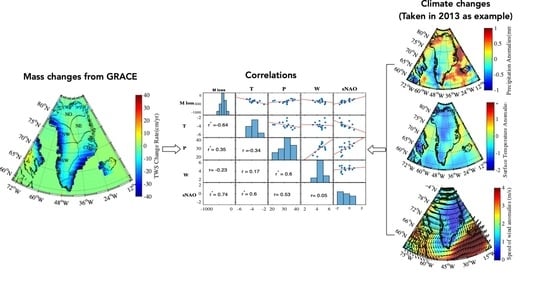
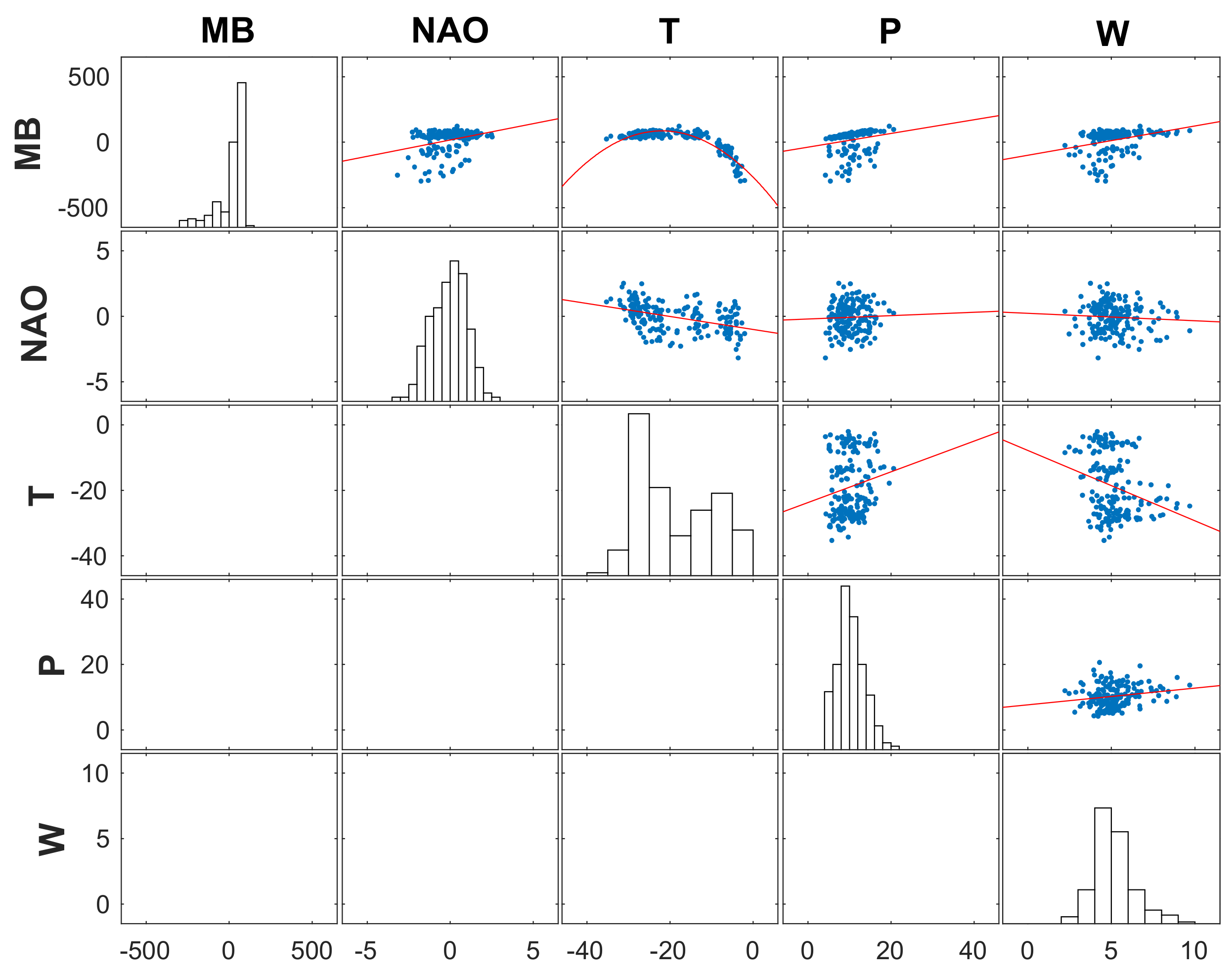
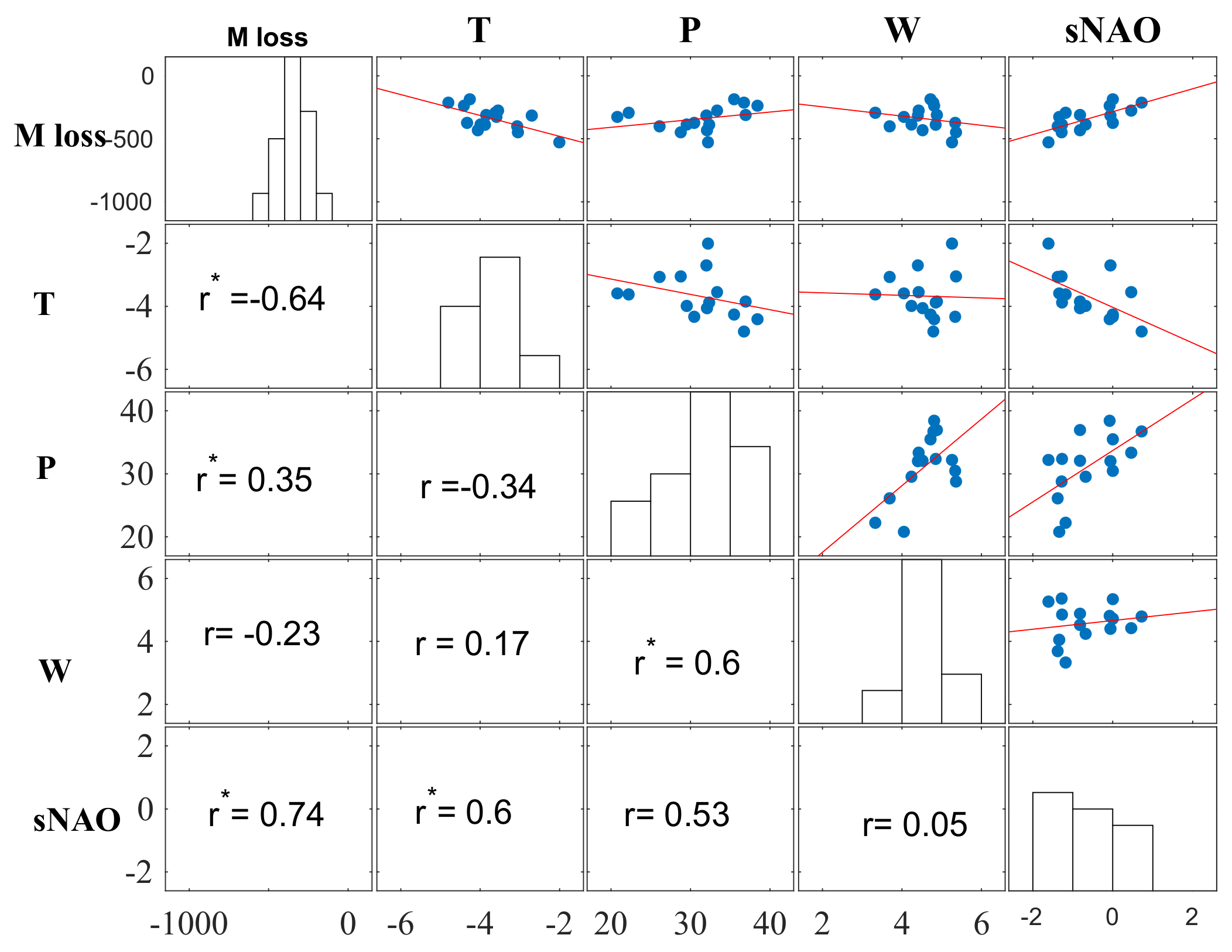
4.2. Relationship Between Mass Changes and Climate Controls
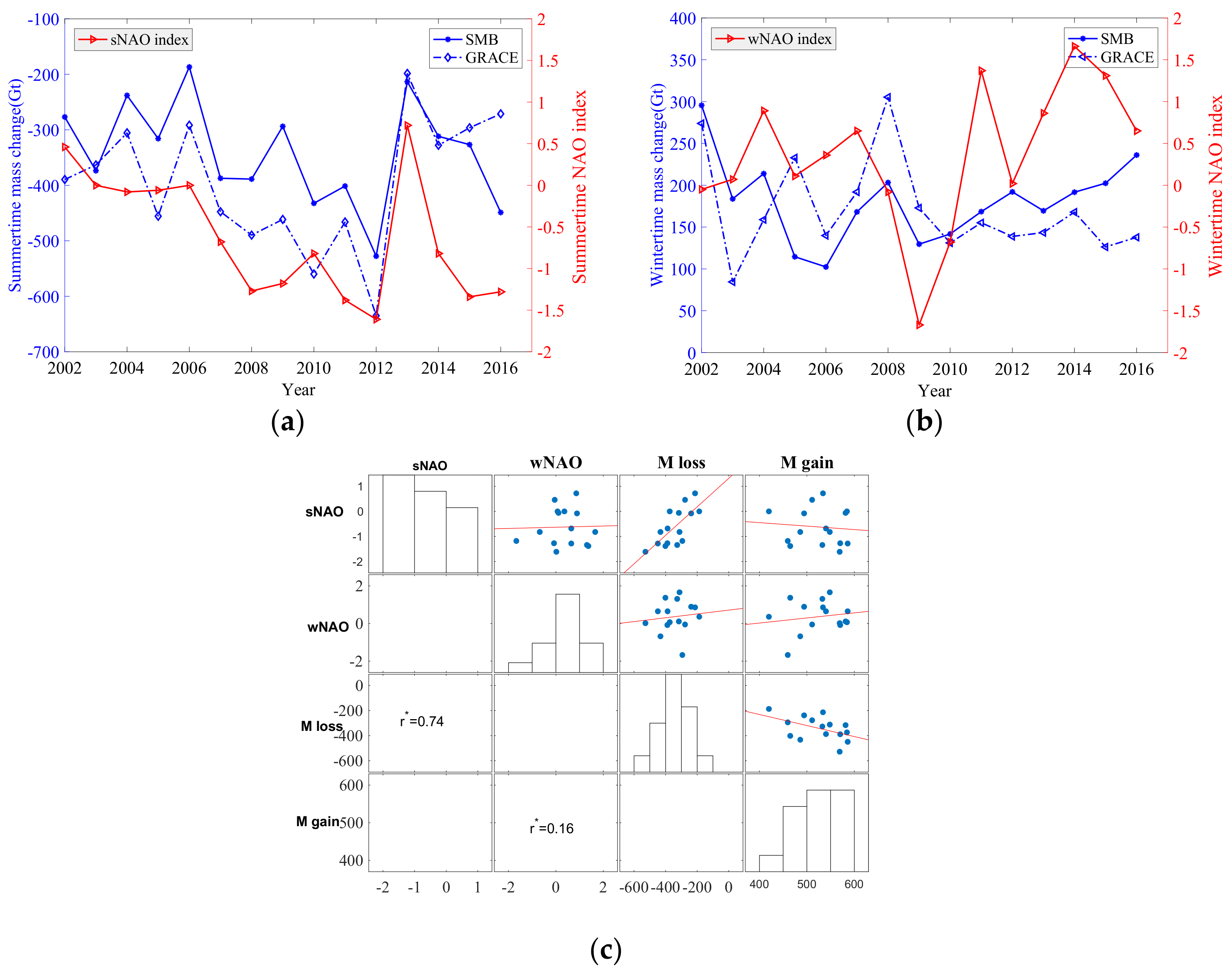
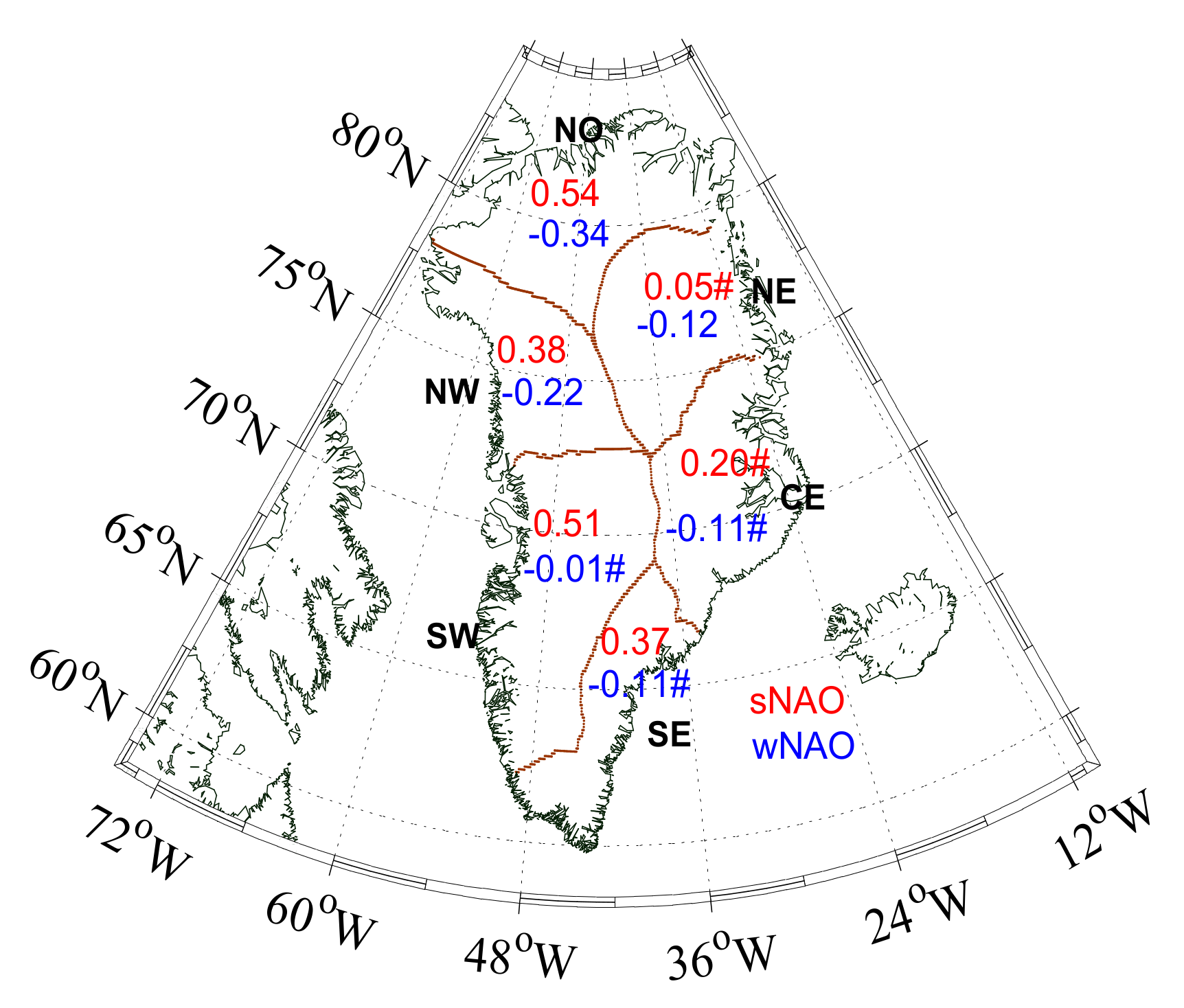
4.2.1. Connections between NAO and Mass Changes
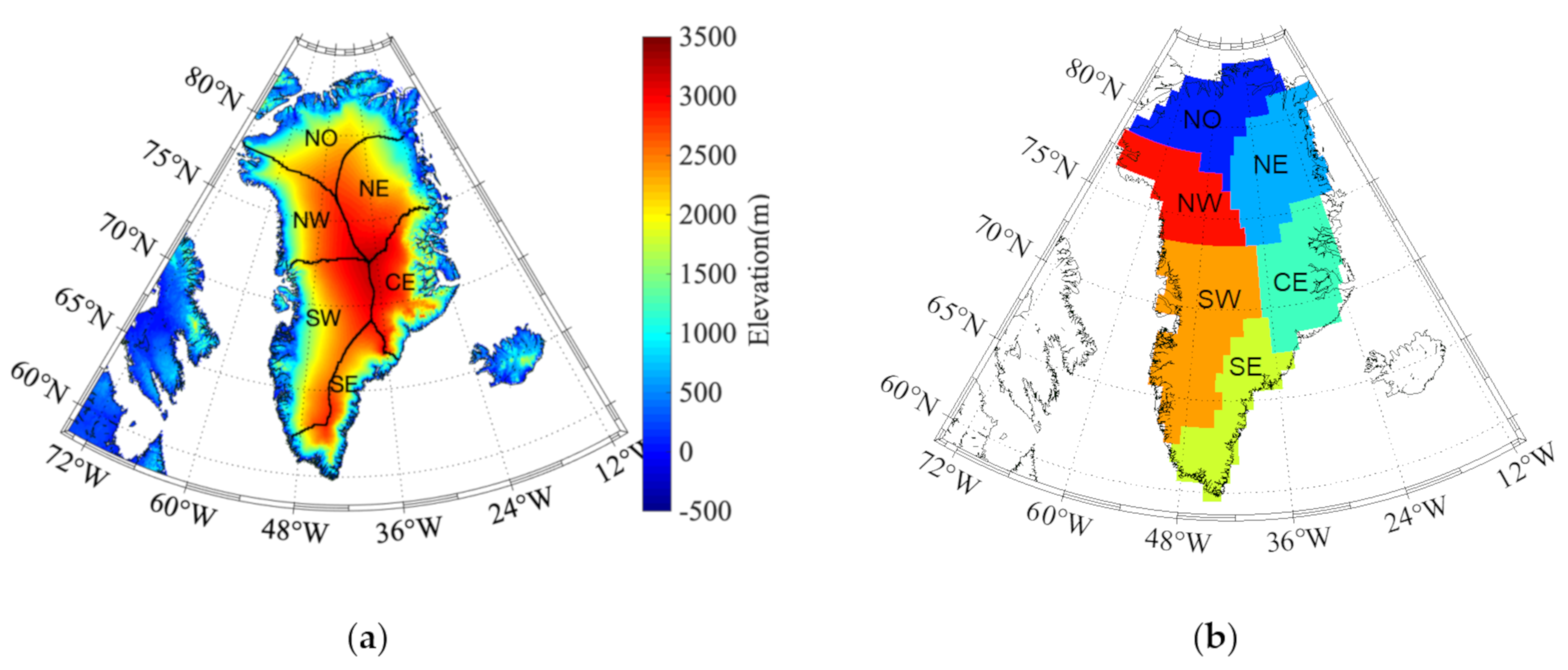
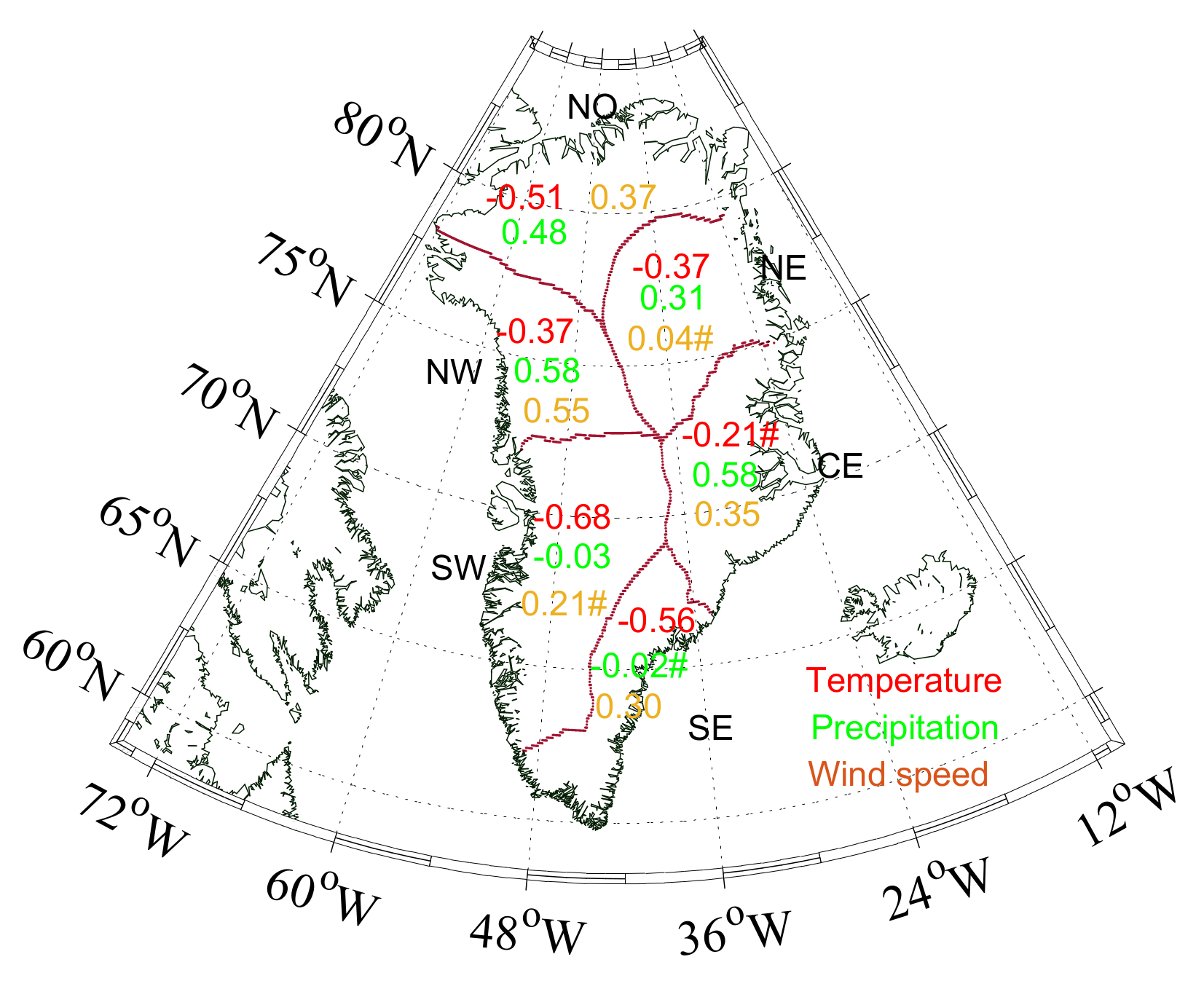
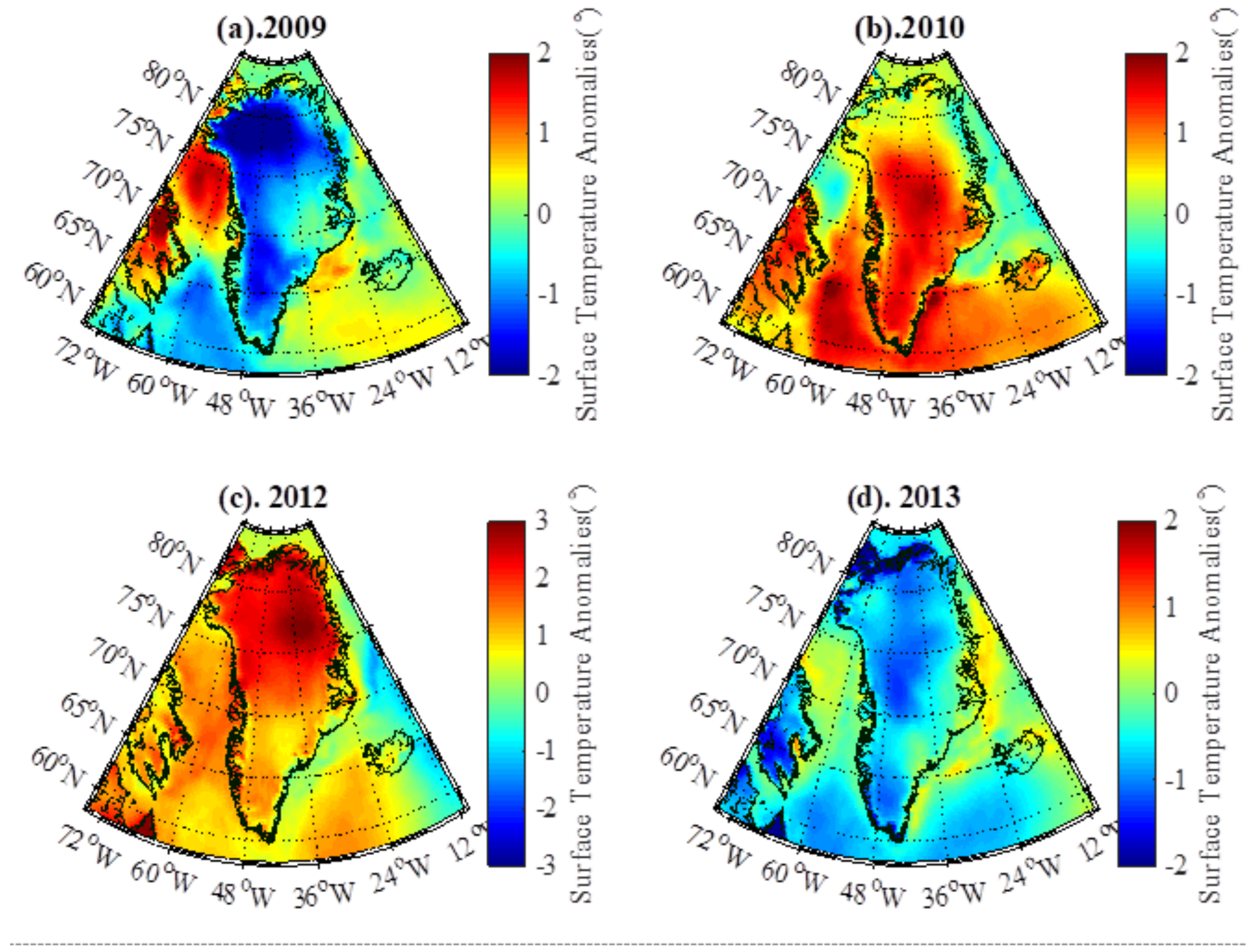
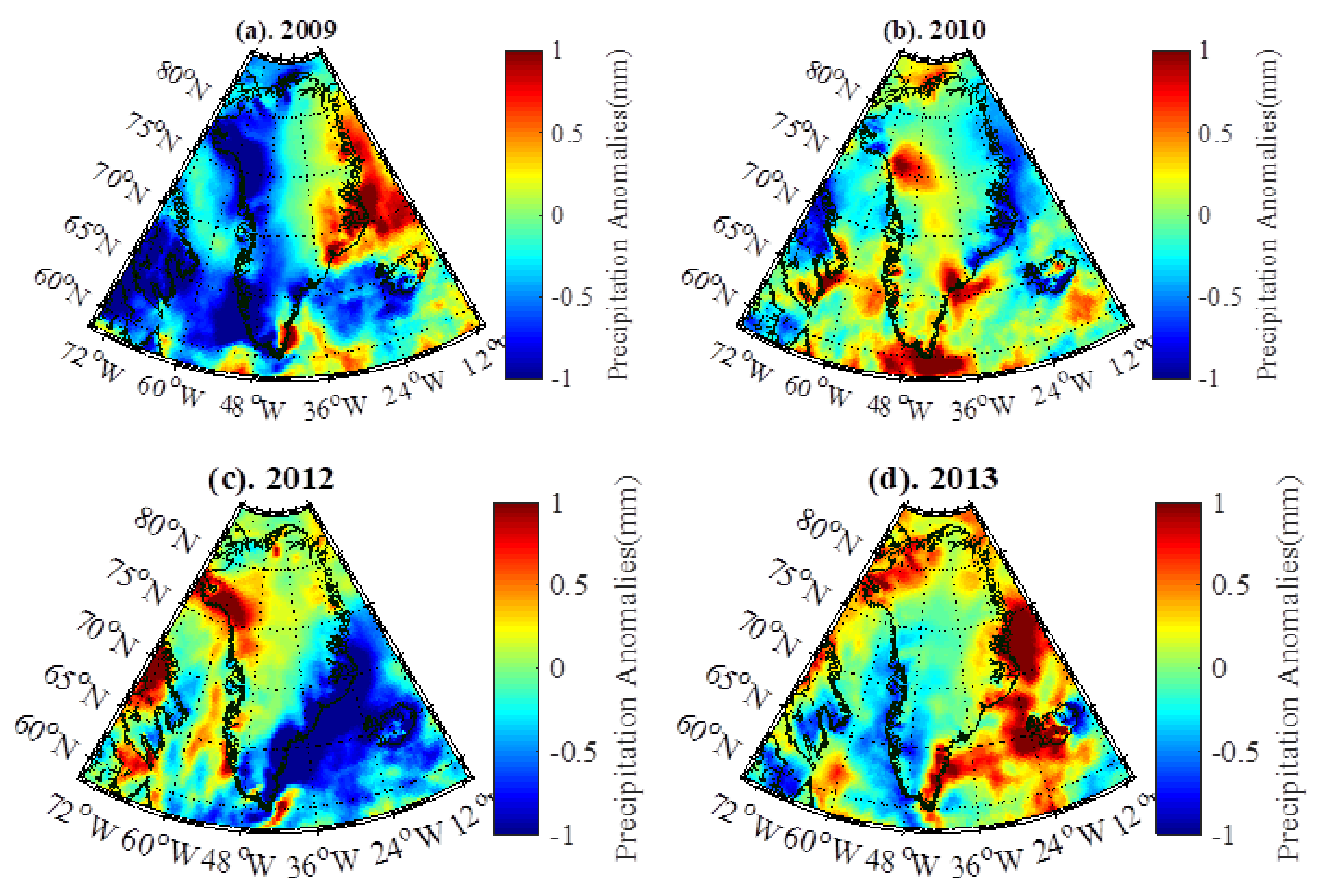
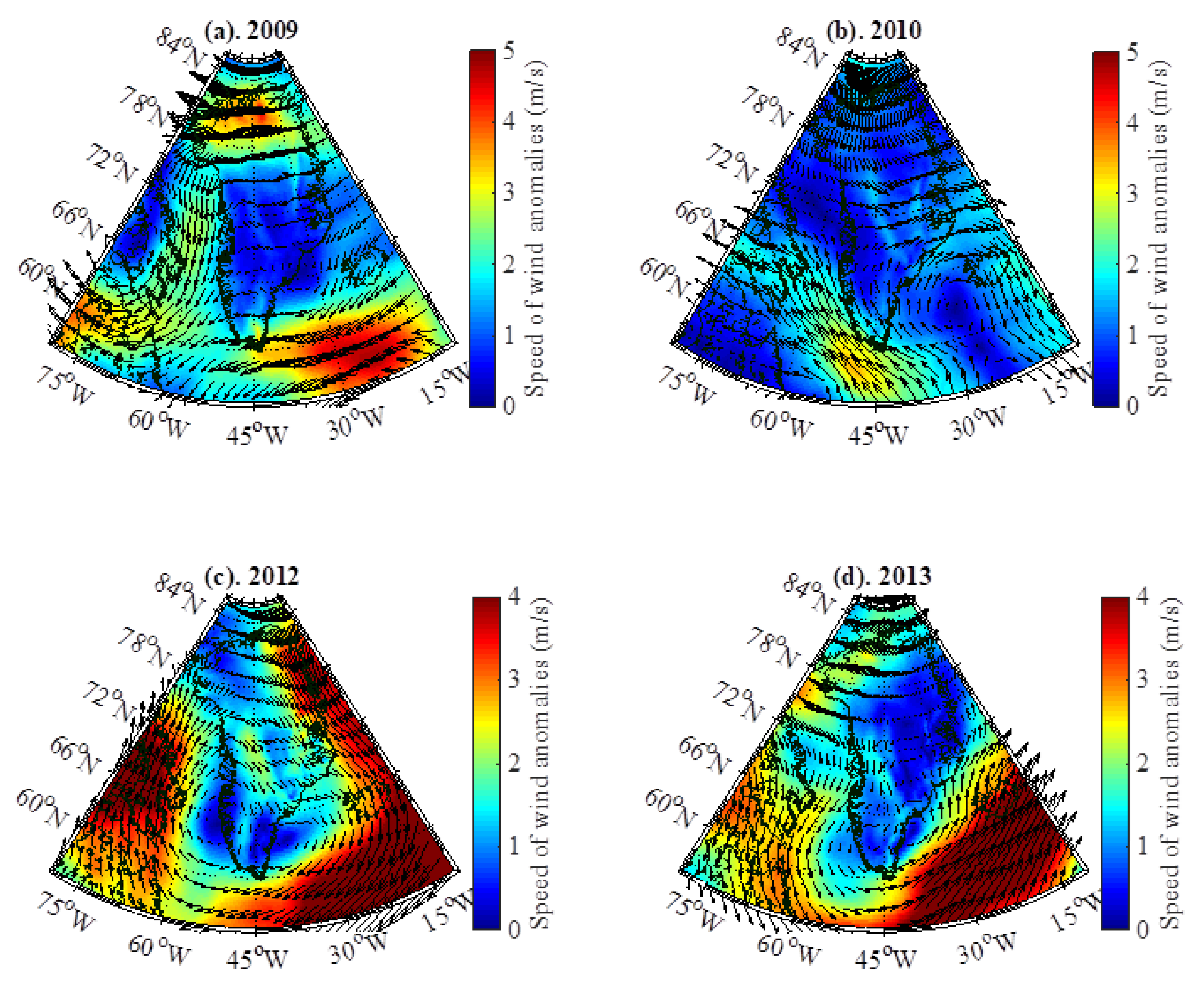
4.2.2. Relationship Between Regional Climate Controls and Mass Changes
4.2.3. Associated Mechanisms
5. Discussion
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bevis, M.; Harig, C.; Khan, S.A.; Brown, A.; Simons, F.J.; Willis, M.; Fettweis, X.; van den Broeke, M.R.; Madsen, F.B.; Kendrick, E.; et al. Accelerating changes in ice mass within Greenland, and the ice sheet’s sensitivity to atmospheric forcing. Proc. Natl. Acad. Sci. USA 2019, 116, 1934–1939. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Contribution of ice sheet and mountain glacier melt to recent sea level rise. Nat. Geosci. 2013, 6, 549–552. [Google Scholar] [CrossRef]
- Graversen, R.G.; Drijfhout, S.; Hazeleger, W.; Wal, R.V.D.; Bintanja, R.; Helsen, M. Greenland’s contribution to global sea-level rise by the end of the 21st century. Clim. Dyn. 2011, 37, 1427–1442. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Rignot, E.; Velicogna, I.; Broeke, M.R.V.D.; Monaghan, A.; Lenaerts, J.T.M. Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Slater, D.A.; Felikson, D.; Straneo, F.; Goelzer, H.; Nowicki, S. Twenty-first century ocean forcing of the Greenland ice sheet for modelling of sea level contribution. Cryosphere 2020, 14, 985–1008. [Google Scholar] [CrossRef]
- Chambers, D.P. Calculating trends from GRACE in the presence of large changes in continental ice storage and ocean mass. Geophys. J. Int. 2009, 176, 415–419. [Google Scholar] [CrossRef]
- Ettema, J.; van den Broeke, M.R.; van Meijgaard, E.; van de Berg, W.J.; Bamber, J.L.; Box, J.E.; Bales, R.C. Higher surface mass balance of the Greenland ice sheet revealed by high-resolution climate modeling. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Simpson, M.J.R.; Wake, L.; Milne, G.A.; Huybrechts, P. The influence of decadal- to millennial-scale ice mass changes on present-day vertical land motion in Greenland: Implications for the interpretation of GPS observations. JGR 2011, 116. [Google Scholar] [CrossRef]
- Wahr, J.; Khan, S.A.; van Dam, T.; Liu, L.; van Angelen, J.H.; van den Broeke, M.R.; Meertens, C.M. The use of GPS horizontals for loading studies, with applications to northern California and southeast Greenland. J. Geophys. Res. Solid Earth 2013, 118, 1795–1806. [Google Scholar] [CrossRef]
- Bolch, T.; Sandberg Sørensen, L.; Simonsen, S.B.; Mölg, N.; Machguth, H.; Rastner, P.; Paul, F. Mass loss of Greenland’s glaciers and ice caps 2003–2008 revealed from ICESat laser altimetry data. Geophys. Res. Lett. 2013, 40, 875–881. [Google Scholar] [CrossRef]
- Ewert, H.; Groh, A.; Dietrich, R. Volume and mass changes of the Greenland ice sheet inferred from ICESat and GRACE. J. Geodyn. 2012, 59–60, 111–123. [Google Scholar] [CrossRef]
- Slobbe, D.C.; Ditmar, P.; Lindenbergh, R.C. Estimating the rates of mass change, ice volume change and snow volume change in Greenland from ICESat and GRACE data. Geophys. J. Int. 2009, 176, 95–106. [Google Scholar] [CrossRef]
- Helm, V.; Humbert, A.; Miller, H. Elevation and elevation change of Greenland and Antarctica derived from CryoSat-2. Cryosphere 2014, 8, 1539–1559. [Google Scholar] [CrossRef]
- Su, X.; Shum, C.K.; Guo, J.; Duan, J.; Howat, I.; Yi, Y. High resolution Greenland ice sheet inter-annual mass variations combining GRACE gravimetry and Envisat altimetry. Earth Planet. Sci. Lett. 2015, 422, 11–17. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Satellite gravity measurements confirm accelerated melting of Greenland ice sheet. Science 2006, 313, 1958–1960. [Google Scholar] [CrossRef]
- Jin, S.; Zou, F. Re-estimation of glacier mass loss in Greenland from GRACE with correction of land–ocean leakage effects. Glob. Planet. Chang. 2015, 135, 170–178. [Google Scholar] [CrossRef]
- Ran, J.; Ditmar, P.; Klees, R. Optimal mascon geometry in estimating mass anomalies within Greenland from GRACE. Geophys. J. Int. 2018, 214, 2133–2150. [Google Scholar] [CrossRef]
- Weigelt, M.; van Dam, T.; Jäggi, A.; Prange, L.; Tourian, M.J.; Keller, W.; Sneeuw, N. Time-variable gravity signal in Greenland revealed by high-low satellite-to-satellite tracking. J. Geophys. Res. Solid Earth 2013, 118, 3848–3859. [Google Scholar] [CrossRef]
- Baur, O.; Kuhn, M.; Featherstone, W.E. GRACE-derived ice-mass variations over Greenland by accounting for leakage effects. JGR 2009, 114. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Sabaka, T.J.; Loomis, B.D.; Arendt, A.A.; McCarthy, J.J.; Camp, J. Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global mascon solution. J. Glaciol. 2017, 59, 613–631. [Google Scholar] [CrossRef]
- Schrama, E.J.O.; Wouters, B.; Rietbroek, R. A mascon approach to assess ice sheet and glacier mass balances and their uncertainties from GRACE data. J. Geophys. Res. Solid Earth 2014, 119, 6048–6066. [Google Scholar] [CrossRef]
- Velicogna, I.; Sutterley, T.C.; van den Broeke, M.R. Regional acceleration in ice mass loss from Greenland and Antarctica using GRACE time-variable gravity data. Geophys. Res. Lett. 2014, 41, 8130–8137. [Google Scholar] [CrossRef]
- Bamber, J.L.; Baldwin, D.J.; Gogineni, S.P. A new bedrock and surface elevation dataset for modelling the Greenland ice sheet. Ann. Glaciol. 2017, 37, 351–356. [Google Scholar] [CrossRef]
- Noel, B.; Fettweis, X.; Van de Berg, W.; Van Den Broeke, M.; Erpicum, M. Sensitivity of Greenland Ice Sheet surface mass balance to perturbations in sea surface temperature and sea ice cover: A study with the regional climate model MAR. Cryosphere 2014, 8, 1871–1883. [Google Scholar] [CrossRef]
- Noël, B.; van de Berg, W.J.; Machguth, H.; Lhermitte, S.; Howat, I.; Fettweis, X.; van den Broeke, M.R. A daily, 1 km resolution data set of downscaled Greenland ice sheet surface mass balance (1958–2015). Cryosphere 2016, 10, 2361–2377. [Google Scholar] [CrossRef]
- Van den Broeke, M.; Box, J.; Fettweis, X.; Hanna, E.; Noël, B.; Tedesco, M.; van As, D.; van de Berg, W.J.; van Kampenhout, L. Greenland ice sheet surface mass loss: Recent developments in observation and modeling. Curr. Clim. Chang. Rep. 2017, 3, 345–356. [Google Scholar] [CrossRef]
- Mouginot, J.; Rignot, E.; Bjørk, A.A.; Michiel, V.D.B.; Millan, R.; Morlighem, M.; Noël, B.; Scheuchl, B.; Wood, M. Forty-six years of Greenland Ice Sheet mass balance from 1972 to 2018. Proc. Natl. Acad. Sci. USA 2019, 116, 9239–9244. [Google Scholar] [CrossRef]
- Zou, F.; Tenzer, R.; Fok, H.S.; Nichol, J.E. Mass Balance of the Greenland Ice Sheet from GRACE and Surface Mass Balance Modelling. Water 2020, 12, 1847. [Google Scholar] [CrossRef]
- Hall, D.K.; Williams, R., Jr.; Casey, K.; Digirolamo, N.E.; Wan, Z. Satellite-derived, melt-season surface temperature of the Greenland Ice Sheet (2000–2005) and its relationship to mass balance. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Tedesco, M.; Serreze, M.; Fettweis, X. Diagnosing the extreme surface melt event over southwestern Greenland in 2007. Cryosphere Discuss. 2008, 2, 383–397. [Google Scholar] [CrossRef]
- Seo, K.-W.; Waliser, D.E.; Lee, C.-K.; Tian, B.; Scambos, T.; Kim, B.-M.; van Angelen, J.H.; van den Broeke, M.R. Accelerated mass loss from Greenland ice sheet: Links to atmospheric circulation in the North Atlantic. Glob. Planet. Chang. 2015, 128, 61–71. [Google Scholar] [CrossRef]
- Box, J. Greenland ice sheet surface mass-balance variability: 1991–2003. Ann. Glaciol. 2005, 42, 90–94. [Google Scholar] [CrossRef]
- Murphy, B.F.; Marsiat, I.; Valdes, P. Atmospheric contributions to the surface mass balance of Greenland in the HadAM3 atmospheric model. J. Geophys. Res. Atmos. 2002, 107, ACL 3-1–ACL 3-20. [Google Scholar] [CrossRef]
- Bezeau, P.; Sharp, M.; Gascon, G. Variability in summer anticyclonic circulation over the Canadian Arctic Archipelago and west Greenland in the late 20th/early 21st centuries and its effect on glacier mass balance. Int. J. Climatol. 2015, 35, 540–557. [Google Scholar] [CrossRef]
- Fettweis, X.; Hanna, E.; Lang, C.; Belleflamme, A.; Erpicum, M.; Gallée, H. Important role of the mid-tropospheric atmospheric circulation in the recent surface melt increase over the Greenland ice sheet. Cryosphere 2013, 7, 241–248. [Google Scholar] [CrossRef]
- Hanna, E.; Fettweis, X.; Mernild, S.H.; Cappelen, J.; Ribergaard, M.H.; Shuman, C.A.; Steffen, K.; Wood, L.; Mote, T.L. Atmospheric and oceanic climate forcing of the exceptional Greenland ice sheet surface melt in summer 2012. Int. J. Climatol. 2014, 34, 1022–1037. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Archie, P.; Shijie, Z.; John, W. Inference of mantle viscosity from GRACE and relative sea level data. Geophys. J. Int. 2007, 171, 492–508. [Google Scholar]
- A, G.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Khan, S.A.; Sasgen, I.; Bevis, M.; Van Dam, T.; Bamber, J.L.; Wahr, J.; Willis, M.; Kjaer, K.H.; Wouters, B.; Helm, V. Geodetic measurements reveal similarities between post–Last Glacial Maximum and present-day mass loss from the Greenland ice sheet. Sci. Adv. 2016, 2, e1600931. [Google Scholar] [CrossRef] [PubMed]
- Fleming, K.; Lambeck, K. Constraints on the Greenland Ice Sheet since the Last Glacial Maximum from sea-level observations and glacial-rebound models. Quat. Sci. Rev. 2004, 23, 1053–1077. [Google Scholar] [CrossRef]
- Fleming, K.; Martinec, Z.; Hagedoorn, J. Geoid displacement about Greenland resulting from past and present-day mass changes in the Greenland Ice Sheet. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Peltier, W.R. GLOBAL GLACIAL ISOSTASY AND THE SURFACE OF THE ICE-AGE EARTH: The ICE-5G (VM2) Model and GRACE. Annu. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Slangen, A.; Katsman, C.; Van de Wal, R.; Vermeersen, L.; Riva, R. Towards regional projections of twenty-first century sea-level change based on IPCC SRES scenarios. Clim. Dyn. 2012, 38, 1191–1209. [Google Scholar] [CrossRef]
- Karegar, M.A.; Dixon, T.H.; Malservisi, R.; Kusche, J.; Engelhart, S.E. Nuisance flooding and relative sea-level rise: The importance of present-day land motion. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- NOAA. North Atlantic Oscillation (NAO). Available online: https://www.ncdc.noaa.gov/teleconnections/nao/ (accessed on 15 May 2020).
- Olauson, J. ERA5: The new champion of wind power modelling? Renew. Energy 2018, 126, 322–331. [Google Scholar] [CrossRef]
- Massey, E.J. The Kolmogorov-Smirnov Test of Goodness of Fit. J. Am. Stat. Assoc. 1951, 46. [Google Scholar] [CrossRef]
- Gauthier, T.D. Detecting Trends Using Spearman’s Rank Correlation Coefficient. Environ. Forensics 2001, 2, 359–362. [Google Scholar] [CrossRef]
- Ni, S.; Chen, J.; Wilson, C.R.; Li, J.; Hu, X.; Fu, R. Global Terrestrial Water Storage Changes and Connections to ENSO Events. Surv. Geophys. 2018, 39, 1–22. [Google Scholar] [CrossRef]
- Saleh, A.K.M.E.; Kibria, B.M.G. Performance of some new preliminary test ridge regression estimators and their properties. Commun. Stat. Theory Methods 1993. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Applications to Nonorthogonal Problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
- Muggeo, V.M. Segmented: An R package to fit regression models with broken-line relationships. R News 2008, 8, 20–25. [Google Scholar]
- Muggeo, V.M. Estimating regression models with unknown break-points. Stat. Med. 2003, 22, 3055–3071. [Google Scholar] [CrossRef]
- Gladish, C.V.; Holland, D.M.; Rosing-Asvid, A.; Behrens, J.W.; Boje, J. Oceanic Boundary Conditions for Jakobshavn Glacier. Part I: Variability and Renewal of Ilulissat Icefjord Waters, 2001–14. J. Phys. Oceanogr. 2015, 45, 3–32. [Google Scholar] [CrossRef]
- Khazendar, A.; Fenty, I.G.; Carroll, D.; Gardner, A.; Lee, C.M.; Fukumori, I.; Wang, O.; Zhang, H.; Seroussi, H.; Moller, D. Interruption of two decades of Jakobshavn Isbrae acceleration and thinning as regional ocean cools. Nat. Geosci. 2019, 12, 277. [Google Scholar] [CrossRef]
- Zwally, H.J.; Giovinetto, M.B.; Beckley, M.A.; Sab, J.L. Antarctic and Greenland Drainage Systems. Available online: http://icesat4.gsfc.nasa.gov/cryo_data/ant_grn_drainage_systems.php (accessed on 3 January 2020).
- Sodemann, H.; Schwierz, C.; Wernli, H. Interannual variability of Greenland winter precipitation sources: Lagrangian moisture diagnostic and North Atlantic Oscillation influence. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Bevis, M.; Wahr, J.; Khan, S.A.; Madsen, F.B.; Brown, A.; Willis, M.; Kendrick, E.; Knudsen, P.; Box, J.E.; van Dam, T. Bedrock displacements in Greenland manifest ice mass variations, climate cycles and climate change. Proc. Natl. Acad. Sci. USA 2012, 109, 11944–11948. [Google Scholar] [CrossRef] [PubMed]
- Tedesco, M.; Fettweis, X.; Mote, T.; Wahr, J.; Alexander, P.; Box, J.; Wouters, B. Evidence and analysis of 2012 Greenland records from spaceborne observations, a regional climate model and reanalysis data. Cryosphere 2013, 7, 615–630. [Google Scholar] [CrossRef]
- Berdahl, M.; Rennermalm, A.; Hammann, A.; Mioduszweski, J.; Hameed, S.; Tedesco, M.; Stroeve, J.; Mote, T.; Koyama, T.; Mcconnell, J.R. Southeast Greenland Winter Precipitation Strongly Linked to the Icelandic Low Position. J. Clim. 2018, 31, 4483–4500. [Google Scholar] [CrossRef]
- Mosley-Thompson, E.; Readinger, C.; Craigmile, P.; Thompson, L.; Calder, C. Regional sensitivity of Greenland precipitation to NAO variability. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- King, M.D.; Howat, I.M.; Candela, S.G.; Noh, M.J.; Negrete, A. Dynamic ice loss from the Greenland Ice Sheet driven by sustained glacier retreat. Commun. Earth Environ. 2020, 1. [Google Scholar] [CrossRef]
- Mankoff, K.D.; Colgan, W.; Solgaard, A.; Karlsson, N.B.; Ahlstrøm, A.P.; Van As, D.; Box, J.E.; Khan, S.A.; Kjeldsen, K.K.; Mouginot, J. Greenland Ice Sheet solid ice discharge from 1986 through 2017. Earth Syst. Sci. Data 2019, 11, 769–786. [Google Scholar] [CrossRef]
- Sasgen, I.; van den Broeke, M.; Bamber, J.L.; Rignot, E.; Sørensen, L.S.; Wouters, B.; Martinec, Z.; Velicogna, I.; Simonsen, S.B. Timing and origin of recent regional ice-mass loss in Greenland. Earth Planet. Sci. Lett. 2012, 333–334, 293–303. [Google Scholar] [CrossRef]
| Year | Summer Loss | Winter Gain | MB(Gt) |
|---|---|---|---|
| 2002 | −389.56 ± 28.61 | 273.88 ± 24.46 | −115.68 ± 6.70 |
| 2003 | −363.35 ± 26.52 | 84.45 ± 9.31 | −278.90 ± 19.76 |
| 2004 | −305.52 ± 21.89 | 158.89 ± 15.26 | −146.63 ± 9.18 |
| 2005 | −455.77 ± 33.91 | 232.82 ± 21.18 | −222.96 ± 15.29 |
| 2006 | −291.76 ± 20.79 | 139.89 ± 13.74 | −151.86 ± 9.60 |
| 2007 | −447.61 ± 33.26 | 191.89 ± 17.90 | −255.72 ± 17.91 |
| 2008 | −489.77 ± 36.63 | 305.34 ± 26.98 | −184.43 ± 12.20 |
| 2009 | −461.52 ± 34.37 | 172.91 ± 16.38 | −288.61 ± 20.54 |
| 2010 | −559.92 ± 42.24 | 131.10 ± 13.04 | −428.81 ± 31.76 |
| 2011 | −466.10 ± 34.74 | 155.12 ± 14.96 | −310.99 ± 22.33 |
| 2012 | −635.08 ± 48.26 | 138.77 ± 13.65 | −496.31 ± 37.15 |
| 2013 | −198.45 ± 13.33 | 143.40 ± 14.02 | −55.05 ± 1.85 |
| 2014 | −327.88 ± 23.68 | 167.88 ± 15.98 | −160.00 ± 10.25 |
| 2015 | −296.35 ± 21.16 | 126.21 ± 12.65 | −170.14 ± 11.06 |
| 2016 | −271.22 ± 19.15 | 137.77 ± 13.57 | −133.45 ± 8.13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, F.; Tenzer, R.; Fok, H.S.; Nichol, J.E. Recent Climate Change Feedbacks to Greenland Ice Sheet Mass Changes from GRACE. Remote Sens. 2020, 12, 3250. https://doi.org/10.3390/rs12193250
Zou F, Tenzer R, Fok HS, Nichol JE. Recent Climate Change Feedbacks to Greenland Ice Sheet Mass Changes from GRACE. Remote Sensing. 2020; 12(19):3250. https://doi.org/10.3390/rs12193250
Chicago/Turabian StyleZou, Fang, Robert Tenzer, Hok Sum Fok, and Janet E. Nichol. 2020. "Recent Climate Change Feedbacks to Greenland Ice Sheet Mass Changes from GRACE" Remote Sensing 12, no. 19: 3250. https://doi.org/10.3390/rs12193250
APA StyleZou, F., Tenzer, R., Fok, H. S., & Nichol, J. E. (2020). Recent Climate Change Feedbacks to Greenland Ice Sheet Mass Changes from GRACE. Remote Sensing, 12(19), 3250. https://doi.org/10.3390/rs12193250