Abstract
Solar radiation significantly affects terrestrial gross primary productivity (GPP). However, the relationship between GPP and solar radiation is nonlinear because it is affected by diffuse radiation. Solar radiation has undergone a shift from darker to brighter values over the past 30 years in China. However, the effects on GPP of variation in solar radiation because of changes in diffuse radiation are unclear. In this study, national global radiation in conjunction with other meteorological data and remotely sensed data were used as input into a two-leaf light use efficiency model (TL-LUE) that simulated GPP separately for sunlit and shaded leaves for the period from 1981 to 2012. The results showed that the nationwide annual global radiation experienced a significant reduction (2.18 MJ m−2 y−1; p < 0.05) from 1981 to 2012, decreasing by 1.3% over this 32-year interval. However, the nationwide annual diffuse radiation increased significantly (p < 0.05). The reduction in global radiation from 1981 to 2012 decreased the average annual GPP of terrestrial ecosystems in China by 0.09 Pg C y−1, whereas the gain in diffuse radiation from 1981 to 2012 increased the average annual GPP in China by about 50%. Therefore, the increase in canopy light use efficiency under higher diffuse radiation only partially offsets the loss of GPP caused by lower global radiation.
1. Introduction
Carbon sequestration is extremely important for global change studies [1]. Terrestrial gross primary productivity (GPP), which indicates the ability of vegetation to use light energy through fixation of carbon dioxide during photosynthesis, is a primary component of the terrestrial carbon cycle [2]. Solar radiation substantially affects the ecosystem GPP [3].
Global radiation (Rg) includes both direct and diffuse components. Compared with direct radiation, diffuse radiation (Rd) is more readily distributed evenly in the canopy and shows higher photosynthetic saturation. Therefore, higher Rd increases the canopy light use efficiency (LUE) and thus leads to the enhancement of GPP [4,5,6,7]. Consequently, under cloudy or severe haze conditions, even if Rg decreased, vegetation GPP can increase as a result of the higher Rd component.
Many studies have quantitatively or mechanistically assessed the influence of changes in Rd on GPP at the site scale. An increase in Rd results in enhanced canopy LUE and hence leads to an increase in vegetation productivity. For example, Gu et al. [8] confirmed that canopy LUE under Rd was higher than that under direct radiation for six vegetation types. Gu et al. [9] observed that after a volcanic eruption, changes in Rd on the GPP of Harvard Forest increased by 3–21% because of the increase in the diffuse radiation fraction.
Previous studies have evaluated the effects of Rd on GPP at the regional scale with ecological models. Black et al. [10] investigated the impact of radiation on GPP over the past 50 years. The effect was greater for agricultural lands and grasslands than for forests, as demonstrated by flux data. Mercado et al. [5] observed that the reduction in global photosynthetically active radiation (PAR) reduced global terrestrial carbon sinks by 14.4%, whereas an increase in Rd increased global terrestrial carbon sinks by 9.3%. Chen et al. [11] coupled a terrestrial ecological model and an atmospheric radiation transmission model to study the direct radiation effect on terrestrial ecosystems from 2003 to 2010, and reported that enhanced Rd led to an increase of global GPP by 4.9 Pg C. Thus, previous studies clearly show that the impacts of Rd on the carbon cycle should be considered in ecological models.
In recent years, given the important influence of Rd on GPP, an increasing body of research has attempted to improve ecological models for simulation of GPP with the inclusion of Rd with LUE models. The two-leaf light use efficiency model (TL-LUE) simulates GPP with the differentiation of direct radiation and Rd [12]. Wang et al. [13,14] incorporated Rd into a LUE model. Yan et al. [15] also established a two-leaf model Terrestrial Ecosystem Carbon flux (DTEC) to separately simulate GPP for sunlit and shaded leaves. Zheng et al. [16] upgraded a large-leaf model, Eddy Covariance - Light Use Efficiency (EC-LUE), into a two-leaf model to separately simulate GPP for sunlit and shaded leaves. The above-mentioned models show that incorporation of Rd into GPP models clearly improves the GPP simulation.
In China, previous studies of changes in Rg and Rd have been based on meteorological data, including global radiation measurements, or global radiation derived from sunshine duration. With regard to Rg, studies of trends in Rg that were conducted around or before 2000 were inconsistent because of limited radiation measurement stations. Previous studies have shown that, during the period from the 1950s to 2000s, Rg changes in China have undergone a shift from darker (decreasing) to brighter (increasing) values [17,18,19,20,21], whereas other studies have shown that Rg in China has experienced a sustained reduction of about 3.1–4.5 W m−2 decade−1 [22,23,24]. Studies on the trend of Rg based on an increased number of radiation measurement stations from the 1980s to the 2010s have shown that global radiation shows a distinct increasing trend [25]. Regarding Rd, previous studies have reported that, in the context of global dimming, Rd and the diffuse radiation fraction are increasing [19,22,25]. For example, Ren et al. [25] observed that national annual mean Rd during the period from 1981 to 2010 increased by 7.03 MJ m−2 y−1 by interpolation from 754 meteorological stations and 122 radiation stations across China. Che et al. [22] reported that the diffuse radiation fraction in China increased by 1.73% per decade from the 1960s to the 1990s.
Several studies have simulated the effects of changes in Rd and Rg on GPP at the site scale in China. He et al. [26] observed that increments in the diffuse radiation fraction enhanced the LUE of the forest canopy, which compensated for the reduction in GPP caused by the decrease in the PAR fraction in three forest ecosystems in China. Li et al. [27] reported that the response of canopy GPP to radiation changes was predominantly determined by the Rd in an evergreen coniferous forest in China. However, at a regional scale in China, the impacts of recent changes in Rg and Rd on GPP are unclear, which demands a better understanding and accurate spatiotemporal estimation of such impacts. The aims of the present study were to (i) analyze the trends of Rd and Rg in China from 1981 to 2012, and (ii) assess the effects of variation in the diffuse radiation fraction on terrestrial GPP in China.
2. Materials and Methods
2.1. Data
The data used in the two-leaf light use efficiency model (TL-LUE) model to simulate GPP in China over the period 1981–2012 were as follows: (i) grid-based meteorological data, including Rg, Rd, air temperature (Ta), minimum temperature (Tamin), maximum air temperature (Tamax), and vapor pressure deficit (VPD) at the daily scale; (ii) 8-day remotely sensed leaf area index (LAI); and (iii) remotely sensed land-cover data.
2.1.1. Meteorological Data
Average daily Ta, Tamin, Tamax, average relative humidity (RH), and sunshine duration for 1981–2012, available from 754 conventional meteorological stations, were used. The average RH was converted to VPD following the reference methodology of Allen et al. [28]. Of the 754 meteorological stations, Rg and Rd were measured at 103 and 81 sites, respectively, and sunshine duration was measured at all 754 sites during 1981–2012 (Figure 1 and Supplementary Figure S1, and Supplementary Tables S1 and S2).
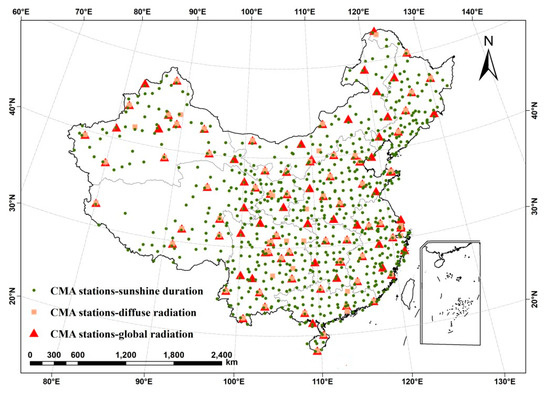
Figure 1.
Distribution in China of meteorological stations recording sunshine duration, and global and diffuse radiation.
The Rg at the site scale was interpolated to the national scale by the following steps. First, the Ångström model (Equation (1)) [29] was calibrated using data from 103 meteorological stations recording both Rg and sunshine duration measurements during 1981–2012. Second, to compensate for the lack of global radiation measurements, Rg for the remaining 651 meteorological stations was calculated by using sunshine duration and the calibrated Ångström model in step 1. Third, data from 12 sites with Rg measurements in 2014 were used to validate the calibrated Ångström model (see Supplementary Materials Figure S2). Finally, using radiation data at the 754 sites, Rg was interpolated to the national scale with an inverse distance weighted method.
Considering the heterogeneity of terrain and climate in China, the country was divided into eight regions: Northeast China (R1), Inner Mongolia (R2), Northwest China (R3), North China (R4), Central China (R5), South China (R6), Southwest China (R7), and the Qinghai–Tibet Plateau (R8). The Rg estimation model was fitted for each region separately to convert sunshine duration into Rg, which was comparable with the method of Ren et al. [25,30]. The Ångström model [29] was selected to estimate Rg because of the advantages of a simple structure, clear physical meaning, stable model coefficients, and good fitting results in addition to its widespread use [31]. This model was as follows:
where Rg is the global radiation reaching the surface, R0 is the daily extraterrestrial radiation, n is the actual daily sunshine duration observed at a given site, N is the potential daily sunshine duration, and a and b are coefficients. Both R0 and N can be calculated based on latitude and date [32]. Root mean square error (RMSE) values of the radiation derived using Ångström models for each of the eight regions of China are shown in Table 1.

Table 1.
Parameter and error values for the various Ångström models used to convert sunshine hours into global radiation (Rg) for eight regions of China.
The Rd at the site scale was interpolated to the national scale based on the following steps. First, data from 81 meteorological stations recording both Rg and Rd during 1981–2012 were used to calibrate the logistic model (Equation (2)) [27,30]. Second, to compensate for the lack of Rd measurements, Rg estimated with the Ångström model was used to calculate Rd for the remaining 673 meteorological stations using the calibrated Equation (2) in step 1. Third, data from 12 sites with Rg measurements in 2014 were used to validate the calibrated Ångström model (see Supplementary Materials, Figure S3). Finally, Rd was interpolated to the national scale using Rd at the 754 sites.
A simple and accurate logistic model [27,30] was used to estimate Rd as follows:
where Rd is the diffuse radiation, and c and d are the nonlinear regression coefficients. Table 2 shows the RMSE values of estimated Rd derived from logistic models for the eight regions of China.

Table 2.
Parameters and error values for various logistic models used to estimate diffuse radiation (Rd) for eight regions of China.
The coefficient of determination (R2) for Rg and Rd measurements and estimations ranged from 0.66 to 0.79 (Table 1) and 0.63 to 0.81 (Table 2), which were comparable with the results of Singh [33] and Ren et al. [30]. Validation (see Supplementary Materials, Figures S2 and S3) indicated that the R2 for Rg measurements and estimations was 0.85–0.96 and that for Rd was 0.55–0.75 at validation sites. Estimated global and Rd in this study showed the similar values to those of Ren et al. [30] (see Supplementary Materials, Figure S4).
2.1.2. LAI Data
The LAI at a 0.0727° grid for 1981–2012 was generated using the Moderate Resolution Imaging Spectroradiometer (MODIS) and the Advanced Very High Resolution Radiometer (AVHRR) data. The dataset was generated by Liu et al. [34] and has been widely used in studies of the carbon cycle and vegetation response to climate change of terrestrial ecosystems [35,36,37,38,39]. GLOBMAP LAI V3 during 1981 to 2012 was generated by fusing LAI inverted from MODIS reflectance data with Global Inventory Modelling and Mapping Studies (GIMMS) AVHRR Normalized Difference Vegetation Index (NDVI) data. The LAI from 2001 to 2012 was first derived from the MODIS land surface reflectance data (MOD09A1) reflectance based on the GLOBCARBON LAI algorithm. For the fusion of MODIS and AVHRR remotely sensed data, the relationships between GIMMS NDVI and MODIS LAI were established pixel by pixel over a period (2001–2006) that they overlap. The AVHRR LAI from 1981 to 2000 was then generated using these relationships.
2.1.3. Land-cover Data
Given the lack of land-cover data before 2000, we used land-cover data in 2001 for the entire period simulations. The MODIS land-cover data at 500-m spatial resolution (MCD12Q1) for 2001 was resampled to 0.0727° to drive the TL-LUE model during 1981 and 2012. The International Geosphere–Biosphere Programme classification system was used in this study, including categories of evergreen needle-leaf forest (ENF), deciduous coniferous forest (DNF), evergreen broad-leaved forest (EBF), deciduous broad-leaved forest (DBF), evergreen broad-leaved forest (ENF), deciduous coniferous forest (DNF), evergreen broad-leaved forest (EBF), mixed forest (MF), sparse shrubland (OS), dense shrubland (CS), grassland (GRASS), farmland (CROP), and other surface cover types (NOV).
2.1.4. GPP Data
Flux data from 13 available flux tower sites of the ChinaFLUX network were compared with the simulated GPP. These sites included three broad-leaved forest (BF), two needle-leaved forest (NF), one MF, one shrubland (Shrub), four GRASS, and two CROP sites, providing a total of 100 site years (Table 3).

Table 3.
Specifications for the 13 flux tower sites. (BF means broad-leaved forest; CROP means crop; GRASS means grass; MF means mixed forest; NF means needle-leaved forest; Shrub means shrubland).
2.2. Modeling
2.2.1. TL-LUE Model
The TL-LUE model [12] is based on MODIS GPP [40] and the Boreal Ecosystem Productivity Simulator (BEPS) model [41]. Model validation was performed at both the site [42,43] and the regional scale [44]. Additional information on the model was introduced in [12,42,43]. The model parameters used for the TL-LUE models followed Zhou et al. [43].
GPP was calculated with the following Equation (3):
where εmsu and εmsh are the maximum LUE of sunlit and shaded leaves, respectively; APARsu and APARsh are the absorbed PAR of sunlit and shaded leaves, respectively; and f(VPD) and f(Tamin) are stress factors of Vapour Pressure Deficiency (VPD) and air temperature, respectively. APARsu and APARsh were calculated with the following Equations (4) and (5):
where α is albedo; PARdif_u is diffuse radiation under the canopy; C is multiple scattered radiation; β is the leaf angle, which was considered to be 60°; θ is the solar zenith angle; PARdif and PARdir are incoming direct and diffuse radiation, respectively (Chen et al., 1999). LAIsu and LAIsh are the LAI of sunlit and shaded leaves and was calculated with Equations (6) and (7):
LAIsh = LAI−LAIsu
On the basis of Equations (3)–(5), GPP derived from diffuse radiation can be calculated with the following Equation (8):
where GPPdif and GPPdir are GPP contributed by diffuse and direct radiation, respectively.
2.2.2. Modeling Scenarios
To quantitatively assess the impacts of variation in Rg and diffuse radiation fractions on GPP, three simulations were performed (see Supplementary Materials, Table S3).
(i) Scenario 1 (Scenario): Both historical meteorological data with temporal variations and LAI were used to simulate GPP for the period 1981–2012.
(ii) Scenario 2 (Scenario_Rg): Temporally constant Rg data, other historical meteorological data with temporal variations, and LAI were used to simulate GPP for the period 1981–2012. The differences between simulated GPP values in S1 and S2 reflect the effects of change in Rg on GPP simulation.
Based on the assumption that the annual Rg remained unchanged from 1981 to 2012, and the variation tendency of daily Rg variation to Rg averaged values during 1981–2012 was consistent, daily radiation for the period 1982–2012 was calibrated using Equation (9):
where i and j are the line and row of any given pixel, and is the daily Rg of pixel (i, j) on the kth day of the mth year.
(iii) Scenario 3 (Scenario_Rd): Temporally constant Rd, other historical meteorological data with temporal variations, and LAI were used to simulate GPP for the period 1981–2012. The difference between simulated GPP values in S1 and S3 reflect the effects of Rd on GPP simulations.
Based on the assumption that the annual diffuse radiation fraction remained constant from 1981 to 2012, and the variation tendency of daily Rd variation to Rd averaged values during 1981–2012 was consistent, the daily diffuse radiation fraction for the period 1982–2012 was calibrated using Equation (10):
where i and j are the row and column of a given pixel, and is the diffuse radiation fraction in pixel (i, j) for the kth day of the mth year. The diffuse radiation fraction was calculated using Equation (11):
where fdif is the diffuse radiation fraction, Rd and Rg are diffuse and global radiation, respectively.
fdif = Rd/Rg
3. Results
3.1. Spatiotemporal Distributions of Annual Radiation in China
The spatial distributions of the average annual and standard deviation of Rg, Rd, and diffuse radiation fraction in China over the period 1981–2012 are shown in Figure 2. The Rg (Figure 2a) was unevenly distributed across China, with a range of 3255–7154 MJ m−2 y−1 and a national average of 5258 MJ m−2 y−1 (Figure 2a). The standard deviation of Rg ranged from 65 to 359 MJ m−2 y−1 (Figure 2b). Generally, Rg values on the western plateau were higher than those on the eastern plain. The highest Rg values were recorded on the southern part of the Qinghai–Tibet Plateau (>6500 MJ m−2 y−1) because of the thin air density in this region. The northeastern part of the Sichuan Basin and the Yunnan–Guizhou Plateau had the lowest annual Rg values (<3800 MJ m−2 y−1).
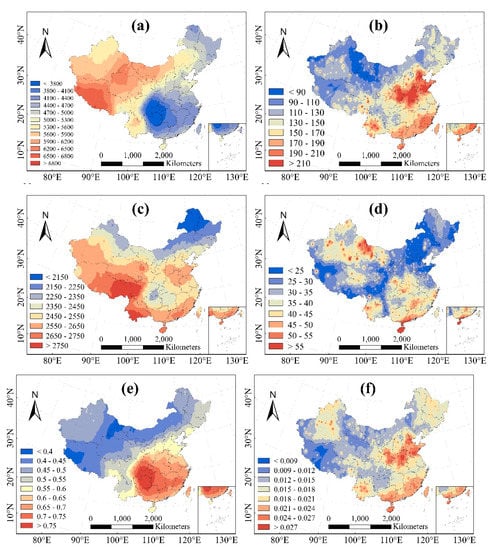
Figure 2.
Spatial distribution of the mean (a) and standard deviation (b) of global radiation (unit: MJ m−2 y−1), the annual mean (c) and standard deviation (d) of diffuse radiation (unit: MJ m−2 y−1), and the mean (e) and standard deviation (f) of diffuse radiation fraction in China for the period 1981–2012 with a spatial resolution of 0.0727°.
Values of Rd (Figure 2c) ranged from 1989 to 3007 MJ m−2 y−1 and showed a national average of 2483 MJ m−2 y−1, which is close to the value of 2477 MJ m−2 y−1 estimated by Ren et al. [25,30]. The standard deviation range of Rg is 15–101 MJ m−2 y−1 with a national average of 33 MJ m−2 y−1 (Figure 2d). In general, Rd was high in the south and west of China and low in the north. The highest values of Rd were on the Qinghai–Tibet Plateau and on the southwestern part of the Yunnan–Guizhou Plateau, with values higher than 2800 MJ m−2 y−1. The lowest values were found for Northeast China, Inner Mongolia, and Northwest China, with values of less than 2300 MJ m−2 y−1. Values of diffuse radiation fraction ranged from 0.34 to 0.83 and showed a national average of 0.52 (Figure 2e), and the diffuse radiation fraction was highest in southern China, especially within the regions of Sichuan and Guizhou. The standard deviation of diffuse radiation fraction ranged from 0.007 to 0.043 with a national average of 0.016 (Figure 2f).
The Rg exhibited broad variability during 1981–2012 but generally showed a significant (p < 0.05) negative trend of 2.18 MJ m−2 y−1, yielding a rate of decrease of 1.3% y−1 (Figure 3a). Specifically, Rg decreased markedly and then increased slightly during the interval 1980–1990. During the interval 1991–1993, Rg declined rapidly, possibly because of the volcanic eruption of Mount Pinatubo in 1991. This volcanic eruption led to the release of about 20 million tonnes of sulfide gas into the stratosphere, producing a reduction in Rg. The Rg values were gradually restored after 1994 [9,25,30]. Values of Rg also decreased slightly after 1999, consistent with the findings of Che et al. [22] and Wild et al. [17].
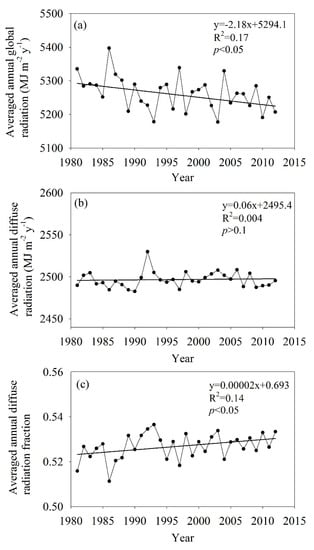
Figure 3.
Linear trends in annual mean (a) global radiation, (b) diffuse radiation, and (c) diffuse radiation fraction across China for the period 1981–2012.
The simple linear trend in the average annual Rd in China was positive from 1981 to 2012, although this trend was not significant (Figure 3b). The Rd decreased during the interval 1981–1990 but increased and then decreased rapidly during the interval 1991–1994 because of the eruption of Mount Pinatubo. From the mid-1990s, Rd increased slightly and then decreased again.
The annual average diffuse radiation fraction in China increased markedly between 1981 and 2012 by 0.0002 y−1 (p < 0.05) (Figure 3c).
The spatial distribution of the variation in annual Rg, Rd, and diffuse radiation fraction in China over the period 1981–2012 is shown in Figure 4. Decreases in Rg mainly occurred in North China, Hainan, and on the Qinghai–Tibet Plateau (Figure 4a), which is consistent with the findings of Tang et al. [45] and Lin et al. [46]. Conversely, Rg increased only over a small part of China during the period 1981–2012. Generally, the changes in Rg over most parts of China were not significant, predominantly because China experienced “dimming” prior to 1990, whereas Rg increased slightly over large parts of China post-1990 [23].
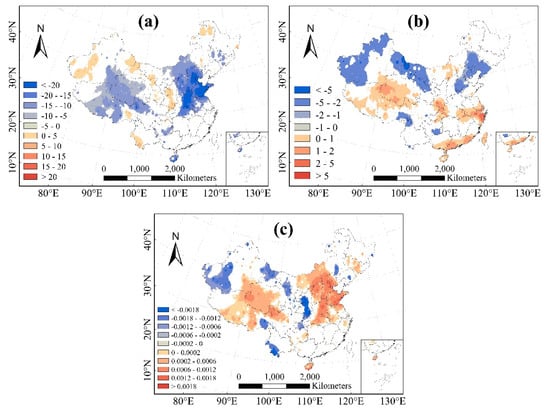
Figure 4.
Spatial distribution of the changing rate in annual mean global radiation ((a), unit: MJ m−2 y−1), diffuse radiation ((b), unit: MJ m−2 y−1), and diffuse radiation fraction (c) in China for the period 1981–2012 (white areas show no significant trends; α = 0.05) with a spatial resolution of 0.0727°.
Increases in Rd predominantly occurred over the Qinghai–Tibet Plateau, Shanghai–Hangzhou–Wuhan region, Guangdong, and Guangxi and its surrounding areas (Figure 4b). Decreases in Rd occurred in the northwestern part of Xinjiang, western parts of Inner Mongolia, and Shenyang. The national average diffuse radiation fraction increased by 0.2% decade−1 during the period 1981–2012 (Figure 4c). Initially, the diffuse radiation fraction increased and then decreased during the 1980s. In 1993, after the eruption of Mount Pinatubo, the diffuse radiation fraction attained its peak during the study period, and then quickly returned to its average value.
3.2. Spatial Distribution of GPP in China over the Period 1981–2012
At the site scale, comparison of the simulated GPP values derived from the TL-LUE model (GPPTL) versus site flux data-derived GPP showed good agreement (R2 = 0.82; N = 100; p < 0.0001) (Figure 5). At the national scale, the average annual GPP value in China was estimated to be 7.64 Pg C y−1, which lies within the range of values reported by previous studies (Table 4). Li et al. [47] estimated the average annual GPP from 2001 to 2010 as 6.04 Pg C y−1, and the annual mean GPP value based on MODIS for China for the same period was estimated as 5.47 Pg C y−1. The GPP estimates based on relationships with meteorological data were 6.06 and 7.78 Pg C y−1 during 2001–2010 with two spatial resolutions [48].
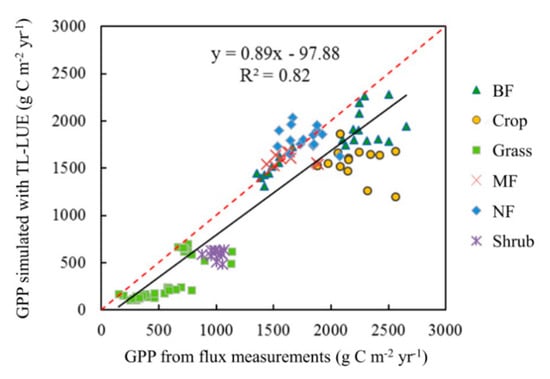
Figure 5.
GPP derived from observations at each of 13 flux tower sites and the GPP values estimated by the TL-LUE model. BF, broad-leaved forest; MF, mixed forest; NF, needle-leaf forest.

Table 4.
Comparison between gross primary productivity (GPP) of major vegetation types and total annual GPP estimated using TL-LUE and other models (ENF means evergreen needle-leaved forest; EBF means evergreen broad-leaved forest; DNF means deciduous needle-leaved forest; DBF means deciduous broad-leaved forest).
The multi-year mean GPP in China for the period 1981–2012 is shown in Fig. 6a. In the southeastern and northeastern parts of China, the GPP was higher than 1000 g C m−2 y−1. On the southeastern coast, Yunnan–Guizhou Plateau, and the southern part of the Qinghai–Tibet Plateau, the GPP was higher than 2500 g C m−2 y−1. Low values of GPP occurred over desert areas of China and the remaining parts of the Qinghai–Tibet Plateau. Given the scarcity of vegetation in these areas, their annual GPP values were less than 50 g C m−2 y−1. The northern Tianshan Mountains showed high GPP values of up to 1000–2000 g C m−2 y−1. Inner Mongolia and the southeastern part of the Qinghai–Tibet Plateau formed part of a transition zone to lower values, showing annual GPP values of 200–1000 g C m−2 y−1. Therefore, the TL-LUE model’s simulation of the average annual distribution of GPP was reasonable and was largely consistent with previous simulations [44,47]. The standard deviation of GPP during 1981–2012 showed a national average of 75 g C m−2 y−1 with a range of 0–838 g C m−2 y−1 (Figure 6b).
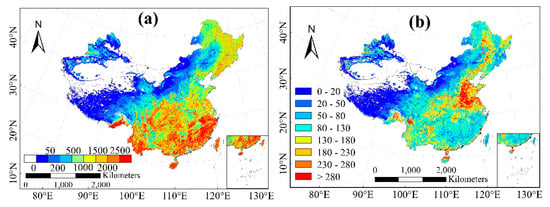
Figure 6.
Spatial distribution of the annual GPP (a) and standard deviation of GPP (b) estimated by the TL-LUE model for the period 1981–2012 (unit: g C m−2 y−1) with a spatial resolution of 0.0727°.
3.3. Spatial Distribution of Diffuse Radiation Contribution to Terrestrial Ecosystem GPP
The spatial distribution of GPP driven by Rd was consistent with that of GPP driven by Rg (Figure 7a–b). GPP driven by Rd ranged from 0 to 4348 g C m−2 y−1 with a national average of 586 g C m−2 y−1 and a national average standard deviation of 56 g C m−2 y−1. Figure 7c,d show the proportion of GPP fixed by Rd to the total GPP and its standard deviation. The proportion of GPP fixed by Rd to the total GPP ranged from 0.43 to 0.88 with a national average of 0.71, with very low standard deviation ranging from 0.0007 to 0.12. The highest proportion was in the northern Sichuan Basin and the northern parts of the Yunnan–Guizhou Plateau, where the diffuse radiation fraction was highest. Conversely, in most parts of northwestern and northeastern China, the diffuse radiation fraction was less than 0.5 (Figure 2e), where the proportion of GPP contributed by Rd to GPP derived from Rg was greater than 0.5, reflecting the higher LUE of Rd.
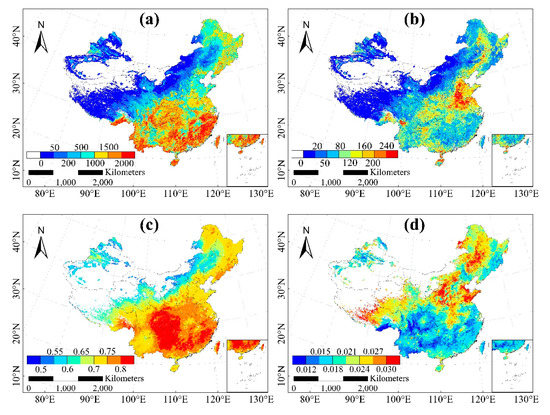
Figure 7.
Spatial distribution of the annual (a) GPP sequestrated by diffuse radiation (unit: g C m−2 y−1) and its standard deviation (b), and the ratio of annual mean (c) GPP sequestrated by diffuse radiation and global radiation and its standard deviation (d) during the period 1981–2012 with a spatial resolution of 0.0727°.
3.4. Impact of Radiation Changes on GPP
3.4.1. Simulated Interannual Variability of Total GPP in China
The total amounts of GPP for China during the period 1981–2012 from three simulations are shown in Figure 8. In S1, the mean annual total GPP for the period 1981–2012 ranged from 7.43 to 8.47 Pg C y−1. The total amount of GPP was lowest in 2000, likely because of the large-scale severe drought in China at that time. In S2, the multi-year mean annual GPP for the period 1981–2012 was 7.73 Pg C y−1, which was 0.09 Pg C y−1 higher than the average value for S1. The difference in GPP between S1 and S2 reflects the effects of the 1.3% reduction in Rg, which caused a reduction of 1.7% in GPP. In S3, the multi-year mean national total GPP was 7.58 Pg C y−1 for the period 1981–2012, which was higher than the average value for S1. The difference in GPP between S1 and S3 reflects the increase in the diffuse radiation fraction over the period 1981–2012, which positively affected GPP in China and partially compensated for the loss in GPP because of the reduction in Rg.
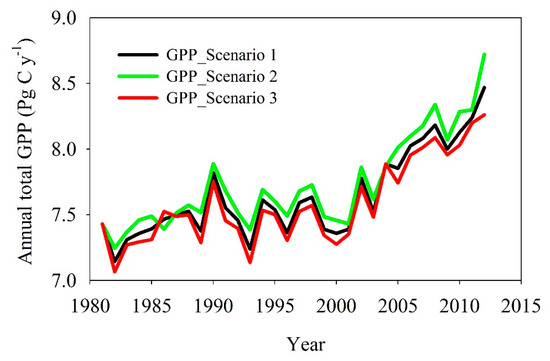
Figure 8.
Interannual variation in total annual GPP for the period 1981–2012 in China for three simulations (GPP_Scenario 1; GPP_Scenario 2; and GPPsi GPP_Scenario 3). Scenario 1 assumed that the global radiation and diffuse radiation ratio changed with time; Scenario 2 assumed that global radiation remained unchanged from 1981 to 2012; and Scenario 3 assumed that the diffuse radiation fraction remained unchanged from 1981 to 2012.
3.4.2. Spatial Distribution of Radiation Effects on GPP
The average GPP in the period 1981–2012 simulated in S2 (Figure 9a) and S3 (Figure 9c) were similar to the distribution for S1 (Figure 6). The difference (Figure 9b) between the multi-year mean GPP simulated in S1 and S2 showed that any reduction in Rg would result in a reduction in GPP over most of China. In North China, the decrease in Rg was significant, simultaneously reducing the GPP by more than 50 g C m−2 y−1. The Rg over Central and Southwest China showed no significant decrease, but these areas experienced a decrease in GPP that was higher than 50 g C m−2 y−1, which was predominantly because of the high LAI in these regions (see Supplementary Materials, Figure S5). Compared with areas with lower LAI, the reduction in Rg substantially reduced GPP for regions with higher LAI. During the period 1981–2012, the areas that showed the highest GPP increase were along the southeastern coast, northern Sichuan, as well as northeastern, northern, and some western parts of Xinjiang.
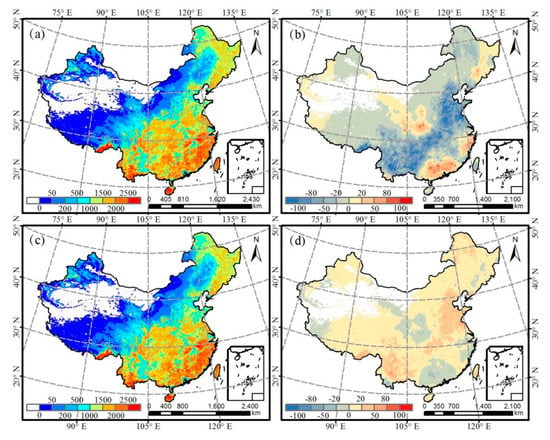
Figure 9.
Spatial distribution of the mean annual GPP simulated by scenario 2 (a); spatial distribution of the difference between the mean annual GPP in simulations 1 and 2 (b); spatial distribution of the annual mean GPP in simulation 3 (c); and spatial distribution of the difference between the mean annual GPP in simulations 1 and 3 (d) (unit: g C m−2 y−1). Simulation 1 assumed that the global radiation and diffuse radiation ratio changed with time; simulation 2 assumed that global radiation remained unchanged from 1981 to 2012; and simulation 3 assumed that the diffuse radiation fraction remained unchanged from 1981 to 2012 with a spatial resolution of 0.0727°.
The difference in GPP values between S1 and S3 are shown in Figure 9d. In most regions of China, the enhanced diffuse radiation fraction led to an increase in GPP, especially in Central China and Yunnan Province. The significant increase in GPP in Central China mainly resulted from the increase in Rd. In Yunnan Province, although the increase in diffuse radiation fraction was not significant, the GPP increased because of the high LAI (see Supplementary Materials, Figure S5). On the Qinghai–Tibet Plateau, although the diffuse radiation fraction significantly increased, the increase in GPP was not as strongly significant as that in Central China because of the scarcity of vegetation in the former region. Similarly, along the southeastern coast, in Xi’an and western parts of Xinjiang, the reduction in diffuse radiation fraction led to a reduction in GPP.
4. Discussion
In China, annual mean Rd has increased during the past 30 years [25]. An increase in Rd leads to an increase in canopy LUE because photosynthetic saturation is reduced, thereby enhancing the ecosystem GPP [3,5]. Therefore, investigating the effect of Rd on GPP is important in studies of the carbon cycle [5,8,9]. There are many causes of radiation changes, such as changes in the solar constant, clouds, aerosols, and water vapor [55]. As the world’s largest developing country, rapid economic development and rapid population growth in China have led to the emission of increasing quantities of man-made aerosols into the atmosphere. Aerosols can simultaneously change the amounts of direct and diffuse radiation reaching the surface [56]. Li et al. [57] reported that radiation decreased by about 24.1 W m−2 from September 2004 to September 2005 because of the higher aerosol concentration by using aerosol observation data from the Xianghe Station in China. In addition, volcanic eruptions can also strongly affect global and diffuse radiation [58,59]. Ren et al. [25] observed that the eruption of Mount Pinatubo in the Philippines in 1991 caused a rapid increase in the amount of diffuse radiation in China in the early 1990s.
The TL-LUE model, which provides a distinct means to investigate the effects of Rd changes on GPP, simulates GPP for sunlit (diffuse and direct radiation) and shaded leaves (diffuse radiation) separately. In the present study, during the period 1981–2012, the average GPP contributed by Rd in China was 5.69 Pg C y−1, which accounted for 74.48% of the total annual GPP. This finding shows that the contribution of Rd to GPP in China was greater than that of direct radiation. The higher contribution of Rd to GPP was largely because of the high fraction of Rd and was also associated with the higher LUE of Rd. The present results showed that the increase in Rd ratio could compensate for the reduction in GPP because of the lower photosynthetically effective radiation. These results will help to quantify the impacts of Rd on GPP and enhance knowledge of the possible causes of carbon budget variation.
Although the mean annual GPP and the GPP of each vegetation type are comparable to those reported by many previous studies (Table 4), some marked differences are apparent. The possible reasons are, first, that model structures are different, not only between process models and LUE models, but also among various LUE models. Second, the modeling area and period are set differently. For example, in the Carnegie-Ames-Stanford approach (CASA) (Table 4), Piao et al. [50] estimated that the total amount of GPP for the period 1982–2009 only varied by 2.66–3.16 Pg C y−1, whereas the average annual GPP reported by Zhu et al. [51] for 1993 was 6.24 Pg C y−1, in which maximum LUE was retrieved based on observations at 690 sites. Third, the types of input data used are inconsistent, covering different time ranges and differing in spatial and temporal resolutions.
Several uncertainties in the present study are acknowledged. First, the Rg of 1981 as a baseline was used to investigate the effect of Rg and diffuse radiation fraction on GPP in terrestrial ecosystems. The advantages of this method were that the annual Rg remained unchanged from 1981 to 2012 and the variation tendency of daily Rg variation to Rg values in 1981 was consistent. However, this method would result in a degree of uncertainty regarding daily Rg. For example, for a year that included many cloudy days, the Rg of a sunny day would be overestimated.
Second, the TL-LUE model has been validated worldwide [42,43,44], showing that the model performance for GPP simulations is satisfactory. In the present study, we obtained a high R2 (0.82) value for comparisons between the model-simulated GPP and observed GPP values. However, an extremely limited number of flux sites in China were used to optimize LUEsun and LUEshaded [43], which would cause their underestimation for some ecosystems, especially for crops. Compared with C3 plants, C4 plants photosynthesize by the combination of vascular bundle sheath cells and mesophyll cells, which have a higher CO2 assimilation rate, resulting in higher LUE [60]. Therefore, the inclusion of a few sites dominated by C4 plants to parameterize the model would result in underestimation of LUEsun and LUEshaded used in the model and the subsequent simulation would underestimate GPP values at some sites in China (Figure 5). Therefore, additional flux tower sites in China should be used to validate the model in the future.
In addition, underestimation of LAI values would result in underestimation of simulated GPP values. For example, the LAI values at the GRASS sites used in the present study were significantly lower than those of the MOD15A2 LAI product (Figure 10), which resulted in underestimation of GPP values at these sites. The GPP uncertainties caused by LAI uncertainties have been investigated and the sensitivity of GPP estimates derived from TL-LUE was lower than that of large-leaf LUE models at the site scale [43]. In the present study, the uncertainties of GPP simulated by the TL-LUE model caused by LAI uncertainties at the national scale were investigated (Figure 10). Overestimation of LAI by 10% would result in GPP overestimation by about 1.2–10%, whereas in most areas with higher LAI the overestimation of GPP was no more than 8%; similarly, underestimation of LAI by 10% would result in GPP overestimation by a similar magnitude to that mentioned above but in the inverse direction (Figure 11).
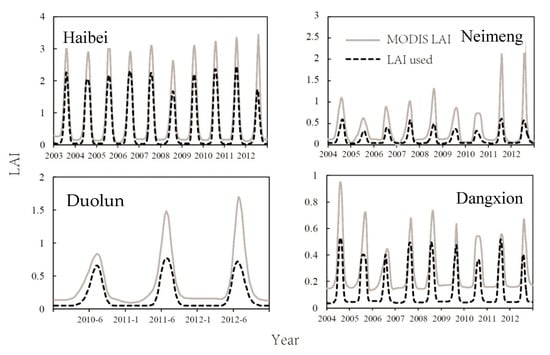
Figure 10.
Comparison of leaf area index (LAI) data used in this study and the MODIS LAI product (MOD15A2) for grassland sites, as part of the validation process for estimation of GPP (details for each site were described in Table 3).
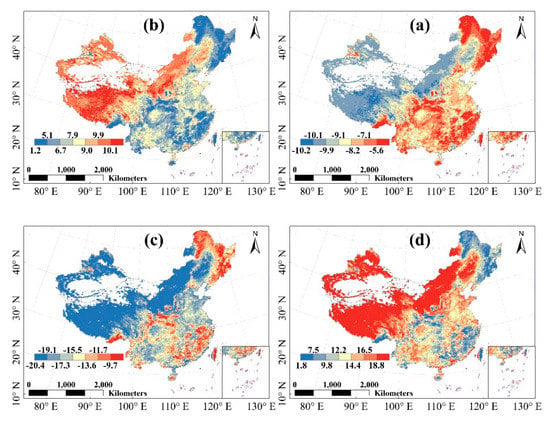
Figure 11.
Uncertainties in GPP simulated by the TL-LUE model caused by LAI uncertainties in China during the period 1981–2012 (unit: %). (a) Decrease in GPP simulated with the TL-LUE model (GPPTL) caused by a decrease in LAI by 10%; (b) increase in GPPTL caused by an increase in LAI by 10%; (c) decrease in GPPTL caused by a decrease in LAI by 20% and (d) increase in GPPTL caused by an increase in LAI by 20%.
Furthermore, radiation measurements in China are extremely limited, comprising 103 and 81 sites for global radiation and diffuse radiation, respectively; therefore, an interpolation method was used to infer the national-scale Rg and Rd. The Ångström model is commonly used for radiation interpolation [29,30]. Interpolated radiation data are widely used for ecosystem-level simulations of water and carbon dynamics [44,61]. However, because of the limited available measurements, national Rg and Rd were interpolated to 500 m based on daily extraterrestrial radiation and sunshine duration, omitting many of the drivers of dimming and Rd, which would result in Rd and Rg uncertainties, especially in heterogeneous areas.
5. Conclusions
In this study, we modeled the effects on GPP of solar radiation variation caused by changes in diffuse radiation in China over the period 1981–2012 using a two-leaf light use efficiency model (TL-LUE), which was driven by national global radiation in conjunction with other meteorological data and remotely sensed data. The main findings are as follows:
(i) The annual mean Rg in China significantly decreased over the period 1981–2012 by 2.18 MJ m−2 y−1, whereas the diffuse radiation increased. A significant reduction in Rg and increases in the diffuse radiation fraction were observed in the Beijing–Tianjin–Hebei region and on the Qinghai–Tibet Plateau. The annual mean Rd predominantly showed an upward trend over the study period, especially on the southeastern coast and the Qinghai–Tibet Plateau.
(ii) During the period 1981–2012, the average annual total GPP of China’s terrestrial ecosystems was 7.64 Pg C y−1, comprising a contribution from Rd of 5.69 Pg C y−1. The total GPP decreased by 0.09 Pg C y−1, although this decrease was partially compensated for by about 50% because of the increase in Rd. Clearly, the increase in LUE of canopy light associated with Rd partly compensated for the reduction in total GPP caused by the reduced Rg in China.
Supplementary Materials
The following are available online at https://www.mdpi.com/2072-4292/12/20/3355/s1, Figure S1: Distribution of sunshine duration, diffuse and global radiation station in China. Figure S2: Observed and interpolated daily global radiation at 12 sites in 2014; Figure S3: Observed and interpolated daily Rd at 12 sites in 2014; Figure S4: Comparisons of estimated Rg and Rd between this study and that of Ren et al. [30]; Figure S5: Spatial distribution of mean annual LAI in China from 1981 to 2012; Table S1: Proportions of sites distributed in different aerosol optical depth (AOD) levels. Table S2: Proportions of sites distributed in different AOD levels. Table S3: Scenario simulations of the impact of radiation change on GPP.
Author Contributions
Conceptualization, W.J.; formal analysis and methodology, X.W.; resources and validation, L.Z., Z.C., Y.L. and Y.S.; writing—original draft preparation, Y.Z.; writing—review and editing, W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (2016YFA0600202) and by the National Natural Science Foundation of China (42077419).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Le, Q.C.; Raupach, M.R.; Canadell, J.G.; Marland, G.; Bopp, L.; Ciais, P.; Conway, T.J.; Doney, S.C.; Feely, R.A.; Foster, P.; et al. Trends in the sources and sinks of carbon dioxide. Nat. Geosci. 2009, 2, 831–836. [Google Scholar]
- Yuan, W.P.; Cai, W.W.; Xia, J.Z. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the LaThuile database. Agric. For. Meteorol. 2014, 192–193, 108–120. [Google Scholar] [CrossRef]
- Kanniah, K.D.; Beringer, J.; North, P.; Hutley, L. Control of atmospheric particles on diffuse radiation and terrestrial plant productivity: A review. Progr. Phys. Geogr. 2012, 36, 209–237. [Google Scholar] [CrossRef]
- Cohan, D.S.; Xu, J.; Greenwald, R.; Bergin, M.H.; Chameides, W.L. Impact of atmospheric aerosol light scattering and absorption on terrestrial net primary productivity. Glob. Biogeochem. Cycle 2002, 16, 37. [Google Scholar] [CrossRef]
- Mercado, L.M.; Bellouin, N.; Sitch, S.; Boucher, O.; Huntingford, C.; Wild, M.; Cox, P.M. Impact of changes in diffuse radiation on the global land carbon sink. Nature 2009, 458, 1014–1017. [Google Scholar] [CrossRef] [PubMed]
- Farquhar, G.D.; Roderick, M.L. Pinatubo diffuse light and the carbon cycle. Science 2003, 299, 1997–1998. [Google Scholar] [CrossRef]
- Gu, L.H.; Fuentes, J.D.; Shugart, H.H.; Staebler, R.M.; Black, T.A. Responses of net ecosystem exchanges of carbon dioxide to changes in cloudiness: Results from two North American deciduous forest. J. Geophys. Res. 1999, 104, 31421–31434. [Google Scholar] [CrossRef]
- Gu, L.H.; Baldocchi, D.; Verma, S.B.; Black, T.A.; Vesala, T.; Falge, E.M.; Dowty, P.R. Advantages of diffuse radiation for terrestrial ecosystem productivity. J. Geophys. Res. 2002, 107, ACL2-1–ACL2-23. [Google Scholar] [CrossRef]
- Gu, L.H.; Baldocchi, D.D.; Wofsy, S.C.; Munger, J.W.; Michalsky, J.J.; Urbanski, S.P.; Boden, T.A. Response of a deciduous forest to the mount Pinatubo eruption: Enhanced photosynthesis. Science 2003, 299, 2035–2038. [Google Scholar] [CrossRef]
- Black, K.; Davis, P.; Lynch, P.; Jones, M.; McGettigan, M.; Osborne, B. Long-term trends in solar irradiance in ireland and their potential effects on gross primary productivity. Agric. For. Meteorol. 2006, 141, 118–132. [Google Scholar] [CrossRef]
- Chen, M.; Zhuang, Q.L. Evaluating aerosol direct radiative effects on global terrestrial ecosystem carbon dynamics from 2003 to 2010. Tellus B 2014, 66, 21808. [Google Scholar] [CrossRef]
- He, M.Z.; Ju, W.M.; Zhou, Y.L.; Chen, J.M.; He, H.L.; Wang, S.Q.; Wang, H.M.; Guan, D.X.; Yan, J.H.; Li, Y.N.; et al. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary production. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Wang, S.Q.; Huang, K.; Yan, H.; Yan, H.M.; Zhou, L.; Wang, H.M.; Zhang, J.H.; Yan, J.H.; Zhao, L.; Wang, Y.F.; et al. Improving the light use efficiency model for simulating terrestrial vegetation gross primary production by the inclusion of diffuse radiation across ecosystems in China. Ecol. Complex. 2015, 23, 1–13. [Google Scholar] [CrossRef]
- Wang, S.; Ibrom, A.; Bauer-Gottwein, P.; Garcia, M. Incorporating diffuse radiation into a light use efficiency and evapotranspiration model: An 11-year study in a high latitude deciduous forest. Agric. For. Meteorol. 2018, 248, 479–493. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.Q.; da Rocha, H.R.; Rap, A.; Bonal, D.; Butt, N.; Coupe, N.R.; Shugart, H.H. Simulation of the unexpected photosynthetic seasonality in Amazonian evergreen forests by using an improved diffuse fraction-based light use efficiency model. J. Geophys. Res. Biogeosci. 2017, 122, 3014–3030. [Google Scholar] [CrossRef]
- Zheng, Y.; Shen, R.Q.; Wang, Y.W.; Li, X.Q.; Liu, S.G.; Liang, S.L.; Chen, J.M.; Ju, W.M.; Zhang, L.; Yuan, W.P. Improved estimate of global gross primary production for reproducing its long-term variation, 1982–2017. Earth Syst. Sci. Data 2019, 126, 1–31. [Google Scholar]
- Wild, M.; Gilgen, H.; Roesch, A.; Ohmura, A.; Long, C.N.; Dutton, E.G.; Forgan, B.; Kallis, A.; Russak, V.; Tsvetkov, A. From dimming to brightening: Decadal changes in solar radiation at earth’s surface. Science 2005, 308, 847–850. [Google Scholar] [CrossRef]
- Ohmura, A. Observed long-term variations of solar irradiance at the earth’s surface. Space Sci. Rev. 2006, 125, 111–128. [Google Scholar] [CrossRef]
- Shi, G.Y.; Hayasaka, T.; Ohmura, A.; Chen, Z.H.; Wang, B.; Zhao, J.Q.; Che, H.Z.; Xu, L. Data quality assessment and the long-term trend of ground solar radiation in China. J. Appl. Meteor. 2008, 47, 1006–1016. [Google Scholar] [CrossRef]
- Norris, J.R.; Wild, M. Trends in aerosol radiative effects over China and Japan inferred from observed cloud cover solar “dimming” and solar “brightening”. J. Geophys. Res. 2009, 114, D15. [Google Scholar] [CrossRef]
- Qi, Y.; Fang, S.B.; Zhou, W.Z. Variation and spatial distribution of surface solar radiation in China over recent 50 years. Acta Ecol. Sin. 2014, 34, 7444–7453. (In Chinese) [Google Scholar]
- Che, H.Z.; Shi, G.Y.; Zhang, X.Y.; Arimoto, R.; Zhao, J.Q.; Xu, L.; Wang, B.; Chen, Z.H. Analysis of 40 years of solar radiation data from China, 1961–2000. Geophys. Res. Lett. 2005, 32, 2341–2352. [Google Scholar] [CrossRef]
- Qian, Y.; Kaiser, D.P.; Leung, L.R.; Xu, M. More frequent cloud-free sky and less surface solar radiation in China from 1955 to 2000. Geophys. Res. Lett. 2006, 33, L01812. [Google Scholar] [CrossRef]
- Yang, H.B.; Yang, D.W. Climatic factors influencing changing pan evaporation across China from 1961 to 2001. J. Hydrol. 2012, 414–415, 184–193. [Google Scholar] [CrossRef]
- Ren, X.L.; He, H.L.; Zhang, L.; Zhou, L.; Yu, G.R.; Fan, J.W. Spatiotemporal variability analysis of diffuse radiation in China during 1981–2010. Ann. Geophys. 2013, 31, 277–289. [Google Scholar] [CrossRef]
- He, X.Z.; Zhou, T.; Jia, G.S.; Zhang, Z.Y.; Li, X.J.; Zhao, C.; Feng, S.H. Modeled effects of changes in the amount and diffuse fraction of PAR on forest GPP. J. Nat. Res. 2011, 26, 619–634. [Google Scholar]
- Li, D.Q.; Zhou, Y.L.; Ju, W.M.; Wang, H.M.; Liu, Y.B.; Wu, X.C. Modelling the effects of changes in solar radiation on gross primary production in subtropical evergreen needle-leaf plantations. Chin. J. Plant Ecol. 2014, 38, 219–230. [Google Scholar]
- Allen, R.G.; Walter, I.A.; Elliott, R.L.; Howell, T.A.; Itenfisu, D.; Jensen, M.E.; Snyder, R.L. The ASCE Standardized Reference Evapotranspiration Equation; Final Report; Environmental and Water Resources Institute of the American Society of Civil Engineers: Reston, VA, USA, 2005. [Google Scholar]
- Ångström, A. Solar and terrestrial radiation. Report to the international commission for solar research on actinometric investigations of solar and atmospheric radiation. Q. J. R. Meteorol. Soc. 1924, 50, 121–126. [Google Scholar] [CrossRef]
- Ren, X.L.; He, H.L.; Zhang, L.; Yu, G.R. Global radiation, photosynthetically active radiation, and the diffuse component dataset of China, 1981–2010. Earth Syst. Sci. Data 2018, 10, 1217–1226. [Google Scholar] [CrossRef]
- Chen, R.S.; Ersi, K.; Yang, J.P.; Lu, S.H.; Zhao, W.Z. Validation of five global radiation models with measured daily data in China. Energy Conv. Manag. 2004, 45, 1759–1769. [Google Scholar] [CrossRef]
- Roderick, M.L. Estimating the diffuse component from daily and monthly measurements of global radiation. Agric. For. Meteorol. 1999, 95, 169–185. [Google Scholar] [CrossRef]
- Singh, U.P. Diffuse Radiation Calculation Methods. Ph.D. Thesis, Science Arizona State University, Tempe, AZ, USA, 2016. [Google Scholar]
- Liu, Y.; Liu, R.G.; Chen, J.M. Retrospective retrieval of long-term consistent global leaf area index (1981–2011) from combined AVHRR and MODIS data. J. Geophys. Res. 2012, 117, G04003. [Google Scholar] [CrossRef]
- Sawada, Y.; Koike, T. Simultaneous estimation of both hydrological and ecological parameters in an ecohydrological model by assimilating microwave signal. J. Geophys. Res. Atmos. 2014, 119, 8839–8857. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, X.J.; Yu, G.R.; He, N.P.; Wang, Q.F.; Tian, J. Water use efficiency threshold for terrestrial ecosystem carbon sequestration in China under afforestation. Agric. For. Meteorol. 2014, 195–196, 32–37. [Google Scholar] [CrossRef]
- Zhu, X.J.; Yu, G.R.; He, H.L.; Wang, Q.F.; Chen, Z.; Gao, Y.N.; Zhang, Y.P.; Zhang, J.H.; Yan, J.H.; Wang, H.M.; et al. Geographical statistical assessments of carbon fluxes in terrestrial ecosystems of China: Results from upscaling network observations. Glob. Planet. Chang. 2014, 118, 52–61. [Google Scholar] [CrossRef]
- Piao, S.L.; Yin, G.D.; Tan, J.G.; Cheng, L.; Huang, M.T.; Li, Y.; Liu, R.G.; Mao, J.F.; Myneni, R.B.; Peng, S.S.; et al. Detection and attribution of vegetation greening trend in China over the last 30 years. Glob. Chang. Biol. 2015, 21, 1601–1609. [Google Scholar] [CrossRef]
- Chen, J.M.; Ju, W.M.; Ciais, P.; Viovy, N.; Liu, R.G.; Liu, Y.; Lu, X.H. Vegetation structural change since 1981 significantly enhanced the terrestrial carbon sink. Nat. Commun. 2019, 10, 1–7. [Google Scholar] [CrossRef]
- Running, S.; Thornton, P.; Nemani, R.; Glassy, J. Global terrestrial gross and net primary productivity from the earth observing system. Methods Ecosyst. Sci. 2000, 3, 44–57. [Google Scholar]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Modell. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- Wu, X.C.; Ju, W.M.; Zhou, Y.L.; He, M.Z.; Law, B.E.; Black, T.A.; Margolis, H.A.; Cescatti, A.; Gu, L.H.; Montagnani, L.; et al. Performance of linear and nonlinear two-leaf light use efficiency models at different temporal scales. Remote Sens. 2015, 7, 2238–2278. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Wu, X.C.; Ju, W.M.; Chen, J.M.; Wang, S.Q.; Yuan, W.P.; Black, T.A.; Jassal, R.; Ibrom, A.; Han, S.J.; et al. Global parameterization and validation of a two-leaf light use efficiency model for predicting gross primary production across FLUXNET sites. J. Geophys. Res. Biogeosci. 2016, 121, 1045–1072. [Google Scholar] [CrossRef]
- Zan, M.; Zhou, Y.L.; Ju, W.M.; Zhang, Y.G.; Zhang, L.M.; Liu, Y.B. Performance of a two-leaf light use efficiency model for mapping gross primary productivity against remotely sensed sun-induced chlorophyll fluorescence data. Sci. Total Environ. 2018, 613–614, 977–989. [Google Scholar] [CrossRef]
- Tang, W.J.; Yang, K.; Qin, J.; Cheng, C.C.K.; He, J. Solar radiation trend across China in recent decades: A revisit with quality-controlled data. Atmos. Chem. Phys. 2011, 11, 393–406. [Google Scholar] [CrossRef]
- Lin, C.G.; Wu, H.P.; Ou, T.H.; Chen, D.L. A new perspective on solar dimming over the Tibetan Plateau. Int. J. Climatol. 2019, 39, 302–316. [Google Scholar] [CrossRef]
- Li, X.L.; Liang, S.L.; Yu, G.R.; Yuan, W.P.; Cheng, X.; Xia, J.Z.; Zhao, T.B.; Feng, J.M.; Ma, Z.G.; Ma, M.G.; et al. Estimation of gross primary production over the terrestrial ecosystems in China. Ecol. Modell. 2013, 261–262, 80–92. [Google Scholar] [CrossRef]
- Wang, Q.F.; Zheng, H.; Zhu, X.J.; Yu, G.R. Primary estimation of Chinese terrestrial carbon sequestration during 2001–2010. Sci. Bull. 2015, 60, 577–590. [Google Scholar] [CrossRef]
- Gao, Z.Q.; Liu, J.Y. Comparative study on net productivity of vegetation in China. Chin. Sci. Bull. 2008, 53, 317–326. [Google Scholar] [CrossRef]
- Piao, S.L.; Fang, J.Y.; Zhou, L.M.; Zhu, B.; Tan, K.; Tao, S. Changes in vegetation net primary productivity from 1982 to 1999 in China. Glob. Biogeochem. Cycle 2005, 19, GB2027. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Pan, Y.Z.; Zhang, J.S. Estimation of net primary productivity of Chinese terrestrial vegetation based on remote sensing. Acta Phytoecol. Sin. 2007, 31, 413–424. (In Chinese) [Google Scholar]
- Feng, X.; Liu, G.H.; Chen, J.; Chen, M.; Liu, J.; Ju, W.M.; Sun, R.; Zhou, W. Net primary productivity of China’s terrestrial ecosystems from a process model driven by remote sensing. J. Environ. Manag. 2007, 85, 563–573. [Google Scholar] [CrossRef]
- Xiao, X.; Melillo, J.M.; Kicklighter, D.W.; Pan, Y.; McGuire, A.D.; Helfrich, J. Net primary production of terrestrial ecosystems in China and its equilibrium responses to changes in climate and atmospheric CO2 concentration. Acta Phytoecol. Sin. 1998, 22, 97–118. [Google Scholar]
- Tao, B.; Li, K.R.; Shao, X.M.; Cao, M.K. The temporal and spatial patterns of terrestrial net primary productivity in China. J. Geogr. Sci. 2003, 13, 163–171. [Google Scholar]
- Stanhill, G.; Cohen, S. Global dimming: A review of the evidence for a widespread and significant reduction in global radiation with discussion of its possible causes and possible agricultural consequences. Agric. For. Meteorol. 2001, 107, 255–278. [Google Scholar] [CrossRef]
- Ramanathan, V.; Crutzen, P.J.; Kiehl, J.T. Atmosphere, aerosols, climate, and the hydrological cycle. Science 2001, 294, 2119–2124. [Google Scholar] [CrossRef]
- Li., Z.; Xia, X.; Cribb, M. Aerosol optical properties and their radiative effects in northern China. J. Geophys. Res. Atmos. 2007, D22S01. [Google Scholar] [CrossRef]
- Qiu, J.H.; Yang, L.Q. Variation characteristics of atmospheric aerosol optical depths and visibility in North China during 1980–1994. Atmos. Environ. 2000, 34, 603–609. [Google Scholar]
- Wild, M.; Trüssel, B.; Ohmura, A. Global dimming and brightening: An update beyond 2000. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Hicks, S.R.A.; Brisk, D.D.; Call, C.A. Co-existence of a perennial C3 bunchgrass in a C4 dominated grassland: An evaluation of gas exchange characteristics. Photosynthetica 1990, 24, 63–74. [Google Scholar]
- Liu, Y.B.; Xiao, J.F.; Ju, W.M.; Zhu, G.L.; Wu, X.C.; Fan, W.L.; Li, D.Q.; Zhou, Y.L. Satellite-derived LAI products exhibit large discrepancies and can lead to substantial uncertainty in simulated carbon and water fluxes. Remote Sens. Environ. 2018, 206, 174–188. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).