Author Contributions
Conceptualization, L.A. and I.P.; methodology, L.A. and I.P.; software, L.A.; validation, L.A., I.P., E.H., and S.T.; formal analysis, L.A.; investigation, L.A.; resources, I.P.; data curation, L.A., I.P., E.H., and S.T.; writing—original draft preparation, L.A.; writing—review and editing, E.H., S.T., I.P., and L.A.; visualization, L.A.; supervision, I.P.; project administration, I.P.; funding acquisition, I.P. All authors have read and agreed to the published version of the manuscript.
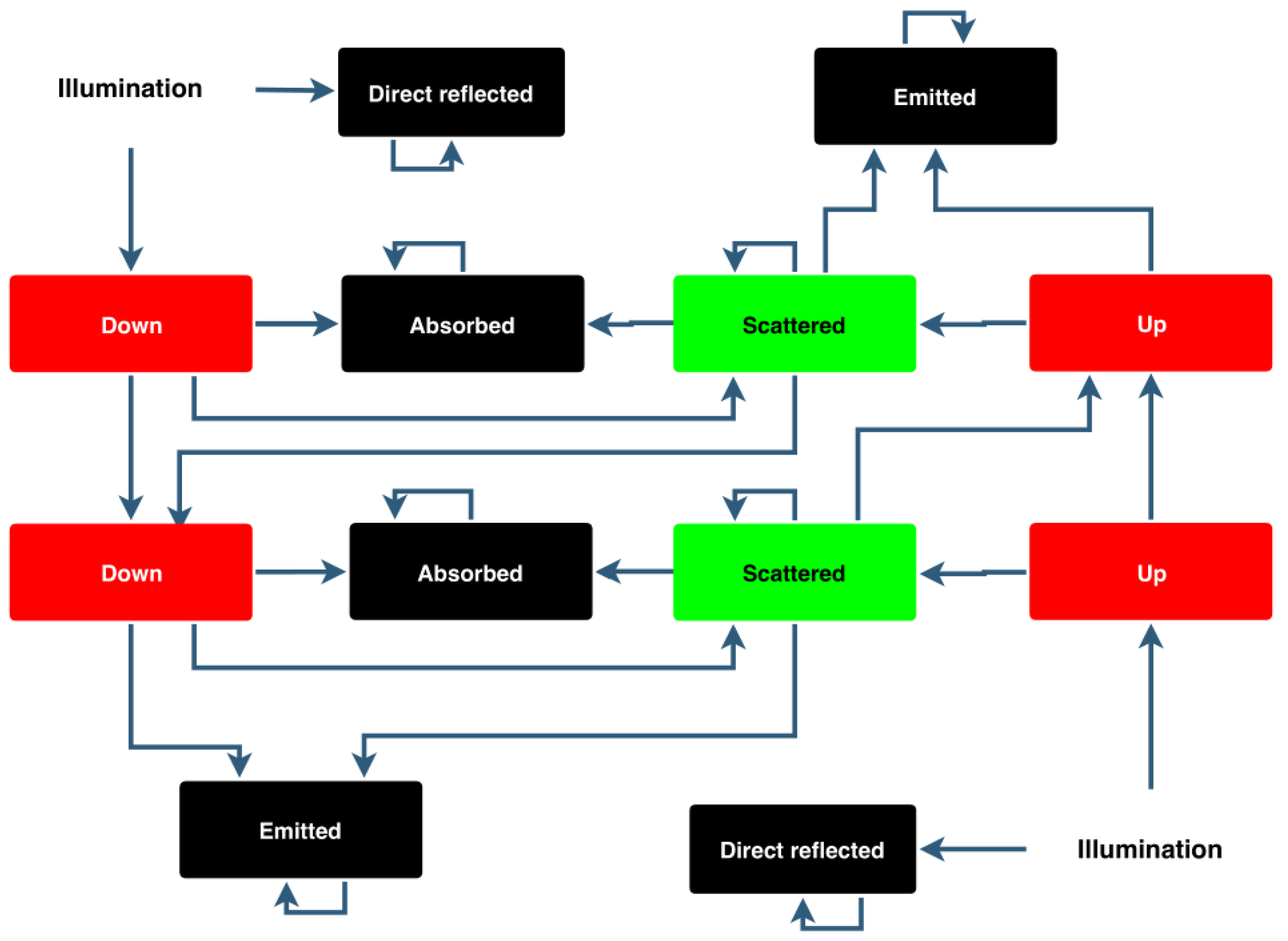
Figure 1.
Diagram representation of stochastic model of leaf optical properties (SLOP). A tree leaf is assumed to have two major layers: a palisade layer and a spongy layer. In both layers, a photon can go straight through, be absorbed or scatter until it is absorbed or it moves to the previous or next layer. Adapted from [
22].
Figure 1.
Diagram representation of stochastic model of leaf optical properties (SLOP). A tree leaf is assumed to have two major layers: a palisade layer and a spongy layer. In both layers, a photon can go straight through, be absorbed or scatter until it is absorbed or it moves to the previous or next layer. Adapted from [
22].
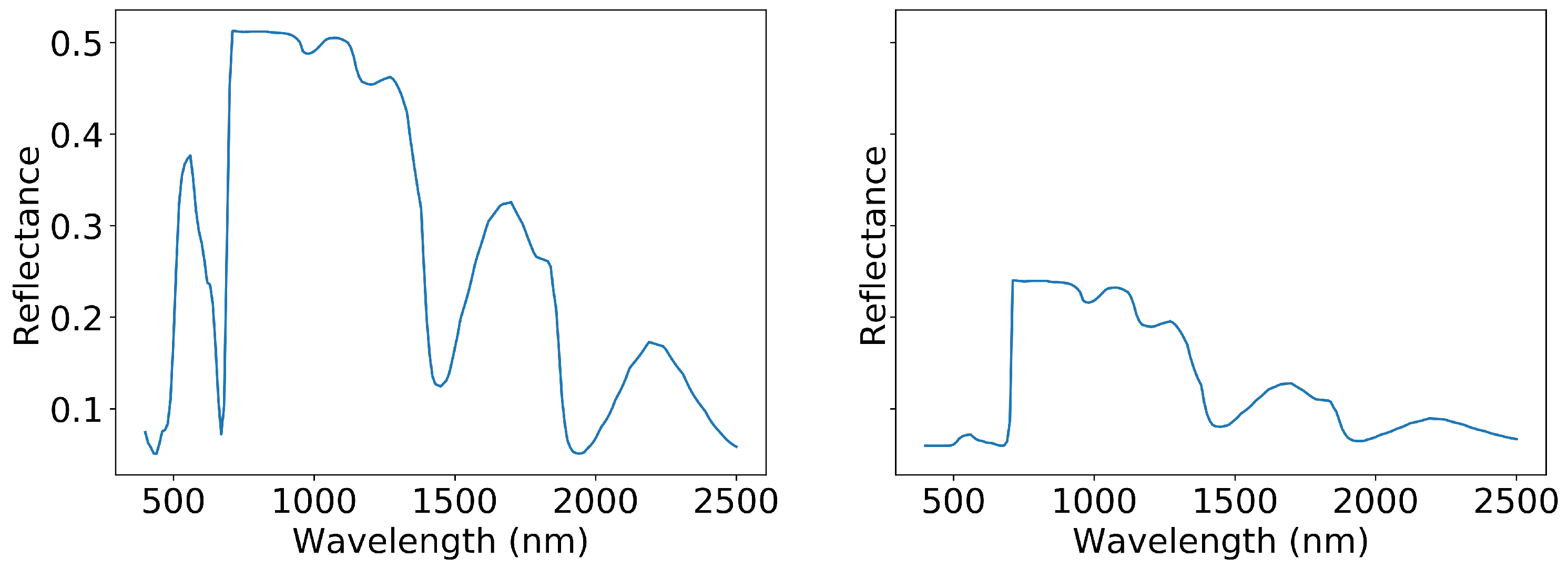
Figure 2.
Two spectra produced with SLOP. The graph on the left is produced with minimum values from
Table 1 while the graph on the right is produced with maximum values.
Figure 2.
Two spectra produced with SLOP. The graph on the left is produced with minimum values from
Table 1 while the graph on the right is produced with maximum values.
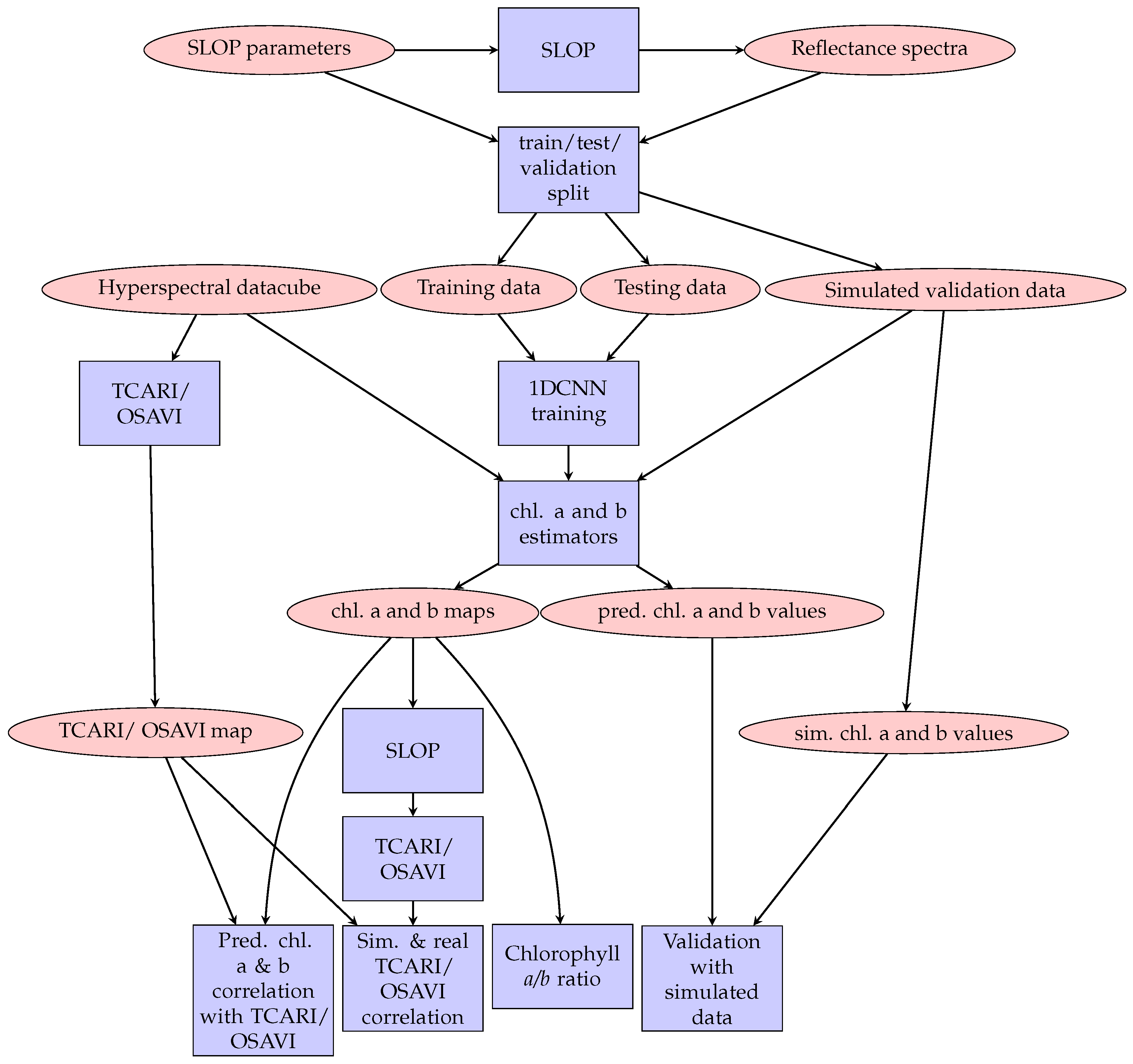
Figure 4.
Flow chart of the research methodology. Ovals represent data and boxes represent methods.
Figure 4.
Flow chart of the research methodology. Ovals represent data and boxes represent methods.
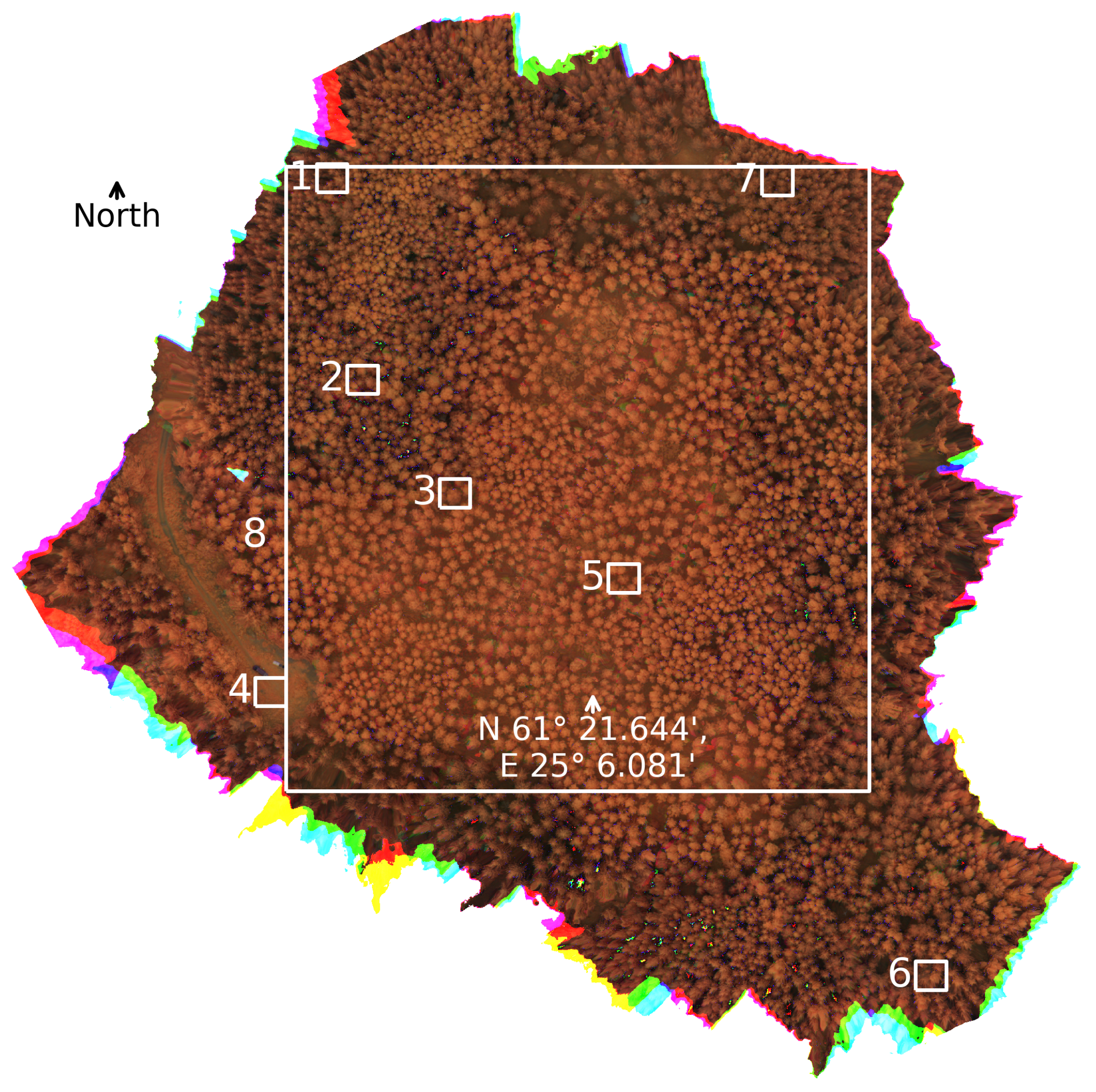
Figure 5.
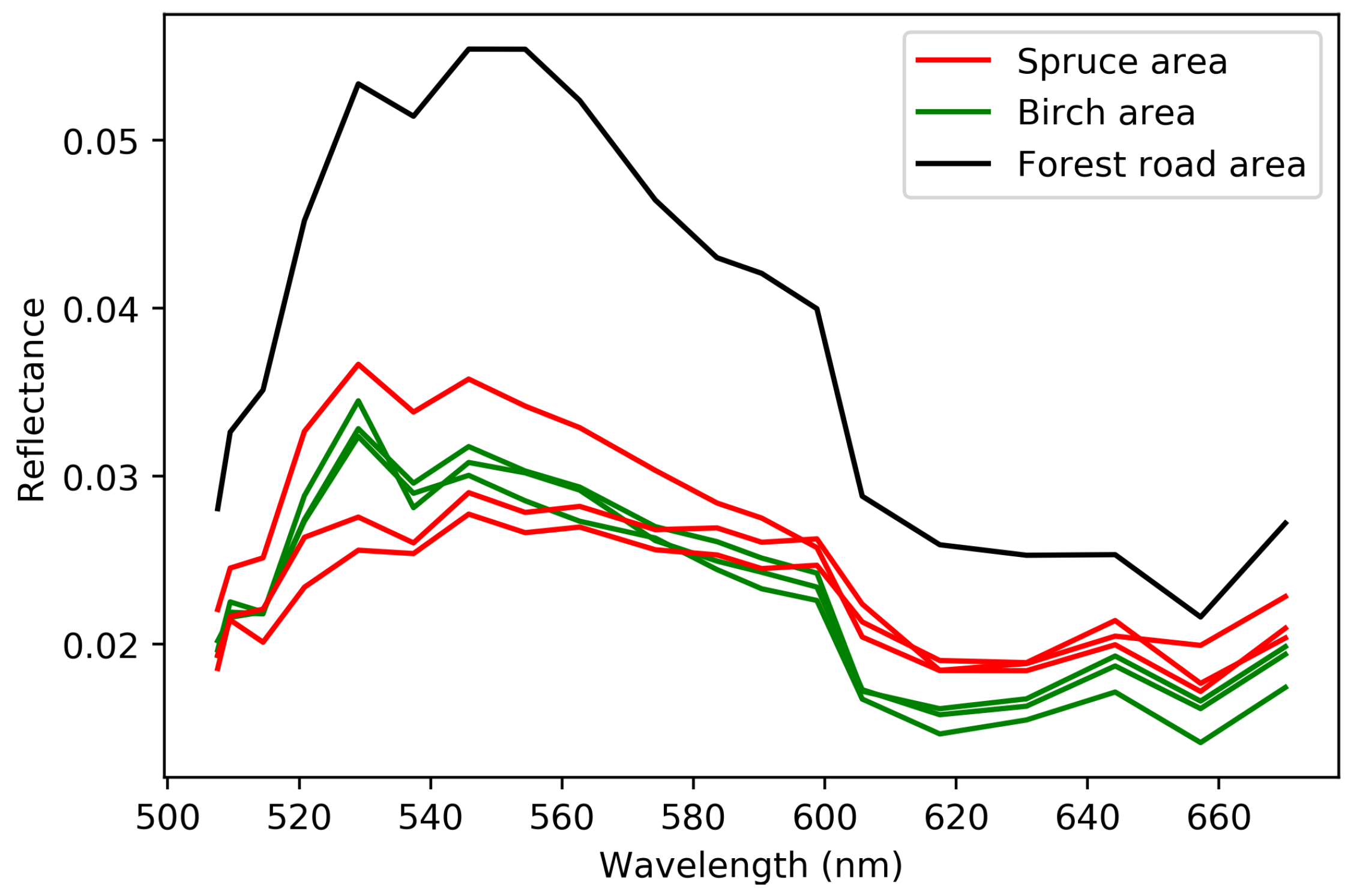
Plots selected for in-depth analysis plotted over a false color image of the research forest. The wavelength bands used in making the figure are approximately 800 , 700 , and 500 . The edges show a rainbow artefact produced by some of the bands being empty in the plot. Plots 1, 5, and 6 are in a spruce-dominated plot, plots 2, 3, and 5 are in a birch-dominated plot and plot 4 is on a forest road. Plot 8 is a larger plot that consists mainly of birch forest, while having a significant amount of spruce on the border plots.
Figure 5.
Plots selected for in-depth analysis plotted over a false color image of the research forest. The wavelength bands used in making the figure are approximately 800 , 700 , and 500 . The edges show a rainbow artefact produced by some of the bands being empty in the plot. Plots 1, 5, and 6 are in a spruce-dominated plot, plots 2, 3, and 5 are in a birch-dominated plot and plot 4 is on a forest road. Plot 8 is a larger plot that consists mainly of birch forest, while having a significant amount of spruce on the border plots.
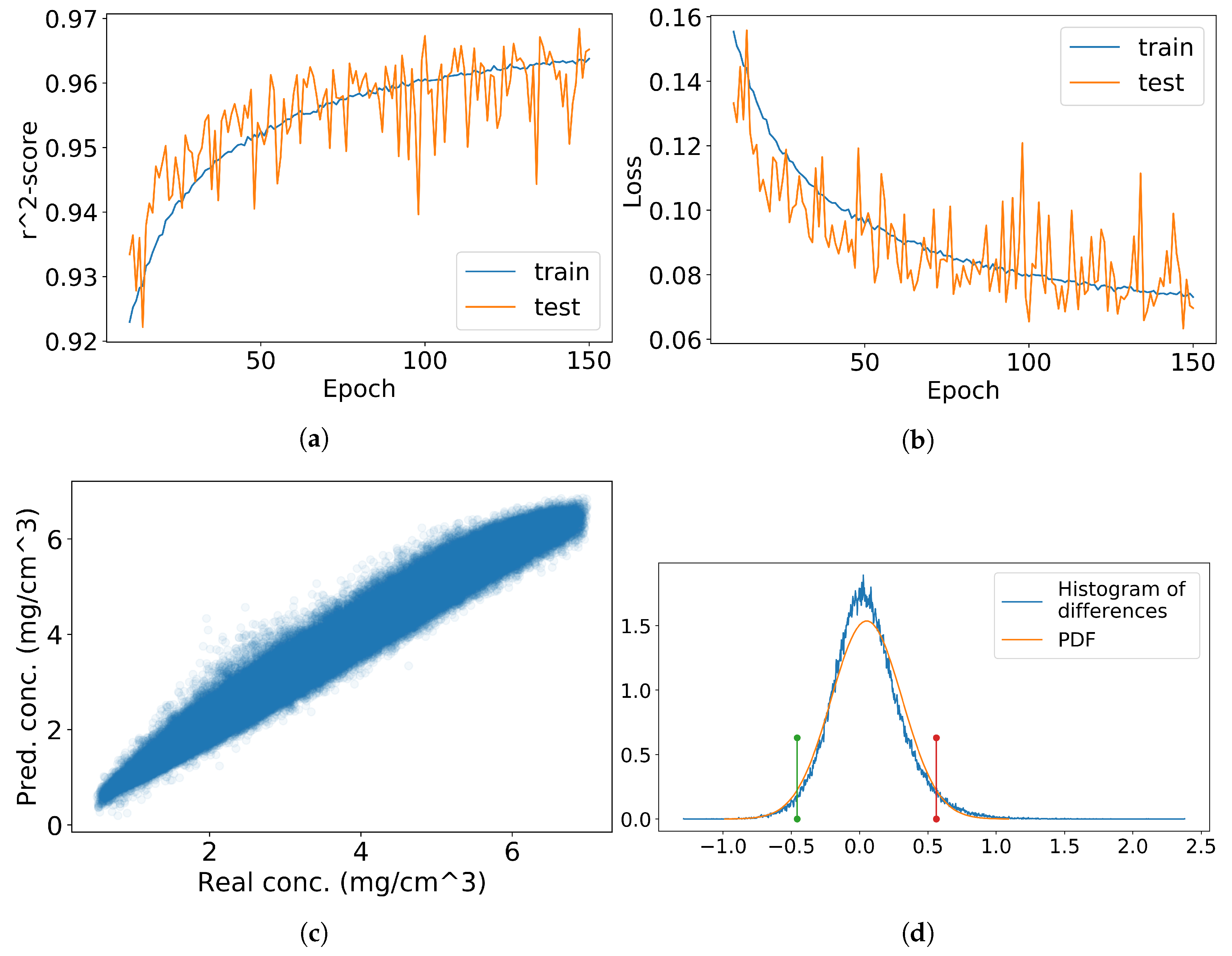
Figure 6.
Convolutional neural network (CNN) training and testing results for chlorophyll a (a–d) and b (e–h). Figures (a,e) contain training and testing scores and figures (b,f) contain training and testing mean square error (MSE) scores. In figures (c,g) the estimated values are compared to the values in the validation dataset and in figures (d,h) their difference is computed and the matching normal distribution is calculated. Red and green lines represent the 95% confidence interval.
Figure 6.
Convolutional neural network (CNN) training and testing results for chlorophyll a (a–d) and b (e–h). Figures (a,e) contain training and testing scores and figures (b,f) contain training and testing mean square error (MSE) scores. In figures (c,g) the estimated values are compared to the values in the validation dataset and in figures (d,h) their difference is computed and the matching normal distribution is calculated. Red and green lines represent the 95% confidence interval.
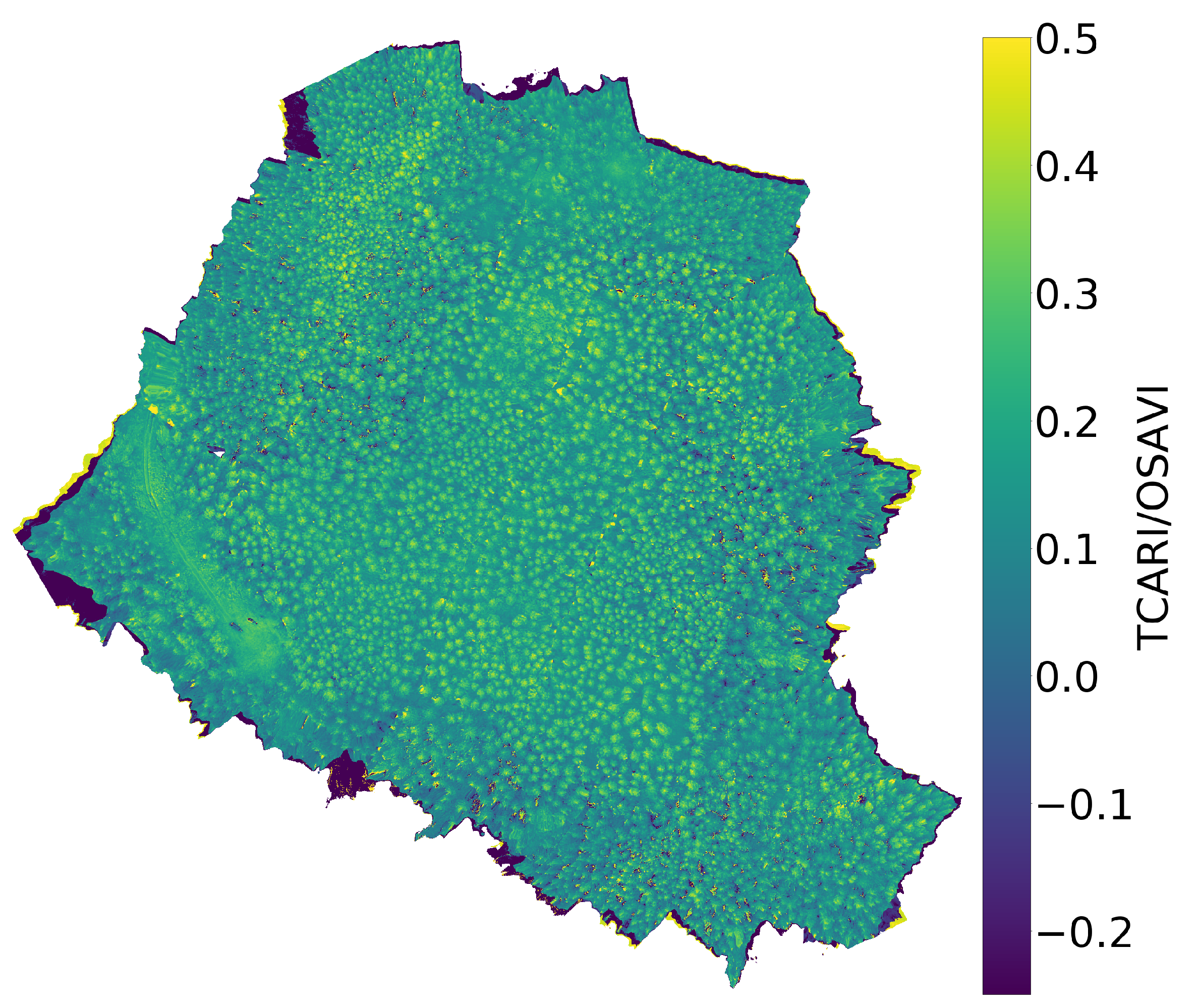
Figure 7.
The chlorophyll a (top), b (middle), and index (bottom) maps. The chlorophyll maps are calculated by feeding the hyperspectral data to the inverse SLOP model.
Figure 7.
The chlorophyll a (top), b (middle), and index (bottom) maps. The chlorophyll maps are calculated by feeding the hyperspectral data to the inverse SLOP model.
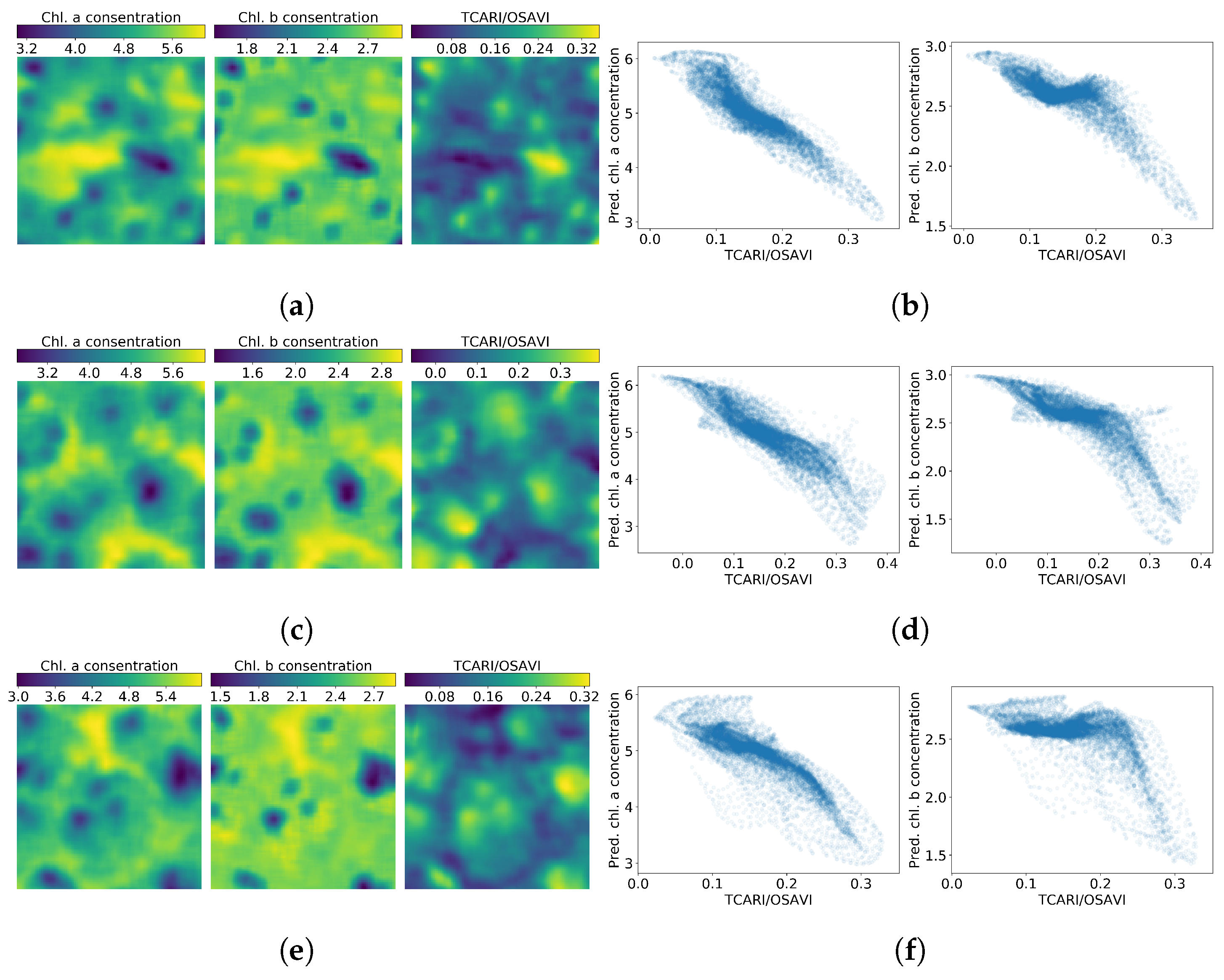
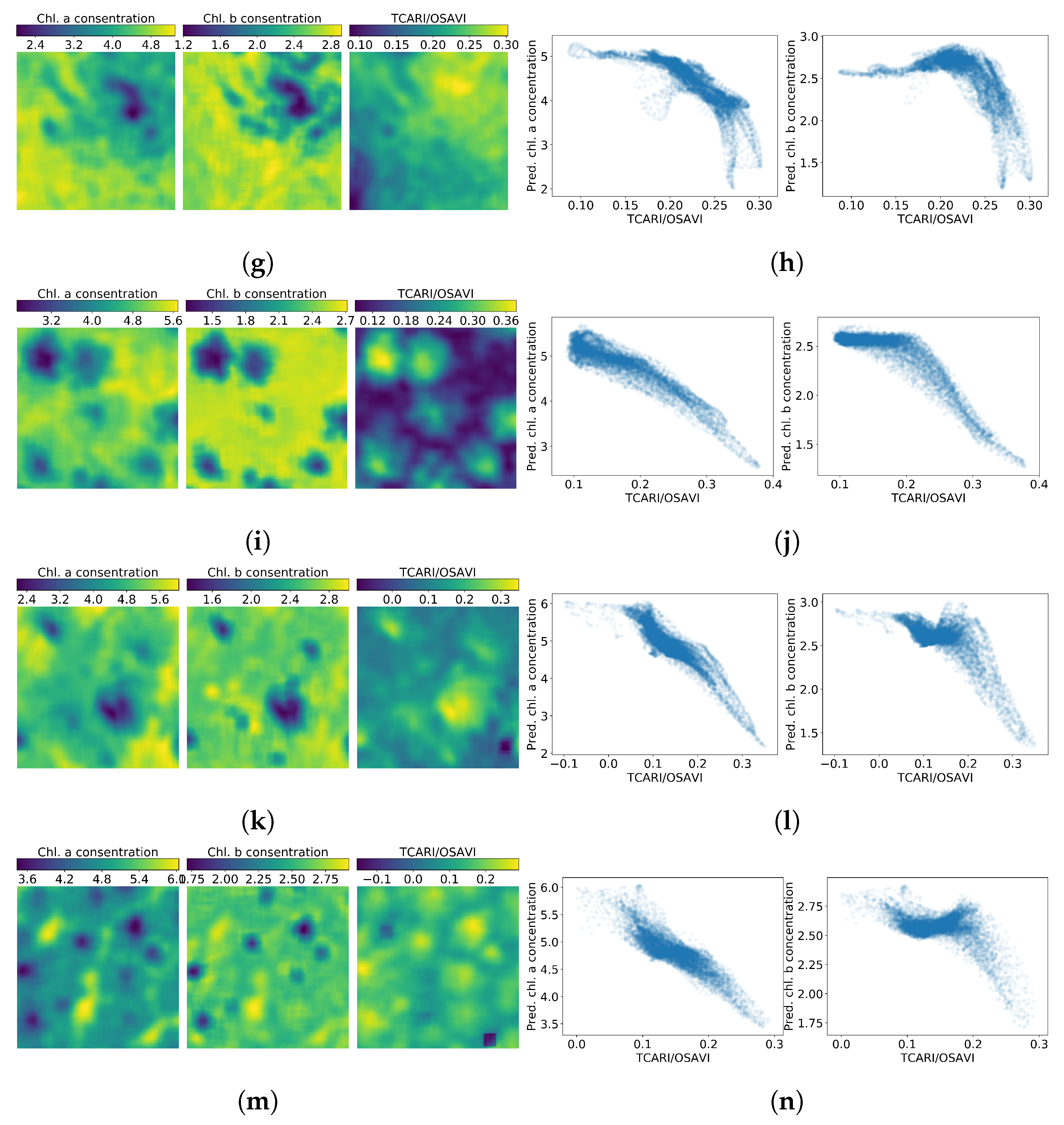
Figure 8.
Chlorophyll a, b and maps (left column) and correlation between the chlorophylls and the index (right column) in plots 1–7. Figures (a,b) are related to plot 1, (c,d) to plot 2, (e,f) to plot 3, (g,h) to plot 4, (i,j) to plot 5, (k,l) to plot 6 and (m,n) to plot 7.
Figure 8.
Chlorophyll a, b and maps (left column) and correlation between the chlorophylls and the index (right column) in plots 1–7. Figures (a,b) are related to plot 1, (c,d) to plot 2, (e,f) to plot 3, (g,h) to plot 4, (i,j) to plot 5, (k,l) to plot 6 and (m,n) to plot 7.
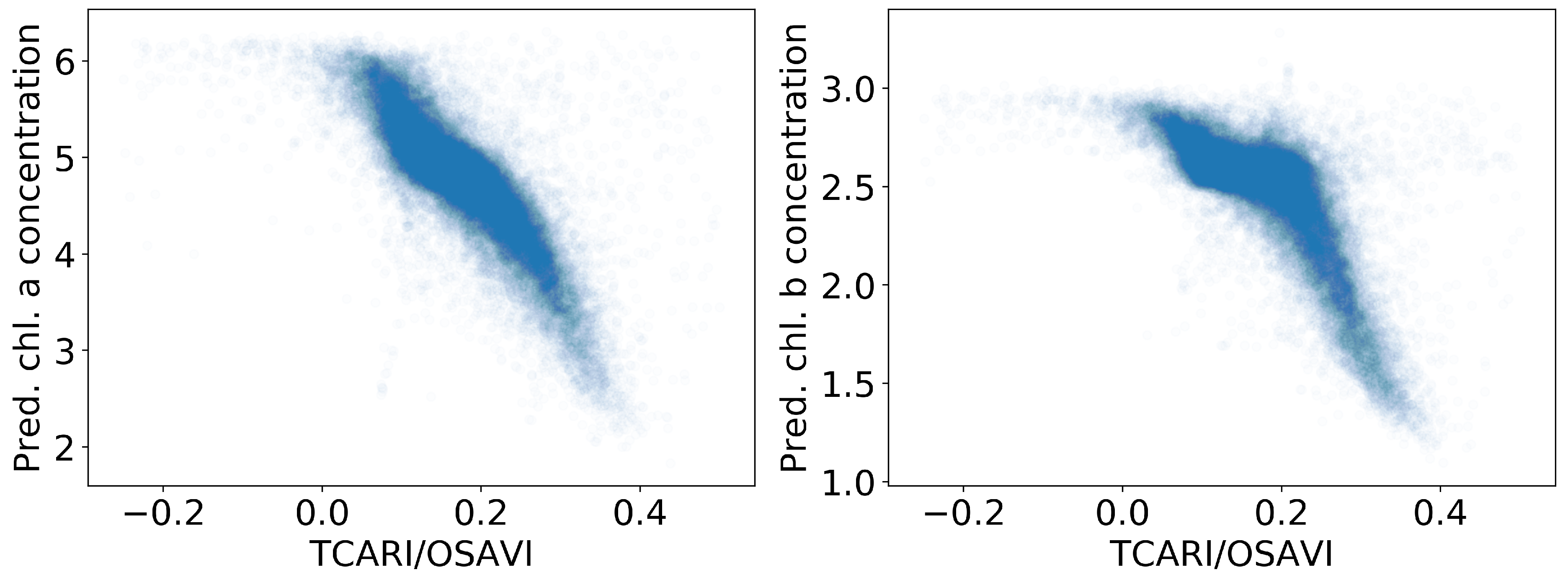
Figure 9.
Correlation between chlorophyll and the index in larger plot 8.
Figure 9.
Correlation between chlorophyll and the index in larger plot 8.
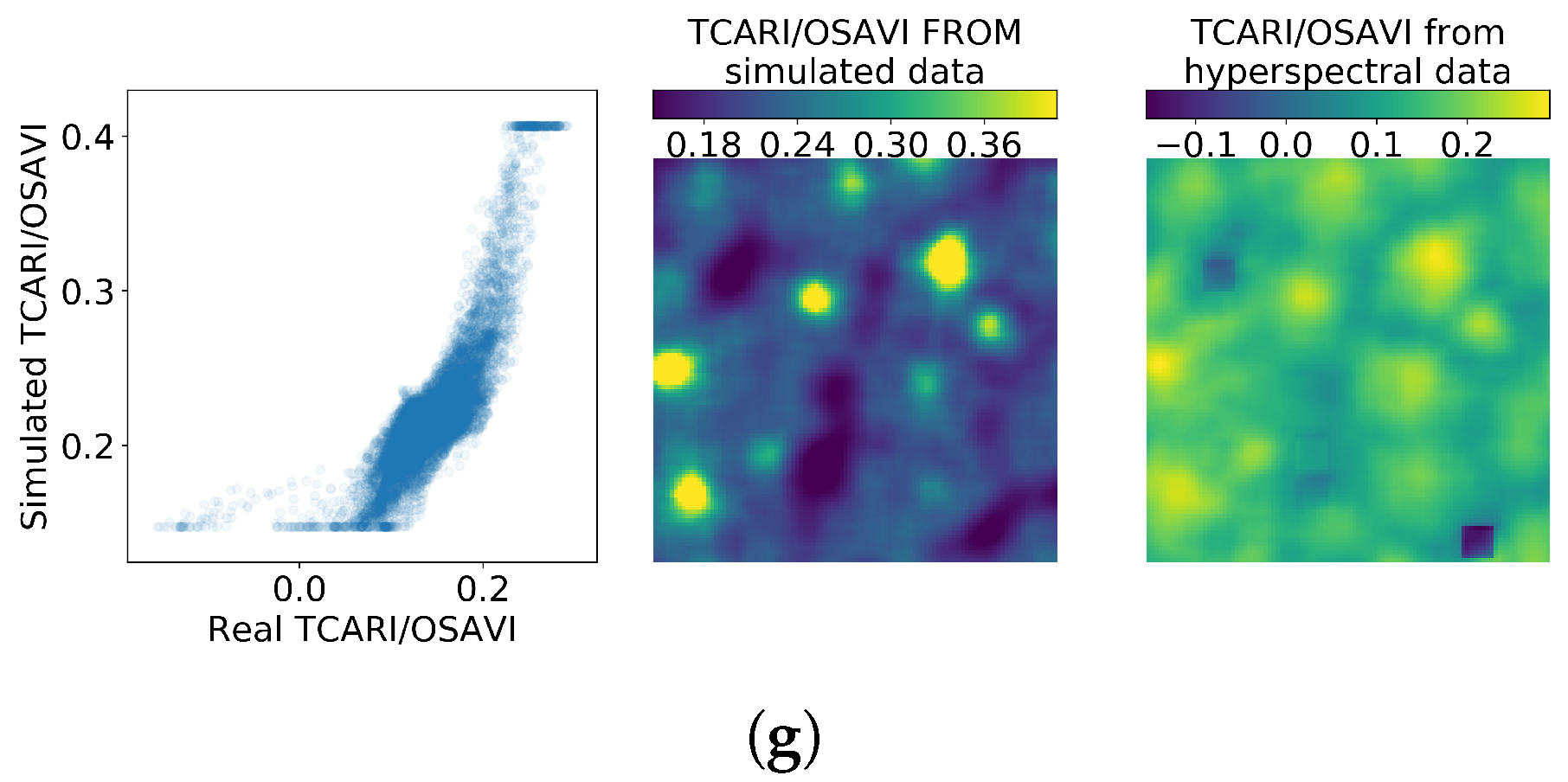
Figure 10.
Comparison between simulated and empirical indexes. The simulated index is calculated from data simulated using SLOP. (a) corresponds to the research plot 1, (b) to plot 2, (c) to 3, (d) to 4, (e) to 5, (f) to 6 and (g) to 7.
Figure 10.
Comparison between simulated and empirical indexes. The simulated index is calculated from data simulated using SLOP. (a) corresponds to the research plot 1, (b) to plot 2, (c) to 3, (d) to 4, (e) to 5, (f) to 6 and (g) to 7.
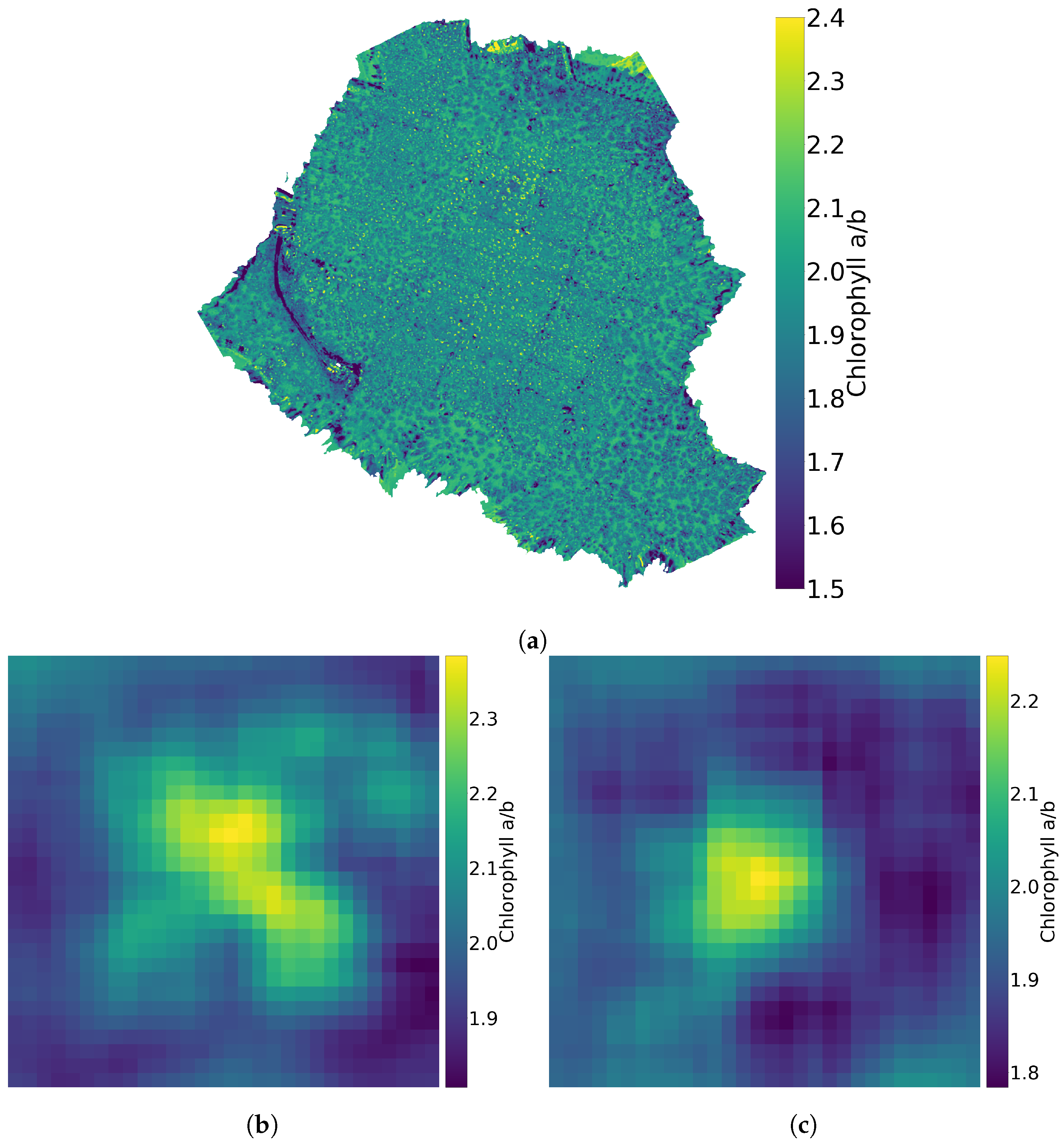
Figure 11.
Chlorophyll a values divided by chlorophyll b values for the whole forest (a), for a birch (b) and for a spruce (c).
Figure 11.
Chlorophyll a values divided by chlorophyll b values for the whole forest (a), for a birch (b) and for a spruce (c).
Table 1.
Constants and variables used in making training, testing, and validation data with SLOP. The training, testing, and validation data consist of 500,000 spectra made with SLOP. Each spectrum is produced by taking a random value from each interval in the table and calculating SLOP for each specified wavelength. The spectra are divided into training, testing, and validation data randomly, with constant sizes.
Table 1.
Constants and variables used in making training, testing, and validation data with SLOP. The training, testing, and validation data consist of 500,000 spectra made with SLOP. Each spectrum is produced by taking a random value from each interval in the table and calculating SLOP for each specified wavelength. The spectra are divided into training, testing, and validation data randomly, with constant sizes.
| | | Leaf Layer |
|---|
| | | Palisade | Spongy |
|---|
| Variables | Chlorophyll a concentration (/) | [1, 10] | [0, 4] |
| Chlorophyll b concentration (/) | [0.5, 5.5] | [0, 3] |
| -carotene concentration (/) | [0, 1] | [0, 0.5] |
| Lutein concentration (/) | [0, 1] | [0, 0.5] |
| Violaxanthin concentration (/) | [0, 0.5] | [0, 0.25] |
| Neoxanthin concentration (/) | [0, 0.5] | [0, 0.25] |
| Water content (/) | [0.8, 1] | [0.1, 0.5] |
| scattering coefficient (1/) | [3.5, 5.5] | [1000, 1100] |
| Probability of direct reflection | [0.4, 0.06] |
| Constants | Chloroplast diameter () | 0.0005 |
| Chloroplast concentration (1/) | | |
| Thickness () | 0.0069 | 0.0069 |
Table 2.
Wavelength and full width of the half maximum (FWHM) values of the measured hyperspectral data [
41].
Table 2.
Wavelength and full width of the half maximum (FWHM) values of the measured hyperspectral data [
41].
| Wavelength (nm): | 507.60, 509.50, 514.50, 520.80, 529.00, 537.40, 545.80, 554.40, 562.70, 574.20, 583.60, 590.40, 598.80, 605.70, 617.50, 630.70, 644.20, 657.20, 670.10, 677.80, 691.10, 698.40, 705.30, 711.10, 717.90, 731.30, 738.50, 751.50, 763.70, 778.50, 794.00, 806.30, 819.70 |
| FWHM (nm): | 11.2, 13.6, 19.4, 21.8, 22.6, 20.7, 22.0, 22.2, 22.1, 21.6, 18.0, 19.8, 22.7, 27.8, 29.3, 29.9, 26.9, 30.3, 28.5, 27.8, 30.7, 28.3, 25.4, 26.6, 27.5, 28.2, 27.4, 27.5, 30.5, 29.5, 25.9, 27.3, 29.9 |
Table 3.
The architecture of the used one-dimensional convolutional neural network (1DCNN).
Table 3.
The architecture of the used one-dimensional convolutional neural network (1DCNN).
| Layer | Kernel/Pool Size and Activation | Filters/Units |
|---|
| Batch Normalization | | |
| Conv1D | 3 ReLU | 64 |
| Batch Normalization | | |
| MaxPooling1D | 3 | |
| Conv1D | 3 ReLU | 128 |
| Batch Normalization | | |
| Dropout (0.15) | | |
| Flatten | | |
| Dense | ReLU | 100 |
| Dense | ReLU | 1 |
| Optimiser: | Adam | |
| Loss: | Mean square error | |
| Accuracy: | -score | |
Table 4.
Results of training and validating the CNN estimators for chlorophyll a and b.
Table 4.
Results of training and validating the CNN estimators for chlorophyll a and b.
| | Chlorophyll a | Chlorophyll b |
|---|
| score between original and predicted values | 0.97 | 0.95 |
| Correlation coefficient between original and predicted values | 0.98 | 0.98 |
| MSE | 0.07 | 0.03 |
| Average difference | 0.05 | 0.02 |
| Standard deviation | 0.26 | 0.18 |
| 95% Confidence interval of the difference between predicted and original values | | |
Table 5.
Correlation coefficients between predicted chlorophyll values and the index in the eight researched plots.
Table 5.
Correlation coefficients between predicted chlorophyll values and the index in the eight researched plots.
| | Correlation Coefficient for Chlorophyll a and Index | Correlation Coefficient for Chlorophyll b and Index | Plot Description |
|---|
| Plot 1 | −0.91 | −0.81 | Spruce |
| Plot 2 | −0.90 | −0.83 | Birch |
| Plot 3 | −0.84 | −0.61 | Birch |
| Plot 4 | −0.81 | −0.61 | Forest road |
| Plot 5 | −0.93 | −0.88 | Birch |
| Plot 6 | −0.91 | −0.74 | Spruce |
| Plot 7 | −0.88 | −0.55 | Spruce |
| Plots 1, 6 and 7 | −0.90 | −0.70 | Spruce |
| Plots 2, 3 and 5 | −0.89 | −0.77 | Birch |
| Plots 1–7 | −0.87 | −0.68 | Spruce and Birch |
| Plot 8 | −0.82 | −0.76 | Larger plot. Mainly birch, spruce on the border areas |
Table 6.
Correlation coefficients between simulated and empirical indexes in the seven investigated plots.
Table 6.
Correlation coefficients between simulated and empirical indexes in the seven investigated plots.
| | Correlation Coefficient between Simulated and Empirical Indexes | Plot Description |
|---|
| Plot 1 | 0.89 | Spruce |
| Plot 2 | 0.83 | Birch |
| Plot 3 | 0.75 | Birch |
| Plot 4 | 0.68 | Forest road |
| Plot 5 | 0.88 | Birch |
| Plot 6 | 0.85 | Spruce |
| Plot 7 | 0.81 | Spruce |