Evaluation of Coherent and Incoherent Landslide Detection Methods Based on Synthetic Aperture Radar for Rapid Response: A Case Study for the 2018 Hokkaido Landslides
Abstract
1. Introduction
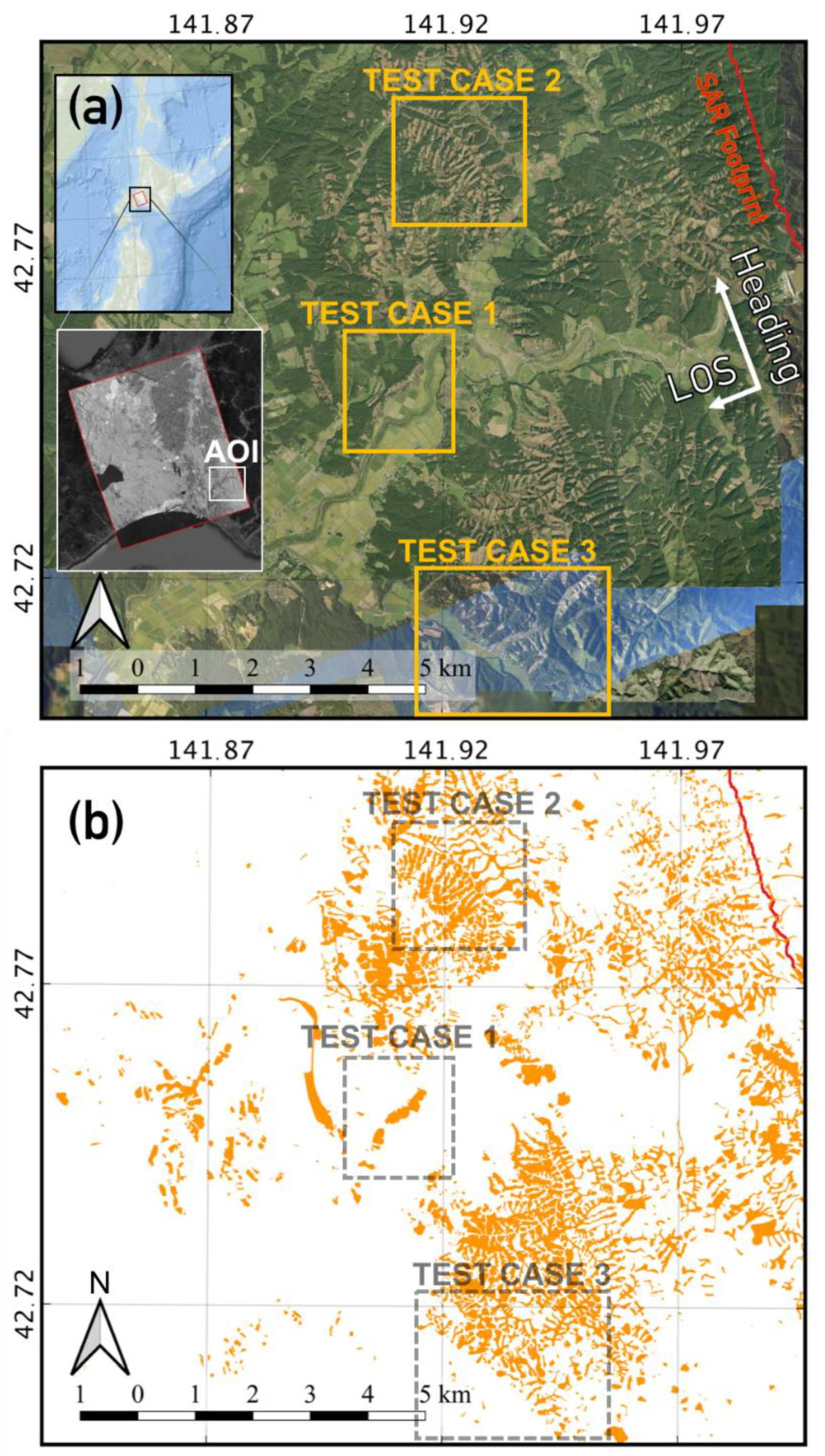
2. Hokkaido (Eastern Iburi) Landslides
3. SAR data and Landslide Detection Methods
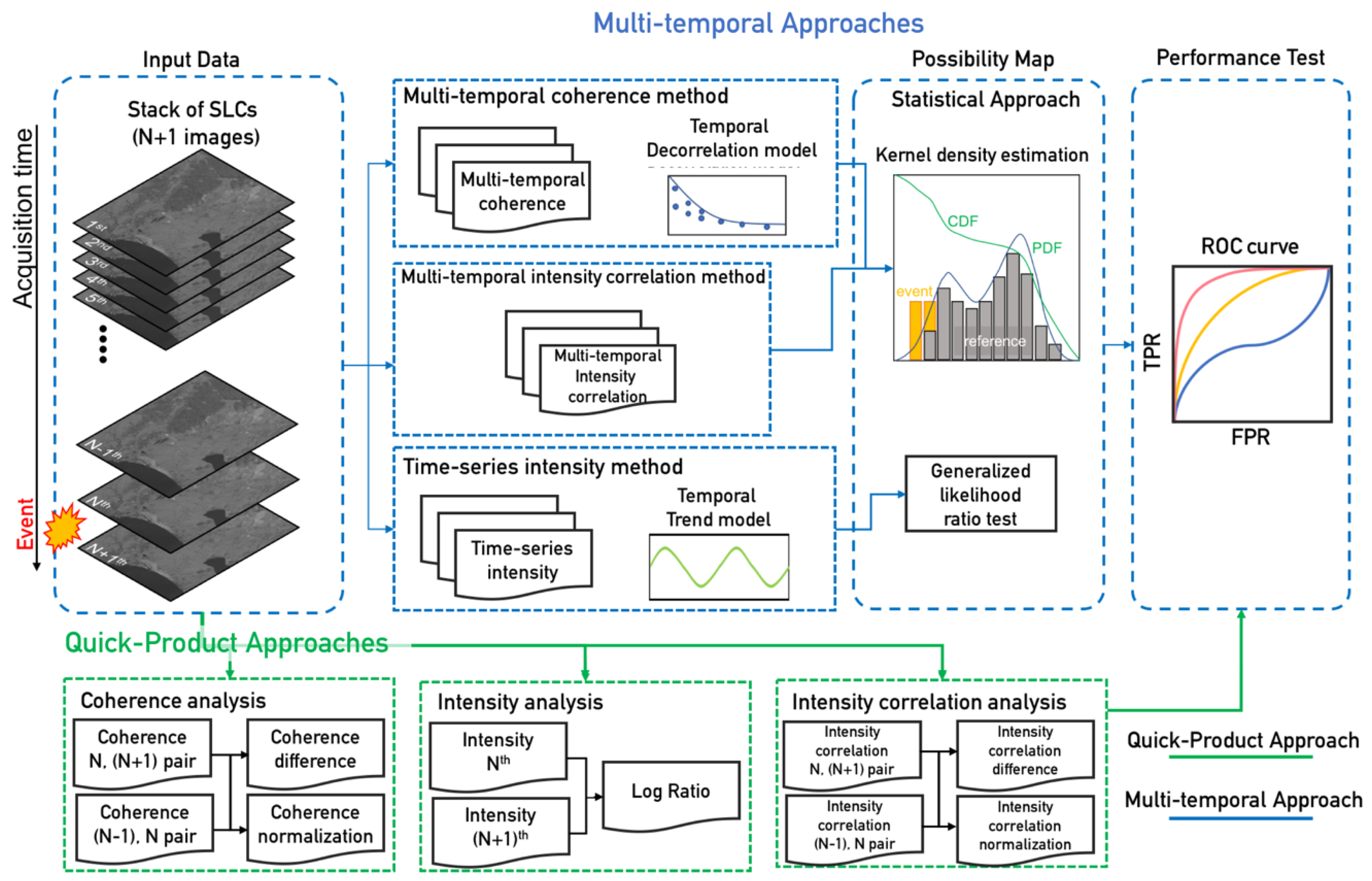
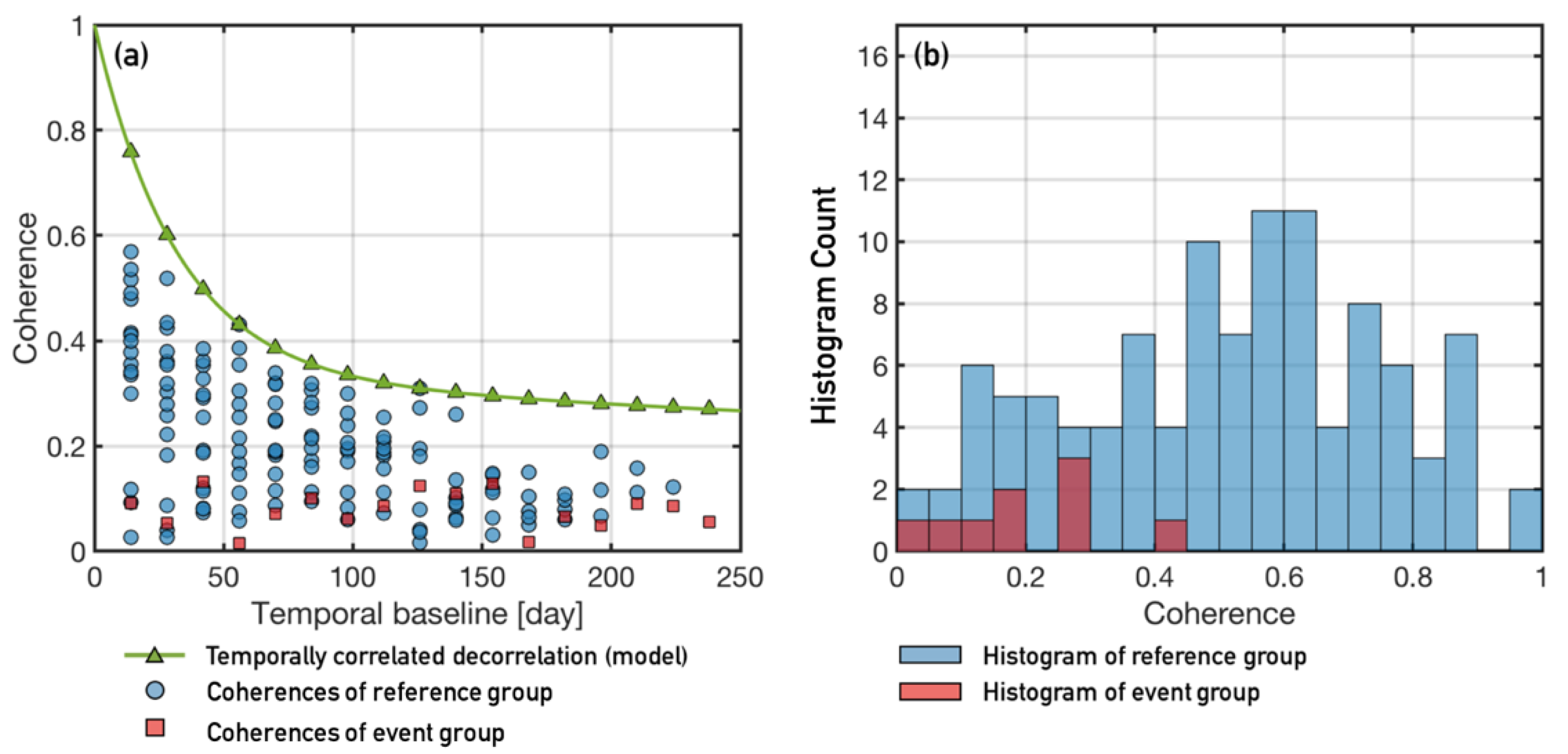
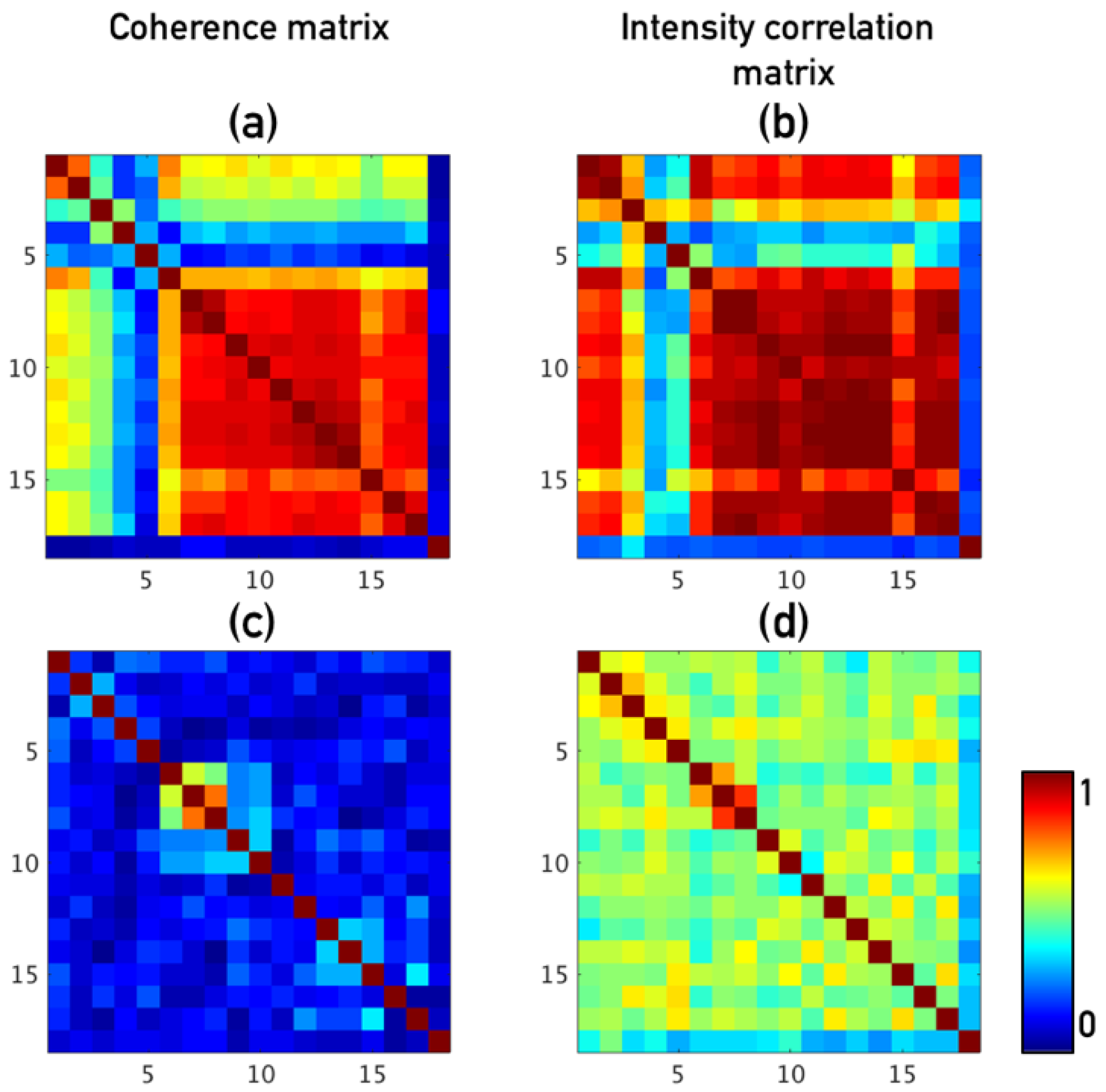
3.1. Coherence-Based Method
3.2. Amplitude-Based Method
3.2.1. Intensity (Amplitude) Analysis
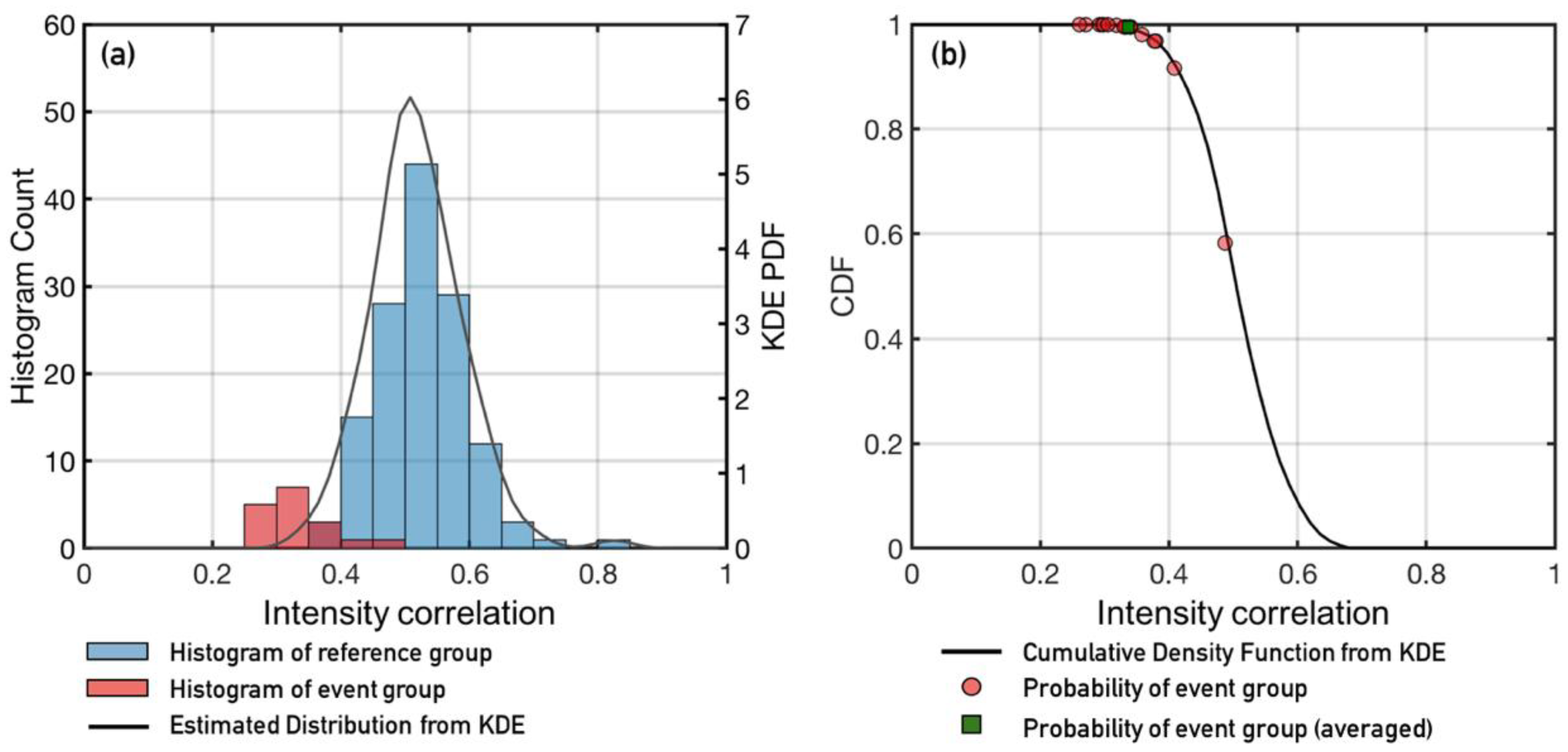
3.2.2. Intensity Correlation Analysis
4. Experimental Results
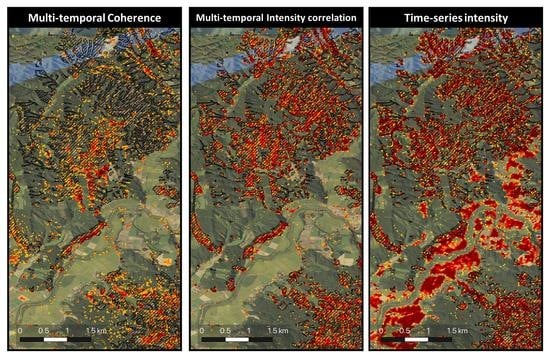
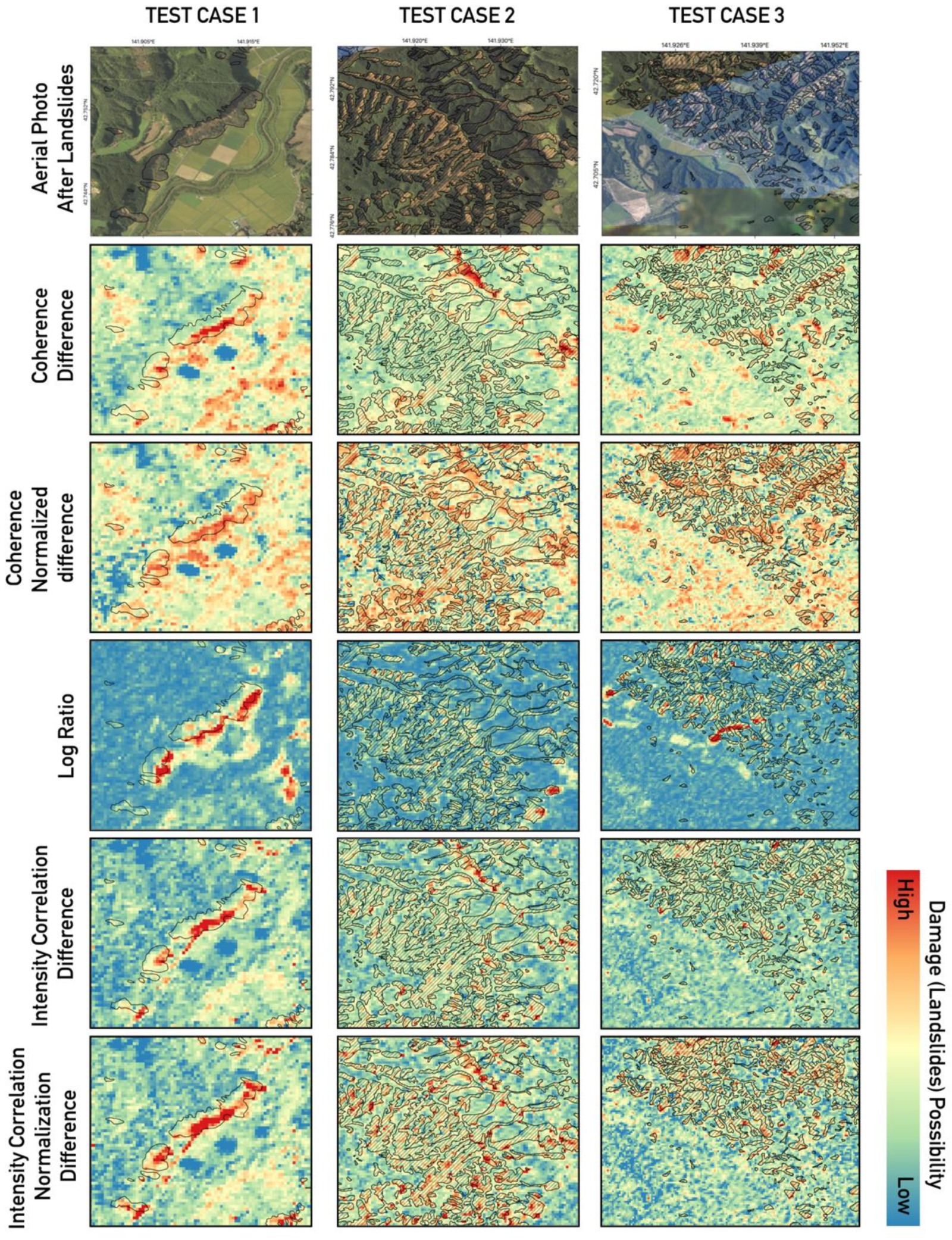
4.1. Quick-Product Analysis
4.2. Multi-Temporal Analysis
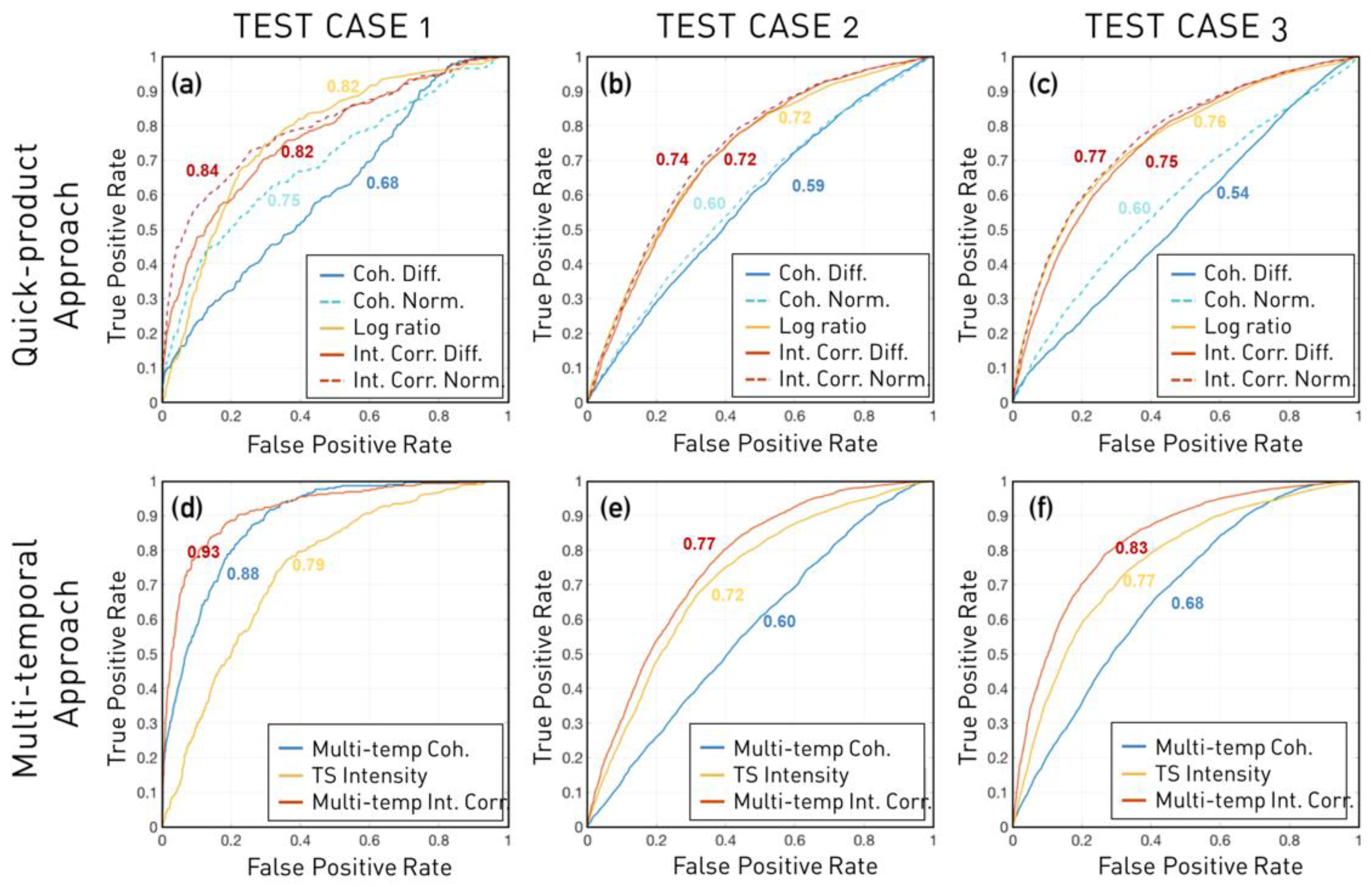
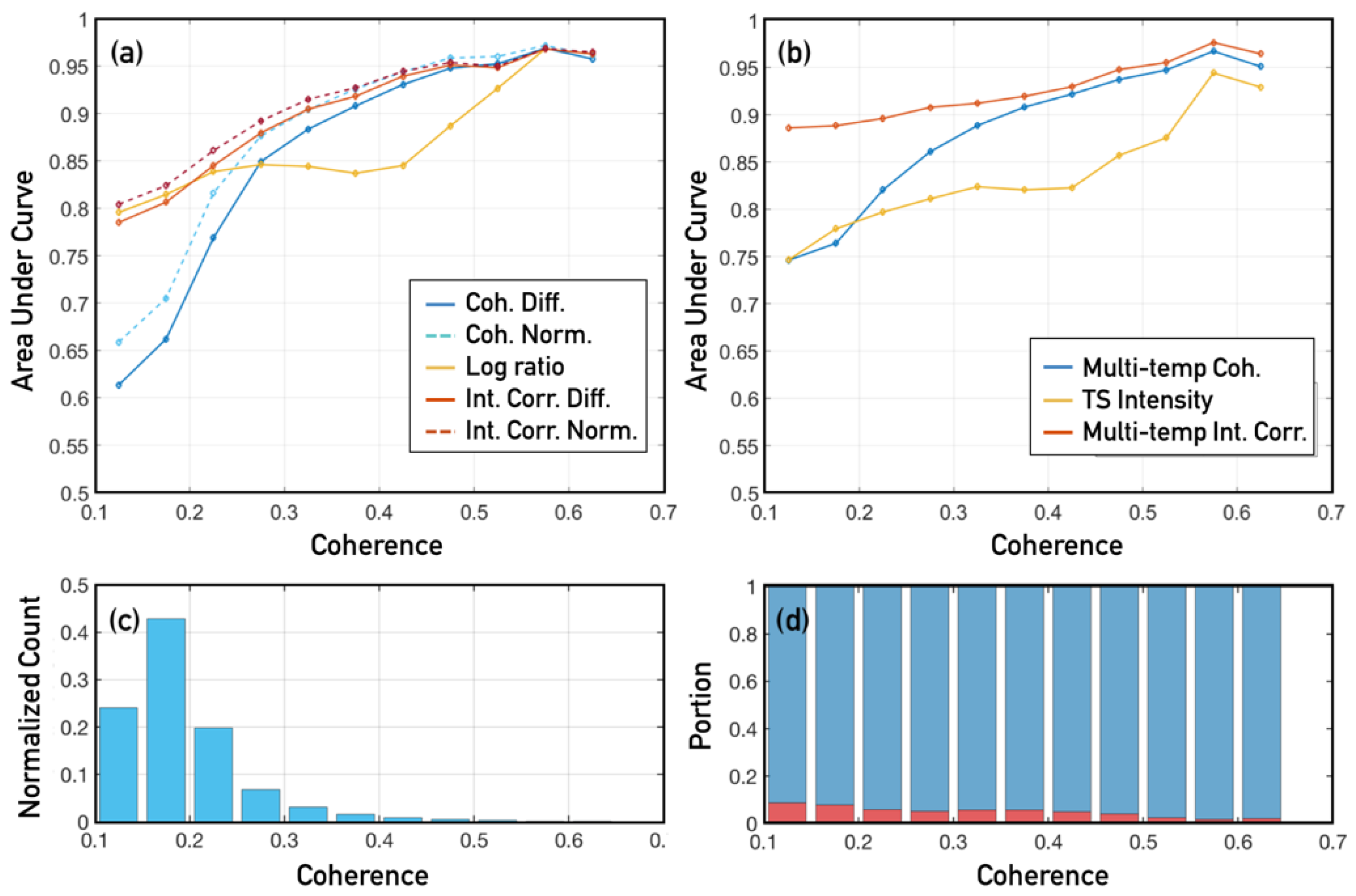
4.3. Performance Test Using ROC Curve Analysis
4.4. Overall Accuracy Comparison
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Remy, D.; Froger, J.-L.; Peltier, A.; Villeneuve, N.; Darrozes, J.; Perfettini, H.; Bonvalot, S. Long-term ground displacement observations using InSAR and GNSS at Piton de la Fournaise volcano between 2009 and 2014. Remote Sens. Environ. 2017, 194, 230–247. [Google Scholar] [CrossRef]
- García-Davalillo, J.C.; Herrera, G.; Notti, D.; Strozzi, T.; Álvarez-Fernández, I.J.L. DInSAR analysis of ALOS PALSAR images for the assessment of very slow landslides: The Tena Valley case study. Landslides 2014, 11, 225–246. [Google Scholar] [CrossRef]
- Tuan, N.A.; Marianne, S.; José, D.; Marc, O.; Gerardo, H.G.; Carlos, G.L.-D.J.; Celestino, G.N.; Inmaculada, Á.F.; Bernard, M.; Joaquim, M.D.P. Spatio-temporal evolution of Ground displacement of the Tena landslide (Spain). In Landslide Science and Practice; Springer: Berlin/Heidelberg, Germany, 2013; pp. 133–140. [Google Scholar]
- Jia, H.; Zhang, H.; Liu, L.; Liu, G.J.R.S. Landslide Deformation Monitoring by Adaptive Distributed Scatterer Interferometric Synthetic Aperture Radar. Remote Sens. 2019, 11, 2273. [Google Scholar] [CrossRef]
- Yonezawa, C.; Takeuchi, S. Decorrelation of SAR data by urban damages caused by the 1995 Hyogoken-nanbu earthquake. Int. J. Remote Sens. 2001, 22, 1585–1600. [Google Scholar] [CrossRef]
- Ito, Y.; Hosokawa, M. Damage estimation model using temporal coherence ratio. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 2859–2861. [Google Scholar]
- Hoffmann, J. Mapping damage during the Bam (Iran) earthquake using interferometric coherence. Int. J. Remote Sens. 2007, 28, 1199–1216. [Google Scholar] [CrossRef]
- Fielding, E.J.; Talebian, M.; Rosen, P.A.; Nazari, H.; Jackson, J.A.; Ghorashi, M.; Walker, R. Surface ruptures and building damage of the 2003 Bam, Iran, earthquake mapped by satellite synthetic aperture radar interferometric correlation. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Yun, S.-H.; Hudnut, K.; Owen, S.; Webb, F.; Simons, M.; Sacco, P.; Gurrola, E.; Manipon, G.; Liang, C.; Fielding, E. Rapid Damage Mapping for the 2015 M w 7.8 Gorkha Earthquake Using Synthetic Aperture Radar Data from COSMO–SkyMed and ALOS-2 Satellites. Seismol. Res. Lett. 2015, 86, 1549–1556. [Google Scholar] [CrossRef]
- Chini, M.; Piscini, A.; Cinti, F.R.; Amici, S.; Nappi, R.; DeMartini, P.M. The 2011 Tohoku (Japan) tsunami inundation and liquefaction investigated through optical, thermal, and SAR data. IEEE Geosci. Remote Sens. Lett. 2012, 10, 347–351. [Google Scholar] [CrossRef]
- Jung, J.; Kim, D.-j.; Lavalle, M.; Yun, S.-H. Coherent Change Detection Using InSAR Temporal Decorrelation Model: A Case Study for Volcanic Ash Detection. IEEE Trans. Geosci.Remote Sens. 2016, 54, 5765–5775. [Google Scholar] [CrossRef]
- Christophe, E.; Chia, A.S.; Yin, T.; Kwoh, L.K. 2009 earthquakes in Sumatra: The use of L-band interferometry in a SAR-hostile environment. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 5–30 July 2010; pp. 1202–1205. [Google Scholar]
- Takeuchi, S.; Yamada, S. Monitoring of forest fire damage by using JERS-1 InSAR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 3290–3292. [Google Scholar]
- Jung, J.; Yun, S.-H.; Kim, D.-J.; Lavalle, M. Damage-Mapping Algorithm Based on Coherence Model Using Multitemporal Polarimetric–Interferometric SAR Data. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1520–1532. [Google Scholar] [CrossRef]
- Robinson, D.; Gardner, C.; Cooper, J. Measurement of relative permittivity in sandy soils using TDR, capacitance and theta probes: Comparison, including the effects of bulk soil electrical conductivity. J. Hydrol. 1999, 223, 198–211. [Google Scholar] [CrossRef]
- Matgen, P.; Hostache, R.; Schumann, G.; Pfister, L.; Hoffmann, L.; Savenije, H. Towards an automated SAR-based flood monitoring system: Lessons learned from two case studies. Phys. Chem. Earth Parts A/B/C 2011, 36, 241–252. [Google Scholar] [CrossRef]
- Martinez, J.-M.; Le Toan, T. Mapping of flood dynamics and spatial distribution of vegetation in the Amazon floodplain using multitemporal SAR data. Remote Sens. Environ. 2007, 108, 209–223. [Google Scholar] [CrossRef]
- Schlaffer, S.; Matgen, P.; Hollaus, M.; Wagner, W. Flood detection from multi-temporal SAR data using harmonic analysis and change detection. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 15–24. [Google Scholar] [CrossRef]
- Tanase, M.A.; Santoro, M.; de La Riva, J.; Fernando, P.; Le Toan, T. Sensitivity of X-, C-, and L-band SAR backscatter to burn severity in Mediterranean pine forests. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3663–3675. [Google Scholar] [CrossRef]
- Gimeno, M.; San-Miguel-Ayanz, J.; Schmuck, G. Identification of burnt areas in Mediterranean forest environments from ERS-2 SAR time series. Int. J. Remote Sens. 2004, 25, 4873–4888. [Google Scholar] [CrossRef]
- Matsuoka, M.; Yamazaki, F. Building damage mapping of the 2003 Bam, Iran, earthquake using Envisat/ASAR intensity imagery. Earthq. Spectra 2005, 21, 285–294. [Google Scholar] [CrossRef]
- Mondini, A. Measures of Spatial Autocorrelation Changes in Multitemporal SAR images for event landslides detection. Remote Sens. 2017, 9, 554. [Google Scholar] [CrossRef]
- Konishi, T.; Suga, Y. Landslide detection using COSMO-SkyMed images: A case study of a landslide event on Kii Peninsula, Japan. Eur. J. Remote Sens. 2018, 51, 205–221. [Google Scholar] [CrossRef]
- Alessandro, C.; Mondini, M.S. Margherita Rocchetti, Enrica Rossetto, Andrea Manconi, Oriol Monserrat. Sentinel-1 SAR Amplitude Imagery for Rapid Landslide Detection. Remote Sens. 2019, 11, 760. [Google Scholar] [CrossRef]
- Uemoto, J.; Moriyama, T.; Nadai, A.; Kojima, S.; Umehara, T.J.N.H. Landslide detection based on height and amplitude differences using pre-and post-event airborne X-band SAR data. Nat. Hazards 2019, 95, 485–503. [Google Scholar] [CrossRef]
- Plank, S. Rapid damage assessment by means of multi-temporal SAR—A comprehensive review and outlook to Sentinel-1. Remote Sens. 2014, 6, 4870–4906. [Google Scholar] [CrossRef]
- Preiss, M.; Gray, D.A.; Stacy, N.J.; Sensing, R. Detecting scene changes using synthetic aperture radar interferometry. IEEE Trans. Geosci. Remote Sens 2006, 44, 2041–2054. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A.V.; Brovelli, M.A.; Manzoni, M.; d’Alessandro, M.M.; Molinari, M.E.; Oxoli, D. Coherent Change Detection for Multipass SAR. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6811–6822. [Google Scholar] [CrossRef]
- Guida, L.; Boccardo, P.; Donevski, I.; Lo Schiavo, L.; Molinari, M.; Monti-Guarnieri, A.; Oxoli, D.; Brovelli, M.J. Post-Disaster damage assessment through coherent change detection on sar imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42. [Google Scholar] [CrossRef]
- Lê, T.T.; Atto, A.M.; Trouvé, E.; Nicolas, J.-M.J.I.G.; Letters, R.S. Adaptive multitemporal SAR image filtering based on the change detection matrix. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1826–1830. [Google Scholar]
- Karimzadeh, S.; Matsuoka, M. A Weighted Overlay Method for Liquefaction-Related Urban Damage Detection: A Case Study of the 6 September 2018 Hokkaido Eastern Iburi Earthquake, Japan. Geosciences 2018, 8, 487. [Google Scholar] [CrossRef]
- Yamagishi, H.; Yamazaki, F. Landslides by the 2018 Hokkaido Iburi-Tobu Earthquake on September 6. Landslides 2018, 15, 2521–2524. [Google Scholar] [CrossRef]
- Wang, F.; Fan, X.; Yunus, A.P.; Subramanian, S.S.; Alonso-Rodriguez, A.; Dai, L.; Xu, Q.; Huang, R.J.L. Coseismic landslides triggered by the 2018 Hokkaido, Japan (M w 6.6), earthquake: Spatial distribution, controlling factors, and possible failure mechanism. Landslides 2019, 16, 1551–1566. [Google Scholar] [CrossRef]
- Mavroeidis, G.P.; Papageorgiou, A.S. A mathematical representation of near-fault ground motions. Bull. Seismol. Soc. Am. 2003, 93, 1099–1131. [Google Scholar] [CrossRef]
- Kameda, J.; Kamiya, H.; Masumoto, H.; Morisaki, T.; Hiratsuka, T.; Inaoi, C.J. Fluidized landslides triggered by the liquefaction of subsurface volcanic deposits during the 2018 Iburi–Tobu earthquake, Hokkaido. Sci. Rep. 2019, 9, 13119. [Google Scholar] [CrossRef] [PubMed]
- Motohka, T.; Isoguchi, O.; Sakashita, M.; Shimada, M. Results of ALOS-2 PALSAR-2 calibration and validation after 3 years of operation. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4169–4170. [Google Scholar]
- Fattahi, H.; Simons, M.; Agram, P. InSAR time-series estimation of the ionospheric phase delay: An extension of the split range-spectrum technique. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5984–5996. [Google Scholar] [CrossRef]
- Rosen, P.A.; Gurrola, E.; Sacco, G.F.; Zebker, H. The InSAR scientific computing environment. In Proceedings of the EUSAR 2012; 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 3–26 April 2012; pp. 730–733. [Google Scholar]
- Van Zyl, J.J. The Shuttle Radar Topography Mission (SRTM): A breakthrough in remote sensing of topography. Acta Astronaut. 2001, 48, 559–565. [Google Scholar] [CrossRef]
- Zebker, H.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Cloude, S.; Papathanassiou, K. Three-stage inversion process for polarimetric SAR interferometry. IEEE Proc. Radar Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef]
- Lavalle, M.; Hensley, S. Extraction of structural and dynamic properties of forests from polarimetric-interferometric SAR data affected by temporal decorrelation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4752–4767. [Google Scholar] [CrossRef]
- Lavalle, M.; Simard, M.; Hensley, S. A temporal decorrelation model for polarimetric radar interferometers. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2880–2888. [Google Scholar] [CrossRef]
- Suga, Y.; Takeuchi, S.; Oguro, Y.; Chen, A.; Ogawa, M.; Konishi, T.; Yonezawa, C. Application of ERS-2/SAR data for the 1999 Taiwan earthquake. Adv. Space Res. 2001, 28, 155–163. [Google Scholar] [CrossRef]
- Wei, M.; Sandwell, D.T. Decorrelation of L-band and C-band interferometry over vegetated areas in California. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2942–2952. [Google Scholar]
- Verbesselt, J.; Zeileis, A.; Herold, M. Near real-time disturbance detection using satellite image time series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
- Moser, G.; Zerubia, J.; Serpico, S.B. SAR amplitude probability density function estimation based on a generalized Gaussian model. IEEE Trans. Image Process. 2006, 15, 1429–1442. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, P.; Oliver, C. Maximum likelihood approach to the detection of changes between multitemporal SAR images. IEE Proc. Radar Sonar Navig. 2001, 148, 200–210. [Google Scholar] [CrossRef]
- Tison, C.; Nicolas, J.-M.; Tupin, F.; Maître, H.J.; Sensing, R. A new statistical model for Markovian classification of urban areas in high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2046–2057. [Google Scholar] [CrossRef]
- Rignot, E.J.M.; Zyl, J.J. Change detection techniques for ERS-1 SAR data. IEEE Tans. Geosci. Remote Sens. 1993, 44, 896–906. [Google Scholar] [CrossRef]
- Lee, J.-S.; Hoppel, K.W.; Mango, S.A.; Miller, A.R. Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1017–1028. [Google Scholar]
- Bowman, A.W.; Azzalini, A. Applied Smoothing Techniques for Data Analysis; Oxford University Press Inc.: New York, NY, USA, 1997. [Google Scholar]
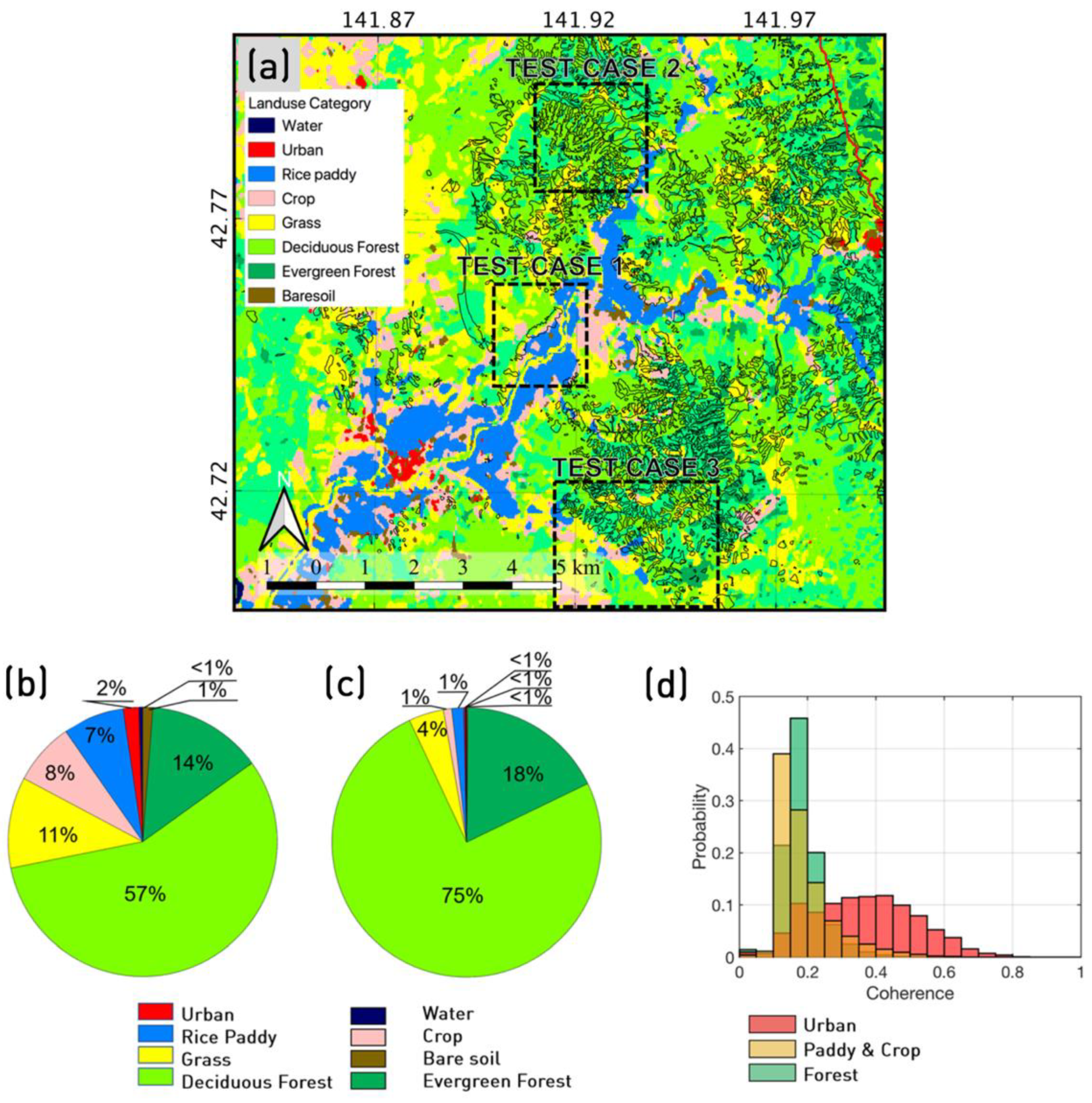
- Takahashi, M.; Nasahara, K.N.; Tadono, T.; Watanabe, T.; Dotsu, M.; Sugimura, T.; Tomiyama, N. JAXA high resolution land-use and land-cover map of Japan. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 2384–2387. [Google Scholar]
- Plank, S.; Twele, A.; Martinis, S.J. Landslide mapping in vegetated areas using change detection based on optical and polarimetric SAR data. Remote Sens. 2016, 8, 307. [Google Scholar] [CrossRef]
| Methods | Test Case 1 | Test Case 2 | Test Case 3 | |
|---|---|---|---|---|
| Quick-Product Approaches | Coherence difference | 0.682 | 0.590 | 0.544 |
| Coherence norm. diff.1 | 0.751 | 0.602 | 0.595 | |
| Log-ratio | 0.817 | 0.724 | 0.758 | |
| Intensity corr. diff. 2 | 0.815 | 0.724 | 0.751 | |
| Intensity corr. norm. diff. 3 | 0.841 | 0.735 | 0.769 | |
| Multi-Temporal Approaches | Multi-temp. coherence 4 | 0.884 | 0.579 | 0.675 |
| T.S. intensity 5 | 0.793 | 0.724 | 0.765 | |
| Multi-temp. intensity corr. 6 | 0.927 | 0.767 | 0.832 |
| Methods | Entire Area | Rice Paddy and Crop | Forest | |
|---|---|---|---|---|
| Quick-Product Approaches | Coherence difference | 75.9% | 65.5% | 75.5% |
| Coherence norm. diff. | 75.9% | 80.9% | 76.0% | |
| Log-ratio | 79.4% | 57.4% | 80.1% | |
| Intensity corr. diff. | 77.7% | 70.6% | 78.8% | |
| Intensity corr. norm. diff. | 78.1% | 72.5% | 79.2% | |
| Multi-Temporal Approaches | Multi-temp. coherence | 76.3% | 93.3% | 76.5% |
| T.S. intensity | 78.9% | 52.8% | 83.2% | |
| Multi-temp. intensity corr. | 80.0% | 83.9% | 80.7% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.; Yun, S.-H. Evaluation of Coherent and Incoherent Landslide Detection Methods Based on Synthetic Aperture Radar for Rapid Response: A Case Study for the 2018 Hokkaido Landslides. Remote Sens. 2020, 12, 265. https://doi.org/10.3390/rs12020265
Jung J, Yun S-H. Evaluation of Coherent and Incoherent Landslide Detection Methods Based on Synthetic Aperture Radar for Rapid Response: A Case Study for the 2018 Hokkaido Landslides. Remote Sensing. 2020; 12(2):265. https://doi.org/10.3390/rs12020265
Chicago/Turabian StyleJung, Jungkyo, and Sang-Ho Yun. 2020. "Evaluation of Coherent and Incoherent Landslide Detection Methods Based on Synthetic Aperture Radar for Rapid Response: A Case Study for the 2018 Hokkaido Landslides" Remote Sensing 12, no. 2: 265. https://doi.org/10.3390/rs12020265
APA StyleJung, J., & Yun, S.-H. (2020). Evaluation of Coherent and Incoherent Landslide Detection Methods Based on Synthetic Aperture Radar for Rapid Response: A Case Study for the 2018 Hokkaido Landslides. Remote Sensing, 12(2), 265. https://doi.org/10.3390/rs12020265