A Geographically Weighted Regression Approach to Understanding Urbanization Impacts on Urban Warming and Cooling: A Case Study of Las Vegas
Abstract
1. Introduction
2. Materials and Methods
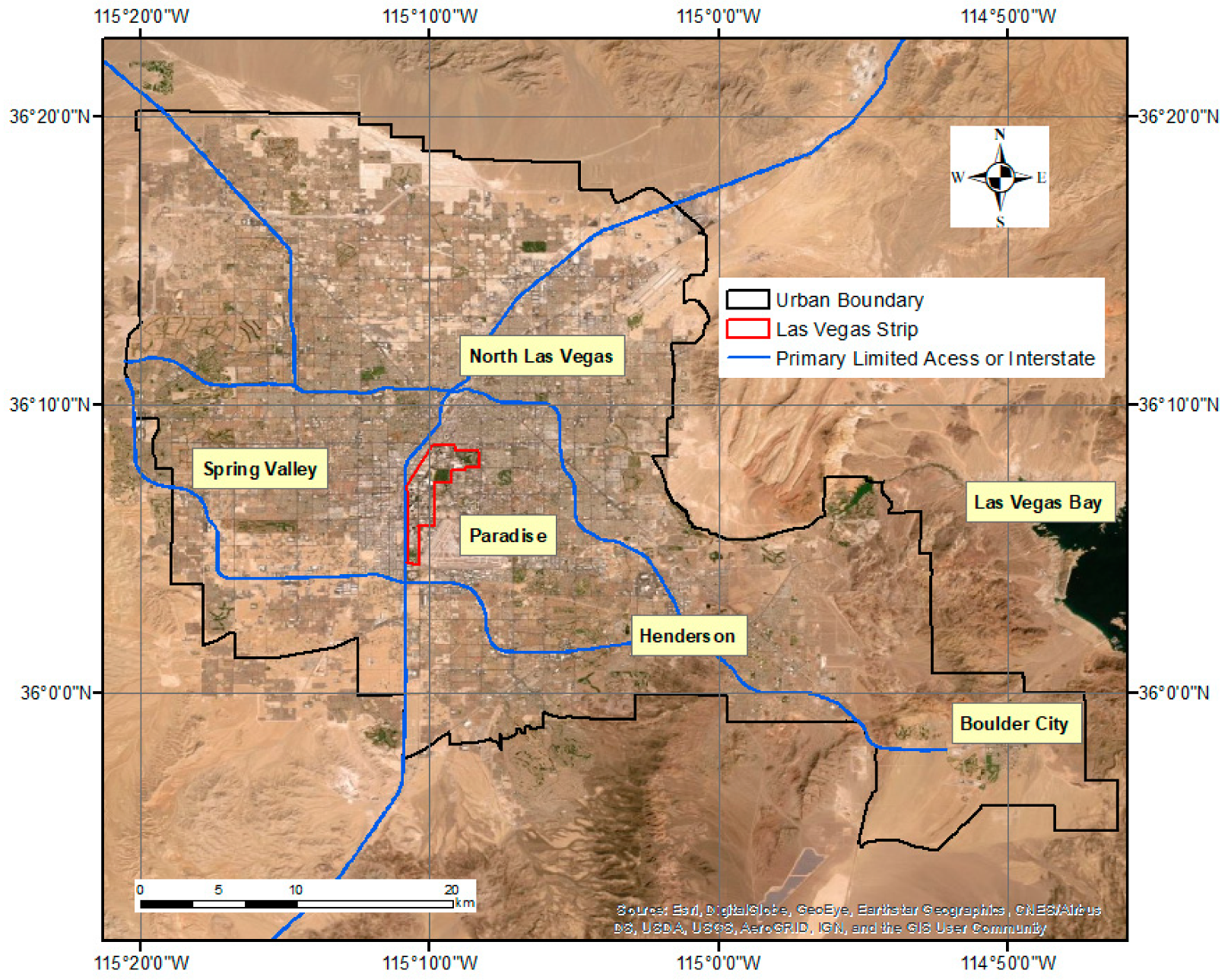
2.1. Study Area
2.2. SUHI Intensity Derivation
2.3. Biophysical Indicators
2.4. Statistical Analysis
2.5. Statistical Summary by LULC Type
3. Results
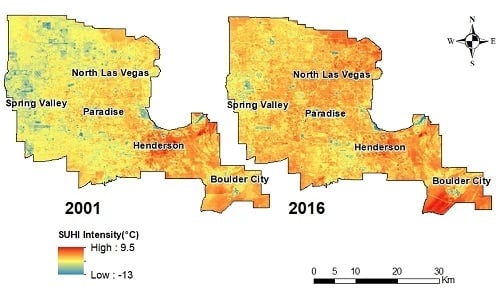
3.1. SUHI Intensity Maps
3.2. Correlation Analysis
3.3. Regression Analysis
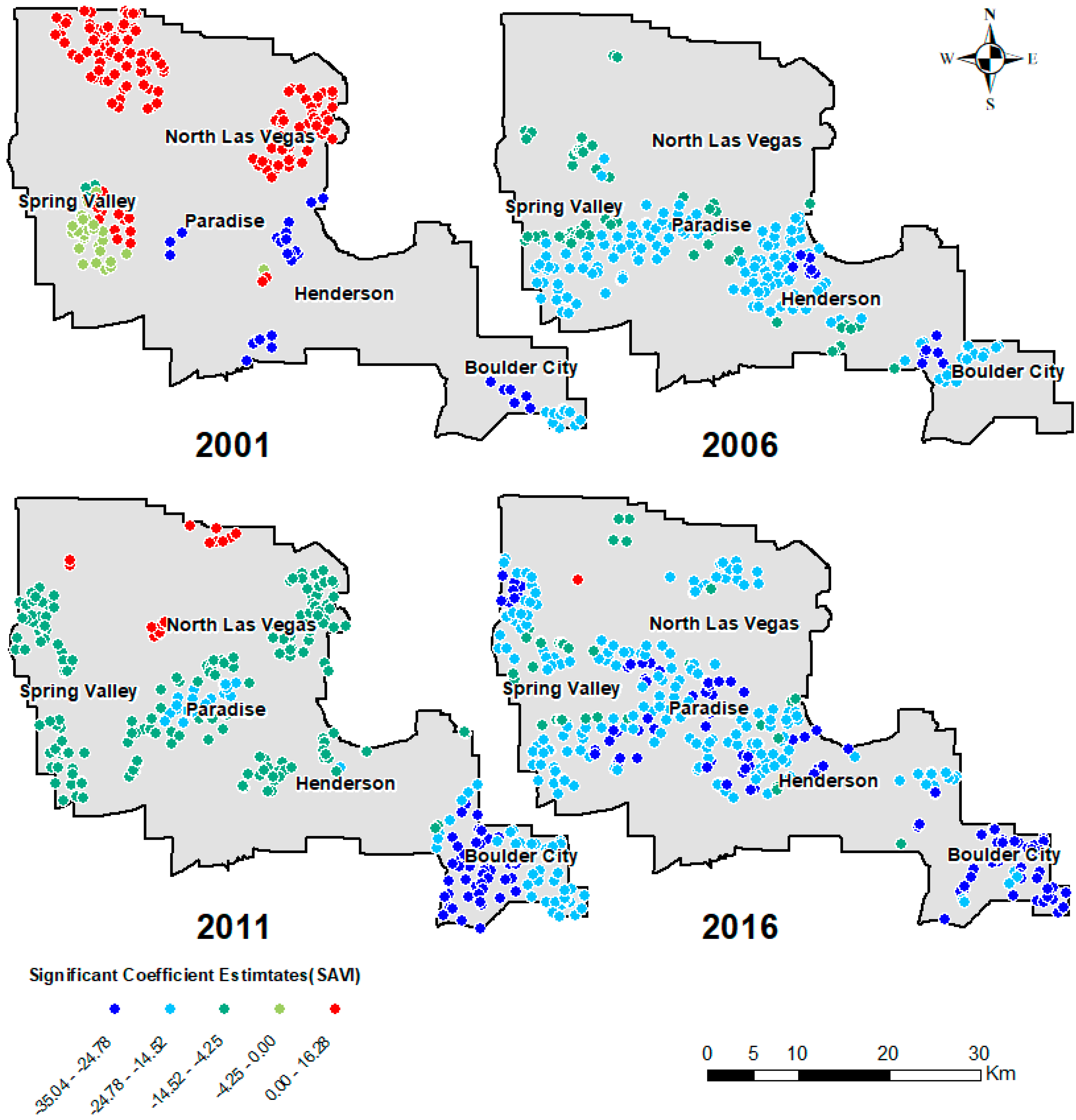
3.4. Spatial Patterns of the GWR Estimates
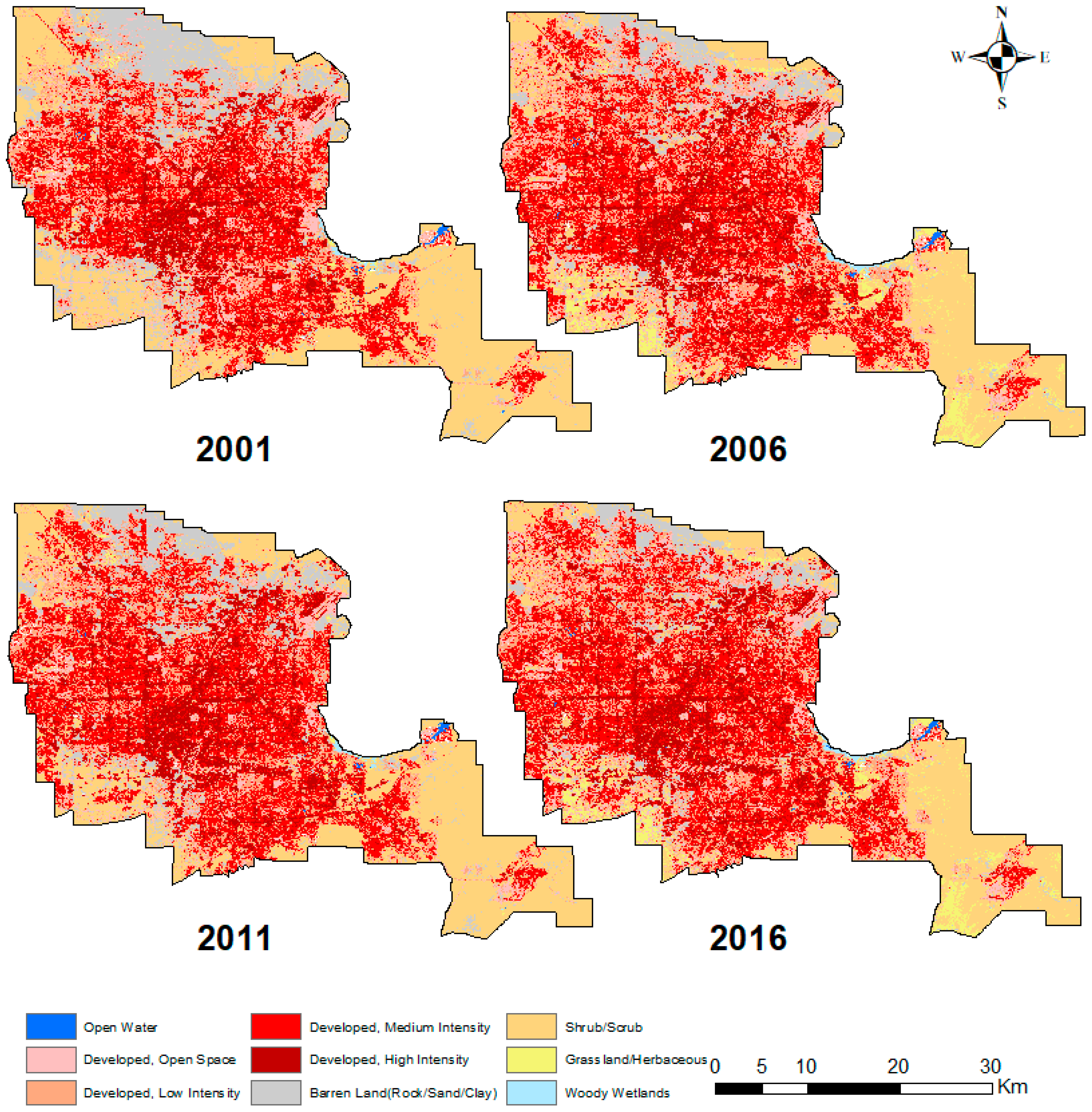
3.5. Summarized Estimates by LULC Types
4. Discussion
4.1. Effects of Land Cover Features on SUHI
4.2. Urban Heat Sink
4.3. Effects of Urbanization on Spatiotemporal Changes of SUHI
4.4. Implications for SUHI Mitigation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Fan, C.; Myint, S.W.; Kaplan, S.; Middel, A.; Zheng, B.; Rahman, A.; Huang, H.-P.; Brazel, A.; Blumberg, D.G. Understanding the impact of urbanization on surface urban heat islands—A longitudinal analysis of the oasis effect in subtropical desert cities. Remote Sens. 2017, 9, 672. [Google Scholar] [CrossRef]
- Guhathakurta, S.; Gober, P. The impact of the phoenix urban heat island on residential water use. J. Am. Plan. Assoc. 2007, 73, 317–329. [Google Scholar] [CrossRef]
- Li, H.; Meier, F.; Lee, X.; Chakraborty, T.; Liu, J.; Schaap, M.; Sodoudi, S. Interaction between urban heat island and urban pollution island during summer in Berlin. Sci. Total Environ. 2018, 636, 818–828. [Google Scholar] [CrossRef]
- Geri, F.; Amici, V.; Rocchini, D. Human activity impact on the heterogeneity of a Mediterranean landscape. Appl. Geogr. 2010, 30, 370–379. [Google Scholar] [CrossRef]
- Harlan, S.L.; Brazel, A.J.; Prashad, L.; Stefanov, W.L.; Larsen, L. Neighborhood microclimates and vulnerability to heat stress. Soc. Sci. Med. 2006, 63, 2847–2863. [Google Scholar] [CrossRef]
- Wang, Y.; Berardi, U.; Akbari, H. Comparing the effects of urban heat island mitigation strategies for Toronto, Canada. Energy Build. 2016, 114, 2–19. [Google Scholar] [CrossRef]
- Zhang, Y.; Murray, A.T.; Turner Ii, B.L. Optimizing green space locations to reduce daytime and nighttime urban heat island effects in Phoenix, Arizona. Landsc. Urban Plan. 2017, 165, 162–171. [Google Scholar] [CrossRef]
- Zhao, Q.; Sailor, D.J.; Wentz, E.A. Impact of tree locations and arrangements on outdoor microclimates and human thermal comfort in an urban residential environment. Urban For. Urban Green. 2018, 32, 81–91. [Google Scholar] [CrossRef]
- Fan, C.; Myint, S.W.; Zheng, B. Measuring the spatial arrangement of urban vegetation and its impacts on seasonal surface temperatures. Prog. Phys. Geogr. 2015, 39, 199–219. [Google Scholar] [CrossRef]
- Li, D.; Bou-Zeid, E.; Oppenheimer, M. The effectiveness of cool and green roofs as urban heat island mitigation strategies. Environ. Res. Lett. 2014, 9, 055002. [Google Scholar] [CrossRef]
- Middel, A.; Chhetri, N.; Quay, R. Urban forestry and cool roofs: Assessment of heat mitigation strategies in Phoenix residential neighborhoods. Urban For. Urban Green. 2015, 14, 178–186. [Google Scholar] [CrossRef]
- Hong, B.; Lin, B. Numerical Study of the Influences of Different Patterns of the Building and Green Space on Micro-Scale Outdoor Thermal Comfort and Indoor Natural Ventilation. In Proceedings of the Building Simulation; Springer: Berlin, Germany, 2014; Volume 7, pp. 525–536. [Google Scholar]
- Ivajnšič, D.; Kaligarič, M.; Žiberna, I. Geographically weighted regression of the urban heat island of a small city. Appl. Geogr. 2014, 53, 341–353. [Google Scholar] [CrossRef]
- Anniballe, R.; Bonafoni, S.; Pichierri, M. Spatial and temporal trends of the surface and air heat island over milan using modis data. Remote Sens. Environ. 2014, 150, 163–171. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Shearer, S. An overview of current and potential applications of thermal remote sensing in precision agriculture. Comput. Electron. Agric. 2017, 139, 22–32. [Google Scholar] [CrossRef]
- Hinkel, K.M.; Nelson, F.E.; Klene, A.E.; Bell, J.H. The urban heat island in winter at Barrow, Alaska. Int. J. Climatol. 2003, 23, 1889–1905. [Google Scholar] [CrossRef]
- Buyantuyev, A.; Wu, J. Urban heat islands and landscape heterogeneity: Linking spatiotemporal variations in surface temperatures to land-cover and socioeconomic patterns. Landsc. Ecol. 2010, 25, 17–33. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y.; Myint, S.W. Effects of landscape composition and pattern on land surface temperature: An urban heat island study in the megacities of southeast Asia. Sci. Total Environ. 2017, 577, 349–359. [Google Scholar] [CrossRef]
- Myint, S.W.; Wentz, E.A.; Brazel, A.J.; Quattrochi, D.A. The impact of distinct anthropogenic and vegetation features on urban warming. Landsc. Ecol. 2013, 28, 959–978. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in landsat imagery. Remote Sens. Environ. 2007, 106, 375–386. [Google Scholar] [CrossRef]
- Chen, X.-L.; Zhao, H.-M.; Li, P.-X.; Yin, Z.-Y. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Wang, C.; Myint, S.W.; Wang, Z.; Song, J. Spatio-temporal modeling of the urban heat island in the Phoenix metropolitan area: Land use change implications. Remote Sens. 2016, 8, 185. [Google Scholar] [CrossRef]
- Zhou, W.; Qian, Y.; Li, X.; Li, W.; Han, L. Relationships between land cover and the surface urban heat island: Seasonal variability and effects of spatial and thematic resolution of land cover data on predicting land surface temperatures. Landsc. Ecol. 2014, 29, 153–167. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, M.; Lu, Y. Spatially varying relationships between surface urban heat islands and driving factors across cities in China. Environ. Plan. B Urban Anal. City Sci. 2019, 46, 377–394. [Google Scholar] [CrossRef]
- Tobler, W.R. Cellular geography. In Philosophy in Geography; Springer: Berlin, Germany, 1979; Volume 20, pp. 379–386. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically weighted regression: A natural evolution of the expansion method for spatial data analysis. Environ. Plan. A 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Getis, A.; Griffith, D.A. Comparative spatial filtering in regression analysis. Geogr. Anal. 2002, 34, 130–140. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Miaomiao, X.; Wang, Y. Investigating spatial non-stationary and scale-dependent relationships between urban surface temperature and environmental factors using geographically weighted regression. Environ. Model. Softw. 2010, 25, 1789–1800. [Google Scholar] [CrossRef]
- Zhao, C.; Jensen, J.; Weng, Q.; Weaver, R. A Geographically weighted regression analysis of the underlying factors related to the surface urban heat island phenomenon. Remote Sens. 2018, 10, 1428. [Google Scholar] [CrossRef]
- US Census Bureau G. TIGER Products. Available online: https://www.census.gov/geo/maps-data/data/tiger.html (accessed on 27 March 2018).
- US Department of Commerce N. NOAA’s National Weather Service—National Climate. Available online: https://w2.weather.gov/climate/ (accessed on 17 October 2019).
- Climate Central: A Science and News Organization. Available online: http://www.climatecentral.org (accessed on 4 February 2018).
- EarthExplorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 9 March 2018).
- Landsat Satellite Missions. Available online: https://www.usgs.gov/land-resources/nli/landsat/landsat-satellite-missions?qt-science_support_page_related_con=2#qt-science_support_page_related_con (accessed on 17 October 2019).
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A generalized single-channel method for retrieving land surface temperature from remote sensing data. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Atmospheric Correction Parameter Calculator. Available online: https://atmcorr.gsfc.nasa.gov/ (accessed on 30 March 2018).
- ENVI—The Leading Geospatial Analytics Software|Harris Geospatial. Available online: http://www.harrisgeospatial.com/SoftwareTechnology/ENVI.aspx (accessed on 27 March 2018).
- Wang, J.; Huang, B.; Fu, D.; Atkinson, P. Spatiotemporal variation in surface urban heat island intensity and associated determinants across major Chinese cities. Remote Sens. 2015, 7, 3670–3689. [Google Scholar] [CrossRef]
- Morini, E.; Castellani, B.; Presciutti, A.; Anderini, E.; Filipponi, M.; Nicolini, A.; Rossi, F. Experimental analysis of the effect of geometry and façade materials on urban district’s equivalent albedo. Sustainability 2017, 9, 1245. [Google Scholar] [CrossRef]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Han-Qiu, X.U. A study on information extraction of water body with the modified normalized difference water index (MNDWI). J. Remote Sen. 2005, 5, 589–595. [Google Scholar]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Esri: GIS Mapping Software, Spatial Data Analytics & Location Intelligence. Available online: https://www.esri.com/en-us/home (accessed on 6 December 2019).
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Spatial variations in school performance: A local analysis using geographically weighted regression. Geogr. Environ. Model. 2001, 5, 43–66. [Google Scholar] [CrossRef]
- Wentz, E.A.; Gober, P. Determinants of small-area water consumption for the city of phoenix, Arizona. Water Res. Manag. 2007, 21, 1849–1863. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Kelly, M.H.; Charlton, M. The demographic impacts of the irish famine: Towards a greater geographical understanding: The demographic impacts of the irish famine. Trans. Inst. Br. Geogr. 2013, 38, 221–237. [Google Scholar] [CrossRef]
- GWR4 for Windows|Geographically Weighted Modelling. Available online: https://scholar.google.com.hk/scholar?hl=zh (accessed on 3 January 2020).
- Multi-Resolution Land Characteristics (MRLC) Consortium|Multi-Resolution Land Characteristics (MRLC) Consortium. Available online: https://www.mrlc.gov/ (accessed on 6 December 2019).
- Dihkan, M.; Karsli, F.; Guneroglu, A.; Guneroglu, N. Evaluation of surface urban heat island (SUHI) effect on coastal zone: The case of Istanbul Megacity. Ocean Coast. Manag. 2015, 118, 309–316. [Google Scholar] [CrossRef]
- Myint, S.W.; Zheng, B.; Talen, E.; Fan, C.; Kaplan, S.; Middel, A.; Smith, M.; Huang, H.-P.; Brazel, A. Does the spatial arrangement of urban landscape matter? Examples of urban warming and cooling in Phoenix and Las Vegas. Ecosyst. Health Sustain. 2015, 1, 1–15. [Google Scholar] [CrossRef]
- Zhao, Q.; Myint, S.W.; Wentz, E.A.; Fan, C. Rooftop surface temperature analysis in an urban residential environment. Remote Sens. 2015, 7, 12135–12159. [Google Scholar] [CrossRef]
- Carnahan, W.H.; Larson, R.C. An analysis of an urban heat sink. Remote Sens. Environ. 1990, 33, 65–71. [Google Scholar] [CrossRef]
- Zheng, B.; Myint, S.W.; Fan, C. Spatial configuration of anthropogenic land cover impacts on urban warming. Landsc. Urban Plan. 2014, 130, 104–111. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y. Monitoring surface urban heat island formation in a tropical mountain city using Landsat data (1987–2015). ISPRS J. Photogramm. Remote Sens. 2017, 133, 18–29. [Google Scholar] [CrossRef]

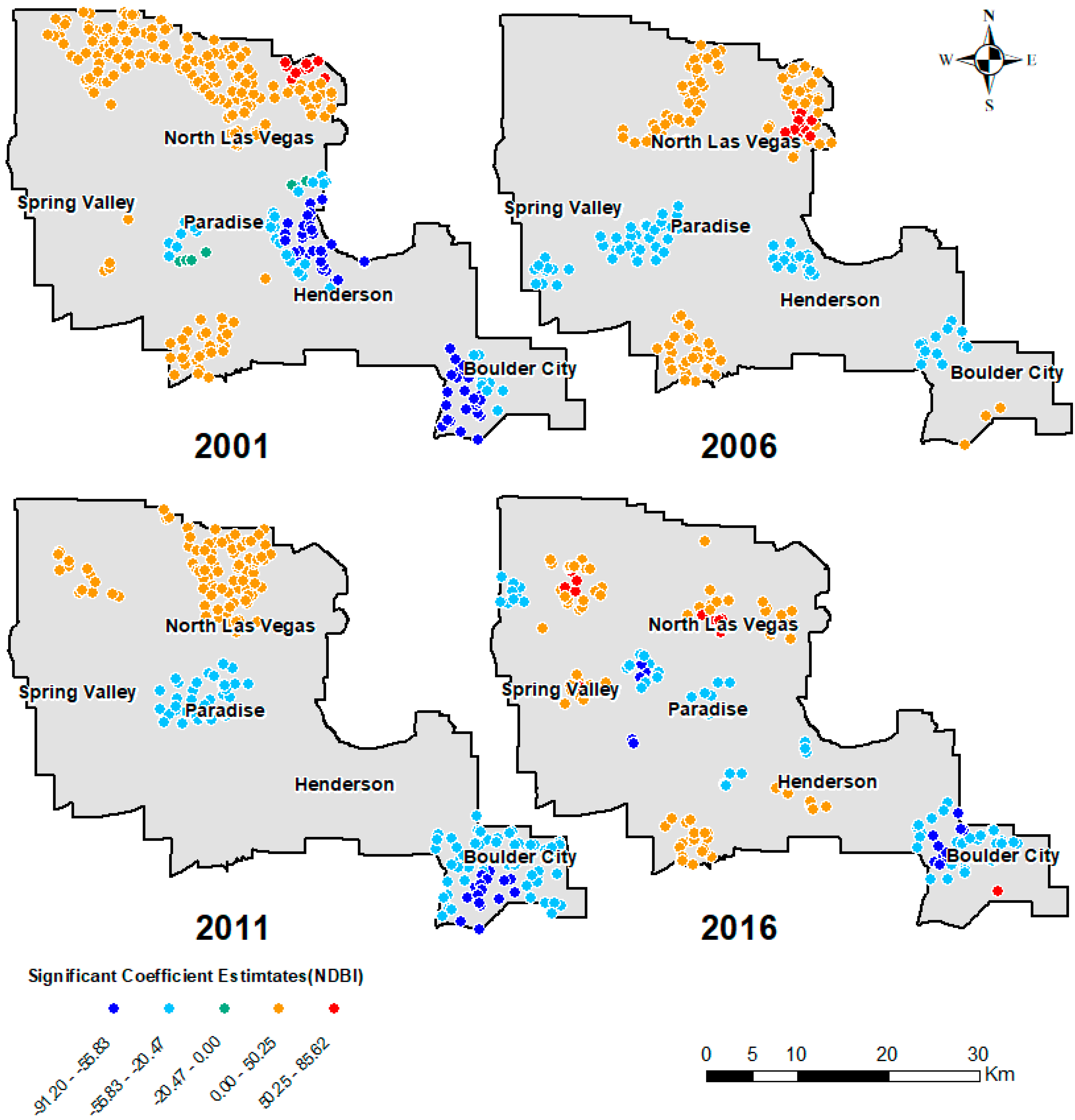
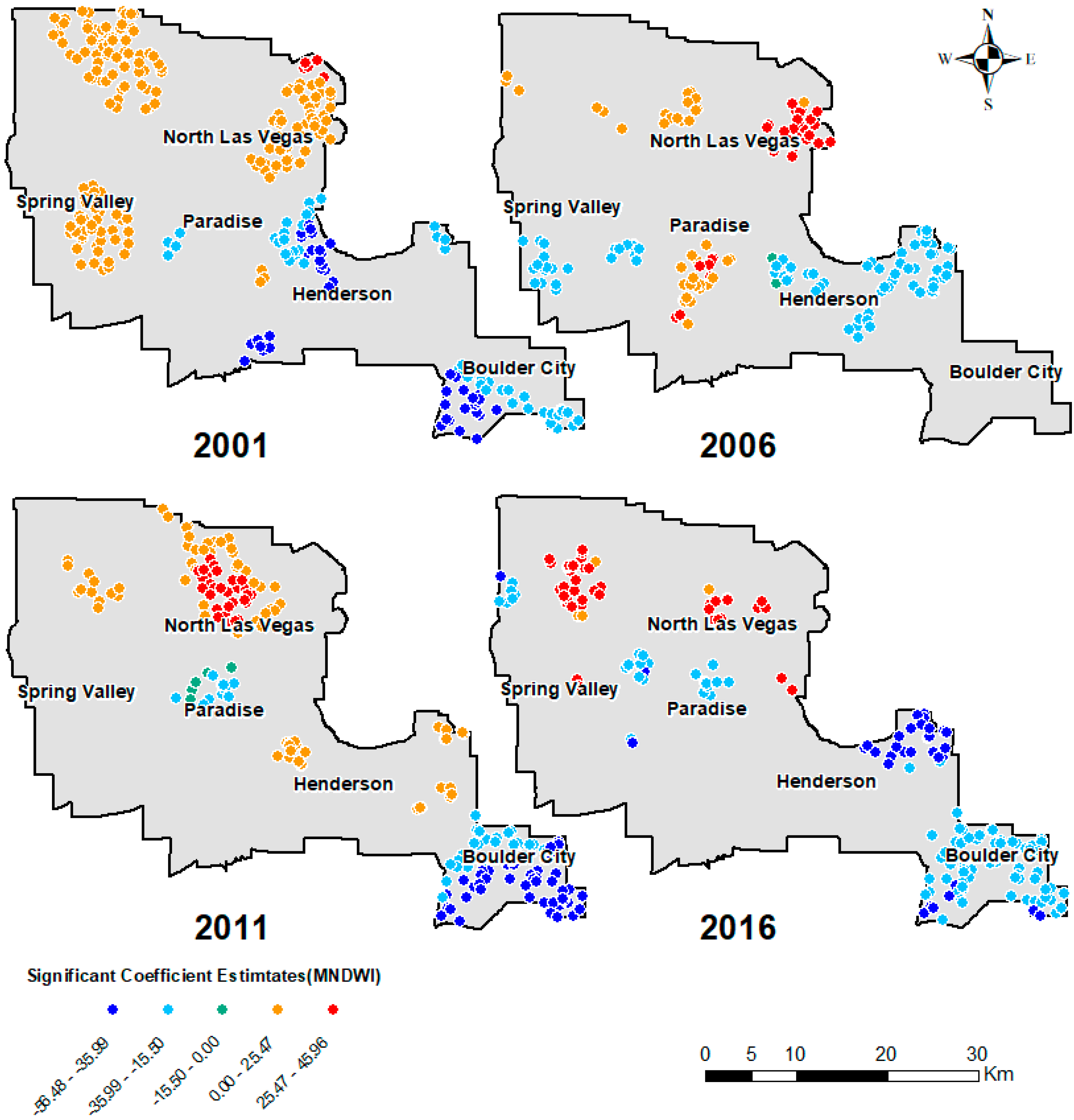
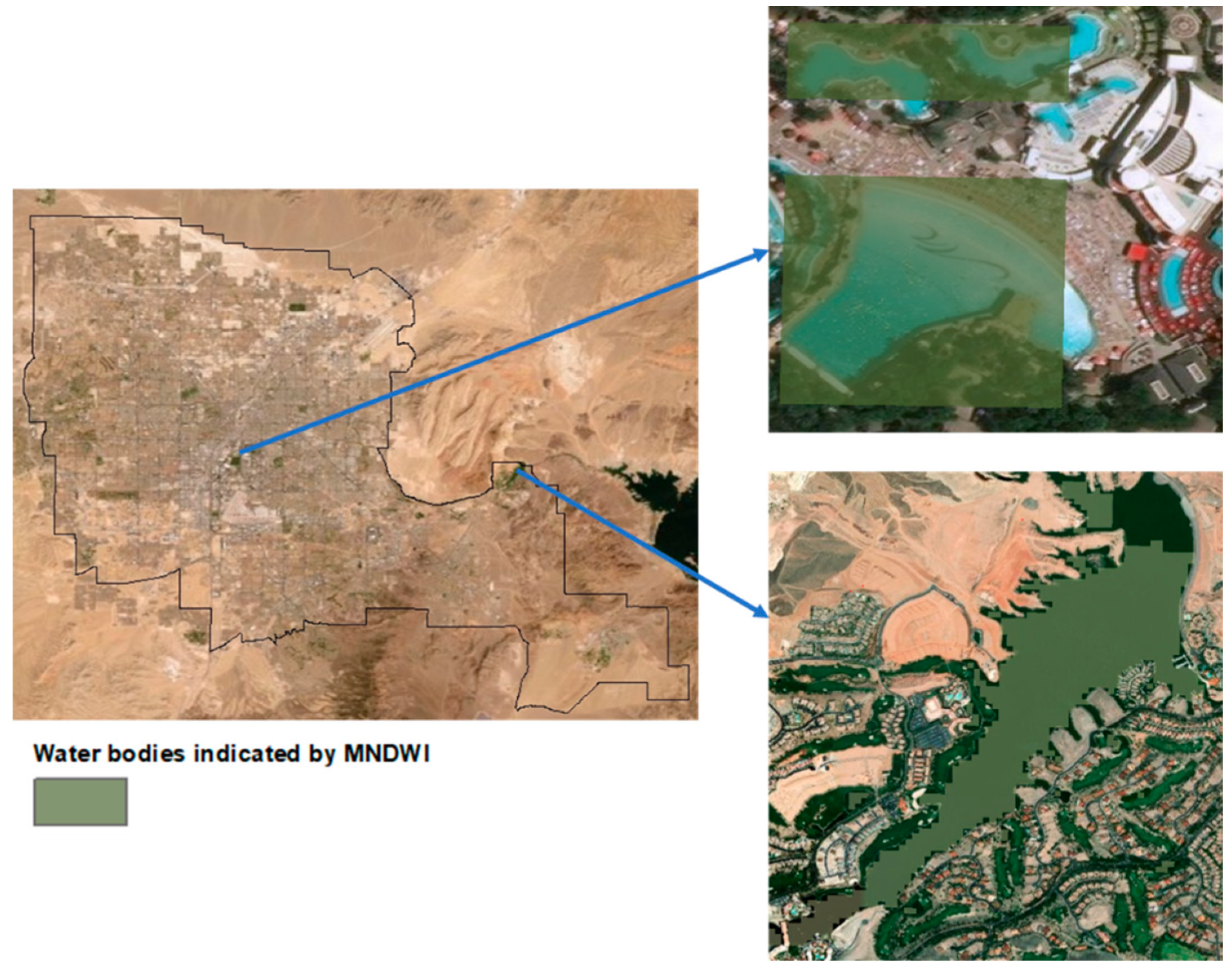
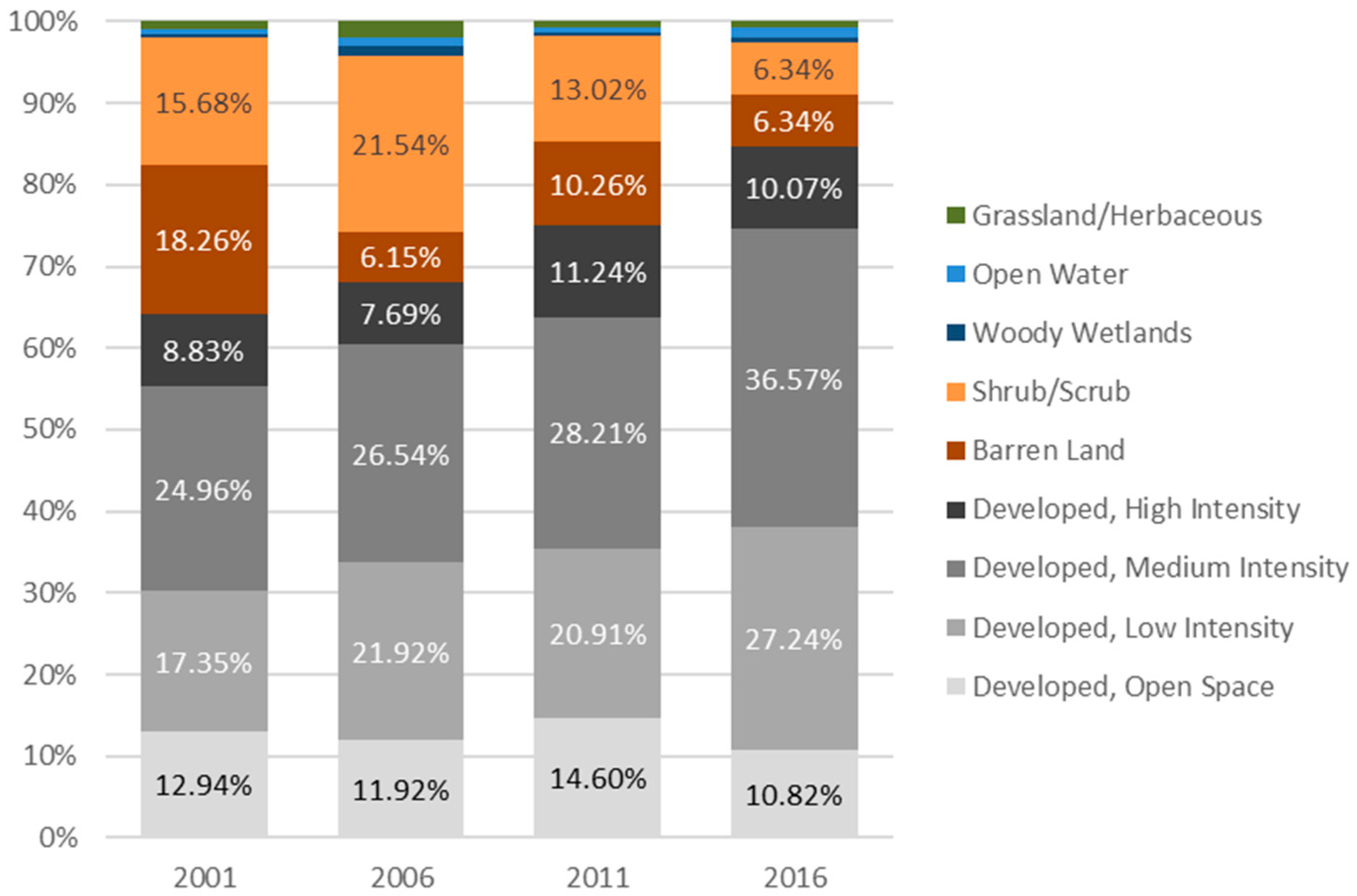
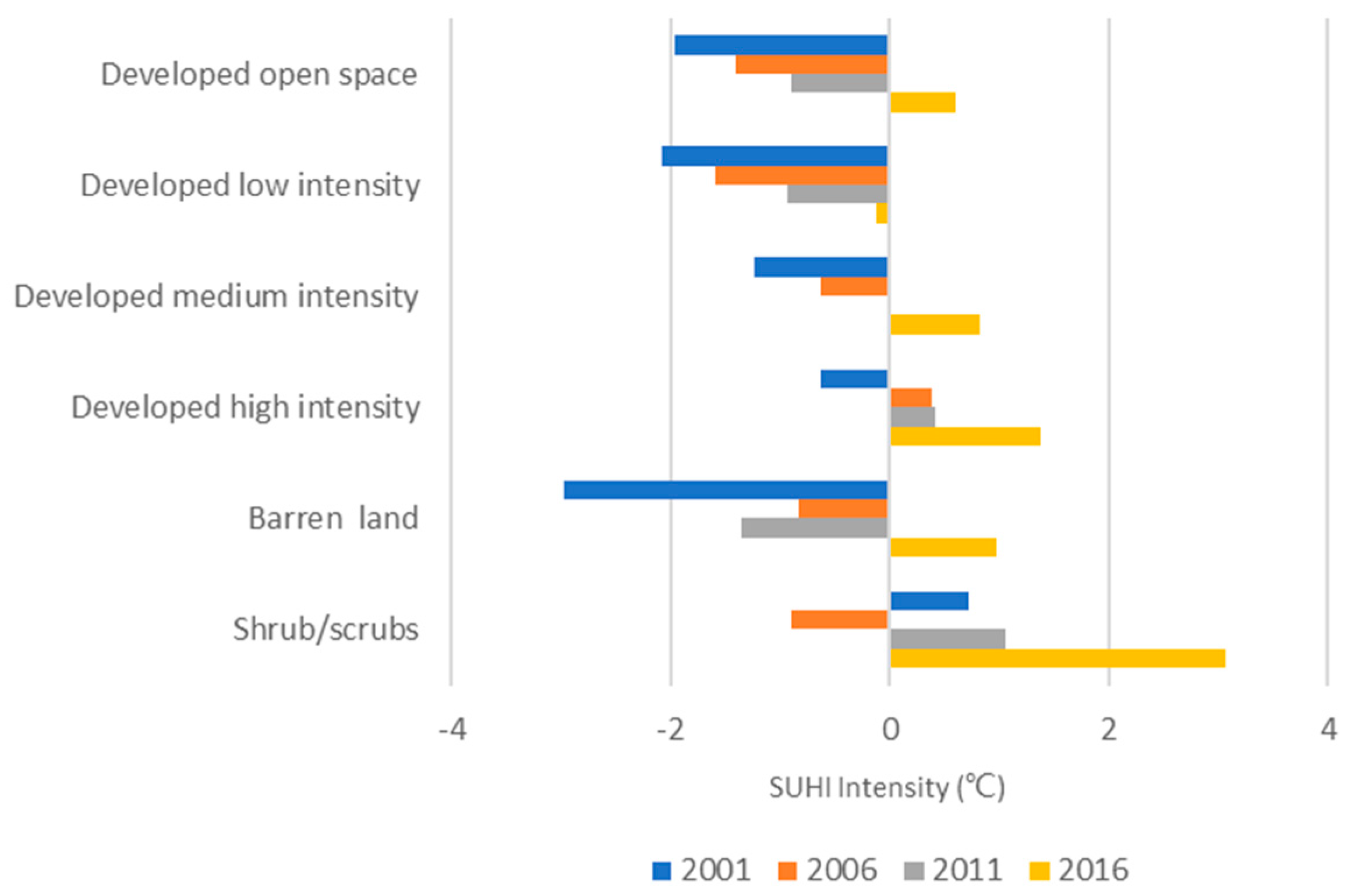
| 2001 | 2006 | 2011 | 2016 | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | StDev | Mean | StDev | Mean | StDev | Mean | StDev | |
| SUHI | −1.11 | 3.19 | −0.99 | 3.03 | −0.12 | 2.80 | 1.12 | 3.03 |
| SAVI | 0.02 | 0.15 | −0.01 | 0.14 | 0.00 | 0.14 | 0.14 | 0.10 |
| NDBI | 0.19 | 0.09 | 0.19 | 0.08 | 0.18 | 0.09 | −0.02 | 0.06 |
| MNDWI | −0.22 | 0.11 | −0.04 | 0.10 | −0.05 | 0.10 | −0.04 | 0.07 |
| SAVI | NDBI | MNDWI | ||
|---|---|---|---|---|
| SUHI | 2001 | −0.253 ** | 0.191 ** | 0.091 ** |
| 2006 | −0.364 ** | 0.290 ** | −0.152 ** | |
| 2011 | −0.247 ** | 0.250 ** | −0.159 ** | |
| 2016 | −0.484 ** | 0.500 ** | −0.285 ** |
| 2001 | Linear regression | GWR | ||||
| β | S.E. a | p-value | VIF | Mean β b | S.D. c | |
| SAVI | −1.85 | 1.34 | 0.167 | 4.12 | −5.92 | 16 |
| NDBI | 6.78 | 2.3 | 0.003 | 4.8 | −0.56 | 26.23 |
| MNDWI | 4.71 | 1.5 | 0.002 | 2.65 | −.28 | 15.91 |
| Diagnostics | ||||||
| AICc | 4992.78 | 4203.26 | ||||
| Adjusted R2 | 0.07 | 0.618 | ||||
| Bandwidth | 1000 | 75.77 | ||||
| 2006 | Linear regression | GWR | ||||
| β | S.E. a | p-value | VIF | Mean β b | S.D. c | |
| SAVI | −8.72 | 1.33 | <0.001 | 3.75 | −6.83 | 9.2 |
| NDBI | −1.96 | 3.56 | 0.038 | 9.59 | 4.93 | 19.51 |
| MNDWI | −7.64 | 2.54 | <0.001 | 6.43 | −0.33 | 13.82 |
| Diagnostics | ||||||
| AICc | 5046.54 | 4400.50 | ||||
| Adjusted R2 | 0.156 | 0.607 | ||||
| Bandwidth | 1000 | 68.22 | ||||
| 2011 | Linear regression | GWR | ||||
| β | S.E. a | p-value | VIF | Mean β b | S.D. c | |
| SAVI | −3.98 | 1.16 | <0.001 | 3.92 | −5.15 | 9.37 |
| NDBI | 6.03 | 2.93 | 0.623 | 9.25 | 1.61 | 20.02 |
| MNDWI | 3.6 | 2.14 | 0.016 | 5.92 | 1.51 | 16.29 |
| Diagnostics | ||||||
| AICc | 4654.97 | 4063.12 | ||||
| Adjusted R2 | 0.100 | 0.557 | ||||
| Bandwidth | 1000 | 69.93 | ||||
| 2016 | Linear regression | GWR | ||||
| β | S.E. a | p-value | VIF | Mean β b | S.D. c | |
| SAVI | −12.32 | 1.62 | <0.001 | 4.43 | −11.41 | 15.26 |
| NDBI | 4.31 | 3.71 | 0.247 | 8.8 | 1.93 | 24.129 |
| MNDWI | −8.66 | 2.66 | 0.001 | 5.15 | −2.11 | 17.48 |
| Diagnostics | ||||||
| AICc | 4648.89 | 4076.65 | ||||
| Adjusted R2 | 0.3 | 0.665 | ||||
| Bandwidth | 1000 | 52.77 | ||||
| 2001 | 2006 | 2011 | 2016 | |||||
|---|---|---|---|---|---|---|---|---|
| SAVI | NDBI | SAVI | NDBI | SAVI | NDBI | SAVI | NDBI | |
| Open Space | −4.34 | 2.92 | −17.98 | 38.03 | −11.65 | 10.67 | −20.57 | 16.86 |
| Low Intensity | −6.08 | 0.70 | −17.53 | 12.13 | −11.70 | 9.32 | −21.97 | 7.04 |
| Medium Intensity | −10.27 | −12.83 | −17.68 | 12.55 | −13.23 | −5.35 | −20.55 | 12.58 |
| High Intensity | −11.02 | −17.57 | −17.20 | −11.98 | −11.59 | −5.45 | −21.20 | −2.74 |
| Barren Land | −0.18 | 15.62 | −19.20 | 31.44 | −7.65 | 21.12 | −15.72 | 2.14 |
| Shrub/Scrub | −20.94 | −3.66 | −17.81 | 11.00 | −21.96 | −23.38 | −28.25 | −21.99 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Fan, C.; Zhao, Q.; Myint, S.W. A Geographically Weighted Regression Approach to Understanding Urbanization Impacts on Urban Warming and Cooling: A Case Study of Las Vegas. Remote Sens. 2020, 12, 222. https://doi.org/10.3390/rs12020222
Wang Z, Fan C, Zhao Q, Myint SW. A Geographically Weighted Regression Approach to Understanding Urbanization Impacts on Urban Warming and Cooling: A Case Study of Las Vegas. Remote Sensing. 2020; 12(2):222. https://doi.org/10.3390/rs12020222
Chicago/Turabian StyleWang, Zhe, Chao Fan, Qunshan Zhao, and Soe Win Myint. 2020. "A Geographically Weighted Regression Approach to Understanding Urbanization Impacts on Urban Warming and Cooling: A Case Study of Las Vegas" Remote Sensing 12, no. 2: 222. https://doi.org/10.3390/rs12020222
APA StyleWang, Z., Fan, C., Zhao, Q., & Myint, S. W. (2020). A Geographically Weighted Regression Approach to Understanding Urbanization Impacts on Urban Warming and Cooling: A Case Study of Las Vegas. Remote Sensing, 12(2), 222. https://doi.org/10.3390/rs12020222