Abstract
Coastal salt marshes are valuable and critical components of tidal landscapes, currently threatened by increasing rates of sea level rise, wave-induced lateral erosion, decreasing sediment supply, and human pressure. Halophytic vegetation plays an important role in salt-marsh erosional and depositional patterns and marsh survival. Mapping salt-marsh halophytic vegetation species and their fractional abundance within plant associations can provide important information on marsh vulnerability and coastal management. Remote sensing has often provided valuable methods for salt-marsh vegetation mapping; however, it has seldom been used to assess the fractional abundance of halophytes. In this study, we developed and tested a novel approach to estimate fractional abundance of halophytic species and bare soil that is based on Random Forest (RF) soft classification. This approach can fully use the information contained in the frequency of decision tree “votes” to estimate fractional abundance of each species. Such a method was applied to WorldView-2 (WV-2) data acquired for the Venice lagoon (Italy), where marshes are characterized by a high diversity of vegetation species. The proposed method was successfully tested against field observations derived from ancillary field surveys. Our results show that the new approach allows one to obtain high accuracy (6.7% < root-mean-square error (RMSE) < 18.7% and 0.65 < R2 < 0.96) in estimating the sub-pixel fractional abundance of marsh-vegetation species. Comparing results obtained with the new RF soft-classification approach with those obtained using the traditional RF regression method for fractional abundance estimation, we find a superior performance of the novel RF soft-classification approach with respect to the existing RF regression methods. The distribution of the dominant species obtained from the RF soft classification was compared to the one obtained from an RF hard classification, showing that numerous mixed areas are wrongly labeled as populated by specific species by the hard classifier. As for the effectiveness of using WV-2 for salt-marsh vegetation mapping, feature importance analyses suggest that Yellow (584–632 nm), NIR 1 (near-infrared 1, 765–901 nm) and NIR 2 (near-infrared 2, 856–1043 nm) bands are critical in RF soft classification. Our results bear important consequences for mapping and monitoring vegetation-species fractional abundance within plant associations and their dynamics, which are key aspects in biogeomorphic analyses of salt-marsh landscapes.
1. Introduction
Salt-marsh ecosystems are transition zones between aquatic and terrestrial systems and provide critical ecological and geomorphological functions in tidal landscapes [1,2,3,4,5]. Salt-marsh ecosystems host high primary productivity [6,7,8], attenuate waves, protect coastal areas from storms [9,10,11,12,13], and act as important global carbon sinks [4,14,15,16,17,18]. Unfortunately, salt marshes are also threatened by accelerating sea-level rise, reduced sediment availability at the coast, wind–wave erosion, and human interventions, especially in recent decades. Salt-marsh deterioration is a consequence of lateral erosion [19,20,21,22] and retreat in the horizontal plane [19,23,24,25], although these processes are rarely studied in a coupled way [26,27,28].
Halophytic vegetation populates marsh areas between mean sea level (MSL) and mean high tide (MHT) [29]. Halophytes can strongly influence erosional and deposition processes, by reducing flow velocity, by attenuating waves, and by trapping suspended sediments [3,30,31,32,33,34,35]. Indeed, halophytes can support salt-marsh survival through biomorphic feedbacks, increasing organic and inorganic deposition [23,24,36,37,38,39,40]. Vegetation spatial patterns are characterized by sharply defined patches of typical species associations [41,42,43,44,45,46,47,48,49]. This spatial organization, or zonation, can be attributed to the adaptation of halophytes to edaphic conditions [50,51,52,53,54,55,56,57,58], species competition [59,60,61,62], and the capability of halophytes to engineer salt-marsh landscapes via biogeomorphic feedbacks [40,48,49,63].
Fractional abundance, i.e., the fraction of the area—projected on the horizontal plane—occupied by plants of a given species, is an important indicator of vegetation distribution [45], with strong links to biomass and salt-marsh surface geomorphology [18] and its time evolution [3,36,40,48,63,64,65,66]. Fractional abundance of bare soil is also an important property of the marsh landscape that has been connected to the marsh sediment budget and marsh vulnerability [67,68]. Hence, accurate vegetation and bare soil mapping is of central interest to understand marsh dynamics and to support coastal management strategies.
Due to the profound influence of halophytic vegetation on ecological and geomorphological processes and their spatial and temporal dynamics [36,38,45,69,70,71,72], analyses of the fractional abundance of salt-marsh vegetation species are required over a large range of spatial scales, from the local (plant) scale to the whole-marsh scale (up to several km2). Remote sensing is an ideal tool to obtain this type of quantitative information and there is an ever-growing amount of research work focusing on the application of remote sensing methods to map fractional abundance of halophytic vegetation in space and time [44,70,73,74,75,76].
Classification methods applied to salt marshes have been developed for and applied to multi- and hyperspectral remote sensing data in a diverse set of biomes worldwide [76,77,78,79,80,81,82]. The large majority of previous approaches to halophytic vegetation mapping determined vegetation abundance by identifying the dominant species in each pixel, using traditional supervised and unsupervised classification algorithms [2,44,76,83,84,85,86]. Nonparametric mapping methods, such as Random Forest (RF) algorithms, have also been applied to halophytic vegetation mapping in the form of pixel-based [84,87] and object-based methods [76,86,88]. However, halophytic vegetation species are highly mixed at the scale of typical satellite sensor resolutions (order of 0.5–1 m) such that the use of hard classification approaches, which attempt to associate a single dominant species to each pixel, is hardly justified. Yet, the number of studies focusing on retrieving the fractional abundance of halophytic vegetation species and bare soil at the sub-pixel scale, i.e., the problem of unmixing, is still limited [65,83]. This is a clear gap that hinders the usefulness of remote sensing retrievals of vegetation distribution and change in salt-marsh studies. Here, we contribute to filling this gap by developing and applying a novel RF-based soft classification method to infer relative species abundance at the sub-pixel scale.
Wang et al. [74] used artificial neural network models to map the fractional abundance of species within associations in salt-marsh landscapes. Artificial neural networks, however, require a relatively time-consuming training phase and the definition and identification of their parameters can be a difficult task [89]. Additionally, artificial neural network performance heavily depends on their structure and design [90], i.e., the number of layers and neurons can significantly influence the accuracy of the method, such that it is difficult to provide a general neural network architecture that can be easily applied in different environments furthermore populated by different species.
RF algorithms [91] have been applied to detect land-use fractional cover [92,93]. However, to our knowledge, the RF approach has never been applied to estimating the fractional abundance of salt-marsh halophytic species at the sub-pixel scale. As marsh vegetation species are particularly highly mixed, here we wonder whether the RF methods may have the ability to provide reliable unmixing results. Furthermore, typical applications of the RF unmixing method to other environments separately estimate single species abundances through regression and subsequently normalize them to sum to 100% [93]. This leads to increased estimation errors, which may be avoided if the RF formulation was better leveraged. To address the latter issue, in this work, we propose a new approach which uses the frequency with which individual “trees” in the RF assign a pixel to each species as reflective of its relative abundance at the sub-pixel scale. This new approach substantially differs from previous analyses based on the RF regression algorithm to estimate fractional abundance at the sub-pixel level, because those analyses do not take advantage of the information contained in the individual tree “votes” and rely on empirical regressions based on field observations. Towards the goal of improving current capability to accurately map fractional abundance of halophytic vegetation in space and time in salt-marsh landscapes, we first explored the possibility of applying the new algorithm based on RF soft classification and then compared the performance of the newly proposed approach to that characterizing existing RF regression methods.
2. Methods
2.1. Study Site—The San Felice Salt Marsh (Venice Lagoon, Italy)
The Venice lagoon (top panels in Figure 1) is located in northeastern Italy and is connected to the Adriatic Sea by three inlets: Lido, Malamocco, and Chioggia. The main rivers that used to debouch into the lagoon were diverted directly to the sea in the XVI–XIX centuries [94], and only a few small rivers now remain, carrying modest amounts of freshwater and sediments into the lagoon. The Venice lagoon has an area of about 550 km2 and is characterized by a semidiurnal tide with an average tidal range of about 1.0 m and a maximum spring tidal range of approximately 1.5 m [95,96].
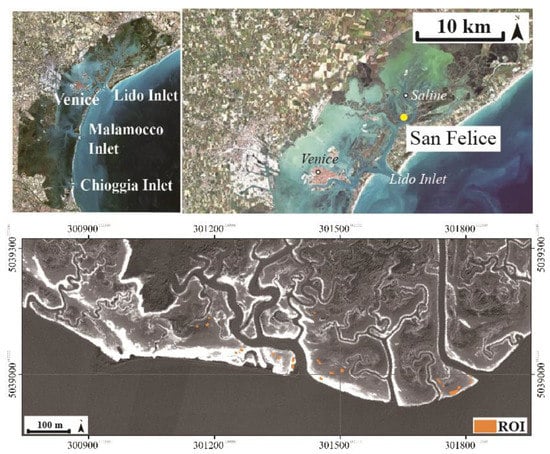
Figure 1.
Research area: the top panels show the map of the Venice lagoon and the position of the San Felice salt marsh; the bottom panel shows the map of the San Felice marsh acquired by WorldView-2 (WV-2) (Red Edge, central wavelength: 724 nm) in 2019 and the positions of the regions of interest (ROIs).
The present study focuses on the San Felice salt marsh (bottom panel in Figure 1), one of the most naturally preserved areas within the northern part of the lagoon, close to the Lido inlet. The San Felice marsh is characterized by relatively healthy vegetation conditions [18,97] and is colonized by halophytic vegetation associations dominated by the following species: Salicornia veneta (hereafter “Salicornia”), Spartina maritima (hereafter “Spartina”), Limonium narbonense (hereafter “Limonium”), Sarcocornia fruticosa (hereafter “Sarcocornia”) and Juncus maritimus (hereafter “Juncus”) [44,45,74,98]. Silvestri et al. [45] reported that each species occupies a preferential range of possible elevations, thus leading to a typical species sequence with increasing elevation. Moreover, due to the strong link between marsh elevation and distance to channels [40], the distribution of halophytic species also varies from the channel edges to the inner portions of the marsh. Specifically, Salicornia and Spartina are preferably found in the lowest areas (inner portions of the marsh), Limonium tends to occupy intermediate marsh elevations, and Sarcocornia is more likely to colonize higher marsh areas, close to marsh edges. Juncus tends to develop where creeks bring litter and organic matter accumulates over time. In general, the density of halophytic vegetation decreases with distance to marsh edges [18].
As mentioned above, halophytic vegetation distribution is strongly linked to marsh morphology through a landscape-forming bio-morphologic process, and species are associated with (possibly overlapping) characteristic elevation ranges [45,48]—the result of species adaption to edaphic factors [43,50,99] and of interspecific competition [60,100]. Productivity and bio-diversity of halophytic vegetation are also linked to elevation [36,71,101]. The presence of these links between morphological and ecological patterns highlights the great value of robust fractional-abundance mapping methods to monitor and analyze salt-marsh bio-morphodynamics. This suggests that robust fractional-abundance mapping algorithms are of critical importance to analyze halophytic vegetation distribution patterns and temporal dynamics at large spatial scales (indicatively 10–10,000 m).
Finally, halophytic vegetation distribution has been observed to change over time scales of a few years [44,62,65,70,102,103], especially in the current accelerating sea-level rise scenario [104,105,106,107,108]. Hence, a proper quantitative description of marsh vegetation space–time dynamics would greatly benefit from robust and highly repeatable quantitative mapping.
2.2. Datasets
2.2.1. WoldView-2 Data
We developed and tested RF unmixing methods with application to WorldView-2 (WV-2) data. The workflow of this study is shown in Figure 2.
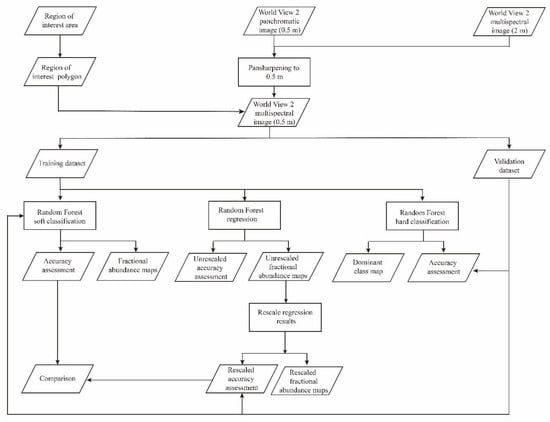
Figure 2.
The workflow of the present study.
The WV-2 sensors included a panchromatic spectral band with a high spatial resolution (0.5 m) and 8 multispectral bands (Table 1) with a lower spatial resolution (2 m), spanning 4 standard bands (red, green, blue, and near-infrared 1) and 4 other application-oriented bands (Coastal, Yellow, Red Edge, and near-infrared 2). The sensor acquired data from an altitude of about 770 km. The data analyzed in this study were acquired at 10:23:00 on 7 November 2019. At the time of acquisition, the tidal level, measured at the Saline tide gauge station, close (about 3 km) to the San Felice marsh, was about 0.76 m above the Punta della Salute datum. As the current MSL is 31 cm higher than the Punta della Salute datum, the water level was about 0.45 m above the MSL at the time of acquisition, which corresponds to water depths ranging between 0 and 30 cm over the marsh platform.

Table 1.
WorldView-2 spectral band edges and center wavelengths. NIR 1 = near-infrared 1; NIR 2 = near-infrared 2.
2.2.2. Field Observations
Field vegetation mapping was performed on Jan 9, 2020. Twenty-four regions of interest (ROIs, i.e., field areas used for training and validating the classification model), were selected, with areas ranging between 18.0 m2 and 106.5 m2 (Table 2 and bottom panel in Figure 1). ROIs were randomly selected across the marsh to include all typical homogeneous associations of species that encroach the San Felice salt marsh. For each ROI, the percentage cover of vegetation species and bare soil was estimated using the standard Braun-Blanquet visual method, which records the presence of each species by 10 intervals between 0% and 100% [44]. The boundaries of the ROIs were accurately delimited through differential GPS (Leica CS15 in RTK mode, minimum accuracy of ±1 cm) (see Table 2 for ROI properties). ROIs were then overlaid on the WV-2 georeferenced image (using ArcGIS 10.5) and only pixels falling entirely within an ROI were used to build the classification dataset, which was then divided into two independent training and validation subsets, as explained in Section 2.3 [74].

Table 2.
Field measurements of fractional abundance of each class in the San Felice salt marsh (Venice, Italy). Jun = Juncus, Lim = Limonium, Sali = Salicornia, Sarc = Sarcocornia and Spar = Spartina.
2.2.3. WorldView-2 Data Preprocessing
Even though the atmospheric correction may not influence the result and accuracy of classifications [109], we applied such a correction to obtain more accurate spectral information to favor the interpretation of the results, and for possible comparisons with past or future acquisitions. The Fast Line-of-sight Atmospheric Analysis of Spectral Hypercubes (FLAASH) algorithm [110,111] was employed to perform atmospheric correction in Envi 5.4. In FLAASH, the “Mid-Latitude Winter” Atmospheric Model and the “Maritime” Aerosol Model were used. Due to the lack of aerosol optical thickness data at the nearest AERONET station on the acquisition date (https://aeronet.gsfc.nasa.gov/) and good weather conditions, according to the instruction [112] the visibility was set to “Clear”, corresponding to 40 km. After atmospheric correction, the multi-spectral bands were pan-sharpened using the panchromatic band, which has a spatial resolution of 0.5 m, through the Gram–Schmidt Pan Sharpening algorithm [113,114]. Both atmospheric correction and pan-sharpening were performed in ENVI 5.4. Water bodies were masked based on negative values of the NDVI (normalized differential vegetation index) [115] derived from “NIR1” and “Red” channels (Table 1).
2.3. Algorithm Description
In this work, the RF algorithm is applied using the Scikit-learn package [116], a freely available machine learning library for the Python programming language.
RF is a machine-learning algorithm based on the Decision Tree method [91], which is being increasingly and successfully used in remote sensing analyses of vegetation species and habitats [76,77,84,93,117,118]. RF classification is a supervised nonparametric classification method that makes predictions through a set of decision trees [91] which form a so-called “forest”. Each decision tree is composed of a set of internal nodes and terminal nodes. Given a set of pixels known to belong to different information classes (i.e., the different vegetation species in the present application), training is performed by feeding each tree with the input spectral reflectance and the associated class for each pixel. Training pixels (samples) are then split into two groups (“left” and “right”) at each node, based on so-called “best split” binary rules [91,119] and decreasing the Gini impurity index (G(I)), which is defined as:
where is the frequency of occurrence of the ith class among the n total classes. G(I) represents the impurity level of information in the current node. Specifically, the highest value of G(I), G(I) = 1 − 1/n, shows each class is equally distributed in this node, while the minimum value of G(I) shows all pixels in this node belong to one class. The best-split is chosen by maximizing the impurity decrease (ID), which can be expressed as:
where N is the total number of samples in the training set, Nt is the number of samples at the current node, Ntl is the number of samples in the left child node, and Ntr is the number of samples in the right child node, and the and are G(I) in the right and left child node, respectively, [116]. In a decision tree, the nodes will be split if this split induces a decrease in the impurity larger than or equal to a determined value, named “min impurity decrease” (hereafter mid). The value of mid is pre-determined as 0, which is the default value in Scikit-learn package. If the growth of a tree is not bounded, the tree would keep growing until there is a terminal node for every single pixel.
In the RF classification, a user-defined large number of decision trees (ntree) is chosen, but each tree has limitations in growth given by specific rules. In particular, each tree learns from a subset of pixels randomly selected from the training dataset. Two-thirds of the pixels present in the training dataset are drawn with replacement (i.e., bootstrapping) to construct each decision tree; thus decision trees are trained on different subsets of the data [91]. Each tree is fed with a subset of the training pixels, those that are left out (out of bag, OOB) are used as validation datasets to test the predictive ability of that individual tree. The proportion of times that OOB samples are incorrectly predicted is recorded and averaged over all cases to produce an OOB error estimate (OOB score). The OOB error estimation has been proven to be unbiased [120].
The training process also makes it possible to evaluate the importance of each spectral band in reducing the classification error. Specifically, at each split, the decrease in G(I) is recorded for each band (Xi) that was used to form the split. The average of all decreases in the G(I) in the forest where band (Xi) is involved yields the Gini variable importance value (IV) [121,122,123]. Scikit-learn normalizes IVs of each band to a value between 0 and 1 by dividing by the sum of all importance values [116]. As for other supervised classification methods, the training dataset may come from ROIs selected in the image. If the ROIs contain mixed vegetation and bare soil areas, as it often happens with marsh sites, the RF classifier allows to include “sample weights”, which, in this study, correspond to the fractional abundance of different vegetation species and bare soil estimated for each ROI during field surveys. Once “sample weights” are defined, the split is determined by the weight of each class at the current node, instead of the number of samples. N, Nt, Ntr, and Ntl in Equation (2) will be the sum of the weight of all species at their corresponding nodes. For example, a node including n pixels, in which fractional abundance belongs to ith species is Fi. N at this node can be obtained by . Once this node acts as a mother node to split, the calculation of Nt, Ntr, and Ntl will follow the same method. Moreover, we use another parameter, i.e., the “min weight fraction”, to control the split process. “Min weight fraction” is defined by Pedregosa et al. [116] as the minimum weighted fraction of the total sum of the weights (of all the input samples) at each child node. Here, we prefer to interpret it as a threshold value to determine whether the child node should be created or not. Specifically, the weight fraction (wf) of each child node creation is defined as follows:
where weightchild and weightmother are the weight sum of classes in the child and mother node, respectively. A child node whose wf is lower than “min weight fraction” should not be created. In this study, the “min weight fraction” is set to 0. The RF is trained based on the provided classes and sample weights (fractional abundances), generating the pruning decision trees. After the training, when an unknown pixel value is input into the model, each decision tree assigns it to a specific class independently. This is usually explained by saying that each tree “votes” for a class, thus suggesting the possibility to consider it as a voting process. The RF classifier records the number of votes associated with the classified pixel for all the classes and the pixel is usually assigned to the class with the highest number of votes. Instead of considering the final association of each pixel to the most-voted class, in this work, we consider the number of votes as the probability value that the pixel belongs to one specific class [91], and then we interpret such probability value as the sub-pixel relative fractional abundance.
An important advantage of the RF classification is that it can manage a large number of input bands [84,88,124] and minimize data dimensionality issues, such as the Hughes phenomenon [117], that make the large amount of information contained in multispectral data difficult to exploit fully. Moreover, unlike some supervised parametric classifiers, such as the Maximum Likelihood method which assumes data are normally distributed [125], RF is also capable of handling multi-modal datasets, whose variables display more than one maximum in their probability distribution [117].
In this work, in order to test the accuracy of our results, we have randomly divided the original dataset into two independent groups, i.e., 75% of the pixels (2804 pixels) from the ROIs were used for model training and 25% of the pixels (935 pixels) were used for testing. Sample weights of training data were passed to the model according to fractional coverages of vegetation species recorded in the field. At the end of the process, we assumed that the predicted probability of each vegetation class (i.e., species) equals its fractional abundance. Results were validated using the fractional abundance of the validation dataset and the error for each vegetation species was calculated.
With the purpose of verifying the effectiveness of this new approach based on RF soft classification for sub-pixel fractional abundance assessment, we used the same dataset to train and test a traditional RF regression method.
Similarly to the RF classification, the RF regression is an ensemble of decision trees, and it is based on the assumption that the relationship between input variables (spectral reflectance) and sub-pixel fractional abundance can be described through a non-linear correspondence [91]. Following the above description of RF classification, it is easy to understand the processes of RF regression, which shares many of the advantages of the RF classifier. RF regression is always characterized by a relatively low risk of overfitting, compared with other regression methods, especially the Decision Tree regression. Similar to its classification counterpart, RF regression can provide a relatively unbiased evaluation of the model (through OOB information). In the RF regression process, the same training and validation datasets of RF soft classification were used to construct and test the RF regression model.
The main steps of the RF regression are: (1) the RF generates a regression model for each vegetation species based on the training dataset; (2) for each unknown pixel, the RF regression model is used to predict the fractional abundance of vegetation species and soil, and the prediction error is calculated using the validation dataset; (3) the results obtained for each pixel are then rescaled to sum to 100% because the method predicts vegetation fractional abundance separately for each vegetation species; (4) the accuracy of the predicted percentage for each class (obtained in Step 3) is again quantified using the validation dataset.
Considering that traditional approaches to mapping halophytic vegetation usually assign pixels to the dominant species [2,44,84,97] and that some of species associations are dominated by one species, we used the fractional abundance maps obtained with the RF soft classification method to produce a map of the most abundant halophytic species across the study site. Specifically, the pixels with percentage cover larger than 60% were considered as colonized by the dominant species [44]. The results were then compared to a map obtained using an RF hard classification trained using only ROIs characterized by relative homogeneous vegetation communities (or bare soil) with the dominant species (or soil) covering more than 60% of the area. A dataset of 2829 pixels was used, but to allow for error assessment, it was randomly divided into two groups: 2121 pixels (about 75% of the dataset) were used in model training and 708 pixels (about 25% of the dataset) were used in model validation. We notice that the number of data used for the hard classification is smaller than that used for soft classification and regression because hard classification just includes pixels with percentage cover greater than 60% [44] while all pixels are used in soft classification and regression processes.
2.4. Estimation of Accuracy
The Confusion Matrix was used to evaluate the performance of the hard classification, which can provide Overall Accuracy (A), describing the ratio between the number of correctly classified validation points and the total number of validation points irrespective of the class [126]. We also used the Kappa coefficient, K, which is defined by the proportion of correctly classified validation sites after random agreements are removed [127]. The root-mean-square error (RMSE) and the coefficient of determination (R2) between predicted fractional abundance and test data were calculated for each class to estimate model performance:
where is the ground referential value, represents the predicted value, is the average of the observed values, and n is the number of test points.
3. Results
3.1. Selection of Ntree
In this work, we selected ntree based on the accuracy of hard classification, testing the overall Accuracy (A) variations when the number of trees ranged from 10 to 1000. Figure 3 shows the results obtained when ntree is in the 10 to 1000 range. We notice that the training accuracy A rapidly increases and stays stable once ntree is larger than 150. The steady increase in A with ntree can be attributed to the reduced risk of overfitting. Indeed, the peak value of A is approached when ntree ranges from 460 to 490. As the RF is a computationally efficient algorithm and a larger ensemble of trees can reduce the risk of overfitting, ntree should be set as large as possible [128]. Considering that several applications of the RF to remote sensing image classification used ntree = 500 [93,129,130,131], we decided to use ntree close to 500 to compare the results obtained with our method to those from previous analyses. We thus selected ntree equal to 490, which was close to the value used in previous studies and also provided the highest value of A in this study. Even though ntree was selected based on RF hard classification, to consistently compare the results, we have maintained ntree = 490 also for RF soft classification and RF regression.
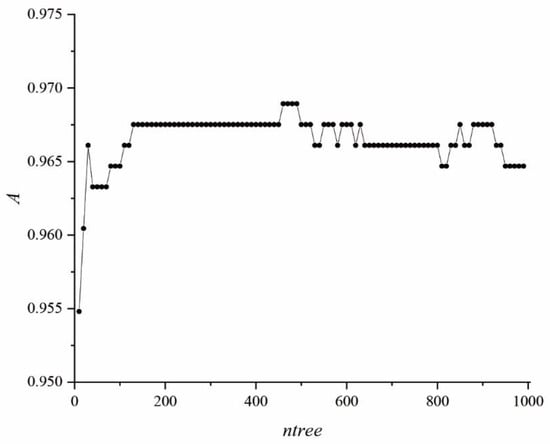
Figure 3.
Overall accuracy (A) of hard classification variations as a function of the number of trees (ntree).
3.2. Fractional Abundance Based on RF Soft Classification Method
As discussed in the Methods section, we use the number of votes resulting from the RF soft classification to determine the probability of each vegetation species. The main advantage of this new approach is that, for each pixel, the sum of the predicted probability of each class is equal to 100%. Indeed, by assuming that the probability of each species represents its fractional abundance, there is no need to rescale the abundance of the different species. This is consistent with the collection of ancillary data because we emphasize that the method used in the field for determining the fractional abundance (i.e., the Braun-Blanquet visual method, commonly used in ecology) is also essentially related to the occurrence probability of each class.
Maps of fractional abundance of Juncus, Limonium, Salicornia, Sarcocornia, Soil, and Spartina generated using the RF soft classification method are shown in Figure 4, while Table 3 shows R2 and RMSE for fractional abundance. We notice that R2 and RMSE values for the RF soft classification range from 0.652 to 0.956 and from 6.753 to 18.667, respectively. This suggests that the RF soft classification method can successfully predict the fractional abundance of each species and bare soil.
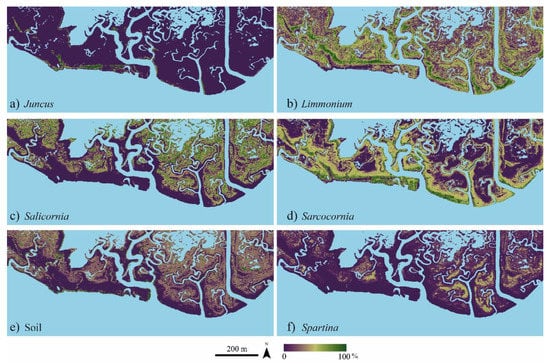
Figure 4.
Maps of fractional abundance of each species and bare soil obtained based on the Random Forest (RF) soft classification method. Specifically, (a–f) are maps of fractional abundance of Juncus, Limonium, Salicornia, Sarcocornia, Soil and Spartina, respectively. Light blue areas represent water.

Table 3.
Accuracy information for RF soft classification. Jun = Juncus, Lim = Limonium, Sali = Salicornia, Sarc = Sarcocornia and Spar = Spartina. RMSE = root-mean-square error.
3.3. Subpixel Classification through RF Regression Method
It has been shown that RF regression can perform well for vegetation species mapping when ntree is large (for example, 500 decision trees) [93]. To compare the performance of the RF regression method with the soft method, 490 decision trees (i.e., ntree = 490) were used to predict the abundance of the six vegetation species individually. Table 4 provides the accuracy retrieved for each class, showing that R2 and RMSE range from 0.74 to 0.98 and from 4.5 to 15.0, respectively. These results confirm that the RF regression is an accurate predictor of percentage for each class when we consider one class at a time (Figure 5). However, once the predicted abundance of each class is simply rescaled to 100% (i.e., the percentage values of the classes are rescaled to sum to 100% for each pixel), the accuracy decreases (Table 4), suggesting that the RF regression method may not be suitable to provide quantitative information on the fractional abundance for highly mixed vegetation species. Due to their low accuracy, the rescaled fractional abundance maps are not shown in this paper.

Table 4.
Accuracy information for RF regression. Jun = Juncus, Lim = Limonium, Sali = Salicornia, Sarc = Sarcocornia and Spar = Spartina.
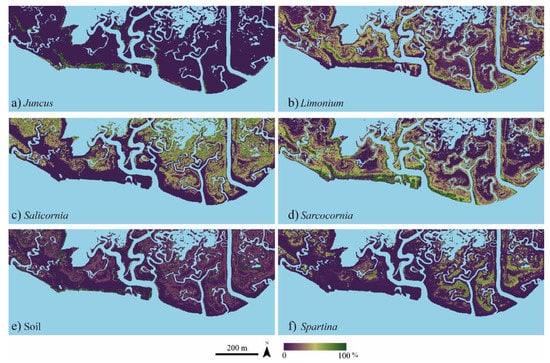
Figure 5.
Maps of the individually predicted abundance of vegetation species obtained based on the RF regression. Specifically, (a–f) are maps of abundance of Juncus, Limonium, Salicornia, Sarcocornia, Soil and Spartina, respectively. Light blue areas represent water.
3.4. RF Hard Classification
Figure 6 shows the results of an RF hard classification with ntree = 490, trained with the same dataset used for the RF soft classification (Figure 6a). The OOB, A, and Kappa coefficient of the RF hard classification are 0.96, 0.97, and 0.96, respectively. Figure 6b shows a majority map created using fractional abundance predicted by the RF soft classification, i.e., a map that shows the spatial distribution of species with fractional abundance higher than 60%. Black pixels in the map indicate the highly mixed locations, where the percentage cover of all classes is lower than 60%. The Confusion Matrix for the RF hard classifier is displayed in Table 5. Our results show that the RF hard classifier can efficiently distinguish different vegetation associations based on the dominant species and bare soil.
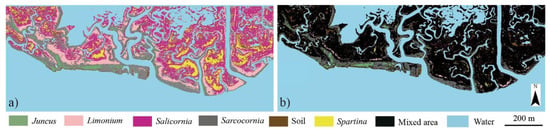
Figure 6.
Maps for dominant species and soil: (a) RF hard classification map results; (b) majority map based on RF soft classification.

Table 5.
Confusion Matrix for WV-2 classification of San Felice marsh through Random Forest (RF) hard classifier. Jun = Juncus, Lim = Limonium, Sali = Salicornia, Sarc = Sarcocornia and Spar = Spartina.
4. Discussion
We developed and tested a new method that uses the frequency with which an individual “tree” in an RF algorithm assigns a pixel to each species as reflecting the fractional abundance of the corresponding species. A comparison of results from the new algorithm to those from existing RF regression methods [132,133,134] shows a superior performance of the proposed method (Table 3), which thus constitutes a powerful method for the analysis of vegetation patterns and their dynamics in salt-marsh landscapes.
4.1. Halophytic Vegetation Distribution Patterns on the San Felice Marsh
The application of the new method of vegetation abundance mapping to marshes in the Venice lagoon allows the quantitative description of some characteristic patterns exhibited by halophytic vegetation. Figure 4a shows that Juncus is more likely to populate marsh edges, while Limonium and Sarcocornia (Figure 4b,d) tend to compete for the same area, located at a moderate distance from the tidal channels. Figure 4c,f show that Salicornia and Spartina tend to cover the inner portions of the marsh. Such patterns nicely agree with those documented through field observations [44,45]. Indeed, as discussed in Section 2, halophytic vegetation distribution is associated with salt-marsh surface morphology. Silvestri et al. [45] showed that, in the study marsh considered, Spartina colonizes the inner and lower part of the marsh, Limonium and Sarcocornia are more likely to be observed at intermediate surface elevations, and Juncus tends to occupy higher-elevation marsh areas. Indeed, the fractional abundance of each species has been considered as an indicator of marsh morphology [53] and of distance to channels [135]. Consistent with observational evidence [2,45,53,74], maps of fractional abundance of each species provided by the “soft” RF algorithm (Figure 4) emphasize the clear link between vegetation distribution and marsh surface morphology, which is strongly related to the distance to main channels representing the source of sediments delivered to the platform [136]. Indeed, inner marsh portions, that are mainly occupied by Salicornia and Spartina (Figure 4c,f), display lower elevations; areas at moderate distance to the channels, that are encroached by Limonium and Sarcocornia, (Figure 4b,d) are characterized by intermediate surface elevations; marsh edges, which are mainly occupied by Juncus, are characterized by higher elevations. The link between plant distribution and marsh morphology, described in Figure 4, is consistent with observational evidence [18,53], and therefore further confirms the robustness of the RF soft classification. The repeated application of the novel soft RF algorithm to a temporal series of remote sensing data from the same marsh can thus allow a quantitative and repeatable monitoring of marsh eco-morphodynamic processes.
4.2. The RF Soft Method Performance Compared to Existing Regression Models
It is worth recalling that the RF regression method [132,133,134,137,138], after simply rescaling abundance of each class to sum to 100%, was observed to perform well when applied, e.g., to map fracitonal abundance of tree species in Bavaria (Germany) (0.72 < R2 < 0.82) [93] and plant types (0.47 < R2 < 0.78) in East Asia steppe (China, Mongolia, and Russia) [133]. However, in our case the accuracy of the RF regression model was not satisfactory (0.14 < R2 < 0.58). This relatively worse performance can probably be attributed to the high small-scale heterogeneity that characterizes marsh vegetation. In particular, the number of classes in Bavaria (two tree species and one class labeled as “other” considered in [93]) and in East Asia steppe (two plant types: woody and herbaceous) was lower than that of the Venice lagoon (five vegetation species and one class representing the bare soil on the marsh). Furthermore, the renormalization of RF regression results summing to 100%, which is necessary to obtain fractional abundances, is likely to increase the estimation error (Table 4 and Figure 7, Figure 8 and Figure 9). Indeed, as Immitzer et al. [93] reported when they estimated the fractional abundance of tree species in Bavaria via the RF regression, the highest value of the sum of the relative abundance of the three considered classes in each pixel was about 102%, while such a value increased to more than 200% in our case. It should be noticed that the renormalization process in the application of the RF regression is performed in this study by assuming that all RF regression models for single species contribute equally, e.g., considering that the sum of the predicted abundance is 100% [139]. In order to improve the accuracy of the RF regression, a weighted contribution of each model on the basis of the documented vegetation distribution patterns could be considered.
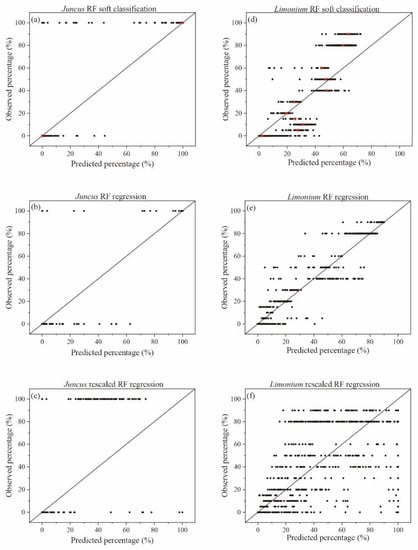
Figure 7.
Validation results for Juncus and Limonium: (a,d) are predicted probabilities (x-axis) plotted against the validation data; (b,e) are regression results (x-axis) plotted against the validation data; (c,f) are rescaled regression results (x-axis) plotted against the validation data. Red dots represent the mean of the predicted percentage using the RF soft classification.
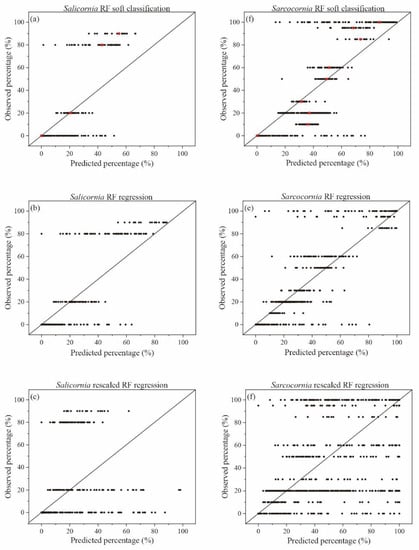
Figure 8.
Validation results for Salicornia and Sarcocornia: (a,d) are predicted probabilities (x-axis) plotted against the validation data; (b,e) are regression results (x-axis) plotted against the validation data; (c,f) are rescaled regression results (x-axis) plotted against the validation data. Red dots represent the mean of the predicted percentage using the RF soft classification.
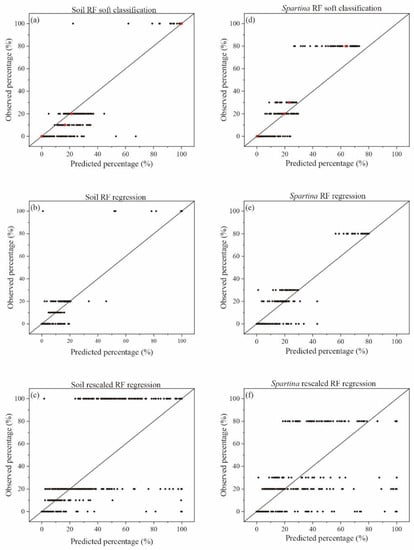
Figure 9.
Validation results for Soil and Spartina: (a,d) are predicted probabilities (x-axis) plotted against the validation data; (b,e) are regression results (x-axis) plotted against the validation data; (c,f) are rescaled regression results (x-axis) plotted against the validation data. Red dots represent the mean of the predicted percentage using the RF soft classification.
Figure 7, Figure 8 and Figure 9 and Table 4 suggest that, although the RF regression model predicts reasonably the relative distribution of each class taken separately, the method that is usually adopted [93,132,133,137] can hardly be applied to accurately estimate the fractional abundance of each species in the case of highly mixed species. Values of R2 and RMSE for fractional abundance derived from RF soft classification and RF regression, respectively (Table 3 and Table 4), suggest that the RF soft classification performs slightly worse than RF regression for single classes, while its performance is considerably higher compared to the rescaled RF regression method. Figure 7, Figure 8 and Figure 9 show the outcome of the test performed to compare field observations with the results obtained with the three different methods (RF soft classification, RF regression, and rescaled RF regression models) for Juncus and Limonium (Figure 7), Salicornia and Sarcocornia (Figure 8), Soil and Spartina (Figure 9) and highlight that the RF soft classification method performs much better than the rescaled RF regression method. The superior performance of the RF soft classification can be attributed i) to the full use of the information provided by each decision tree, and ii) to the simultaneous consideration of all classes which avoids the need to perform ad hoc renormalizations.
4.3. Drawbacks of Dominant Species Maps
Due to the high biodiversity of halophytic vegetation species on marshes, we argue that traditional hard classification methods (i.e., where classifiers tend to associate each pixel to an individual species or to bare soil) [44,70] cannot provide accurate information on vegetation distribution. Indeed, pixels (whose sizes are in the order of 0.5–1 m) in remote sensing images are often composed of highly mixed vegetation associations [53,74], particularly over salt marshes. The results obtained with the hard classification (Figure 6a) allow us to perform a further analysis of the results obtained with the RF soft classification (Figure 6b). Specifically, we notice that the position of patches occupied by dominant classes agrees quite well with those obtained with a RF hard classification, thus suggesting the robustness of the RF soft method. Furthermore, we notice that some large mixed areas, composed by more than one species (or bare soil), cannot be detected by the hard classification method. These areas are mostly located in the inner portions of the marsh, where topographic elevations are relatively low [18,45] and inner species (Salicornia and Spartina) are always mixed with bare soil. Finally, we also notice that mixed areas are observed in Limonium-dominated areas in the hard classification results. This can be attributed to the fact that Limonium and Sarcocornia tend to colonize the same areas.
We further compared our results to those obtained by Belluco et al. [44] using ML (Maximum Likelihood) and SAM (Spectral Angle Mapper) hard classifiers applied to a 2001 IKONOS dataset over the same study site. The map obtained with the RF hard classification and the majority map obtained from the RF soft classification are both very similar to that of ML and slightly better than its SAM counterparts, based on the comparison of A and Kappa coefficient, indicating that RF is a reliable classifier for halophytic species.
We therefore conclude that, in highly mixed vegetation environments like salt marshes, traditional hard classification methods do not provide sufficient information on species distribution since they must necessarily label mixed areas with the dominant species. On the contrary, soft classification methods, when properly applied, provide essential information about species presence (also within mixed pixels). Majority maps obtained from RF soft methods are consistent with those produced with hard classification methods, lending further support to the method introduced here.
4.4. Feature Importance Analyses
An advantage of the RF algorithm is that it allows the quantification of the importance of each spectral band (i.e., feature) used in the classification. In our case, we analyzed IV values of each WV-2 band for the detection of salt marsh vegetation and bare soil. As for the hard classification method, Figure 10a shows that the Yellow band (wavelength: 584–632 nm) is the most important band among those provided by WV-2. One possible explanation for this could be that the Yellow band facilitates the detection of bare soil, which has higher reflectance at this wavelength compared to vegetation (Figure 10c). As for the subpixel classification based on RF soft method, Yellow band, NIR 1, and NIR 2 bands are those that provide the majority of information (Figure 10b), possibly due to the difference of reflectance characteristics in the NIR 1 and NIR 2 bands of different vegetation species (Figure 10c). Table 6 suggests that the Yellow band is of critical importance in Soil and Limonium percentage regression. Moreover, Table 6 also shows that the NIR 1 and NIR 2 bands are critical in regression practice for other classes. These analyses suggest the NIR 1 and NIR 2 bands provided by WV-2 can improve the accuracy of halophytic classification. This can be explained because, as shown in Figure 10c, in the visible range, reflectance values of vegetation species are similar, while the variability increases in the NIR 1 and NIR 2 bands.
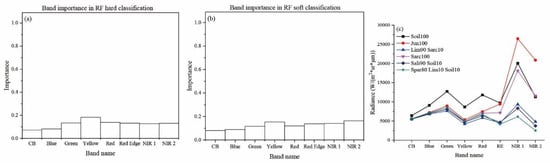
Figure 10.
Band importance for different methods and reflectance characteristics of each class: (a,b) are the relative importance of each band for RF hard classification and RF soft classification, respectively; (c) is calculated by average radiance value of corresponding ROI (CB is Coastal Blue, RE is Red Edge).

Table 6.
Feature importance of each band in RF regression (CB is Coastal Blue). Jun = Juncus, Lim = Limonium, Sali = Salicornia, Sarc = Sarcocornia and Spar = Spartina.
An important source of uncertainty in this study may be related to the interference of water with species reflectance. The tidal elevation at the time of acquisition was about 0.45 m above MSL, suggesting that large portions of the marsh, whose elevations range from 0.15 m to 0.60 m above MSL, were flooded with water depths up to 30 cm. Kearney et al. [140] documented that tidal inundation can result in a significant reduction in NIR 2 (856–1043 nm) and greatly affects the Red Edge band (699–749 nm). High water levels thus increase noise in spectral reflectance information, in particular for NIR bands and significantly affect the outcome of hard and soft classifiers.
5. Conclusions
Halophytic vegetation, an important component of salt marshes, is typically organized in patches of species associations. In this study, we focus on the development of a new approach based on the application of RF soft classification for estimating fractional abundance of each species within vegetation associations and applied it to a WV-2 multispectral image. In particular, we make full use of the information contained in the distribution of “votes” from individual decision trees and interpret their distribution across classes as the corresponding fractional abundance. This approach yields high classification accuracies (6.7% < RMSE < 18.7% and 0.65 < R2 < 0.96). We found that, while the RF regression can predict the percentage of each class accurately when each class is considered separately, the overall accuracy decreases significantly when relative abundances are rescaled to sum to 100%. Comparisons of RF soft classification results to rescaled RF regression results (Figure 6, Figure 7 and Figure 8) suggest that the former is more suitable to accurately map fractional abundance in highly mixed halophytic associations. Our results show that the RF soft-classifier predicted distribution patterns are in very good agreement with halophytic vegetation patterns documented by previous analyses [18,44,45,83], thus confirming the usefulness of the method.
We show that the results obtained with the RF soft classification can be used to produce a map of the dominant species within the plant association (i.e., with percentage cover higher than 60% in our case). This map nicely agrees with an RF hard classification map (Kappa = 0.962, A = 0.970) produced for the same study site, thus emphasizing the RF soft-classifier robustness. Our comparison also highlights that the traditional hard classifiers force the pixels to be assigned to a specific class, which is unrealistic when dealing with mixed vegetation associations as in the case of salt marshes, thus neglecting the heterogeneous contribution to the spectral signal associated with the mixture.
In conclusion, we developed a robust RF soft classification approach to assess the fractional abundance of halophytic vegetation and bare soil. This approach uses the frequency of “votes” to each species to represent corresponding fractional abundance. We applied this method to estimate the fractional abundance of halophytic vegetation species within our study site, which is characterized by high biodiversity of salt-marsh vegetation and where halophytic species are organized in mixed vegetation associations at the scale of the satellite sensor resolution (0.5 m). The proposed method allowed us to obtain high accuracy in the current application, suggesting it can be a valuable tool to analyze the distribution pattern of fractional abundance of salt-marsh vegetation species. The comparison between the results obtained with the RF soft classifier to those drawn from its regression counterpart shows its superior robustness. We suggest that the RF soft classification allows one to monitor the temporal evolution of halophytic vegetation, such as dieback and replacement. We, therefore, suggest that the RF soft classification method should be considered to analyze salt-marsh response to sea-level changes and for the development and testing of biogeomorphic models.
Author Contributions
Conceptualization, Z.Y., A.D., M.M. and S.S.; Methodology and Validation Z.Y. and S.S.; Formal Analysis, Z.Y.; Investigation Z.Y., A.D., M.M. and S.S.; Data Curation Z.Y., A.D., M.M. and S.S.; Writing-Original Draft Preparation Z.Y. and S.S.; Writing-Review & Editing, Z.Y., A.D., M.M. and S.S.; Funding Acquisition, A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project “VENEZIA 2021: Scientific Research Program for a Regulated Lagoon – Research Line 3.2 (PI Andrea D’Alpaos)”.
Acknowledgments
Reviewers and editors will be acknowledged. We thank recommendation from Hugo Coasta and Markus Immitzer to develop the models. We also thank Davide Tognin, Alice Puppin and Alvise Finotello for their kind support in field work and ROI selection.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cronk, J.K.; Fennessy, M.S. Wetland Plants: Biology and Ecology; Lewis Publishers: Boca Raton, FL, USA, 2001. [Google Scholar]
- Marani, M.; Belluco, E.; Ferrari, S.; Silvestri, S.; D’Alpaos, A.; Lanzoni, S.; Feola, A.; Rinaldo, A. Analysis, synthesis and modelling of high-resolution observations of salt-marsh eco-geomorphological patterns in the Venice lagoon. Estuar. Coast. Shelf Sci. 2006, 69, 414–426. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Kirwan, M.L.; Mudd, S.M.; Guntenspergen, G.R.; Temmerman, S.; D’Alpaos, A.; van de Koppel, J.; Rybczyk, J.M.; Reyes, E.; Craft, C.; et al. Numerical models of salt marsh evolution: Ecological, geomorphic, and climatic factors. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Fitzgerald, D.M.; Hughes, Z. Marsh processes and their response to climate change and sea-level rise. Annu. Rev. Earth Planet. Sci. 2019, 47, 481–517. [Google Scholar] [CrossRef]
- D’Alpaos, A.; Lanzoni, S.; Marani, M.; Rinaldo, A. Landscape evolution in tidal embayments: Modeling the interplay of erosion, sedimentation, and vegetation dynamics. J. Geophys. Res. Space Phys. 2007, 112, 1–17. [Google Scholar] [CrossRef]
- Morris, J.T.; Haskin, B. A 5-yr record of aerial primary production and stand characteristics of Spartina alterniflora. Ecology 1990, 71, 2209–2217. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Gosselink, J.G. The value of wetlands: Importance of scale and landscape setting. Ecol. Econ. 2000, 35, 25–33. [Google Scholar] [CrossRef]
- Zedler, J.B.; Kercher, S. Wetland resources: Status, trends, ecosystem services, and restorability. Annu. Rev. Environ. Resour. 2005, 30, 39–74. [Google Scholar] [CrossRef]
- Moller, I.; Spencer, T. Wave dissipation over macro-tidal saltmarshes: Effects of marsh edge typology and vegetation change. J. Coast. Res. 2002, 36, 506–521. [Google Scholar] [CrossRef]
- Loder, N.; Irish, J.L.; Cialone, M.; Wamsley, T. Sensitivity of hurricane surge to morphological parameters of coastal wetlands. Estuar. Coast. Shelf Sci. 2009, 84, 625–636. [Google Scholar] [CrossRef]
- Howes, N.C.; Fitzgerald, D.M.; Hughes, Z.J.; Georgiou, I.Y.; Kulp, M.A.; Miner, M.D.; Smith, J.M.; Barras, J.A. Hurricane-induced failure of low salinity wetlands. Proc. Natl. Acad. Sci. USA 2010, 107, 14014–14019. [Google Scholar] [CrossRef]
- Möller, I.; Kudella, M.; Rupprecht, F.; Spencer, T.; Paul, M.; Van Wesenbeeck, B.K.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-Lange, M.; et al. Wave attenuation over coastal salt marshes under storm surge conditions. Nat. Geosci. 2014, 7, 727–731. [Google Scholar] [CrossRef]
- Silinski, A.; Fransen, E.; Bouma, T.J.; Meire, P.; Temmerman, S. Unravelling the controls of lateral expansion and elevation change of pioneer tidal marshes. Geomorphology 2016, 274, 106–115. [Google Scholar] [CrossRef]
- Chmura, G.L.; Anisfeld, S.C.; Cahoon, D.R.; Lynch, J.C. Global carbon sequestration in tidal, saline wetland soils. Glob. Biogeochem. Cycles 2003, 17. [Google Scholar] [CrossRef]
- McLeod, E.; Chmura, G.L.; Bouillon, S.; Salm, R.; Björk, M.; Duarte, C.M.; Lovelock, C.E.; Schlesinger, W.H.; Silliman, B.R. A blueprint for blue carbon: Toward an improved understanding of the role of vegetated coastal habitats in sequestering CO2. Front. Ecol. Environ. 2011, 9, 552–560. [Google Scholar] [CrossRef]
- Mudd, S.M.; Howell, S.M.; Morris, J.T. Impact of dynamic feedbacks between sedimentation, sea-level rise, and biomass production on near-surface marsh stratigraphy and carbon accumulation. Estuar. Coast. Shelf Sci. 2009, 82, 377–389. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Mudd, S.M. Response of salt-marsh carbon accumulation to climate change. Nature 2012, 489, 550–553. [Google Scholar] [CrossRef]
- Roner, M.; D’Alpaos, A.; Ghinassi, M.; Marani, M.; Silvestri, S.; Franceschinis, E.; Realdon, N. Spatial variation of salt-marsh organic and inorganic deposition and organic carbon accumulation: Inferences from the Venice lagoon, Italy. Adv. Water Resour. 2016, 93, 276–287. [Google Scholar] [CrossRef]
- Marani, M.; D’Alpaos, A.; Lanzoni, S.; SantaLucia, M. Understanding and predicting wave erosion of marsh edges. Geophys. Res. Lett. 2011, 38, 38. [Google Scholar] [CrossRef]
- Mariotti, G.; Fagherazzi, S. Critical width of tidal flats triggers marsh collapse in the absence of sea-level rise. Proc. Natl. Acad. Sci. USA 2013, 110, 5353–5356. [Google Scholar] [CrossRef]
- Leonardi, N.; Defne, Z.; Ganju, N.K.; Fagherazzi, S. Salt marsh erosion rates and boundary features in a shallow Bay. J. Geophys. Res. Earth Surf. 2016, 121, 1861–1875. [Google Scholar] [CrossRef]
- Tommasini, L.; Carniello, L.; Ghinassi, M.; Roner, M.; D’Alpaos, A. Changes in the wind-wave field and related salt-marsh lateral erosion: Inferences from the evolution of the Venice Lagoon in the last four centuries. Earth Surf. Process. Landf. 2019, 44, 1633–1646. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Murray, A.B. A coupled geomorphic and ecological model of tidal marsh evolution. Proc. Natl. Acad. Sci. USA 2007, 104, 6118–6122. [Google Scholar] [CrossRef] [PubMed]
- D’Alpaos, A.; Mudd, S.M.; Carniello, L. Dynamic response of marshes to perturbations in suspended sediment concentrations and rates of relative sea level rise. J. Geophys. Res. Space Phys. 2011, 116, 1–13. [Google Scholar] [CrossRef]
- Bendoni, M.; Mel, R.; Solari, L.; Lanzoni, S.; Francalanci, S.; Oumeraci, H. Insights into lateral marsh retreat mechanism through localized field measurements. Water Resour. Res. 2016, 52, 1446–1464. [Google Scholar] [CrossRef]
- Mariotti, G.; Carr, J. Dual role of salt marsh retreat: Long-term loss and short-term resilience. Water Resour. Res. 2014, 50, 2963–2974. [Google Scholar] [CrossRef]
- Hopkinson, C.S.; Morris, J.T.; Fagherazzi, S.; Wollheim, W.M.; Raymond, P.A. Lateral marsh edge erosion as a source of sediments for vertical marsh accretion. J. Geophys. Res. Biogeosci. 2018, 123, 2444–2465. [Google Scholar] [CrossRef]
- Lalimi, F.Y.; Marani, M.; Heffernan, J.B.; D’Alpaos, A.; Murray, A.B. Watershed and ocean controls of salt marsh extent and resilience. Earth Surf. Process. Landf. 2020, 45, 1456–1468. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Guntenspergen, G.R. Influence of tidal range on the stability of coastal marshland. J. Geophys. Res. Space Phys. 2010, 115, 1–11. [Google Scholar] [CrossRef]
- Leonard, L.A.; Luther, M.E. Flow hydrodynamics in tidal marsh canopies. Limnol. Oceanogr. 1995, 40, 1474–1484. [Google Scholar] [CrossRef]
- Leonard, L.A.; Croft, A.L. The effect of standing biomass on flow velocity and turbulence in Spartina alterniflora canopies. Estuar. Coast. Shelf Sci. 2006, 69, 325–336. [Google Scholar] [CrossRef]
- Bouma, T.J.; Van Duren, L.; Temmerman, S.; Claverie, T.; Blanco-Garcia, A.; Ysebaert, T.; Herman, P.M.J. Spatial flow and sedimentation patterns within patches of epibenthic structures: Combining field, flume and modelling experiments. Cont. Shelf Res. 2007, 27, 1020–1045. [Google Scholar] [CrossRef]
- Marani, M.; D’Alpaos, A.; Lanzoni, S.; Carniello, L.; Rinaldo, A. The importance of being coupled: Stable states and catastrophic shifts in tidal biomorphodynamics. J. Geophys. Res. Space Phys. 2010, 115, 1–15. [Google Scholar] [CrossRef]
- Mudd, S.M.; D’Alpaos, A.; Morris, J.T. How does vegetation affect sedimentation on tidal marshes? Investigating particle capture and hydrodynamic controls on biologically mediated sedimentation. J. Geophys. Res. Space Phys. 2010, 115, 1–14. [Google Scholar] [CrossRef]
- Brisson, C.; Coverdale, T.C.; Bertness, M.D. Salt marsh die-off and recovery reveal disparity between the recovery of ecosystem structure and service provision. Boil. Conserv. 2014, 179, 1–5. [Google Scholar] [CrossRef]
- Morris, J.T.; Sundareshwar, P.V.; Nietch, C.T.; Kjerfve, B.; Cahoon, D.R. Sea level of coastal wetlands to rising responses. Ecology 2002, 83, 2869–2877. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Guntenspergen, G.R.; D’Alpaos, A.; Morris, J.T.; Mudd, S.M.; Temmerman, S. Limits on the adaptability of coastal marshes to rising sea level. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Temmerman, S.; Skeehan, E.E.; Guntenspergen, G.R.; Fagherazzi, S. Overestimation of marsh vulnerability to sea level rise. Nat. Clim. Chang. 2016, 6, 253–260. [Google Scholar] [CrossRef]
- Marani, M.; D’Alpaos, A.; Lanzoni, S.; Carniello, L.; Rinaldo, A. Biologically-controlled multiple equilibria of tidal landforms and the fate of the Venice lagoon. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- D’Alpaos, A.; Marani, M. Reading the signatures of biologic–geomorphic feedbacks in salt-marsh landscapes. Adv. Water Resour. 2016, 93, 265–275. [Google Scholar] [CrossRef]
- Van Wijnen, H.J.; Bakker, J.P.; De Vries, Y. Twenty years of salt marsh succession on a Dutch coastal barrier island. J. Coast. Conserv. 1997, 3, 9–18. [Google Scholar] [CrossRef]
- Costa, C.S.B.; Marangoni, J.C.; Azevedo, A.M.G. Plant zonation in irregularly flooded salt marshes: Relative importance of stress tolerance and biological interactions. J. Ecol. 2003, 91, 951–965. [Google Scholar] [CrossRef]
- Pennings, S.C.; Selig, E.R.; Houser, L.T.; Bertness, M.D. Geographic variation in positive and negative interactions among salt marsh plants. Ecology 2003, 84, 1527–1538. [Google Scholar] [CrossRef]
- Belluco, E.; Camuffo, M.; Ferrari, S.; Modenese, L.; Silvestri, S.; Marani, A.; Marani, M. Mapping salt-marsh vegetation by multispectral and hyperspectral remote sensing. Remote Sens. Environ. 2006, 105, 54–67. [Google Scholar] [CrossRef]
- Silvestri, S.; Defina, A.; Marani, M. Tidal regime, salinity and salt marsh plant zonation. Estuar. Coast. Shelf Sci. 2005, 62, 119–130. [Google Scholar] [CrossRef]
- Moffett, K.B.; Robinson, D.A.; Gorelick, S.M. Relationship of salt marsh vegetation zonation to spatial patterns in soil moisture, salinity, and topography. Ecosystems 2010, 13, 1287–1302. [Google Scholar] [CrossRef]
- Moffett, K.B.; Gorelick, S.M.; McLaren, R.G.; Sudicky, E.A. Salt marsh ecohydrological zonation due to heterogeneous vegetation-groundwater-surface water interactions. Water Resour. Res. 2012, 48, 48. [Google Scholar] [CrossRef]
- Marani, M.; Da Lio, C.; D’Alpaos, A. Vegetation engineers marsh morphology through multiple competing stable states. Proc. Natl. Acad. Sci. USA 2013, 110, 3259–3263. [Google Scholar] [CrossRef]
- Ratliff, K.M.; Braswell, A.E.; Marani, M. Spatial response of coastal marshes to increased atmospheric CO2. Proc. Natl. Acad. Sci. USA 2015, 112, 15580–15584. [Google Scholar] [CrossRef]
- Adams, J.; Bate, G. Ecological implications of tolerance of salinity and inundation by Spartina maritima. Aquat. Bot. 1995, 52, 183–191. [Google Scholar] [CrossRef]
- Álvarez-Rogel, J.; Silla, R.O.; Ariza, F.A. Edaphic characterization and soil ionic composition influencing plant zonation in a semiarid Mediterranean salt marsh. Geoderma 2001, 99, 81–98. [Google Scholar] [CrossRef]
- Bockelmann, A.-C.; Bakker, J.P.; Neuhaus, R.; Lage, J. The relation between vegetation zonation, elevation and inundation frequency in a Wadden Sea salt marsh. Aquat. Bot. 2002, 73, 211–221. [Google Scholar] [CrossRef]
- Silvestri, S.; Marani, M. Salt-marsh vegetation and morphology: Basic physiology, modelling and remote sensing observations. In The Ecogeomorphology of Tidal Marshes; Fagherazzi, S., Marani, M., Blum, L., Eds.; Coastal and Estuarine Monograph Series; American Geophysical Union: Washington, DC, USA, 2004; Volume 59, pp. 5–25. [Google Scholar]
- Marani, M.; Lanzoni, S.; Silvestri, S.; Rinaldo, A. Tidal landforms, patterns of halophytic vegetation and the fate of the lagoon of Venice. J. Mar. Syst. 2004, 51, 191–210. [Google Scholar] [CrossRef]
- Marani, M.; Silvestri, S.; Belluco, E.; Ursino, N.; Comerlati, A.; Tosatto, O.; Putti, M. Spatial organization and ecohydrological interactions in oxygen-limited vegetation ecosystems. Water Resour. Res. 2006, 42, 1–12. [Google Scholar] [CrossRef]
- Watson, E.; Byrne, R. Abundance and diversity of tidal marsh plants along the salinity gradient of the San Francisco Estuary: Implications for global change ecology. Plant Ecol. 2009, 205, 113–128. [Google Scholar] [CrossRef]
- Moffett, K.B.; Gorelick, S.M. Alternative stable states of tidal marsh vegetation patterns and channel complexity. Ecohydrology 2016, 9, 1639–1662. [Google Scholar] [CrossRef]
- Fariña, J.M.; He, Q.; Silliman, B.R.; Bertness, M.D. Biogeography of salt marsh plant zonation on the Pacific coast of South America. J. Biogeogr. 2017, 45, 238–247. [Google Scholar] [CrossRef]
- Pennings, S.C.; Callaway, R.M. Salt marsh plant zonation: The relative importance of competition and physical factors. Ecology 1992, 73, 681–690. [Google Scholar] [CrossRef]
- Pennings, S.C.; Grant, M.-B.; Bertness, M.D. Plant zonation in low-latitude salt marshes: Disentangling the roles of flooding, salinity and competition. J. Ecol. 2005, 93, 159–167. [Google Scholar] [CrossRef]
- Marani, M.; Zillio, T.; Belluco, E.; Silvestri, S.; Maritan, A. Non-neutral vegetation dynamics. PLoS ONE 2006, 1, e78. [Google Scholar] [CrossRef]
- Strain, E.M.; Van Belzen, J.; Comandini, P.; Wong, J.; Bouma, T.J.; Airoldi, L. The role of changing climate in driving the shift from perennial grasses to annual succulents in a Mediterranean saltmarsh. J. Ecol. 2017, 105, 1374–1385. [Google Scholar] [CrossRef]
- Da Lio, C.; D’Alpaos, A.; Marani, M. The secret gardener: Vegetation and the emergence of biogeomorphic patterns in tidal environments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120367. [Google Scholar] [CrossRef] [PubMed]
- Temmerman, S.; Bouma, T.; Van De Koppel, J.; Van Der Wal, D.; De Vries, M.; Herman, P.M.J. Vegetation causes channel erosion in a tidal landscape. Geology 2007, 35, 631. [Google Scholar] [CrossRef]
- Taramelli, A.; Valentini, E.; Cornacchia, L.; Monbaliu, J.; Sabbe, K. Indications of dynamic effects on scaling relationships between channel sinuosity and vegetation patch size across a salt marsh platform. J. Geophys. Res. Earth Surf. 2018, 123, 2714–2731. [Google Scholar] [CrossRef]
- Zhu, Z.; Van Belzen, J.; Zhu, Q.; Van De Koppel, J.; Bouma, T.J. Vegetation recovery on neighboring tidal flats forms an Achilles’ heel of saltmarsh resilience to sea level rise. Limnol. Oceanogr. 2019, 65, 51–62. [Google Scholar] [CrossRef]
- Ganju, N.K.; Defne, Z.; Kirwan, M.L.; Fagherazzi, S.; D’Alpaos, A.; Carniello, L. Spatially integrative metrics reveal hidden vulnerability of microtidal salt marshes. Nat. Commun. 2017, 8, 14156. [Google Scholar] [CrossRef] [PubMed]
- Ladd, C.J.; Duggan-Edwards, M.F.; Bouma, T.J.; Pagès, J.F.; Skov, M.W. Sediment supply explains long-term and large-scale patterns in salt marsh lateral expansion and erosion. Geophys. Res. Lett. 2019, 46, 11178–11187. [Google Scholar] [CrossRef]
- Van De Koppel, J.; Van Der Wal, D.; Bakker, J.P.; Herman, P.M.J. Self-organization and vegetation collapse in salt marsh ecosystems. Am. Nat. 2005, 165, E1–E12. [Google Scholar] [CrossRef]
- Van Der Wal, D.; Dool, A.W.-V.D.; Herman, P.M.J. Spatial patterns, rates and mechanisms of saltmarsh cycles. Estuar. Coast. Shelf Sci. 2008, 76, 357–368. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Guntenspergen, G.R. Feedbacks between inundation, root production, and shoot growth in a rapidly submerging brackish marsh. J. Ecol. 2012, 100, 764–770. [Google Scholar] [CrossRef]
- Bernhardt, J.R.; Leslie, H.M. Resilience to climate change in coastal marine ecosystems. Annu. Rev. Mar. Sci. 2013, 5, 371–392. [Google Scholar] [CrossRef]
- Artigas, F.J.; Yang, J. Spectral Discrimination of Marsh Vegetation Types in the New Jersey Meadowlands, USA. Wetlands 2006, 26, 271–277. [Google Scholar] [CrossRef]
- Wang, C.; Menenti, M.; Stoll, M.-P.; Belluco, E.; Marani, M. Mapping mixed vegetation communities in salt marshes using airborne spectral data. Remote Sens. Environ. 2007, 107, 559–570. [Google Scholar] [CrossRef]
- Gilmore, M.S.; Wilson, E.H.; Barrett, N.; Civco, D.L.; Prisloe, S.; Hurd, J.D.; Chadwick, C. Integrating multi-temporal spectral and structural information to map wetland vegetation in a lower Connecticut River tidal marsh. Remote Sens. Environ. 2008, 112, 4048–4060. [Google Scholar] [CrossRef]
- Berhane, T.M.; Costa, H.; Lane, C.R.; Anenkhonov, O.A.; Chepinoga, V.V.; Autrey, B.C. The influence of region of interest heterogeneity on classification accuracy in Wetland systems. Remote Sens. 2019, 11, 551. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Goodin, D.G.; Anibas, K.L.; Bezymennyi, M. Mapping land cover and land use from object-based classification: An example from a complex agricultural landscape. Int. J. Remote Sens. 2015, 36, 4702–4723. [Google Scholar] [CrossRef]
- Kulkarni, A.D.; Lowe, B. Random forest algorithm for land cover classification. Int. J. Recent Innov. Trends Comput. Commun. 2016, 4, 58–63. [Google Scholar]
- Costa, H.; Foody, G.M.; Boyd, D.S. Using mixed objects in the training of object-based image classifications. Remote Sens. Environ. 2017, 190, 188–197. [Google Scholar] [CrossRef]
- Kumar, U.; Ganguly, S.; Nemani, R.R.; Raja, K.S.; Milesi, C.; Sinha, R.; Michaelis, A.; Votava, P.; Hashimoto, H.; Li, S.; et al. Exploring subpixel learning algorithms for estimating global land cover fractions from satellite data using high performance computing. Remote Sens. 2017, 9, 1105. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Silvestri, S.; Marani, M.; Marani, A. Hyperspectral remote sensing of salt marsh vegetation, morphology and soil topography. Phys. Chem. Earth Parts A/B/C 2003, 28, 15–25. [Google Scholar] [CrossRef]
- Van Beijma, S.; Comber, A.J.; Lamb, A. Random forest classification of salt marsh vegetation habitats using quad-polarimetric airborne SAR, elevation and optical RS data. Remote Sens. Environ. 2014, 149, 118–129. [Google Scholar] [CrossRef]
- Moffett, K.B.; Nardin, W.; Silvestri, S.; Wang, C.; Temmerman, S. Multiple stable states and catastrophic shifts in coastal wetlands: Progress, challenges, and opportunities in validating theory using remote sensing and other methods. Remote Sens. 2015, 7, 10184–10226. [Google Scholar] [CrossRef]
- Campbell, A.; Wang, Y.; Christiano, M.; Stevens, S. Salt marsh monitoring in Jamaica Bay, New York from 2003 to 2013: A decade of change from restoration to hurricane Sandy. Remote Sens. 2017, 9, 131. [Google Scholar] [CrossRef]
- Timm, B.C.; McGarigal, K. Fine-scale remotely-sensed cover mapping of coastal dune and salt marsh ecosystems at Cape Cod National Seashore using random forests. Remote Sens. Environ. 2012, 127, 106–117. [Google Scholar] [CrossRef]
- Juel, A.; Groom, G.; Svenning, J.-C.; Ejrnæs, R. Spatial application of Random Forest models for fine-scale coastal vegetation classification using object based analysis of aerial orthophoto and DEM data. Int. J. Appl. Earth Obs. Geoinf. 2015, 42, 106–114. [Google Scholar] [CrossRef]
- Müller, A.C.; Sarah, G. Introduction to Machine Learning with Python: A Guide for Data Scientists; O’Reilly Media, Inc.: California, CA, USA, 2016. [Google Scholar]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties-A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Sanpayao, M.; Kasetkasem, T.; Rakwatin, P.; Isshiki, T.; Chanwimaluang, T. A Subpixel Classification Algorithm Based on a Random Forest Approach. In Proceedings of the 8th International Conference of Information and Communication Technology for Embedded Systems, Jeju Island, Korea, 18–20 October 2017; pp. 182–187. [Google Scholar]
- Immitzer, M.; Böck, S.; Einzmann, K.; Vuolo, F.; Pinnel, N.; Wallner, A.; Atzberger, C. Fractional cover mapping of spruce and pine at 1 ha resolution combining very high and medium spatial resolution satellite imagery. Remote Sens. Environ. 2018, 204, 690–703. [Google Scholar] [CrossRef]
- D’Alpaos, L. Fatti e Misfatti di Idraulica Lagunare: La Laguna di Venezia Dalla Diversione dei Fiumi Alle Nuove Opere Alle Bocche di Porto; Istituto Veneto di Scienze Lettere ed Arti: Venezia, Italy, 2010. [Google Scholar]
- D’Alpaos, A.; Carniello, L.; Rinaldo, A. Statistical mechanics of wind wave-induced erosion in shallow tidal basins: Inferences from the Venice Lagoon. Geophys. Res. Lett. 2013, 40, 3402–3407. [Google Scholar] [CrossRef]
- Silvestri, S.; D’Alpaos, A.; Nordio, G.; Carniello, L. Anthropogenic modifications can significantly influence the local mean sea level and affect the survival of salt marshes in shallow tidal systems. J. Geophys. Res. Earth Surf. 2018, 123, 996–1012. [Google Scholar] [CrossRef]
- Marani, M.; Silverstri, S.; Belluco, E.; Camuffo, M.; D’Alpaos, A.; Lanzoni, S.; Marani, A.; Rinaldo, A. Patterns in tidal environments: Salt-marsh channel networks and vegetation. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2004. [Google Scholar]
- Silvestri, S.; Marani, M.; Settle, J.; Benvenuto, F.; Marani, A. Salt marsh vegetation radiometry: Data analysis and scaling. Remote Sens. Environ. 2002, 80, 473–482. [Google Scholar] [CrossRef]
- Moffett, K.B.; Gorelick, S.M. Distinguishing wetland vegetation and channel features with object-based image segmentation. Int. J. Remote Sens. 2012, 34, 1332–1354. [Google Scholar] [CrossRef]
- Morris, J.T. Competition among marsh macrophytes by means of geomorphological displacement in the intertidal zone. Estuar. Coast. Shelf Sci. 2006, 69, 395–402. [Google Scholar] [CrossRef]
- Janousek, C.N.; Buffington, K.; Thorne, K.; Guntenspergen, G.; Takekawa, J.; Dugger, B. Potential effects of sea-level rise on plant productivity: Species-specific responses in northeast Pacific tidal marshes. Mar. Ecol. Prog. Ser. 2016, 548, 111–125. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, L.-Q.; Wang, N.; Schwarz, C.; Ysebaert, T. Interactions between the range expansion of saltmarsh vegetation and hydrodynamic regimes in the Yangtze Estuary, China. Estuar. Coast. Shelf Sci. 2012, 96, 273–279. [Google Scholar] [CrossRef]
- Schepers, L.; Kirwan, M.L.; Guntenspergen, G.; Temmerman, S. Spatio-temporal development of vegetation die-off in a submerging coastal marsh. Limnol. Oceanogr. 2016, 62, 137–150. [Google Scholar] [CrossRef]
- Donnelly, J.P.; Bertness, M.D. Rapid shoreward encroachment of salt marsh cordgrass in response to accelerated sea-level rise. Proc. Natl. Acad. Sci. USA 2001, 98, 14218–14223. [Google Scholar] [CrossRef]
- Feagin, R.A.; Martinez, M.L.; Mendoza-Gonzalez, G.; Costanza, R. Salt marsh zonal migration and ecosystem service change in response to global sea level rise: A case study from an urban region. Ecol. Soc. 2010, 15, 15. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Walters, D.; Reay, W.G.; Carr, J. Sea level driven marsh expansion in a coupled model of marsh erosion and migration. Geophys. Res. Lett. 2016, 43, 4366–4373. [Google Scholar] [CrossRef]
- Ge, Z.-M.; Wang, H.; Cao, H.-B.; Zhao, B.; Zhou, X.; Peltola, H.; Cui, L.-F.; Li, X.-Z.; Zhang, L.-Q. Responses of eastern Chinese coastal salt marshes to sea-level rise combined with vegetative and sedimentary processes. Sci. Rep. 2016, 6, 28466. [Google Scholar] [CrossRef] [PubMed]
- Fagherazzi, S.; Anisfeld, S.C.; Blum, L.K.; Long, E.V.; Feagin, R.A.; Fernandes, A.; Kearney, W.S.; Williams, K. Sea level rise and the dynamics of the marsh-upland boundary. Front. Environ. Sci. 2019, 7, 25. [Google Scholar] [CrossRef]
- Hoffbeck, J.P.; Landgrebe, D.A. Effect of radiance-to-reflectance transformation and atmosphere removal on maximum likelihood classification accuracy of high-dimensional remote sensing data. In Proceedings of the IGARSS ’94–1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; pp. 2538–2540. [Google Scholar]
- Cooley, T.; Anderson, G.; Felde, G.; Hoke, M.; Ratkowski, A.; Chetwynd, J.; Gardner, J.; Adler-Golden, S.; Matthew, M.; Berk, A.; et al. FLAASH, a MODTRAN4- based atmospheric correction algorithm, its application and validation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium 2003, Toronto, ON, Canada, 24–28 June 2002; pp. 1414–1418. [Google Scholar]
- Matthew, M.; Adler-Golden, S.; Berk, A.; Felde, G.; Anderson, G.; Gorodetzky, D.; Paswaters, S.; Shippert, M. Atmospheric correction of spectral imagery: Evaluation of the FLAASH algorithm with AVIRIS data. In Proceedings of the 2002 Applied Imagery Pattern Recognition Workshop, Washington, DC, USA, 16–18 October 2002; pp. 157–163. [Google Scholar]
- ENVI FLAASH Version. FLAASH User’s Guide; Research Systems, Inc.: Boulder, CO, USA, 2004. [Google Scholar]
- Palubinskas, G. Fast, simple, and good pan-sharpening method. J. Appl. Remote Sens. 2013, 7, 073526. [Google Scholar] [CrossRef]
- Maurer, T. How to pan-sharpen images using the Gram-Schmidt pan-sharpen method-A recipe. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 239–244. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1974; pp. 309–317. [Google Scholar]
- Varoquaux, G.; Buitinck, L.; Louppe, G.; Grisel, O.; Pedregosa, F.; Mueller, A. Scikit-learn. GetMobile Mob. Comput. Commun. 2015, 19, 29–33. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First experience with Sentinel -2 data for crop and tree species classifications in Central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Xu, M.; Watanachaturaporn, P.; Varshney, P.K.; Arora, M.K. Decision tree regression for soft classification of remote sensing data. Remote Sens. Environ. 2005, 97, 322–336. [Google Scholar] [CrossRef]
- Breiman, L. Out-of-Bag Estimation. 1996. Available online: https://www.stat.berkeley.edu/pub/users/breiman/OOBestimation.pdf (accessed on 3 October 2020).
- Archer, K.J.; Kimes, R.V. Empirical characterization of random forest variable importance measures. Comput. Stat. Data Anal. 2008, 52, 2249–2260. [Google Scholar] [CrossRef]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef]
- Jiang, R.; Tang, W.; Wu, X.; Fu, W. A random forest approach to the detection of epistatic interactions in case-control studies. BMC Bioinform. 2009, 10, S65. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Liu, K.; Shi, W.Z.; Zhang, H. A fuzzy topology-based maximum likelihood classification. ISPRS J. Photogramm. Remote Sens. 2011, 66, 103–114. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Rosenfield, G.H.F.-L.K. A coefficient of agreement as a measure of thematic classification accuracy. Photogramm. Eng. Remote Sens. 1986, 52, 223–227. [Google Scholar]
- Guan, H.; Li, J.; Chapman, M.; Deng, F.; Ji, Z.; Yang, X. Integration of orthoimagery and lidar data for object-based urban thematic mapping using random forests. Int. J. Remote Sens. 2013, 34, 5166–5186. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez, S. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree Species Classification with Random Forest Using Very High Spatial Resolution 8-Band WorldView-2 Satellite Data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Liu, M.; Yang, W.; Chen, J.; Chen, X. An orthogonal Fisher transformation-based unmixing method toward estimating fractional vegetation cover in semiarid areas. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1–5. [Google Scholar] [CrossRef]
- Liu, X.; Liu, H.; Qiu, S.; Wu, X.; Tian, Y.; Hao, Q. An improved estimation of regional fractional woody/herbaceous cover using combined satellite data and high-quality training samples. Remote Sens. 2017, 9, 32. [Google Scholar] [CrossRef]
- Schwieder, M.; Leitão, P.J.; Suess, S.; Senf, C.; Hostert, P. Estimating fractional shrub cover using simulated EnMAP data: A comparison of three machine learning regression techniques. Remote Sens. 2014, 6, 3427–3445. [Google Scholar] [CrossRef]
- Sanderson, E.W.; Foin, T.C.; Ustin, S.L. A simple empirical model of salt marsh plant spatial distributions with respect to a tidal channel network. Ecol. Model. 2001, 139, 293–307. [Google Scholar] [CrossRef]
- D’Alpaos, A.; Lanzoni, S.; Marani, M.; Bonometto, A.; Cecconi, G.; Rinaldo, A. Spontaneous tidal network formation within a constructed salt marsh: Observations and morphodynamic modelling. Geomorphology 2007, 91, 186–197. [Google Scholar] [CrossRef]
- Melville, B.; Fisher, A.G.; Lucieer, A. Ultra-high spatial resolution fractional vegetation cover from unmanned aerial multispectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 14–24. [Google Scholar] [CrossRef]
- Lopatin, J.; Dolos, K.; Hernández, J.; Galleguillos, M.; Fassnacht, F.E. Comparing generalized linear models and random forest to model vascular plant species richness using LiDAR data in a natural forest in central Chile. Remote Sens. Environ. 2016, 173, 200–210. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Scarth, P.; McVicar, T.R.; Renzullo, L.J.; Malthus, T.J.; Stewart, J.B.; Rickards, J.E.; Trevithick, R. Assessing the effects of site heterogeneity and soil properties when unmixing photosynthetic vegetation, non-photosynthetic vegetation and bare soil fractions from Landsat and MODIS data. Remote Sens. Environ. 2015, 161, 12–26. [Google Scholar] [CrossRef]
- Kearney, M.S.; Stutzer, D.; Turpie, K.; Stevenson, J.C. The effects of tidal inundation on the reflectance characteristics of coastal marsh vegetation. J. Coast. Res. 2009, 256, 1177–1186. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).