Abstract
The monitoring of wetland methane (CH4) emission is essential in the context of global CH4 emission and climate change. The remotely sensed multitemporal Atmospheric Infrared Sounder (AIRS) CH4 data and the Breaks for Additive Season and Trend (BFAST) algorithm were used to detect atmospheric CH4 dynamics in the Zoige wetland, China between 2002 and 2018. The overall atmospheric CH4 concentration increased steadily with a rate of 5.7 ± 0.3 ppb/year. After decomposing the time-series of CH4 data using the BFAST algorithm, we found no anomalies in the seasonal and error components. The trend component increased with time, and a total of seven breaks were detected within four cells. Six were well-explained by the air temperature anomalies primarily, but one break was not. The effect of parameter h on decomposition outcomes was studied because it could influence the number of breaks in the trend component. As h increased, the number of breaks decreased. The interplays of the observations of interest, break numbers, and statistical significance should determine the h value.
1. Introduction
Among all natural and anthropogenic sources, wetlands are the single largest methane (CH4) source and contribute 20%~40% of the total global CH4 emission [1]. Wetland CH4 emissions result from interactions between several biological, chemical, and physical processes that primarily include CH4 production, transportation, and oxidation. Methanogenic bacteria carry out the production by decomposing a limited number of relatively simple substrates under strictly anaerobic conditions. Thus, the production rate is limited by the availability of substrate and regulated by climatic and edaphic factors such as temperature, water table position, and pH [2,3,4,5,6]. CH4 can be transported to the atmospheric through various pathways: molecular diffusion, ebullition, and via vascular plant stems [7]. The produced CH4 is mostly oxidized by methanotrophs present at the oxic-anoxic boundary in the soil before emitting into the atmosphere [8]. Thus, the difference between the production and oxidation rates determines the rate of CH4 emission into the atmosphere.
Paleo records and recent studies suggest vital positive feedback of wetlands to global warming through CH4 emissions [9,10]. Therefore, the long-term variation and abrupt changes in wetland CH4 emissions are essential elements to understand the present conditions of the global CH4 emissions and climate changes [11,12]. An abrupt change or break usually denotes a rupture in the established range of observations. In this study, a breakpoint occurs when the wetland CH4 emission is beyond a given threshold value, as observed in the remote-sensing time-series and delineated by an algorithm, triggering a discontinuous transition where a new starting point and rate are initiated.
Within the context of climate change, continuous monitoring of wetland CH4 emissions is essential. With available multitemporal remote-sensing observations and datasets, various long-term change detection methods have been proposed. Temporal decomposition techniques have shown the ability to account for seasonal, gradual, and abrupt changes or breaks in terrestrial ecosystems. An early LandTrendr (Landsat-based detection of Trends in Disturbance and Recovery) algorithm divides long-term trends into piecewise-linear segments to characterize long-term changes in forest properties [13,14]. The algorithm captures changes at an annual scale but not at an intra-annual one. The Detecting Breakpoints and Estimating Segments in Trend (DBEST) can detect both abrupt and non-abrupt changes [15]. All the above methods are generally used to detect changes in the trend components, while seasonality is ignored.
The Seasonal-Trend decomposition based on a locally weighted regression smoother (STL) can identify both the phenological cycle and gradual change [16]. The STL cannot detect abrupt changes, as it assumed that the trend component varies smoothly [17]. Based on the STL algorithm, Verbesselt et al. [18] developed the Breaks for Additive Season and Trend (BFAST) algorithm that detects seasonal, gradual, and abrupt changes in a time-series simultaneously. The algorithm has been used and validated in many studies. For instance, Verbesselt et al. [19] detected drought-related vegetation disturbances. Saatchi et al. [20] examined the impact of the water deficit on the Amazon forest. Watts and Laffan [21] assessed the effectiveness of the algorithm in semi-arid regions, where the vegetation response is typically aseasonal. Hamunyela et al. [22] studied deforestation from the same data in dry and humid tropical forest areas.
CH4 studies have been conducted in the Zoige wetland, mainly using in situ measurements [23,24]. However, the measurements are sparse and cannot be representative on a large scale. Systematic observation of the vertical variation of CH4 is scarce. Therefore, space-borne measures become crucial as they provide broad spatial and multitemporal coverage, helping to understand better variations (e.g., abrupt changes or breaks) of the wetlands CH4 emission and its impact on global climate change. Although the BFAST method has received much attention, no study has been conducted to use the technique coupled with the multitemporal remote-sensing data to understand the variations of the atmospheric CH4 concentrations over wetlands. Thus, our aims are (i) to capture the CH4 dynamic in the Zoige wetland using the BFAST algorithm coupled with remote-sensing observations of a time-series and (ii) to investigate the role of air temperature in altering a CH4 time-series. Like any study using an algorithm, the algorithm parameterization is anticipated. The parameterization of h, a key parameter in the BFAST algorithm, is evaluated as the third objective. Thus, the impact of h on the outcome is studied.
2. Study Area, Datasets, and Methodology
2.1. Study Area
The Zoige Plateau (100°34′–103°45′ E, 31°40′–34°48′ N) is at the eastern edge of the Qinghai-Tibetan Plateau, China. Elevations of the plateau range from about 2400 to 5000 m above the mean sea level. The mean is ~3500 m (Figure 1). The wetland in the Zoige Plateau, approximately 4600 km2, consists mainly of peatland that is about 40% of the peat stock in China. The peatland is regarded as one of the largest alpine peatlands in the world [25]. The area is within the high-altitude temperate humid climate region. The annual precipitation ranges from 400 to 800 mm [26]. The temperature varies considerably, with a yearly mean near 0 °C. The long cold-dry winters but short warm-humid summers generally make the accumulation rate of organic matter in soil higher than the decomposition rate. Methanogens use organic matter to generate CH4.
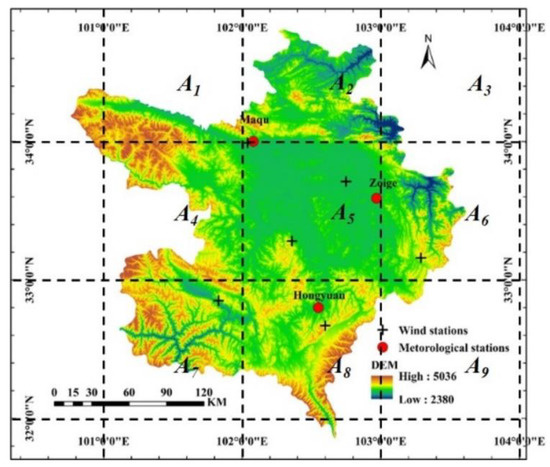
Figure 1.
Digital elevation model (DEM) of the Zoige wetland, China. Three meteorological stations (red dots) and six wind measurement sites (black crosses) are identified.
2.2. Datasets
2.2.1. Meteorological and GLDAS Datasets
Three meteorological stations are located at Maqu, Zoige, and Hongyuan (Figure 1). The air pressure and temperature, wind direction and speed, humidity, and precipitation are measured. The data between September of 2002 and March of 2017 are available and downloadable at the China Meteorological Data Service Center (http://data.cma.cn/site/index.html).
The wind speed and direction are also measured at 90 m above the ground surface at six sites (Figure 1). After analyzing all the wind data from September of 2002 to March of 2018, we found that the wind direction changes annually with an inter-annual cyclic variation. The wind speed varies annually but may not have a clear high or low period intra-annually. The average wind speed between 2002 and 2018 was ~4 m/s. There was not a noticeable trend of increase or decrease. With the spatial resolution of the rasterized CH4 data of 1° (longitude) × 1° (latitude) or ~100 km by ~100 km in the study area, the CH4 diffusion and transport caused by winds were not considered.
The Global Land Data Assimilation System (GLDAS) (https://ldas.gsfc.nasa.gov/gldas/) is a global land-data assimilation system established in recent years, aimed at using satellite- and ground-based observation data products, advanced land surface models, and data assimilation technology to generate optimal surface conditions and flux data. The GLDAS data are downloadable at the NASA Goddard Earth Science Data and Information Services Center (http://disc.sci.gsfc.nasa.gov/datasets). The soil moisture (0–10 cm, 10–40 cm, 40–100 cm, and 100–200 cm) and soil temperature (0–10 cm, 10–40 cm, 40–100 cm, and 100–200 cm) data of GLDAS-Noah Version 2 between September of 2002 and March of 2018 were downloaded. They are monthly datasets with a spatial resolution of 1° (longitude) × 1° (latitude).
2.2.2. CH4 and Landcover Datasets
The Atmospheric Infrared Sounder (AIRS) instrument on-board the NASA Earth Observing System Aqua satellite was launched into space in May of 2002. The AIRS is hyperspectral, having 2378 detectors in the infrared spectra from 3.7 to 15.4 μm [27]. The spatial resolution of AIRS is 13.5 km at nadir. Within a 24-h period, AIRS usually observes the globe twice. AIRS methane retrievals are broadly sensitive, ranging between 850 hPa (hectopascal) and the lower stratosphere, with peak sensitivity around 300–400 hPa. The AIRS Standard Version 6 Level 3 monthly data (AIRS3STM) of the atmospheric CH4 concentration [28] were chosen. The data were divided into twenty-four layers corresponding to different atmospheric pressures or heights above the mean sea level. Here, the CH4 concentration (parts per billion, ppb) at 600 hPa atmospheric pressure was extracted. The equivalent elevation is ~3600 m, which is about 100 m higher than the mean elevation of the study area. The data between September of 2002 and March of 2018 was downloaded from the NASA Goddard Data and Information Services Center at https://disc.gsfc.nasa.gov/datasets. Since the data at a single pixel was analyzed, a 3 × 3 AIRS sub-image covered the Zoige wetland spatially (Figure 1). The cells are named as A1–A9 from left to right and then from top to bottom.
We used the recently created China land cover products provided by the Resource and Environment Science and Data Center. Multiyear products in 2000, 2005, 2010, 2015, and 2018 are available and downloadable at http://www.resdc.cn/Default.aspx. The original land cover type is designed as a hierarchical classification scheme that allows one to adjust the thematic detail that describes each land cover class. Here, we first grouped the “level 2” classes into four categories: cropland, grassland, forest, and water body. Peatland in “level 2” remained as a category. The rest land cover types were classified as other. Thus, we had six land cover types. At such an aggregation level, the six land cover types did not change much from 2000 to 2018. The land cover data in 2010, which was near the middle of the studied time-series, was chosen. It should be noted that the peatland with high grassland coverage (>20%) might be classified into grassland in the downloaded datasets. Thus, some grassland, when the ground is wet, can be considered as wetland, per se.
Within the overlapped area of the study area and each cell, percentages of the six cover types were calculated and are shown in Table 1. Grassland and forest are the primary land cover in A1, whose ground area is only about 25% within the study area. A2 is the mixture of peatland, grassland, and forest, with the grassland cover type being dominant. About 65% area of A2 is inside of the study area. A3 is the grassland area having the lowest elevation in the study area (i.e., Figure 1). The majority of A3 is outside of the study area. In A4, the grassland, forest, and peatland are the major land cover types. More than one-half of the site is within the study area. A5, entirely within the study area, is covered by the peatland, grassland, and forest, with a small part of the waterbody. A6 is the mixture of peatland and grassland, with the grassland being dominant. About 70% of the area of A6 is inside the study area. A7 is covered by the grassland and forest, with a percentage of the peatland. More than one-half of the site is within the study area. The land cover types in A8 are like those in A7. More than 50% area of A8 is located inside of the study area. A small northwestern corner of A9 is inside the study area. Since A1, A3, or A9 is mostly outside of the study area, the atmospheric CH4 concentrations over each cell were not studied. Thus, we focused on A2, A4, A5, A6, A7, and A8.

Table 1.
Percent of each land cover type of the overlapped area within the study area and each cell.
2.3. The BFAST Algorithm
The algorithm decomposes the multitemporal AIRS CH4 data, Y(t), into three components, as
where S(t) is the seasonal component, T(t) is the trend component, and E(t) the error one. All are functions of time t. If there is no single abrupt change point or breakpoint, S(t) is continuous over the entire period. If one breakpoint occurs, S(t) becomes two piecewise functions. If multiple breakpoints exist, one piecewise function is developed between two adjacent breakpoints. With the anticipated periodic characteristics of S(t), a harmonic function is used. Assume p breakpoints occur at times , with being the start of the time-series and the end of the series. Then, between and (j = 1, 2, …, p), one can express S(t) as
where k is the kth number of the harmonic term. K is the highest-order harmonic term used in the algorithm. f is the frequency. Since the period for S(t) is annual, f is one cycle per year. and . is amplitude and phase, and both are segment-specific parameters. In this study, we are interested in the S(t) on an annual basis. The highest order of harmonic terms used in (2) cannot be greater than three [17,29,30], such that we can focus on changes using an entire season as the smallest timespan and eliminate unnecessary high-frequency variations in the AIRS data. Thus, K is set to 3.
T(t) is continuous over the entire period if a single breakpoint does not occur. If breaks happen, T(t) is expressed as piecewise functions as well. Assume m breakpoints happen at times , with being the start of the time-series and the end of the series. A piecewise linear function within (i = 1, 2, …, m) is
where αi is the ith intercept and βi the ith slope. Breakpoints that occur in T(t) or S(t) can generally differ in time or magnitude. Finally, the error term of E(t) is obtained in the decomposition.
2.4. The Effect of the h Parameter on the Decomposition
The BFAST algorithm uses the ordinary least squares residuals-based moving sum (OLS-MOSUM) to evaluate whether one or more breakpoints happen in the trend component or seasonal component [31]. The sum of a fixed number of residuals in a moving data window, whose size was determined by the bandwidth parameter, h(0, 1), moving over the whole sample period, was analyzed. If the evaluation indicated a significant change (with the significance level of p < 0.05), the break was estimated [32]. As implemented ([33]), the Bayesian information criterion determined the number of breakpoints. The date and confidence interval (CI) of each breakpoint was estimated at 95%. Additionally, h determined the minimal segment size between two potential breakpoints in the time-series and was the ratio of the number of observations within a segment divided by the total length of a time-series. The two-end points of the segment or the entire time-series were excluded before the division. Although h(0, 1), the maximum h was ≤ 0.5 if one breakpoint was to occur [21]. Per recommendations in [21] and [34], the minimum h was at least ≥ 5% of the observations within the time-series. Therefore, we varied h between 0.05 and 0.5 to understand its impact on the outcome and determine an h value to link the breaks with abnormal natural events (e.g., temperature).
3. Results
3.1. Increase of Atmospheric CH4 Concentration Derived From AIRS Data
The time-series of the atmospheric CH4 concentrations over A2, A4, A5, A6, A7, and A8 were studied individually. Figure 2 demonstrates an annual cyclic pattern and a persistent increase in the CH4 concentrations at the Zoige wetland during 2002–2018. In the figure, each dot is one observation or one month. A linear fit line was added and is shown as a red, dashed line. The parameters of the linear fit lines over the six cells are listed in Table 2. The slopes of the lines are between 0.015 and 0.017 ppb/day. With each fit line, the atmospheric CH4 concentrations in September of 2002 and March of 2018 were calculated. The concentration values ranged from 1811.357 to 1854.134 ppb in September of 2002 and from 1901.917 to 1944.989 ppb in March of 2018. The increases, after nearly 16 years, were 96.220, 90.560, 90.560, 84.900, 84.900, and 84.900 ppb in A2, A4, A5, A6, A7, and A8, respectively. The average annual rate was 5.7 ± 0.3 ppb/year. The globally averaged annual rate was 5.1 ± 0.6 ppb/year using the marine surface data between 2002 and 2017 (E. Dlugokencky, National Oceanic and Atmospheric Administration (NOAA)/Earth System Research Laboratory (ESRL), https://www.esrl.noaa.gov/gmd/ccgg/trends_ch4/). Regarding the global data, an increase in the atmospheric CH4 concentration at the Zoige wetland is likely true quantitatively.
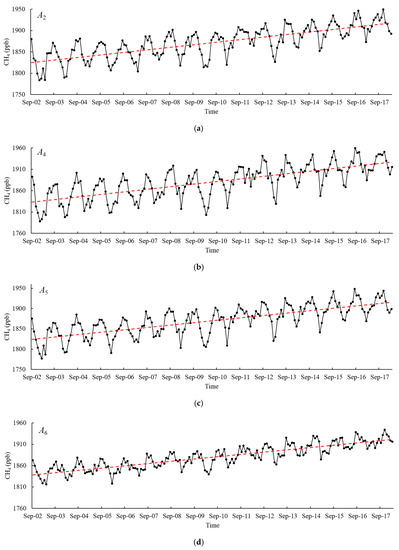
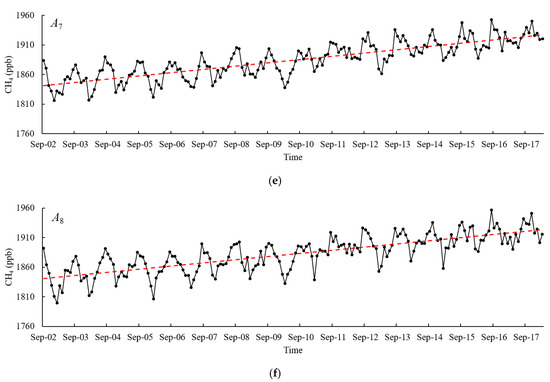
Figure 2.
Atmospheric Infrared Sounder (AIRS) atmospheric CH4 concentration data between 2002 and 2018, shown as a black curve. Each dot is an observation or one month in the monthly AIRS data. The red, dashed line is a linear fit line. (a) A2, (b) A4, (c) A5, (d) A6, (e) A7, and (f) A8.

Table 2.
Intercept and slope values of linear fit lines for A2, A4, A5, A6, A7, and A8.
3.2. Decomposition of the CH4 Time-Series
The decomposition for each of the six cells was conducted individually. No breaks in S(t) for each cell were found. Values of the crest, trough, height, and mean are tabulated in Table 3. The seasonal component of each cell has a mean value near zero, which suggests normality. As an example, Figure 3 shows an S(t) of A5 between 2002 and 2018. It is annually cyclic, which is anticipated. The parameters of S(t) for A5 are given in Table 4. In short, no further analysis of S(t) in each cell was carried out.

Table 3.
Descriptive summary of the seasonal and error components of A2, A4, A5, A6, A7, and A8. The unit is ppb. S(t): seasonal component and E(t): trend component.
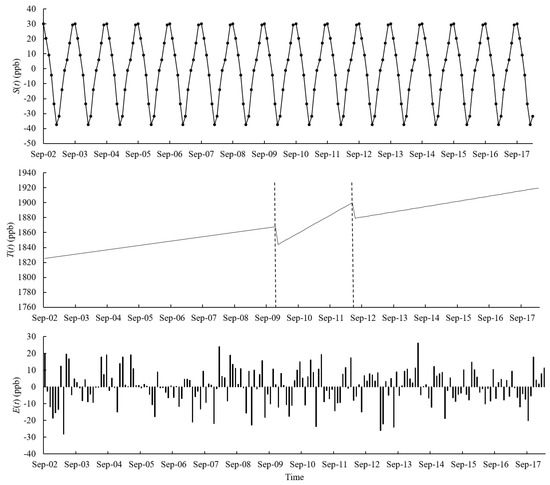
Figure 3.
Decomposition of the atmospheric CH4 concentration data over A5. S(t), T(t), and E(t) are the seasonal, trend, and error components, respectively. Two breakpoints were detected in the trend component. The vertical dotted lines in T(t) indicate the beginnings of breakpoints (December of 2009 and May of 2012).

Table 4.
Parameters of S(t) shown in Figure 3a and θi (i = 1, 2, 3) are the coefficients of the sine and cosine terms, respectively. The unit for and θi is ppb. f is the frequency (once per year).
The mean and standard deviation of the error component of the six cells were also analyzed, respectively. The annual mean value for each of the six cells is 0.000 ppb. The standard deviations range from 9.344 to 12.784 ppb and are ~0.57% of the average atmospheric CH4 concentration within the study period. Thus, E(t) is considered normal. The E(t) of A5 between 2002 and 2018 are shown in Figure 3 as well. No particular patterns exist.
In the trend components, two breakpoints were detected at A2, A4, and A5. A7 had one. No breaks were found at A6 and A8. The time and magnitude of the changes are shown in Table 5. Timewise, two breakpoints occurred in December of 2009, one in January of 2010, one in October of 2010, and three in May of 2012. Additionally, a negative magnitude value indicates a drop, whereas a positive value, an increase. Thus, there are six decreases and one increase. Figure 3 shows the trend component of A5 between 2002 and 2018. There are two drops and three segments or piecewise functions.

Table 5.
Atmospheric CH4 changes in the trend components over A2, A4, A5, and A7 at each breakpoint. At a breakpoint, an increase is positive, but a decrease negative.
Each piecewise linear function within each segment was derived for A2, A4, A5, A6, A7, and A8, respectively. The intercept and slope of each function for each cell are tabulated in Table 6. Of A2, A4, A5, and A7, there is at least one break in the trend components. The intercept values vary and are linked to the breaks. The intercept value of A6, 1285.509, is similar to that in the fit line (1289.315, Table 2). The similarity repeats for A8 (Table 6 confer, c.f., Table 2). All slope values are positive, showing an increasing trend. The values range from 0.011 to 0.076 ppb/day. Moreover, the slope in the final segment for A2, A4, A5, or A7 is always steeper than the counterpart in the first segment. The timing of the acceleration is mostly in agreement with previous studies. The growth rate is plateaued in the mid-2000s, and then, the rate accelerates onwards [35,36].

Table 6.
Intercept and slope values of each segment of T(t) of A2, A4, A5, A6, A7, and A8.
3.3. Parameterization of h and Its Impact on the Decomposition
As one knows that the number of breakpoints decreases when h increases, the negative and monotonic relationship suggests two aspects. First, an h value cannot be too large. An excessively large one can unnecessarily smoothen the trend component. Second, an h value or values exist after considering the interplays of the observations of interest, break numbers, and statistical significance. In this study, we were interested in CH4 variations in the trend components using monthly remote-sensing time-series data. Factors such as an abnormal temperature event or events very likely affecting the observed atmospheric CH4 concentrations were of interest.
As discussed previously, h was between 0.05 and 0.5. At h = 0.05, seven breakpoints over A2, A4, A5, and A7 occurred from September of 2002 to March of 2018 (Table 7). The total number of monthly observations within September of 2002 and March of 2018 was 185. Thus, at h = 0.05, the corresponding number of observations within two breakpoints was 9.3. Statistically, the number is too small. One needs to increase the h, boosting the number of observations while keeping the same number of breakpoints, if possible. Then, an exploratory approach is taken at an increment step of h = 0.01. As h changes from 0.05 to 0.13, the number of observations, no, and the seven breakpoints remain. Once h ≥ 0.14, the number of breakpoints decreases. All the breakpoints disappear when h ≥ 0.17 (Table 7).

Table 7.
Of an h value, number of observations (no), and number of breakpoints detected in the trend components of A2, A4, A5, and A7 of the time-series. h is the ratio of the number of observations within a segment divided by the total length of a time-series, excluding the beginning and end observations.
Using the times that breaks happened in Table 5, we calculated the number of observations between two breakpoints in A2, A4, and A5. The numbers are 26, 27, and 27, respectively. For the three cells, h at 0.13 is the maximum value if all six breaks are desired. Furthermore, h ≥ 0.17 should not be considered if one breakpoint is wanted (Table 7). Therefore, h does influence decomposition. To maintain the maximum number of breakpoints in the trend components at A2, A4, and A5, we should set h ≤ 0.13. Unfortunately, the h value of 0.17 and a corresponding number of observations of 31.5 could not be used to explain the disappearance of the breakpoint at A7. The number of monthly observations between September of 2002 (the starting month of the time-series) and October of 2010 was 96. The number of observations between November of 2010 and March of 2018 (the end of the time-series) was 87.
4. Discussion
4.1. Interpretation of Breaks With Air Temperature Variations
With the occurrence of a breakpoint in the trend component, one is interested to know what the possible causes are. In Table 5, there are six breakpoints linked to decreasing values but one increasing value. As illustrated and stated previously, the topography and land cover types differ among A2, A4, A5, and A7. Logically, one reason is whether a more or less uniform physical feature or event exists and predominantly causes the change.
The soil temperature and water table level are two main factors that influence CH4 emissions from the wetlands into the atmosphere [2,3]. The soil moisture at the surface is usually positively related to the water table position [37]. Thus, the abnormal changes in soil temperature and moisture content may be responsible for the abrupt changes in the trend components. With the available GLDAS monthly soil moisture and soil temperature data, three data points (before the breakpoint, breakpoint, and after the breakpoint) at each breakpoint seem normal. The data cannot be used to interpret the delineated breaks. The aggregation of both types of GLDAS data at a monthly scale might overly smooth the intra-month variations.
We have the daily air temperature data at Maqu (located in A2), Zoige (A5), and Hongyuan (A8) meteorological stations and articulate the following to use variations of the air temperature to explain the breaks. First, to establish the relationship between the air temperature data and soil temperature data, we aggregated the available daily air temperature data into monthly data between 2002 and 2017. Then, the correlation analyses between the monthly air temperature data at Maqu and soil temperature at A2, between the monthly air temperature data at Zoige and soil temperature at A5, and between the monthly air temperature data at Hongyuan and soil temperature at A8 were, respectively, conducted. The correlation coefficients are summarized in Table 8. In the table, the soil temperature data at 0–100-cm depths are the average of the available temperature data at 0–10 cm, 10–40 cm, and 40–100 cm. The correlation coefficients are ≥0.921. For the top layer (0–10 cm), the coefficients are 0.979 or higher. Thus, the air temperature can be a surrogate for the soil temperature. If the daily soil temperature data are not available, one can use the daily air temperature alternatively.

Table 8.
The correlations between the monthly air temperature at three stations and the monthly soil temperature and moisture of the cell where the station is located. Data at two soil depths are analyzed.
Similarly, we analyzed the correlation of the aggregated air temperature data and soil moisture monthly data. The correlation coefficients are tabulated in Table 8. The coefficients between the air temperature and soil moisture contents at the 0–10-cm soil depth were at least 0.713 or higher, although the coefficients decreased as the depth increased (Table 8). Again, with the missing daily soil moisture data, the daily air temperature is an alternative.
A cold front moved across the area in the middle of December 2009, causing a significant temperature drop. The mean air temperature between the 16th and 31st of December was 5.5 °C lower than that from the 1st to 15th of December (Table 9). The t-test using the 1–15 temperature data (n1 = 45, the sample size) versus 16–31 temperature data (n2 = 48) at three meteorological stations resulted in a p-value = 0.000. Thus, the temperature drop was significant.

Table 9.
Descriptive statistics of daily temperatures (°C) in December of 2009 after combining the daily datasets at the Maqu, Zoige, and Hongyuan meteorological stations.
To verify whether the temperature drop of 16–31 December 2009 was abnormal between 2002 and 2018, the daily temperature data of 16–31 December 2009, the averaged 16–31 December daily temperature data between 2002 and 2018, and the averaged 16–31 December daily temperature data without the 16–31 December 2009 temperature were plotted at the meteorological stations. As shown in Figure 4, the temperature data of 16–31 December 2009 differs from the other two averaged daily temperature datasets in December. The matched-pairs t-test of the former versus either of the latter two results in a p-value = 0.000. Thus, the 16–31 December 2009 temperature drop was abnormal.
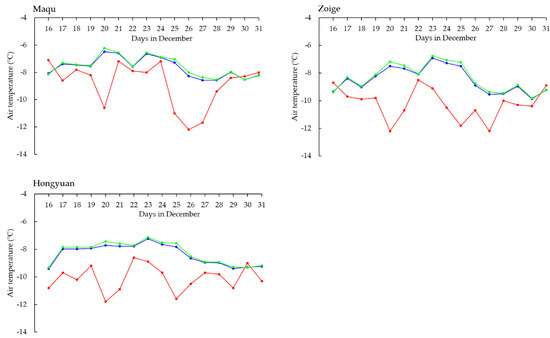
Figure 4.
The daily temperature data of 16–31 December 2009 (red line), average 16–31 December temperature data between 2002 and 2018 (green line), and average 16–31 December temperature data without the 16–31 December 2009 temperature data (blue line) at the three meteorological stations at Maqu, Zoige, and Hongyuan.
Most of the microorganisms of methanogens are thermophilic. The abnormally cold weather in the second part of December 2009 could slow down their CH4 production generally. The CH4 emissions into the atmosphere decreased, and so did the atmospheric CH4 concentrations. Although the drop in soil temperature is typically lagged compared with the air temperature decrease [38], the below-0 °C air temperature in December of 2009, and mainly, the colder air temperature in the late month (Table 9) further froze the soil column downward. Then, the chance that CH4 escaped from the frozen soil column into the atmosphere decreased. With the cold temperature (mean = −6.3 °C and standard deviation = 2.2 °C) in January of 2010, the frozen soil column remained, or even deepened into the column, reducing the CH4 escape further. Consequently, the trend components of A4 and A5 dropped from December of 2009 to January of 2010. The drop of atmospheric CH4 concentrations from January to February of 2010 over A2 could be attributed to the temperature drop in December of 2009, coupled with the elevation difference. The average elevation of A2 is about 500 m lower than that of A4 or A5. The air temperature at A2 is typically about 3 °C warmer than that at A4 or A5. The warmer temperature postponed the above-discussed processes, including the CH4 production reductions in the soil column and the CH4 emissions decrease from the soil into the atmosphere. Therefore, the drop was delayed for one month.
Similarly, the abnormal temperature variation was used to interpret the drop between May and June of 2012 at A2, A4, and A5. Descriptive statistics of the air temperatures in April of 2011, 2012, and 2013 and in May of 2012 are given in Table 10. The mean values in April of 2012 were lower than those in April of 2011 or April of 2013. Then, due to the lower air temperature, CH4 in the soil column of the subsurface that was frozen in early spring might not have easily escaped into the air in April of 2012, as compared to CH4 in April of 2011 or 2013 did. Additionally, the mean value of the daily air temperature in May of 2012 was 7.4 °C. The temperature in May 2012 was almost 5 °C higher than that in April 2012. The colder temperature in April of 2012 dampened the CH4 emissions from the soil into the atmosphere, but the subsequent warmer temperatures in May sped up the escape processes of CH4 [39]. An elevated atmospheric CH4 concentration in May of 2012 occurred. Therefore, relative to the spike of the trend components in May of 2012, the atmospheric CH4 concentration in June of 2012 dropped.

Table 10.
Descriptive statistics of the daily temperature (°C) in April of 2011, 2012, and 2013 and in May of 2012. Daily air temperature data at the three stations were combined.
An increase in the atmospheric CH4 concentration over A7 was detected (Table 5). No anomaly was identified in September, October, and November of 2010. The change in atmospheric CH4 concentrations for A2, A4, A5, A6, or A8 between September of 2002 and March of 2018 did not show any apparent anomaly. Therefore, the cause of the increase is not clear.
4.2. Atmospheric CH4 Concentration Differences of Western Cells Versus Eastern Cells
One or two breakpoints occurred in trend components of A2, A4, A5, and A7 but no breakpoints in A6 and A8. Concerning Figure 1, A6 and A8 were east of A2, A4, A5, and A7. Then, component-by-component, average values of A6 and A8 and average values of A2, A4, and A7 were calculated. The matched-pairs t-test of the average values of A6 and A8 versus the average ones of A2, A4, and A7 was conducted. As shown in Table 11, the trend components differed significantly, but the seasonal and error components did not. The matched-pairs t-test for the average AIRS data was significantly different as well. Further studies will be pursued to understand not only the difference but also the possible causes.

Table 11.
The p-values of the matched-pairs t-test for the western and eastern cells. AIRS: Atmospheric Infrared Sounder.
4.3. Possible Impact on the Decomposition if Random Noisy Observations Exist in the Time-Series
The time-series of the observed monthly atmospheric CH4 concentration may consist of random noise that can affect the decomposition results. One feasible way to evaluate the impact of the noisy observations is to remove some observations randomly first and then replace them through the imputation [40] of the time-series. The imputation is not only widely used statistically in handling missing data but also is needed before running the BFAST algorithm. Without imputing a missing observation, the algorithm would move to the next observation in the time-series to fill in the missing one. The moving and filling continue until reaching the end of the time-series. Then, mixed matches of CH4 observations and months occur and can eventually invalidate the time-series analysis. Therefore, two types of removal and imputation were considered, with A5 as an example.
At h = 0.13, two breakpoints were identified (Table 5). The number of observations was 24.1 (Table 7). As 24 was the nearest integer for 24.1, we chronologically split the 24 observations with the 1st–12th observations and the breakpoint and the 13th–24th observations after the breakpoint. Using the Statistical Package for the Social Sciences (SPSS) software (https://www.ibm.com/analytics/spss-statistics-software), one observation in the 1st–12th observations and one in the 13th–24th observations were randomly selected and removed. The selection and then removal were performed twice, one for each breakpoint. The observation months and corresponding CH4 values are given in Table 12. Then, we used the multiple imputation algorithm of the SPSS software to impute the four missing values. In the imputation, m was set to 5, and the Markov Chain Monte Carlo (MCMC) method was chosen. The imputed values are tabulated in Table 12. The original value and imputed value differed in each of the four cases. After replacing the original value with the related imputed one, the BFAST algorithm was applied to the new time-series, A5_r, again. No breakpoint was found in the seasonal component, whereas two breakpoints were delineated (Table 13). Then, the piecewise functions were derived within each segment. The intercepts and slopes are shown in Table 14. The drop at the 2009/12–2010/01 breakpoint was comparable, and so was the drop at the 2012/05–2012/06 breakpoint (Table 13 c.f. Table 5). The piecewise linear equations were similar as well (Table 14 c.f. Table 6). Therefore, although the removal and imputation of four observations altered the time-series values of A5, the changes might not significantly affect the outcomes from the BFAST algorithm decomposition.

Table 12.
Four randomly removed observations, and the observed and imputed atmospheric CH4 concentration values (ppb) of A5.

Table 13.
Atmospheric CH4 concentration changes at each breakpoint in the trend component of A5_r.

Table 14.
Intercept and slope of each segment of T(t) in A5_r.
To further explore the removal and imputation influences on the decomposition outcomes, we randomly removed and imputed observations at 5%, 6%, …, of the entire time-series of A5. The increment was 1%. At h = 0.13, two breakpoints were still obtained until 7% or the removal and imputation of 13 observations. The drop values at the breakpoints and piecewise linear functions in the three segments varied. At 8% or above, the decomposition outcomes fluctuated with the disappearance of one or both breaks. Thus, caution should be exercised if numerous erroneous observations exist. In this study, without a significant impact on the outcomes, the ceiling number of erroneous observations for A5 was 14.96 (15 as an integer). It should be noted that Watts et al. [41] reported the BFAST algorithm was sensitive to the time-series datasets of vegetation indices collected by the Moderate Resolution Imaging Spectroradiometer (MODIS) Aqua and Terra remote sensors, although the time-series datasets themselves were highly correlated. Thus, one should consider the impact of erroneous data points on outcomes, and one possible way to conduct the sensitivity study to reveal and quantify the effect was suggested.
5. Conclusions
The multitemporal remotely sensed methane (CH4) data from the Atmospheric Infrared Sounder (AIRS) instrument, on-board the NASA Earth Observing System Aqua satellite, were studied to understand the variations of atmospheric CH4 over the Zoige wetland, China. The time spanned from September of 2002 to March of 2018. The Breaks for Additive Season and Trend (BFAST) algorithm was used to decompose the remotely sensed CH4 data into the seasonal, trend, and error components. The meteorological and GLDAS datasets were auxiliary. They were used to interpret multitemporal CH4 data and decomposition outcomes.
The overall pattern of the atmospheric CH4 concentrations was derived from the AIRS data first. The concentrations increased steadily during 2002 and 2018. The average annual rate was on par with the globally average yearly rate. Thus, the annual rate at the Zoige wetland is likely valid.
Cell-by-cell, the seasonal, trend, and error components were next delineated by the BFAST algorithm. We analyzed the seasonal component, considering the crest, trough, height, and mean values. The components showed annual cycles with a mean value of 0. No anomaly was found. The error components varied from 2002 to 2018, but no particular intra- or inter-annual patterns were found. The mean and standard deviations were calculated. With the mean value of 0 and one standard deviation of ~0.5% or less of the average AIRS data, no anomaly was detected in the error components. The trend components increased gradually, with no breakpoints delineated in A6 and A8 but seven breakpoints collectively in A2, A4, A5, and A7. The timing and magnitude of each breakpoint were analyzed. After establishing significant correlations between the air temperature and soil temperature, and between the air temperature and soil moisture, we concluded that the temperature anomalies were primarily responsible for six breakpoints decomposing. However, the temperature anomaly could not explain the occurrence of one breakpoint.
The parameterization of the h parameter in the BFAST algorithm can be the most critical because it considerably influences the detection of breaks and the number of breakpoints. The minimum h is ≥0.05 statistically, but it cannot be >0.5 if one wants to identify one breakpoint. As h increases, the number of breakpoints decreases. Thus, a large h value can adversely smoothen the decomposed component. One may miss the critical and explainable breakpoints in the time-series. An optimized h value may be found after studying the interplays of the observation of interest, break numbers, and statistical significance. In this study, h = 0.13 was found.
Finally, erroneous observations can exist in time-series data, impacting the outcomes using the BFAST algorithm. The removal of one observation or observations and then the imputation of the removed observation or observations, can be one possible approach to conduct a sensitivity study. Thus, one can delineate and quantify the potential impact of the erroneous data point or points.
Author Contributions
Y.Y. and Y.W. conceived the study. Y.Y. studied the BFAST algorithm and analyzed the multitemporal AIRS data in consultation with Y.W. Both wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grants #41771401 and #41471361 to the University of Electronic Science and Technology of China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ciais, P.; Sabine, C.; Bala, G.; Bopp, L.; Brovkin, V.; Canadell, J.; Chhabra, A.; DeFries, R.; Galloway, J.; Heimann, M.; et al. Carbon and Other Biogeochemical Cycles; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 465–570. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/WG1AR5_all_final.pdf (accessed on 29 September 2020).
- Conrad, R. Control of methane production in terrestrial ecosystems. In Exchange of Trace Gases between Terrestrial Ecosystems and the Atmosphere; Andreae, M.O., Schimel, D.S., Eds.; Wiley: Chichester, UK; New York, NY, USA, 1989; pp. 39–58. [Google Scholar]
- Valentine, D.W.; Holland, E.A.; Schimel, D.S. Ecosystem and physiological controls over methane production in northern wetlands. J. Geophys. Res. Space Phys. 1994, 99, 1563. [Google Scholar] [CrossRef]
- Christensen, T.R.; Ekberg, A.; Ström, L.; Mastepanov, M.; Panikov, N.; Öquist, M.; Svensson, B.H.; Nykänen, H.; Martikainen, P.J.; Oskarsson, H. Factors controlling large scale variations in methane emissions from wetlands. Geophys. Res. Lett. 2003, 30, 1414. [Google Scholar] [CrossRef]
- Christensen, T.R.; Prentice, I.C.; Kaplan, J.; Haxeltine, A.; Sitch, S. Methane flux from northern wetlands and tundra. Tellus B Chem. Phys. Meteorol. 1996, 48, 652–661. [Google Scholar] [CrossRef]
- Moore, T.; Roulet, N.T.; Waddington, J. Uncertainty in predicting the effect of climatic change on the carbon cycling of Canadian peatlands. Clim. Chang. 1998, 40, 229–245. [Google Scholar] [CrossRef]
- Walter, B.P.; Heimann, M. A process-based, climate-sensitive model to derive methane emissions from natural wetlands: Application to five wetland sites, sensitivity to model parameters, and climate. Glob. Biogeochem. Cycles 2000, 14, 745–765. [Google Scholar] [CrossRef]
- King, G.M. Regulation by light of methane emissions from a wetland. Nature 1990, 345, 513–515. [Google Scholar] [CrossRef]
- Nisbet, E.G.; Chappellaz, J. Shifting gear, quickly. Science 2009, 324, 477–478. [Google Scholar] [CrossRef]
- Petrenko, V.V.; Smith, A.M.; Brook, E.J.; Lowe, D.; Riedel, K.; Brailsford, G.; Hua, Q.; Schaefer, H.; Reeh, N.; Weiss, R.F.; et al. 14CH4 measurements in greenland ice: Investigating last glacial termination CH4 sources. Science 2009, 324, 506–508. [Google Scholar] [CrossRef]
- Forster, P.; Ramaswamy, V.; Artaxo, P.; Berntsen, T.; Betts, R.; Fahey, D.W.; Haywood, J.; Lena, J.; Lowe, D.C.; Myhre, G.; et al. Changes in atmospheric constituents and in radiative forcing. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M.T., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; pp. 129–234. Available online: http://www.ipcc.ch/pdf/assessment-report/ar4/wg1/ar4-wg1-chapter2.pdf (accessed on 29 September 2020).
- Shindell, D.; Faluvegi, G.; Koch, R.M.; Schmidt, G.; Unger, N.; Bauer, S.E. Improved attribution of climate forcing to emissions. Science 2009, 326, 716–718. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Kennedy, R. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. TimeSync—Tools for calibration and validation. Remote Sens. Environ. 2010, 114, 2911–2924. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Jamali, S.; Jönsson, P.; Eklundh, L.; Ardö, J.; Seaquist, J. Detecting changes in vegetation trends using time series segmentation. Remote Sens. Environ. 2015, 156, 182–195. [Google Scholar] [CrossRef]
- Jacquin, A.; Sheeren, D.; Lacombe, J.-P. Vegetation cover degradation assessment in Madagascar savanna based on trend analysis of MODIS NDVI time series. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S3–S10. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.J.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.J.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Verbesselt, J.; Zeileis, A.; Herold, M. Near real-time disturbance detection using satellite image time series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
- Saatchi, S.; Asefi-Najafabady, S.; Malhi, Y.; Aragão, L.E.O.C.; Anderson, L.O.; Myneni, R.B.; Nemani, R. Persistent effects of a severe drought on Amazonian forest canopy. Proc. Natl. Acad. Sci. USA 2012, 110, 565–570. [Google Scholar] [CrossRef]
- Watts, L.M.; Laffan, S.W. Effectiveness of the BFAST algorithm for detecting vegetation response patterns in a semi-arid region. Remote Sens. Environ. 2014, 154, 234–245. [Google Scholar] [CrossRef]
- Hamunyela, E.; Verbesselt, J.; Herold, M. Using spatial context to improve early detection of deforestation from Landsat time series. Remote Sens. Environ. 2016, 172, 126–138. [Google Scholar] [CrossRef]
- Chen, H.; Yao, S.; Wu, N.; Wang, Y.; Luo, P.; Tian, J.; Gao, Y.; Sun, G. Determinants influencing seasonal variations of methane emissions from alpine wetlands in Zoige Plateau and their implications. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Chen, H.; Wu, N.; Gao, Y.; Wang, Y.; Luo, P.; Tian, J. Spatial variations on methane emissions from Zoige alpine wetlands of Southwest China. Sci. Total. Environ. 2009, 407, 1097–1104. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Yang, G.; Gao, Y.; Chen, H.; Wu, N.; Peng, C.; Zhu, Q.; Zhu, D.; Wu, J.; He, Y.; et al. Higher recent peat C accumulation than that during the Holocene on the Zoige Plateau. Quat. Sci. Rev. 2015, 114, 116–125. [Google Scholar] [CrossRef]
- Li, J.; Wang, W.; Hu, G.; Wei, Z. Changes in ecosystem service values in Zoige Plateau, China. Agric. Ecosyst. Environ. 2010, 139, 766–770. [Google Scholar] [CrossRef]
- Xiong, X.; Barnet, C.; Maddy, E.; Sweeney, C.; Liu, X.; Zhou, L.; Goldberg, M. Characterization and validation of methane products from the Atmospheric Infrared Sounder (AIRS). J. Geophys. Res. Space Phys. 2008, 113, 00 01. [Google Scholar] [CrossRef]
- Tian, B.; Manning, E.; Fetzer, E.; Olsen, E.; Wong, S.; Susskind, J.; Iredell, L. AIRS/AMSU/HSB Version 6 Level 3 Product User Guide; Jet Propulsion Laboratory: Pasadena, CA, USA, 2013. Available online: http://disc.sci.gsfc.nasa.gov/AIRS/documentation/v6_docs/v6releasedocs1/V6_L3_User_Guide.pdf (accessed on 29 September 2020).
- Geerken, R.A. An algorithm to classify and monitor seasonal variations in vegetation phenologies and their inter-annual change. ISPRS J. Photogramm. Remote Sens. 2009, 64, 422–431. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A. Comparison of cloud-reconstruction methods for time series of composite NDVI data. Remote Sens. Environ. 2010, 114, 618–625. [Google Scholar] [CrossRef]
- Zeileis, A. A unified approach to structural change tests based on ML scores, FStatistics, and OLS residuals. Econ. Rev. 2005, 24, 445–466. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econ. 2003, 18, 1–22. [Google Scholar] [CrossRef]
- Zeileis, A.; Leisch, F.; Hornik, K.; Kleiber, C. Strucchange: An R package for testing for structural change in linear regression models. J. Stat. Softw. 2002, 7, 1–38. [Google Scholar] [CrossRef]
- Chu, C.-S.J.; Kaun, C.-M.; Hornik, K. MOSUM tests for parameter constancy. Biometrika 1995, 82, 603–617. [Google Scholar] [CrossRef]
- McKain, K.; Down, A.; Raciti, S.M.; Budney, J.; Hutyra, L.R.; Floerchinger, C.; Herndon, S.C.; Nehrkorn, T.; Zahniser, M.S.; Jackson, R.B.; et al. Methane emissions from natural gas infrastructure and use in the urban region of Boston, Massachusetts. Proc. Natl. Acad. Sci. USA 2015, 112, 1941–1946. [Google Scholar] [CrossRef] [PubMed]
- Zou, M.; Xiong, X.; Wu, Z.; Li, S.; Zhang, Y.; Li, S. Increase of atmospheric methane observed from space-borne and ground-based measurements. Remote Sens. 2019, 11, 964. [Google Scholar] [CrossRef]
- Price, J. Soil moisture, water tension, and water table relationships in a managed cutover bog. J. Hydrol. 1997, 202, 21–32. [Google Scholar] [CrossRef]
- Gabriel, C.-E.; Kellman, L. Investigating the role of moisture as an environmental constraint in the decomposition of shallow and deep mineral soil organic matter of a temperate coniferous soil. Soil Boil. Biochem. 2014, 68, 373–384. [Google Scholar] [CrossRef]
- Feng, X.; Deventer, M.J.; Lonchar, R.; Ng, G.H.C.; Sebestyen, S.D.; Roman, D.T.; Griffis, T.J.; Millet, D.B.; Kolka, R.K. Climate sensitivity of peatland methane emissions mediated by seasonal hydrologic dynamics. Geophys. Res. Lett. 2020, 47, e2020GL088875. [Google Scholar] [CrossRef]
- Graham, J.W. Missing Data: Analysis and Design. Springer: New York, NY, USA; Heidelberg, Germany; Dordrecht, The Netherlands; London, UK, 2012; 323p. [Google Scholar]
- Watts, L.M.; Laffan, S.W. Sensitivity of the BFAST Algorithm to MODIS Satellite and Vegetation Index. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013; pp. 1638–1644. Available online: https://mssanz.org.au/modsim2013/H2/watts.pdf (accessed on 29 September 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).