Estimation of Winter Wheat Grain Protein Content Based on Multisource Data Assimilation
Abstract
1. Introduction
2. Materials and Methods
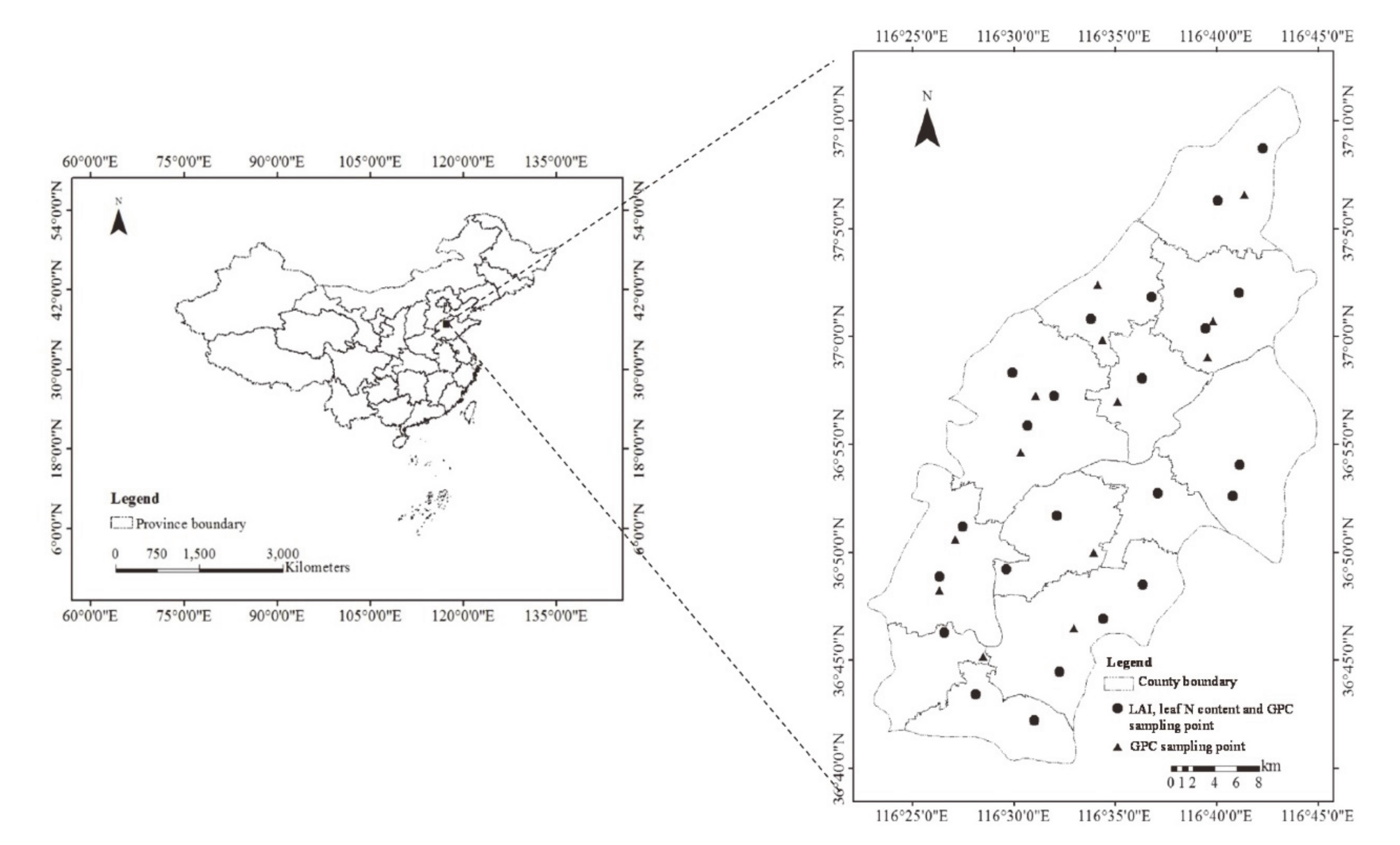
2.1. Study Site
2.2. Crop Growth Model
2.3. Data Acquisition
2.3.1. Field Experimental Data
2.3.2. Regional Sampling Data
2.3.3. Remote Sensing Data
2.3.4. Meteorological Data
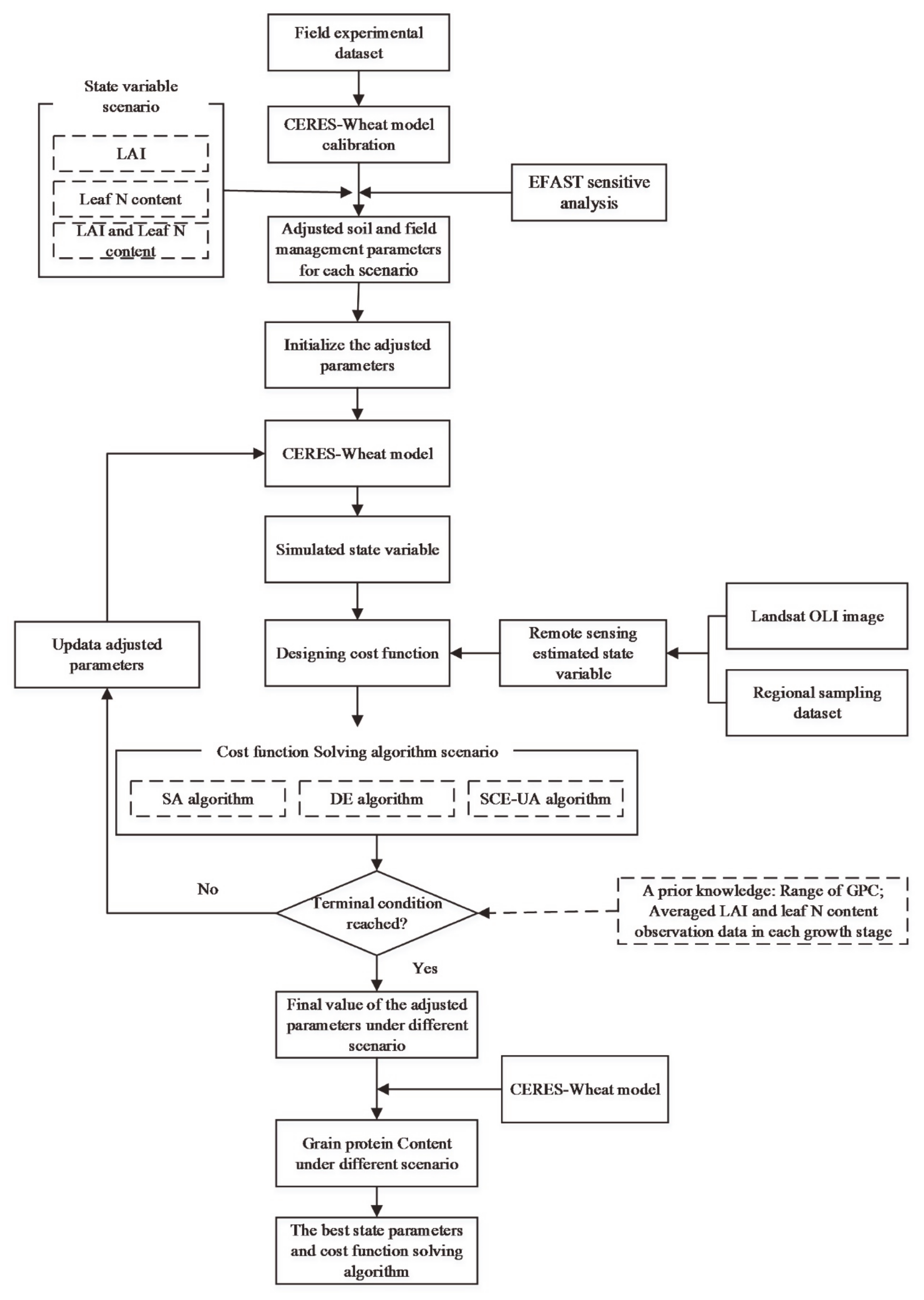
2.4. Data Analysis Method
3. Results
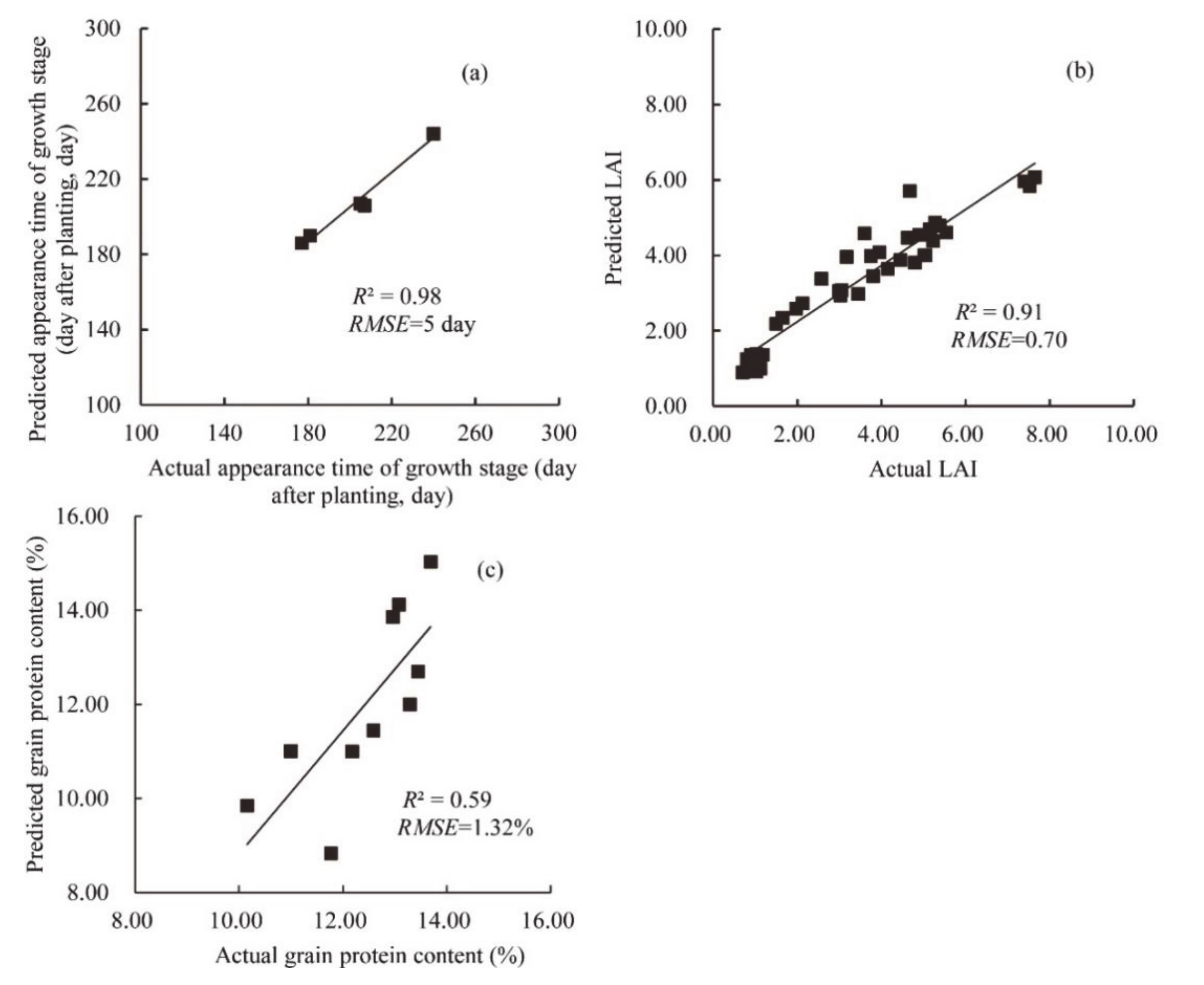
3.1. CERES-Wheat Model Calibration Results
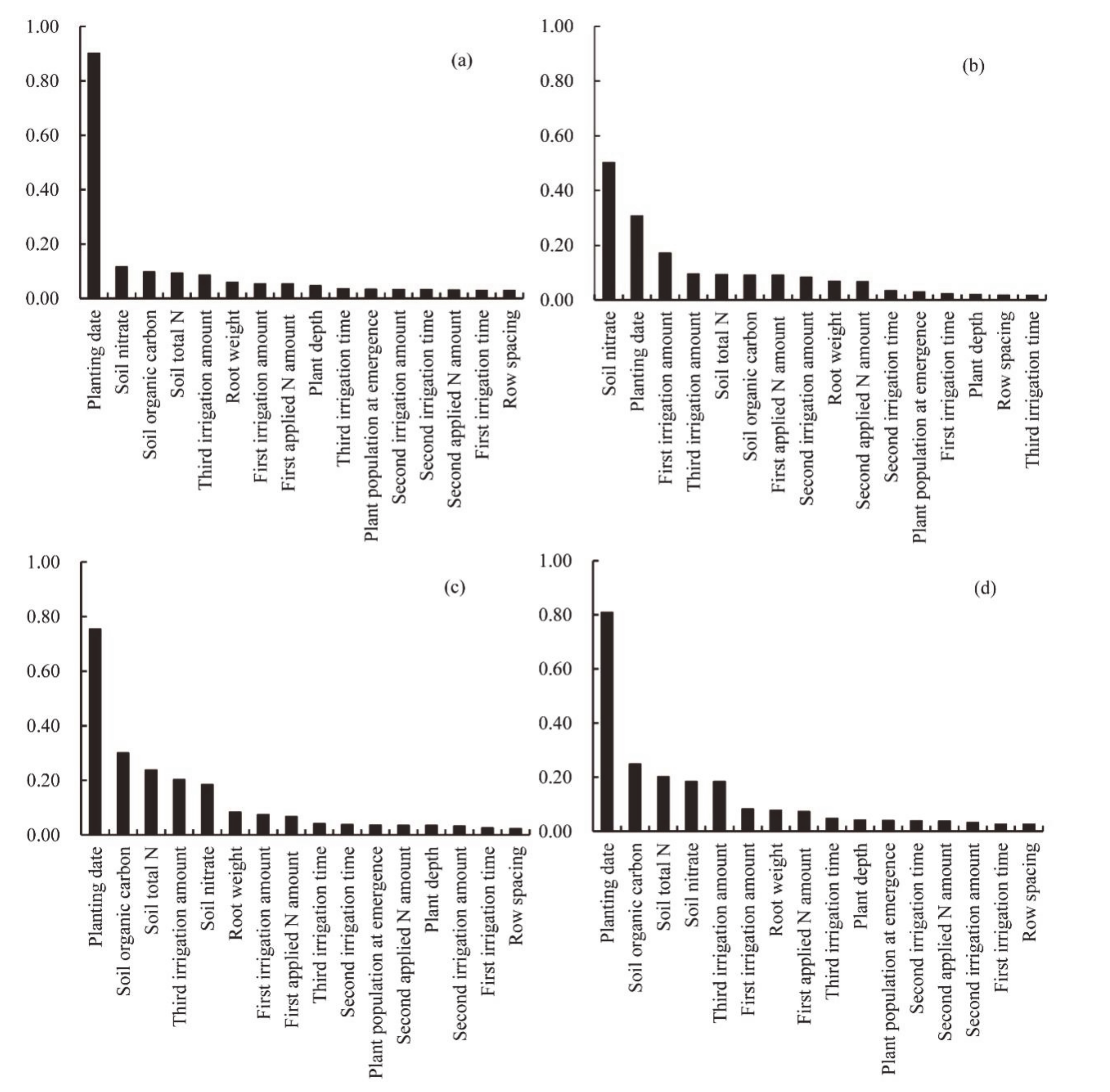
3.2. Selected Adjusted Soil and Field Management Input Variables for Each State Variable Scenario
3.3. Results for Remote Sensing Observation
3.4. Data Assimilation Results
4. Discussion
4.1. Optimal State Variables and Cost Function Solving Algorithm
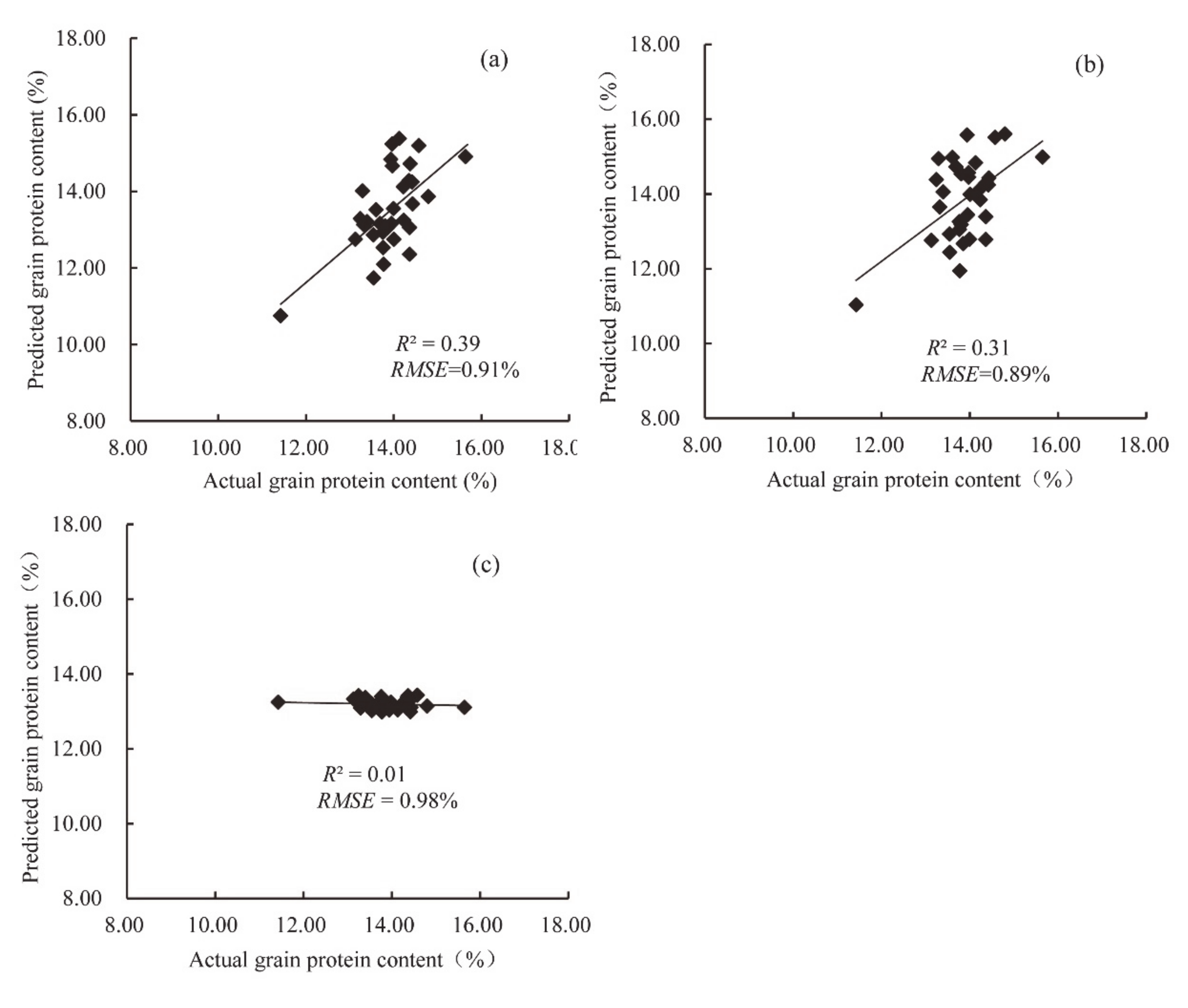
4.2. Effect of a Priori Knowledge on Gpc Prediction Results Using Data Assimilation
4.3. Data Assimilation vs. Only Crop Growth Model
4.4. Comparison with Existing Studies, and Future Development
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, X.; Teng, C.; Zhao, Y.; Du, Y.; Zhao, C.; Yang, G.; Jin, X.; Song, X.; Gu, X.; Casa, R.; et al. Prediction of wheat grain protein by coupling multisource remote sensing imagery and ECMWF data. Remote Sens. 2020, 12, 1349. [Google Scholar] [CrossRef]
- Song, X.; Wang, J.; Yang, G.; Feng, H. Winter wheat cropland GPC evaluation through remote sensing. Intell. Autom. Soft Comput. 2014, 20, 599–609. [Google Scholar] [CrossRef]
- Asseng, S.; Milroy, S.P. Simulation of environmental and genetic effects on grain protein concentration in wheat. Eur. J. Agron. 2006, 25, 119–128. [Google Scholar] [CrossRef]
- Orlando, F.; Marta, A.D.; Mancini, M.; Motha, R.; Qu, J.J.; Orlandini, S. Integration of remote sensing and crop modeling for the early assessment of durum wheat harvest at the field scale. Crop Sci. 2015, 55, 1280–1289. [Google Scholar] [CrossRef]
- Asseng, S.; Bar-Tal, A.; Bowden, J.W.; Keating, B.A.; Van Herwaarden, A.; Palta, J.A.; Huth, N.I.; Probert, M.E. Simulation of grain protein content with APSIM-Nwheat. Eur. J. Agron. 2002, 16, 25–42. [Google Scholar] [CrossRef]
- Anwar, M.R.; Takahashi, S.; Itoh, S.; Nakatsuji, T. Modeling yield and grain protein of Japanese wheat by DSSAT cropping system model. In Proceeding of Plant Growth Modeling and Applications; Hu, B.G., Jaeger, M., Eds.; Liama, Chinese Agricultural University: Beijing, China, 2003; pp. 312–320. [Google Scholar]
- Pan, J.; Zhu, Y.; Jiang, D.; Dai, T.; Li, Y.; Cao, W. Modeling plant nitrogen uptake and grain nitrogen accumulation in wheat. Field Crop. Res. 2006, 97, 322336. [Google Scholar] [CrossRef]
- Basnet, B.B.; Apan, A.A.; Kelly, R.M.; Jensen, T.; Strong, W.M.; Butler, D.G. Relating satellite imagery with gain protein content. In Proceedings of the 2003 Spatial Science Institute Biennial Conference: Spatial Knowledge Without Boundaries (SSC2003); Spatial Sciences Institute: Canberra, Australia, 2003; pp. 22–27. [Google Scholar]
- Zhao, H.; Song, X.; Yang, G.; Li, Z.; Zhang, D.; Feng, H. Monitoring of nitrogen and GPC in winter wheat based on sentinel-2A data. Remote Sens. 2019, 11, 1724. [Google Scholar] [CrossRef]
- Kasampalis, D.A.; Alexandridis, T.K.; Deva, C.; Challinor, A.; Moshou, D.; Zalidis, G. Contribution of remote sensing on crop models: A review. J. Imaging 2018, 4, 52. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.; Liang, S.; Chen, Z.; Xue, J.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276–277, 107609. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.Y.; Chen, Y.; Zhang, L.; Tao, F. Improving regional wheat yields estimations by multi-step assimilating of a crop model with multi-source data. Agric. For. Meteorol. 2020, 290, 107993. [Google Scholar] [CrossRef]
- Talagrand, O. Assimilation of observations, an introduction. J. Meteorol. Soc. Jpn. 1997, 75, 191–209. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaeman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Li, Z.; Jin, X.; Zhao, C.; Wang, J.; Xu, X.; Yang, G.; Li, C.; Shen, J. Estimating wheat yield and quality by coupling the DSSAT-CERES model and proximal remote sensing. Eur. J. Agron. 2015, 71, 53–62. [Google Scholar] [CrossRef]
- Thorp, K.R.; Wang, G.; West, A.; Moran, M.; Bronson, K.; White, J.; Mon, J. Estimating crop biophysical properties from remote sensing data by inverting liked radiative transfer and ecophysiological models. Remote Sens. Environ. 2012, 124, 224–233. [Google Scholar] [CrossRef]
- Mass, S.J. Use of remotely sensed information in agricultural crop growth models. Ecol. Model. 1988, 41, 247–268. [Google Scholar] [CrossRef]
- Thorp, K.R.; Hunsaker, D.J.; French, A.N. Assimilating leaf area index estimates from remote sensing into the simulations of a cropping systems model. Trans. ASABE 2010, 53, 251–262. [Google Scholar] [CrossRef]
- Li, R.; Li, C.J.; Dong, Y.; Feng, L.; Wang, J.; Yang, X.; Pan, Y. Assimilation of remote sensing and crop model for LAI estimation based on ensemble kaiman filter. Agric. Sci. China 2011, 10, 1595–1602. [Google Scholar] [CrossRef]
- Dong, Y.; Zhao, C.; Yang, G.; Chen, L.; Wang, J.; Feng, H. Integrating a very fast simulated annealing optimization algorithm for crop leaf area index variational assimilation. Math. Comput. Model. 2013, 58, 877–885. [Google Scholar] [CrossRef]
- Yao, F.; Tang, Y.; Wang, P.; Zhang, J. Estimation of maize yield by using a process-based model and remote sensing data in the northeast China plain. Phys. Chem. Earth 2015, 87, 142–152. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Su, W.; Zhang, X.; Huang, Y.; Fan, J.; Wu, W. Jointly assimilating MODIS LAI and ET products into the SWAP model for winter wheat yield estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4060–4071. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Xu, X.; Zhao, C.; Jin, X.; Yang, G.; Feng, H. Assimilation of two variables derived from hyperspectral data into the DSSAT-CERES model for grain yield and quality estimation. Remote Sens. 2015, 7, 12400–12418. [Google Scholar] [CrossRef]
- Cui, S.; Yang, S.; Zhu, C.; Wen, N. Remote sensing of surface reflective properties: Role of regularization and a priori knowledge. Optik 2014, 125, 7106–7112. [Google Scholar] [CrossRef]
- Liang, S.; Qin, J. Data Assimilation Methods for Land Surface Variable Estimation, in Advances in Land Remote Sensing: System, Modeling, Inversion and Application; Liang, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 319–339. [Google Scholar]
- Chen, P.; Jing, Q. A comparison of two adaptive multivariate analysis methods (PLSR and ANN) for winter wheat yield forecasting using Landsat-8 OLI images. Adv. Space Res. 2017, 59, 987–995. [Google Scholar] [CrossRef]
- Palosuo, T.; Kersebaum, K.C.; Angulo, C.; Hlavinka, P.; Moriondo, M.; Olesen, J.E.; Patil, R.H.; Ruget, F.; Rumbaur, C.; Takáč, J.; et al. Simulation of winter wheat yield and its variability in different climates of Europe: A comparison of eight crop growth models. Eur. J. Agron. 2011, 35, 103–114. [Google Scholar] [CrossRef]
- Nuttall, J.G.; O’Leary, G.J.; Panozzo, J.F.; Walker, C.K.; Barlow, K.M.; Fitzgerald, G.J. Models of grain quality in wheat-A review. Field Crop. Res. 2017, 202, 136–145. [Google Scholar] [CrossRef]
- Teh, C. Introduction to Mathematical Modeling of Crop Growth; Brown Walker Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Chan, K.P.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Carboni, J.; Gatelli, D.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons Ltd: West Sussex, UK, 2008. [Google Scholar]
- Jin, X.; Li, Z.; Nie, C.; Xu, X.; Feng, H.; Guo, W.; Wang, J. Parameter sensitivity analysis of the AquaCrop model based on extended Fourier amplitude sensitivity under different agro-meteorological conditions and application. Field Crop. Res. 2018, 226, 1–15. [Google Scholar] [CrossRef]
- Baret, F. Contribution au Suivi Radiométrique de Cultures de Céréales. Ph.D. Thesis, Université de Paris-Sud Orsay, Paris, France, 1986. [Google Scholar]
- Casa, R.; Varella, H.; Buis, S.; Guérif, M.; De Solan, B.; Baret, F. Forcing a wheat crop model with LAI data to access agronomic variables: Evaluation of the impact of model and LAI uncertainties and comparison with an empirical approach. Eur. J. Agron. 2012, 37, 1–10. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement of Retrogradation (Green Wave Effect) of Natural Vegetation; Type III, Final Report; NASA/GSFC: Greenbelt, MD, USA, 1974; pp. 1–371. [Google Scholar]
- Pearson, R.L.; Miller, L.D. Remote Mapping of Standing Crop Biomass for Estimation of the Productivity of the Short-Grass Prairie, Pawnee National Grasslands, Colorado; ERIM: Ann Arbor, MI, USA, 1972. [Google Scholar]
- Huete, A.; Justice, C.; Liu, H. Development of vegetation and soil indices for MODIS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.; Merzlyak, M. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Lu, L.; Fang, F. Estimating near future regional corn yields by integrating multi-source observations into a crop growth model. Eur. J. Agron. 2013, 49, 126–140. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Sedano, F.; Lewis, P.; Liang, S.; Wu, Q.; Su, W.; Zhang, X.; Zhu, D. Evaluation of regional estimates of winter wheat yield by assimilating three remotely sensed reflectance datasets into the coupled WOFOST-PROSAIL model. Eur. J. Agron. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Shi, L.; Lin, L.; Wang, S.; Chen, R. Image fusion based on data assimilation and differential evolution algorithm. Acta Photonica Sin. 2010, 39, 1688–1692, (in Chinese with English abstract). [Google Scholar]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Mercier, A.; Betbeder, J.; Rapinel, S.; Jegou, N.; Baudry, J.; Hubert-Moy, L. Evaluation of sentinel-1 and-2 time series for estimating LAI and biomass of wheat and rapeseed crop types. J. Appl. Remote Sens. 2020, 14, 024512. [Google Scholar] [CrossRef]
- Janusauskaite, D.; Feiziene, D.; Feiza, V. Relationship between spring triticale physiological traits and productivity changes as affected by different N rates. Acta Agric. Scand. Sect. B Soil Plant Sci. 2017, 67, 534–541. [Google Scholar] [CrossRef]
- Xing, H.; Li, Z.; Xu, X.; Feng, H.; Yang, G.; Chen, Z. Multi-assimilation methods based on AquaCrop model and remote sensing data. (Trans. Chin. Soc. Agric. Eng.) Trans. Csae. 2017; 33, 183–192, (in Chinese with English abstract). [Google Scholar]
- Pinnington, E.M.; Casella, E.; Dance, S.L.; Lawless, A.S.; Marison, J.I.L.; Nichols, N.K.; Wilkinson, M.; Quaife, T.L. Investigating the role of prior and observation error correlations in improving a model forecast of forest carbon balance using four-dimensional variational data assimilation. Agric. For. Meteorol 2016, 228–229, 299–314. [Google Scholar] [CrossRef]
- Wang, D.W.; Wang, J.D.; Liang, S.L. Retrieving crop leaf area index by assimilation of MODIS data into a crop growth model. Sci. China Earth Sci. 2010, 53, 721–730. [Google Scholar] [CrossRef]
- Marin, F.; Jones, J.W.; Boote, K.J. A stochastic method for crop models: Including uncertainty in a sugarcane model. Agron. J. 2017, 109, 483–495. [Google Scholar] [CrossRef]


| Parameter | Default | Range |
|---|---|---|
| Vernalization time parameter (P1V) | 5.00 | 0.0–60.00 |
| Photoperiod parameter (P1D) | 75.00 | 0.0–200.00 |
| Grain filling phase duration parameter (P5) | 450.00 | 100.00–999.00 |
| Kernel number parameter (G1) | 30.00 | 10.00–50.00 |
| Kernel size parameter (G2) | 35.00 | 10.00–80.00 |
| Tiller weight parameter (G3) | 1.00 | 0.50–8.00 |
| Phyllochron interval parameter (PHINT) | 60.00 | 30.00–150.00 |
| Photosynthetically active radiation conversion ratio parameter (PARUE) | 2.70 | 1.00–6.00 |
| Root depth growth rate (RDGS) | 3.00 | 1.00–5.00 |
| Duration of phase end juvenile to terminal spikelet parameter (P1) | 200.00 | 100.00–500.00 |
| Duration of phase terminal spikelet to end leaf growth parameter (P2) | 200.00 | 100.00–500.00 |
| Vernalization effect parameter (VEFF) | 0.60 | 0.00–1.00 |
| Vegetative phase parameter (LAFV) | 0.10 | 0.01–0.80 |
| Specific leaf area parameter (SLAS) | 400.00 | 100.00–600.00 |
| Parameter | Default | Ranges |
|---|---|---|
| Planting date | 17 October | 4–28 October # |
| Plant population at emergence (10,000 ha−1) | 450.00 | 300.00–450.00 # |
| Row spacing (cm) | 20.00 | 15.00–20.00 # |
| Plant depth (cm) | 3.00 | 3.00–6.00 # |
| First irrigation time | 21 November | 20 November–10 December # |
| First irrigation amount (mm) | 150.00 | 80.00–150.00 # |
| Second irrigation time | 23 March | 15–31 March # |
| Second irrigation amount (mm) | 100.00 | 80.00–150.00 # |
| Third irrigation time | 19 April | 17 April–10 May # |
| Third irrigation amount (mm) | 100.00 | 80.00–150.00 # |
| First fertilization time (conventionally the same as first irrigation time) | 17 October | 4–28 October # |
| First applied N amount (kg N ha−1) | 105.00 | 140.00–200.00 # |
| Fertilizer type for first fertilization | Urea | – |
| Second fertilization time (conventionally the same as third irrigation time) | 19 April | 17 April–10 May |
| Second applied N amount (kg N ha−1) | 105.00 | 140.00–200.00 # |
| Fertilizer type for second fertilization | Urea | – |
| Soil nitrate (g N Mg−1) | 21.60 | 10–30 $ |
| Root weight (kg ha−1) | 1,658.00 | 800.00–1,800.00 $ |
| Water table depth (cm) | 190.00 * | – |
| Albedo | 0.11 * | – |
| Evaporation limit (mm) | 6.00 * | – |
| Drainage rate (% day−1) | 0.10 * | – |
| Runoff curve number | 80.00 * | – |
| Mineralization factor | 1.00 * | – |
| Photosynthesis factor | 1.00 * | – |
| Soil lower limit (cm3 cm−3) | 0.10 * | – |
| Soil upper limit (cm3 cm−3) | 0.30 * | – |
| Soil upper limit (cm3 cm−3) | 0.45 * | – |
| Bulk density (g cm−3) | 1.54 * | – |
| Soil clay content (%) | 3.00 * | – |
| Soil silt content (%) | 90.00 * | – |
| Root growth factor | 1.00 * | – |
| Soil organic carbon (%) | 1.00 | 0.30–2.60 $ |
| Soil total N (%) | 0.09 | 0.05–0.15 $ |
| Soil pH in water | 8.20 * | – |
| Cation exchange capacity (mol kg−1) | 10.00 * | – |
| Index | Full Name | Formula | Developed by |
|---|---|---|---|
| NDVI | Normalized difference vegetation index | (R800 − R670) / (R800 + R670) | Rouse et al. [36] |
| RVI | Ratio vegetation index | R800 / R670 | Pearson et al. [37] |
| EVI | Enhanced vegetation index | 2.5(R800 − R670) / R800 + 6R670 − 7.5R470 + 1) | Huete et al. [38] |
| TVI | Triangular vegetation index | 0.5(120(R750 − R550) − 200(R670 − R550)) | Broge and Leblanc [39] |
| MSAVI | Modified soil-adjusted vegetation index | (2R800 + 1 − sqrt((2R800 + 1)2 − 8(R800 − R670))) / 2 | Qi et al. [40] |
| OSAVI | Optimization of soil-adjusted vegetation index | 1.16(R800 − R670) / (R800 + R670 + 0.16) | Rondeaux et al. [41] |
| GNDVI | Green normalized difference vegetation index | (R800 − R550) / (R800 + R550) | Gitelson et al. [42] |
| MTVI2 | Modified triangular vegetation index 2 | 1.5(1.2(R800 − R550) − 2.5(R670 − R550)) / sqrt((2R800 + 1)2 − (6R800 − 5sqrt(R670)) − 0.5) | Haboudane et al. [43] |
| Spectral Index | LAI | LNC | ||
|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE (kg ha−1) | |
| EVI | 0.63 | 1.44 | 0.76 | 26.26 |
| NDVI | 0.40 | 1.73 | 0.44 | 39.98 |
| RVI | 0.37 | 1.67 | 0.41 | 42.54 |
| TVI | 0.67 | 1.21 | 0.77 | 28.06 |
| MSAVI | 0.61 | 1.32 | 0.68 | 32.67 |
| OSAVI | 0.64 | 1.22 | 0.73 | 25.68 |
| GNDVI | 0.29 | 1.86 | 0.29 | 44.35 |
| MTVI2 | 0.60 | 1.33 | 0.69 | 32.42 |
| State Variable Scenario | Cost Function Solving Algorithm Scenario | R2 | RMSE (%) |
|---|---|---|---|
| LAI | DE | 0.14 | 1.20 |
| SCE-UA | 0.18** | 1.08 | |
| SA | 0.07 | 1.27 | |
| Leaf N content | DE | 0.11 | 1.44 |
| SCE-UA | 0.21** | 1.29 | |
| SA | 0.05 | 1.29 | |
| LAI and leaf N content | DE | 0.26 ** | 1.25 |
| SCE-UA | 0.39 ** | 0.91 | |
| SA | 0.09 | 1.11 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P. Estimation of Winter Wheat Grain Protein Content Based on Multisource Data Assimilation. Remote Sens. 2020, 12, 3201. https://doi.org/10.3390/rs12193201
Chen P. Estimation of Winter Wheat Grain Protein Content Based on Multisource Data Assimilation. Remote Sensing. 2020; 12(19):3201. https://doi.org/10.3390/rs12193201
Chicago/Turabian StyleChen, Pengfei. 2020. "Estimation of Winter Wheat Grain Protein Content Based on Multisource Data Assimilation" Remote Sensing 12, no. 19: 3201. https://doi.org/10.3390/rs12193201
APA StyleChen, P. (2020). Estimation of Winter Wheat Grain Protein Content Based on Multisource Data Assimilation. Remote Sensing, 12(19), 3201. https://doi.org/10.3390/rs12193201





