Abstract
Image segmentation is a cost-effective way to obtain information about the sizes and structural composition of agricultural parcels in an area. To accurately obtain such information, the parameters of the segmentation algorithm ought to be optimized using supervised or unsupervised methods. The difficulty in obtaining reference data makes unsupervised methods indispensable. In this study, we evaluated an existing unsupervised evaluation metric that minimizes a global score (GS), which is computed by summing up the intra-segment uniformity and inter-segment dissimilarity within a segmentation output. We modified this metric and proposed a new metric that uses absolute difference to compute the GS. We compared this proposed metric with the existing metric in two optimization approaches based on the Multiresolution Segmentation (MRS) algorithm to optimally delineate agricultural parcels from Sentinel-2 images in Lower Saxony, Germany. The first approach searches for optimal scale while keeping shape and compactness constant, while the second approach uses Bayesian optimization to optimize the three main parameters of the MRS algorithm. Based on a reference data of agricultural parcels, the optimal segmentation result of each optimization approach was evaluated by calculating the quality rate, over-segmentation, and under-segmentation. For both approaches, our proposed metric outperformed the existing metric in different agricultural landscapes. The proposed metric identified optimal segmentations that were less under-segmented compared to the existing metric. A comparison of the optimal segmentation results obtained in this study to existing benchmark results generated via supervised optimization showed that the unsupervised Bayesian optimization approach based on our proposed metric can potentially be used as an alternative to supervised optimization, particularly in geographic regions where reference data is unavailable or an automated evaluation system is sought.
1. Introduction
Agriculture is the single largest land use (LU) covering the Earth’s land surface [1]. The increasing global population and the accompanying increase in food consumption are placing unparalleled demands on agricultural lands [2]. Some of the negative impacts of these demands include the loss of biodiversity [1], the degradation and destruction of natural ecosystems [3], and an increase in greenhouse gas (GHG) emission [4]. Ensuring food security while minimizing the negative impact of agriculture on the environment requires the use of sustainable agricultural practices [2,5]. Formulating agricultural and environmental policies that ensure sustainable agriculture requires the development of an agricultural monitoring system. The foundation of such a system is accurate and up-to-date agricultural LU maps [6,7]. Agricultural LU maps are essential input data for various processes such as the estimation of biomass and yield [7], monitoring of the phenology of different agricultural LU types [7], modeling of GHG variability [8], estimation of the area of agricultural lands [9], and control of area-based subsidies paid to farmers [9].
The generation and continuous update of agricultural LU maps using traditional methods such as field surveys are inefficient and expensive [8]. Remote Sensing (RS) provides a better alternative due to the frequency at which data can be acquired over large geographical areas [10,11]. The availability of high-resolution satellite images has increased the popularity of Object-Based Image Analysis (OBIA) over traditional pixel-based image analysis [12]. Unlike pixels, which carry only spectral information, image objects additionally carry contextual and spatial information [12], thereby making them more useful for subsequent processes such as classification. The advantages of OBIA over pixel analysis for generating agricultural LU maps have been reported by these authors [10,13,14].
Image segmentation, which is the process of clustering image pixels into homogeneous objects, is a critical step in OBIA [15]. Various authors [16,17,18,19,20] have proved that the quality of segmentation has a direct impact on classification accuracy. One of the most popular segmentation algorithms is the Multiresolution Segmentation (MRS) algorithm proposed by Baatz et al. [21]. MRS is a bottom–up region merging algorithm that starts with one-pixel objects and then in a pairwise manner merges smaller objects into bigger ones until a user-given scale threshold is met [22]. In a recent review article by Ma et al. [23], the MRS algorithm as implemented in the eCognition software [24] accounted for 80.9% of 254 case studies the authors reviewed. This overwhelming popularity hinges on the fact that some exhaustive evaluation studies [25,26,27] have had eCognition coming up tops. In eCognition, the three main parameters that influence the quality of the MRS segmentation are scale, shape, and compactness. To obtain optimal segmentation results, it is imperative to optimize these parameters.
To optimize any segmentation algorithm, the quality of the segmentation output of that algorithm for different parameter combinations ought to be evaluated. This can be done through visual inspection, supervised segmentation evaluation, or unsupervised segmentation evaluation [28,29]. Visual inspection is subjective and inherently limits the number of segmentation evaluations that can be done due to its laborious nature [29]. The supervised evaluation methods assess a segmentation result by comparing it to a reference data and computing a global score (GS) that represents the degree of similarity between the segmentation result and the reference data [29]. The main limitation of supervised segmentation evaluation is that the acquisition of reference data is expensive and time-consuming [29]. This makes unsupervised segmentation evaluation indispensable, as it does not rely on reference data but purely on the content of an image to evaluate the segmentation result [29]. For the unsupervised evaluation methods, the GS is a statistical measure that indicates the level of intra-region uniformity and/or inter-region dissimilarity within the segmentation result [30]. In RS, two of the most used methods are the estimation of scale parameter (ESP) [31,32] tool and the objective function [33]. The ESP tool only addresses the intra-region uniformity of segments by making use of local variance graphs [34]. The objective function of Espindola et al. [33] is a combined measure that addresses intra-region uniformity through average area-weighted variance (WV) and inter-region dissimilarity through spatial autocorrelation using the global Moran’s I (MI) [35]. A comparative analysis by Grybas et al. [36] showed that the objective function outperformed the ESP tool. Various variations [19,37,38,39,40,41,42] of the objective function have been used in the literature.
To compute the GS for each input image band, Espindola et al. [33] separately normalized the WV and MI between zero and one before summing them up. Böck et al. [43] identified a weakness with this normalization step, pointing out that the selection of which segmentation is optimal was dependent on the user-defined scale parameter range. They subsequently proposed the use of fixed ranges to normalize the WV and MI. This produced stable results regardless of the input range of the scale parameter. In the remainder of the paper, we call this modification of Böck et al. [43] the Böck metric. Georganos et al. [16] identified some limitations with the normalization approach of the Böck metric, which triggered them to propose a different approach. The problem with their approach is that it adds some level of subjectivity to the evaluation process, because it requires some initial empirical tests. This makes their proposal unusable within our context of having a metric that can be used for automated segmentation evaluation without any human intervention.
In this study, we aimed at proposing a new unsupervised evaluation metric for assessing the segmentation output of any segmentation algorithm. To do so, we modified the Böck metric and proposed absolute difference (AD) as a means of computing the GS. We compared the Böck and AD metrics by separately using each of them in two unsupervised optimization approaches to optimize the parameters of the MRS algorithm to delineate agricultural parcels from 21 Sentinel-2 images of 10 × 10 km sizes in Lower Saxony, Germany. In the first optimization approach, as is mostly done in the literature [20,31,37,38,39,43,44,45], we optimized scale while keeping the shape and compactness parameters constant at their default values. In the second optimization approach, we employed Bayesian optimization to optimize all three MRS parameters. The optimal segmentation results identified by each metric were evaluated with parcels from the Land Parcel Identification System (LPIS), which is a spatial database of agricultural parcels and their land-use types as declared by farmers within the European Union (EU) [46,47]. The optimal segmentation results of the Böck and AD metrics were compared to each other per each optimization approach. Further, we compared the optimal segmentation results of the unsupervised Bayesian optimization approaches based on the Böck and AD metrics to the benchmark segmentation results of Tetteh et al. [47], where they used supervised Bayesian optimization.
2. Study Area and Data
In this study, we used cloud-free Sentinel-2 images downloaded from the Copernicus Open Access Hub (https://scihub.copernicus.eu) covering the German federal state of Lower Saxony. The images were pre-processed in the previous study of Tetteh et al. [47] using the standard procedure of converting the top-of-atmosphere Level-1C images to the bottom-of-atmosphere Level-2A images with Sen2Cor [48] in the Sentinel Application Platform (SNAP) software. For each Level-2A image, the visible (red, green, blue) and near-infrared bands were extracted and composed into an image made up of four bands. This image is henceforth named VNIR. Each VNIR image has a spatial resolution of 10 m. To identify the optimal MRS parameters needed for segmenting agricultural parcels for every part of Lower Saxony, Tetteh et al. [47] clipped the VNIR images with 10 × 10 km tile grids numbering 562 and additionally masked out all non-agricultural areas such as forests, built-up areas, water bodies, and roads. Out of these 562 images, we selected 21 tiles that spread across Lower Saxony as our study sites (Figure 1). These 21 tiles have diverse agricultural landscapes. The approach we used to select the 21 tiles can be found in the methodology section. Additional pieces of information such as the image acquisition date, percentage coverage of agricultural lands, and other descriptive statistics of the reference agricultural parcels in the LPIS per tile can be found in Appendix A (Table A1). The variation in the sizes of agricultural parcels per tile can also be found in Appendix A (Figure A1).
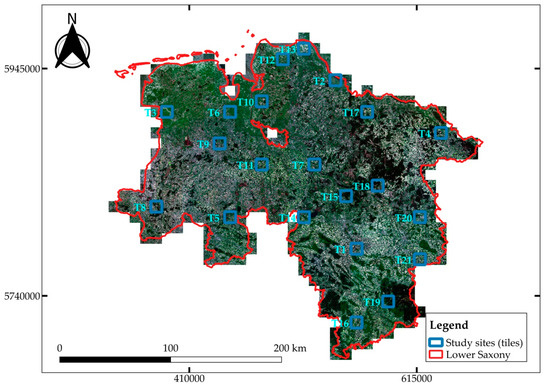
Figure 1.
The study sites (tiles) overlaid on a mosaic of cloud-free and non-masked Sentinel-2 images captured in May 2018. The coordinates are in UTM Zone 32N (EPSG:32632).
3. Methodology
The simplified workflow we used to obtain the results is outlined in Figure 2. The core components of our workflow consist of image segmentation, modification of the existing unsupervised segmentation evaluation metric, unsupervised optimization of segmentation, and empirical evaluation of the segmentation results with reference parcels in the LPIS. These components will be fully covered in the proceeding subsections.

Figure 2.
The simplified workflow we used in this study. Böck refers to the unsupervised segmentation evaluation metric proposed by Böck et al. [43], and absolute difference (AD) is the modified version we proposed in this study.
3.1. Selection of the 21 Tiles
The goal here is to reduce the number of tiles from 562 to a number that will lead to a reduction in the computational time needed for segmentation optimization. The 21 tiles were selected in a way that they were representative of the structural composition of the other tiles that were not used for further processing. The methodology we used to identify these 21 tiles is explained in this section.
For each reference parcel in the LPIS of the 562 tiles, we extracted the minimum bounding rectangle (MBR). The width and length of each MBR were calculated. Aspect was computed by dividing the width by the length. Then, we clustered the 562 tiles based on the average aspect per tile using the k-means method. The determination of the appropriate number of clusters was done using the silhouette analysis [49]. This analysis is used to measure the internal consistency of clusters and the separability of those clusters. To perform the analysis, we clustered the average aspect of the 562 tiles using an incremental approach in which the number of clusters was initiated with two and increased by one in subsequent steps up to 21. For each cluster number, a silhouette coefficient was computed. The silhouette coefficients range from −1 to 1, with high values being more desirable, as it indicates the consistency within clusters and good separability among them. In our case, at cluster number 16, the silhouette coefficient was the highest (0.543), so we kept that. Then, we manually selected a tile from each of the 16 clusters and additionally included five more tiles to ensure a better spatial distribution over Lower Saxony, Germany.
3.2. Image Segmentation
In this study, image segmentation was done based on the implementation of the Multiresolution Segmentation (MRS) algorithm in eCognition Developer 9.5.0 [24]. Starting with one-pixel objects as seed points, in numerous subsequent steps, where the difference in heterogeneity between an object and any of its neighbors is minimal, the two objects are merged into a bigger one [22]. The heterogeneity of an object is calculated using the color and shape of that object [22,47]. The pairwise merging process is terminated when a user-given threshold is met [22]. In eCognition, three parameters (scale, shape, and compactness) influence the segmentation results of the MRS algorithm. Scale defines the minimum size of an object and is used as the threshold criterion to terminate the merging process. Shape refers to the weight placed on an object’s form against its color information during the clustering process [47]. Shape and color add up to 1. In eCognition, one can only pass the shape weight, which then inversely modifies the color weight. Color is a requirement; hence, shape ranges from 0 to 0.9 [47]. Compactness defines the weight of an objects’ squareness against its smoothness during the clustering process [47]. The compactness and smoothness weights also add up to 1. In eCognition, one passes the compactness weight, which inversely changes the smoothness weight. Extensive details about the MRS algorithm can be found in these pieces of literature [21,22,24]. Generating optimal segments requires the optimization of the MRS parameters [47].
3.3. Segmentation Optimization
To optimize any segmentation algorithm, one needs to be able to assess the quality of the segmentation results churned out by the algorithm for different parameter combinations. In this study, we used unsupervised segmentation evaluation metrics that measure the quality of the segmentation results purely based on the spectral values of the underlying image.
3.3.1. Existing Unsupervised Segmentation Evaluation Metrics
To evaluate a segmentation result, Espindola et al. [33] used average area-weighted variance (WV) and Moran’s I (MI) [35]. The WV measures intra-segment homogeneity [33]. Therefore, it shows the level of under-segmentation in a segmentation result. Lower WV values indicate lower under-segmentation [38]. It is derived by first calculating the variance of pixels within each segment per image band, weighting the variance by each segment’s area, and then averaging over all segments to obtain one global value per band. Equation (1) shows the formulation of WV, where represents the area of a segment, is the variance of pixels within a segment, and n is the number of segments.
MI measures the inter-segment heterogeneity [33] within the segmentation result, thereby being indicative of the level of over-segmentation. Lower MI values indicate lower over-segmentation [38]. Similar to the WV, it is also computed per image band. Its formulation is shown by Equation (2), where n is the number of segments, and are the respective mean values of an image band for segments i and j, is the mean band value of the entire image, and is a weight matrix that measures the spatial contiguity [43] between a segment and its neighbors. The elements of the matrix are either zero or one. One indicates that segments i and j have a common boundary, and zero indicates they do not.
MI ranges from −1 (perfect dispersion of segments) to 1 (perfect clustering of segments). Lower MI values indicate that the mean spectral values of neighboring segments within a segmentation layer are more different from each other, thereby indicating lower over-segmentation. Higher MI values show that the mean spectral values of the neighboring segments are more similar, which means that there is more over-segmentation present in the segmentation layer.
To compute a single global score (GS) per image band for a segmentation result, the WV and MI values are individually normalized using Equation (3) [37], where is either the WV or MI. Then, the normalized WV (nWV) and normalized MI (nMI) are summed up to obtain the GS per image band [33]. Then, the final GS for the segmentation result is computed with Equation (4), where represents the number of bands in the image, which is four in our case.
The GS ranges from zero (best quality) to one (worst quality). Given a set of segmentation results generated with different segmentation parameters, the parameter combination that results in the lowest GS is deemed as optimal. Böck et al. [43] observed that the identification of the optimal GS based on the definition of Espindola et al. [33] is highly influenced by the range of the user-defined scale parameter. Different scale parameter ranges yield different optimal segmentation results for the same image. According to Böck et al. [43], this instability is due to the normalization process in Equation (3). To deal with this problem, Böck et al. [43] proposed fixed range normalization for WV and MI as respectively captured by Equation (5) and Equation (6) before computing the final GS, where is the variance of the entire image per band. To obtain Equation (6), Böck et al. [43] respectively replaced and in Equation (3) with −1 and 1, which are the theoretical extrema of MI.
The Böck metric also ranges from zero (best quality) to one (worst quality).
3.3.2. Metric Proposal Based on Absolute Difference (AD)
According to Georganos et al. [16], the fixed ranged normalization proposal put forward by Böck et al. [43] makes two problematic assumptions. The first one is that where there is complete under-segmentation, i.e., where one segment is created for the entire image, the WV becomes equal to the image variance; hence, nWV becomes 1. When this happens, the equivalent value of MI and by extension nMI becomes undefined, because a spatial network of more than one segment is required to compute MI. Secondly, in the case of complete over-segmentation, i.e., where each pixel in the image is a segment, MI is −1 and nMI becomes 0, but the corresponding value of WV may be very low and not necessarily zero. In RS, it is highly implausible to obtain complete over-segmentation; hence, an MI value of −1 is hardly realized [16]. Furthermore, Georganos et al. [16] did some tests and observed that the Böck metric has the potential of selecting under-segmented objects as optimal. We tested this hypothesis using some simulated segmentation data captured by Figure 3. Figure 3a shows the reference data, while Figure 3b–d captures three different corresponding segmentation results. For each dataset in Figure 3, each row represents a segment; hence, there are four segments for each dataset. Figure 3b captures a situation where there is a lot of clustering with minimal under-segmentation, Figure 3c is a situation where there is a balance between clustering and dispersion with moderate under-segmentation, and Figure 3d represents a situation where there is a lot of dispersion with a high level of under-segmentation. The MI, nMI, nWV, and GS of the Böck metric computed for the simulated segmentation results (Figure 3b–d) are captured by Table 1. As postulated by Georganos et al. [16], the Böck metric selected the segmentation result with the highest level of under-segmentation as optimal, given that it had the lowest GS value.
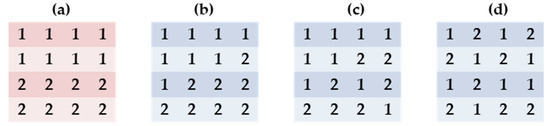
Figure 3.
Simulated reference and segmentation data. The reference dataset is represented by (a). Three different corresponding segmentation results are represented by (b–d), respectively. Each row in each dataset represents a segment; hence, there are four segments in all.

Table 1.
The Moran’s I (MI), normalized MI (nMI), normalized weighted variance (nWV), and global score (GS) of the Böck metric computed for the simulated data at Figure 3. The bold-faced text within the body of the table is the optimal result.
The issues raised by Georganos et al. [16] point to the problem posed by Equation (6), where the theoretical extrema of MI are used to normalize the MI. As visible in Table 1, after normalizing the MI, the numerical difference between the nWV and MI increased in Figure 3b, where the MI was positive. However, for Figure 3c,d, the numerical differences diminished substantially. Therefore, in areas with more dispersion, the Böck metric has the potential of selecting under-segmented results as optimal, as it would be more biased toward nMI [16]. To overcome these issues, we used two steps. First, we did not normalize the MI given that by definition, it lies between −1 and 1. We maintained the nWV. Therefore, the minimum and maximum values of nWV will correspond to the minimum and maximum of MI. Second, to obtain the final GS, we computed the absolute difference between the MI and nWV per band and then averaged over all bands as shown by Equation (7), where the notations have the same meaning as Equation (4). This ensures that the MI and nWV have a fair chance of influencing the GS depending on their respective magnitudes. Similar to the Böck metric, low values mean good quality, and high values mean bad quality. The outcome of this modification, named the AD metric, for the simulated segmentation results (Figure 3b–d) is shown in Table 2. The AD metric correctly selected the least under-segmented result as optimal, followed by the moderately under-segmented. We tested another distance metric, specifically Euclidean Distance (ED), to combine the MI and nWV values at the 21 tiles, but the AD metric proved superior, so we maintained that as our proposal. The difficulty with using ED to compute the GS lies in the fact that given any two numbers, here MI and nWV, it places more emphasis on the larger number than the smaller one, thereby accentuating the influence of the larger number on the overall outcome.

Table 2.
The MI, nWV, and GS of the AD metric computed for the simulated data in Figure 3. The bold-faced text within the body of the table is the optimal result.
3.3.3. Unsupervised Segmentation Optimization
The point of optimization within the context of this study is to identify the MRS parameter combination that yields the lowest GS per metric. The segmentation output corresponding to this combination is the optimal result. We tested two optimization approaches in this study.
For the first approach, which we termed default optimization, we optimized the scale parameter while keeping the shape and compactness parameters constant at their default, as is mostly done in the literature [20,31,37,38,39,43,44,45]. Shape was kept at 0.1, and compactness was kept at 0.5. The scale ranged from 10 to 300 with intervals of 10. The segmentation output corresponding to the scale parameter with the lowest GS is the optimal output.
The second optimization approach is Bayesian optimization, which was used to optimize all three MRS parameters. We adopted the Bayesian optimization approach of Tetteh et al. [47] but used it within an unsupervised optimization framework. Applying Bayesian optimization requires four main definitions:
- The domain space (minimum and maximum values) of each input parameter. The domain space of scale was defined as 20 and 200, for shape 0.0 and 0.9, and for compactness 0.0 and 1.0. These parameter ranges were also used by Tetteh et al. [47] in their approach.
- An objective function to optimize. For our study, the objective function to optimize is f(x), where x is a parameter combination of scale, shape, and compactness. The function takes the parameter combination, performs image segmentation, computes the GS of the segmentation output, and finally returns the GS.
- A surrogate model for the objective function. To build the surrogate model, one has to first define a prior probability distribution that captures the prior behavior of the objective function. We chose Gaussian Processes (GP) [50] as the prior probability distribution. Then, some initial parameter combinations together with their corresponding GS are used to initialize the whole optimization process. We used 125 parameter combinations as initialization samples. These 125 parameter combinations were selected in a way to ensure uniform and representative distribution over each parameter space. For scale, the values were (40, 80, 120, 160, 200), and for both shape and compactness, the values were (0.1, 0.3, 0.5, 0.7, 0.9). The grid search method was used to calculate the corresponding GS for the 125 samples. These samples were used to update the GP to obtain posterior probability distribution over the objective function.
- An acquisition function to be used in sampling new parameter combinations to be evaluated with the objective function. For the acquisition function, we used expected improvement (EI) [51]. EI is used to iteratively select new parameter combinations with the highest probability of optimizing the objection function. We sampled 50 new parameter combinations with the EI function in 50 iterations. At each iteration, out of 10,000 parameter combinations randomly sampled from the domain space, the combination with the highest likelihood of improving upon the current optimal parameter combination is identified by the EI function using the current posterior probability distribution. Then, this identified parameter combination is evaluated with the objective function, and the corresponding GS is used to update the current posterior probability distribution. In all, 175 combinations were used within the Bayesian optimization approach to identify the optimal one.
A more detailed explanation of Bayesian optimization can be found here [52,53,54,55]. The Böck and AD metrics were separately used in the two optimization approaches to optimize the segmentation of agricultural parcels. The optimal segmentation identified by each metric was further evaluated through empirical discrepancy measures. Given the sheer number of segmentations that had to be done, we used eCognition Server 9.5.0 and the eCognition command-line interface (CLI) to automate the segmentation process [47]. For the initial 125 parameter combinations that were used to initialize the Bayesian optimization method, two parallel processes were executed, as our eCognition Server license was limited to two [47]. The Python programming language was used to glue everything together. The implementation of Bayesian optimization via Scikit-optimize in Python was used [47].
3.4. Empirical Discrepancy Measures
To identify which optimization approach and metric performed better per tile, we computed four empirical discrepancy measures (Table 3) by comparing the optimal segmentation results to the reference agricultural parcels in the LPIS. The quality rate (QR) [56] measures the level of geometric match between the segmentation result and the reference parcels. It is the only measure that takes into account both the amount of agreement and disagreement between the reference parcels and their corresponding segments [57]. Therefore, it can single-handedly be used to judge the quality of segmentation. When a reference parcel is larger than its corresponding segment, over-segmentation (OR) [57] occurs, and when the segment is larger, under-segmentation (UR) [57] occurs. The root mean square (RMS) [56] combines the OR and UR into a single measure. In the formulas in Table 3, is a reference parcel and is its corresponding segment, and n is the total number of segments. The discrepancy measures are first computed per segment in a segmentation result. To obtain a single discrepancy measure for an entire segmentation result, an area-weighted average was used (Table 3).

Table 3.
Empirical discrepancy measures used to evaluate the optimal segmentations.
4. Results
4.1. Optimal Segmentation Based on Default Optimization
For each tile, Figure 4 shows the QR for the optimal segmentations identified by the AD and Böck metrics using the default shape value of 0.1 and 0.5 for compactness. The other empirical evaluation measures (OR, UR, and RMS) are captured by Appendix A (Table A2). At T11, the two metrics obtained the same result. Except for T3 and T18, where the Böck metric was marginally better, the AD metric was remarkably better at the other tiles. The highest difference between the two metrics was recorded at T1, where the AD metric exceeded the Böck metric by 17%. The lowest differences were recorded at T2 and T19, where the AD metric was about 1% better. The optimal segmentation results identified by our metric were the least under-segmented except for T2 and T19, where our metric was rather the least over-segmented. The RMS values of our metric were lower at all tiles except T19.
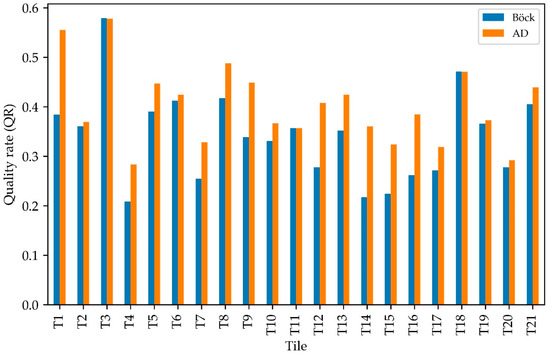
Figure 4.
The quality rate (QR) measure computed for each optimal segmentation result identified by the AD and Böck metrics based on the default optimization (shape = 0.1, compactness = 0.5).
The Böck metric often selected higher scale values than the AD metric, even to the extent that at T1, it chose the highest scale value as the optimal. This led to massive under-segmentation, an example of which is shown in Figure 5a at T1. Four different LU types—namely, winter wheat, winter rapeseed, spring barley, and pastures—are present in this area. Due to the high scale value selected by the Böck metric, only one segment was created containing all the aforementioned LU types, leading to massive under-segmentation. The AD metric did a better job of separating the different LU types, hence reducing under-segmentation (Figure 5b). The segments generated based on the AD metric had a better geometric match to the LPIS reference parcels.
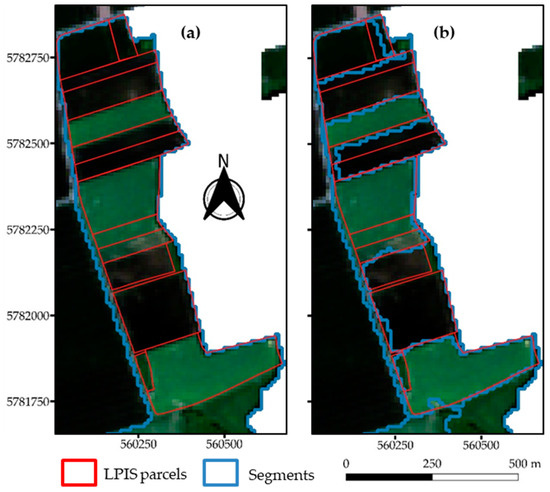
Figure 5.
Examples of segments identified as optimal at T1 using the default shape and compactness parameters. (a) An example based on the optimal segmentation identified by the Böck metric showing massive under-segmentation and (b) based on the AD metric, which shows a better delineation of the agricultural parcels with lower under-segmentation compared to Böck. The coordinates are in UTM Zone 32N (EPSG:32632).
To understand the different behaviors of the Böck and AD metrics, we explored the nWV, MI, nMI, and the corresponding GS computed for each scale value at T1, where the AD metric was substantially better, and then T3, where the Böck metric was marginally better. For both metrics, the nWV increased with increasing scale as the pixels in each segment became more varied, while the MI and nMI exhibited an opposite behavior (Figure 6 and Figure 7). Figure 6a shows that as the scale increased, the Böck metric decreased in response until it reached its minimum at scale 300. As a reminder, lower GS values of a metric correspond to more accurate segmentation results. Our metric, on the other hand, as captured by Figure 6b, exhibited a decreasing trend up to scale 190 and then started to increase in response to increasing nWV and decreasing MI. The GS was at its lowest at scale 190. At T3 (Figure 7), where the Böck metric was marginally better, the GS of both metrics had one commonality. After some initial decreasing behavior, they both started to continuously increase around the median of the scale range, which is 155. The optimal scale selected by the Böck metric was 150, and that of the AD metric was 140.
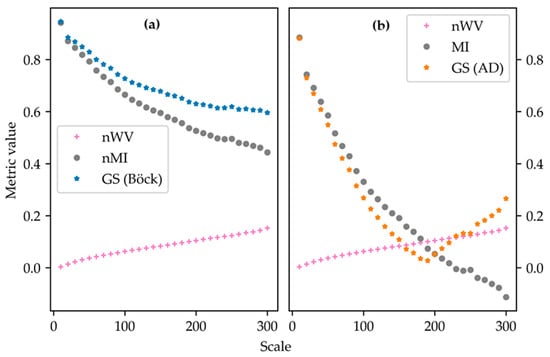
Figure 6.
The normalized average area-weighted variance (nWV), Moran’s I (MI), normalized Moran’s I (nMI), and global score (GS) computed for each scale at T1 based on (a) the Böck metric and (b) the AD metric.
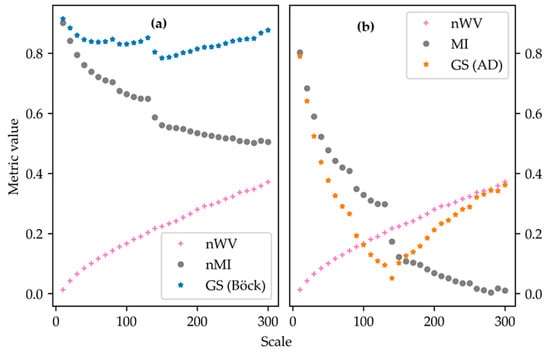
Figure 7.
The normalized average area-weighted variance (nWV), Moran’s I (MI), normalized Moran’s I (nMI), and global score (GS) computed for each scale at T3 based on (a) the Böck metric and (b) the AD metric.
4.2. Optimal Segmentation Based on Bayesian Optimization
We employed Bayesian optimization to respectively minimize the two unsupervised metrics (Böck and AD) at the 21 tiles to optimize the MRS parameters. To identify the optimal MRS parameters, Tetteh et al. [47] used their supervised Bayesian optimization approach to directly maximize the QR. We consider the results achieved by their approach as the benchmark results. For the analysis here, we compared the results achieved by the two unsupervised Bayesian optimization approaches to each other and in parallel compared both to the benchmark results. The QR measures of the optimal segmentations obtained by the supervised and the two unsupervised approaches for the 21 tiles used in this research are captured by Figure 8. The other empirical evaluation measures can be found in Appendix A (Table A3). The unsupervised Bayesian optimization approach based on the AD metric outperformed the Böck metric at all tiles. The approach based on the AD metric was over 22% better at T1 and T15, and it was about 1% better at T6 in comparison with the unsupervised Bayesian approach based on the Böck metric. The supervised approach was expectedly better than both unsupervised approaches at all tiles. At T7 and T17, the segmentation quality of the supervised approach was over 20% higher than the unsupervised AD approach. However, at T2 and T19, the supervised approach was just about 2% better. Regarding the Böck metric, the supervised approach was over 30% better at T1, T14, and T15, and it was about 5% better at T2. The segmentation results of the unsupervised approaches were generally more under-segmented but less over-segmented compared to the supervised approach. The RMS measure was in favor of the supervised approach at all tiles. The optimal segmentation results of the three Bayesian optimization approaches symbolized by the QR calculated per segment at T1, T2, and T17 are captured by Figure 9, Figure 10 and Figure 11, respectively. For all three figures, panel (a) captures the Sentinel-2 image, panel (b) shows the Böck results, panel (c) shows the supervised Bayesian optimization results, and panel (d) captures the AD results. Figure 12 shows a specific case of segments within the optimal results of the three Bayesian optimization approaches at T1 for the same area shown in Figure 5.
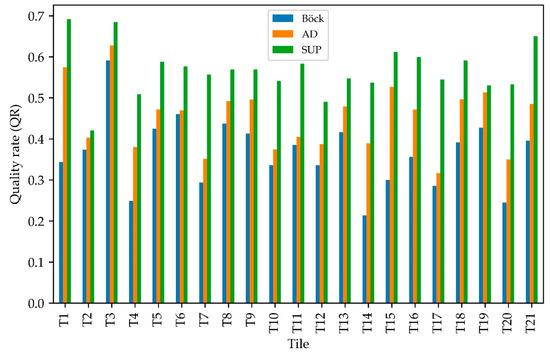
Figure 8.
The quality rate (QR) measure computed for the unsupervised Bayesian optimization approaches based on the Böck and AD metrics, and the supervised Bayesian optimization (SUP) approach that was used to maximize the QR measure by Tetteh et al. [47].
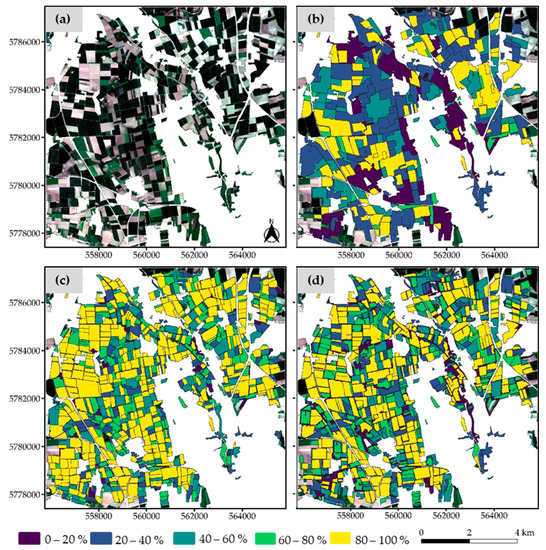
Figure 9.
The outcome of the three Bayesian optimization approaches at T1. The Sentinel-2 image is shown by (a). The optimal segments as identified by (b) the Böck metric, (c) the supervised Bayesian optimization approach, and (d) the AD metric are symbolized by their respective QR measures. The coordinates are in UTM Zone 32N (EPSG:32632).
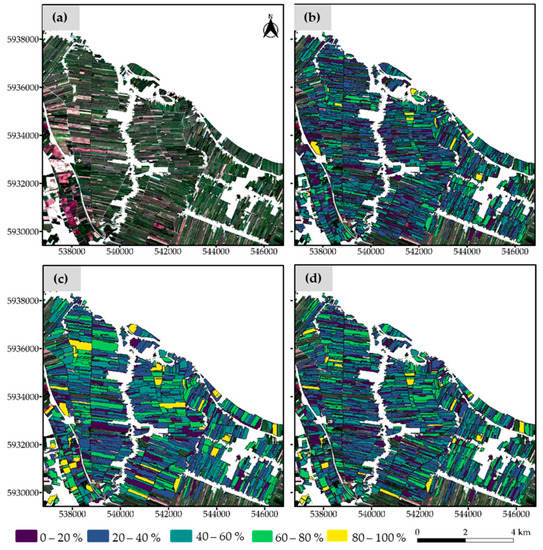
Figure 10.
The outcome of the three Bayesian optimization approaches at T2. The Sentinel-2 image is shown by (a). The optimal segments as identified by (b) the Böck metric, (c) the supervised Bayesian optimization approach, and (d) the AD metric are symbolized by their respective QR measures. The coordinates are in UTM Zone 32N (EPSG:32632).
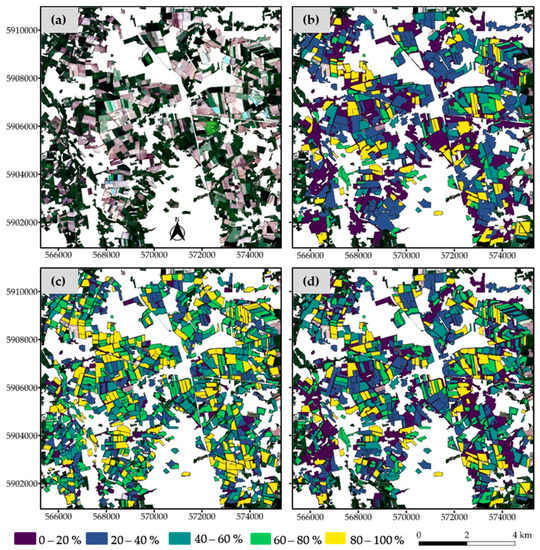
Figure 11.
The outcome of the three Bayesian optimization approaches at T17. The Sentinel-2 image is shown by (a). The optimal segments as identified by (b) the Böck metric, (c) the supervised Bayesian optimization approach, and (d) the AD metric are symbolized by their respective QR measures. The coordinates are in UTM Zone 32N (EPSG:32632).
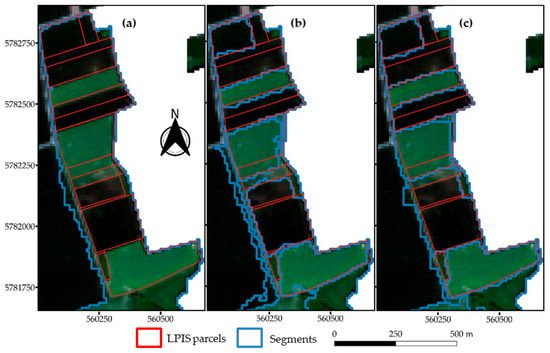
Figure 12.
An example of segments created at T1 using the unsupervised Bayesian optimization approach based on (a) the Böck metric and (b) the AD metric. (c) Segments generated by the supervised Bayesian optimization approach (SUP) based on the QR metric. The coordinates are in UTM Zone 32N (EPSG:32632).
To understand the reason behind the differences in QR between the supervised optimization approach and the unsupervised Bayesian optimization approaches, we analyzed the linear relationship (Figure 13) between the differences in QR and the number of land-use types present at each tile. For each metric, the Pearson correlation coefficient (r) was high, and the p-value was less than 0.05. Therefore, the relationship between the number of crop types and the differences in QR between the supervised approach and each unsupervised approach is significant.
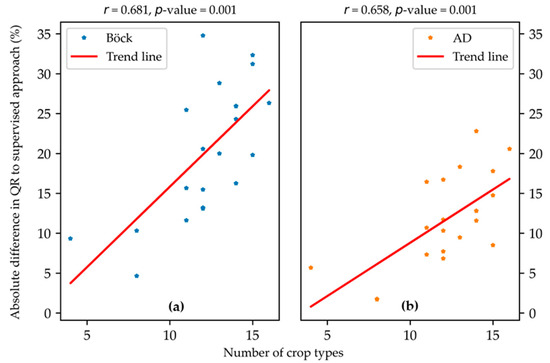
Figure 13.
Correlation between the number of land use (LU) types and the difference in QR between the supervised benchmark results and the unsupervised Bayesian optimization approaches based on (a) the Böck metric and (b) the AD metric.
5. Discussion
The analysis of which metric was optimal for unsupervised segmentation evaluation within our experimental setup of using 21 tiles revealed that our metric (AD) was better than the Böck metric, whether one uses it within a default or Bayesian optimization approach. Visually and quantitatively, the segmentation results yielded by the AD metric were better than the Böck metric in different landscapes composed of diverse agricultural LU types.
For the default optimization approach, at tiles such as T3, where the Böck and AD metrics yielded very similar segmentation results, this is attributable to the fact that there was more clustering of objects as the scale was increased. This is captured by Figure 7b, where all the MI values were positive. Clustering normally occurs in areas where there are different LU types but with similar spectral behaviors sharing the same neighborhood or in areas highly dominated by a single LU type such as grasslands, as was the case of T3. Under those conditions, the GS values of the Böck and AD metrics exhibited a common behavior (Figure 7) and consequently selected similar scale values, leading to very similar segmentation results.
At other tiles such as T1, where there was an enormous disparity between the two metrics, the agricultural landscape is more diverse and interspersed with different LU types such as winter wheat, sugar beet, and maize. Consequently, they had more negative MI values with increasing scale (Figure 6b), which is indicative of the dispersion of objects. The Böck and AD metrics on such occasions differed in curve behavior and global minimum position (Figure 6). Based on the trajectory of the Böck metric in Figure 6a, one can safely conclude that the Böck metric would have further decreased if the scale value had further been increased. Our metric, on the other hand, as captured by Figure 6b, exhibited a decreasing trend up to scale 190 and then started to increase in response to increasing nWV and decreasing MI. The benefit of not normalizing the MI and using absolute difference to compute the GS became manifest on such occasions, where there was a greater dispersion of agricultural parcels. The AD metric was initially more influenced by the MI, but it was later more influenced by the nWV as the scale increased and more MI values became negative (Figure 6b). With the AD metric, the MI and nWV values have a fair chance of impacting the GS value depending on their respective magnitudes. The Böck metric, on the other hand, was continuously impacted by the nMI (Figure 6a). This can be attributed to the normalization approach applied to the MI by the Böck metric. As captured by Figure 6b, before normalization, all the originally negative MI values were numerically smaller than their corresponding nWV values. After normalizing the MI to obtain the nMI (Figure 6a), those negative MI values became numerically higher than their corresponding nWV values, thereby continuously influencing the GS of the Böck metric (Figure 6a).
The Böck metric is more impacted by the nMI than the nWV in all agricultural landscapes. This behavior of the Böck metric has the potential of selecting large-scale values as optimal, thereby leading to the identification of under-segmented objects as optimal. This observation was also made by Georganos et al. [16]. This particular behavior of the Böck metric becomes more problematic in areas with diverse LU types and a greater dispersion of objects, as previously shown in Figure 5a. The more diverse the LU types and the more spectrally similar they behave, the higher the probability of selecting under-segmented objects as optimal using any segmentation evaluation metric, especially a metric that is purely based on the image content. Therefore, a good unsupervised segmentation evaluation metric must reduce over-segmentation but more importantly under-segmentation as the AD metric proved to be able to do, at least in comparison with the Böck metric. For subsequent processes such as object classification, under-segmentation is preferable to over-segmentation [26,58,59]. In general, under-segmentation can largely be dealt with by using very high-resolution images in which visible boundaries between adjacent but spectrally similar parcels can be identified [47].
For the unsupervised Bayesian optimization approach, the approach based on the AD metric outperformed that of the Böck metric at all the tiles, especially at T1, which is composed of diverse LU types. Interestingly, at T3, the Bayesian optimization approach based on the AD metric became better than the Böck metric. This is opposite to the default optimization results at T3, where Böck was marginally better than AD. Overall, in both optimization approaches, the AD metric consistently proved to be better suited for optimizing the segmentation of agricultural parcels in different landscapes. A look at the segmentation results for T1 (Figure 9) clearly shows that the Bayesian optimization approach based on the AD metric generated more segments (Figure 9d) with a higher segmentation quality than the results of the Bayesian approach based on the Böck metric (Figure 9b). There was a greater clustering of objects at T2 (Figure 10) and T17 (Figure 11) based on the computed MI values; hence, the Bayesian optimization approach based on the Böck (Figure 10b and Figure 11b) and the AD (Figure 10d and Figure 11d) metrics yielded very similar segmentation results.
As expected, the supervised Bayesian optimization approach performed better than all the unsupervised Bayesian optimization approaches at all the tiles used in our experiment. This is especially true for T1 (Figure 9c) and T17 (Figure 11c), where the landscape has diversified LU types. At T2, which is highly dominated by pome fruits, the segmentation quality was bad for all the optimization methods. Tetteh et al. [47] in using the supervised Bayesian optimization approach to delineate agricultural parcels made this observation as well for T2 and attributed it to the small size and elongation of agricultural parcels present at that tile. This also holds for the unsupervised Bayesian optimization approaches tested in this research. The high correlation between the number of LU types and the difference in QR between the supervised Bayesian optimization approach and the two unsupervised Bayesian optimization approaches as captured by Figure 13 indicated that at tiles with a smaller number of LU types, the unsupervised Bayesian approaches obtained results similar to the supervised approach. The supervised Bayesian approach was able to adapt more to diverse agricultural landscapes than the unsupervised Bayesian approaches. An example of this can be seen in Figure 12c, where the supervised approach generated segments with well-defined boundaries and a better geometric match to the LPIS parcels than the two unsupervised Bayesian approaches in Figure 12a,b, respectively. The adaptability of supervised segmentation optimization was also asserted by Yang et al. [39] after testing a supervised optimization approach based on the information gain ratio and an unsupervised optimization approach based on MI and WV as was proposed by Espindola et al. [33]. The major defect of any supervised optimization method is the reliance on reference data, which are tedious to obtain [29]. An unsupervised method such as the Bayesian optimization approach based on our proposed AD metric provides a good alternative to supervised segmentation optimization.
Unlike the proposition of Georganos et al. [16], our proposed metric is objective and fully automated. It does not require any human intervention to identify the optimal segmentation. The approach of Georganos et al. [16] requires the user to compute a certain number of initial segmentations with unknown step intervals, something the authors mentioned has a great impact on the results. Additionally, using locally estimated scatterplot smoothing (LOESS) requires a user to specify the order of the polynomial and a span, which controls the level of smoothing. Since the optimal values of those user inputs cannot be known beforehand, the user has to experiment to identify the optimal settings for normalization, which violates the principle behind unsupervised segmentation evaluation.
6. Conclusions
In this study, we modified an existing unsupervised segmentation evaluation metric based on global variance and spatial autocorrelation [43]. We proposed the use of absolute difference (AD) to combine the global variance and spatial autocorrelation. We tested the AD metric and the existing metric, named Böck, in identifying the optimal parameters for delineating agricultural parcels from Sentinel-2 images using the Multiresolution Segmentation (MRS) algorithm. We first tested both metrics at 21 tiles with different agricultural landscapes to optimize the scale parameter of the MRS algorithm through default optimization. In this default approach, we kept the shape and compactness parameters constant and increased the scale at equal intervals to determine the optimal one. The AD metric proved superior to the Böck metric in identifying the segmentation result with a better geometric match to reference agricultural parcels in the Land Parcel Identification System (LPIS). On average, the segmentation quality of the AD metric was over 6% higher than the Böck metric in this default approach. Our metric often identified segmentations that were least under-segmented as optimal, unlike the Böck metric. We separately used each metric in a Bayesian optimization routine to optimize the three main parameters of the MRS algorithm at the same 21 tiles. The Bayesian optimization approach based on the AD metric performed better than that of the Böck metric at all tiles. In the Bayesian optimization approach, the quality of the segmentation result of the AD metric was on average about 9% better than the Böck metric. A comparison of the segmentation results in this study to existing benchmark results obtained via supervised Bayesian optimization showed that the unsupervised Bayesian optimization approach based on the AD metric can be a good alternative. In areas where the number of land-use (LU) types was small, supervised and unsupervised Bayesian optimization obtained similar segmentation results. Supervised segmentation optimization methods require reference data, which are generally difficult and time-consuming to generate, especially for wide geographic areas such as regions and countries. The Bayesian optimization approach based on the AD metric solely depends on the image content to fine-tune the optimization process without any human intervention; hence, it can easily be used in any operational OBIA workflow to generate segmentations in near real time.
In a nutshell, our proposed metric performed better than its predecessor in identifying optimal segmentation. Identifying optimal segmentation is important for purposes of obtaining correct agricultural statistics such as the sizes of agricultural parcels. In the absence of reference data, a Bayesian optimization approach based on the AD metric can provide a means of fulfilling the aforementioned purpose in an automated and efficient manner with no human interaction. Even though we tested this optimization approach on the MRS algorithm within the thematic area of agriculture, it is easily applicable to any segmentation algorithm and different thematic areas.
Going into the future, one possible way of improving the results of the segmentation optimization process with our proposed metric will be to incorporate local variance and spatial autocorrelation in a multi-scale approach to refine under-segmented and over-segmented objects in subsequent steps as was done by Johnson et al. [37]. Different weighting schemes for different agricultural landscapes can be applied to the normalized weighted variance and spatial autocorrelation before the computation of the global score for the AD metric. The impact of this weighting scheme on the identification of the optimal segmentation result would be analyzed accordingly. The impact of the segmentation results identified by the supervised and unsupervised Bayesian optimization approaches on object classification would be assessed. The 21 tiles we used in our experimental setup had relatively flat terrains. However, our proposed metric should work fairly well in other terrains as long as there is enough spectral dissimilarity (dispersion) between adjacent parcels in any geographical area. This hypothesis will be tested in the future.
Author Contributions
Conceptualization, G.O.T.; methodology, G.O.T., A.G.; software, G.O.T.; formal analysis, G.O.T. and A.G.; writing—original draft preparation, G.O.T.; writing—review and editing, A.G., M.S., S.E. and C.C.; visualization, G.O.T.; supervision, A.G., M.S. and S.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We are grateful to the Ministry of Food, Agriculture and Consumer Protection of Lower Saxony for providing the LPIS reference parcels. We appreciate the constructive feedbacks of Antonia Ortmann and Ann-Kathrin Holtgrave on this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Description of the test sites (tiles) used in this study.
Table A1.
Description of the test sites (tiles) used in this study.
| Tile | Image Date | Agric. Land Cover | No. of Land-Use Types | No. of LPIS Parcels | Min. Area (Ha) | Max. Area (Ha) | Mean Area (Ha) |
|---|---|---|---|---|---|---|---|
| T1 | 20 May 2018 | 62.29% | 12 | 1308 | 0.232 | 25.777 | 4.097 |
| T2 | 5 May 2018 | 62.76% | 8 | 1344 | 0.173 | 21.726 | 2.398 |
| T3 | 8 May 2018 | 80.91% | 4 | 2341 | 0.191 | 53.279 | 2.924 |
| T4 | 7 May 2018 | 53.30% | 14 | 1671 | 0.169 | 35.281 | 2.522 |
| T5 | 5 May 2018 | 76.83% | 14 | 1957 | 0.180 | 18.888 | 3.219 |
| T6 | 5 May 2018 | 79.61% | 11 | 2500 | 0.168 | 22.639 | 2.565 |
| T7 | 5 May 2018 | 68.08% | 16 | 2140 | 0.203 | 25.181 | 2.579 |
| T8 | 8 May 2018 | 50.17% | 12 | 1100 | 0.199 | 30.562 | 3.704 |
| T9 | 5 May 2018 | 70.43% | 11 | 1613 | 0.190 | 44.890 | 3.699 |
| T10 | 5 May 2018 | 70.13% | 12 | 2441 | 0.177 | 26.253 | 2.243 |
| T11 | 5 May 2018 | 71.41% | 15 | 1625 | 0.172 | 30.012 | 3.709 |
| T12 | 5 May 2018 | 90.15% | 12 | 1798 | 0.171 | 50.494 | 3.127 |
| T13 | 5 May 2018 | 92.31% | 12 | 1221 | 0.181 | 64.772 | 6.203 |
| T14 | 5 May 2018 | 63.62% | 15 | 1894 | 0.176 | 26.646 | 2.637 |
| T15 | 5 May 2018 | 36.63% | 15 | 809 | 0.203 | 23.687 | 3.580 |
| T16 | 5 May 2018 | 58.45% | 14 | 1752 | 0.181 | 29.022 | 2.781 |
| T17 | 5 May 2018 | 61.10% | 14 | 1538 | 0.180 | 28.160 | 2.994 |
| T18 | 5 May 2018 | 37.26% | 13 | 729 | 0.193 | 28.514 | 4.158 |
| T19 | 7 May 2018 | 14.29% | 8 | 420 | 0.217 | 25.855 | 2.471 |
| T20 | 7 May 2018 | 33.35% | 13 | 744 | 0.191 | 36.408 | 3.111 |
| T21 | 7 May 2018 | 90.84% | 11 | 1340 | 0.213 | 62.730 | 5.883 |
Figure A1.
Boxplot of agricultural parcel sizes per tile.

Table A2.
Empirical discrepancy measures computed for each optimal segmentation result identified by the AD and Böck metrics based on the default optimization (shape = 0.1, compactness = 0.5). The bold-faced texts within the body of the table are the optimal results.
Table A2.
Empirical discrepancy measures computed for each optimal segmentation result identified by the AD and Böck metrics based on the default optimization (shape = 0.1, compactness = 0.5). The bold-faced texts within the body of the table are the optimal results.
| Tile | Scale | Shape | Compactness | QR | OR | UR | RMS | Metric |
|---|---|---|---|---|---|---|---|---|
| T1 | 190 | 0.100 | 0.500 | 55.53% | 0.115 | 0.375 | 0.278 | AD |
| T1 | 300 | 0.100 | 0.500 | 38.42% | 0.057 | 0.597 | 0.424 | Böck |
| T2 | 80 | 0.100 | 0.500 | 36.94% | 0.334 | 0.467 | 0.406 | AD |
| T2 | 70 | 0.100 | 0.500 | 36.07% | 0.387 | 0.427 | 0.407 | Böck |
| T3 | 150 | 0.100 | 0.500 | 57.91% | 0.183 | 0.304 | 0.251 | Böck |
| T3 | 140 | 0.100 | 0.500 | 57.80% | 0.192 | 0.296 | 0.250 | AD |
| T4 | 200 | 0.100 | 0.500 | 28.33% | 0.121 | 0.685 | 0.492 | AD |
| T4 | 280 | 0.100 | 0.500 | 20.84% | 0.076 | 0.779 | 0.553 | Böck |
| T5 | 160 | 0.100 | 0.500 | 44.69% | 0.163 | 0.477 | 0.356 | AD |
| T5 | 200 | 0.100 | 0.500 | 39.00% | 0.122 | 0.563 | 0.407 | Böck |
| T6 | 170 | 0.100 | 0.500 | 42.45% | 0.169 | 0.502 | 0.375 | AD |
| T6 | 180 | 0.100 | 0.500 | 41.24% | 0.161 | 0.520 | 0.385 | Böck |
| T7 | 190 | 0.100 | 0.500 | 32.84% | 0.128 | 0.631 | 0.455 | AD |
| T7 | 270 | 0.100 | 0.500 | 25.46% | 0.084 | 0.729 | 0.519 | Böck |
| T8 | 120 | 0.100 | 0.500 | 48.77% | 0.274 | 0.339 | 0.308 | AD |
| T8 | 170 | 0.100 | 0.500 | 41.78% | 0.150 | 0.513 | 0.378 | Böck |
| T9 | 170 | 0.100 | 0.500 | 44.88% | 0.215 | 0.446 | 0.350 | AD |
| T9 | 300 | 0.100 | 0.500 | 33.86% | 0.101 | 0.635 | 0.454 | Böck |
| T10 | 180 | 0.100 | 0.500 | 36.66% | 0.143 | 0.584 | 0.425 | AD |
| T10 | 210 | 0.100 | 0.500 | 33.06% | 0.126 | 0.631 | 0.455 | Böck |
| T11 | 230 | 0.100 | 0.500 | 35.67% | 0.127 | 0.595 | 0.430 | AD |
| T11 | 230 | 0.100 | 0.500 | 35.67% | 0.127 | 0.595 | 0.430 | Böck |
| T12 | 150 | 0.100 | 0.500 | 40.77% | 0.209 | 0.504 | 0.386 | AD |
| T12 | 270 | 0.100 | 0.500 | 27.78% | 0.126 | 0.697 | 0.501 | Böck |
| T13 | 240 | 0.100 | 0.500 | 42.42% | 0.177 | 0.495 | 0.372 | AD |
| T13 | 300 | 0.100 | 0.500 | 35.18% | 0.142 | 0.601 | 0.436 | Böck |
| T14 | 160 | 0.100 | 0.500 | 36.03% | 0.162 | 0.574 | 0.422 | AD |
| T14 | 280 | 0.100 | 0.500 | 21.74% | 0.077 | 0.768 | 0.546 | Böck |
| T15 | 220 | 0.100 | 0.500 | 32.40% | 0.090 | 0.648 | 0.463 | AD |
| T15 | 300 | 0.100 | 0.500 | 22.41% | 0.062 | 0.764 | 0.542 | Böck |
| T16 | 180 | 0.100 | 0.500 | 38.46% | 0.114 | 0.566 | 0.408 | AD |
| T16 | 280 | 0.100 | 0.500 | 26.20% | 0.064 | 0.723 | 0.513 | Böck |
| T17 | 200 | 0.100 | 0.500 | 31.89% | 0.137 | 0.634 | 0.459 | AD |
| T17 | 240 | 0.100 | 0.500 | 27.14% | 0.111 | 0.700 | 0.501 | Böck |
| T18 | 200 | 0.100 | 0.500 | 47.11% | 0.167 | 0.434 | 0.329 | Böck |
| T18 | 190 | 0.100 | 0.500 | 47.06% | 0.168 | 0.427 | 0.325 | AD |
| T19 | 210 | 0.100 | 0.500 | 37.29% | 0.092 | 0.595 | 0.426 | AD |
| T19 | 50 | 0.100 | 0.500 | 36.58% | 0.552 | 0.207 | 0.417 | Böck |
| T20 | 220 | 0.100 | 0.500 | 29.21% | 0.123 | 0.676 | 0.486 | AD |
| T20 | 260 | 0.100 | 0.500 | 27.79% | 0.102 | 0.698 | 0.499 | Böck |
| T21 | 270 | 0.100 | 0.500 | 43.91% | 0.133 | 0.499 | 0.365 | AD |
| T21 | 300 | 0.100 | 0.500 | 40.52% | 0.117 | 0.546 | 0.395 | Böck |

Table A3.
Empirical discrepancy measures computed for the unsupervised Bayesian optimization approaches based on the Böck and AD metrics, and the supervised Bayesian optimization approach (SUP) that was used to maximize the QR measure. The bold-faced texts within the body of the table are the optimal results.
Table A3.
Empirical discrepancy measures computed for the unsupervised Bayesian optimization approaches based on the Böck and AD metrics, and the supervised Bayesian optimization approach (SUP) that was used to maximize the QR measure. The bold-faced texts within the body of the table are the optimal results.
| Tile | Scale | Shape | Compactness | QR | OR | UR | RMS | Metric |
|---|---|---|---|---|---|---|---|---|
| T1 | 51 | 0.900 | 0.966 | 69.17% | 0.117 | 0.224 | 0.178 | SUP |
| T1 | 160 | 0.300 | 0.500 | 57.47% | 0.126 | 0.349 | 0.263 | AD |
| T1 | 200 | 0.841 | 0.917 | 34.39% | 0.035 | 0.648 | 0.459 | Böck |
| T2 | 40 | 0.900 | 0.300 | 42.04% | 0.219 | 0.479 | 0.372 | SUP |
| T2 | 42 | 0.792 | 0.176 | 40.28% | 0.309 | 0.429 | 0.374 | AD |
| T2 | 56 | 0.415 | 0.192 | 37.40% | 0.402 | 0.395 | 0.398 | Böck |
| T3 | 77 | 0.842 | 0.906 | 68.46% | 0.117 | 0.235 | 0.186 | SUP |
| T3 | 117 | 0.420 | 1.000 | 62.79% | 0.164 | 0.263 | 0.219 | AD |
| T3 | 138 | 0.279 | 0.175 | 59.14% | 0.165 | 0.304 | 0.245 | Böck |
| T4 | 34 | 0.900 | 0.410 | 50.84% | 0.290 | 0.297 | 0.293 | SUP |
| T4 | 116 | 0.655 | 1.000 | 38.04% | 0.121 | 0.576 | 0.416 | AD |
| T4 | 174 | 0.666 | 0.753 | 24.88% | 0.076 | 0.738 | 0.524 | Böck |
| T5 | 42 | 0.900 | 0.783 | 58.78% | 0.205 | 0.273 | 0.242 | SUP |
| T5 | 132 | 0.468 | 0.701 | 47.21% | 0.149 | 0.459 | 0.341 | AD |
| T5 | 162 | 0.395 | 0.452 | 42.52% | 0.124 | 0.524 | 0.381 | Böck |
| T6 | 40 | 0.900 | 0.500 | 57.67% | 0.225 | 0.269 | 0.248 | SUP |
| T6 | 127 | 0.422 | 0.083 | 46.98% | 0.172 | 0.442 | 0.335 | AD |
| T6 | 144 | 0.377 | 0.000 | 46.05% | 0.161 | 0.466 | 0.348 | Böck |
| T7 | 40 | 0.900 | 0.500 | 55.70% | 0.209 | 0.307 | 0.263 | SUP |
| T7 | 183 | 0.088 | 0.401 | 35.14% | 0.142 | 0.601 | 0.436 | AD |
| T7 | 178 | 0.686 | 0.611 | 29.39% | 0.071 | 0.692 | 0.492 | Böck |
| T8 | 46 | 0.853 | 0.665 | 56.91% | 0.261 | 0.240 | 0.251 | SUP |
| T8 | 120 | 0.100 | 0.300 | 49.20% | 0.261 | 0.339 | 0.303 | AD |
| T8 | 160 | 0.300 | 0.100 | 43.71% | 0.145 | 0.499 | 0.367 | Böck |
| T9 | 56 | 0.900 | 0.548 | 56.93% | 0.191 | 0.310 | 0.258 | SUP |
| T9 | 129 | 0.398 | 1.000 | 49.61% | 0.212 | 0.384 | 0.310 | AD |
| T9 | 200 | 0.300 | 0.500 | 41.28% | 0.148 | 0.532 | 0.390 | Böck |
| T10 | 40 | 0.900 | 0.700 | 54.15% | 0.196 | 0.336 | 0.275 | SUP |
| T10 | 189 | 0.000 | 0.380 | 37.43% | 0.152 | 0.573 | 0.419 | AD |
| T10 | 184 | 0.587 | 0.633 | 33.58% | 0.084 | 0.641 | 0.457 | Böck |
| T11 | 50 | 0.900 | 0.699 | 58.31% | 0.200 | 0.277 | 0.241 | SUP |
| T11 | 200 | 0.100 | 0.900 | 40.52% | 0.143 | 0.528 | 0.386 | AD |
| T11 | 108 | 0.900 | 0.777 | 38.50% | 0.073 | 0.595 | 0.424 | Böck |
| T12 | 40 | 0.900 | 0.100 | 49.05% | 0.254 | 0.354 | 0.308 | SUP |
| T12 | 163 | 0.000 | 0.605 | 38.73% | 0.197 | 0.536 | 0.404 | AD |
| T12 | 200 | 0.500 | 0.700 | 33.57% | 0.119 | 0.635 | 0.457 | Böck |
| T13 | 63 | 0.900 | 0.371 | 54.74% | 0.231 | 0.293 | 0.264 | SUP |
| T13 | 151 | 0.643 | 0.272 | 47.92% | 0.168 | 0.434 | 0.329 | AD |
| T13 | 165 | 0.819 | 0.614 | 41.67% | 0.091 | 0.551 | 0.395 | Böck |
| T14 | 42 | 0.900 | 0.576 | 53.68% | 0.204 | 0.328 | 0.273 | SUP |
| T14 | 120 | 0.500 | 0.100 | 38.92% | 0.156 | 0.539 | 0.397 | AD |
| T14 | 200 | 0.700 | 0.100 | 21.35% | 0.059 | 0.778 | 0.552 | Böck |
| T15 | 40 | 0.900 | 0.300 | 61.17% | 0.200 | 0.252 | 0.228 | SUP |
| T15 | 63 | 0.900 | 0.428 | 52.67% | 0.106 | 0.421 | 0.307 | AD |
| T15 | 109 | 0.900 | 0.000 | 29.95% | 0.064 | 0.687 | 0.488 | Böck |
| T16 | 45 | 0.842 | 0.923 | 59.96% | 0.206 | 0.251 | 0.229 | SUP |
| T16 | 101 | 0.652 | 0.762 | 47.17% | 0.116 | 0.470 | 0.342 | AD |
| T16 | 154 | 0.569 | 0.621 | 35.65% | 0.086 | 0.615 | 0.439 | Böck |
| T17 | 45 | 0.900 | 0.632 | 54.49% | 0.205 | 0.320 | 0.269 | SUP |
| T17 | 200 | 0.104 | 0.192 | 31.68% | 0.133 | 0.637 | 0.460 | AD |
| T17 | 185 | 0.603 | 0.800 | 28.57% | 0.093 | 0.691 | 0.493 | Böck |
| T18 | 57 | 0.889 | 0.897 | 59.15% | 0.199 | 0.265 | 0.234 | SUP |
| T18 | 116 | 0.653 | 0.370 | 49.68% | 0.172 | 0.398 | 0.307 | AD |
| T18 | 160 | 0.700 | 0.300 | 39.16% | 0.094 | 0.572 | 0.410 | Böck |
| T19 | 54 | 0.730 | 1.000 | 53.04% | 0.262 | 0.290 | 0.276 | SUP |
| T19 | 40 | 0.900 | 0.700 | 51.35% | 0.221 | 0.343 | 0.288 | AD |
| T19 | 40 | 0.601 | 0.000 | 42.72% | 0.460 | 0.223 | 0.362 | Böck |
| T20 | 40 | 0.900 | 0.900 | 53.31% | 0.221 | 0.319 | 0.274 | SUP |
| T20 | 200 | 0.154 | 0.961 | 34.98% | 0.131 | 0.604 | 0.437 | AD |
| T20 | 200 | 0.700 | 0.500 | 24.48% | 0.067 | 0.743 | 0.528 | Böck |
| T21 | 63 | 0.899 | 0.868 | 64.99% | 0.157 | 0.231 | 0.198 | SUP |
| T21 | 170 | 0.627 | 0.582 | 48.55% | 0.129 | 0.447 | 0.329 | AD |
| T21 | 200 | 0.813 | 0.173 | 39.54% | 0.074 | 0.579 | 0.412 | Böck |
References
- Dudley, N.; Alexander, S. Agriculture and biodiversity: A review. Biodiversity 2017, 18, 45–49. [Google Scholar] [CrossRef]
- Foley, J.A.; Ramankutty, N.; Brauman, K.A.; Cassidy, E.S.; Gerber, J.S.; Johnston, M.; Mueller, N.D.; O’Connell, C.; Ray, D.K.; West, P.C.; et al. Solutions for a cultivated planet. Nature 2011, 478, 337–342. [Google Scholar] [CrossRef] [PubMed]
- Rey Benayas, J.M.; Bullock, J.M. Restoration of biodiversity and ecosystem services on agricultural land. Ecosystems 2012, 15, 883–899. [Google Scholar] [CrossRef]
- Beach, R.H.; DeAngelo, B.J.; Rose, S.; Li, C.; Salas, W.; DelGrosso, S.J. Mitigation potential and costs for global agricultural greenhouse gas emissions1. Agric. Econ. 2008, 38, 109–115. [Google Scholar] [CrossRef]
- Adams, C.R.; Eswaran, H. Global land resources in the context of food and environmental security. In Advances in Land Resources Management for the 20th Century; Soil Conservation Society of India: New Delhi, India, 2000; pp. 35–50. [Google Scholar]
- Forkuor, G.; Conrad, C.; Thiel, M.; Ullmann, T.; Zoungrana, E. integration of optical and synthetic aperture radar imagery for improving crop mapping in Northwestern Benin, West Africa. Remote Sens. 2014, 6, 6472–6499. [Google Scholar] [CrossRef]
- Villa, P.; Stroppiana, D.; Fontanelli, G.; Azar, R.; Brivio, P. In-season mapping of crop type with optical and X-band SAR data: A classification tree approach using synoptic seasonal features. Remote Sens. 2015, 7, 12859–12886. [Google Scholar] [CrossRef]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Blaes, X.; Vanhalle, L.; Defourny, P. Efficiency of crop identification based on optical and SAR image time series. Remote Sens. Environ. 2005, 96, 352–365. [Google Scholar] [CrossRef]
- Castillejo-González, I.L.; López-Granados, F.; García-Ferrer, A.; Peña-Barragán, J.M.; Jurado-Expósito, M.; de la Orden, M.S.; González-Audicana, M. Object- and pixel-based analysis for mapping crops and their agro-environmental associated measures using QuickBird imagery. Comput. Electron. Agric. 2009, 68, 207–215. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Blaschke, T.; Lang, S.; Lorup, E.; Strobl, J.; Zeil, P. Object-oriented image processing in an integrated GIS/remote sensing environment and perspectives for environmental applications. Environ. Inf. Plan. Polit. Public 2000, 2, 555–570. [Google Scholar]
- Whiteside, T.G.; Boggs, G.S.; Maier, S.W. Comparing object-based and pixel-based classifications for mapping savannas. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 884–893. [Google Scholar] [CrossRef]
- Robertson, L.D.; King, D.J. Comparison of pixel- and object-based classification in land cover change mapping. Int. J. Remote Sens. 2011, 32, 1505–1529. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Georganos, S.; Lennert, M.; Grippa, T.; Vanhuysse, S.; Johnson, B.; Wolff, E. Normalization in unsupervised segmentation parameter optimization: A solution based on local regression trend analysis. Remote Sens. 2018, 10, 222. [Google Scholar] [CrossRef]
- Akcay, O.; Avsar, E.O.; Inalpulat, M.; Genc, L.; Cam, A. Assessment of segmentation parameters for object-based land cover classification using color-infrared imagery. ISPRS Int. J. Geo-Inf. 2018, 7, 424. [Google Scholar] [CrossRef]
- Gao, Y.; Mas, J.F.; Kerle, N.; Pacheco, J.A.N. Optimal region growing segmentation and its effect on classification accuracy. Int. J. Remote Sens. 2011, 32, 3747–3763. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Lennert, M.; Vanhuysse, S.; Johnson, B.A.; Wolff, E. Scale Matters: Spatially Partitioned Unsupervised Segmentation Parameter Optimization for Large and Heterogeneous Satellite Images. Remote Sens. 2018, 10, 1440. [Google Scholar] [CrossRef]
- Liu, D.; Xia, F. Assessing object-based classification: Advantages and limitations. Remote Sens. Lett. 2010, 1, 187–194. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, A. Multiresolution segmentation: An optimization approach for high quality multi-scale image segmentation. In Proceedings of the Angewandte Geographische Informations-Verarbeitung XII, Karlsruhe, Germany, 30 June 2000; Strobl, J., Blaschke, T., Griesebner, G., Eds.; Wichmann Verlag: Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Trimble Germany GmbH. eCognition Developer 9.5.0 Reference Book; Trimble Germany GmbH: Munich, Germany, 2019. [Google Scholar]
- Marpu, P.R.; Neubert, M.; Herold, H.; Niemeyer, I. Enhanced evaluation of image segmentation results. J. Spat. Sci. 2010, 55, 55–68. [Google Scholar] [CrossRef]
- Neubert, M.; Herold, H.; Meinel, G. Assessing image segmentation quality—Concepts, methods and application. In Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G.J., Eds.; Lecture Notes in Geoinformation and Cartography; Springer: Berlin/Heidelberg, Germany, 2008; pp. 769–784. ISBN 978-3-540-77058-9. [Google Scholar]
- Neubert, M.; Meinel, G. Evaluation of segmentation programs for high resolution remote sensing applications. In Proceedings of the Joint ISPRS/EARSeL Workshop “High Resolution Mapping from Space 2003”, Hannover, Germany, 8 October 2003. [Google Scholar]
- Zhang, Y.-J. A survey on evaluation methods for image segmentation. Pattern Recognit. 1996, 29, 1335–1346. [Google Scholar] [CrossRef]
- Zhang, H.; Fritts, J.E.; Goldman, S.A. Image segmentation evaluation: A survey of unsupervised methods. Comput. Vis. Image Underst. 2008, 110, 260–280. [Google Scholar] [CrossRef]
- Chabrier, S.; Emile, B.; Rosenberger, C.; Laurent, H. Unsupervised Performance Evaluation of Image Segmentation. EURASIP J. Adv. Signal Process. 2006, 2006, 096306. [Google Scholar] [CrossRef]
- Drăguţ, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterisation for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef]
- Drǎguţ, L.; Tiede, D.; Levick, S.R. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Grybas, H.; Melendy, L.; Congalton, R.G. A comparison of unsupervised segmentation parameter optimization approaches using moderate- and high-resolution imagery. GISci. Remote Sens. 2017, 54, 515–533. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Johnson, B.A.; Bragais, M.; Endo, I.; Magcale-Macandog, D.B.; Macandog, P.B.M. Image segmentation parameter optimization considering within- and between-segment heterogeneity at multiple scale levels: Test case for mapping residential areas using landsat imagery. ISPRS Int. J. Geo-Inf. 2015, 4, 2292–2305. [Google Scholar] [CrossRef]
- Yang, L.; Mansaray, L.R.; Huang, J.; Wang, L. Optimal Segmentation Scale Parameter, Feature Subset and Classification Algorithm for Geographic Object-Based Crop Recognition Using Multisource Satellite Imagery. Remote Sens. 2019, 11, 514. [Google Scholar] [CrossRef]
- Kim, M.; Madden, M.; Warner, T. Estimation of optimal image object size for the segmentation of forest stands with multispectral IKONOS imagery. In Object-Based Image Analysis; Blaschke, T., Lang, S., Hay, G.J., Eds.; Lecture Notes in Geoinformation and Cartography; Springer: Berlin/Heidelberg, Germany, 2008; pp. 291–307. ISBN 978-3-540-77057-2. [Google Scholar]
- Martha, T.R.; Kerle, N.; van Westen, C.J.; Jetten, V.; Kumar, K.V. Segment optimization and data-driven thresholding for knowledge-based landslide detection by object-based image analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4928–4943. [Google Scholar] [CrossRef]
- Chen, J.; Deng, M.; Mei, X.; Chen, T.; Shao, Q.; Hong, L. Optimal segmentation of a high-resolution remote-sensing image guided by area and boundary. Int. J. Remote Sens. 2014, 35, 6914–6939. [Google Scholar] [CrossRef]
- Böck, S.; Immitzer, M.; Atzberger, C. On the objectivity of the objective function—Problems with unsupervised segmentation evaluation based on global score and a possible remedy. Remote Sens. 2017, 9, 769. [Google Scholar] [CrossRef]
- Kim, M.; Warner, T.A.; Madden, M.; Atkinson, D.S. Multi-scale GEOBIA with very high spatial resolution digital aerial imagery: Scale, texture and image objects. Int. J. Remote Sens. 2011, 32, 2825–2850. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Classifying a high resolution image of an urban area using super-object information. ISPRS J. Photogramm. Remote Sens. 2013, 83, 40–49. [Google Scholar] [CrossRef]
- Taşdemir, K.; Wirnhardt, C. Neural network-based clustering for agriculture management. EURASIP J. Adv. Signal Process. 2012, 2012. [Google Scholar] [CrossRef]
- Tetteh, G.O.; Gocht, A.; Conrad, C. Optimal parameters for delineating agricultural parcels from satellite images based on supervised Bayesian optimization. Comput. Electron. Agric. 2020, 178, 105696. [Google Scholar] [CrossRef]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. In Proceedings of the Image and Signal Processing for Remote Sensing XXIII, Warsaw, Poland, 11–13 September 2017; Bruzzone, L., Bovolo, F., Benediktsson, J.A., Eds.; SPIE: Warsaw, Poland, 2017; p. 3. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2006; ISBN 978-0-262-18253-9. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Dewancker, I.; McCourt, M.; Clark, S. Bayesian Optimization Primer. Available online: https://app.sigopt.com/static/pdf/SigOpt_Bayesian_Optimization_Primer.pdf (accessed on 4 March 2020).
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Brochu, E.; Cora, V.M.; de Freitas, N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. arXiv 2010, arXiv:10122599. [Google Scholar]
- Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:180702811. [Google Scholar]
- Weidner, U. Contribution to the assessment of segmentation quality for remote sensing applications. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 479–484. [Google Scholar]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.; Gong, P. Accuracy assessment measures for object-based image segmentation goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Liu, Y.; Bian, L.; Meng, Y.; Wang, H.; Zhang, S.; Yang, Y.; Shao, X.; Wang, B. Discrepancy measures for selecting optimal combination of parameter values in object-based image analysis. ISPRS J. Photogramm. Remote Sens. 2012, 68, 144–156. [Google Scholar] [CrossRef]
- Belgiu, M.; Drǎguţ, L. Comparing supervised and unsupervised multiresolution segmentation approaches for extracting buildings from very high resolution imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 67–75. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).