Analysis of the Contribution Rate of the Influencing Factors to Land Subsidence in the Eastern Beijing Plain, China Based on Extremely Randomized Trees (ERT) Method
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Input Data
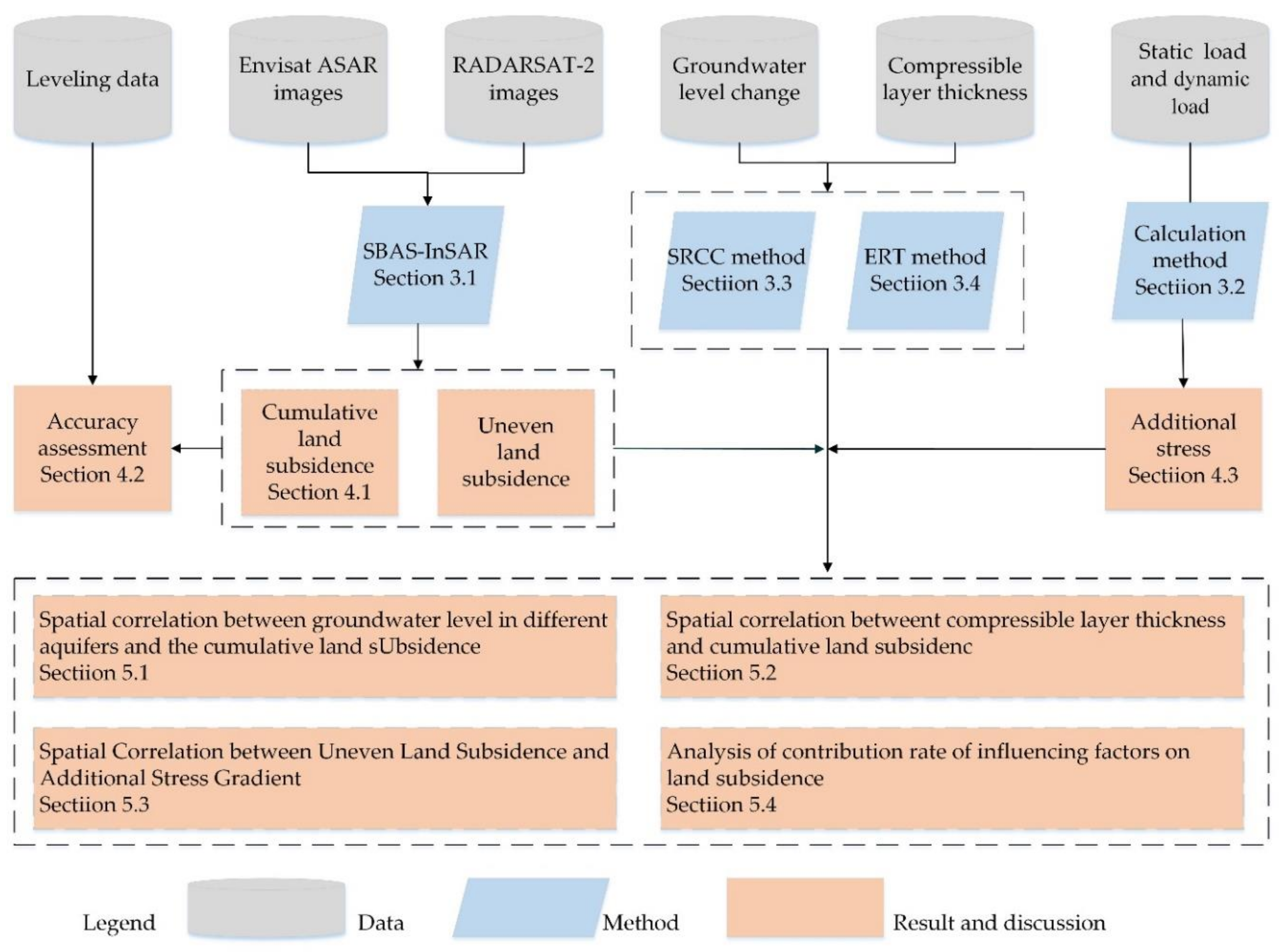
3. Methodology
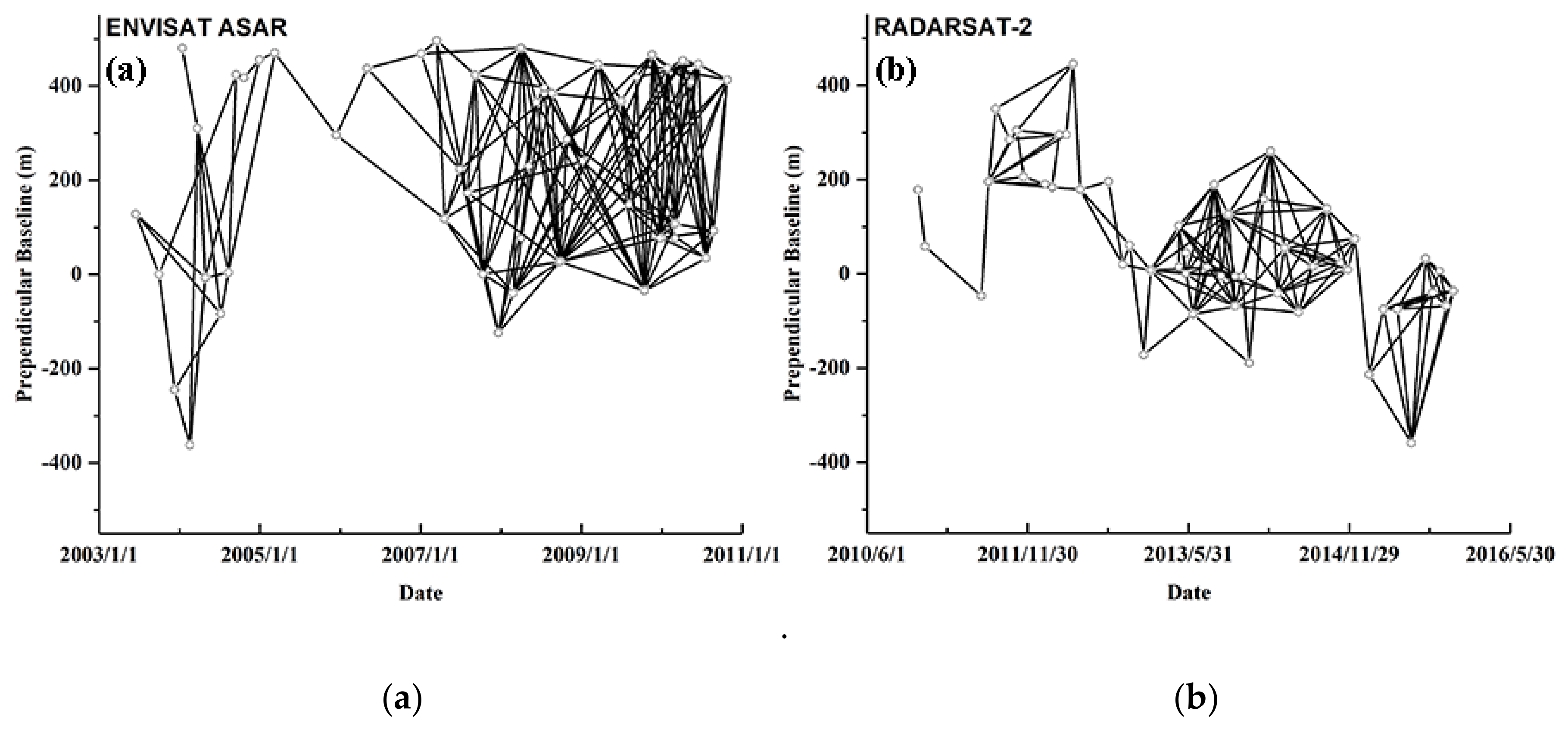
3.1. SBAS-InSAR Processing for the EA and R2 Datasests
3.2. Additional Stress Engendered from Static and Dynamic Loads
3.3. Spearman’s Rank Correlation Coefficient
3.4. Extremely Randomized Trees
4. Results
4.1. Surface Deformation Measured by SBAS-InSAR in Two Time Periods
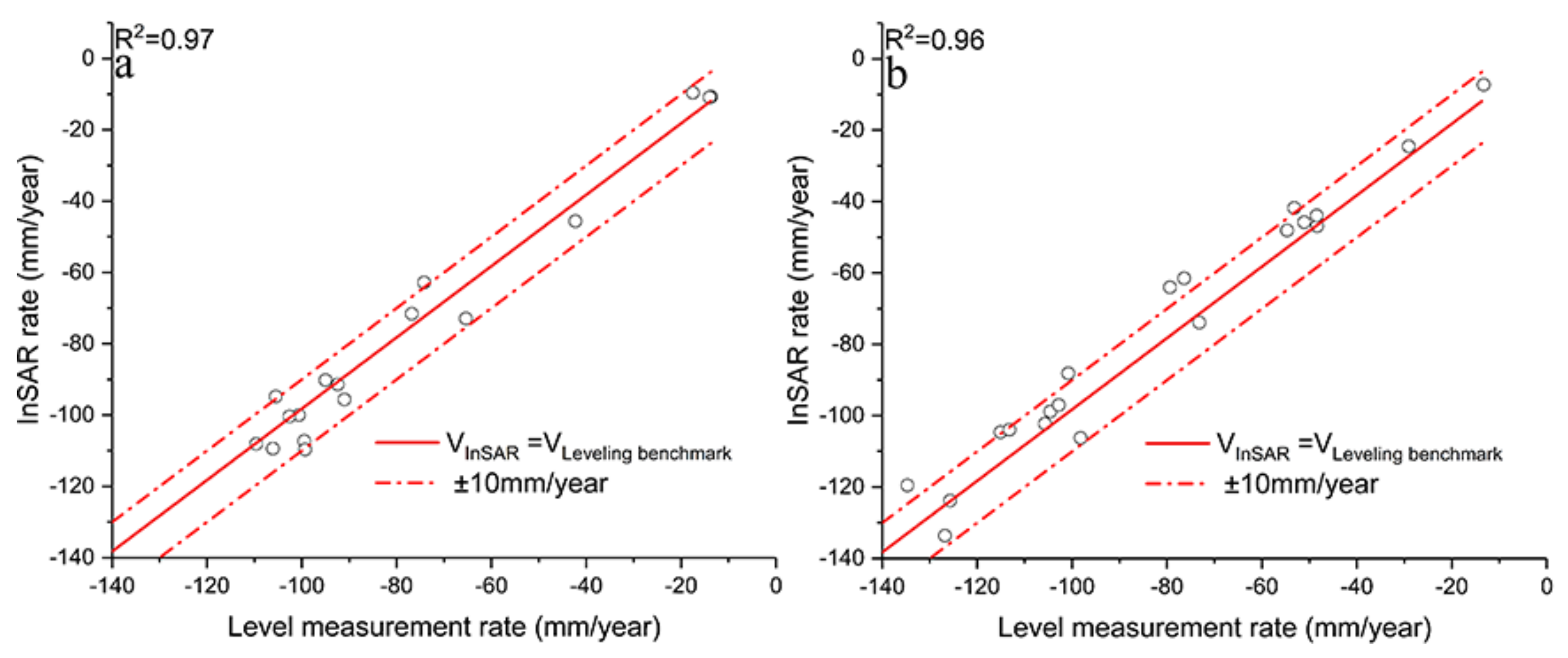
4.2. Accuracy Assessment of the SBAS-InSAR Results
4.3. Acquisition of Additional Stress Engendered from Static and Dynamic Loads
5. Discussion
5.1. Evaluating the Spatial Correlation between Groundwater Level in Different Aquifers and the Cumulative Land Subsidence
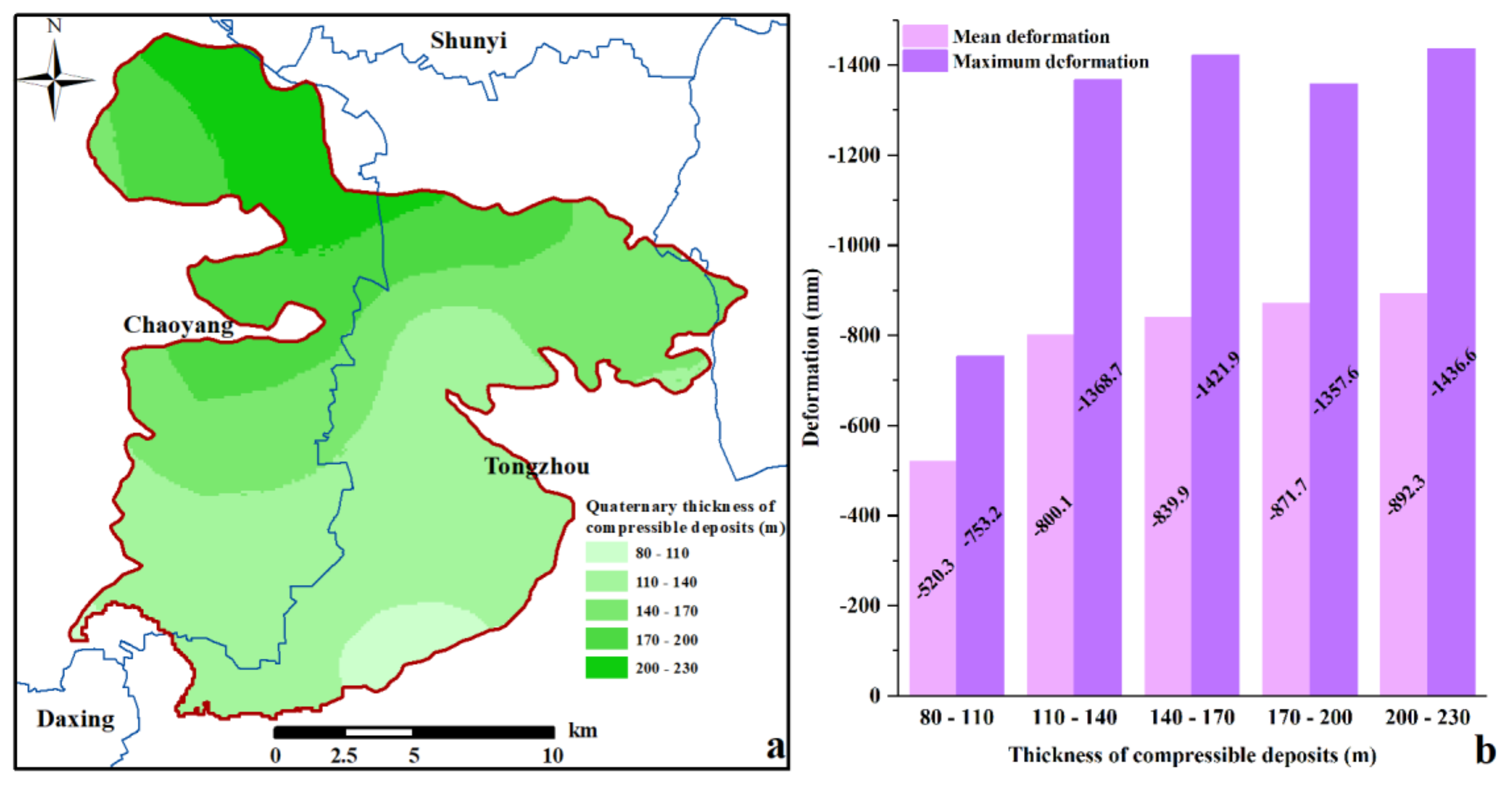
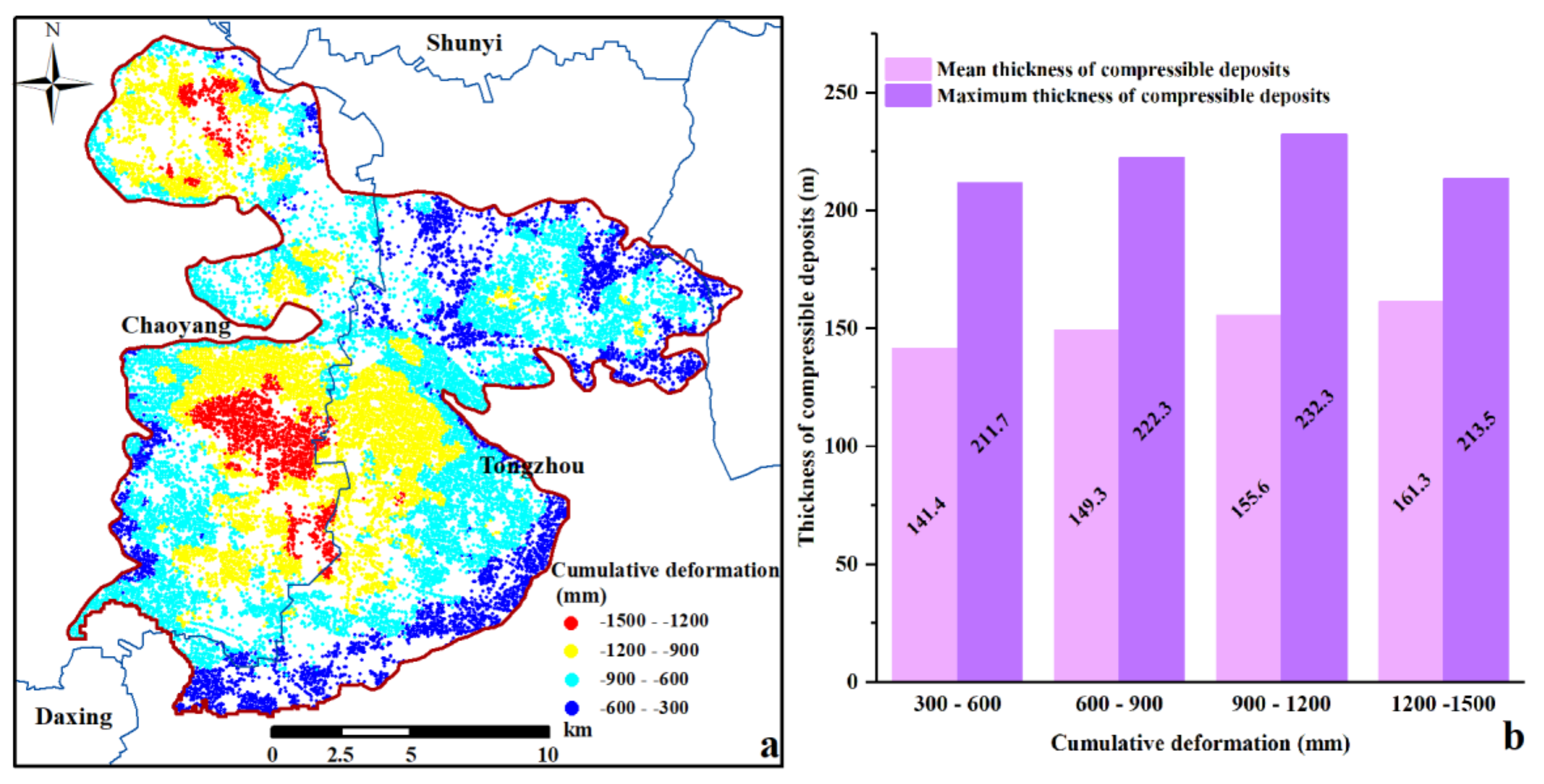
5.2. Evaluation of the Spatial Correlation betweent Compressible Layers of Different Thicknesses and Cumulative Land Subsidence
5.3. Evaluation of the Spatial Correlation between Uneven Land Subsidence and Additional Stress Gradients
5.4. Quantitative Analysis of the Contribution Rate of the Influencing Factors on Land Subsidence Using the ERT Method
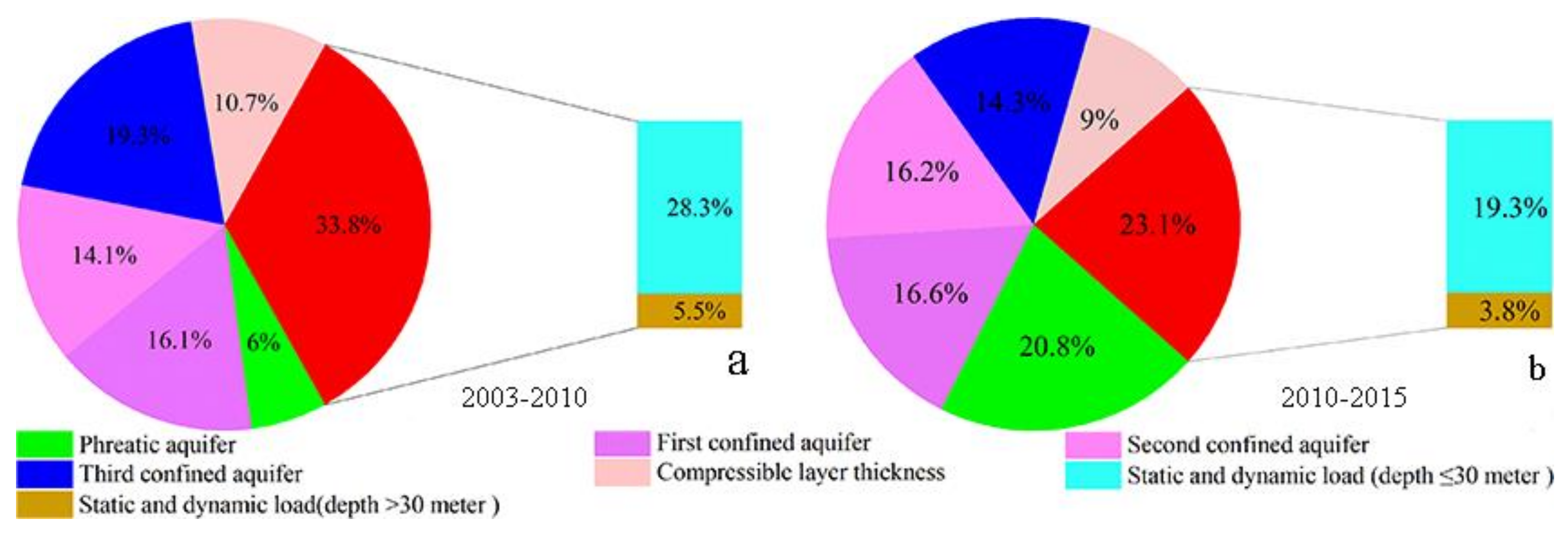
5.4.1. Contribution Rate of the Influencing Factors to Cumulative Land Subsidence
5.4.2. Contribution Rate of the Influencing Factors to Uneven Land Subsidence
6. Conclusions
- (1)
- The maximum land subsidence rate reached 110.7 mm/year and 144.4 mm/year during the 2003–2010 and 2010–2015 periods, respectively. Land subsidence experienced rapid expansion from 2003 to 2010. The maximum land subsidence rate and area with a land subsidence rate greater than 100 mm/year increased from 111.8 to 157.6 mm/year and from 0.1 to 68.9 km2, respectively. Land subsidence showed a decreasing trend from 2010 to 2011 and then remained in a relatively stable stage from 2011 to 2015. The SBAS-InSAR results agree well with the leveling benchmark monitoring results, and the correlation coefficient was 0.97 from 2003 to 2010 and 0.96 from 2013 to 2015.
- (2)
- We found that the greatest contribution to cumulative land subsidence was the second confined aquifer from 2003 to 2010, with a contribution rate of 49.3%. However, its contribution rate decreased to 23.4% from 2010 to 2015. The phreatic aquifer was the main contribution layer from 2010 to 2015, with a contribution rate of 33.9%. The contribution rate of the third confined aquifer increased from 2003 to 2015 due to the upper part of third confined aquifer gradually becoming the main mining layer. We innovatively calculated additional stress to represent static and dynamic load information to show the superposition of additional stress; however, the influence of additional stress engendered from the static and dynamic loads on cumulative land subsidence was slight.
- (3)
- The contribution rate of the static and dynamic loads to uneven land subsidence was 33.8% from 2003 to 2010 and 23.1% from 2010 to 2015, accounting for the largest proportion. The contribution rate of static and dynamic loads with depths of less than 30 m accounted for more than 80% of the total contribution rate of said static and dynamic loads. This result shows that said additional stress has a significant effect on the distribution of uneven settlement, especially in the stratum with a depth of less than 30 m.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, R.L.; Yue, Z.Q.; Wang, L.U.; Wang, S.J. Review on current status and challenging issues of land subsidence in China. Eng. Geol. 2004, 76, 65–77. [Google Scholar] [CrossRef]
- Castellazzi, P.; Garfias, J.; Martel, R.; Brouard, C.; Rivera, A. InSAR to support sustainable urbanization over compacting aquifers: The case of Toluca Valley, Mexico. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 33–44. [Google Scholar] [CrossRef]
- Galloway, D.; Hudnut, K.; Ingebritsen, S.; Ingebritsen, S.; Phillips, S.; Peltzer, S.; Rogez, F.; Rosen, P. Detection of aquifer system compaction and land subsidence using interferometric synthetic aperture radar, Antelope Valley, Mojave Desert, California. Water Resour. Res. 1998, 34, 2573–2585. [Google Scholar] [CrossRef]
- Strozzi, T.; Caduff, R.; Wegmüller, U.; Raetzo, H.; Hauser, M. Widespread surface subsidence measured with satellite SAR interferometry in the Swiss alpine range associated with the construction of the Gotthard BaseTunnel. Remote Sens. Environ. 2017, 190, 1–12. [Google Scholar] [CrossRef]
- Ng, A.H.M.; Ge, L.; Li, X.; Abidin, H.Z.; Andreas, H.; Zhang, K. Mapping land subsidence in Jakarta, Indonesia using persistent scatterer interferometry (PSI) technique with ALOS PALSAR. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 232–242. [Google Scholar] [CrossRef]
- Gao, M.; Gong, H.; Chen, B.; Li, X.; Zhou, C.; Min, S.; Yuan, S.; Zheng, C.; Duan, G. Regional Land Subsidence Analysis in Eastern Beijing Plain by InSAR Time Series and Wavelet Transforms. Remote Sens. 2018, 10, 365. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Oreye, N.; Gonzalez, P.J.; Tiampo, K.F.; Ertolahti, L.; Clague, J.J. Rapidly accelerating subsidence in the Greater Vancouver region from two decades of ERS-ENVISAT-RADARSAT-2 DInSAR measurements. Remote Sens. Environ. 2014, 143, 180–191. [Google Scholar] [CrossRef]
- Du, Z.; Ge, L.; Ng, A.; Yang, X.; Liyuan, L. Correlating the subsidence pattern and land use in Bandung, Indonesia with both Sentinel-1/2 and ALOS-2 satellite images. Int. J. Appl. Earth Obs. Geoinf. 2018, 7, 54–68. [Google Scholar] [CrossRef]
- Zhou, C.; Gong, H.; Chen, B.; Gao, M.; Cao, Q.; Cao, J.; Duan, L.; Zuo, J.; Shi, M. Land Subsidence Response to Different Land Use Types and Water Resource Utilization in Beijing-Tianjin-Hebei, China. Remote Sens. 2020, 12, 457. [Google Scholar] [CrossRef]
- Yu, H.; Gong, H.; Chen, B.; Liu, K.; Gao, M. Analysis of the influence of groundwater on land subsidence in Beijing based on the geographical weighted regression (GWR) model. Sci. Total Environ. 2020, 738, 139405. [Google Scholar] [CrossRef]
- Chen, B.; Gong, H.; Chen, Y.; Li, X.; Zhou, C.; Lei, K.; Zhu, L.; Duan, L.; Zhao, X. Land subsidence and its relation with groundwater aquifers in Beijing Plain of China. Sci. Total Environ. 2020, 735, 139111. [Google Scholar] [CrossRef]
- Zuo, J.; Gong, H.; Chen, B.; Liu, K.; Zhou, C.; Ke, Y. Time-series evolution patterns of land subsidence in the eastern Beijing Plain, China. Remote Sens. 2019, 11, 539. [Google Scholar] [CrossRef]
- Yang, Q.; Ke, Y.; Zhang, D.; Chen, B.; Gong, H.; Lv, M.; Zhu, L.; Li, X. Multi-Scale Analysis of the Relationship between Land Subsidence and Buildings: A Case Study in an Eastern Beijing Urban Area Using the PS-InSAR Technique. Remote Sens. 2018, 10, 1006. [Google Scholar] [CrossRef]
- Yan, X.; Gong, S.; Zeng, Z. Relationship between building density and land subsidence in Shanghai urban zone. Hydrogeol. Eng. Geol. 2002, 29, 21–25. [Google Scholar]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Chaussard, E.; Wdowinski, S.; Cabral-Cano, E.; Amelung, F. Land subsidence in central Mexico detected by ALOS InSAR time-series. Remote Sens. Environ. 2014, 140, 94–106. [Google Scholar] [CrossRef]
- Chen, B.; Gong, H.; Lei, K.; Li, J.; Zhou, C.; Gao, M.; Guan, H.; Lv, W. Land subsidence lagging quantification in the main exploration aquifer layers in Beijing plain, China. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 54–67. [Google Scholar] [CrossRef]
- Abdollahi, S.; Pourghasemi, H.; Ghanbarian, G.; Safaeian, R. Prioritization of effective factors in the occurrence of land subsidence and its susceptibility mapping using an SVM model and their different kernel functions. Bull. Eng. Geol. Environ. 2019, 78, 4017–4034. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Naghibi, S.; Biggs, T.; Soltani, M.; Cerda, A.; Mohammadi, F.; Bui, T. Land subsidence modelling using tree-based machine learning algorithms. Sci. Total Environ. 2019, 672, 239–252. [Google Scholar] [CrossRef]
- Zamanirad, M.; Sarraf, A.; Sedghi, H.; Saremi, A.; Rezaee, P. Modeling the Influence of Groundwater Exploitation on Land Subsidence Susceptibility Using Machine Learning Algorithms. Nat. Resour. Res. 2020, 29, 1127–1141. [Google Scholar] [CrossRef]
- Zhou, C.; Gong, H.; Chen, B.; Li, X.; Li, J.; Wang, X.; Gao, M.; Si, Y.; Guo, L.; Shi, M.; et al. Quantifying the contribution of multiple factors to land subsidence in the Beijing Plain, China with machine learning technology. Geomorphology 2019, 335, 48–61. [Google Scholar] [CrossRef]
- Guo, L.; Gong, H.; Zhu, F.; Zhu, L.; Zhang, Z.; Zhou, C.; Gao, M.; Sun, Y. Analysis of the Spatiotemporal Variation in Land Subsidence on the Beijing Plain, China. Remote Sens. 2019, 11, 1170. [Google Scholar] [CrossRef]
- Chen, B.; Gong, H.; Li, X.; Lei, K.; Zhu, L.; Gao, M.; Zhou, C. Characterization and causes of land subsidence in Beijing, China. Int. J. Remote Sens. 2017, 38, 808–826. [Google Scholar] [CrossRef]
- Zhou, C.; Gong, H.; Chen, B.; Zhu, F.; Duan, G.; Gao, M.; Lu, W. Land subsidence under different land use in the eastern Beijing plain, China 2005-2013 revealed by InSAR timeseries analysis. GISci. Remote Sens. 2016, 53, 671–688. [Google Scholar] [CrossRef]
- Xue, X.; Wei, Y. Boussinesq-Mindlin united solution for pile-net compound foundation additional stress. High. Speed Railw. Technol. 2010, 1, 1–4. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Liu, M.; Song, H.; Li, J. Long-term Settlement of Saturated Soft Clay under Subway Loading. Chin. J. Under Ground Space Eng. 2006, 2, 813–817. [Google Scholar]
- Li, F.; Gong, H.; Chen, B.; Gao, M.; Zhou, C. Subsidence monitoring with TerraSAR-X data in Beijing Central Business District and subway tunnelings, China. IAHS 2020, 382, 125–130. [Google Scholar] [CrossRef]




| Line | Operating Speed (km/h) | Load (t) | Equivalent Static Load (t) |
|---|---|---|---|
| Line 1 | 55 | 26.9 | 8.5 |
| Line 6 | 55 | 25.6 | 8.1 |
| Line 7 | 55 | 25.4 | 8.1 |
| Line Yizhuang | 55 | 25.9 | 8.2 |
| Vehicle | Proportion (%) | Operating Speed (km/h) | Load (t) | Equivalent Static Load (t) |
|---|---|---|---|---|
| Car | 76.3 | 90 | 2.8 | 1 |
| Bus | 12.1 | 90 | 20 | 7.1 |
| Truck | 11.6 | 90 | 9.4 | 3.3 |
| Parameters | Meaning |
|---|---|
| σ | Additional stress engendered from the static and dynamic loads of the grid point |
| Pb | Additional stress engendered from the building load |
| Pt | Additional stress engendered from the subway load |
| Pv | Additional stress engendered from the expressway load |
| n | Number of buildings |
| j | Number of equivalent static loads of the subway load |
| e | Number of average equivalent static loads of the expressway load |
| Pi | Gravity of building i |
| Pj | Gravity of the equivalent static load of subway load j |
| Pk | Gravity of the average equivalent static load of expressway load k |
| X | Projection coordinate of a point in the grid along the longitude in WGS84 |
| Y | Projection coordinate of a point in the grid along the latitude in WGS84 |
| Z | Depth of the point in the grid in WGS84 |
| Xi | Projection coordinate of building i along the longitude in WGS84 |
| Yi | Projection coordinate of building i along the latitude in WGS84 |
| Zi | Foundation depth of building i in WGS84 |
| Xj | Projection coordinate of equivalent static load of subway load j along the longitude in WGS84 |
| Yj | Projection coordinate of the equivalent static load of subway load j along the latitude in WGS84 |
| Zj | Foundation height of the equivalent static load of subway load j in WGS84 |
| Xk | Projection coordinate of the average equivalent static load of expressway load k along the longitude in WGS84 |
| Yk | Projection coordinate of the average equivalent static load of expressway load k along the latitude in WGS84 |
| Zk | Foundation height of the equivalent static load of expressway load k in WGS84 |
| Soil Name | Density (kg/m3) |
|---|---|
| Silty soil | 2014 |
| Artificial fill soil | 1930 |
| Silty clay soil | 2010 |
| Sandy soil | 2000 |
| Gravel | 2200 |
| SRCC | 2003–2010 | 2010–2015 |
|---|---|---|
| The phreatic aquifer | 0.02 | 0.50 |
| The first confined aquifer | 0.29 | 0.19 |
| The second confined aquifer | 0.67 | 0.20 |
| The third confined aquifer | 0.13 | 0.14 |
| Influencing Factors | 2003–2010 | 2010–2015 |
|---|---|---|
| The phreatic aquifer groundwater level gradient | 0.03 | 0.14 |
| The first confined aquifer groundwater level gradient | 0.02 | −0.04 |
| The second confined aquifer groundwater level gradient | 0.04 | 0.01 |
| The third confined aquifer groundwater level gradient | 0.03 | 0.05 |
| The gradient of compressible layers of different thicknesses | 0.07 | 0.07 |
| The additional stress gradient | 0.42 | 0.35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Gong, H.; Chen, B.; Zhou, C.; Guo, L. Analysis of the Contribution Rate of the Influencing Factors to Land Subsidence in the Eastern Beijing Plain, China Based on Extremely Randomized Trees (ERT) Method. Remote Sens. 2020, 12, 2963. https://doi.org/10.3390/rs12182963
Li F, Gong H, Chen B, Zhou C, Guo L. Analysis of the Contribution Rate of the Influencing Factors to Land Subsidence in the Eastern Beijing Plain, China Based on Extremely Randomized Trees (ERT) Method. Remote Sensing. 2020; 12(18):2963. https://doi.org/10.3390/rs12182963
Chicago/Turabian StyleLi, Fengkai, Huili Gong, Beibei Chen, Chaofan Zhou, and Lin Guo. 2020. "Analysis of the Contribution Rate of the Influencing Factors to Land Subsidence in the Eastern Beijing Plain, China Based on Extremely Randomized Trees (ERT) Method" Remote Sensing 12, no. 18: 2963. https://doi.org/10.3390/rs12182963
APA StyleLi, F., Gong, H., Chen, B., Zhou, C., & Guo, L. (2020). Analysis of the Contribution Rate of the Influencing Factors to Land Subsidence in the Eastern Beijing Plain, China Based on Extremely Randomized Trees (ERT) Method. Remote Sensing, 12(18), 2963. https://doi.org/10.3390/rs12182963






