VIIRS Nighttime Light Data for Income Estimation at Local Level
Abstract
1. Introduction
2. Research Overview
3. Study Area and Data
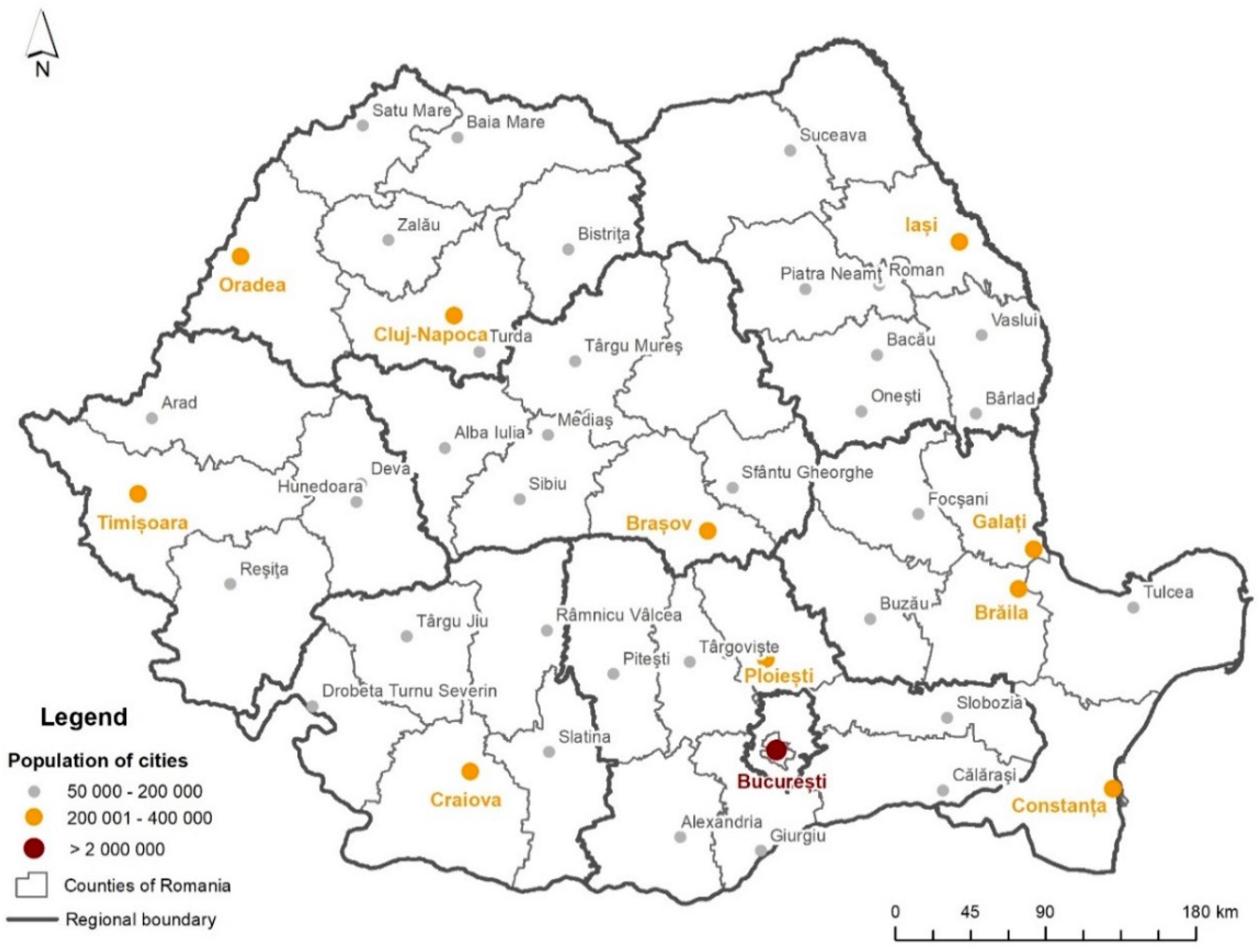
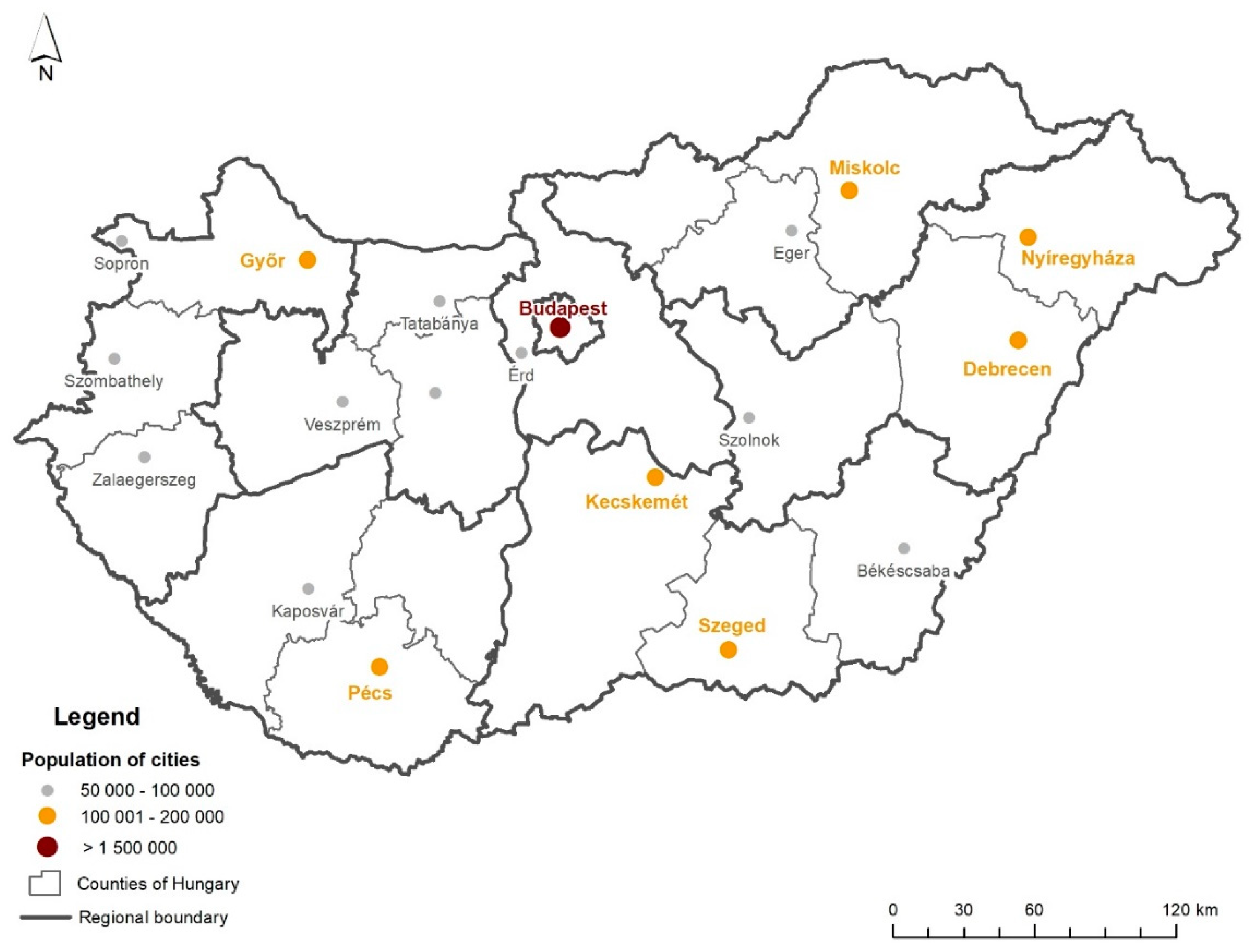
3.1. Study Area
3.2. Data Collection
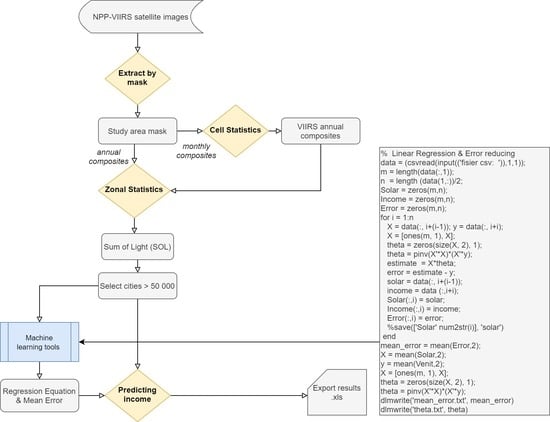
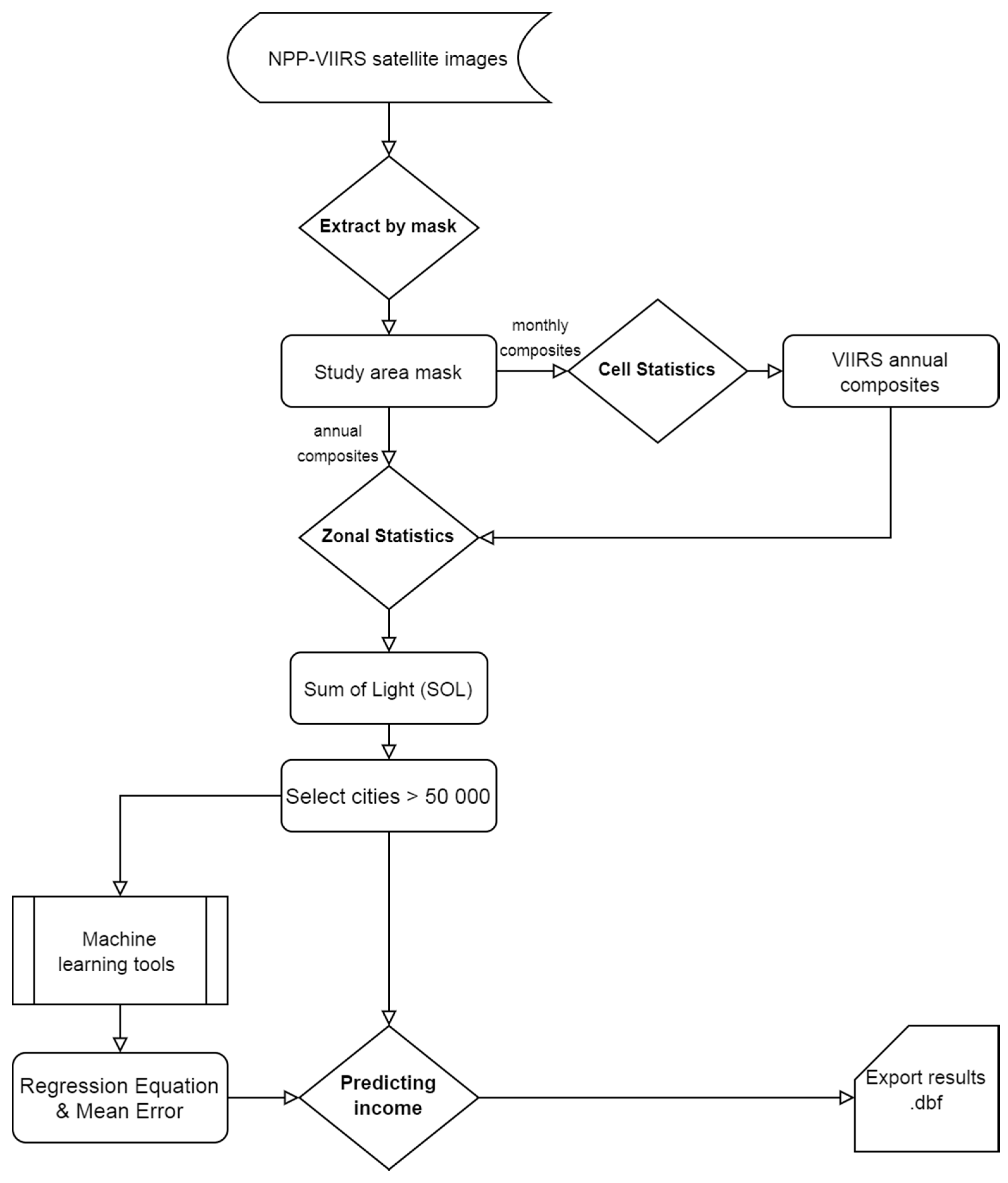
4. Methodology
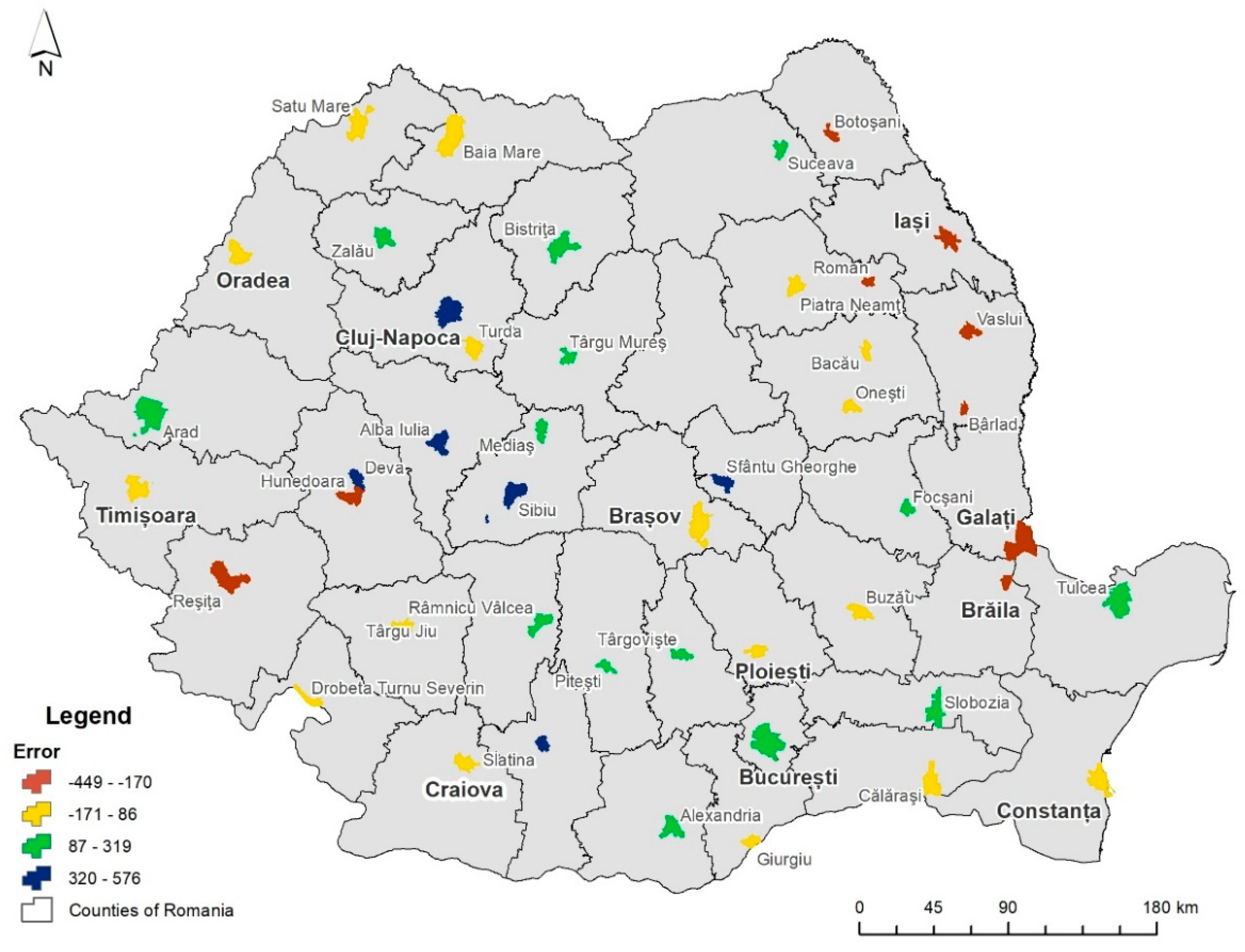
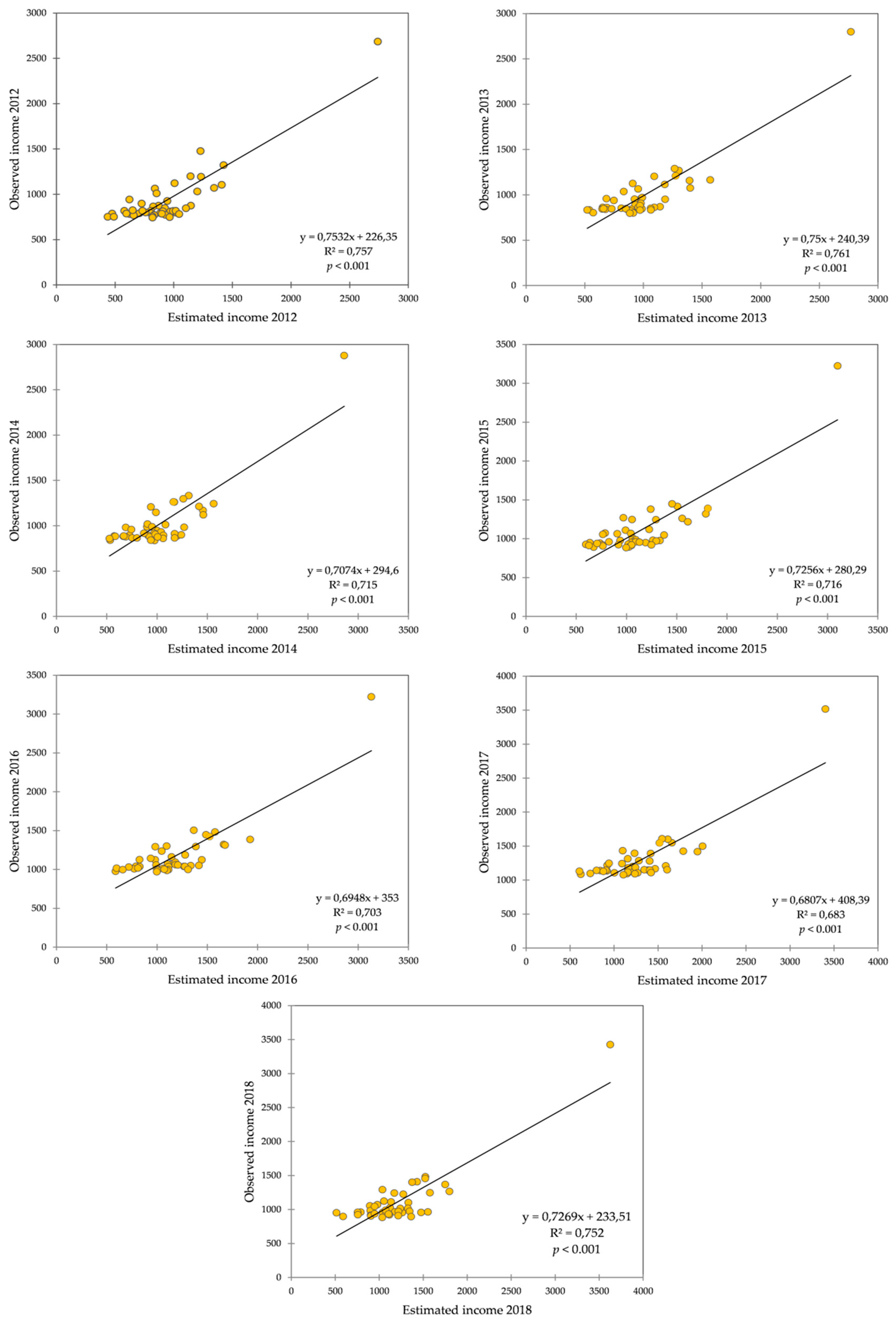
5. Results
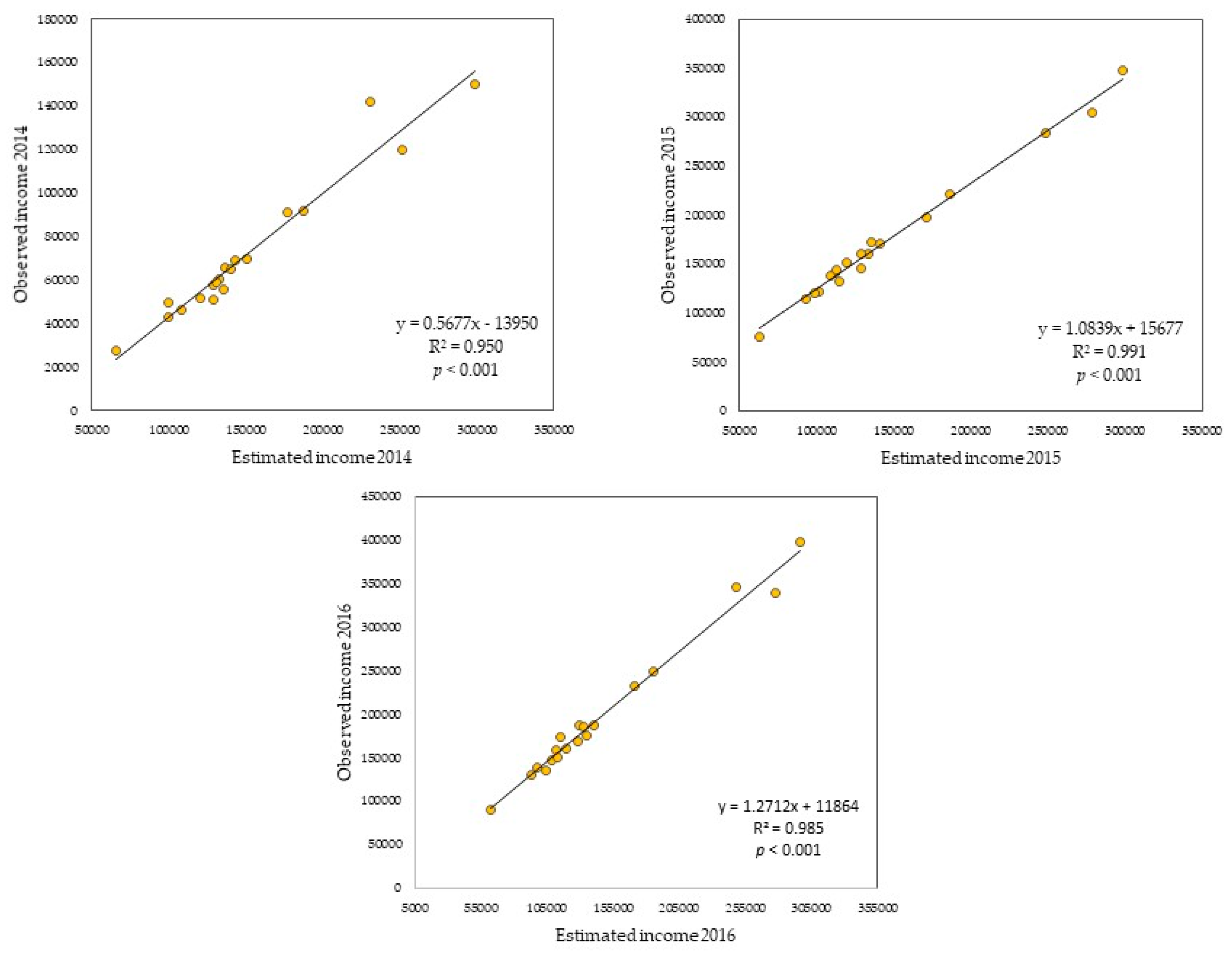
6. Validation of the Results and Discussions
Limitations
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
Appendix C
| Romania | ||
| City | Population | |
| 1 | București | 2,112,483 |
| 2 | Iași | 373,507 |
| 3 | Timișoara | 330,014 |
| 4 | Cluj-Napoca | 323,484 |
| 5 | Constanța | 314,816 |
| 6 | Galați | 303,069 |
| 7 | Craiova | 302,783 |
| 8 | Brașov | 289,878 |
| 9 | Ploiești | 229,641 |
| 10 | Oradea | 221,796 |
| 11 | Brăila | 205,172 |
| 12 | Bacău | 197,285 |
| 13 | Arad | 177,464 |
| 14 | Pitești | 175,047 |
| 15 | Sibiu | 169,177 |
| 16 | Târgu Mureș | 148,490 |
| 17 | Baia Mare | 146,241 |
| 18 | Buzău | 133,376 |
| 19 | Suceava | 122,231 |
| 20 | Botoșani | 120,902 |
| 21 | Satu Mare | 120,736 |
| 22 | Râmnicu Vâlcea | 118,111 |
| 23 | Piatra Neamț | 113,396 |
| 24 | Vaslui | 113,272 |
| 25 | Drobeta Turnu Severin | 107,614 |
| 26 | Târgu Jiu | 95,869 |
| 27 | Bistrița | 93,950 |
| 28 | Focșani | 92,936 |
| 29 | Târgoviște | 92,090 |
| 30 | Tulcea | 87,698 |
| 31 | Reșița | 86,554 |
| 32 | Slatina | 83,389 |
| 33 | Călărași | 76,380 |
| 34 | Alba Iulia | 74,574 |
| 35 | Hunedoara | 72,971 |
| 36 | Bârlad | 71,431 |
| 37 | Deva | 69,527 |
| 38 | Zalău | 69,518 |
| 39 | Roman | 69,479 |
| 40 | Giurgiu | 67,721 |
| 41 | Sfântu Gheorghe | 64,428 |
| 42 | Mediaș | 57,701 |
| 43 | Turda | 56,146 |
| 44 | Slobozia | 51,999 |
| 45 | Onești | 51,580 |
| 46 | Alexandria | 50,832 |
| Hungary | ||
| City | Population | |
| 1 | Budapest | 169,3051 |
| 2 | Debrecen | 203,493 |
| 3 | Szeged | 163,763 |
| 4 | Miskolc | 160,325 |
| 5 | Pécs | 149,030 |
| 6 | Győr | 124,743 |
| 7 | Nyiregyháza | 120,086 |
| 8 | Kecskemét | 110,974 |
| 9 | Székesfehérvár | 97,190 |
| 10 | Szombathely | 76,528 |
| 11 | Szolnok | 71,084 |
| 12 | Tatabánya | 69,092 |
| 13 | Érd | 68,039 |
| 14 | Kaposvár | 63,778 |
| 15 | Békéscsaba | 60,137 |
| 16 | Sopron | 58,458 |
| 17 | Zalaegerszeg | 57,914 |
| 18 | Veszprém | 56,361 |
| 19 | Eger | 53,091 |
References
- O’Grady, M.; O’Hare, G. How Smart Is Your City? Science 2012, 335, 1581–1582. [Google Scholar] [CrossRef] [PubMed]
- United Nations. World Urbanization Prospects: The 2018 Revision. Available online: https://population.un.org/wup/Publications/Files/WUP2018-Report.pdf. (accessed on 13 February 2020).
- Caragliu, A.; Del Bo, C.; Nijkamp, P. Smart Cities in Europe. J. Urban Technol. 2011, 18, 65–82. [Google Scholar] [CrossRef]
- Schaffers, H.; Ratti, C.; Komninos, N. Special issue on smart applications for smart cities: New approaches to innovation: Guest editors’ introduction. J. Theor. Appl. Electron. Commer. Res. 2012, 7, 2–5. [Google Scholar] [CrossRef]
- Turcu, C. Re-thinking sustainability indicators: Local perspectives of urban sustainability. J. Environ. Plan. Manag. 2013, 56, 695–719. [Google Scholar] [CrossRef]
- Berardi, U. Sustainability Assessments of urban Communities through Rating Systems. Environ. Dev. Sustain. 2013, 15, 1573–1591. [Google Scholar] [CrossRef]
- Zhuhadar, L.; Thrasher, E.; Marklin, S.; de Pablos, P.O. The next wave of innovation—Review of smart cities intelligent operation systems. Comput. Hum. Behav. 2017, 66, 273–281. [Google Scholar] [CrossRef]
- Peng, G.; Nunes, M.; Zheng, L. Impacts of low citizen awareness and usage in smart city services: The case of London’s smart parking system. Inf. Syst. e-Bus. Manag. 2017, 15, 845–876. [Google Scholar] [CrossRef]
- Guo, J.; Ma, J.; Li, X.; Zhang, J.; Zhang, T. An attribute-based trust negotiation protocol for D2D communication in smart city balancing trust and privacy. J. Inf. Sci. Eng. 2017, 33, 1007–1023. [Google Scholar] [CrossRef]
- Chong, M.; Habib, A.; Evangelopoulos, N.; Park, H.W. Dynamic capabilities of a smart city: An innovative approach to discovering urban problems and solutions. Gov. Inf. Q. 2018, 35, 682–692. [Google Scholar] [CrossRef]
- Hollands, R.G. Critical interventions into the corporate smart city. Camb. J. Reg. Econ. Soc. 2015, 8, 61–77. [Google Scholar] [CrossRef]
- Colding, J.; Barthel, S. An urban ecology critique on the “Smart City” model. J. Clean. Prod. 2017, 164, 95–101. [Google Scholar] [CrossRef]
- Marsal-Llacuna, M.L.; Segal, M.E. The Intelligenter Method (II) for “smarter” urban policy-making and regulation drafting. Cities 2017, 61, 83–95. [Google Scholar] [CrossRef]
- Mora, L.; Bolici, R.; Deakin, M. The first two decades of Smart-city research: A bibliometric analysis. J. Urban Technol. 2017, 24, 3–27. [Google Scholar] [CrossRef]
- Allam, Z.; Newman, P. Redefining the smart city: Culture, metabolism & governance. Smart Cities 2018, 1, 4–25. [Google Scholar] [CrossRef]
- Yigitcanlar, T.; Kamruzzaman, M.; Foth, M.; Sabatini-Marques, J.; Costa, E.; Ioppolo, G. Can cities become smart without being sustainable? A systematic review of the literature. Sustain. Cities Soc. 2019, 45, 348–365. [Google Scholar] [CrossRef]
- Huovila, A.; Bosch, P.; Airaksinen, M. Comparative analysis of standardized indicators for Smart sustainable cities: What indicators and standards to use and when? Cities 2019, 89, 141–153. [Google Scholar] [CrossRef]
- Nichol, J.; King, B.; Quattrochi, D.; Dowman, I.; Ehlers, M.; Ding, X. Earth Observation for Urban Planning and Management: State of the Art and Recommendations for Application of Earth Observation in Urban Planning. Photogramm. Eng. Remote Sens. 2007, 73, 973–979. [Google Scholar] [CrossRef]
- Musakwa, W.; van Niekerk, A. Earth Observation for Sustainable Urban Planning in Developing Countries: Needs, Trends, and Future Directions. J. Plan. Lit. 2015, 30, 149–160. [Google Scholar] [CrossRef]
- Hall, O. Remote Sensing in Social Science Research. Open Remote Sens. J. 2010, 3, 1–16. [Google Scholar] [CrossRef]
- Santos, T.; Freire, S.; Tenedório, J.A.; Fonseca, A.; Afonso, N.; Navarro, A.; Soares, F. The GeoSat Project: Using Remote Sensing to Keep Pace with Urban Dynamics. IEEE Earthzine. 2011. Available online: http://www.earthzine.org/themes-page/urban-monitoring/ (accessed on 24 February 2020).
- Musakwa, W.; van Niekerk, A. Monitoring sustainable urban development using built-up area indicators: A case study of Stellenbosch, South Africa. Environ. Dev. Sustain. 2015, 17, 547–566. [Google Scholar] [CrossRef]
- Patino, J.E.; Duque, J.C. A review of regional science applications of satellite remote sensing in urban settings. Comput. Environ. Urban Syst. 2013, 37, 1–17. [Google Scholar] [CrossRef]
- Kohli, D.; Sliuzas, R.; Kerle, N.; Stein, A. An ontology of slums for image based classification. Comput. Environ. Urban Syst. 2012, 36, 154–163. [Google Scholar] [CrossRef]
- Novack, T.; Kux, H.J.H. Urban land cover and land use classification of an informal settlement area using the open-source knowledge-based system InterIMAGE. J. Spat. Sci. 2010, 55, 23–41. [Google Scholar] [CrossRef]
- Kadhim, N.; Mourshed, M.; Bray, M. Advances in remote sensing applications for urban sustainability. Euro-Mediterr. J. Environ. Integr. 2016, 1, 1–22. [Google Scholar] [CrossRef]
- Hillson, R.; Coates, A.; Alejandre, J.D.; Jacobsen, K.H.; Ansumana, R.; Bockarie, A.S.; Bangura, U.; Lamin, J.M.; Stenger, D.A. Estimating the size of urban populations using Landsat images: A case study of Bo, Sierra Leone. West Africa. Int. J. Health Geogr. 2019, 18, 16. [Google Scholar] [CrossRef]
- Weng, Q.H. Remote sensing of impervious surfaces in the urban areas: Requirements, methods, and trends. Remote Sens. Environ. 2012, 117, 34–49. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus William, D. VIIRS Nighttime Lights in the Estimation of Cross-Sectional and Time-Series GDP. Remote Sens. 2019, 11, 1057. [Google Scholar] [CrossRef]
- Ivan, K.; Holobâcă, I.-H.; Benedek, J.; Török, I. Potential of Night-Time Lights to Measure Regional Inequality. Remote Sens. 2020, 12, 33. [Google Scholar] [CrossRef]
- Ebener, S.; Murray, C.; Tandon, A.; Elvidge, C. From wealth to health: Modeling the distribution of income per capita at the sub-national level using nighttime lights imagery. Int. J. Health Geogr. 2005, 4, 5–11. [Google Scholar] [CrossRef]
- Li, X.; Ge, L.L.; Chen, X.L. Detecting Zimbabwe’s decadal economic decline using nighttime light imagery. Remote Sens. 2013, 5, 4551–4570. [Google Scholar] [CrossRef]
- Ghosh, T.; Powell, R.L.; Elvidge, C.D.; Baugh, K.E.; Sutton, P.C.; Anderson, S. Shedding Light on the Global Distribution of Economic Activity. Open Geogr. J. 2010, 3, 148–161. [Google Scholar] [CrossRef]
- Bhandari, L.; Roychowdhury, K. Night lights and economic activity in India: A study using DMSP-OLS night time images. Proc. Asia Pac. Adv. Netw. 2011, 32, 218–236. [Google Scholar] [CrossRef]
- Dai, Z.; Hu, Y.; Zhao, G. The Suitability of Different Nighttime Light Data for GDP Estimation at Different Spatial Scales and Regional Levels. Sustainability 2017, 9, 305. [Google Scholar] [CrossRef]
- Basihos, S. Nightlights as a Development Indicator: The Estimation of Gross Provincial Product (GPP) in Turkey (5 May 2016). Available online: https://ssrn.com/abstract=2885518 (accessed on 15 January 2020).
- Jean, N.; Burke, M.; Xie, M.; Davis, W.M.; Lobell, D.B.; Ermon, S. Combining satellite imagery and machine learning to predict poverty. Science 2016, 353, 790–794. [Google Scholar] [CrossRef] [PubMed]
- Määttä, I.; Lessmann, C. Human Lights. Remote Sens. 2019, 11, 2194. [Google Scholar] [CrossRef]
- Subash, S.P.; Kumar, R.R.; Aditya, K.S. Satellite data and machine learning tools for predicting poverty in rural India. Agric. Econ. Res. Rev. 2018, 31, 231–240. [Google Scholar] [CrossRef]
- Benedek, J. Urban policy and urbanisation in the transititon Romania. Rom. Rev. Reg. Stud. 2006, 1, 51–64. [Google Scholar]
- Benedek, J. The Role of Urban Growth Poles in Regional Policy: The Romanian Case. Special Issue. In 2nd International Symposium on New Metropolitan Perspectives–Strategic Planning, Spatial Planning, Economic Programs and Decision Support Tools, Through the Implementation of Horizon/Europe2020. ISTH2020, Reggio Calabria, Italy, 18–20 May 2016; Calabró, F., della Spina, L., Eds.; Springer: Amsterdam, The Netherlands, 2016; Volume 223, pp. 285–290. [Google Scholar] [CrossRef]
- Benedek, J. Spatial differentiation and core-periphery structures in Romania. East. J. Eur. Stud. 2015, 6, 49–61. [Google Scholar]
- Benedek, J.; Lembcke, A.C. Characteristics of recovery and resilience in the Romanian regions. East. J. Eur. Stud. 2017, 8, 95–126. [Google Scholar]
- Ivan, K.; Benedek, J.; Ciobanu, S.M. School-Aged Pedestrian–Vehicle Crash Vulnerability. Sustainability 2019, 11, 1214. [Google Scholar] [CrossRef]
- National Institute of Statistics. Bucharest, Romania. Available online: http://www.insse.ro (accessed on 12 February 2020).
- Török, I.; Benedek, J. Spatial patterns of local income inequalities. J. Settl. Spat. Plan. 2018, 2, 77–91. [Google Scholar] [CrossRef]
- Benedek, J.; Varvari, Ș.; Litan, C. Urban Growth Pole Policy and Regional Development: Old Vine in New Bottles. In Regional and Local Development in Times of Polarization. Re-Thinking Spatial Policies in Europe; Lang, T., Görmar, F., Eds.; Palgrave/MacMillan: Basingstoke, UK, 2019; pp. 173–196. [Google Scholar] [CrossRef]
- Version 1 VIIRS Day/Night Band Nighttime Lights. The Earth Observations Group (EOG). Available online: https://eogdata.mines.edu/download_dnb_composites.html (accessed on 8 January 2020).
- Wu, R.; Yang, D.; Dong, J.; Zhang, L.; Xia, F. Regional inequality in China based on NPP-VIIRS night-time light imagery. Remote Sens. 2018, 10, 240. [Google Scholar] [CrossRef]
- Ministry of Regional Development and Public Administration (MRDPA). Bucharest, Romania. Available online: https://www.mdrap.ro/en/ (accessed on 12 January 2020).
- Pinkovskiy, M.; Sala-i-Martin, X. Lights, camera income! Illuminating the national accounts-household surveys debate. Q. J. Econ. 2016, 131, 579–631. [Google Scholar] [CrossRef]
- Mellander, C.; Lobo, J.; Stolarick, K.; Matheson, Z. Night-Time Light Data: A Good Proxy Measure for Economic Activity? PLoS ONE 2015, 10, e0139779. [Google Scholar] [CrossRef]
- Benedek, J.; Ivan, K. Remote sensing based assessment of variation of spatial disparities. Geogr. Tech. 2018, 13, 1–9. [Google Scholar] [CrossRef]
- Angelescu, I. New Eastern Perspectives? A critical analysis of Romania’s Relations with Moldova, Ukraine and the Black Sea Region. Perspectives 2011, 19, 123–142. [Google Scholar]
- Cristea, M.; Mare, C.; Moldovan, C.; China, A.; Farole, T.; Vințan, A.; Park, J.; Garrett, K.P.; Ionescu-Heroiu, M. Magnet Cities: Migration and Commuting in Romania; World Bank Group: Washington, DC, USA, 2017. [Google Scholar]
- Dospinescu, A.; Russo, G. Romania Systematic Country Diagnostic. Background Notes. Migration. 2018. Available online: https://www.worldbank.org/en/country/romania/publication/romania-systematic-country-diagnostic (accessed on 16 March 2020).
- Bluhm, R.; Krause, M. Top lights—bright cities and their contribution to economic development. CESifo 2018, 7411. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3338765 (accessed on 16 June 2020).
- Godfrey, K. Simple linear regression in medical research. New Engl. J. Med. 1985, 313, 1629–1636. [Google Scholar] [CrossRef]
- Kyba, C.C.M.; Küster, T.; De Miguel, A.S.; Baugh, K.; Jechow, A.; Hölker, F.; Bennie, J.; Elvidge, C.D.; Gaston, K.J.; Guanter, L. Artificially lit surface of Earth at night increasing in radiance and extent. Sci. Adv. 2017, 3, e1701528. [Google Scholar] [CrossRef]
- Kolláth, Z.; Dömény, A.; Kolláth, K.; Nagy, B. Qualifying lighting remodelling in a Hungarian city based on light pollution effects. J. Quant. Spectrosc. Radiat. Transf. 2016, 181, 46–51. [Google Scholar] [CrossRef]
- Hungarian Central Statistical Office. Budapest, Hungary. Available online: https://www.ksh.hu/engstadat (accessed on 29 March 2020).
- Rab, J.; Szemerey, S. About the Smart City Development Model. Inf. Tarsad. 2016, 3, 146–156. [Google Scholar] [CrossRef]
- Egedy, T. Urban development paradigms in the new millennium—The creative city and the smart city. Geogr. Rev. 2017, 3, 254–262. [Google Scholar]
- European Statistics (Eurostat). Available online: https://www.ec.europa.eu/eurostat (accessed on 3 April 2020).
- Li, C.; Zou, L.; Wu, Y.; Xu, H. Potentiality of Using Luojia1-01 Night-Time Light Imagery to Estimate Urban Community Housing Price-A Case Study in Wuhan, China. Sensors 2019, 19, 3167. [Google Scholar] [CrossRef] [PubMed]
- Levin, N.; Kyba, C.C.; Zhang, Q.; De Miguel, A.S.; Román, M.O.; Li, X.; Portnov, B.A.; Molthan, A.L.; Jechow, A.; Miller, S.D.; et al. Remote sensing of night lights: A review and an outlook for the future. Remote. Sens. Environ. 2020, 237, 111443. [Google Scholar] [CrossRef]
| 2012 | 2013 | 2014 | ||||
| Population | r | R2 | r | R2 | r | R2 |
| 40,000 | 0.791 | 0.625 | 0.810 | 0.656 | 0.789 | 0.622 |
| 50,000 | 0.867 | 0.751 | 0.864 | 0.747 | 0.839 | 0.703 |
| 60,000 | 0.873 | 0.762 | 0.873 | 0.762 | 0.850 | 0.722 |
| 70,000 | 0.881 | 0.776 | 0.874 | 0.764 | 0.856 | 0.733 |
| 80,000 | 0.898 | 0.807 | 0.893 | 0.798 | 0.873 | 0.761 |
| 2015 | 2016 | 2017 | ||||
| Population | r | R2 | r | R2 | r | R2 |
| 40,000 | 0.767 | 0.589 | 0.609 | 0.371 | 0.605 | 0.366 |
| 50,000 | 0.829 | 0.687 | 0.831 | 0.690 | 0.826 | 0.682 |
| 60,000 | 0.837 | 0.700 | 0.836 | 0.700 | 0.831 | 0.691 |
| 70,000 | 0.839 | 0.704 | 0.838 | 0.702 | 0.839 | 0.703 |
| 80,000 | 0.848 | 0.719 | 0.854 | 0.730 | 0.853 | 0.728 |
| Before Error Reduction | After Error Reduction | ||
|---|---|---|---|
| r | 0.86 | r | 0.93 |
| R² | 0.75 | R² | 0.87 |
| RMSE 1 | 247 | RMSE | 181 |
| AIC 1 | 404 | AIC | 368 |
| 2014 | 2015 | 2016 | ||||||
|---|---|---|---|---|---|---|---|---|
| r | R2 | RMSE | r | R2 | RMSE | r | R2 | RMSE |
| 0.975 | 0.950 | 19066 | 0.995 | 0.991 | 6678 | 0.992 | 0.985 | 12591 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivan, K.; Holobâcă, I.-H.; Benedek, J.; Török, I. VIIRS Nighttime Light Data for Income Estimation at Local Level. Remote Sens. 2020, 12, 2950. https://doi.org/10.3390/rs12182950
Ivan K, Holobâcă I-H, Benedek J, Török I. VIIRS Nighttime Light Data for Income Estimation at Local Level. Remote Sensing. 2020; 12(18):2950. https://doi.org/10.3390/rs12182950
Chicago/Turabian StyleIvan, Kinga, Iulian-Horia Holobâcă, József Benedek, and Ibolya Török. 2020. "VIIRS Nighttime Light Data for Income Estimation at Local Level" Remote Sensing 12, no. 18: 2950. https://doi.org/10.3390/rs12182950
APA StyleIvan, K., Holobâcă, I.-H., Benedek, J., & Török, I. (2020). VIIRS Nighttime Light Data for Income Estimation at Local Level. Remote Sensing, 12(18), 2950. https://doi.org/10.3390/rs12182950