Satellite Determination of Peatland Water Table Temporal Dynamics by Localizing Representative Pixels of A SWIR-Based Moisture Index
Abstract
1. Introduction
- evaluate the applicability of OPTRAM based on long-term remotely sensed data of different spatial resolutions (namely, Landsat, MODIS, and Landsat spatially rescaled to the MODIS resolution) for monitoring temporal changes in WTD;
- analyze the effects of the vegetation type on the OPTRAM sensitivity to temporal changes in WTD based on available vegetation maps and literature;
- compare the performance of applying in situ and PEATCLSM WTD data for selecting the ‘best pixels’, i.e., OPTRAM pixels with the highest sensitivity to the in situ WTD fluctuations in peatlands;
- assess the quality of ‘best pixels’ selected based on in situ WTD in comparison to PEATCLSM WTD data for WTD monitoring.
2. Materials and Methods
2.1. Study Sites and In Situ WTD Measurements
2.2. The OPtical TRApezoid Model (OPTRAM)
2.2.1. Theoretical Background
2.2.2. OPTRAM Parameterization
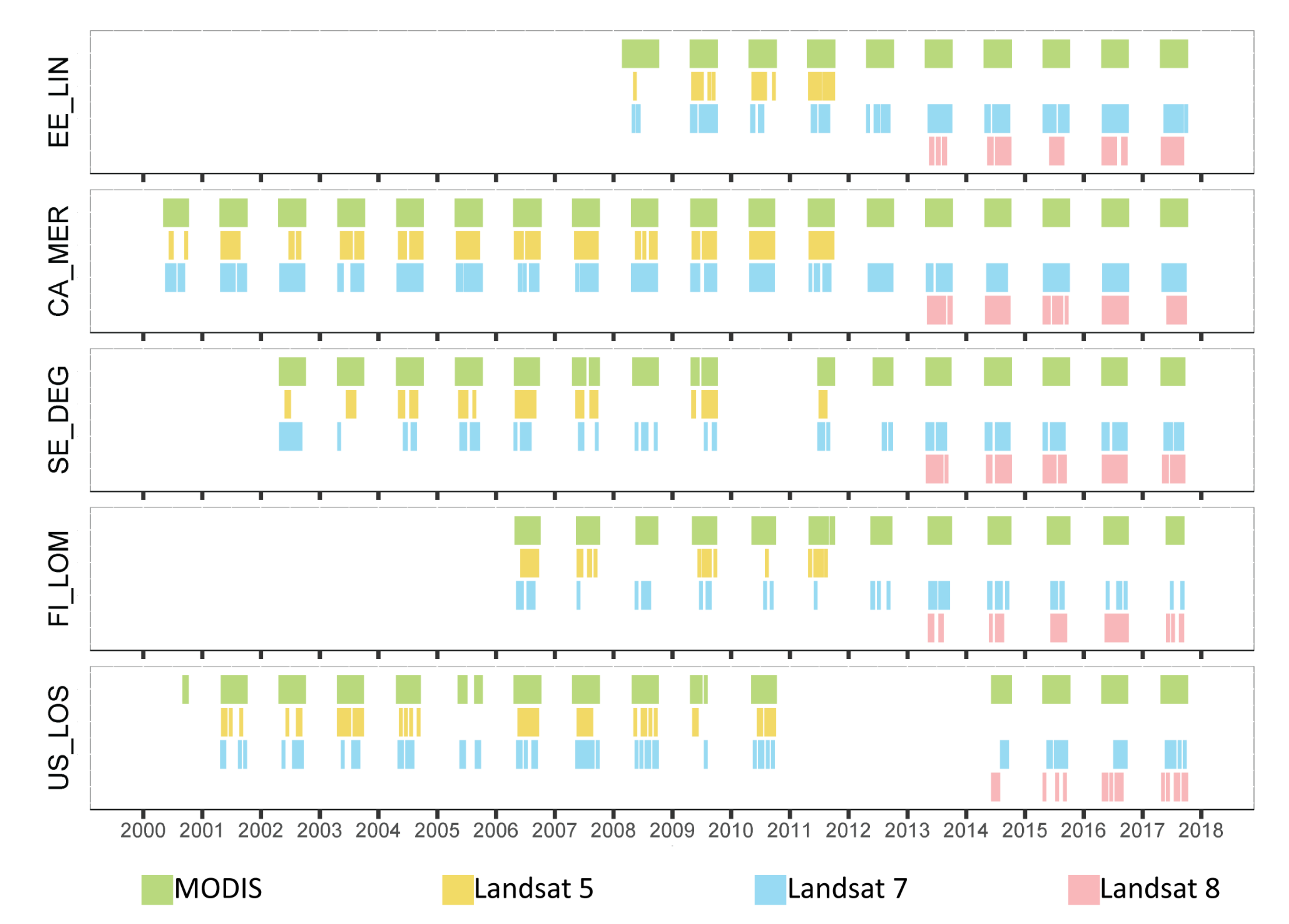
2.3. Satellite Data
2.4. PEATCLSM Data
2.5. Statistical Analysis
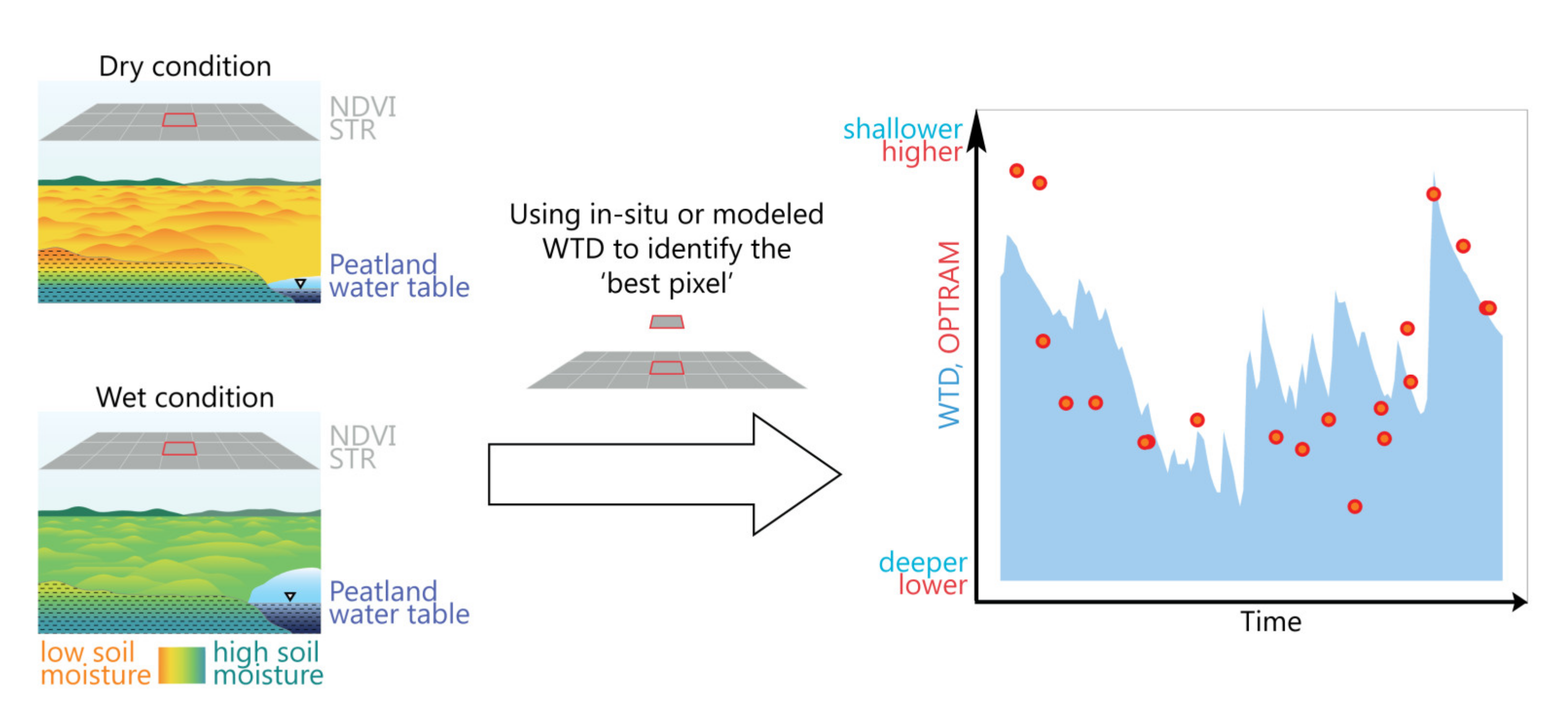
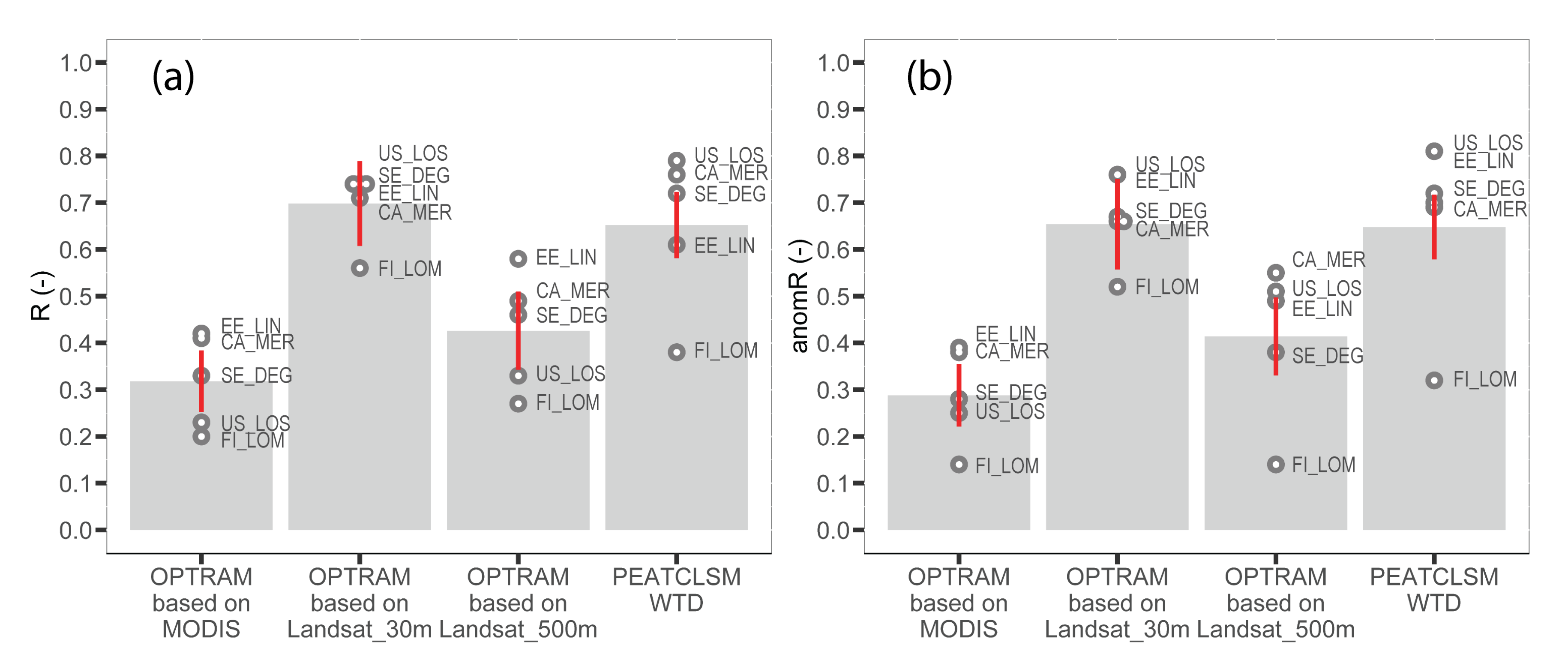
2.6. Selection of the OPTRAM Pixel with the Highest R (‘Best Pixel’)
3. Results
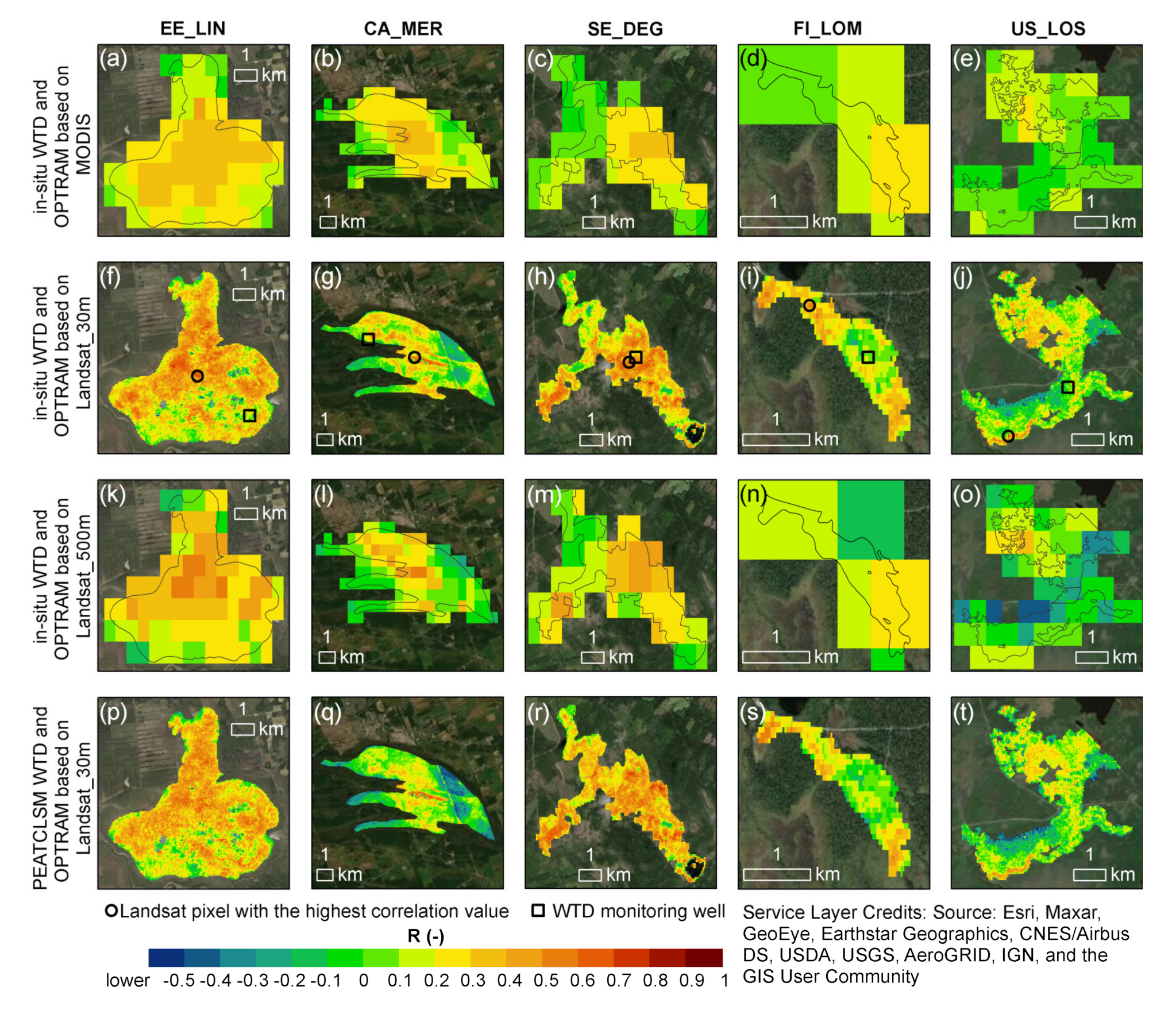
3.1. Spatial Patterns of Temporal Correlation between OPTRAM and WTD
3.2. Dependency of the Temporal Correlation between OPTRAM and WTD on Vegetation Cover
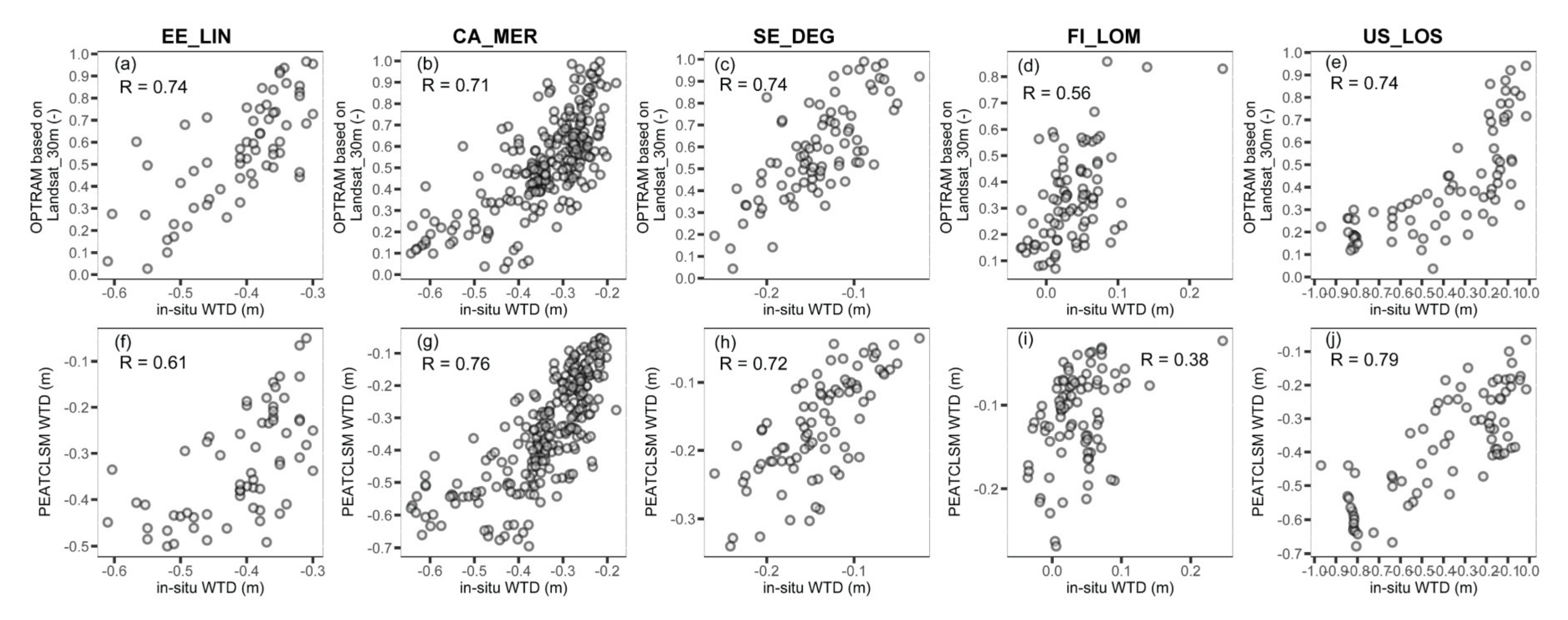
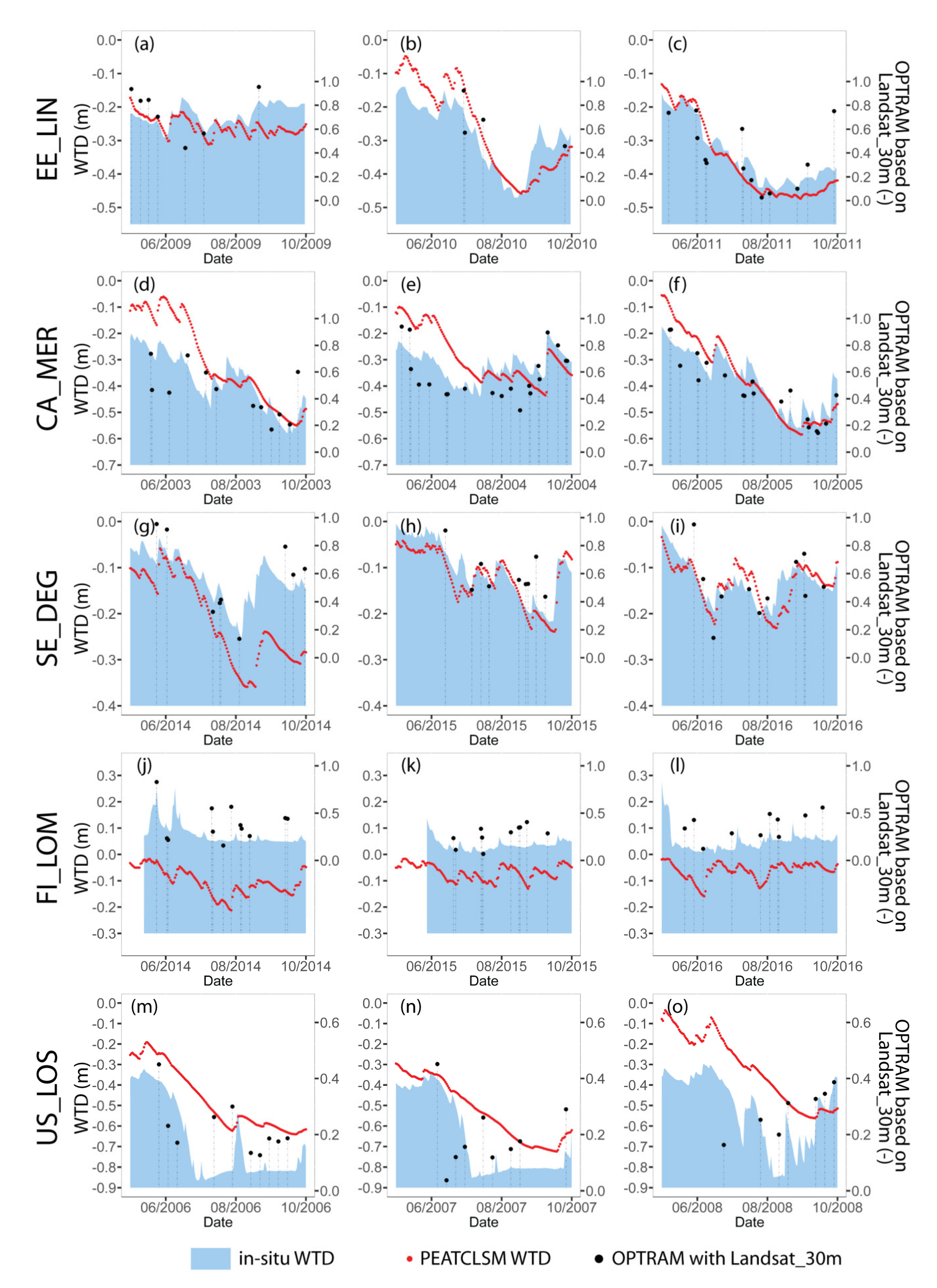
3.3. Temporal Relationships between In Situ WTD and OPTRAM, and between In Situ and Modeled WTD
4. Discussion
4.1. Factors Affecting the Ability of OPTRAM Index to Reveal the Changes in WTD
4.2. Potential of Using In Situ and PEATCLSM WTD for Selecting the OPTRAM Pixels with the Highest Sensitivity to WTD Fluctuations
4.3. Quality Assessment of OPTRAM Index in Comparison to PEATCLSM
5. Conclusions
- OPTRAM is applicable for monitoring WTD dynamics in both bogs and fen peatland types;
- the spatial resolution of remotely sensed data can impact the quality of OPTRAM index, with better results obtained for high spatial resolution Landsat_30m data;
- the highest temporal correlation coefficients (R = 0.56–0.74, an average of 0.7) between in situ WTD and OPTRAM based on Landsat_30m were observed for pixels with dominantly hollow and lawn microtopography covered with mosses and graminoids with little or no shrubs or trees; and
- either historical in situ WTD or PEATCLSM WTD can be used to detect ‘best’ OPTRAM pixels allowing for subsequent near real-time WTD monitoring using OPTRAM.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roulet, N.T.; Lafleur, P.M.; Richard, P.J.H.; Moore, T.R.; Humphreys, E.R.; Bubier, J. Contemporary carbon balance and late Holocene carbon accumulation in a northern peatland. Glob. Chang. Biol. 2007, 13, 397–411. [Google Scholar] [CrossRef]
- Yu, Z.; Loisel, J.; Brosseau, D.P.; Beilman, D.W.; Hunt, S.J. Global peatland dynamics since the Last Glacial Maximum. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Damman, A.W.H. Peat accumulation in fens and bogs: Effects of hydrology and fertility. In Proceedings of the Northern Peatlands in Global Climatic Change; Publications of the Academy of Finland: Helsinki, Finland, 1996; pp. 213–222. [Google Scholar]
- Yu, Z.; Beilman, D.W.; Frolking, S.; MacDonald, G.M.; Roulet, N.T.; Camill, P.; Charman, D.J. Peatlands and Their Role in the Global Carbon Cycle. EOS Trans. Am. Geophys. Union 2011, 92, 97–98. [Google Scholar] [CrossRef]
- Frolking, S.; Roulet, N.T. Holocene radiative forcing impact of northern peatland carbon accumulation and methane emissions. Glob. Chang. Biol. 2007, 13, 1079–1088. [Google Scholar] [CrossRef]
- Helbig, M.; Waddington, J.M.; Alekseychik, P.; Amiro, B.D.; Aurela, M.; Barr, A.G.; Black, T.A.; Blanken, P.D.; Carey, S.K.; Chen, J.; et al. Increasing contribution of peatlands to boreal evapotranspiration in a warming climate. Nat. Clim. Chang. 2020, 10, 555–560. [Google Scholar] [CrossRef]
- Hilbert, D.W.; Roulet, N.; Moore, T. Modelling and analysis of peatlands as dynamical systems. J. Ecol. 2000, 88, 230–242. [Google Scholar] [CrossRef]
- Sulman, B.N.; Desai, A.R.; Saliendra, N.Z.; Lafleur, P.M.; Flanagan, L.B.; Sonnentag, O.; Mackay, D.S.; Barr, A.G.; van der Kamp, G. CO 2 fluxes at northern fens and bogs have opposite responses to inter-annual fluctuations in water table. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Lafleur, P.M.; Moore, T.R.; Roulet, N.T.; Frolking, S. Ecosystem Respiration in a Cool Temperate Bog Depends on Peat Temperature But Not Water Table. Ecosystems 2005, 8, 619–629. [Google Scholar] [CrossRef]
- Lindholm, T.; Markkula, I. Moisture conditions in hummocks and hollows in virgin and drained sites on the raised bog Laaviosuo, southern Finland. Ann. Bot. Fenn. 1984, 21, 241–255. [Google Scholar] [CrossRef]
- Kellner, E.; Halldin, S. Water budget and surface-layer water storage in a Sphagnum bog in central Sweden. Hydrol. Process. 2002, 16, 87–103. [Google Scholar] [CrossRef]
- Price, J.S.; Schlotzhauer, S.M. Importance of shrinkage and compression in determining water storage changes in peat: The case of a mined peatland. Hydrol. Process. 1999, 13, 2591–2601. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.Ö.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Wetland Water Level Monitoring Using Interferometric Synthetic Aperture Radar (InSAR): A Review. Can. J. Remote Sens. 2018, 44, 247–262. [Google Scholar] [CrossRef]
- Asmuß, T.; Bechtold, M.; Tiemeyer, B. On the Potential of Sentinel-1 for High Resolution Monitoring of Water Table Dynamics in Grasslands on Organic Soils. Remote Sens. 2019, 11, 1659. [Google Scholar] [CrossRef]
- Bauer-Marschallinger, B.; Freeman, V.; Cao, S.; Paulik, C.; Schaufler, S.; Stachl, T.; Modanesi, S.; Massari, C.; Ciabatta, L.; Brocca, L.; et al. Toward Global Soil Moisture Monitoring with Sentinel-1: Harnessing Assets and Overcoming Obstacles. IEEE Trans. Geosci. Remote Sens. 2019, 57, 520–539. [Google Scholar] [CrossRef]
- Tiner, R.W.; Lang, M.W.; Klemas, V. V Remote Sensing of Wetlands: Applications and Advances; CRC Press: Boca Raton, FL, USA, 2015; ISBN 1482237385. [Google Scholar]
- Bechtold, M.; Schlaffer, S.; Tiemeyer, B.; De Lannoy, G. Inferring Water Table Depth Dynamics from ENVISAT-ASAR C-Band Backscatter over a Range of Peatlands from Deeply-Drained to Natural Conditions. Remote Sens. 2018, 10, 536. [Google Scholar] [CrossRef]
- Jackson, T.J.; Chen, D.; Cosh, M.; Li, F.; Anderson, M.; Walthall, C.; Doriaswamy, P.; Hunt, E.R. Vegetation water content mapping using Landsat data derived normalized difference water index for corn and soybeans. In Proceedings of the Remote Sensing of Environment; Elsevier: Amsterdam, The Netherlands, 2004; Volume 92, pp. 475–482. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The optical trapezoid model: A novel approach to remote sensing of soil moisture applied to Sentinel-2 and Landsat-8 observations. Remote Sens. Environ. 2017, 198, 52–68. [Google Scholar] [CrossRef]
- Goward, S.N.; Cruickshanks, G.D.; Hope, A.S. Observed relation between thermal emission and reflected spectral radiance of a complex vegetated landscape. Remote Sens. Environ. 1985, 18, 137–146. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Franz, T.E.; Jones, S.; Tuller, M. Mapping soil moisture with the OPtical TRApezoid Model (OPTRAM) based on long-term MODIS observations. Remote Sens. Environ. 2018, 211, 425–440. [Google Scholar] [CrossRef]
- Huang, F.; Wang, P.; Ren, Y.; Liu, R. Estimating Soil Moisture Using the Optical Trapezoid Model (OPTRAM) in a Semi-Arid Area of SONGNEN Plain, China Based on Landsat-8 Data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS); Institute of Electrical and Electronics Engineers Inc., Yokohama, Japan, 28 July–2 August 2019; pp. 7010–7013. [Google Scholar] [CrossRef]
- Babaeian, E.; Sidike, P.; Newcomb, M.S.; Maimaitijiang, M.; White, S.A.; Demieville, J.; Ward, R.W.; Sadeghi, M.; LeBauer, D.S.; Jones, S.B.; et al. A New Optical Remote Sensing Technique for High-Resolution Mapping of Soil Moisture. Front. Big Data 2019, 2, 37. [Google Scholar] [CrossRef]
- Burdun, I.; Bechtold, M.; Sagris, V.; Komisarenko, V.; De Lannoy, G.; Mander, Ü. A comparison of three trapezoid models using optical and thermal satellite imagery for water table depth monitoring in Estonian bogs. Remote Sens. 2020, 12, 1980. [Google Scholar] [CrossRef]
- Harris, A.; Bryant, R.G.; Baird, A.J. Detecting near-surface moisture stress in Sphagnum spp. Remote Sens. Environ. 2005, 97, 371–381. [Google Scholar] [CrossRef]
- Bryant, R.G.; Baird, A.J. The spectral behaviour of Sphagnum canopies under varying hydrological conditions. Geophys. Res. Lett. 2003, 30, 1134. [Google Scholar] [CrossRef]
- Harris, A. Spectral reflectance and photosynthetic properties of Sphagnum mosses exposed to progressive drought. Ecohydrology 2008, 1, 35–42. [Google Scholar] [CrossRef]
- Rydin, H.; McDonald, A.J.S. Tolerance of Sphagnum to water level. J. Bryol. 1985, 13, 571–578. [Google Scholar] [CrossRef]
- Murphy, M.T.; Moore, T.R. Linking root production to aboveground plant characteristics and water table in a temperate bog. Plant Soil 2010, 336, 219–231. [Google Scholar] [CrossRef]
- Strack, M.; Waddington, J.M.; Rochefort, L.; Tuittila, E.S. Response of vegetation and net ecosystem carbon dioxide exchange at different peatland microforms following water table drawdown. J. Geophys. Res. Biogeosciences 2006, 111. [Google Scholar] [CrossRef]
- Lafleur, P.M.; Hember, R.A.; Admiral, S.W.; Roulet, N.T. Annual and seasonal variability in evapotranspiration and water table at a shrub-covered bog in southern Ontario, Canada. Hydrol. Process. 2005, 19, 3533–3550. [Google Scholar] [CrossRef]
- Finlayson, C.M.; Milton, G.R. Peatlands. In The Wetland Book II: Distribution, Description, and Conservation; Springer Nature: Berlin/Heidelberg, Germany, 2018; Volume 1, pp. 227–244. ISBN 9789400740013. [Google Scholar]
- Ivanov, K.E. Water Movement in Mirelands; Academic Press: London, UK, 1981. [Google Scholar]
- Letts, M.G.; Comer, N.T.; Roulet, N.T.; Skarupa, M.R.; Verseghy, D.L. Parametrization of peatland hydraulic properties for the Canadian land surface scheme. Atmos. Ocean 2000, 38, 141–160. [Google Scholar] [CrossRef]
- Malhotra, A.; Roulet, N.T.; Wilson, P.; Giroux-Bougard, X.; Harris, L.I. Ecohydrological feedbacks in peatlands: An empirical test of the relationship among vegetation, microtopography and water table. Ecohydrology 2016, 9, 1346–1357. [Google Scholar] [CrossRef]
- Wilson, P. The Relationship among Micro-Topographic Variation, Water Table Depth and Biogeochemistry in an Ombrotrophic Bog; McGill University: Montreal, QC, Canada, 2012. [Google Scholar]
- Hokanson, K.J.; Moore, P.A.; Lukenbach, M.C.; Devito, K.J.; Kettridge, N.; Petrone, R.M.; Mendoza, C.A.; Waddington, J.M. A hydrogeological landscape framework to identify peatland wildfire smouldering hot spots. Ecohydrology 2018, 11, e1942. [Google Scholar] [CrossRef]
- Howie, S.A.; van Meerveld, H.J. Regional and local patterns in depth to water table, hydrochemistry and peat properties of bogs and their laggs in coastal British Columbia. Hydrol. Earth Syst. Sci. 2013, 17, 3421–3435. [Google Scholar] [CrossRef]
- Bechtold, M.; De Lannoy, G.; Koster, R.D.; Reichle, R.H.; Mahanama, S.; Bleuten, W.; Bourgault, M.A.; Brümmer, C.; Burdun, I.; Desai, A.R.; et al. PEAT-CLSM: A Specific Treatment of Peatland Hydrology in the NASA Catchment Land Surface Model. J. Adv. Model. Earth Syst. 2019, 11, 2130–2162. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J.; Ducharne, A.; Stieglitz, M.; Kumar, P. A catchment-based approach to modeling land surface processes in a general circulation model 1. Model structure. J. Geophys. Res. Atmos. 2000, 105, 24809–24822. [Google Scholar] [CrossRef]
- Ducharne, A.; Koster, R.D.; Suarez, M.J.; Stieglitz, M.; Kumar, P. A catchment-based approach to modeling land surface processes in a general circulation model 2. Parameter estimation and model demonstration. J. Geophys. Res. Atmos. 2000, 105, 24823–24838. [Google Scholar] [CrossRef]
- Xu, J.; Morris, P.J.; Liu, J.; Holden, J. PEATMAP: Refining estimates of global peatland distribution based on a meta-analysis. Catena 2018, 160, 134–140. [Google Scholar] [CrossRef]
- Burdun, I.; Sagris, V.; Mander, Ü. Relationships between field-measured hydrometeorological variables and satellite-based land surface temperature in a hemiboreal raised bog. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 295–301. [Google Scholar] [CrossRef]
- Strilesky, S.L.; Humphreys, E.R. A comparison of the net ecosystem exchange of carbon dioxide and evapotranspiration for treed and open portions of a temperate peatland. Agric. For. Meteorol. 2012, 153, 45–53. [Google Scholar] [CrossRef]
- Peichl, M.; Sagerfors, J.; Lindroth, A.; Buffam, I.; Grelle, A.; Klemedtsson, L.; Laudon, H.; Nilsson, M.B. Energy exchange and water budget partitioning in a boreal minerogenic mire. J. Geophys. Res. Biogeosci. 2013, 118, 1–13. [Google Scholar] [CrossRef]
- Aurela, M.; Lohila, A.; Tuovinen, J.-P.; Hatakka, J.; Penttilä, T.; Laurila, T. Carbon dioxide and energy flux measurements in four northern-boreal ecosystems at Pallas. Boreal Environ. Res. 2015, 20, 455–473. [Google Scholar]
- Aurela, M.; Lohila, A.; Tuovinen, J.-P.; Hatakka, J.; Laurila, T.; Riutta, T. Carbon dioxide exchange on a northern boreal fen. J. Name Boreal Environ. Res. 2009, 14, 699–710. [Google Scholar]
- Räsänen, A.; Aurela, M.; Juutinen, S.; Kumpula, T.; Lohila, A.; Penttilä, T.; Virtanen, T. Detecting northern peatland vegetation patterns at ultra-high spatial resolution. Remote Sens. Ecol. Conserv. 2019, 2, 140. [Google Scholar] [CrossRef]
- Sulman, B.N.; Desai, A.R.; Cook, B.D.; Saliendra, N.; Mackay, D.S. Contrasting carbon dioxide fluxes between a drying shrub wetland in Northern Wisconsin, USA, and nearby forests. Biogeosciences 2009, 6, 1115–1126. [Google Scholar] [CrossRef]
- Carlson, T. An Overview of the “Triangle Method” for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Sadeghi, M.; Jones, S.B.; Philpot, W.D. A linear physically-based model for remote sensing of soil moisture using short wave infrared bands. Remote Sens. Environ. 2015, 164, 66–76. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, Y.; Yao, Y.; Lu, J.; Pu, X.; Hu, T.; Wang, P. Evaluation of an OPtical TRApezoid Model (OPTRAM) to retrieve soil moisture in the Sanjiang Plain of Northeast China. Earth Space Sci. 2020, 7. [Google Scholar] [CrossRef]
- Ambrosone, M.; Matese, A.; Di Gennaro, S.F.; Gioli, B.; Tudoroiu, M.; Genesio, L.; Miglietta, F.; Baronti, S.; Maienza, A.; Ungaro, F.; et al. Retrieving soil moisture in rainfed and irrigated fields using Sentinel-2 observations and a modified OPTRAM approach. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102113. [Google Scholar] [CrossRef]
- Mananze, S.; Pôças, I. Agricultural drought monitoring based on soil moisture derived from the optical trapezoid model in Mozambique. J. Appl. Remote Sens. 2019, 13, 1. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Bechtold, M.; De Lannoy, G.; Reichle, R.H. PEAT-CLSM Simulation Output (Northern Peatlands) Version 1. Available online: https://osf.io/e58ym/ (accessed on 1 July 2020).
- De Lannoy, G.J.M.; Reichle, R.H. Global assimilation of multiangle and multipolarization SMOS brightness temperature observations into the GEOS-5 catchment land surface model for soil moisture estimation. J. Hydrometeorol. 2016, 17, 669–691. [Google Scholar] [CrossRef]
- Bechtold, M.; De Lannoy, G.; Reichle, R.H.; Roose, D.; Balliston, N.; Burdun, I.; Devito, K.; Kurbatova, J.; Munir, T.M.; Zarov, E.A. Improved Groundwater Table and L-band Brightness Temperature Estimates for Northern Hemisphere Peatlands Using New Model Physics and SMOS Observations in a Global Data Assimilation Framework. Remote Sens. Environ. 2020, 246, 111805. [Google Scholar] [CrossRef]
- Estonian Land Board Download Topographic Data. Available online: https://geoportaal.maaamet.ee/index.php?lang_id=2&page_id=618 (accessed on 21 February 2020).
- Estonian Land Board Orthophotos. Available online: https://geoportaal.maaamet.ee/index.php?page_id=309&lang_id=2 (accessed on 2 July 2020).
- Lode, E.; Küttim, M.; Kiivit, I.K. Indicative effects of climate change on groundwater levels in estonian raised bogs over 50 years. Mires Peat 2017, 19. [Google Scholar] [CrossRef]
- Keskkonnaagentuur. Maastike Kaugseire 2002; Keskkonnaagentuur: Tallinn, Estonia, 2002. [Google Scholar]
- Arroyo-Mora, J.P.; Kalacska, M.; Soffer, R.J.; Moore, T.R.; Roulet, N.T.; Juutinen, S.; Ifimov, G.; Leblanc, G.; Inamdar, D.; Arroyo-Mora, J.P.; et al. Airborne Hyperspectral Evaluation of Maximum Gross Photosynthesis, Gravimetric Water Content, and CO2 Uptake Efficiency of the Mer Bleue Ombrotrophic Peatland. Remote Sens. 2018, 10, 565. [Google Scholar] [CrossRef]
- Li, J.; Chen, W.; Touzi, R. Optimum RADARSAT-1 configurations for wetlands discrimination: A case study of the Mer Bleue peat bog. Can. J. Remote Sens. 2007, 33, S46–S55. [Google Scholar] [CrossRef]
- Sonnentag, O.; Chen, J.M.; Roberts, D.A.; Talbot, J.; Halligan, K.Q.; Govind, A. Mapping tree and shrub leaf area indices in an ombrotrophic peatland through multiple endmember spectral unmixing. Remote Sens. Environ. 2007, 109, 342–360. [Google Scholar] [CrossRef]
- Kalacska, M.; Arroyo-Mora, J.; de Gea, J.; Snirer, E.; Herzog, C.; Moore, T. Videographic Analysis of Eriophorum Vaginatum Spatial Coverage in an Ombotrophic Bog. Remote Sens. 2013, 5, 6501–6512. [Google Scholar] [CrossRef]
- Talbot, J.; Richard, P.J.H.; Roulet, N.T.; Booth, R.K. Assessing long-term hydrological and ecological responses to drainage in a raised bog using paleoecology and a hydrosequence. J. Veg. Sci. 2010, 21, 143–156. [Google Scholar] [CrossRef]
- Arens, M. The Effect of Spatial Organization of Peatland Patterns on the Hydrology. Master’s Thesis, Wageningen University, Wageningen, The Netherlands, 2017. [Google Scholar]
- Osterwalder, S.; Sommar, J.; Åkerblom, S.; Jocher, G.; Fritsche, J.; Nilsson, M.B.; Bishop, K.; Alewell, C. Comparative study of elemental mercury flux measurement techniques over a Fennoscandian boreal peatland. Atmos. Environ. 2018, 172, 16–25. [Google Scholar] [CrossRef]
- Nijp, J.J.; Metselaar, K.; Limpens, J.; Bartholomeus, H.M.; Nilsson, M.B.; Berendse, F.; van der Zee, S.E.A.T.M. High-resolution peat volume change in a northern peatland: Spatial variability, main drivers, and impact on ecohydrology. Ecohydrology 2019, 12, e2114. [Google Scholar] [CrossRef]
- ICOS Degerö Vegetation. Available online: https://www.icos-sweden.se/station_degero.html (accessed on 1 July 2020).
- Wiscland 2 Land Cover Database. Available online: https://dnr.wisconsin.gov/maps/WISCLAND.html (accessed on 26 June 2020).
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- DuBois, S.; Desai, A.R.; Singh, A.; Serbin, S.P.; Goulden, M.L.; Baldocchi, D.D.; Ma, S.; Oechel, W.C.; Wharton, S.; Kruger, E.L.; et al. Using imaging spectroscopy to detect variation in terrestrial ecosystem productivity across a water-stressed landscape. Ecol. Appl. 2018, 28, 1313–1324. [Google Scholar] [CrossRef] [PubMed]
- Serbin, S.P.; Singh, A.; Desai, A.R.; Dubois, S.G.; Jablonski, A.D.; Kingdon, C.C.; Kruger, E.L.; Townsend, P.A. Remotely estimating photosynthetic capacity, and its response to temperature, in vegetation canopies using imaging spectroscopy. Remote Sens. Environ. 2015, 167, 78–87. [Google Scholar] [CrossRef]
- Firigato, J.O. Soil_Moisture_OPTRAM_Sentinel2. Available online: https://github.com/joaootavio007/Google-Earth-Engine/blob/a57546b6da32bb3df2b672cdc1714b71b75954f1/Soil_Moisture_OPTRAM_Sentinel2.js (accessed on 22 August 2020).
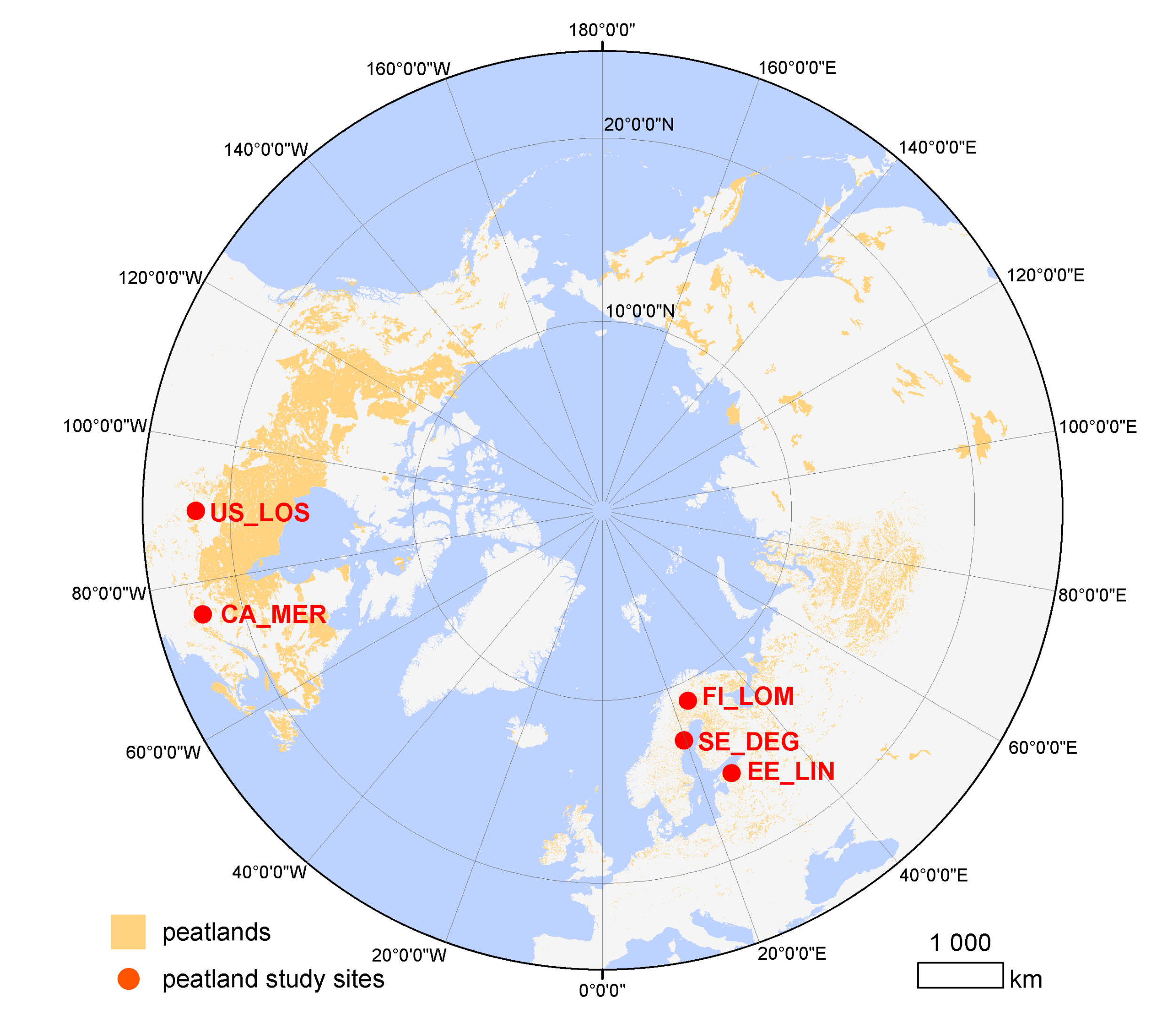


| Site Name and Location | Site Code | WTD Data Period | Peatland Type | Dominant Vegetation | Lat. | Lon. | Ref. |
|---|---|---|---|---|---|---|---|
| Linnusaare, Estonia | EE_LIN | 2008–2017 | bog | Mosses, sedges, shrubs, sparse dwarf pines | 58.88 | 26.20 | [46] |
| Mer Bleue, Canada | CA_MER | 2000–2017 | bog | Shrubs, sedges, black spruce, mosses | 45.41 | −75.52 | [34,47] |
| Degerö Stormyr, Sweden | SE_DEG | 2002–2017 | fen | Sedges, mosses, shrubs | 64.18 | 19.55 | [48] |
| Lompolo-jänkkä, Finland | FI_LOM | 2006–2017 | fen | Sedges, low shrubs, mosses, downy willows, and dwarf birch | 67.99 | 24.20 | [49,50,51] |
| Lost Creek, USA | US_LOS | 2000–2017 | fen | Alder, willow, sedges | 46.08 | −89.97 | [52] |
| Site Code | Characteristics of Sites with High R | Characteristics of Sites with Low R |
|---|---|---|
| EE_LIN | Hollow-ridge complex with permanently flooded depressions. Pixels’ area is mainly covered with hollows [62,63]. The dominant vegetation is Sphagnum species and graminoids [64]. | Hummocks covered with dwarf pines, graminoids, and Sphagnum species [65]. |
| CA_MER | A higher density of hollows microtopography with lower plant area index [66]. Vegetation is dominated by Sphagnum species, evergreen shrubs, deciduous shrubs, and sedges [67,68,69]. | Relatively dense tree canopy of black spruce and tamarack [47,66]; drained areas east of ditch with gray birch, tamarack, and white pine [70]. |
| SE_DEG | Permanently flooded Sphagnum-dominated hollows, lawns, and flarks [71,72,73]. | Forested peatland with pine and spruce [74]. |
| FI_LOM * | A high percentage of Sphagnum cover (70–98%). Sites are covered with mosses, graminoids, shrubs, and trees. This territory matches with the area covered by vegetation community described as cluster 3 [51]. | Corresponds to riparian areas of the stream running through the FI_LOM site. It is primarily vegetated by 60-cm-high Salix [51]. |
| US_LOS | Emergent or wet meadows, and lowland shrubs [75]. | Forested wetland and shrubs [75]. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burdun, I.; Bechtold, M.; Sagris, V.; Lohila, A.; Humphreys, E.; Desai, A.R.; Nilsson, M.B.; De Lannoy, G.; Mander, Ü. Satellite Determination of Peatland Water Table Temporal Dynamics by Localizing Representative Pixels of A SWIR-Based Moisture Index. Remote Sens. 2020, 12, 2936. https://doi.org/10.3390/rs12182936
Burdun I, Bechtold M, Sagris V, Lohila A, Humphreys E, Desai AR, Nilsson MB, De Lannoy G, Mander Ü. Satellite Determination of Peatland Water Table Temporal Dynamics by Localizing Representative Pixels of A SWIR-Based Moisture Index. Remote Sensing. 2020; 12(18):2936. https://doi.org/10.3390/rs12182936
Chicago/Turabian StyleBurdun, Iuliia, Michel Bechtold, Valentina Sagris, Annalea Lohila, Elyn Humphreys, Ankur R. Desai, Mats B. Nilsson, Gabrielle De Lannoy, and Ülo Mander. 2020. "Satellite Determination of Peatland Water Table Temporal Dynamics by Localizing Representative Pixels of A SWIR-Based Moisture Index" Remote Sensing 12, no. 18: 2936. https://doi.org/10.3390/rs12182936
APA StyleBurdun, I., Bechtold, M., Sagris, V., Lohila, A., Humphreys, E., Desai, A. R., Nilsson, M. B., De Lannoy, G., & Mander, Ü. (2020). Satellite Determination of Peatland Water Table Temporal Dynamics by Localizing Representative Pixels of A SWIR-Based Moisture Index. Remote Sensing, 12(18), 2936. https://doi.org/10.3390/rs12182936








