New Insights into Long-Term Aseismic Deformation and Regional Strain Rates from GNSS Data Inversion: The Case of the Pollino and Castrovillari Faults
Abstract
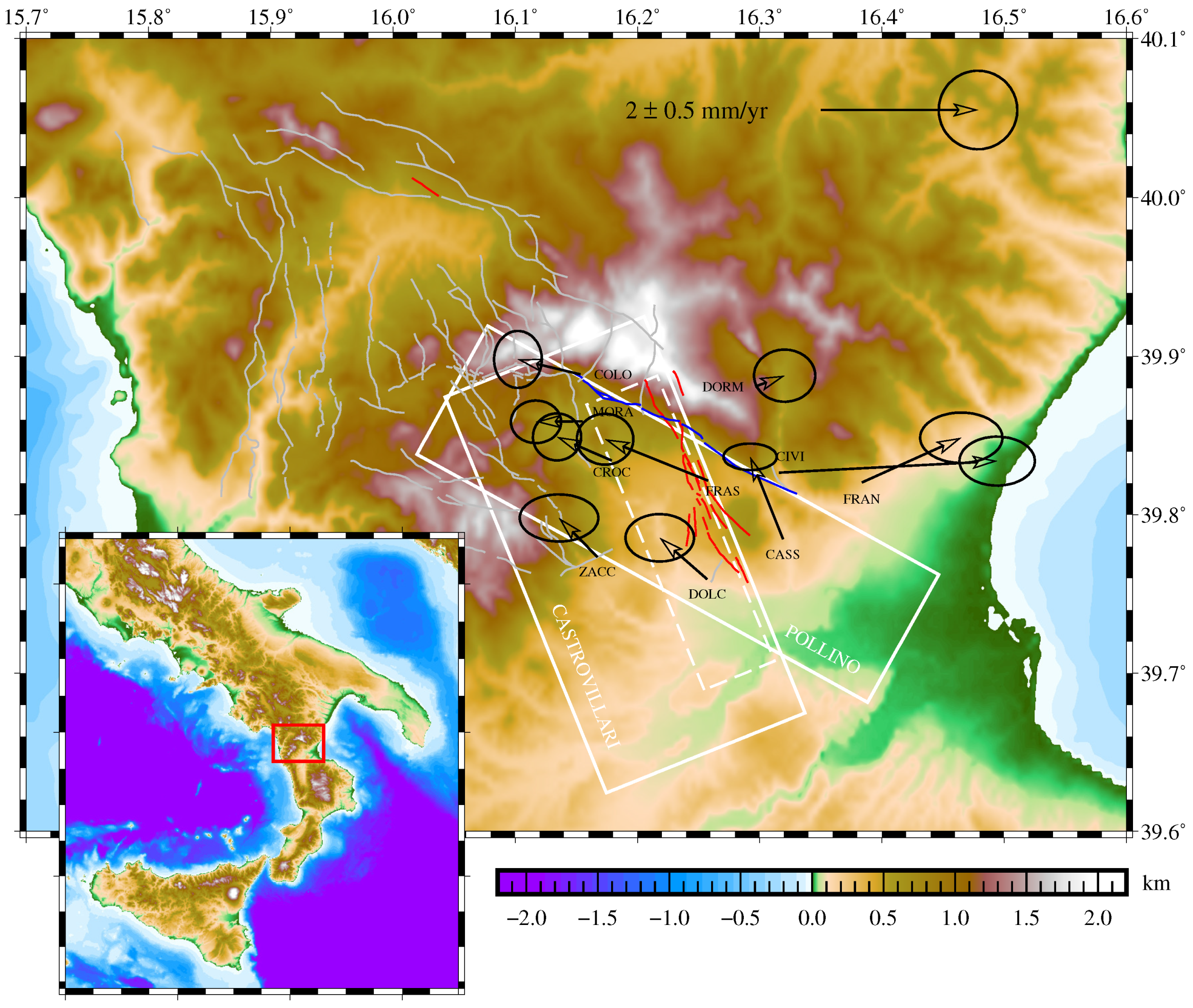
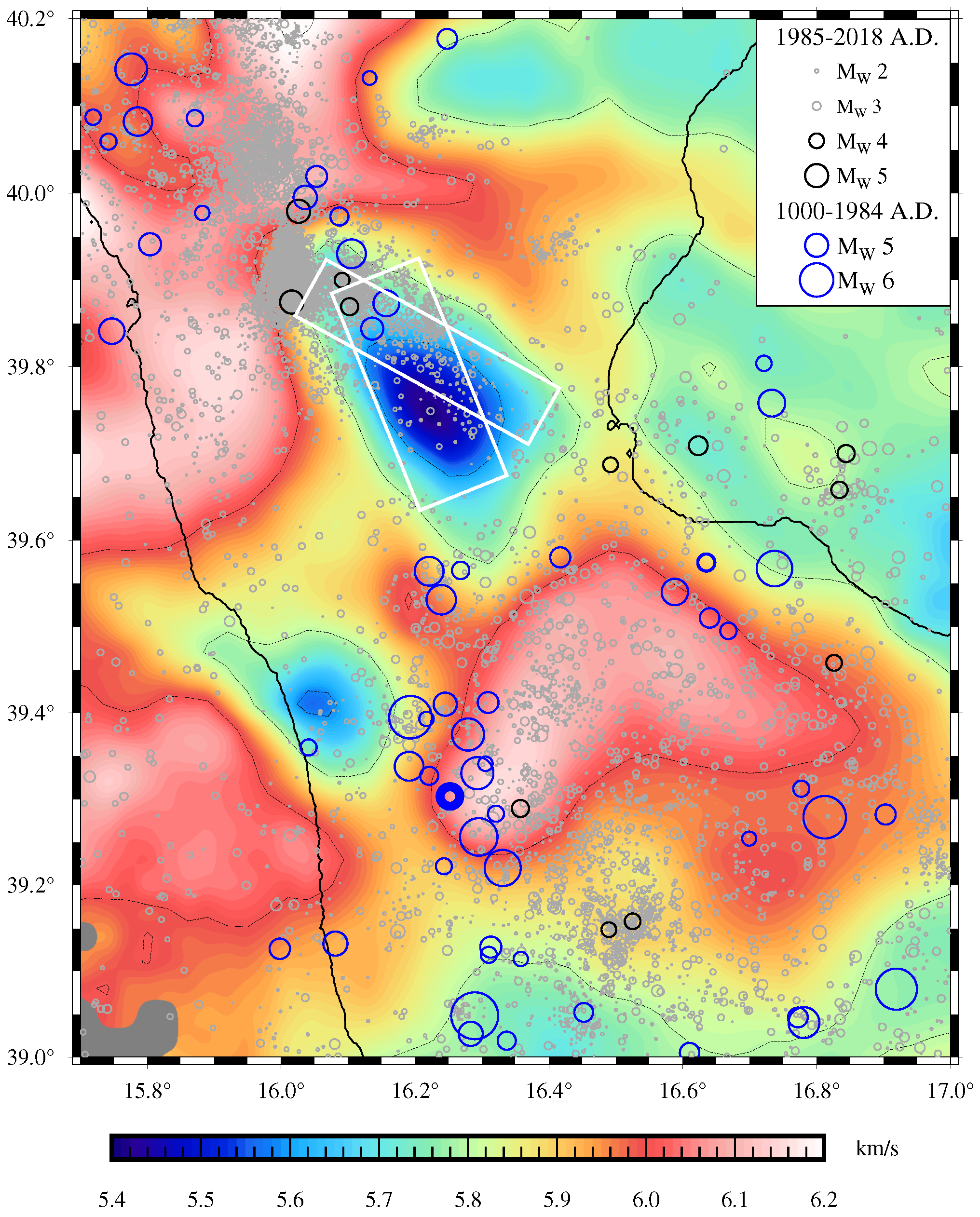
1. Introduction
2. Forward Model
2.1. Regional Deformation
2.2. Fault Creep
3. Inverse Problem
3.1. Information from Observations and a Priori Constraints
3.2. Posterior Probability Density Function
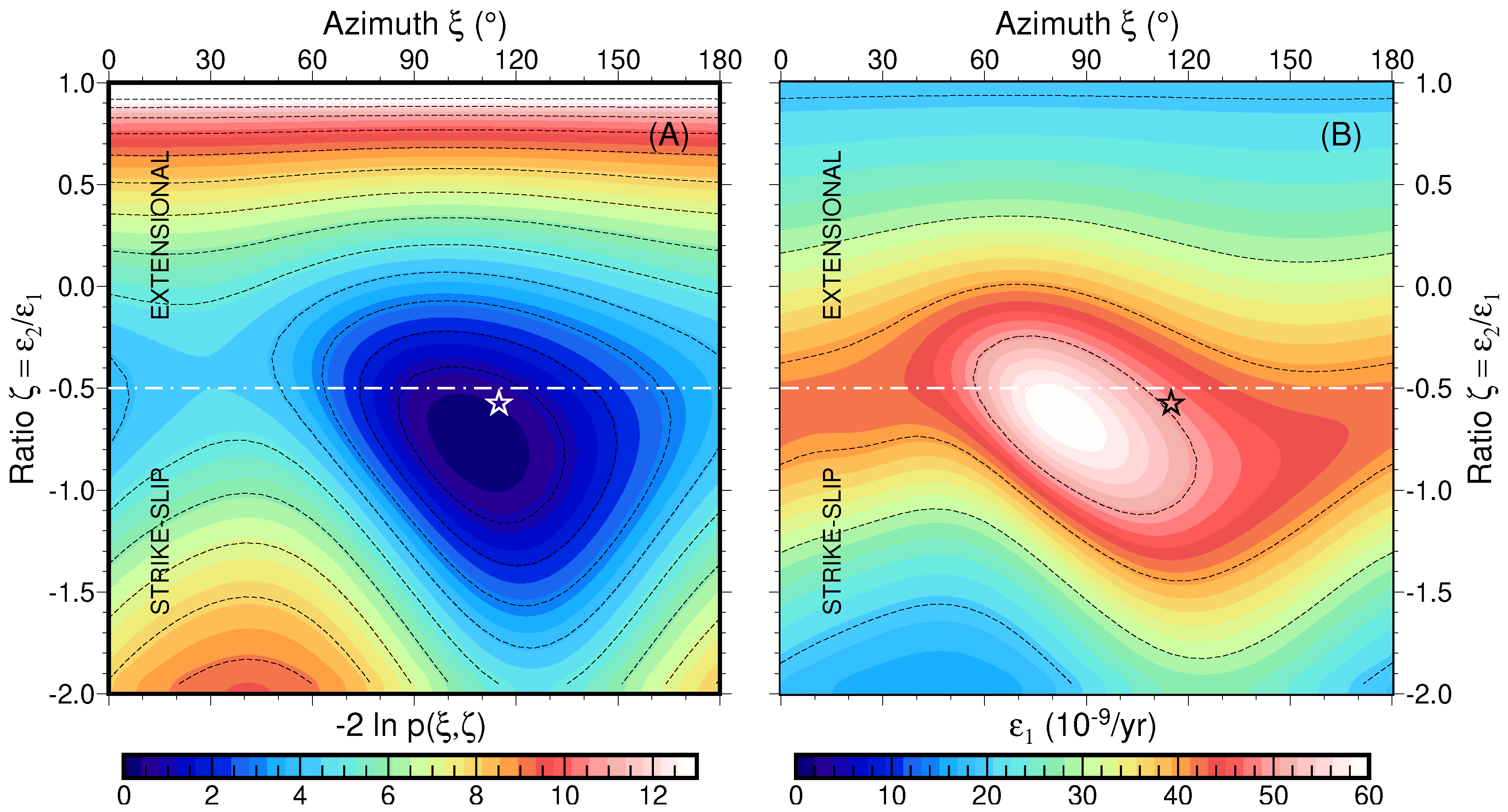
3.3. Prior Information on the Tectonic Regimes
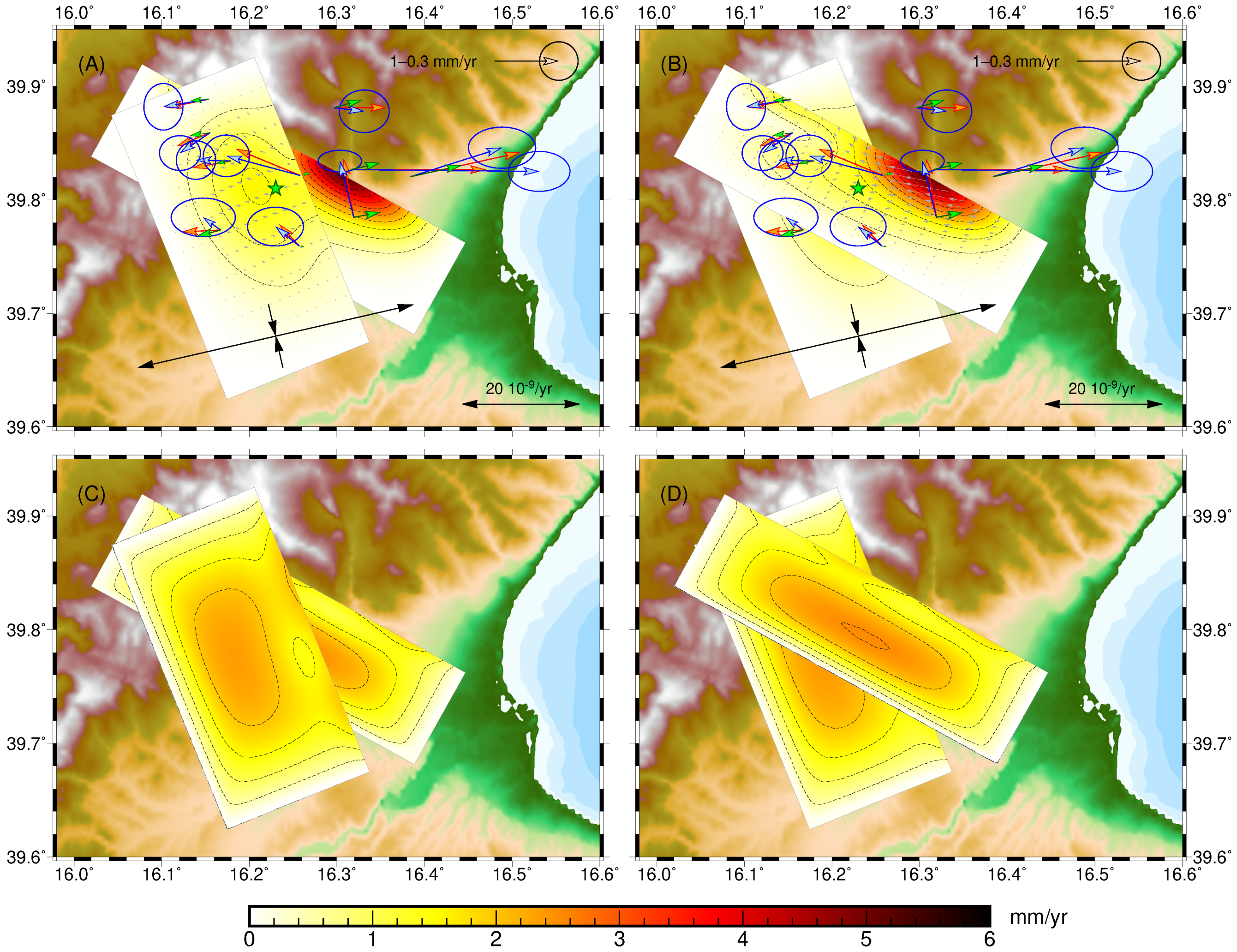
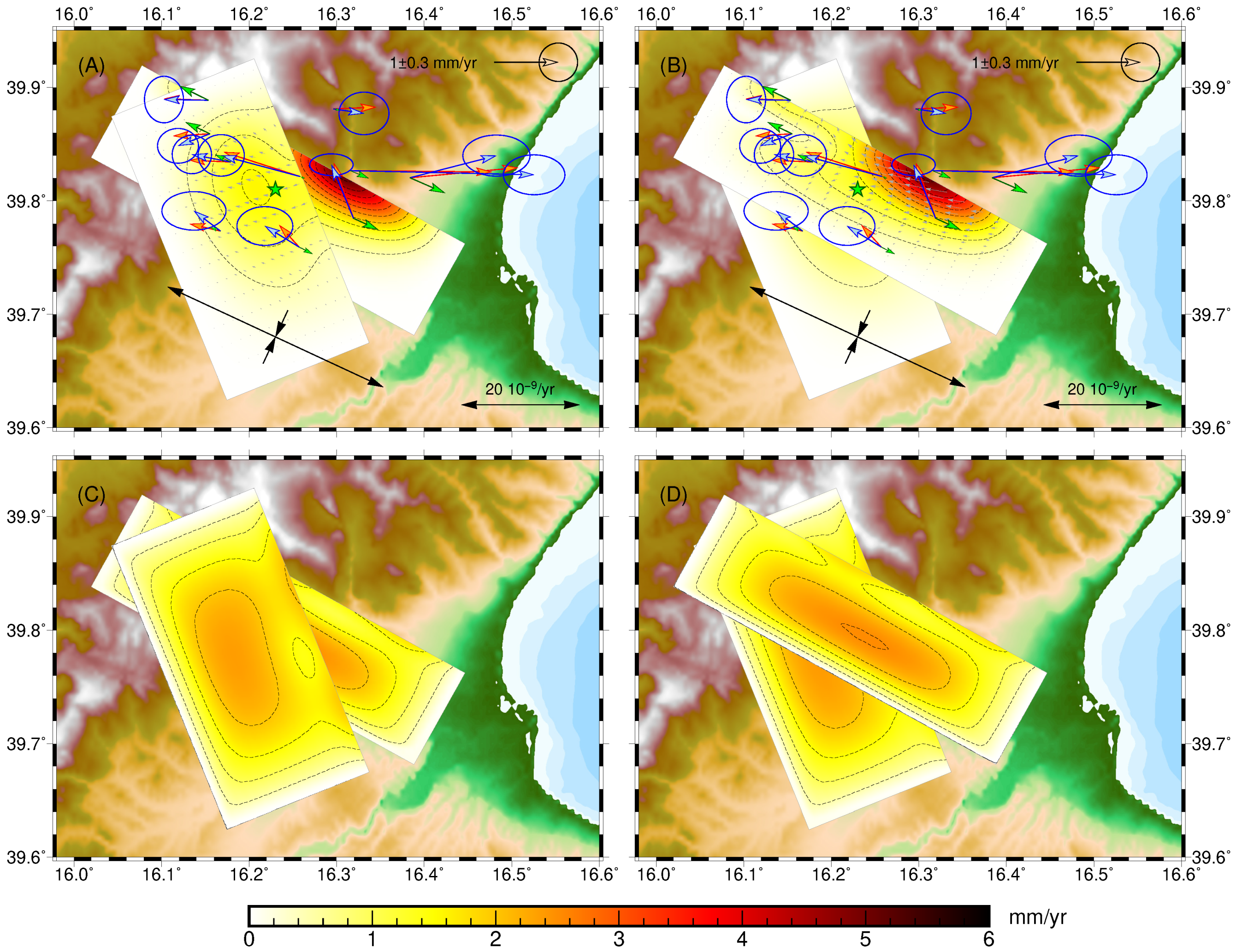
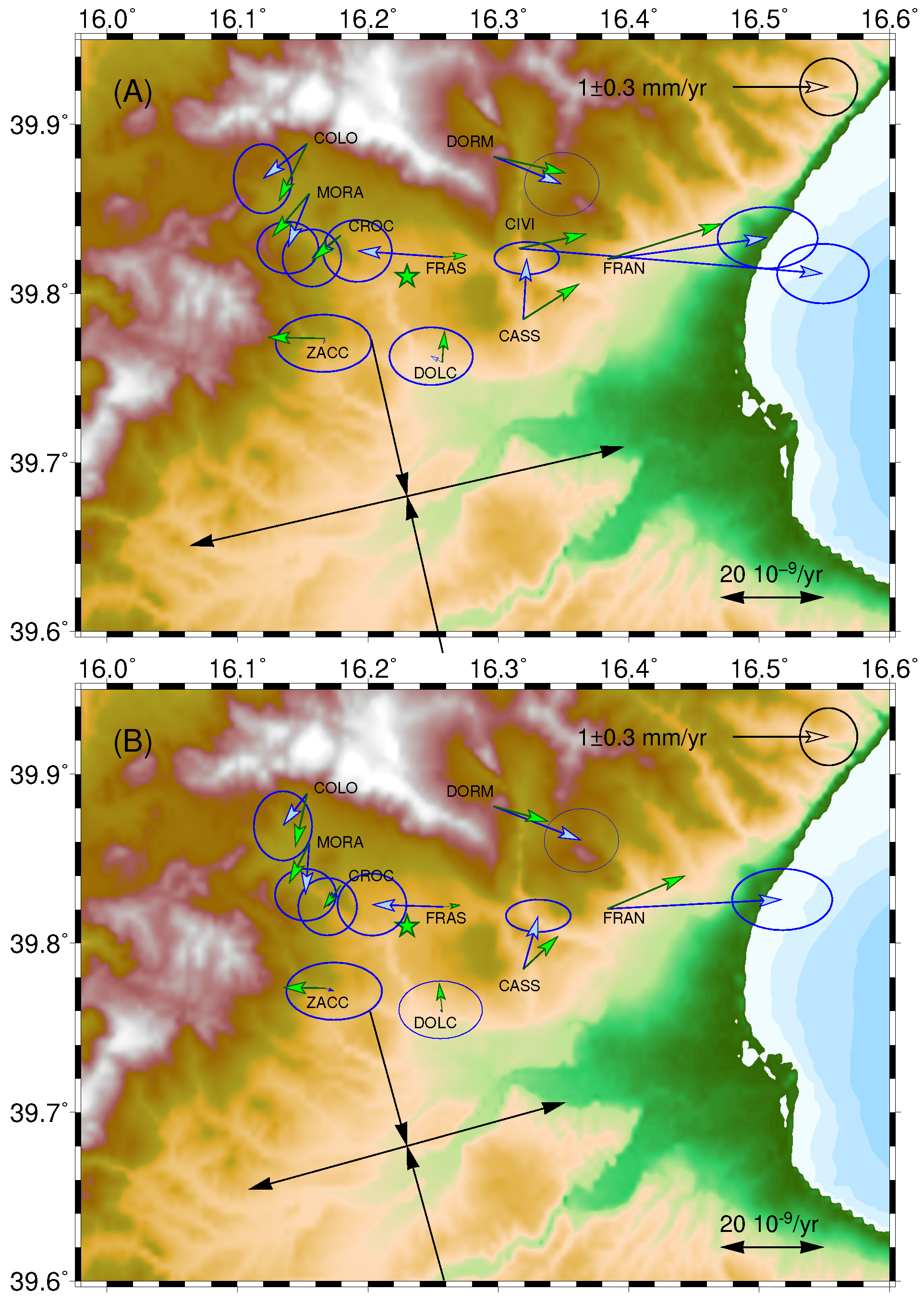
4. Results
4.1. Regional Deformations without Fault Creep
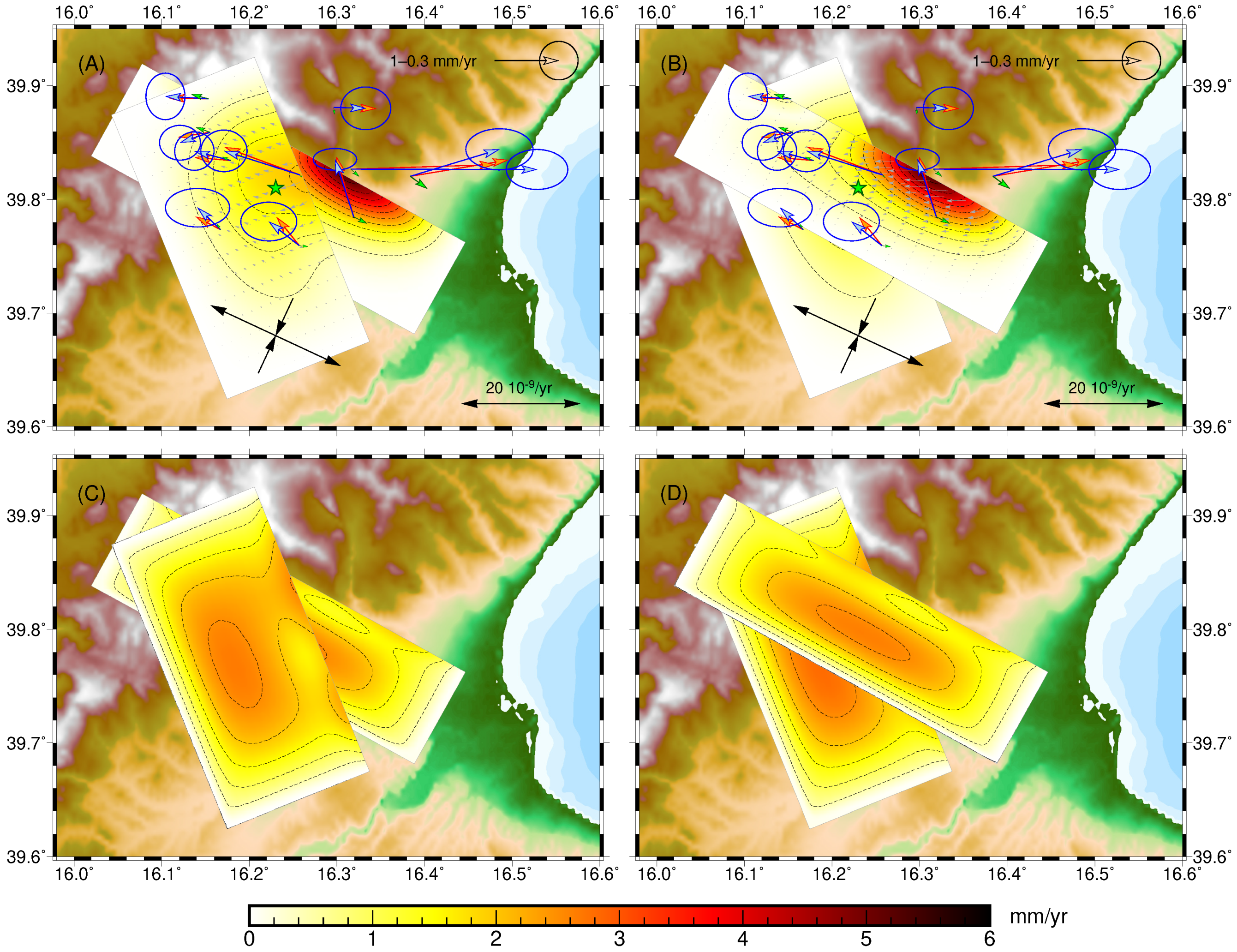
4.2. Regional Deformations and Fault Creep
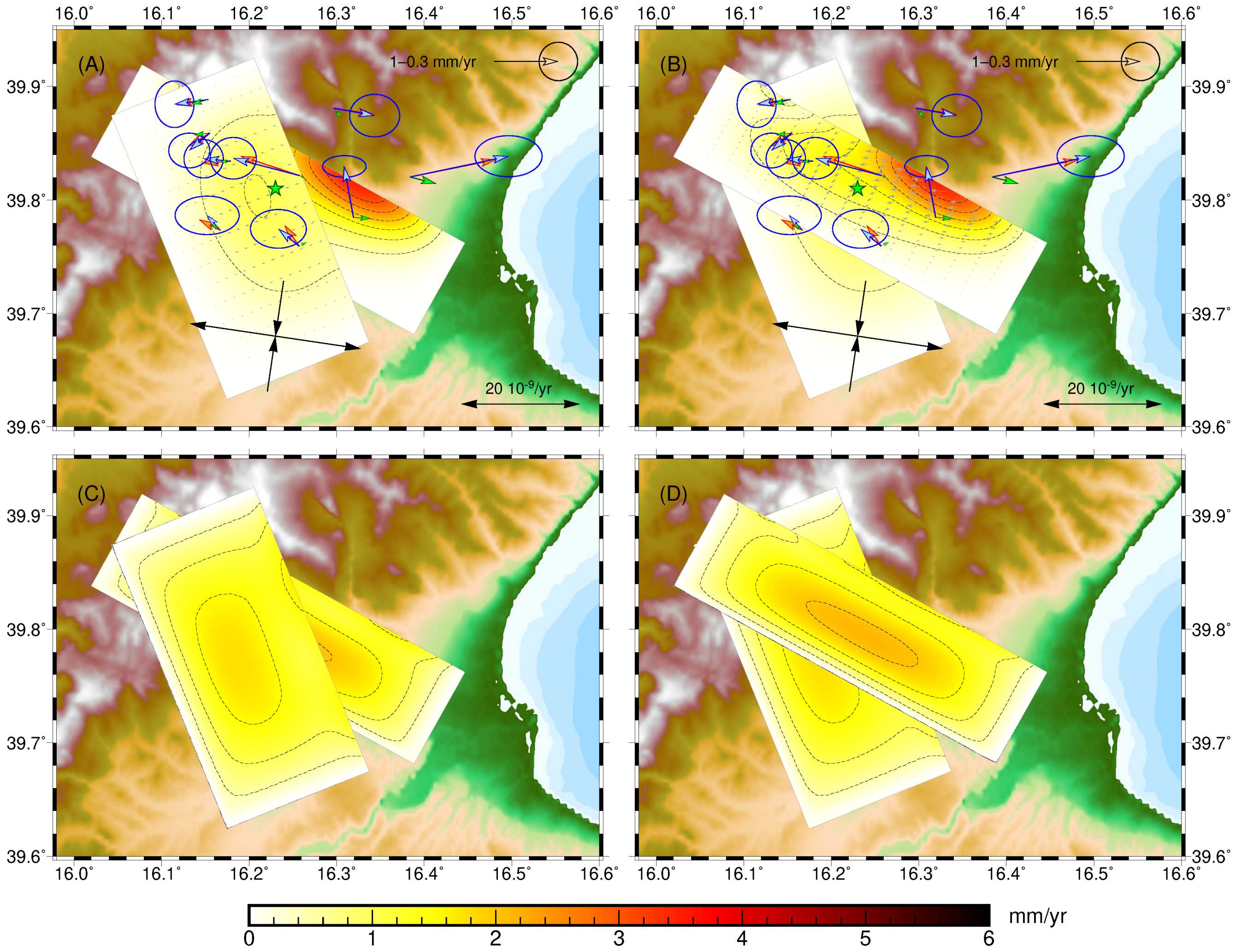
4.3. Regional Deformations and Fault Creep and Prior Information about the Tectonic Regimes
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Modified Bicubic Splines
References
- Clarke, P.J.; Davies, R.R.; England, P.C.; Parsons, B.; Billiris, H.; Paradissis, D.; Veis, G.; Cross, P.A.; Denys, P.H.; Ashkenazi, V.; et al. Crustal strain in central Greece from repeated GPS measurements in the interval 1989–1997. Geophys. J. Int. 1998, 135, 195–214. [Google Scholar] [CrossRef]
- Mazzotti, S.; Leonard, L.; Cassidy, J.; Rogers, G.; Halchuk, S. Seismic hazard in western Canada from GPS strain rates versus earthquake catalog. J. Geophys. Res. 2011, 116, B12310. [Google Scholar] [CrossRef]
- Palano, M.; Imprescia, P.; Agnon, A.; Gresta, S. An improved evaluation of the seismic/geodetic deformation-rate ratio for the Zagros Fold-and-Thrust collisional belt. Geophys. J. Int. 2018, 213, 194–209. [Google Scholar] [CrossRef]
- Masson, F.; Chery, J.; Hatzfeld, D.; Martinod, J.; Vernant, P.; Tavakoli, F.; Ghafory-Ashtiani, M. Seismic versus aseismic deformation in Iran inferred from earthquakes and geodetic data. Geophys. J. Int. 2005, 160, 217–226. [Google Scholar] [CrossRef]
- Savage, J.C.; Burford, R.O. Geodetic determination of relative plate motion in Central California. J. Geophys. Res. 1973, 78, 832–845. [Google Scholar] [CrossRef]
- Savage, J.C. A dislocation mode of strain accumulation and release at a subduction zone. J. Geophys. Res. 1983, 88, 4984–4996. [Google Scholar] [CrossRef]
- McCaffrey, R. lnterseismic locking on the Hikurangi subduction zone: Uncertainties from slow-slip events. J. Geophys. Res. 2014, 119, 7874–7888. [Google Scholar] [CrossRef]
- Li, S.; Moreno, M.; Bedford, J.; Rosenau, M.; Oncken, O. Revisiting viscoelastic effects on interseismic deformation and locking degree: A case study of the Peru-North Chile subduction zone. J. Geophys. Res. 2015, 120, 4522–4538. [Google Scholar] [CrossRef]
- Ranalli, G. Rheology of the Earth, 2nd ed.; Chapman and Hall: London, UK, 1995. [Google Scholar]
- Splendore, R.; Marotta, A. Crust-mantle mechanical structure in the Central Mediterranean region. Tectonophysics 2013, 603, 89–103. [Google Scholar] [CrossRef]
- England, P.; McKenzie, D. A thin viscous sheet model for continental deformation. R. Astron. Soc. Geophys. J. 1982, 70, 295–321, Erratum in 1983, 73, 523–532. [Google Scholar] [CrossRef]
- Medvedev, S.; Podladchikov, Y. New extended thin-sheet approximation for geodynamic applications–I. Model formulation. Geophys. J. Int. 1999, 136, 567–585. [Google Scholar] [CrossRef]
- Marotta, A.; Sabadini, R. The signatures of tectonics and glacial isostatic adjustment revealed by the strain rate in Europe. Geophys. J. Int. 2004, 157, 865–870. [Google Scholar] [CrossRef]
- Marotta, A.; Mitrovica, J.; Sabadini, R.; Milne, G. Combined effects of tectonics and glacial isostatic adjustment on intraplate deformation in central and northern Europe: Applications to geodetic baseline analyses. J. Geophyis. Res. 2004, 109, B01413. [Google Scholar] [CrossRef]
- Jiménez-Munt, I.; Garcia-Castellanos, D.; Negredo, A.; Platt, J. Gravitational and tectonic forces controlling postcollisional deformation and the present-day stress field of the Alps: Constraints from numerical modeling. Tectonics 2005, 24, TC5009. [Google Scholar] [CrossRef]
- Hearn, E. What can GPS data tell us about the dynamics of post-seismic deformation? Geophys. J. Int. 2003, 155, 753–777. [Google Scholar] [CrossRef]
- Hutton, W.; DeMets, C.; Sanchez, O.; Suarez, G.; Stock, J. Slip kinematics and dynamics during and after the 1995 October 9 Mw = 8.0 Colima-Jalisco earthquake, Mexico, from GPS geodetic constraints. Geophys. J. Int. 2001, 146, 637–658. [Google Scholar] [CrossRef]
- Cheloni, D.; D’Agostino, N.; Selvaggi, G.; Avallone, A.; Fornaro, G.; Giuliani, R.; Reale, D.; Sansosti, E.; Tizzani, P. Aseismic transient during the 2010–2014 seismic swarm: Evidence for longer recurrence of M ≥ 6.5 earthquakes in the Pollino gap (Southern Italy)? Sci. Rep. 2017, 7, 576. [Google Scholar] [CrossRef]
- Murray, J.; Minson, S.; Svarc, J. Slip rates and spatially variable creep on faults of the northern San Andreas system inferred through Bayesian inversion of Global Positioning System data. J. Geophys. Res. 2014, 119, 6023–6047. [Google Scholar] [CrossRef]
- Cinti, F.; Moro, M.; Pantosti, D.; Cucci, L.; D’Addezio, G. New constraints on the seismic history of the Castrovillari fault in the Pollino gap (Calabria, southern Italy). J. Seismol. 2002, 6, 199–217. [Google Scholar] [CrossRef]
- Michetti, A.; Ferreli, L.; Serva, L.; Vittori, E. Geological evidence for strong historical earthquakes in an “aseismic” region: The Pollino case. J. Geodyn. 1997, 24, 67–86. [Google Scholar] [CrossRef]
- Totaro, C.; Presti, D.; Billi, A.; Gervasi, A.; Orecchio, B.; Guerra, I.; Neri, G. The ongoing seismic sequence at the Pollino Mountains. Italy Seismol. Res. Lett. 2013, 84, 955–962. [Google Scholar] [CrossRef]
- Totaro, C.; Koulakov, I.; Orecchio, B.; Presti, D. Detailed crustal structure in the area of the southern Apennines–Calabrian Arc border from local earthquake tomography. J. Geodyn. 2014, 82, 87–97. [Google Scholar] [CrossRef]
- Chiarabba, C.; Agostinetti, N.; Bianchi, I. Lithospheric fault and kinematic decoupling of the Apennines system across the Pollino range. Geophys. Res. Lett. 2016, 43, 3201–3207. [Google Scholar] [CrossRef]
- Sabadini, R.; Aoudia, A.; Barzaghi, R.; Crippa, B.; Marotta, A.; Borghi, A.; Cannizzaro, L.; Calcagni, L.; Dalla Via, G.; Rossi, G.; et al. First evidences of fast creeping on a long-lasting quiescent earthquake normal-fault in the Mediterranean. Geophys. J. Int. 2009, 179, 720–732. [Google Scholar] [CrossRef]
- Brozzetti, F.; Cirillo, D.; de Nardis, R.; Cardinali, M.; Lavecchia, G.; Orecchio, B.; Presti, D.; Totaro, C. Newly identified active faults in the Pollino seismic gap, southern Italy, and their seismotectonic significance. J. Struct. Geol. 2017, 94, 13–31. [Google Scholar] [CrossRef]
- DISS Working Group. Database of Individual Seismogenic Sources (DISS), Version 3.0.4: A Compilation of Potential Sources for Earthquakes Larger than M 5.5 in Italy and Surrounding Areas. 2007. Available online: http://www.ingv.it/DISS/ (accessed on 15 July 2017).
- Rovida, A.; Camassi, R.; Gasperini, P.; Stucchi, M. CPTI11, la versione 2011 del Catalogo Parametrico dei Terremoti Italiani, Milano, Bologna. 2011. Available online: http://emidius.mi.ingv.it/CPTI (accessed on 15 July 2017).
- ISIDe Working Group. Italian Seismological Instrumental and Parametric Databases. 2016. Available online: http://cnt.rm.ingv.it/iside (accessed on 15 July 2017).
- Savage, J.; Gan, W.; Svarc, J. Strain accumulation and rotation in the Eastern California Shear Zone. J. Geophys. Res. 2001, 106, 21995–22007. [Google Scholar] [CrossRef]
- Shen, Z.K.; Jackson, D.; Ge, B. Crustal deformation across and beyond the Los Angeles basin from geodetic measurements. J. Geophys. Res. 1996, 101, 27957–27980. [Google Scholar] [CrossRef]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar]
- Ferranti, L.; Palano, M.; Cannavò, F.; Mazzella, M.; Oldow, J.; Gueguen, E.; Mattia, M.; Monaco, C. Rates of geodetic deformation across active faults in southern Italy. Tectonophysics 2014, 621, 101–122. [Google Scholar] [CrossRef]
- Yabuki, T.; Matsu’ura, M. Geodetic data inversion using a Bayesian information criterion for spatial distribution of fault slip. Geophys. J. Int. 1992, 109, 363–375. [Google Scholar] [CrossRef]
- Cambiotti, G.; Zhou, X.; Sparacino, F.; Sabadini, R.; Sun, W. Joint estimate of the rupture area and slip distribution of the 2009 L’Aquila earthquake by a Bayesian inversion of GPS data. Geophys. J. Int. 2017, 209, 992–1003. [Google Scholar] [CrossRef]
- Fukuda, J.; Johnson, K. A fully Bayesian inversion for spatial distribution of fault slip with objective smoothing. Bull. Seism. Soc. Am. 2008, 98, 1128–1146. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Devoti, R.; Esposito, A.; Pietrantonio, G.; Pisani, A.; Riguzzi, F. Evidence of large scale deformation patterns from GPS data in the Italian subduction boundary. EPSL 2011, 311, 230–241. [Google Scholar] [CrossRef]
- Orecchio, B.; Prestia, D.; Totaro, C.; D’Amico, S.; Neri, G. Investigating slab edge kinematics through seismological data: Thenorthern boundary of the Ionian subduction system (south Italy). J. Geodyn. 2015, 88, 23–35. [Google Scholar] [CrossRef]
- Totaro, C.; Orecchio, B.; Presti, D.; Scolaro, S.; Neri, G. Seismogenic stress field estimation in the Calabrian Arc region (south Italy) from a Bayesian approach. Geophys. Res. Lett. 2016, 43, 8960–8969. [Google Scholar] [CrossRef]

| Castrovillari | Pollino | |
|---|---|---|
| dip | ||
| strike | ||
| length | km | km |
| width | km | km |
| top depth | 0 km | 0 km |
| GNSS Data | ||||||
|---|---|---|---|---|---|---|
| CASS | 16.31969 | 39.78493 | 1.33 | 4.95 | 0.34 | 0.18 |
| COLO | 16.15402 | 39.88887 | 0.99 | 4.14 | 0.31 | 0.37 |
| CROC | 16.17953 | 39.83458 | 1.07 | 4.24 | 0.32 | 0.31 |
| DOLC | 16.25764 | 39.75962 | 1.14 | 4.45 | 0.44 | 0.31 |
| DORM | 16.29699 | 39.88124 | 2.16 | 4.05 | 0.39 | 0.34 |
| FRAN | 16.38424 | 39.82068 | 3.03 | 4.46 | 0.52 | 0.33 |
| FRAS | 16.25836 | 39.82188 | 0.45 | 4.45 | 0.36 | 0.33 |
| MORA | 16.15572 | 39.85936 | 1.18 | 3.94 | 0.32 | 0.28 |
| ZACC | 16.16781 | 39.77370 | 1.26 | 4.44 | 0.50 | 0.31 |
| CIVI | 16.31628 | 39.82693 | 4.54 | 4.05 | 0.48 | 0.32 |
| Inversion Scheme | |||||||
|---|---|---|---|---|---|---|---|
| Nickname | R | FR | FR-E | FR-E | R* | FR* | |
| Features | Creep | no | yes | yes | yes | no | yes |
| Regime | all | all | Extensional | Extensional | all | all | |
| Azimuth | all | all | all | all | |||
| Estimates | 4.75 | 1.10 | 1.32 | 1.05 | 2.11 | 0.46 | |
| 0 | 0 | ||||||
| Figure 3A | Figure 4 | Figure 8 | Figure 9 | Figure 3B | Figure 5 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cambiotti, G.; Palano, M.; Orecchio, B.; Marotta, A.M.; Barzaghi, R.; Neri, G.; Sabadini, R. New Insights into Long-Term Aseismic Deformation and Regional Strain Rates from GNSS Data Inversion: The Case of the Pollino and Castrovillari Faults. Remote Sens. 2020, 12, 2921. https://doi.org/10.3390/rs12182921
Cambiotti G, Palano M, Orecchio B, Marotta AM, Barzaghi R, Neri G, Sabadini R. New Insights into Long-Term Aseismic Deformation and Regional Strain Rates from GNSS Data Inversion: The Case of the Pollino and Castrovillari Faults. Remote Sensing. 2020; 12(18):2921. https://doi.org/10.3390/rs12182921
Chicago/Turabian StyleCambiotti, Gabriele, Mimmo Palano, Barbara Orecchio, Anna Maria Marotta, Riccardo Barzaghi, Giancarlo Neri, and Roberto Sabadini. 2020. "New Insights into Long-Term Aseismic Deformation and Regional Strain Rates from GNSS Data Inversion: The Case of the Pollino and Castrovillari Faults" Remote Sensing 12, no. 18: 2921. https://doi.org/10.3390/rs12182921
APA StyleCambiotti, G., Palano, M., Orecchio, B., Marotta, A. M., Barzaghi, R., Neri, G., & Sabadini, R. (2020). New Insights into Long-Term Aseismic Deformation and Regional Strain Rates from GNSS Data Inversion: The Case of the Pollino and Castrovillari Faults. Remote Sensing, 12(18), 2921. https://doi.org/10.3390/rs12182921