Analyzing Spatio-Temporal Factors to Estimate the Response Time between SMOS and In-Situ Soil Moisture at Different Depths
Abstract
1. Introduction
2. Data and Methods
2.1. Time Series Datasets
2.1.1. SMOS Soil Moisture
2.1.2. REMEDHUS Soil Moisture and Climate Data
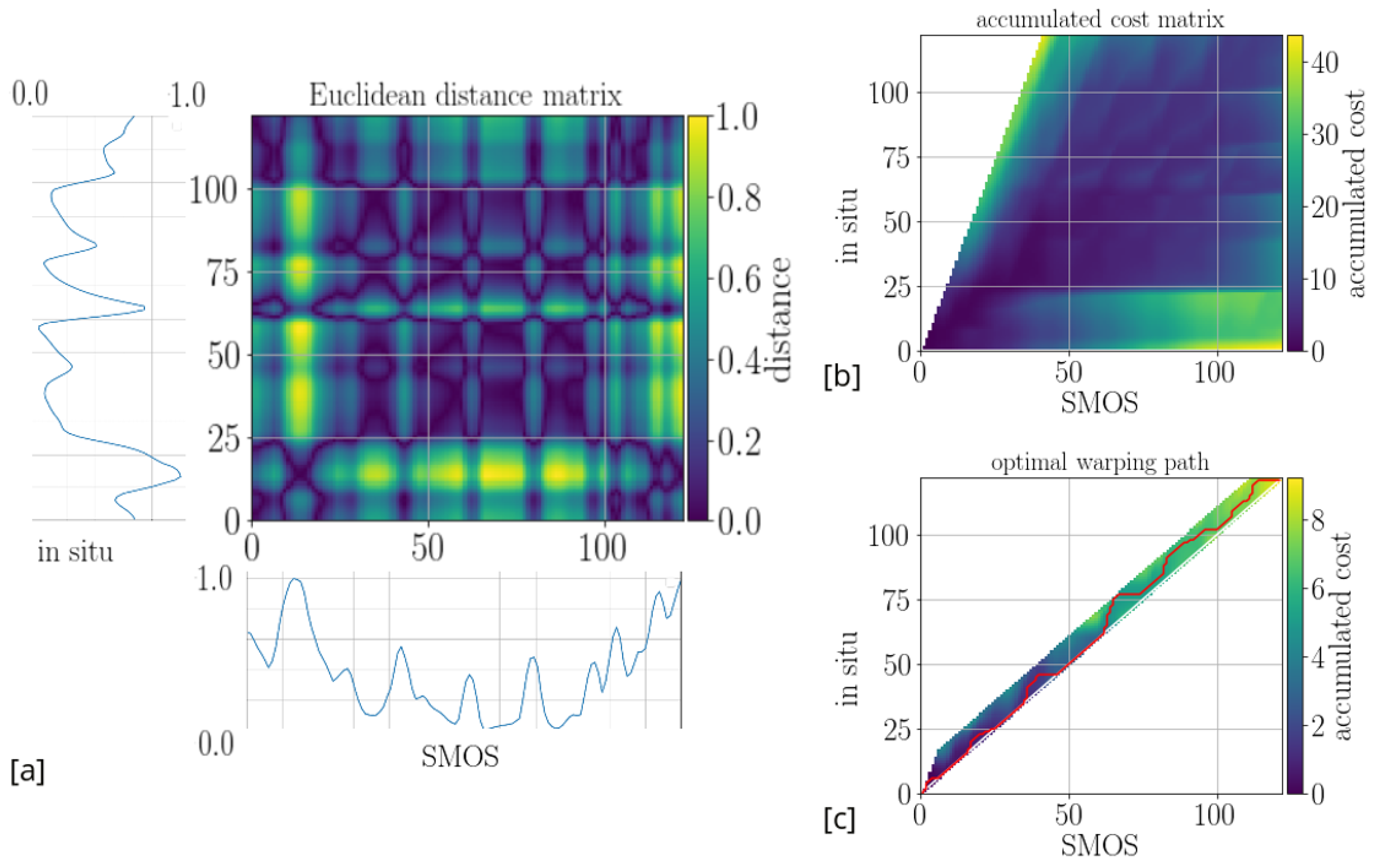
2.2. DTW Technique
2.2.1. Fundamentals of DTW
- (i)
- boundary condition:
- (ii)
- monotonicity condition:
- (iii)
- step-size condition (simple version): .
- (i)
- Computation of the local distance matrix
- (ii)
- Building the accumulated cost matrix
- (iii)
- Retrieval of the optimal warping path
2.2.2. Customization of DTW
Maximum Allowed Time Lag
Adjustment of Step-Size Condition
Determination of Onsets of Pronounced Precipitation Events
2.3. Comparison of SMOS and In-Situ SM
3. Results
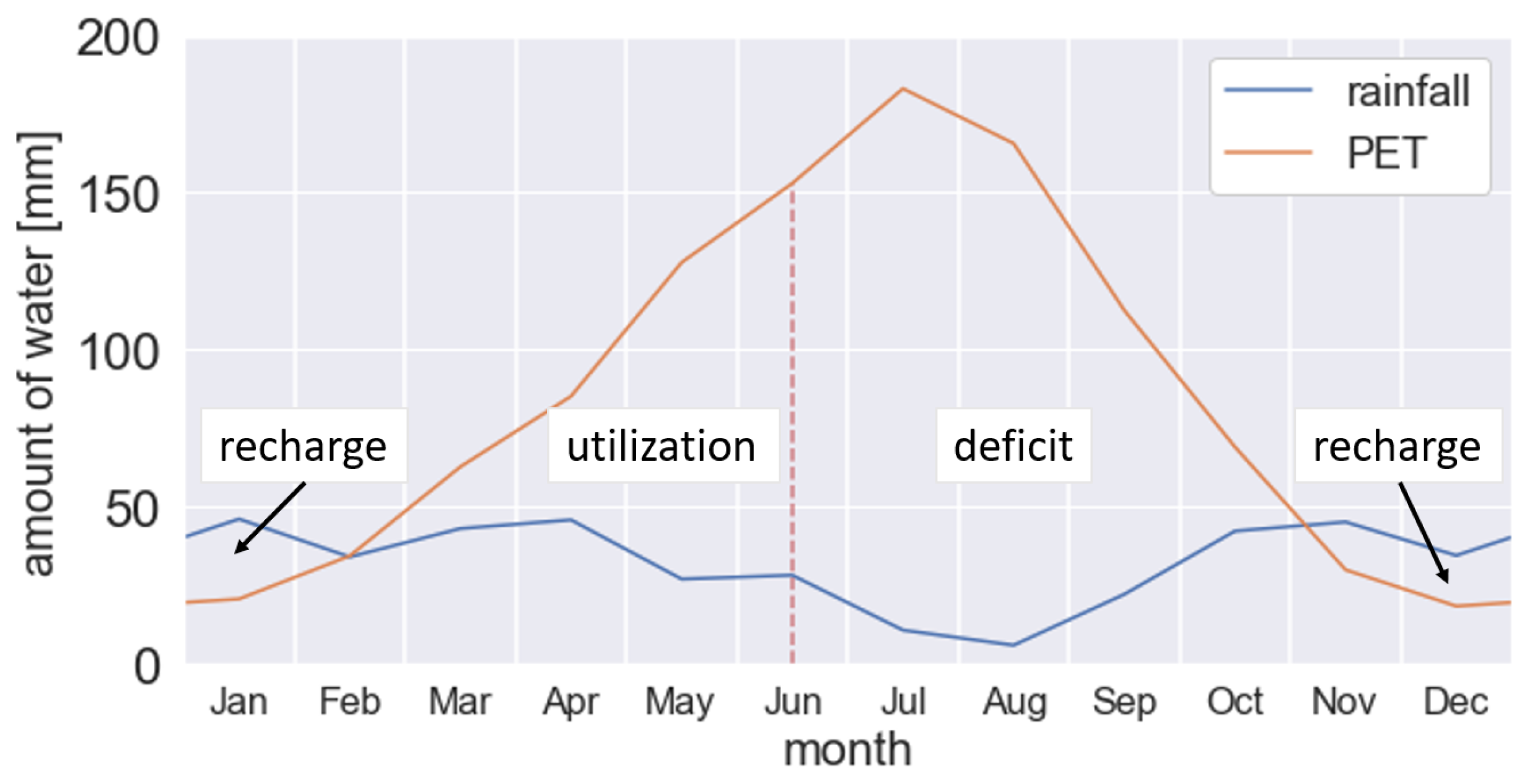
3.1. Temporal Variability of Climate Factors
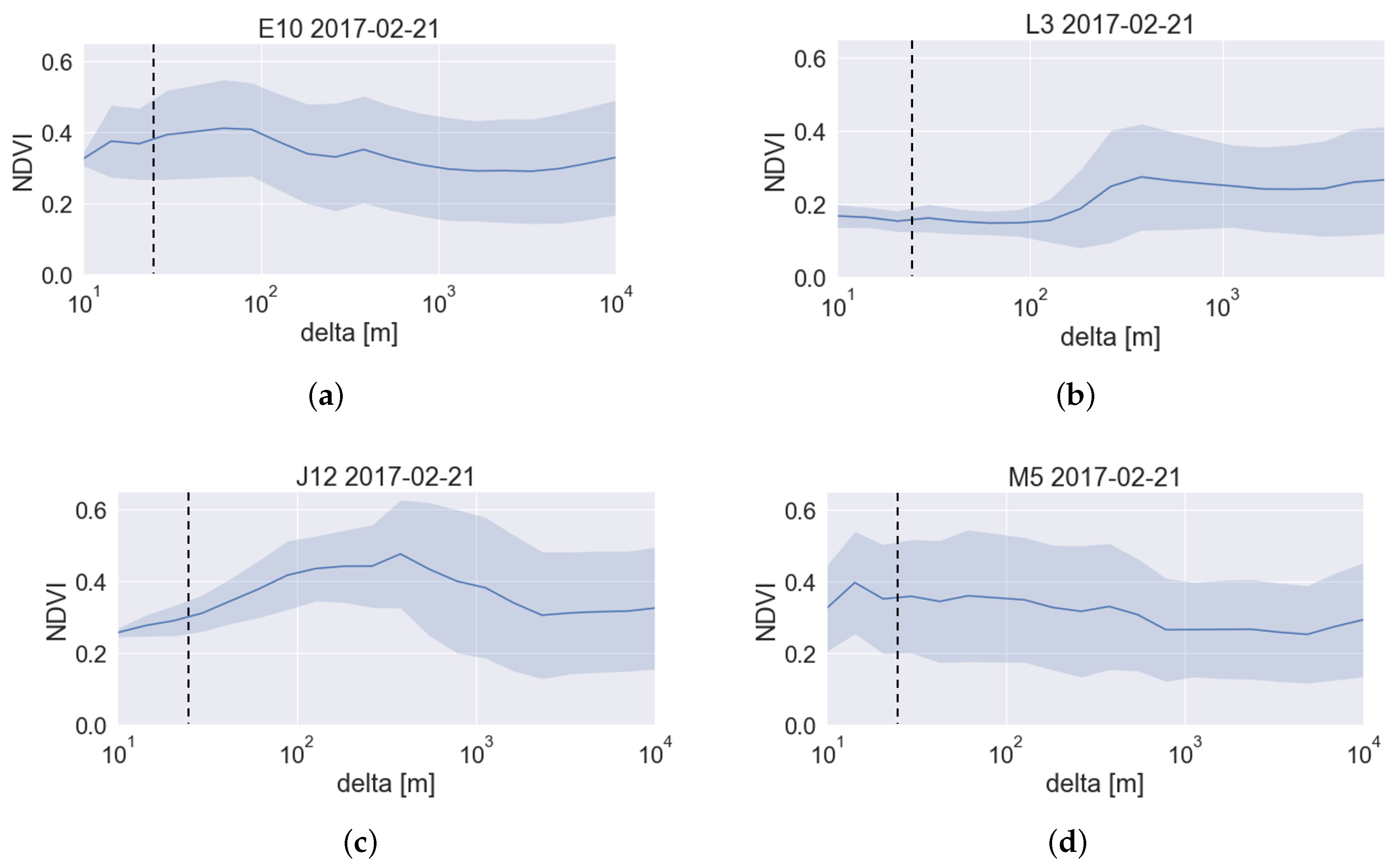
3.2. Spatial Heterogeneity of Land Coverage
3.3. Interim Results of DTW and Customization
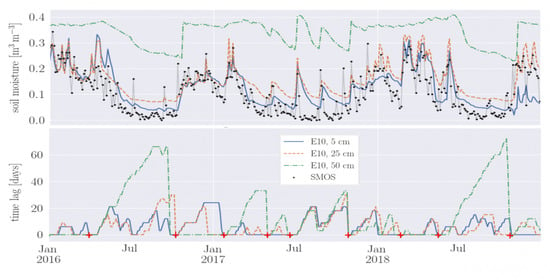
3.4. Final Results of the Evolution of Time Lag
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Basara, J.B.; Crawford, K.C. Linear relationships between root-zone soil moisture and atmospheric processes in the planetary boundary layer. J. Geophys. Res. Atmos. 2002, 107, ACL 10-1–ACL 10-18. [Google Scholar] [CrossRef]
- Fan, J.; McConkey, B.; Wang, H.; Janzen, H. Root distribution by depth for temperate agricultural crops. Field Crop Res. 2016, 189, 68–74. [Google Scholar] [CrossRef]
- Jiménez-Martínez, J.; Skaggs, T.; Van Genuchten, M.T.; Candela, L. A root zone modelling approach to estimating groundwater recharge from irrigated areas. J. Hydrol. 2009, 367, 138–149. [Google Scholar] [CrossRef]
- Kang, Y.; Khan, S.; Ma, X. Climate change impacts on crop yield, crop water productivity and food security—A review. Prog. Nat. Sci. 2009, 19, 1665–1674. [Google Scholar] [CrossRef]
- Batool, A.; Cheng, Z.G.; Akram, N.A.; Lv, G.C.; Xiong, J.L.; Zhu, Y.; Ashraf, M.; Xiong, Y.C. Partial and full root-zone drought stresses account for differentiate root-sourced signal and yield formation in primitive wheat. Plant Methods 2019, 15, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Falkenmark, M. Growing water scarcity in agriculture: Future challenge to global water security. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120410. [Google Scholar] [CrossRef]
- Bell, T.H.; Barrow, B.J.; Miller, J.T. Subsurface discrimination using electromagnetic induction sensors. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1286–1293. [Google Scholar] [CrossRef]
- Jol, H.M. Ground Penetrating Radar Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Su, S.L.; Singh, D.; Baghini, M.S. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Jackson, T.J. Remote sensing of soil moisture: Implications for groundwater recharge. Hydrogeol. J. 2002, 10, 40–51. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Chan, S.K.; Bindlish, R.; O’Neill, P.E.; Njoku, E.; Jackson, T.; Colliander, A.; Chen, F.; Burgin, M.; Dunbar, S.; Piepmeier, J.; et al. Assessment of the SMAP passive soil moisture product. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4994–5007. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; Oevelen, P.V.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; Ceballos, A. Temporal stability of soil moisture in a large-field experiment in Spain. Soil Sci. Soc. Am. J. 2003, 67, 1647–1656. [Google Scholar] [CrossRef]
- Pablos, M.; Martínez-Fernández, J.; Piles, M.; Sánchez, N.; Vall-llossera, M.; Camps, A. Multi-temporal evaluation of soil moisture and land surface temperature dynamics using in situ and satellite observations. Remote Sens. 2016, 8, 587. [Google Scholar] [CrossRef]
- Pablos, M.; González-Zamora, Á.; Sánchez, N.; Martínez-Fernández, J. Assessment of root zone soil moisture estimations from SMAP, SMOS and MODIS observations. Remote Sens. 2018, 10, 981. [Google Scholar] [CrossRef]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Sanchez, N.; Martínez-Fernández, J.; Scaini, A.; Perez-Gutierrez, C. Validation of the SMOS L2 soil moisture data in the REMEDHUS network (Spain). IEEE Trans. Geosci. Remote Sens. 2012, 50, 1602–1611. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.; Cosh, M.; Dunbar, R.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Portal, G.; Jagdhuber, T.; Vall-llossera, M.; Camps, A.; Pablos, M.; Entekhabi, D.; Piles, M. Assessment of Multi-Scale SMOS and SMAP Soil Moisture Products across the Iberian Peninsula. Remote Sens. 2020, 12, 570. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Chanzy, A.; Wigneron, J.P.; Kerr, Y. Effective soil moisture sampling depth of L-band radiometry: A case study. Remote Sens. Environ. 2010, 114, 995–1001. [Google Scholar] [CrossRef]
- Owe, M.; Van de Griend, A.A. Comparison of soil moisture penetration depths for several bare soils at two microwave frequencies and implications for remote sensing. Water Resour. Res. 1998, 34, 2319–2327. [Google Scholar] [CrossRef]
- Rondinelli, W.J.; Hornbuckle, B.K.; Patton, J.C.; Cosh, M.H.; Walker, V.A.; Carr, B.D.; Logsdon, S.D. Different rates of soil drying after rainfall are observed by the SMOS satellite and the South Fork in situ soil moisture network. J. Hydrometeorol. 2015, 16, 889–903. [Google Scholar] [CrossRef]
- Shellito, P.J.; Small, E.E.; Colliander, A.; Bindlish, R.; Cosh, M.H.; Berg, A.A.; Bosch, D.D.; Caldwell, T.G.; Goodrich, D.C.; McNairn, H.; et al. SMAP soil moisture drying more rapid than observed in situ following rainfall events. Geophys. Res. Lett. 2016, 43, 8068–8075. [Google Scholar] [CrossRef]
- Pablos, M.; Martínez-Fernández, J.; Sánchez, N.; González-Zamora, Á. Temporal and spatial comparison of agricultural drought indices from moderate resolution satellite soil moisture data over Northwest Spain. Remote Sens. 2017, 9, 1168. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Berg, A.; Bosch, D.; Caldwell, T.; Chan, S.; Cosh, M.H.; Collins, C.H.; Martínez-Fernández, J.; McNairn, H.; et al. Effect of rainfall events on SMAP radiometer-based soil moisture accuracy using core validation sites. J. Hydrometeorol. 2020, 21, 255–264. [Google Scholar] [CrossRef]
- De Lannoy, G.J.; Houser, P.R.; Verhoest, N.E.; Pauwels, V.R.; Gish, T.J. Upscaling of point soil moisture measurements to field averages at the OPE3 test site. J. Hydrol. 2007, 343, 1–11. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Wang, J.; Ge, Y.; Heuvelink, G.; Zhou, C. Upscaling in situ soil moisture observations to pixel averages with spatio-temporal geostatistics. Remote Sens. 2015, 7, 11372–11388. [Google Scholar] [CrossRef]
- Ogden, F.L.; Allen, M.B.; Lai, W.; Zhu, J.; Seo, M.; Douglas, C.C.; Talbot, C.A. The soil moisture velocity equation. J. Adv. Model. Earth Syst. 2017, 9, 1473–1487. [Google Scholar] [CrossRef]
- Skøien, J.O.; Blöschl, G.; Western, A.W. Characteristic space scales and timescales in hydrology. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Rosenbaum, U.; Bogena, H.R.; Herbst, M.; Huisman, J.; Peterson, T.; Weuthen, A.; Western, A.; Vereecken, H. Seasonal and event dynamics of spatial soil moisture patterns at the small catchment scale. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Dorigo, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Larson, K.M.; Njoku, E.G.; Small, E.E.; et al. State of the art in large-scale soil moisture monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Barrett, B. Surface soil moisture retrievals from remote sensing: Current status, products & future trends. Phys. Chem. Earth Parts A/B/C 2015, 83, 36–56. [Google Scholar]
- Mohanty, B.P.; Cosh, M.H.; Lakshmi, V.; Montzka, C. Soil moisture remote sensing: State-of-the-science. Vadose Zone J. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Ceballos, A.; Scipal, K.; Wagner, W.; Martínez-Fernández, J. Validation of ERS scatterometer-derived soil moisture data in the central part of the Duero Basin, Spain. Hydrol. Process. Int. J. 2005, 19, 1549–1566. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. [Google Scholar] [CrossRef]
- Ford, T.; Harris, E.; Quiring, S. Estimating Root Zone Soil Moisture Using Near-Surface Observations from SMOS. Hydrol. Earth Syst. Sci. 2014, 18, 139–154. [Google Scholar] [CrossRef]
- González-Zamora, Á.; Sánchez, N.; Martínez-Fernández, J.; Wagner, W. Root-zone plant available water estimation using the SMOS-derived soil water index. Adv. Water Resour. 2016, 96, 339–353. [Google Scholar] [CrossRef]
- Wu, W.; Geller, M.A.; Dickinson, R.E. The response of soil moisture to long-term variability of precipitation. J. Hydrometeorol. 2002, 3, 604–613. [Google Scholar] [CrossRef]
- Wang, X.; Mueen, A.; Ding, H.; Trajcevski, G.; Scheuermann, P.; Keogh, E. Experimental comparison of representation methods and distance measures for time series data. Data Min. Knowl. Discov. 2013, 26, 275–309. [Google Scholar] [CrossRef]
- Liu, Y. Spatial patterns of soil moisture connected to monthly-seasonal precipitation variability in a monsoon region. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. Eur. Geosci. Union (EGU) 1994, 11, 561–566. [Google Scholar] [CrossRef]
- Qi, P.; Zhang, G.; Xu, Y.J.; Wang, L.; Ding, C.; Cheng, C. Assessing the influence of precipitation on shallow groundwater table response using a combination of singular value decomposition and cross-wavelet approaches. Water 2018, 10, 598. [Google Scholar] [CrossRef]
- Rakthanmanon, T.; Campana, B.; Mueen, A.; Batista, G.; Westover, B.; Zhu, Q.; Zakaria, J.; Keogh, E. Searching and mining trillions of time series subsequences under dynamic time warping. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 23–27 August 2012; pp. 262–270. [Google Scholar] [CrossRef]
- Berndt, D.J.; Clifford, J. Using Dynamic Time Warping to Find Patterns in Time Series; KDD Workshop: Seattle, WA, USA, 1994; Volume 10, pp. 359–370. [Google Scholar]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Maus, V.; Câmara, G.; Cartaxo, R.; Sanchez, A.; Ramos, F.M.; de Queiroz, G.R. A time-weighted dynamic time warping method for land-use and land-cover mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3729–3739. [Google Scholar] [CrossRef]
- Belgiu, M.; Csillik, O. Sentinel-2 cropland mapping using pixel-based and object-based time-weighted dynamic time warping analysis. Remote Sens. Environ. 2018, 204, 509–523. [Google Scholar] [CrossRef]
- Csillik, O.; Belgiu, M.; Asner, G.P.; Kelly, M. Object-based time-constrained dynamic time warping classification of crops using Sentinel-2. Remote Sens. 2019, 11, 1257. [Google Scholar] [CrossRef]
- Lee, C.S.; Sohn, E.; Park, J.D.; Jang, J.D. Estimation of soil moisture using deep learning based on satellite data: A case study of South Korea. GISci. Remote Sens. 2019, 56, 43–67. [Google Scholar] [CrossRef]
- Portal, G.; Vall-Llossera, M.; Piles, M.; Camps, A.; Chaparro, D.; Pablos, M.; Rossato, L. A spatially consistent downscaling approach for SMOS using an adaptive moving window. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1883–1894. [Google Scholar] [CrossRef]
- Masialeti, I.; Egbert, S.; Wardlow, B.D. A comparative analysis of phenological curves for major crops in Kansas. GISci. Remote Sens. 2010, 47, 241–259. [Google Scholar] [CrossRef]
- Atchley, A.L.; Maxwell, R.M. Influences of subsurface heterogeneity and vegetation cover on soil moisture, surface temperature and evapotranspiration at hillslope scales. Hydrogeol. J. 2011, 19, 289–305. [Google Scholar] [CrossRef]
- Sentinel Ltd. Modified Copernicus Sentinel Data 2020/Sentinel Hub. 2020. Available online: https://sentinel-hub.com (accessed on 22 June 2020).
- Rodriguez-Fernandez, N.; Al Bitar, A.; Colliander, A.; Zhao, T. Soil Moisture Remote Sensing across Scales. Remote Sens. 2019, 11, 190. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Font, J.; Camps, A.; Borges, A.; Martín-Neira, M.; Boutin, J.; Reul, N.; Kerr, Y.H.; Hahne, A.; Mecklenburg, S. SMOS: The challenging sea surface salinity measurement from space. Proc. IEEE 2009, 98, 649–665. [Google Scholar] [CrossRef]
- Corbella, I.; Torres, F.; Camps, A.; Colliander, A.; Martín-Neira, M.; Ribó, S.; Rautiainen, K.; Duffo, N.; Vall-llossera, M. MIRAS end-to-end calibration: Application to SMOS L1 processor. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1126–1134. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Pablos, M.; Piles, M.; González-Haro, C. BEC SMOS Land Products Description. Available online: http://bec.icm.csic.es/doc/BEC-SMOS-0003-PD-Land.pdf (accessed on 15 September 2019).
- Piles, M.; Sánchez, N.; Vall-llossera, M.; Camps, A.; Martínez-Fernández, J.; Martínez, J.; González-Gambau, V. A downscaling approach for SMOS land observations: Evaluation of high-resolution soil moisture maps over the Iberian Peninsula. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3845–3857. [Google Scholar] [CrossRef]
- Martín-Neira, M.; Oliva, R.; Corbella, I.; Torres, F.; Duffo, N.; Durán, I.; Kainulainen, J.; Closa, J.; Zurita, A.; Cabot, F.; et al. SMOS instrument performance and calibration after six years in orbit. Remote Sens. Environ. 2016, 180, 19–39. [Google Scholar] [CrossRef]
- González-Zamora, Á.; Sanchez, N.; Gumuzzio, A.; Piles, M.; Olmedo, E.; Martínez-Fernández, J. Validation of SMOS L2 and L3 soil moisture products over the Duero Basin at different spatial scales. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 1183. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Müller, M. Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germany, 2007; Volume 2. [Google Scholar]
- Ainsworth, W. Speech Recognition by Machine Peter Peregrinus; IEE: London, UK, 1988. [Google Scholar]
- Laguna, P.; Jané, R.; Caminal, P. Automatic detection of wave boundaries in multilead ECG signals: Validation with the CSE database. Comput. Biomed. Res. 1994, 27, 45–60. [Google Scholar] [CrossRef] [PubMed]
- Zifan, A.; Saberi, S.; Moradi, M.H.; Towhidkhah, F. Automated ECG segmentation using piecewise derivative dynamic time warping. Int. J. Biol. Med Sci. 2006, 1. [Google Scholar] [CrossRef]
- Houle, M.E.; Kriegel, H.P.; Kröger, P.; Schubert, E.; Zimek, A. Can shared-neighbor distances defeat the curse of dimensionality? In International Conference on Scientific and Statistical Database Management; Springer: Berlin/Heidelberg, Germany, 2010; pp. 482–500. [Google Scholar]
- Wagner, W.; Naeimi, V.; Scipal, K.; de Jeu, R.; Martínez-Fernández, J. Soil moisture from operational meteorological satellites. Hydrogeol. J. 2007, 15, 121–131. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A. A soil water based index as a suitable agricultural drought indicator. J. Hydrol. 2015, 522, 265–273. [Google Scholar] [CrossRef]
- Pietola, L.; Alakukku, L. Root growth dynamics and biomass input by Nordic annual field crops. Agric. Ecosyst. Environ. 2005, 108, 135–144. [Google Scholar] [CrossRef]
- Agrarian Technological Institute of Castilla and León (ITACyL): Maps of Soil Types. Available online: http://suelos.itacyl.es/ (accessed on 1 August 2020).
- Guddat, C.; Deger, J.; Marschall, K.; Zorn, W.; Götz, R. Guidelines for efficient and environmentally sustainable production of winter wheat. Thuring. Reg. Inst. Agric. 2015, 8, 6. [Google Scholar]
- Dorigo, W.; Gruber, A.; De Jeu, R.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Entin, J.K.; Robock, A.; Vinnikov, K.Y.; Hollinger, S.E.; Liu, S.; Namkhai, A. Temporal and spatial scales of observed soil moisture variations in the extratropics. J. Geophys. Res. Atmos. 2000, 105, 11865–11877. [Google Scholar] [CrossRef]
- De Lannoy, G.J.; Pauwels, V.R.; Houser, P.R.; Gish, T.; Verhoest, N.E. Representativeness of Point Soil Moisture Observations, Upscaling and Assimilation. In Symposium HS2004 at IUGG2007, Date: 2007/07/09-2007/07/13, Location: Perugia, Italy; IAHS-AISH Publication: Wallingford, Oxfordshire, UK, 2007; Volume 313, p. 249. [Google Scholar]
- Monerris, A.; Vall-llossera, M.; Camps, A.; Sabia, R.; Villarino, R.; Cardona, M.; Alvarez, E.; Sosa, S. Soil moisture retrieval using L-band radiometry: Dependence on soil type and moisture profiles. In Proceedings of the 2006 IEEE MicroRad, SanJuan, Puerto Rico, 28 February–3 March 2006; pp. 171–175. [Google Scholar]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance metrics for soil moisture retrievals and application requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]









| Station | Land Use | Soil Type | Depth | Sand | Silt | Clay | WP | FC |
|---|---|---|---|---|---|---|---|---|
| [2016–2018] | [cm] | [%] | [%] | [%] | [m m] | [m m] | ||
| Gleyic | 5 | 75.11 | 16.35 | 8.54 | 0.028 | 0.088 | ||
| E10 | Vineyard | and | 25 | 73.74 | 15.71 | 10.55 | 0.047 | 0.108 |
| albic luvisol | 50 | 66.79 | 4.96 | 28.25 | 0.099 | 0.193 | ||
| Cambic arenosol | 5 | 82.25 | 6.44 | 11.31 | 0.040 | 0.125 | ||
| L3 | Vineyard | and | 25 | 82.45 | 6.27 | 11.28 | 0.056 | 0.146 |
| calcaric cambisol | 50 | 80.20 | 11.90 | 7.90 | 0.043 | 0.130 | ||
| Fallow (2016), | Gleyic | 5 | 60.94 | 16.85 | 22.21 | 0.096 | 0.236 | |
| J12 | winter cereals | and | 25 | 59.10 | 16.76 | 24.14 | 0.113 | 0.228 |
| (2017/2018) | albic luvisol | 50 | 59.99 | 14.97 | 25.04 | 0.168 | 0.265 | |
| Calcaric | 5 | 81.64 | 8.31 | 10.05 | 0.057 | 0.100 | ||
| M5 | Winter cereals | and | 25 | 81.41 | 7.87 | 10.72 | 0.042 | 0.125 |
| eutric cambisol | 50 | 84.75 | 5.37 | 9.88 | 0.043 | 0.071 |
| SM Season | Period | Criterion | Prevailing Processes | SM Condition |
|---|---|---|---|---|
| Recharge | November– | PrecipitationPET; | Precipitation | SM storage increases |
| Mid-February | initial plant growth | |||
| Utilization | Mid-February– | PrecipitationPET; | Strong root-water uptake | SM decreases |
| mid-June | main growing season | and evapotranspiration | due to consumption | |
| Deficit | Mid-June– | Precipitation PET; | Evaporation at | Continuous drying; SM |
| October | crops are harvested | maximum | at minimum in the end |
| Station | Local Land Use | SMOS Land Use | Spatial Heterogeneity | Representativeness |
|---|---|---|---|---|
| NDVI Mean/StDev | NDVI Mean/StDev | (SMOS to In-Situ) | ||
| E10 | Vineyard | Mixed land use | Homogeneous up to m, | Given; but station |
| 0.380.12 | 0.340.15 | then heterogeneous | bordering on cereals! | |
| L3 | Vineyard | Mixed land use | Homogeneous up to ±100 m, | Not given |
| 0.170.04 | 0.280.12 | then heterogeneous | ||
| J12 | Rainfed cereals | Rainfed cereals | Proportionally increasing | Conditionally given; |
| 0.310.05 | 0.450.19 | heterogeneity with resolution | variability is diverging | |
| M5 | Rainfed cereals | Mixed land use | Heterogeneous | Given |
| 0.340.17 | 0.260.15 |
| Station | Depth | Time Lag [Days] | |||||
|---|---|---|---|---|---|---|---|
| [cm] | Recharge | Utilization | Deficit | ||||
| Mean | Maximum | Mean | Maximum | Mean | Maximum | ||
| 5 | 5 | 12 | 4 | 16 | 6 | 16 | |
| E10 | 25 | 6 | 18 | 3 | 13 | 7 | 22 |
| 50 | 3 | 7 | 4 | 19 | 38 | 69 | |
| 5 | 7 | 24 | 7 | 22 | 11 | 34 | |
| L3 | 25 | 4 | 19 | 5 | 18 | 8 | 25 |
| 50 | 1 | 4 | 3 | 13 | 23 | 45 | |
| 5 | 3 | 13 | 6 | 22 | 26 | 51 | |
| J12 | 25 | 8 | 19 | 4 | 15 | 7 | 21 |
| 50 | 1 | 4 | 8 | 24 | 13 | 21 | |
| 5 | 6 | 22 | 6 | 27 | 13 | 27 | |
| M5 | 25 | 8 | 24 | 9 | 25 | 23 | 43 |
| 50 | 7 | 19 | 11 | 30 | 38 | 72 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herbert, C.; Pablos, M.; Vall-llossera, M.; Camps, A.; Martínez-Fernández, J. Analyzing Spatio-Temporal Factors to Estimate the Response Time between SMOS and In-Situ Soil Moisture at Different Depths. Remote Sens. 2020, 12, 2614. https://doi.org/10.3390/rs12162614
Herbert C, Pablos M, Vall-llossera M, Camps A, Martínez-Fernández J. Analyzing Spatio-Temporal Factors to Estimate the Response Time between SMOS and In-Situ Soil Moisture at Different Depths. Remote Sensing. 2020; 12(16):2614. https://doi.org/10.3390/rs12162614
Chicago/Turabian StyleHerbert, Christoph, Miriam Pablos, Mercè Vall-llossera, Adriano Camps, and José Martínez-Fernández. 2020. "Analyzing Spatio-Temporal Factors to Estimate the Response Time between SMOS and In-Situ Soil Moisture at Different Depths" Remote Sensing 12, no. 16: 2614. https://doi.org/10.3390/rs12162614
APA StyleHerbert, C., Pablos, M., Vall-llossera, M., Camps, A., & Martínez-Fernández, J. (2020). Analyzing Spatio-Temporal Factors to Estimate the Response Time between SMOS and In-Situ Soil Moisture at Different Depths. Remote Sensing, 12(16), 2614. https://doi.org/10.3390/rs12162614