Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake
Abstract
1. Introduction
2. Geologic Setting and Aftershock Sequence
3. InSAR Data and Processing Methodology
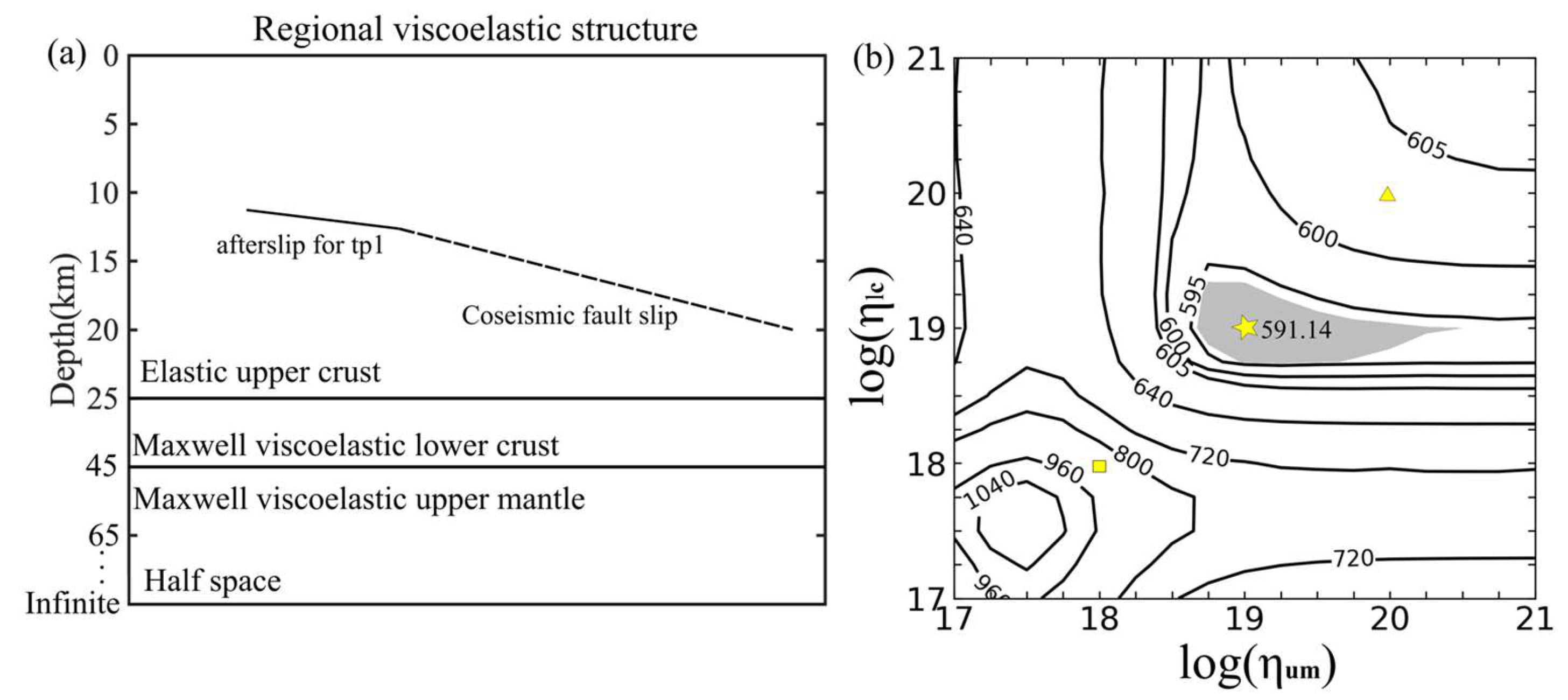
4. Modelling Approach
5. Results
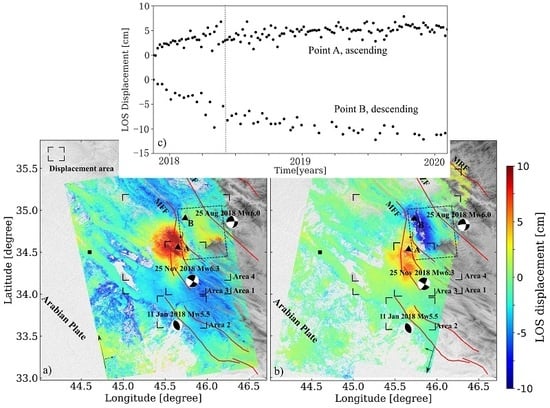
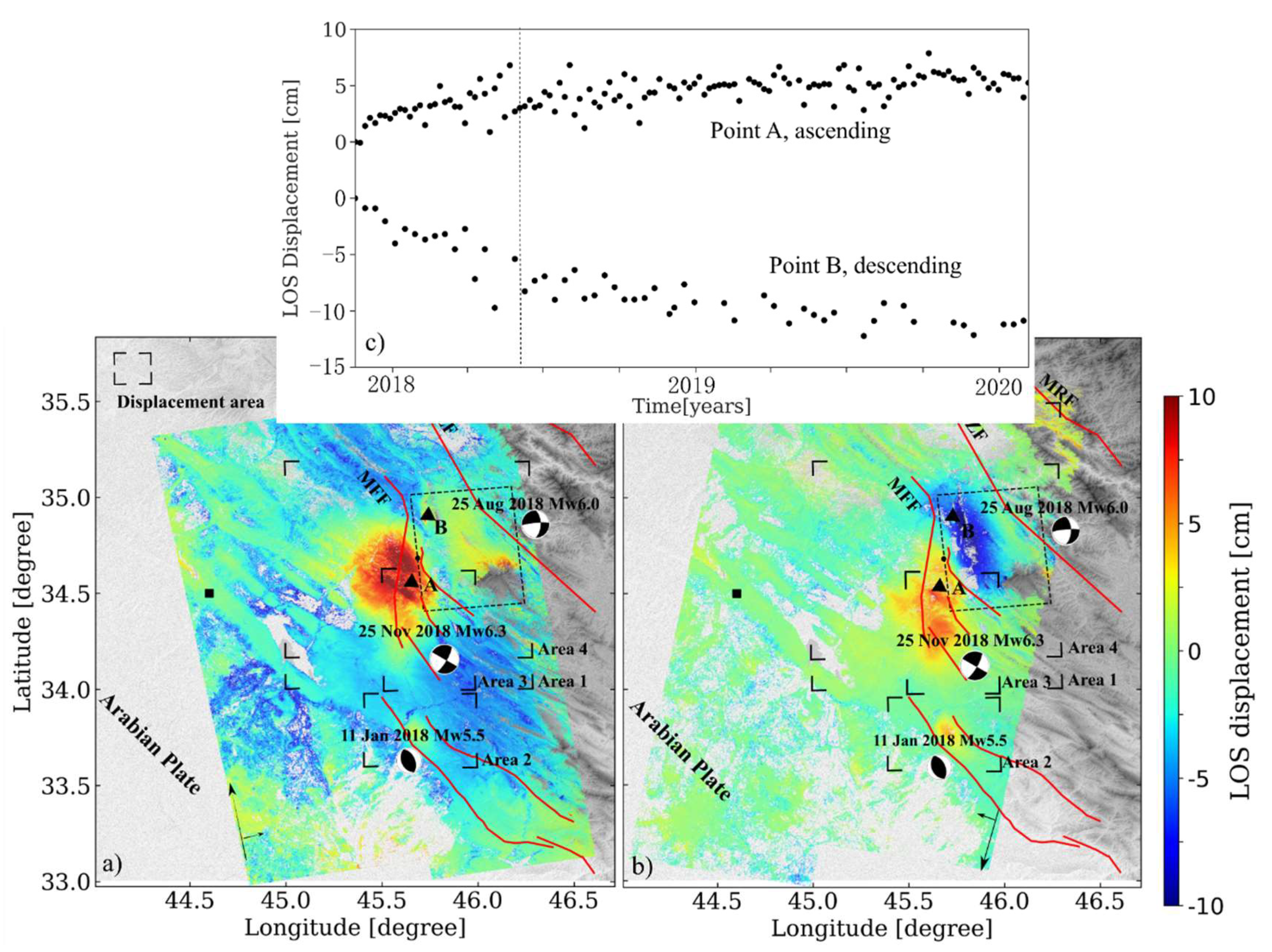
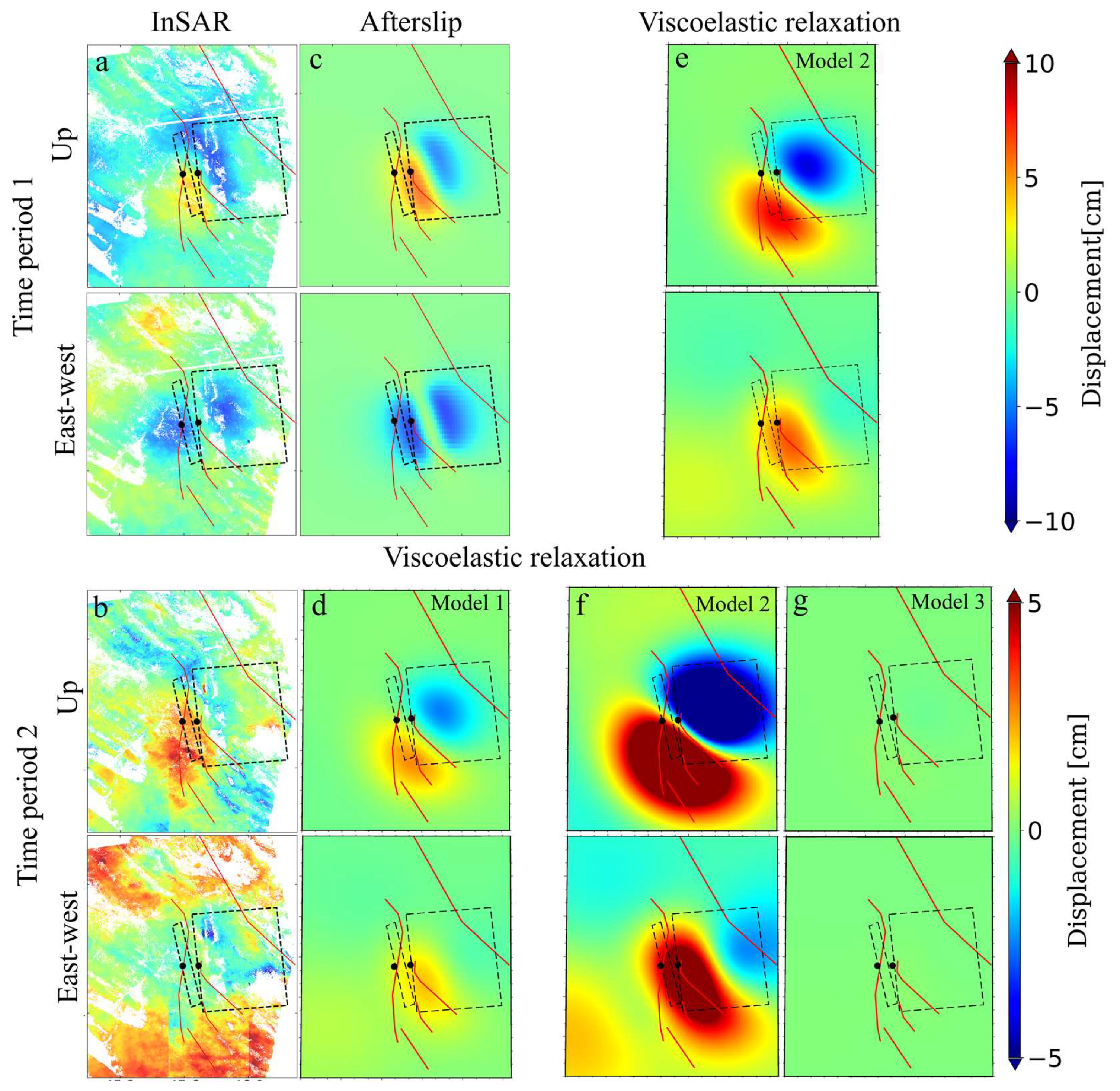
5.1. Post-Seismic Displacement Field
5.2. Aftershocks
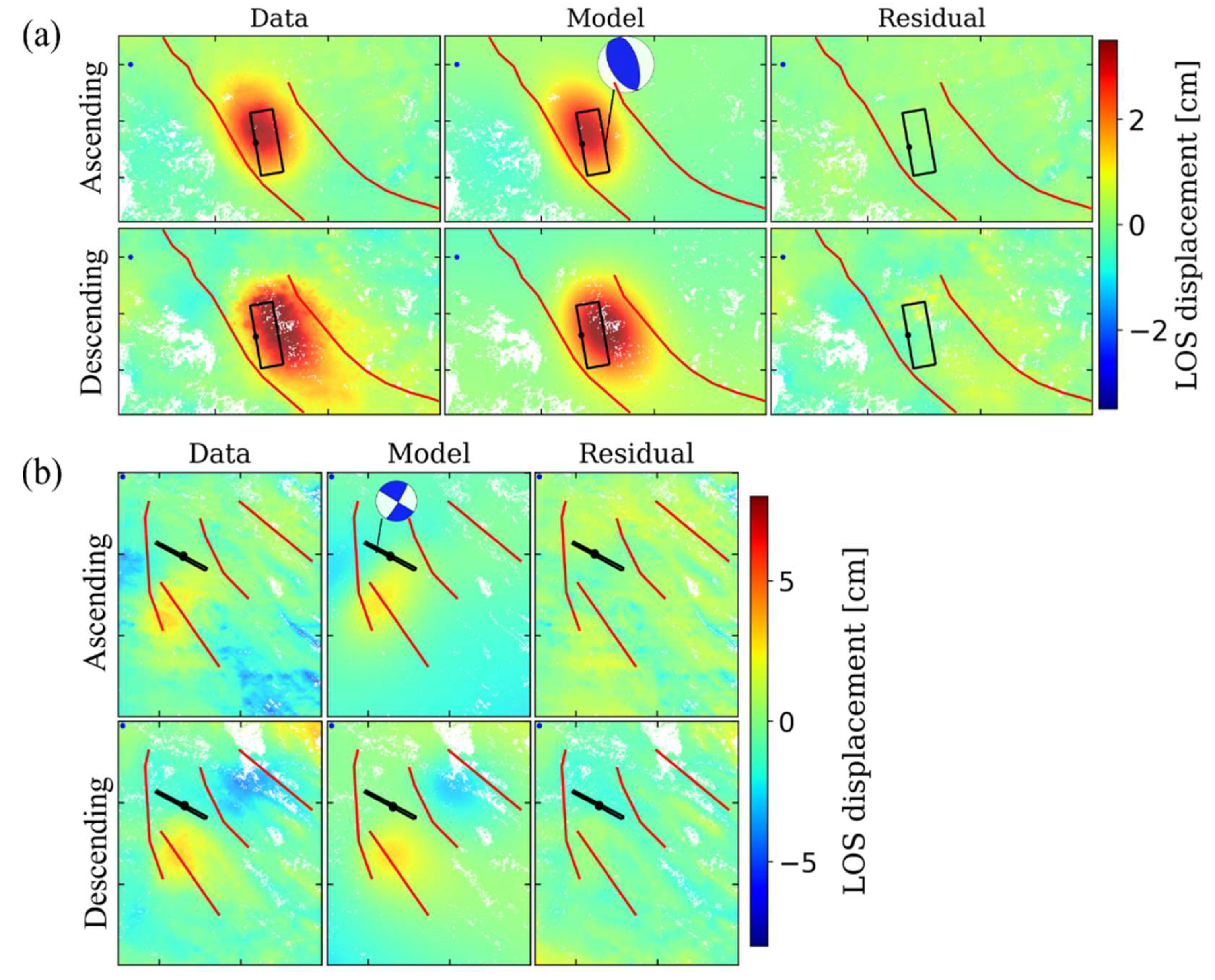
5.3. Afterslip for Time Period 1
5.4. Viscoelastic Relaxation for Time Period 2
5.5. Summary of Post-Seismic Models
6. Discussion
6.1. Afterslip for Time Period 1
6.2. Viscoelastic Relaxation for Time Period 2
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zare, M.; Kamranzad, F.; Parcharidis, I. Preliminary Report of Mw7.3 Sarpol-e Zahab, Iran Earthquake on November 12. 2017; EMSC Report; EMSC/CSEM: Essonne, France, 2018. [Google Scholar]
- Peyret, M.; Rolandone, F.; Dominguez, S.; Djamour, Y.; Meyer, B. Source model for the Mw 6.1, 31 March 2006, Chalan-Chulan Earthquake (Iran) from InSAR. Terra Nova 2008, 20, 126–133. [Google Scholar] [CrossRef]
- Vajedian, S.; Motagh, M.; Mousavi, Z.; Motaghi, K.; Fielding, E.; Akbari, B.; Wetzel, H.-U.; Darabi, A. Coseismic Deformation Field of the Mw 7.3 12 November 2017 Sarpol-e Zahab (Iran) Earthquake: A Decoupling Horizon in the Northern Zagros Mountains Inferred from InSAR Observations. Remote Sens. 2018, 10, 1589. [Google Scholar] [CrossRef]
- Shen, Z.-K.; Jackson, D.D.; Feng, Y.; Cline, M.; Kim, M.; Fang, P.; Bock, Y. Postseismic deformation following the Landers earthquake, California, 28 June 1992. Bull. Seismol. Soc. Am. 1994, 84, 780–791. [Google Scholar]
- Freed, A.M. Earthquake triggering by static, dynamic, and postseismic stress transfer. Annu. Rev. Earth Planet. Sci. 2005, 33, 335–367. [Google Scholar] [CrossRef]
- Wei, S.; Barbot, S.; Graves, R.; Lienkaemper, J.J.; Wang, T.; Hudnut, K.; Fu, Y.; Helmberger, D. The 2014 Mw 6.1 South Napa Earthquake: A Unilateral Rupture with Shallow Asperity and Rapid Afterslip. Seismol. Res. Lett. 2015, 86, 344–354. [Google Scholar] [CrossRef]
- Avouac, J.-P. From Geodetic Imaging of Seismic and Aseismic Fault Slip to Dynamic Modeling of the Seismic Cycle. Annu. Rev. Earth Planet. Sci. 2015, 43, 233–271. [Google Scholar] [CrossRef]
- Deng, J.; Gurnis, M.; Kanamori, H.; Hauksson, E. Viscoelastic Flow in the Lower Crust after the 1992 Landers, California, Earthquake. Science 1998, 282, 1689. [Google Scholar] [CrossRef]
- Wiseman, K.; Bürgmann, R.; Freed, A.M.; Banerjee, P. Viscoelastic relaxation in a heterogeneous Earth following the 2004 Sumatra–Andaman earthquake. Earth Planet. Sci. Lett. 2015, 431, 308–317. [Google Scholar] [CrossRef]
- Pollitz, F.F. Lithosphere and shallow asthenosphere rheology from observations of post-earthquake relaxation. Phys. Earth Planet. Inter. 2019, 293, 106271. [Google Scholar] [CrossRef]
- Peltzer, G.; Rosen, P.; Rogez, F.; Hudnut, K. Poroelastic rebound along the Landers 1992 earthquake surface rupture. J. Geophys. Res. Solid Earth 1998, 103, 30131–30145. [Google Scholar] [CrossRef]
- Hughes, K.L.H.; Masterlark, T.; Mooney, W.D. Poroelastic stress-triggering of the 2005 M8.7 Nias earthquake by the 2004 M9.2 Sumatra–Andaman earthquake. Earth Planet. Sci. Lett. 2010, 293, 289–299. [Google Scholar] [CrossRef]
- Hu, Y.; Bürgmann, R.; Freymueller, J.T.; Banerjee, P.; Wang, K. Contributions of poroelastic rebound and a weak volcanic arc to the postseismic deformation of the 2011 Tohoku earthquake. Earth Planets Space 2014, 66, 106. [Google Scholar] [CrossRef]
- Zhao, B.; Bürgmann, R.; Wang, D.; Tan, K.; Du, R.; Zhang, R. Dominant Controls of Downdip Afterslip and Viscous Relaxation on the Postseismic Displacements Following the Mw7.9 Gorkha, Nepal, Earthquake. J. Geophys. Res. Solid Earth 2017, 122, 8376–8401. [Google Scholar] [CrossRef]
- Mikumo, T.; Yagi, Y.; Singh, S.K.; Santoyo, M.A. Coseismic and postseismic stress changes in a subducting plate: Possible stress interactions between large interplate thrust and intraplate normal-faulting earthquakes. J. Geophys. Res. Solid Earth 2002, 107, ESE 5-1–ESE 5-12. [Google Scholar] [CrossRef]
- Cattania, C.; Hainzl, S.; Wang, L.; Enescu, B.; Roth, F. Aftershock triggering by postseismic stresses: A study based on Coulomb rate-and-state models. J. Geophys. Res. Solid Earth 2015, 120, 2388–2407. [Google Scholar] [CrossRef]
- Verdecchia, A.; Pace, B.; Visini, F.; Scotti, O.; Peruzza, L.; Benedetti, L. The Role of Viscoelastic Stress Transfer in Long-Term Earthquake Cascades: Insights After the Central Italy 2016–2017 Seismic Sequence. Tectonics 2018, 37, 3411–3428. [Google Scholar] [CrossRef]
- Barnhart, W.D.; Brengman, C.M.J.; Li, S.; Peterson, K.E. Ramp-flat basement structures of the Zagros Mountains inferred from co-seismic slip and afterslip of the 2017 Mw7.3 Darbandikhan, Iran/Iraq earthquake. Earth Planet. Sci. Lett. 2018, 496, 96–107. [Google Scholar] [CrossRef]
- Vernant, P.; Nilforoushan, F.; Hatzfeld, D.; Abbassi, M.R.; Vigny, C.; Masson, F.; Nankali, H.; Martinod, J.; Ashtiani, A.; Bayer, R.; et al. Present-day crustal deformation and plate kinematics in the Middle East constrained by GPS measurements in Iran and northern Oman. Geophys. J. Int. 2004, 157, 381–398. [Google Scholar] [CrossRef]
- Chen, K.; Xu, W.; Mai, P.M.; Gao, H.; Zhang, L.; Ding, X. The 2017 Mw 7.3 Sarpol Zahāb Earthquake, Iran: A compact blind shallow-dipping thrust event in the mountain front fault basement. Tectonophysics 2018, 747–748, 108–114. [Google Scholar] [CrossRef]
- Feng, W.; Samsonov, S.; Almeida, R.; Yassaghi, A.; Li, J.; Qiu, Q.; Li, P.; Zheng, W. Geodetic Constraints of the 2017 Mw7.3 Sarpol Zahab, Iran Earthquake, and Its Implications on the Structure and Mechanics of the Northwest Zagros Thrust-Fold Belt. Geophys. Res. Lett. 2018, 45, 6853–6861. [Google Scholar] [CrossRef]
- Ding, K.; He, P.; Wen, Y.; Chen, Y.; Wang, D.; Li, S.; Wang, Q. The 2017 Mw 7.3 Ezgeleh, Iran earthquake determined from InSAR measurements and teleseismic waveforms. Geophys. J. Int. 2018, 215, 1728–1738. [Google Scholar] [CrossRef]
- Yang, Y.H.; Hu, J.C.; Yassaghi, A.; Tsai, M.C.; Zare, M.; Chen, Q.; Wang, Z.G.; Rajabi, A.M.; Kamranzad, F. Midcrustal Thrusting and Vertical Deformation Partitioning Constraint by 2017 Mw 7.3 Sarpol Zahab Earthquake in Zagros Mountain Belt, Iran. Seismol. Res. Lett. 2018, 89, 2204–2213. [Google Scholar] [CrossRef]
- Yang, C.; Han, B.; Zhao, C.; Du, J.; Zhang, D.; Zhu, S. Co-and post-seismic Deformation Mechanisms of the MW 7.3 Iran Earthquake (2017) Revealed by Sentinel-1 InSAR Observations. Remote Sens. 2019, 11, 418. [Google Scholar] [CrossRef]
- Rosen, P.A.; Gurrola, E.; Sacco, G.F.; Zebker, H. The InSAR scientific computing environment. In Proceedings of the EUSAR 2012; 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012; pp. 730–733. [Google Scholar]
- Fattahi, H.; Agram, P.; Simons, M. A Network-Based Enhanced Spectral Diversity Approach for TOPS Time-Series Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 777–786. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338–351. [Google Scholar] [CrossRef]
- Yunjun, Z.; Fattahi, H.; Amelung, F. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar] [CrossRef]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar]
- Barbot, S.; Fialko, Y.; Sandwell, D. Three-dimensional models of elastostatic deformation in heterogeneous media, with applications to the Eastern California Shear Zone. Geophys. J. Int. 2009, 179, 500–520. [Google Scholar] [CrossRef]
- Barbot, S.; Fialko, Y. Fourier-domain Green’s function for an elastic semi-infinite solid under gravity, with applications to earthquake and volcano deformation. Geophys. J. Int. 2010, 182, 568–582. [Google Scholar] [CrossRef]
- Barbot, S.; Fialko, Y. A unified continuum representation of post-seismic relaxation mechanisms: Semi-analytic models of afterslip, poroelastic rebound and viscoelastic flow. Geophys. J. Int. 2010, 182, 1124–1140. [Google Scholar] [CrossRef]
- Bagnardi, M.; Hooper, A. Inversion of Surface Deformation Data for Rapid Estimates of Source Parameters and Uncertainties: A Bayesian Approach. Geochem. Geophys. Geosyst. 2018, 19, 2194–2211. [Google Scholar] [CrossRef]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1.0—A 1-degree Global Model of Earth’s Crust. Geophys. Res. Abstr. 2013, 15, 2658. [Google Scholar]
- Hatzfeld, D.; Tatar, M.; Priestley, K.; Ghafory-Ashtiany, M. Seismological constraints on the crustal structure beneath the Zagros Mountain belt (Iran). Geophys. J. Int. 2003, 155, 403–410. [Google Scholar] [CrossRef]
- Stein, S.; Gordon, R.G. Statistical tests of additional plate boundaries from plate motion inversions. Earth Planet. Sci. Lett. 1984, 69, 401–412. [Google Scholar] [CrossRef]
- Hao, M.; Shen, Z.-K.; Wang, Q.; Cui, D. Postseismic deformation mechanisms of the 1990 Mw 6.4 Gonghe, China earthquake constrained using leveling measurements. Tectonophysics 2012, 532–535, 205–214. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Peltzer, G.; Bürgmann, R. Mobility of continental mantle: Evidence from postseismic geodetic observations following the 1992 Landers earthquake. J. Geophys. Res. Solid Earth 2000, 105, 8035–8054. [Google Scholar] [CrossRef]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geopyhs. Res. Lett. 2004, 31, L01607. [Google Scholar] [CrossRef]
- Marone, C.J.; Scholtz, C.H.; Bilham, R. On the mechanics of earthquake afterslip. J. Geophys. Res. Solid Earth 1991, 96, 8441–8452. [Google Scholar] [CrossRef]
- Mahsas, A.; Lammali, K.; Yelles, K.; Calais, E.; Freed, A.M.; Briole, P. Shallow afterslip following the 2003 May 21, Mw = 6.9 Boumerdes earthquake, Algeria. Geophys. J. Int. 2008, 172, 155–166. [Google Scholar] [CrossRef]
- Cetin, E.; Meghraoui, M.; Cakir, Z.; Akoglu, A.M.; Mimouni, O.; Chebbah, M. Seven years of postseismic deformation following the 2003 Mw = 6.8 Zemmouri earthquake (Algeria) from InSAR time series. Geopyhs. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Jiang, G.; Wang, Y.; Wen, Y.; Liu, Y.; Xu, C.; Xu, C. Afterslip evolution on the crustal ramp of the Main Himalayan Thrust fault following the 2015 Mw 7.8 Gorkha (Nepal) earthquake. Tectonophysics 2019, 758, 29–43. [Google Scholar] [CrossRef]
- Ozawa, S.; Nishimura, T.; Suito, H.; Kobayashi, T.; Tobita, M.; Imakiire, T. Coseismic and postseismic slip of the 2011 magnitude-9 Tohoku-Oki earthquake. Nature 2011, 475, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, S.; Nishimura, T.; Munekane, H.; Suito, H.; Kobayashi, T.; Tobita, M.; Imakiire, T. Preceding, coseismic, and postseismic slips of the 2011 Tohoku earthquake, Japan. J. Geophys. Res.Solid Earth 2012, 117, 7404. [Google Scholar] [CrossRef]
- Noda, A.; Takahama, T.; Kawasato, T.; Matsu’ura, M. Interpretation of Offshore Crustal Movements Following the 2011 Tohoku-Oki Earthquake by the Combined Effect of Afterslip and Viscoelastic Stress Relaxation. Pure Appl. Geophys. 2018, 175, 559–572. [Google Scholar] [CrossRef]
- Diao, F.; Wang, R.; Wang, Y.; Xiong, X.; Walter, T.R. Fault behavior and lower crustal rheology inferred from the first seven years of postseismic GPS data after the 2008 Wenchuan earthquake. Earth Planet. Sci. Lett. 2018, 495, 202–212. [Google Scholar] [CrossRef]
- Lienkaemper, J.J.; McFarland, F.S. Long-Term Afterslip of the 2004 M 6.0 Parkfield, California, Earthquake—Implications for Forecasting Amount and Duration of Afterslip on Other Major Creeping Faults. Bull. Seismol. Soc. Am. 2017, 107, 1082–1093. [Google Scholar] [CrossRef]
- Wright, T.J.; Elliott, J.R.; Wang, H.; Ryder, I. Earthquake cycle deformation and the Moho: Implications for the rheology of continental lithosphere. Tectonophysics 2013, 609, 504–523. [Google Scholar] [CrossRef]
- Afsari, N.; Sodoudi, F.; Taghizadeh Farahmand, F.; Ghassemi, M.R. Crustal structure of Northwest Zagros (Kermanshah) and Central Iran (Yazd and Isfahan) using teleseismic Ps converted phases. J. Seismol. 2011, 15, 341–353. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Wicks, C.; Thatcher, W. Mantle Flow Beneath a Continental Strike-Slip Fault: Postseismic Deformation After the 1999 Hector Mine Earthquake. Science 2001, 293, 1814. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Bürgmann, R.; Thatcher, W. Illumination of rheological mantle heterogeneity by the M7.2 2010 El Mayor-Cucapah earthquake. Geochem. Geophys. Geosyst. 2012, 13, Q06002. [Google Scholar] [CrossRef]
- Jónsson, S. Importance of post-seismic viscous relaxation in southern Iceland. Nat. Geosci. 2008, 1, 136–139. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Bürgmann, R.; Segall, P. Joint estimation of afterslip rate and postseismic relaxation following the 1989 Loma Prieta earthquake. J. Geophys. Res. Solid Earth 1998, 103, 26975–26992. [Google Scholar] [CrossRef]
- Dalla Via, G.; Sabadini, R.; De Natale, G.; Pingue, F. Lithospheric rheology in southern Italy inferred from postseismic viscoelastic relaxation following the 1980 Irpinia earthquake. J. Geophys. Res. Solid Earth 2005, 110, B06311. [Google Scholar] [CrossRef]
- Wimpenny, S.; Copley, A.; Ingleby, T. Fault mechanics and post-seismic deformation at Bam, SE Iran. Geophys. J. Int. 2017, 209, 1018–1035. [Google Scholar] [CrossRef]
- Gourmelen, N.; Amelung, F. Postseismic Mantle Relaxation in the Central Nevada Seismic Belt. Science 2005, 310, 1473. [Google Scholar] [CrossRef]
- Nishimura, T.; Thatcher, W. Rheology of the lithosphere inferred from postseismic uplift following the 1959 Hebgen Lake earthquake. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Deng, J.; Hudnut, K.; Gurnis, M.; Hauksson, E. Stress loading from viscous flow in the lower crust and triggering of aftershocks following the 1994 Northridge, California, Earthquake. Geopyhs. Res. Lett. 1999, 26, 3209–3212. [Google Scholar] [CrossRef]
- Wang, L.; Wang, R.; Roth, F.; Enescu, B.; Hainzl, S.; Ergintav, S. Afterslip and viscoelastic relaxation following the 1999 M 7.4 İzmit earthquake from GPS measurements. Geophys. J. Int. 2009, 178, 1220–1237. [Google Scholar] [CrossRef]
- Sheu, S.; Shieh, C. Viscoelastic–afterslip concurrence: A possible mechanism in the early post-seismic deformation of the Mw 7.6, 1999 Chi-Chi (Taiwan) earthquake. Geophys. J. Int. 2004, 159, 1112–1124. [Google Scholar] [CrossRef]
- Ryder, I.; Parsons, B.; Wright, T.J.; Funning, G.J. Post-seismic motion following the 1997 Manyi (Tibet) earthquake: InSAR observations and modelling. Geophys. J. Int. 2007, 169, 1009–1027. [Google Scholar] [CrossRef]
- Vergnolle, M.; Pollitz, F.; Calais, E. Constraints on the viscosity of the continental crust and mantle from GPS measurements and postseismic deformation models in western Mongolia. J. Geophys. Res. Solid Earth 2003, 108, 2502. [Google Scholar] [CrossRef]
- Reddy, C.D.; Sunil, P.S.; Bürgmann, R.; Chandrasekhar, D.V.; Kato, T. Postseismic relaxation due to Bhuj earthquake on January 26, 2001: Possible mechanisms and processes. Nat. Hazards 2013, 65, 1119–1134. [Google Scholar] [CrossRef]
- Ryder, I.; Bürgmann, R.; Pollitz, F. Lower crustal relaxation beneath the Tibetan Plateau and Qaidam Basin following the 2001 Kokoxili earthquake. Geophys. J. Int. 2011, 187, 613–630. [Google Scholar] [CrossRef]
- Johnson, K.M.; Bürgmann, R.; Freymueller, J.T. Coupled afterslip and viscoelastic flow following the 2002 Denali Fault, Alaska earthquake. Geophys. J. Int. 2009, 176, 670–682. [Google Scholar] [CrossRef]
- Bruhat, L.; Barbot, S.; Avouac, J.-P. Evidence for postseismic deformation of the lower crust following the 2004 Mw6.0 Parkfield earthquake. J. Geophys. Res. Solid Earth 2011, 116, B08401. [Google Scholar] [CrossRef]
- Dixon, J.E.; Dixon, T.H.; Bell, D.R.; Malservisi, R. Lateral variation in upper mantle viscosity: Role of water. Earth Planet. Sci. Lett. 2004, 222, 451–467. [Google Scholar] [CrossRef]
- Hirth, G.; Kohlstedt, D. Rheology of the Upper Mantle and the Mantle Wedge: A View from the Experimentalists. In Inside the Subduction Factory; Geophysical Monograph Series; Eiler, J., Ed.; Blackwell Publishing Ltd.: Oxford, UK, 2004; pp. 83–105. [Google Scholar]
- Bürgmann, R.; Dresen, G. Rheology of the Lower Crust and Upper Mantle: Evidence from Rock Mechanics, Geodesy, and Field Observations. Annu. Rev. Earth Planet. Sci. 2008, 36, 531–567. [Google Scholar] [CrossRef]
- Batir, J.F.B.; David, D.; Richards, M.C. Updated Surface Heat Flow Map of Alaska. In Proceedings of the Geothermal Resources Council Transactions, 2013 Annual Meeting, Las Vegas, NV, USA, 30 September–3 October 2013. [Google Scholar]
- Hjartarson, Á. Heat Flow in Iceland. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Mahmoodabadi, M.; Yaminifard, F.; Tatar, M.; Kaviani, A.; Motaghi, K. Upper-mantle velocity structure beneath the Zagros collision zone, Central Iran and Alborz from nonlinear teleseismic tomography. Geophys. J. Int. 2019, 218, 414–428. [Google Scholar] [CrossRef]
- Chen, C.-H.; Wang, W.-H.; Teng, T.-L. 3D Velocity Structure around the Source Area of the 1999 Chi-Chi, Taiwan, Earthquake: Before and After the Mainshock. Bull. Seismol. Soc. Am. 2001, 91, 1013–1027. [Google Scholar] [CrossRef]
- Moreno, M.; Haberland, C.; Oncken, O.; Rietbrock, A.; Angiboust, S.; Heidbach, O. Locking of the Chile subduction zone controlled by fluid pressure before the 2010 earthquake. Nat. Geosci. 2014, 7, 292–296. [Google Scholar] [CrossRef]
- Freed, A.M.; Bürgmann, R. Evidence of power-law flow in the Mojave desert mantle. Nature 2004, 430, 548–551. [Google Scholar] [CrossRef] [PubMed]
| Time (UTC) | Magnitude (Mw) | Type | Depth (km) |
|---|---|---|---|
| Aftershock sequence on 11 January 2018 (aftershock sequence 1) | |||
| 06:59:30 | 5.5 | Thrust | 13.5 |
| 07:00:52 | 5.3 | No information | No information |
| 07:14:15 | 5.3 | Thrust | 13.5 |
| 07:55:00 | 5.1 | No information | No information |
| 08:00:39 | 5.3 | Thrust | 17.5 |
| Aftershock sequence on 25 November 2018 (aftershock sequence 2) | |||
| 16:37:32 | 6.3 | Strike-slip | 23.5 |
| 17:09:36 | 5.2 | Thrust | 17.5 |
| 23:00:46 | 5.0 | No information | No information |
| Length (km) | Width (km) | Depth (km) | Dip (°) | Strike (°) | Dip Slip b (m) | Strike Slip c (m) | Lat d,e | Lon d,e | Mw e | Rms (m) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Aftershocks 1 (Mw5.5) | |||||||||||
| Lower | 5 | 5 | 1 | −90 | 90 | 0 | −0.2 | — | — | — | |
| Upper | 50 | 35 | 30 | 90 | 360 | 6 | 0.2 | — | — | — | |
| Optimal | 12.9 | 5.4 | 13.0 | 51 | 344 | 0.39 | −0.08 | 33.71 | 45.68 | 5.94 | 0.002 |
| 2.5% a | 8.7 | 1.8 | 11. 9 | 42 | 335 | 0.21 | −0.25 | — | — | — | |
| 97.5% a | 15.3 | 10.1 | 15.3 | 58 | 352 | 0.59 | 0.05 | — | — | — | |
| Aftershocks 2 (Mw6.3) | |||||||||||
| Lower | 5 | 5 | 1 | 50 | 90 | −0.3 | −2 | — | — | — | |
| Upper | 30 | 30 | 40 | 90 | 360 | 0 | 2 | — | — | — | |
| Optimal | 12.7 | 8.8 | 22.0 | 90 | 302 | −0.29 | 1.80 | 34.36 | 45.70 | 6.52 | 0.008 |
| 2.5% | 6.2 | 2.9 | 13.2 | 87 | 292 | −0.41 | 0.91 | — | — | — | |
| 97.5% | 21.2 | 14.7 | 32.0 | 90 | 310 | −0.02 | 2.25 | — | — | — | |
| Afterslip | |||||||||||
| Lower | 5 | 1 | 5 | −20 | 330 | 0 | −3 | — | — | — | |
| Upper | 70 | 50 | 20 | 20 | 360 | 5 | 3 | — | — | — | |
| Optimal | 45.5 | 6.4 | 11.5 | −4 | 346 | 0.69 | −0.45 | 34.45 | 45.62 | 6.56 | 0.018 |
| 2.5% | 38.9 | 1.0 | 10.3 | −10 | 340 | 0.13 | −0.76 | — | — | — | |
| 97.5% | 54.6 | 11.5 | 13.6 | 5 | 350 | 1.56 | −0.24 | — | — | — | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, X.; Amelung, F.; Shao, Y.; Ye, S.; Liu, M.; Xie, C. Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake. Remote Sens. 2020, 12, 2032. https://doi.org/10.3390/rs12122032
Lv X, Amelung F, Shao Y, Ye S, Liu M, Xie C. Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake. Remote Sensing. 2020; 12(12):2032. https://doi.org/10.3390/rs12122032
Chicago/Turabian StyleLv, Xiaoran, Falk Amelung, Yun Shao, Shu Ye, Ming Liu, and Chou Xie. 2020. "Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake" Remote Sensing 12, no. 12: 2032. https://doi.org/10.3390/rs12122032
APA StyleLv, X., Amelung, F., Shao, Y., Ye, S., Liu, M., & Xie, C. (2020). Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake. Remote Sensing, 12(12), 2032. https://doi.org/10.3390/rs12122032