Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake
Abstract
:1. Introduction
2. Geologic Setting and Aftershock Sequence
3. InSAR Data and Processing Methodology
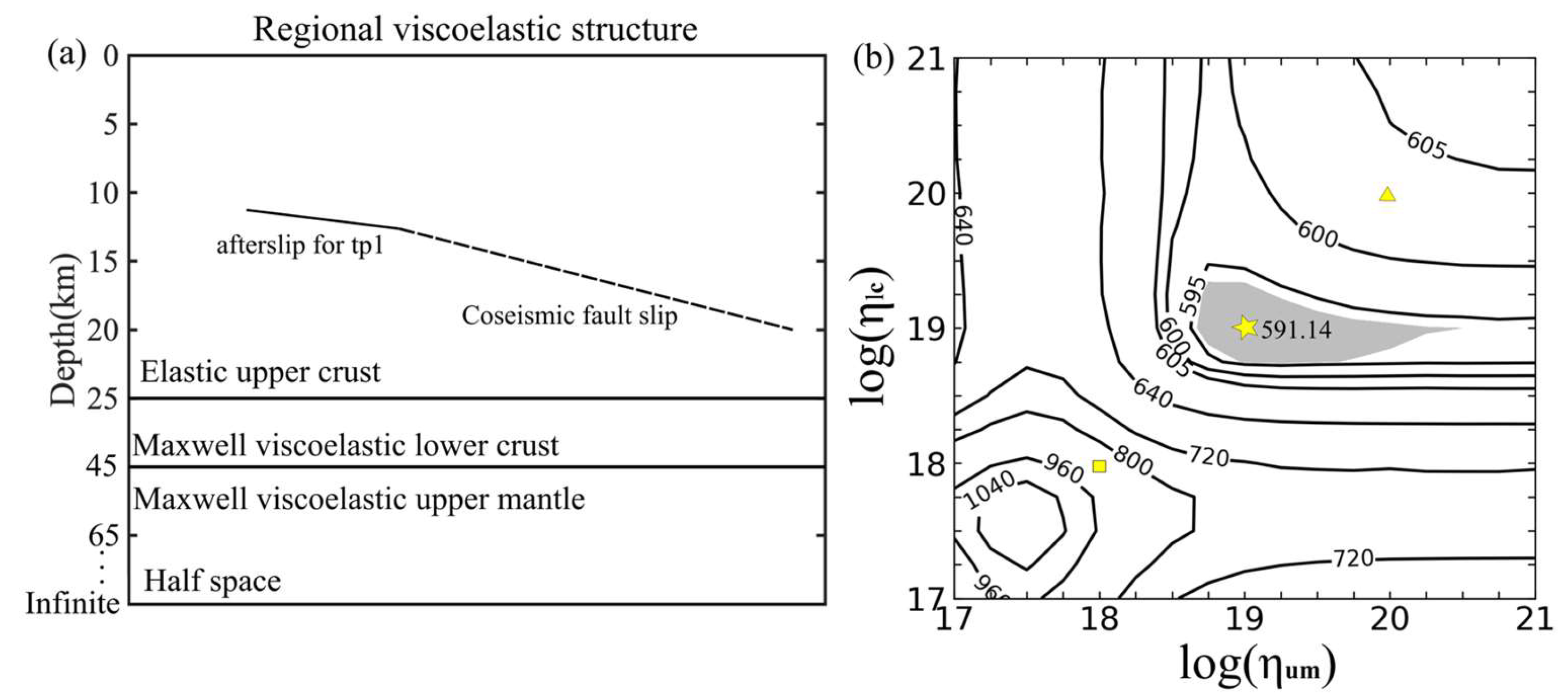
4. Modelling Approach
5. Results
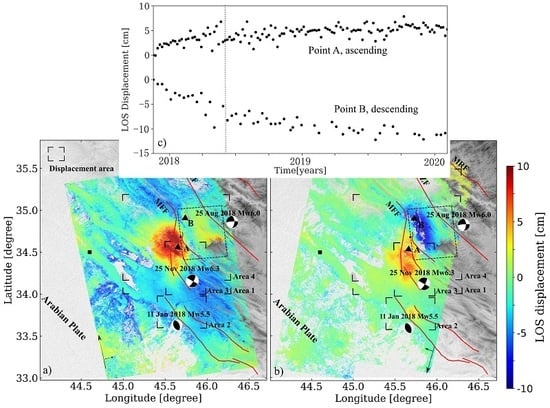
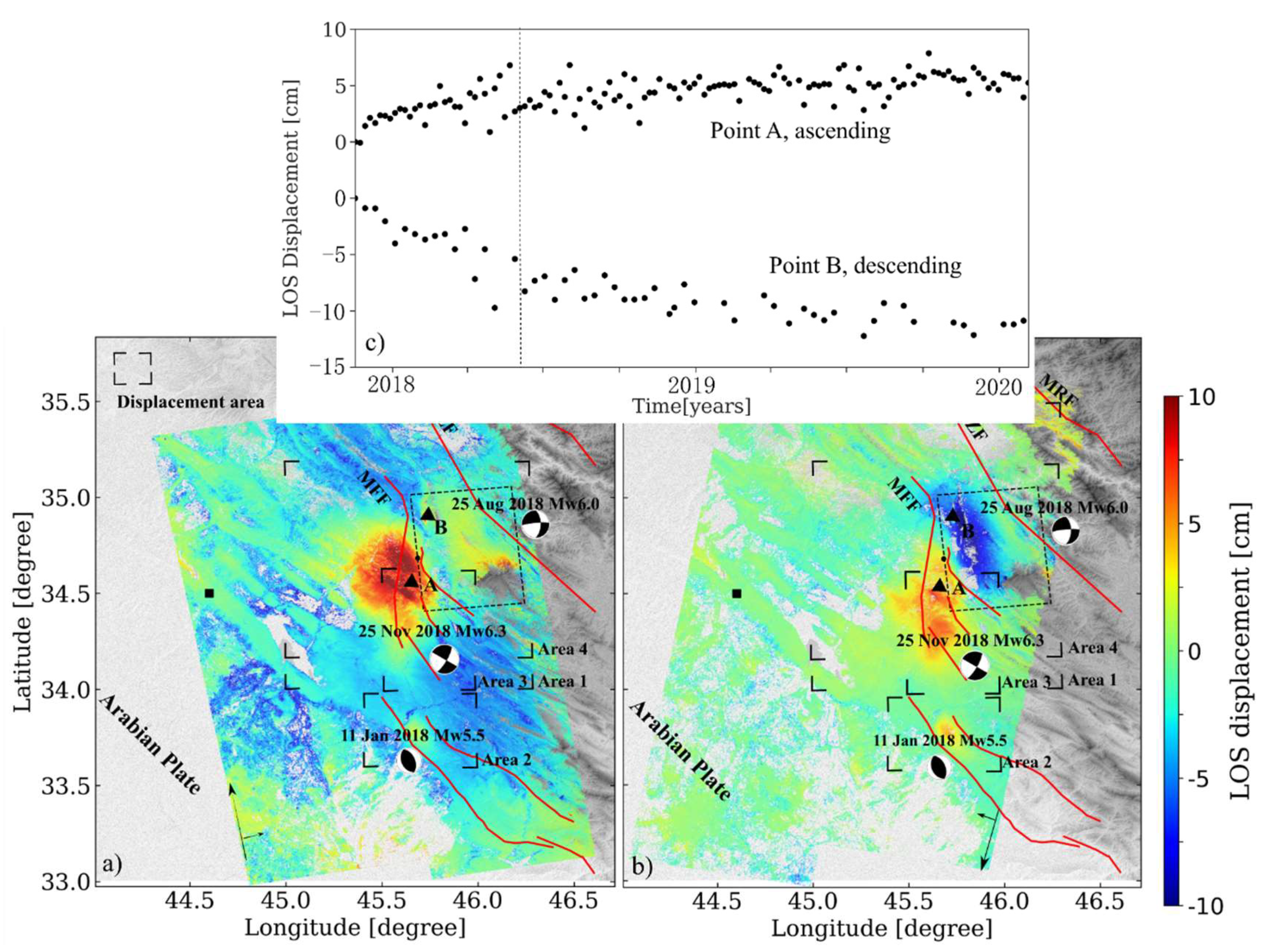
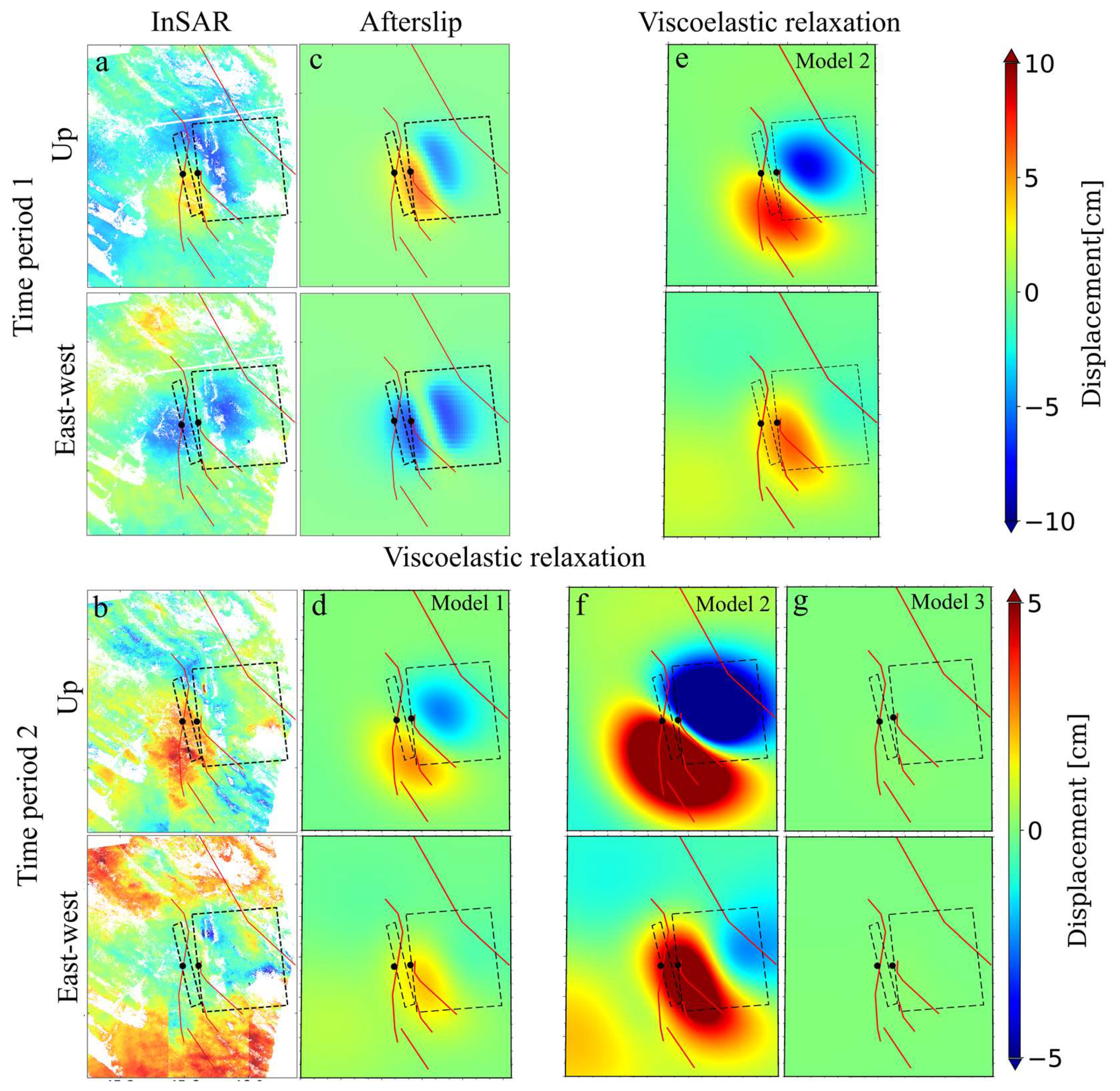
5.1. Post-Seismic Displacement Field
5.2. Aftershocks
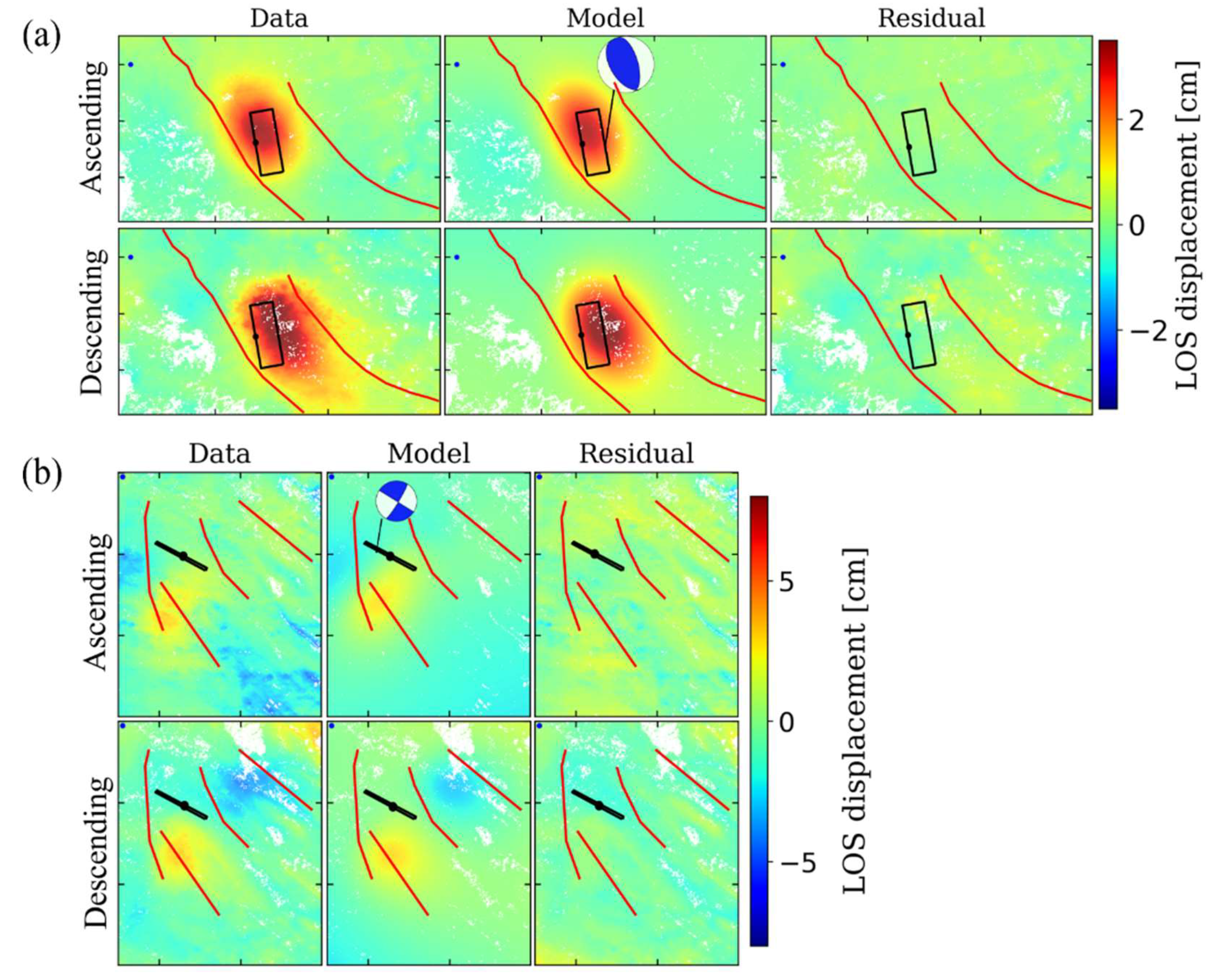
5.3. Afterslip for Time Period 1
5.4. Viscoelastic Relaxation for Time Period 2
5.5. Summary of Post-Seismic Models
6. Discussion
6.1. Afterslip for Time Period 1
6.2. Viscoelastic Relaxation for Time Period 2
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zare, M.; Kamranzad, F.; Parcharidis, I. Preliminary Report of Mw7.3 Sarpol-e Zahab, Iran Earthquake on November 12. 2017; EMSC Report; EMSC/CSEM: Essonne, France, 2018. [Google Scholar]
- Peyret, M.; Rolandone, F.; Dominguez, S.; Djamour, Y.; Meyer, B. Source model for the Mw 6.1, 31 March 2006, Chalan-Chulan Earthquake (Iran) from InSAR. Terra Nova 2008, 20, 126–133. [Google Scholar] [CrossRef]
- Vajedian, S.; Motagh, M.; Mousavi, Z.; Motaghi, K.; Fielding, E.; Akbari, B.; Wetzel, H.-U.; Darabi, A. Coseismic Deformation Field of the Mw 7.3 12 November 2017 Sarpol-e Zahab (Iran) Earthquake: A Decoupling Horizon in the Northern Zagros Mountains Inferred from InSAR Observations. Remote Sens. 2018, 10, 1589. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.-K.; Jackson, D.D.; Feng, Y.; Cline, M.; Kim, M.; Fang, P.; Bock, Y. Postseismic deformation following the Landers earthquake, California, 28 June 1992. Bull. Seismol. Soc. Am. 1994, 84, 780–791. [Google Scholar]
- Freed, A.M. Earthquake triggering by static, dynamic, and postseismic stress transfer. Annu. Rev. Earth Planet. Sci. 2005, 33, 335–367. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.; Barbot, S.; Graves, R.; Lienkaemper, J.J.; Wang, T.; Hudnut, K.; Fu, Y.; Helmberger, D. The 2014 Mw 6.1 South Napa Earthquake: A Unilateral Rupture with Shallow Asperity and Rapid Afterslip. Seismol. Res. Lett. 2015, 86, 344–354. [Google Scholar] [CrossRef] [Green Version]
- Avouac, J.-P. From Geodetic Imaging of Seismic and Aseismic Fault Slip to Dynamic Modeling of the Seismic Cycle. Annu. Rev. Earth Planet. Sci. 2015, 43, 233–271. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.; Gurnis, M.; Kanamori, H.; Hauksson, E. Viscoelastic Flow in the Lower Crust after the 1992 Landers, California, Earthquake. Science 1998, 282, 1689. [Google Scholar] [CrossRef]
- Wiseman, K.; Bürgmann, R.; Freed, A.M.; Banerjee, P. Viscoelastic relaxation in a heterogeneous Earth following the 2004 Sumatra–Andaman earthquake. Earth Planet. Sci. Lett. 2015, 431, 308–317. [Google Scholar] [CrossRef] [Green Version]
- Pollitz, F.F. Lithosphere and shallow asthenosphere rheology from observations of post-earthquake relaxation. Phys. Earth Planet. Inter. 2019, 293, 106271. [Google Scholar] [CrossRef]
- Peltzer, G.; Rosen, P.; Rogez, F.; Hudnut, K. Poroelastic rebound along the Landers 1992 earthquake surface rupture. J. Geophys. Res. Solid Earth 1998, 103, 30131–30145. [Google Scholar] [CrossRef]
- Hughes, K.L.H.; Masterlark, T.; Mooney, W.D. Poroelastic stress-triggering of the 2005 M8.7 Nias earthquake by the 2004 M9.2 Sumatra–Andaman earthquake. Earth Planet. Sci. Lett. 2010, 293, 289–299. [Google Scholar] [CrossRef]
- Hu, Y.; Bürgmann, R.; Freymueller, J.T.; Banerjee, P.; Wang, K. Contributions of poroelastic rebound and a weak volcanic arc to the postseismic deformation of the 2011 Tohoku earthquake. Earth Planets Space 2014, 66, 106. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Bürgmann, R.; Wang, D.; Tan, K.; Du, R.; Zhang, R. Dominant Controls of Downdip Afterslip and Viscous Relaxation on the Postseismic Displacements Following the Mw7.9 Gorkha, Nepal, Earthquake. J. Geophys. Res. Solid Earth 2017, 122, 8376–8401. [Google Scholar] [CrossRef] [Green Version]
- Mikumo, T.; Yagi, Y.; Singh, S.K.; Santoyo, M.A. Coseismic and postseismic stress changes in a subducting plate: Possible stress interactions between large interplate thrust and intraplate normal-faulting earthquakes. J. Geophys. Res. Solid Earth 2002, 107, ESE 5-1–ESE 5-12. [Google Scholar] [CrossRef] [Green Version]
- Cattania, C.; Hainzl, S.; Wang, L.; Enescu, B.; Roth, F. Aftershock triggering by postseismic stresses: A study based on Coulomb rate-and-state models. J. Geophys. Res. Solid Earth 2015, 120, 2388–2407. [Google Scholar] [CrossRef] [Green Version]
- Verdecchia, A.; Pace, B.; Visini, F.; Scotti, O.; Peruzza, L.; Benedetti, L. The Role of Viscoelastic Stress Transfer in Long-Term Earthquake Cascades: Insights After the Central Italy 2016–2017 Seismic Sequence. Tectonics 2018, 37, 3411–3428. [Google Scholar] [CrossRef] [Green Version]
- Barnhart, W.D.; Brengman, C.M.J.; Li, S.; Peterson, K.E. Ramp-flat basement structures of the Zagros Mountains inferred from co-seismic slip and afterslip of the 2017 Mw7.3 Darbandikhan, Iran/Iraq earthquake. Earth Planet. Sci. Lett. 2018, 496, 96–107. [Google Scholar] [CrossRef]
- Vernant, P.; Nilforoushan, F.; Hatzfeld, D.; Abbassi, M.R.; Vigny, C.; Masson, F.; Nankali, H.; Martinod, J.; Ashtiani, A.; Bayer, R.; et al. Present-day crustal deformation and plate kinematics in the Middle East constrained by GPS measurements in Iran and northern Oman. Geophys. J. Int. 2004, 157, 381–398. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Xu, W.; Mai, P.M.; Gao, H.; Zhang, L.; Ding, X. The 2017 Mw 7.3 Sarpol Zahāb Earthquake, Iran: A compact blind shallow-dipping thrust event in the mountain front fault basement. Tectonophysics 2018, 747–748, 108–114. [Google Scholar] [CrossRef] [Green Version]
- Feng, W.; Samsonov, S.; Almeida, R.; Yassaghi, A.; Li, J.; Qiu, Q.; Li, P.; Zheng, W. Geodetic Constraints of the 2017 Mw7.3 Sarpol Zahab, Iran Earthquake, and Its Implications on the Structure and Mechanics of the Northwest Zagros Thrust-Fold Belt. Geophys. Res. Lett. 2018, 45, 6853–6861. [Google Scholar] [CrossRef]
- Ding, K.; He, P.; Wen, Y.; Chen, Y.; Wang, D.; Li, S.; Wang, Q. The 2017 Mw 7.3 Ezgeleh, Iran earthquake determined from InSAR measurements and teleseismic waveforms. Geophys. J. Int. 2018, 215, 1728–1738. [Google Scholar] [CrossRef]
- Yang, Y.H.; Hu, J.C.; Yassaghi, A.; Tsai, M.C.; Zare, M.; Chen, Q.; Wang, Z.G.; Rajabi, A.M.; Kamranzad, F. Midcrustal Thrusting and Vertical Deformation Partitioning Constraint by 2017 Mw 7.3 Sarpol Zahab Earthquake in Zagros Mountain Belt, Iran. Seismol. Res. Lett. 2018, 89, 2204–2213. [Google Scholar] [CrossRef]
- Yang, C.; Han, B.; Zhao, C.; Du, J.; Zhang, D.; Zhu, S. Co-and post-seismic Deformation Mechanisms of the MW 7.3 Iran Earthquake (2017) Revealed by Sentinel-1 InSAR Observations. Remote Sens. 2019, 11, 418. [Google Scholar] [CrossRef] [Green Version]
- Rosen, P.A.; Gurrola, E.; Sacco, G.F.; Zebker, H. The InSAR scientific computing environment. In Proceedings of the EUSAR 2012; 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012; pp. 730–733. [Google Scholar]
- Fattahi, H.; Agram, P.; Simons, M. A Network-Based Enhanced Spectral Diversity Approach for TOPS Time-Series Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 777–786. [Google Scholar] [CrossRef] [Green Version]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338–351. [Google Scholar] [CrossRef] [Green Version]
- Yunjun, Z.; Fattahi, H.; Amelung, F. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar] [CrossRef] [Green Version]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar]
- Barbot, S.; Fialko, Y.; Sandwell, D. Three-dimensional models of elastostatic deformation in heterogeneous media, with applications to the Eastern California Shear Zone. Geophys. J. Int. 2009, 179, 500–520. [Google Scholar] [CrossRef] [Green Version]
- Barbot, S.; Fialko, Y. Fourier-domain Green’s function for an elastic semi-infinite solid under gravity, with applications to earthquake and volcano deformation. Geophys. J. Int. 2010, 182, 568–582. [Google Scholar] [CrossRef] [Green Version]
- Barbot, S.; Fialko, Y. A unified continuum representation of post-seismic relaxation mechanisms: Semi-analytic models of afterslip, poroelastic rebound and viscoelastic flow. Geophys. J. Int. 2010, 182, 1124–1140. [Google Scholar] [CrossRef] [Green Version]
- Bagnardi, M.; Hooper, A. Inversion of Surface Deformation Data for Rapid Estimates of Source Parameters and Uncertainties: A Bayesian Approach. Geochem. Geophys. Geosyst. 2018, 19, 2194–2211. [Google Scholar] [CrossRef]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1.0—A 1-degree Global Model of Earth’s Crust. Geophys. Res. Abstr. 2013, 15, 2658. [Google Scholar]
- Hatzfeld, D.; Tatar, M.; Priestley, K.; Ghafory-Ashtiany, M. Seismological constraints on the crustal structure beneath the Zagros Mountain belt (Iran). Geophys. J. Int. 2003, 155, 403–410. [Google Scholar] [CrossRef]
- Stein, S.; Gordon, R.G. Statistical tests of additional plate boundaries from plate motion inversions. Earth Planet. Sci. Lett. 1984, 69, 401–412. [Google Scholar] [CrossRef]
- Hao, M.; Shen, Z.-K.; Wang, Q.; Cui, D. Postseismic deformation mechanisms of the 1990 Mw 6.4 Gonghe, China earthquake constrained using leveling measurements. Tectonophysics 2012, 532–535, 205–214. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Peltzer, G.; Bürgmann, R. Mobility of continental mantle: Evidence from postseismic geodetic observations following the 1992 Landers earthquake. J. Geophys. Res. Solid Earth 2000, 105, 8035–8054. [Google Scholar] [CrossRef]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geopyhs. Res. Lett. 2004, 31, L01607. [Google Scholar] [CrossRef] [Green Version]
- Marone, C.J.; Scholtz, C.H.; Bilham, R. On the mechanics of earthquake afterslip. J. Geophys. Res. Solid Earth 1991, 96, 8441–8452. [Google Scholar] [CrossRef]
- Mahsas, A.; Lammali, K.; Yelles, K.; Calais, E.; Freed, A.M.; Briole, P. Shallow afterslip following the 2003 May 21, Mw = 6.9 Boumerdes earthquake, Algeria. Geophys. J. Int. 2008, 172, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Cetin, E.; Meghraoui, M.; Cakir, Z.; Akoglu, A.M.; Mimouni, O.; Chebbah, M. Seven years of postseismic deformation following the 2003 Mw = 6.8 Zemmouri earthquake (Algeria) from InSAR time series. Geopyhs. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Jiang, G.; Wang, Y.; Wen, Y.; Liu, Y.; Xu, C.; Xu, C. Afterslip evolution on the crustal ramp of the Main Himalayan Thrust fault following the 2015 Mw 7.8 Gorkha (Nepal) earthquake. Tectonophysics 2019, 758, 29–43. [Google Scholar] [CrossRef]
- Ozawa, S.; Nishimura, T.; Suito, H.; Kobayashi, T.; Tobita, M.; Imakiire, T. Coseismic and postseismic slip of the 2011 magnitude-9 Tohoku-Oki earthquake. Nature 2011, 475, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, S.; Nishimura, T.; Munekane, H.; Suito, H.; Kobayashi, T.; Tobita, M.; Imakiire, T. Preceding, coseismic, and postseismic slips of the 2011 Tohoku earthquake, Japan. J. Geophys. Res.Solid Earth 2012, 117, 7404. [Google Scholar] [CrossRef]
- Noda, A.; Takahama, T.; Kawasato, T.; Matsu’ura, M. Interpretation of Offshore Crustal Movements Following the 2011 Tohoku-Oki Earthquake by the Combined Effect of Afterslip and Viscoelastic Stress Relaxation. Pure Appl. Geophys. 2018, 175, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Diao, F.; Wang, R.; Wang, Y.; Xiong, X.; Walter, T.R. Fault behavior and lower crustal rheology inferred from the first seven years of postseismic GPS data after the 2008 Wenchuan earthquake. Earth Planet. Sci. Lett. 2018, 495, 202–212. [Google Scholar] [CrossRef] [Green Version]
- Lienkaemper, J.J.; McFarland, F.S. Long-Term Afterslip of the 2004 M 6.0 Parkfield, California, Earthquake—Implications for Forecasting Amount and Duration of Afterslip on Other Major Creeping Faults. Bull. Seismol. Soc. Am. 2017, 107, 1082–1093. [Google Scholar] [CrossRef] [Green Version]
- Wright, T.J.; Elliott, J.R.; Wang, H.; Ryder, I. Earthquake cycle deformation and the Moho: Implications for the rheology of continental lithosphere. Tectonophysics 2013, 609, 504–523. [Google Scholar] [CrossRef]
- Afsari, N.; Sodoudi, F.; Taghizadeh Farahmand, F.; Ghassemi, M.R. Crustal structure of Northwest Zagros (Kermanshah) and Central Iran (Yazd and Isfahan) using teleseismic Ps converted phases. J. Seismol. 2011, 15, 341–353. [Google Scholar] [CrossRef] [Green Version]
- Pollitz, F.F.; Wicks, C.; Thatcher, W. Mantle Flow Beneath a Continental Strike-Slip Fault: Postseismic Deformation After the 1999 Hector Mine Earthquake. Science 2001, 293, 1814. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Bürgmann, R.; Thatcher, W. Illumination of rheological mantle heterogeneity by the M7.2 2010 El Mayor-Cucapah earthquake. Geochem. Geophys. Geosyst. 2012, 13, Q06002. [Google Scholar] [CrossRef]
- Jónsson, S. Importance of post-seismic viscous relaxation in southern Iceland. Nat. Geosci. 2008, 1, 136–139. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Bürgmann, R.; Segall, P. Joint estimation of afterslip rate and postseismic relaxation following the 1989 Loma Prieta earthquake. J. Geophys. Res. Solid Earth 1998, 103, 26975–26992. [Google Scholar] [CrossRef] [Green Version]
- Dalla Via, G.; Sabadini, R.; De Natale, G.; Pingue, F. Lithospheric rheology in southern Italy inferred from postseismic viscoelastic relaxation following the 1980 Irpinia earthquake. J. Geophys. Res. Solid Earth 2005, 110, B06311. [Google Scholar] [CrossRef]
- Wimpenny, S.; Copley, A.; Ingleby, T. Fault mechanics and post-seismic deformation at Bam, SE Iran. Geophys. J. Int. 2017, 209, 1018–1035. [Google Scholar] [CrossRef] [Green Version]
- Gourmelen, N.; Amelung, F. Postseismic Mantle Relaxation in the Central Nevada Seismic Belt. Science 2005, 310, 1473. [Google Scholar] [CrossRef] [Green Version]
- Nishimura, T.; Thatcher, W. Rheology of the lithosphere inferred from postseismic uplift following the 1959 Hebgen Lake earthquake. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Deng, J.; Hudnut, K.; Gurnis, M.; Hauksson, E. Stress loading from viscous flow in the lower crust and triggering of aftershocks following the 1994 Northridge, California, Earthquake. Geopyhs. Res. Lett. 1999, 26, 3209–3212. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, R.; Roth, F.; Enescu, B.; Hainzl, S.; Ergintav, S. Afterslip and viscoelastic relaxation following the 1999 M 7.4 İzmit earthquake from GPS measurements. Geophys. J. Int. 2009, 178, 1220–1237. [Google Scholar] [CrossRef] [Green Version]
- Sheu, S.; Shieh, C. Viscoelastic–afterslip concurrence: A possible mechanism in the early post-seismic deformation of the Mw 7.6, 1999 Chi-Chi (Taiwan) earthquake. Geophys. J. Int. 2004, 159, 1112–1124. [Google Scholar] [CrossRef] [Green Version]
- Ryder, I.; Parsons, B.; Wright, T.J.; Funning, G.J. Post-seismic motion following the 1997 Manyi (Tibet) earthquake: InSAR observations and modelling. Geophys. J. Int. 2007, 169, 1009–1027. [Google Scholar] [CrossRef] [Green Version]
- Vergnolle, M.; Pollitz, F.; Calais, E. Constraints on the viscosity of the continental crust and mantle from GPS measurements and postseismic deformation models in western Mongolia. J. Geophys. Res. Solid Earth 2003, 108, 2502. [Google Scholar] [CrossRef] [Green Version]
- Reddy, C.D.; Sunil, P.S.; Bürgmann, R.; Chandrasekhar, D.V.; Kato, T. Postseismic relaxation due to Bhuj earthquake on January 26, 2001: Possible mechanisms and processes. Nat. Hazards 2013, 65, 1119–1134. [Google Scholar] [CrossRef]
- Ryder, I.; Bürgmann, R.; Pollitz, F. Lower crustal relaxation beneath the Tibetan Plateau and Qaidam Basin following the 2001 Kokoxili earthquake. Geophys. J. Int. 2011, 187, 613–630. [Google Scholar] [CrossRef] [Green Version]
- Johnson, K.M.; Bürgmann, R.; Freymueller, J.T. Coupled afterslip and viscoelastic flow following the 2002 Denali Fault, Alaska earthquake. Geophys. J. Int. 2009, 176, 670–682. [Google Scholar] [CrossRef] [Green Version]
- Bruhat, L.; Barbot, S.; Avouac, J.-P. Evidence for postseismic deformation of the lower crust following the 2004 Mw6.0 Parkfield earthquake. J. Geophys. Res. Solid Earth 2011, 116, B08401. [Google Scholar] [CrossRef] [Green Version]
- Dixon, J.E.; Dixon, T.H.; Bell, D.R.; Malservisi, R. Lateral variation in upper mantle viscosity: Role of water. Earth Planet. Sci. Lett. 2004, 222, 451–467. [Google Scholar] [CrossRef]
- Hirth, G.; Kohlstedt, D. Rheology of the Upper Mantle and the Mantle Wedge: A View from the Experimentalists. In Inside the Subduction Factory; Geophysical Monograph Series; Eiler, J., Ed.; Blackwell Publishing Ltd.: Oxford, UK, 2004; pp. 83–105. [Google Scholar]
- Bürgmann, R.; Dresen, G. Rheology of the Lower Crust and Upper Mantle: Evidence from Rock Mechanics, Geodesy, and Field Observations. Annu. Rev. Earth Planet. Sci. 2008, 36, 531–567. [Google Scholar] [CrossRef] [Green Version]
- Batir, J.F.B.; David, D.; Richards, M.C. Updated Surface Heat Flow Map of Alaska. In Proceedings of the Geothermal Resources Council Transactions, 2013 Annual Meeting, Las Vegas, NV, USA, 30 September–3 October 2013. [Google Scholar]
- Hjartarson, Á. Heat Flow in Iceland. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Mahmoodabadi, M.; Yaminifard, F.; Tatar, M.; Kaviani, A.; Motaghi, K. Upper-mantle velocity structure beneath the Zagros collision zone, Central Iran and Alborz from nonlinear teleseismic tomography. Geophys. J. Int. 2019, 218, 414–428. [Google Scholar] [CrossRef]
- Chen, C.-H.; Wang, W.-H.; Teng, T.-L. 3D Velocity Structure around the Source Area of the 1999 Chi-Chi, Taiwan, Earthquake: Before and After the Mainshock. Bull. Seismol. Soc. Am. 2001, 91, 1013–1027. [Google Scholar] [CrossRef]
- Moreno, M.; Haberland, C.; Oncken, O.; Rietbrock, A.; Angiboust, S.; Heidbach, O. Locking of the Chile subduction zone controlled by fluid pressure before the 2010 earthquake. Nat. Geosci. 2014, 7, 292–296. [Google Scholar] [CrossRef]
- Freed, A.M.; Bürgmann, R. Evidence of power-law flow in the Mojave desert mantle. Nature 2004, 430, 548–551. [Google Scholar] [CrossRef] [PubMed]
| Time (UTC) | Magnitude (Mw) | Type | Depth (km) |
|---|---|---|---|
| Aftershock sequence on 11 January 2018 (aftershock sequence 1) | |||
| 06:59:30 | 5.5 | Thrust | 13.5 |
| 07:00:52 | 5.3 | No information | No information |
| 07:14:15 | 5.3 | Thrust | 13.5 |
| 07:55:00 | 5.1 | No information | No information |
| 08:00:39 | 5.3 | Thrust | 17.5 |
| Aftershock sequence on 25 November 2018 (aftershock sequence 2) | |||
| 16:37:32 | 6.3 | Strike-slip | 23.5 |
| 17:09:36 | 5.2 | Thrust | 17.5 |
| 23:00:46 | 5.0 | No information | No information |
| Length (km) | Width (km) | Depth (km) | Dip (°) | Strike (°) | Dip Slip b (m) | Strike Slip c (m) | Lat d,e | Lon d,e | Mw e | Rms (m) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Aftershocks 1 (Mw5.5) | |||||||||||
| Lower | 5 | 5 | 1 | −90 | 90 | 0 | −0.2 | — | — | — | |
| Upper | 50 | 35 | 30 | 90 | 360 | 6 | 0.2 | — | — | — | |
| Optimal | 12.9 | 5.4 | 13.0 | 51 | 344 | 0.39 | −0.08 | 33.71 | 45.68 | 5.94 | 0.002 |
| 2.5% a | 8.7 | 1.8 | 11. 9 | 42 | 335 | 0.21 | −0.25 | — | — | — | |
| 97.5% a | 15.3 | 10.1 | 15.3 | 58 | 352 | 0.59 | 0.05 | — | — | — | |
| Aftershocks 2 (Mw6.3) | |||||||||||
| Lower | 5 | 5 | 1 | 50 | 90 | −0.3 | −2 | — | — | — | |
| Upper | 30 | 30 | 40 | 90 | 360 | 0 | 2 | — | — | — | |
| Optimal | 12.7 | 8.8 | 22.0 | 90 | 302 | −0.29 | 1.80 | 34.36 | 45.70 | 6.52 | 0.008 |
| 2.5% | 6.2 | 2.9 | 13.2 | 87 | 292 | −0.41 | 0.91 | — | — | — | |
| 97.5% | 21.2 | 14.7 | 32.0 | 90 | 310 | −0.02 | 2.25 | — | — | — | |
| Afterslip | |||||||||||
| Lower | 5 | 1 | 5 | −20 | 330 | 0 | −3 | — | — | — | |
| Upper | 70 | 50 | 20 | 20 | 360 | 5 | 3 | — | — | — | |
| Optimal | 45.5 | 6.4 | 11.5 | −4 | 346 | 0.69 | −0.45 | 34.45 | 45.62 | 6.56 | 0.018 |
| 2.5% | 38.9 | 1.0 | 10.3 | −10 | 340 | 0.13 | −0.76 | — | — | — | |
| 97.5% | 54.6 | 11.5 | 13.6 | 5 | 350 | 1.56 | −0.24 | — | — | — | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, X.; Amelung, F.; Shao, Y.; Ye, S.; Liu, M.; Xie, C. Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake. Remote Sens. 2020, 12, 2032. https://doi.org/10.3390/rs12122032
Lv X, Amelung F, Shao Y, Ye S, Liu M, Xie C. Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake. Remote Sensing. 2020; 12(12):2032. https://doi.org/10.3390/rs12122032
Chicago/Turabian StyleLv, Xiaoran, Falk Amelung, Yun Shao, Shu Ye, Ming Liu, and Chou Xie. 2020. "Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake" Remote Sensing 12, no. 12: 2032. https://doi.org/10.3390/rs12122032
APA StyleLv, X., Amelung, F., Shao, Y., Ye, S., Liu, M., & Xie, C. (2020). Rheology of the Zagros Lithosphere from Post-Seismic Deformation of the 2017 Mw7.3 Kermanshah, Iraq, Earthquake. Remote Sensing, 12(12), 2032. https://doi.org/10.3390/rs12122032