Extracting Seasonal Signals in GNSS Coordinate Time Series via Weighted Nuclear Norm Minimization
Abstract
:1. Introduction
2. Model and Method
2.1. Model
2.2. Weighted Nuclear Norm Minimization
| Algorithm 1 WNNM for GNSS time series |
Input: Noisy time series y, the constant C, and . Output: Extracted time series
|
3. Results of Simulation
3.1. Case 1: Pure FN
3.2. Case 2: WN+FN
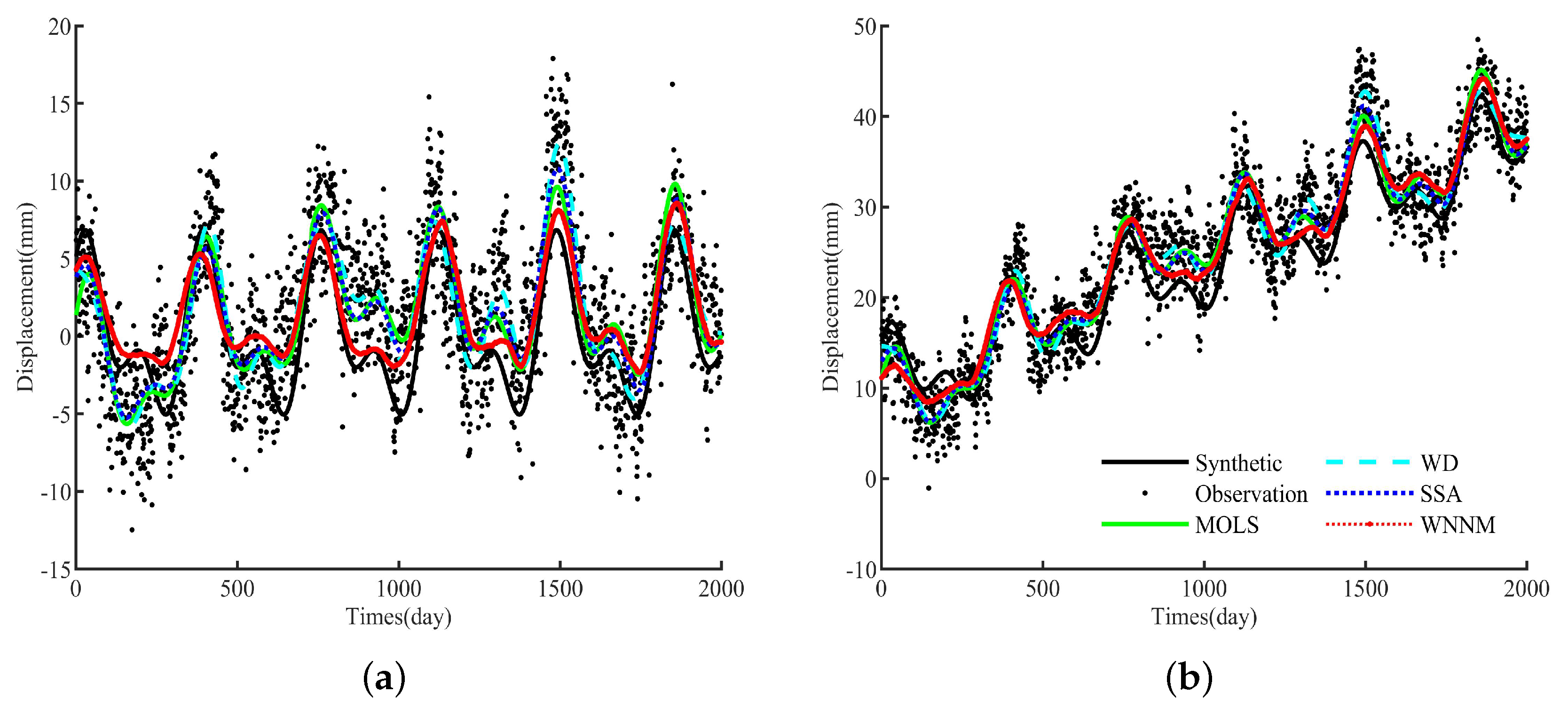
4. Application to Real Data
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
References
- Zhang, J.; Bock, Y.; Johnson, H.; Fang, P.; Williams, S.; Genrich, J.; Wdowinski, S.; Behr, J. Southern California Permanent GPS Geodetic Array: Error analysis of daily position estimates and site velocities. J. Geophys. Res. Earth 1997, 102, 18035–18055. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Earth 2002, 107, ETG-9. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.L.; Wernicke, B.P.; Tamisiea, M.E. On seasonal signals in geodetic time series. J. Geophys. Res. Earth 2012, 117, 1403. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Jiang, W.; Chen, H.; An, X.; Zhou, X.; Yuan, P.; Chen, Q. Analysis of seasonal signal in GPS short-baseline time series. Pure Appl. Geophys. 2018, 175, 3485–3509. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. Solid Earth 2002, 107, ETG9. [Google Scholar] [CrossRef] [Green Version]
- Zou, R.; Freymueller, J.T.; Ding, K.; Yang, S.; Wang, Q. Evaluating seasonal loading models and their impact on global and regional reference frame alignment. J. Geophys. Res. Solid Earth 2014, 119, 1337–1358. [Google Scholar] [CrossRef]
- Bogusz, J.; Klos, A. On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut. 2016, 20, 655–664. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Zhao, Q.; Zhang, B.; Wu, W. Characterizing the seasonal crustal motion in Tianshan area using GPS, GRACE and Surface loading models. Remote Sens. 2017, 9, 1303. [Google Scholar] [CrossRef] [Green Version]
- Klos, A.; Olivares, G.; Teferle, F.N.; Hunegnaw, A.; Bogusz, J. On the combined effect of periodic signals and colored noise on velocity uncertainties. GPS Solut. 2018, 22, 1. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Zhao, Q.; Wei, N.; Liu, J. Impacts on noise analysis of GNSS position time series caused by seasonal signal, weight matrix, offset, and Helmert transformation parameters. Remote Sens. 2018, 10, 1584. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Dam, T.V.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Pan, Y.; Shen, W.; Ding, H.; Hwang, C.; Li, J.; Zhang, T. The Quasi-Biennial vertical oscillations at Global GPS stations: Identification by ensemble empirical mode decomposition. Sensors 2015, 15, 26096–26114. [Google Scholar] [CrossRef] [PubMed]
- Bogusz, J. Geodetic aspects of GPS permanent station non-linearity studies. Acta Geodyn. Et Geomater. 2015, 12, 323–333. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Simkooei, A.R. Non-negative least-squares variance component estimation with application to GPS time series. J. Geod. 2016, 90, 451–466. [Google Scholar] [CrossRef]
- Ming, F.; Yang, Y.; Zeng, A.; Jing, Y. Analysis of seasonal signals and long-term trends in the height time series of IGS sites in China. Sci. China Earth Sci. 2016, 59, 1283–1291. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Y.; Wu, S.; Zhang, K. An enhanced singular spectrum analysis method for constructing nonsecular model of GPS site movement. J. Geophys. Res. Earth 2016, 121, 2193–2211. [Google Scholar] [CrossRef] [Green Version]
- Klos, A.; Bos, M.S.; Bogusz, J. Detecting time-varying seasonal signal in GPS position time series with different noise levels. GPS Solut. 2018, 22, 21. [Google Scholar] [CrossRef] [Green Version]
- Ji, K.; Shen, Y.; Wang, F. Signal extraction from GNSS position time series using weighted wavelet analysis. Remote Sens. 2020, 12, 992. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Montillet, J.P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]
- Elsner, J.B. Analysis of time series structure: SSA and related techniques. J. Am. Stat. Assoc. 2012, 97, 1207–1208. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 24–27 June 2014; pp. 2862–2869. [Google Scholar]
- Xu, J.; Zhang, L.; Zhang, D.; Feng, X. Multi-channel weighted nuclear norm minimization for real color image denoising. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Gu, S.; Xie, Q.; Meng, D.; Zuo, W.; Feng, X.; Zhang, L. Weighted nuclear norm minimization and its applications to low level vision. Int. J. Comput. Vis. 2017, 121, 183–208. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Ji, S.; Li, Y.; Qian, Z. Seismic noise suppression using weighted nuclear norm minimization method. J. Appl. Geophys. 2017, 146, 214–220. [Google Scholar] [CrossRef]
- VaniDevi, M. Weighted Nuclear Norm Minimization Method for Massive MIMO Low Rank Channel Estimation Problem. Ph.D. Thesis, Indian Institute of Space Science and Technology, Kerala, India, 2018. [Google Scholar]
- Zha, Z.; Yuan, X.; Li, B.; Zhang, X.; Liu, X.; Tang, L.; Liang, Y. Analyzing the weighted nuclear norm minimization and nuclear norm minimization based on group sparse representation. arXiv 2017, arXiv:1702.04463. [Google Scholar]
- Cai, J.F.; Wang, T.; Wei, K. Fast and provable algorithms for spectrally sparse signal reconstruction via low-rank Hankel matrix completion. Appl. Comput. Harmon. Anal. 2019, 46, 94–121. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.D.P.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time series. J. Geophys. Res. 2004, 109, B03412. [Google Scholar] [CrossRef] [Green Version]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef] [Green Version]
- Klos, A.; Bogusz, J.; Figurski, M.; Gruszczynski, M. Error analysis for European IGS stations. Stud. Geophys. Et Geod. 2016, 60, 17–34. [Google Scholar] [CrossRef]
- Mao, A.; Harrison, C.G.A. Noise in GPS coordinate time series. J. Geophys. Res. 1999, 104, 2797–2816. [Google Scholar] [CrossRef] [Green Version]
- Santamaría-Gómez, A.; Bouin, M.N.; Collilieux, X.; Wöppelmann, G. Correlated errors in GPS position time series: Implications for velocity estimates. J. Geophys. Res. 2011, 116, B01405. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GPS observations. J. Geod. 2008, 82, 157–166. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.D.P. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- He, Y.; Zhang, S.; Wang, Q.; Liu, Q.; Qu, W.; Hou, X. HECTOR for analysis of GPS time series. In China Satellite Navigation Conference (CSNC) 2018 Proceedings; Sun, J., Yang, C., Guo, S., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2018; Volume 497. [Google Scholar]
- Li, Z.; Jiang, W.; Liu, H.; Qu, X. Noise model establishment and analysis of IGS reference station coordinate time series inside China. Acta Geod. Et Cartogr. Sin. Chin. 2012, 41, 496–503. [Google Scholar]
- Liu, N.; Dai, W.; Santerre, R.; Kuang, C. A MATLAB-based Kriged Kalman Filter software for interpolating missing data in GNSS coordinate time series. GPS Solut. 2018, 22, 25. [Google Scholar] [CrossRef]
- Gazeaux, J.; Williams, S.; King, M.; Bos, M.; Dach, R.; Deo, M.; Moore, A.W.; Ostini, L.; Petrie, E.; Roggero, M. Detecting offsets in GPS time series: First results from the detection of offsets in GPS experiment. J. Geophys. Res. Earth 2013, 118, 2397–2407. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Lu, N.; Zou, J.; Guo, S. An improved 3σ gross error detection method for GNSS deformation monitoring time series. Geomater. Inf. Sci. Wuhan Univ. 2019, 44, 1282–1288. [Google Scholar]








| Method | Without Trend | With Trend | ||||||
|---|---|---|---|---|---|---|---|---|
| Trend Uncertainty () | k | () | Misfit () | Trend Uncertainty () | k | () | Misfit () | |
| MOLS | 0.017 | −0.04 | 1.10 | 0.21 | 0.019 | −0.06 | 1.25 | 0.21 |
| WD | 0.017 | −0.03 | 1.18 | 0.29 | 0.017 | −0.01 | 1.15 | 0.30 |
| SSA | 0.032 | −0.62 | 0.90 | 0.13 | 0.018 | −0.05 | 1.21 | 0.22 |
| WNNM | 0.041 | −0.67 | 1.05 | 0.13 | 0.021 | −0.31 | 0.94 | 0.20 |
| Actual | 0.067 | −1 | 1.00 | ∖ | 0.067 | −1 | 1.00 | ∖ |
| Method | Without Trend | With Trend | ||||||
|---|---|---|---|---|---|---|---|---|
| Trend Uncertainty () | k | () | Misfit () | Trend Uncertainty () | k | () | Misfit () | |
| MOLS | 0.378 | −0.78 | 8.14 | 1.71 | 0.360 | −0.76 | 7.99 | 1.92 |
| WD | 0.287 | −0.69 | 7.13 | 2.32 | 0.288 | −0.69 | 7.15 | 2.33 |
| SSA | 0.392 | −0.79 | 8.29 | 1.80 | 0.329 | −0.73 | 7.67 | 2.05 |
| WNNM | 0.495 | −0.89 | 8.90 | 1.39 | 0.452 | −0.85 | 8.68 | 1.85 |
| Actual | 0.667 | −1 | 10.00 | ∖ | 0.667 | −1 | 10.00 | ∖ |
| Method | Without Trend | With Trend | ||||||
|---|---|---|---|---|---|---|---|---|
| Trend Uncertainty () | k | () | Misfit () | Trend Uncertainty () | k | () | Misfit () | |
| MOLS | 0.024 | −0.13 | 1.41 | 0.24 | 0.017 | −0.02 | 1.16 | 0.24 |
| WD | 0.021 | −0.08 | 1.32 | 0.32 | 0.015 | −0.04 | 1.06 | 0.34 |
| SSA | 0.022 | −0.10 | 1.36 | 0.24 | 0.016 | −0.01 | 1.13 | 0.24 |
| WNNM | 0.050 | −0.78 | 1.07 | 0.16 | 0.046 | −0.76 | 1.03 | 0.24 |
| Actual | 0.050 | –0.83 | 1.00 | ∖ | 0.050 | –0.83 | 1.00 | ∖ |
| Method | Without Trend | With Trend | ||||||
|---|---|---|---|---|---|---|---|---|
| Trend Uncertainty () | k | () | Misfit () | Trend Uncertainty () | k | () | Misfit () | |
| MOLS | 0.351 | −0.76 | 7.81 | 1.96 | 0.357 | −0.76 | 7.94 | 1.96 |
| WD | 0.263 | −0.66 | 6.85 | 2.38 | 0.281 | −0.68 | 7.09 | 2.38 |
| SSA | 0.307 | −0.71 | 7.39 | 2.01 | 0.326 | −0.73 | 7.59 | 2.01 |
| WNNM | 0.514 | −0.92 | 8.80 | 1.67 | 0.448 | −0.85 | 8.60 | 1.95 |
| Actual | 0.583 | −0.92 | 10 | ∖ | 0.583 | −0.92 | 10 | ∖ |
| Site | Longitude | Latitude | Span | Numbers | Epochs of Offset | Miss Rate | ONM (U) |
|---|---|---|---|---|---|---|---|
| BJFS | 115.8924 | 39.6086 | 1999.8041–2019.7795 | 5500 | 2010.3877, 2011.1904 2015.9027, 2016.2309 | 24.63% | WN+FN |
| KUNM | 102.7971 | 25.0295 | 1998.7685–2013.0836 | 3892 | 2004.9850 | 25.58% | WN+FN |
| LHAS | 91.1039 | 29.6573 | 1995.3740–2007.0699 | 2790 | \ | 34.69% | WN+FN |
| SHAO | 121.2004 | 31.0996 | 1995.0233–2019.2133 | 6049 | 2011.1904 | 31.54% | WN+FN |
| TCMS | 120.9873 | 24.7979 | 2002.7481–2019.5356 | 4270 | \ | 31.46% | WN+FN |
| TNML | 120.9873 | 24.7979 | 2002.7481–2019.2370 | 3949 | \ | 35.48% | WN+FN |
| URUM | 87.6000 | 43.8079 | 1998.8342–2018.9575 | 5044 | 2008.7172 | 25.13% | WN+PL |
| WUHN | 114.3572 | 30.5316 | 1993.3630–2016.7363 | 5464 | 2002.0699, 2002.8315 2011.2233, 2013.8808 | 26.54% | WN+BPPL |
| GUAO | 87.1773 | 43.4711 | 2002.4534–2016.2008 | 3134 | \ | 34.04% | WN+BPPL |
| Method | North | East | Up | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Trend Uncertainty () | k | () | Trend Uncertainty () | k | () | Trend Uncertainty () | k | () | |
| MOLS | 0.4436 | −1.3172 | 3.8570 | 0.6391 | −1.3815 | 4.9550 | 1.6703 | −1.3381 | 13.9940 |
| WD | 0.3567 | −1.2500 | 3.4910 | 0.5611 | −1.3422 | 4.6670 | 1.6771 | −1.3393 | 14.0210 |
| SSA | 0.3890 | −1.2776 | 3.6270 | 0.4166 | −1.2500 | 4.0770 | 1.6238 | −1.3296 | 13.8120 |
| WNNM | 0.4650 | −1.3320 | 3.9380 | 0.6720 | −1.3970 | 5.0670 | 1.7151 | −1.3466 | 14.1540 |
| North | MOLS | WD | SSA | WNNM | |
| MOLS | 1 | ||||
| WD | 0.9621 | 1 | |||
| SSA | 0.9666 | 0.9896 | 1 | ||
| WNNM | 0.9868 | 0.9624 | 0.9741 | 1 | |
| East | MOLS | WD | SSA | WNNM | |
| MOLS | 1 | ||||
| WD | 0.9095 | 1 | |||
| SSA | 0.9298 | 0.9051 | 1 | ||
| WNNM | 0.9574 | 0.8537 | 0.9279 | 1 | |
| Up | MOLS | WD | SSA | WNNM | |
| MOLS | 1 | ||||
| WD | 0.9860 | 1 | |||
| SSA | 0.9920 | 0.9962 | 1 | ||
| WNNM | 0.9935 | 0.9861 | 0.9917 | 1 |
| Site | Method | North | East | Up | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Trend Uncertainty () | k | () | Trend Uncertainty () | k | () | Trend Uncertainty () | k | () | ||
| KUNM | MOLS | 0.5403 | −1.2692 | 5.1130 | 0.6734 | −1.3104 | 5.9260 | 1.4175 | −1.1684 | 15.9820 |
| WD | 0.3862 | −1.1670 | 4.3650 | 0.5635 | −1.2564 | 5.4530 | 1.2566 | −1.1314 | 15.0970 | |
| SSA | 0.4086 | −1.1844 | 4.4820 | 0.5505 | −1.2495 | 5.3920 | 1.2674 | −1.1341 | 15.1560 | |
| WNNM | 0.5519 | −1.2766 | 5.1550 | 0.6605 | −1.3055 | 5.8630 | 1.3195 | −1.1478 | 15.4130 | |
| LHAS | MOLS | 0.1635 | −1.1480 | 1.9090 | 0.2534 | −1.1514 | 2.9420 | 0.1502 | −0.8226 | 3.0180 |
| WD | 0.1243 | −1.0636 | 1.6760 | 0.2048 | −1.0859 | 2.6580 | 0.1159 | −0.7407 | 2.6580 | |
| SSA | 0.1308 | −1.0793 | 1.7170 | 0.2047 | −1.0861 | 2.6570 | 0.1206 | −0.7534 | 2.7100 | |
| WNNM | 0.1665 | −1.1535 | 1.9260 | 0.2661 | −1.1675 | 3.0050 | 0.1376 | −0.7958 | 2.8860 | |
| SHAO | MOLS | 0.9741 | −1.4123 | 7.1450 | 0.7676 | −1.3828 | 5.9370 | 0.9421 | −1.2500 | 9.2200 |
| WD | 0.8581 | −1.3743 | 6.7390 | 0.7161 | −1.3619 | 5.7500 | 0.9414 | −1.2500 | 9.2130 | |
| SSA | 0.8663 | −1.3771 | 6.7700 | 0.7124 | −1.3604 | 5.7360 | 1.0464 | −1.2833 | 9.6600 | |
| WNNM | 1.0508 | −1.4355 | 7.3900 | 0.8549 | −1.4157 | 6.2320 | 0.9408 | −1.2500 | 9.2070 | |
| TCMS | MOLS | 0.5611 | −1.3687 | 4.4510 | 0.4083 | −1.3541 | 3.3250 | 0.6230 | −1.1870 | 6.8030 |
| WD | 0.4971 | −1.3323 | 4.2080 | 0.2916 | −1.2500 | 2.8540 | 0.4834 | −1.1087 | 6.0370 | |
| SSA | 0.5185 | −1.3450 | 4.2910 | 0.2910 | −1.2500 | 2.8480 | 0.4949 | −1.1164 | 6.1000 | |
| WNNM | 0.6298 | −1.4038 | 4.6910 | 0.4110 | −1.3567 | 3.3310 | 0.6355 | −1.1934 | 6.8630 | |
| TNML | MOLS | 0.3574 | −1.2884 | 3.2700 | 0.2995 | −1.2626 | 2.8670 | 0.2857 | −0.9614 | 4.5710 |
| WD | 0.2943 | −1.2291 | 2.9870 | 0.2631 | −1.2225 | 2.7010 | 0.2663 | −0.9393 | 4.4190 | |
| SSA | 0.3048 | −1.2398 | 3.0370 | 0.2627 | −1.2222 | 2.6990 | 0.2410 | −0.9088 | 4.2050 | |
| WNNM | 0.3496 | −1.2820 | 3.2350 | 0.3443 | −1.3050 | 3.0590 | 0.2799 | −0.9556 | 4.5210 | |
| URUM | MOLS | 1.9938 | −1.6179 | 10.0000 | 1.0745 | −1.5159 | 6.5220 | 5.6630 | −1.6241 | 28.0710 |
| WD | 1.8614 | −1.5973 | 9.7060 | 0.9353 | −1.4741 | 6.1310 | 6.0291 | −1.6447 | 28.7380 | |
| SSA | 1.8756 | −1.5998 | 9.7340 | 0.8497 | −1.4456 | 5.8670 | 4.3477 | −1.5439 | 25.0540 | |
| WNNM | 2.0304 | −1.6248 | 10.0510 | 0.9936 | −1.4936 | 6.2840 | 4.5277 | −1.5565 | 25.4860 | |
| WUHN | MOLS | 0.3617 | −1.2291 | 3.6710 | 0.4067 | −1.2921 | 3.6970 | 2.1608 | −1.3929 | 16.4130 |
| WD | 0.2908 | −1.1622 | 3.3140 | 0.3580 | −1.2533 | 3.4830 | 2.2150 | −1.4000 | 16.6110 | |
| SSA | 0.2905 | −1.1622 | 3.3110 | 0.3597 | −1.2549 | 3.4900 | 1.8447 | −1.3459 | 15.2420 | |
| WNNM | 0.3332 | −1.2052 | 3.5250 | 0.4157 | −1.2992 | 3.7310 | 1.9788 | −1.3676 | 15.7290 | |
| GUAO | MOLS | 0.1713 | −1.2190 | 1.7700 | 0.5416 | −1.4204 | 3.9150 | 2.6531 | −1.4944 | 16.7550 |
| WD | 0.2454 | −1.4750 | 1.6060 | 0.4770 | −1.3820 | 3.6950 | 2.5835 | −1.4867 | 16.5480 | |
| SSA | 0.1480 | −1.1702 | 1.6630 | 0.4670 | −1.3758 | 3.6580 | 2.6268 | −1.4918 | 16.6680 | |
| WNNM | 0.1612 | −1.1970 | 1.7300 | 0.5469 | −1.4239 | 3.9280 | 2.6674 | −1.4977 | 16.7430 | |
| Component | Method | Trend Uncertainty () | k | |
|---|---|---|---|---|
| North | MOLS | 0.6185 | −1.3189 | 4.5762 |
| WD | 0.5460 | −1.2945 | 4.2324 | |
| SSA | 0.5480 | −1.2706 | 4.2924 | |
| WNNM | 0.6376 | −1.3234 | 4.6268 | |
| East | MOLS | 0.5627 | −1.3412 | 4.4540 |
| WD | 0.4856 | −1.2920 | 4.1547 | |
| SSA | 0.4572 | −1.2772 | 4.0471 | |
| WNNM | 0.5739 | −1.3516 | 4.5000 | |
| Up | MOLS | 1.7295 | −1.2488 | 12.7586 |
| WD | 1.7298 | −1.2268 | 12.5936 | |
| SSA | 1.5126 | −1.2119 | 12.0674 | |
| WNNM | 1.5780 | −1.2346 | 12.3336 |
| Site | Correlation Coefficients | Site | Correlation Coefficients | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| KUNM | Method | MOLS | WD | SSA | WNNM | MOLS | WD | SSA | WNNM | |
| MOLS | 1 | TNML | 1 | |||||||
| WD | 0.9586 | 1 | 0.9823 | 1 | ||||||
| SSA | 0.9625 | 0.9945 | 1 | 0.9844 | 0.9927 | 1 | ||||
| WNNM | 0.9693 | 0.9879 | 0.9917 | 1 | 0.9895 | 0.9908 | 0.9942 | 1 | ||
| LHAS | MOLS | 1 | URUM | 1 | ||||||
| WD | 0.9468 | 1 | 0.5664 | 1 | ||||||
| SSA | 0.9593 | 0.9945 | 1 | 0.5581 | 0.9826 | 1 | ||||
| WNNM | 0.9738 | 0.9741 | 0.9846 | 1 | 0.5969 | 0.9552 | 0.9557 | 1 | ||
| SHAO | MOLS | 1 | WUHN | 1 | ||||||
| WD | 0.9821 | 1 | 0.9346 | 1 | ||||||
| SSA | 0.9889 | 0.9965 | 1 | 0.9368 | 0.9897 | 1 | ||||
| WNNM | 0.9871 | 0.9852 | 0.9913 | 1 | 0.9450 | 0.9885 | 0.9890 | 1 | ||
| TCMS | MOLS | 1 | GUAO | 1 | ||||||
| WD | 0.8186 | 1 | 0.9553 | 1 | ||||||
| SSA | 0.8286 | 0.9925 | 1 | 0.9723 | 0.9912 | 1 | ||||
| WNNM | 0.9446 | 0.8540 | 0.8751 | 1 | 0.9723 | 0.9774 | 0.9875 | 1 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Bian, J.; Ding, K.; Wu, H.; Li, H. Extracting Seasonal Signals in GNSS Coordinate Time Series via Weighted Nuclear Norm Minimization. Remote Sens. 2020, 12, 2027. https://doi.org/10.3390/rs12122027
Chen B, Bian J, Ding K, Wu H, Li H. Extracting Seasonal Signals in GNSS Coordinate Time Series via Weighted Nuclear Norm Minimization. Remote Sensing. 2020; 12(12):2027. https://doi.org/10.3390/rs12122027
Chicago/Turabian StyleChen, Baozhou, Jiawen Bian, Kaihua Ding, Haochen Wu, and Hongwei Li. 2020. "Extracting Seasonal Signals in GNSS Coordinate Time Series via Weighted Nuclear Norm Minimization" Remote Sensing 12, no. 12: 2027. https://doi.org/10.3390/rs12122027
APA StyleChen, B., Bian, J., Ding, K., Wu, H., & Li, H. (2020). Extracting Seasonal Signals in GNSS Coordinate Time Series via Weighted Nuclear Norm Minimization. Remote Sensing, 12(12), 2027. https://doi.org/10.3390/rs12122027






