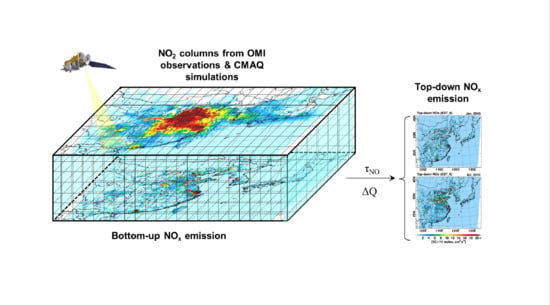
An Estimation of Top-Down NOx Emissions from OMI Sensor Over East Asia
Abstract
:1. Introduction
2. Experimental Methods
2.1. Description of WRF-CMAQ Model Simulations
2.2. Description of OMI NO2 Columns
3. Algorithm for Top-Down Estimation of NOx Emissions
3.1. General Concept
3.2. NOx Transported from Adjacent Cells (Qin)
3.3. NOx Transported to Adjacent Cells (Qout)
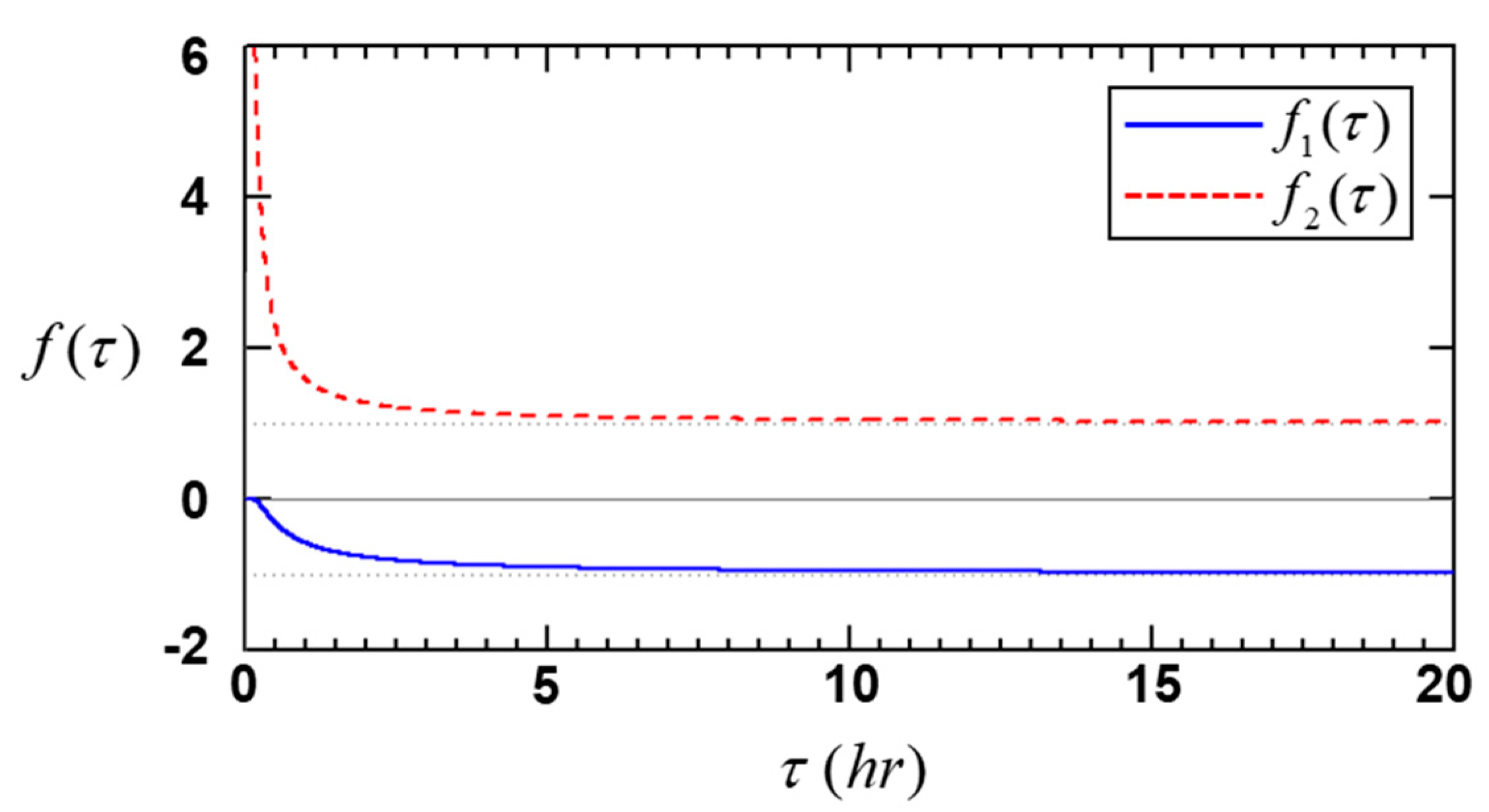
3.4. Column NOx Lifetimes and Sensitivity Analysis
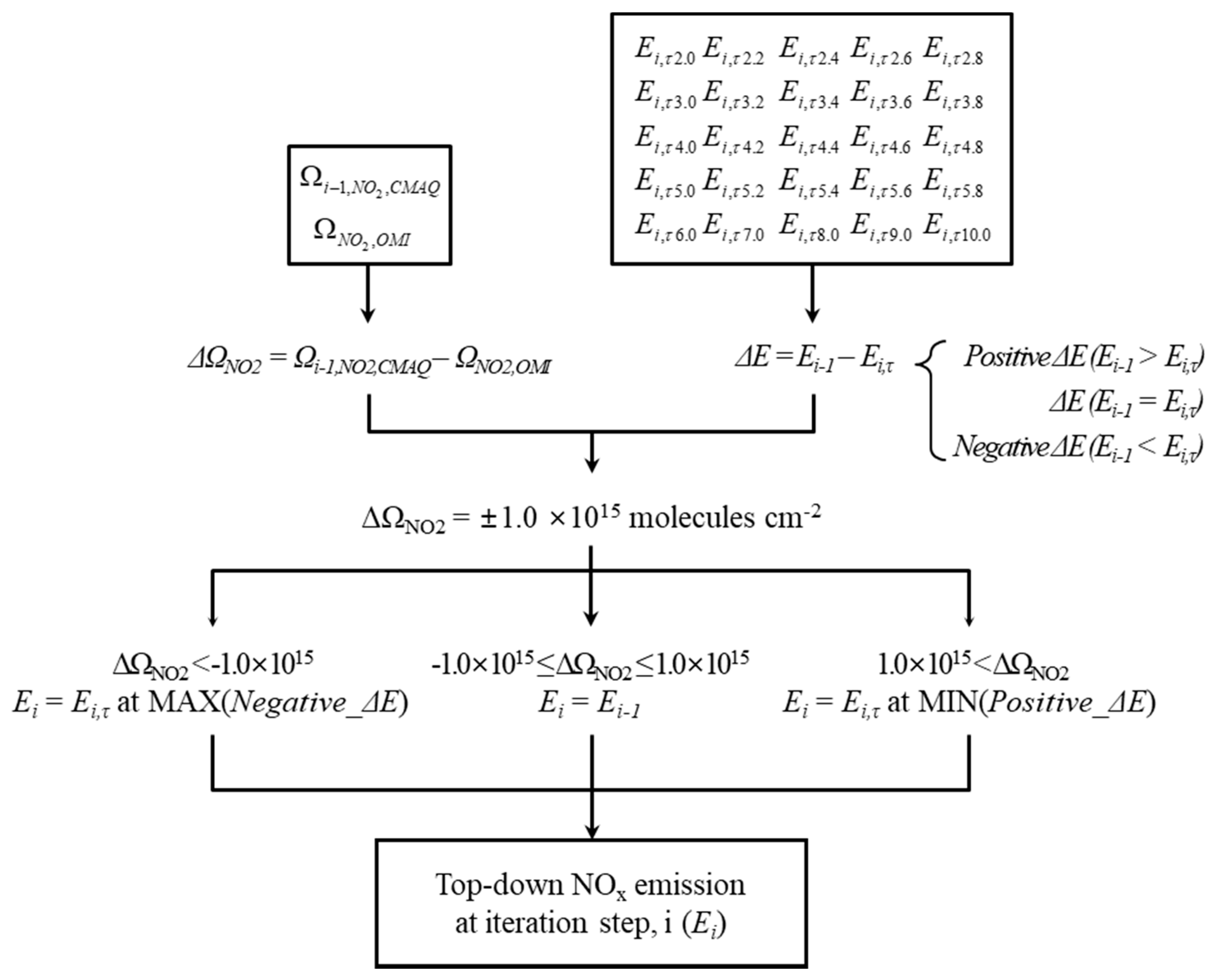
3.4.1. Determination of Lifetimes of Column NOx (τ)
3.4.2. Sensitivity Analysis of τ
3.5. Satellite-Derived NOx Columns
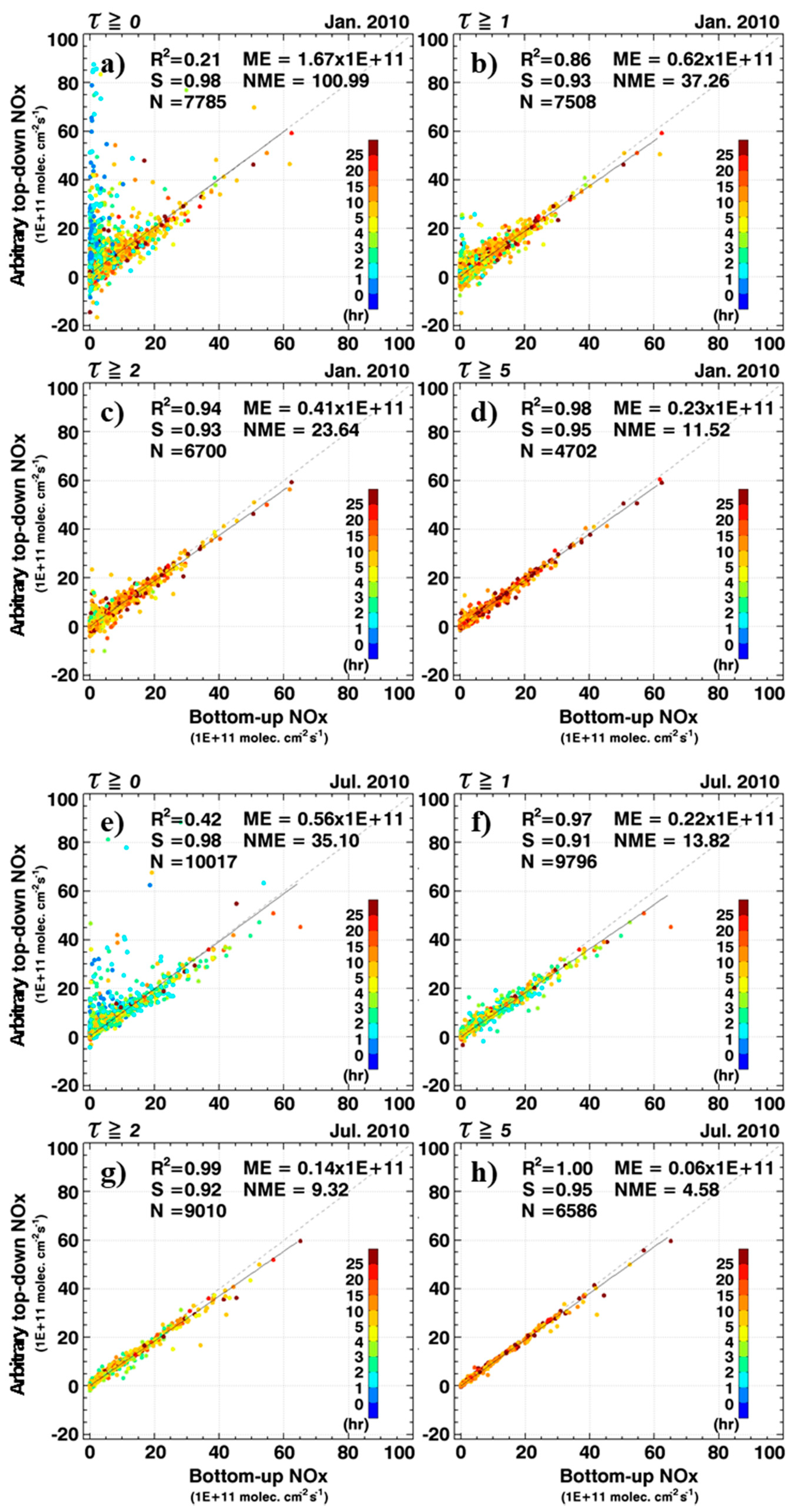
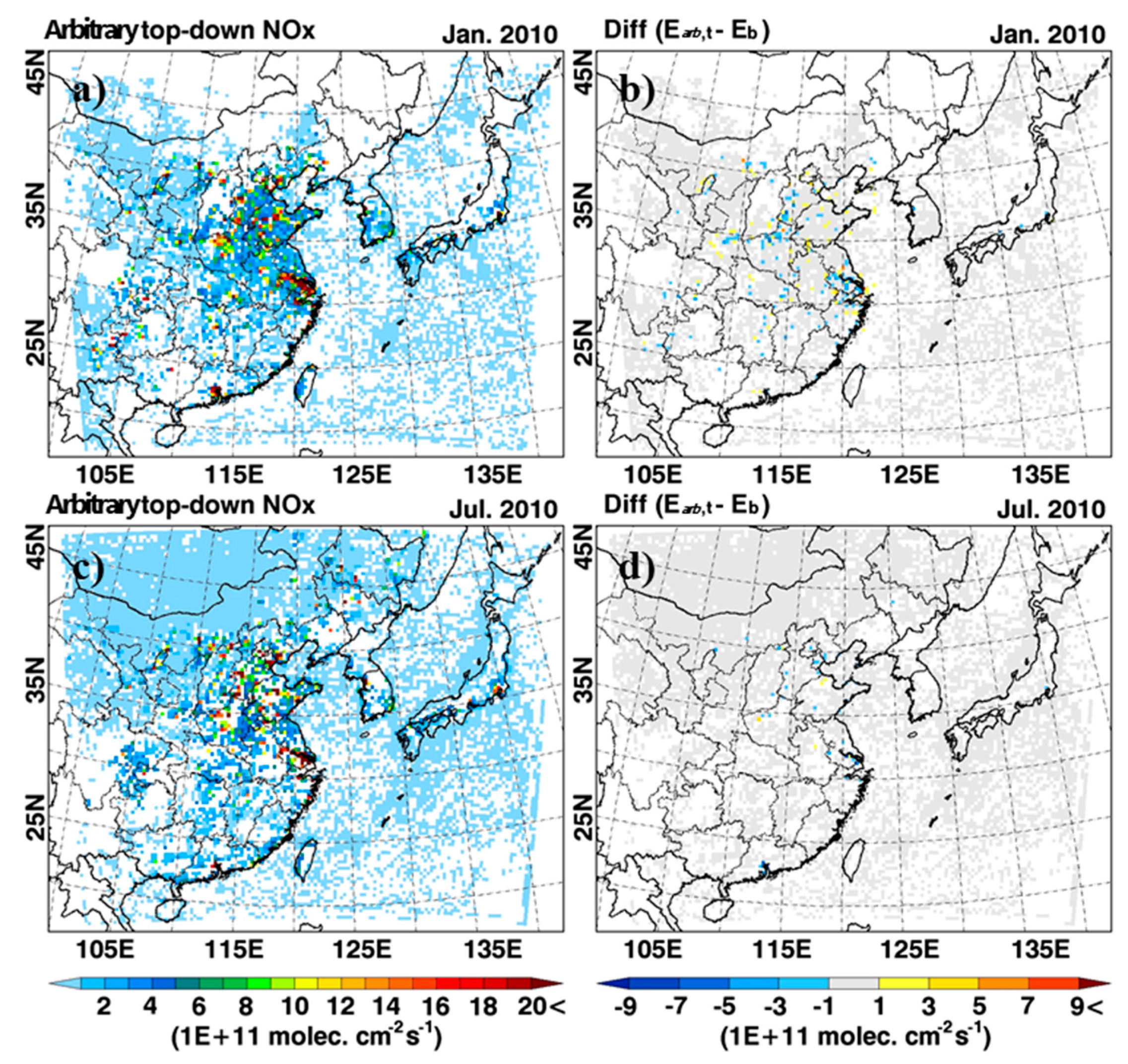
3.6. Optimal Conditions for the Top-Down NOx Estimation
4. Results and Discussions
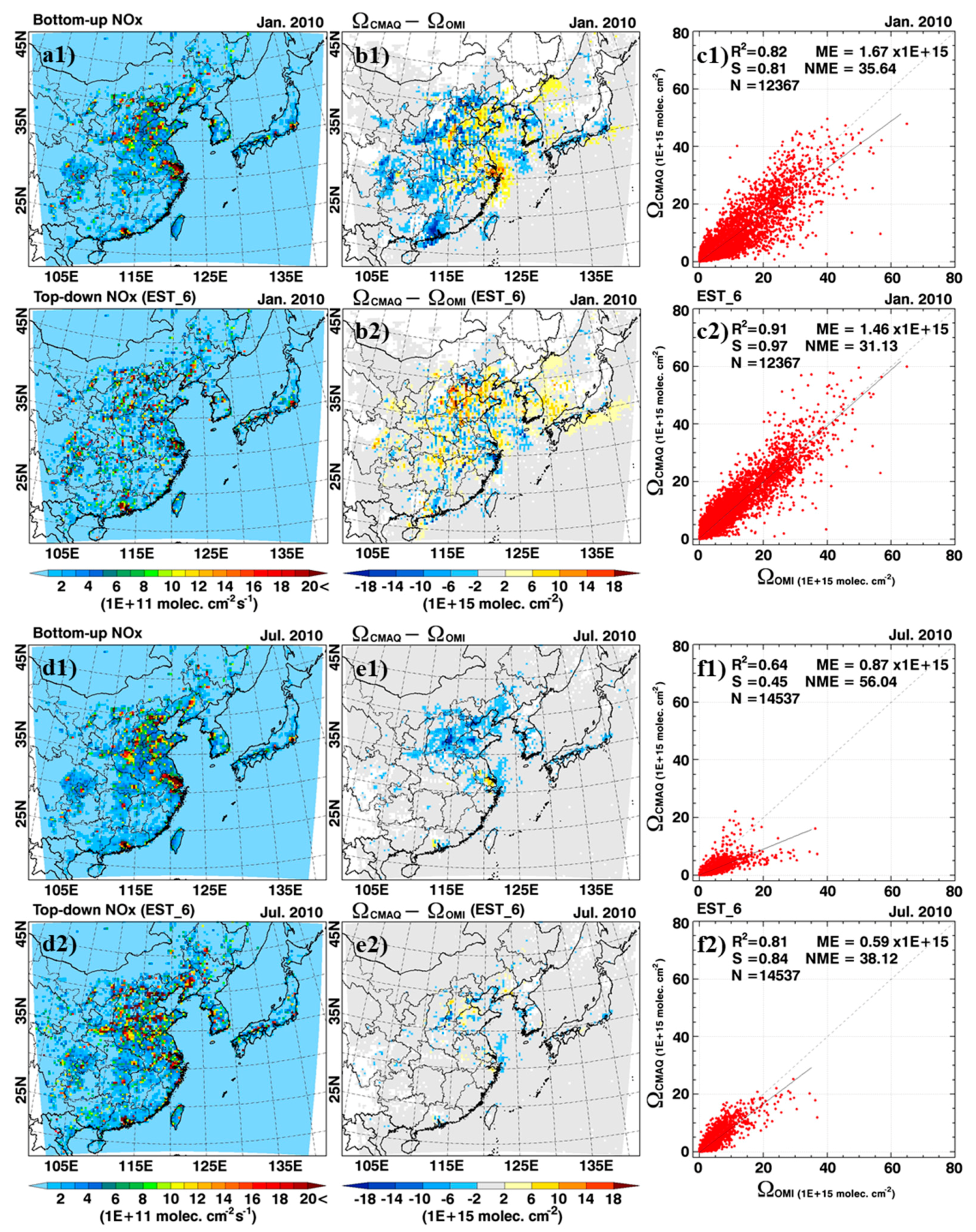
4.1. Comparison between ΩNO2,CMAQ and ΩNO2,OMI from Initial CMAQ Simulation
4.2. Top-Down NOx Estimation and Comparisons between ΩNO2,CMAQ and ΩNO2,OMI
4.2.1. East Asia
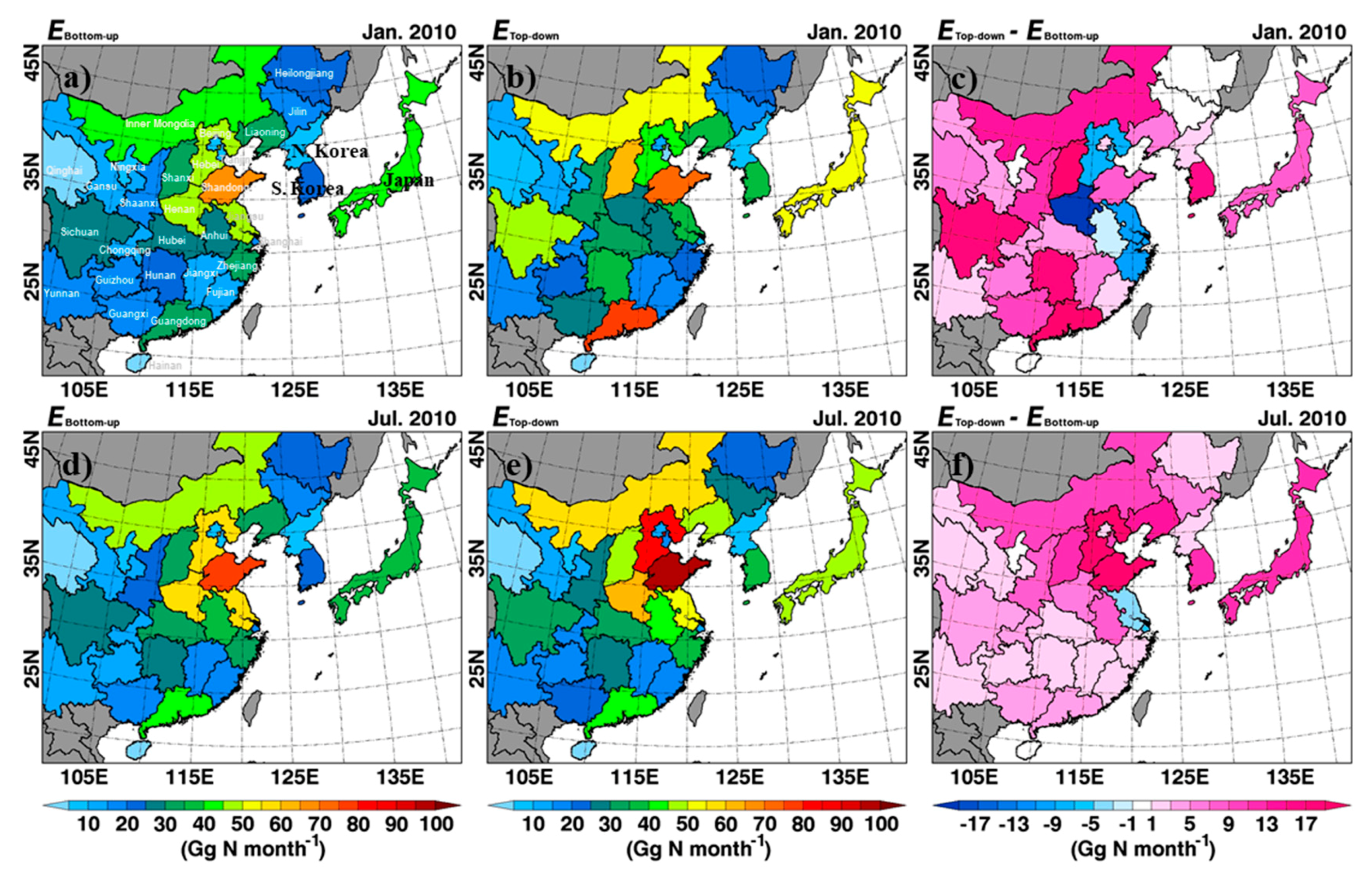
4.2.2. China, North Korea, South Korea, and Japan
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Zhao, C.S.; Ma, N.; Liu, P.F.; Göbel, T.; Hallbauer, E.; Deng, Z.Z.; Ran, L.; Xu, W.Y.; Liang, Z.; et al. A parameterization of low visibilities for hazy days in the North China Plain. Atmos. Chem. Phys. 2012, 12, 4935–4950. [Google Scholar] [CrossRef] [Green Version]
- Fu, G.Q.; Xu, W.Y.; Yang, R.F.; Li, J.B.; Zhao, C.S. The distribution and trends of fog and haze in the North China Plain over the past 30 years. Atmos. Chem. Phys. 2014, 14, 11949–11958. [Google Scholar] [CrossRef] [Green Version]
- Zheng, G.J.; Duan, F.K.; Su, H.; Ma, Y.L.; Cheng, Y.; Zheng, B.; Zhang, Q.; Huang, T.; Kimoto, T.; Chang, D.; et al. Exploring the severe winter haze in Beijing: The impact of synoptic weather, regional transport and heterogeneous reactions. Atmos. Chem. Phys. 2015, 15, 2969–2983. [Google Scholar] [CrossRef] [Green Version]
- Bytnerowicz, A.; Omasa, K.; Paoletti, E. Integrated effects of air pollution and climate change on forests: A northern hemisphere perspective. Environ. Pollut. 2007, 147, 438–445. [Google Scholar] [CrossRef]
- United Nation Environment Program (UNEP). Forests suffer from air pollution. In Vital Forest Graphics; UNEP/GRID: Arendal, Norway, 2009; pp. 50–51. [Google Scholar]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef]
- Hanna, S.R.; Chang, J.C.; Fernau, M.E. Monte Carlo estimates of uncertainties in predictions by a photochemical grid model (UAM-IV) due to uncertainties in input variables. Atmos. Environ. 1998, 32, 3619–3628. [Google Scholar] [CrossRef]
- Zhang, Y.; Bocquet, M.; Mallet, V.; Seigneur, C.; Baklanov, A. Real-time air quality forecasting, part I: History, techniques, and current status. Atmos. Environ. 2012, 60, 632–655. [Google Scholar] [CrossRef]
- Zhang, Y.; Bocquet, M.; Mallet, V.; Seigneur, C.; Baklanov, A. Real-time air quality forecasting, part II: State of the science, current research needs, and future prospects. Atmos. Environ. 2012, 60, 656–676. [Google Scholar] [CrossRef]
- Streets, D.G.; Bond, T.C.; Carmichael, G.R.; Fernandes, S.D.; Fu, Q.; He, D.; Klimont, Z.; Nelson, S.M.; Tsai, N.Y.; Wang, M.Q.; et al. An inventory of gaseous and primary aerosol emissions in Asia in the year 2000. J. Geophys. Res. 2003, 108, 8809. [Google Scholar] [CrossRef]
- Zhang, Q.; Streets, D.G.; He, K.; Wang, Y.; Richter, A.; Burrows, J.P.; Uno, I.; Jang, C.J.; Chen, D.; Yao, Z.; et al. NOx emission trends for China, 1995–2004: The view from the ground and the view from space. J. Geophys. Res. 2007, 112, D22306. [Google Scholar] [CrossRef] [Green Version]
- Xing, J.; Wang, S.X.; Chatani, S.; Zhang, C.Y.; Wei, W.; Hao, J.M.; Klimont, Z.; Cofala, J.; Amann, M. Projections of air pollutant emissions and its impacts on regional air quality in China in 2020. Atmos. Chem. Phys. 2011, 11, 3119–3136. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Nielsen, C.P.; Lei, Y.; McElroy, M.B.; Hao, J. Quantifying the uncertainties of a bottom-up emission inventory of anthropogenic atmospheric pollutants in China. Atmos. Chem. Phys. 2011, 11, 2295–2308. [Google Scholar] [CrossRef] [Green Version]
- Han, K.M.; Lee, S.; Chang, L.S.; Song, C.H. A comparison study between CMAQ-simulated and OMI-retrieved NO2 columns over East Asia for evaluation of NOx emission fluxes of INTEX-B, CAPSS, and REAS inventories. Atmos. Chem. Phys. 2015, 15, 1913–1938. [Google Scholar] [CrossRef] [Green Version]
- Beirle, S.; Boersma, K.F.; Platt, U.; Lawrence, M.G.; Wagner, T. Megacity emissions and lifetimes of nitrogen oxides probed from space. Science 2011, 333, 1737–1739. [Google Scholar] [CrossRef] [PubMed]
- de Foy, B.; Lu, Z.; Streets, D.G.; Lamsal, L.N.; Duncan, B.N. Estimates of power plant NOx emissions and lifetimes from OMI NO2 satellite retrievals. Atmos. Environ. 2015, 116, 1–11. [Google Scholar] [CrossRef]
- Souri, A.H.; Choi, Y.; Pan, S.; Curci, G.; Nowlan, C.R.; Janz, S.J.; Kowalewski, M.G.; Liu, J.; Herman, J.G.; Weinheimer, A.J. First top-down estimates of anthropogenic NOx emissions using high-resolution airborne remote sensing observations. J. Geophys. Res. Atmos. 2018, 123, 3269–3284. [Google Scholar] [CrossRef]
- Goldberg, D.; Lu, Z.; Oda, T.; Lamsal, L.; Liu, F.; Griffin, D.; McLinden, C.; Krotkov, N.A.; Duncan, B.; Streets, D. Exploiting OMI NO2 satellite observations to infer fossil-fuel CO2 emissions from U.S. megacities. Sci. Total Environ. 2019, 695, 133805. [Google Scholar] [CrossRef]
- Beirle, S.; Borger, C.; Dörner, S.; Li, A.; Hu, Z.; Liu, F.; Wang, Y.; Wagner, T. Pinpointing nitrogen oxide emissions from space. Sci. Adv. 2019, 5, eaax9800. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Wang, Y. Assimilated inversion of NOx emissions over East Asia using OMI NO2 column measurements. Geophys. Res. Lett. 2009, 36, L06805. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.-T.; McElroy, M.B.; Boersma, K.F. Constraint of anthropogenic NOx emissions in China from different sectors: A new methodology using multiple satellite retrievals. Atmos. Chem. Phys. 2010, 10, 63–78. [Google Scholar] [CrossRef] [Green Version]
- Ghude, S.D.; Pfister, G.G.; Jena, C.; van der A, R.J.; Emmons, L.K.; Kumar, R. Satellite constraints of nitrogen oxide (NOx) emissions from India based on OMI observations and WRF-Chem simulations. Geophys. Res. Lett. 2013, 40, 423–428. [Google Scholar] [CrossRef]
- Itahashi, S.; Yumimoto, K.; Kurokawa, J.; Morino, Y.; Nagashima, T.; Miyazaki, K.; Maki, T.; Ohara, T. Inverse estimation of NOx emissions over China and India 2005–2016; contrasting recent trends and future perspectives. Environ. Res. Lett. 2019, 14, 124020. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Beirle, S.; Zhang, Q.; van der A, R.J.; Zheng, B.; Tong, D.; He, K. NOx emission trends over Chinese cities estimated from OMI observations during 2005 to 2015. Atmos. Chem. Phys. 2017, 17, 9261–9275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qu, Z.; Henze, D.K.; Capps, S.L.; Wang, Y.; Xu, X.; Wang, J.; Keller, M. Monthly top-down NOx emissions for China (2005–2012): A hybrid inversion method and trend analysis. J. Geophys. Res. Atmos. 2017, 122, 4600–4625. [Google Scholar] [CrossRef]
- Goldberg, D.; Lu, Z.; Streets, D.G.; de Foy, B.; Griffin, D.; McLinden, C.; Lamsal, L.; Krotkov, N.; Eskes, H. Enhanced capabilities of TROPOMI NO2: Estimating NOx from North American cities and power plants. Environ. Sci. Technol. 2019, 53, 12594–12601. [Google Scholar] [CrossRef] [PubMed]
- Konovalov, I.B.; Beekmann, M.; Burrows, J.P.; Richter, A. Satellite measurement based estimates of decadal changes in European nitrogen oxides emissions. Atmos. Chem. Phys. 2008, 8, 2623–2641. [Google Scholar] [CrossRef] [Green Version]
- Vinken, G.C.M.; Boersma, K.F.; van Donkelaar, A.; Zhang, L. Constraints on ship NOx emissions in Europe using GEOS-Chem and OMI satellite NO2 observations. Atmos. Chem. Phys. 2014, 14, 1353–1369. [Google Scholar] [CrossRef] [Green Version]
- Zyrichidou, I.; Koukouli, M.E.; Balis, D.; Markakis, K.; Poupkou, A.; Katragkou, E.; Kioutsioukis, I.; Melas, D.; Boersma, K.F.; van Roozendael, M. Identification of surface NOx emission sources on a regional scale using OMI NO2. Atmos. Environ. 2015, 101, 82–93. [Google Scholar] [CrossRef]
- Boersma, K.F.; Jacob, D.J.; Bucsela, E.J.; Perring, A.E.; Dirksen, R.; van der A, R.J.; Yantosca, R.M.; Park, R.J.; Wenig, M.O.; Bertram, T.H.; et al. Validation of OMI tropospheric NO2 observations during INTEX-B and application to constrain NOx emissions over the eastern United States and Mexico. Atmos. Environ. 2008, 42, 4480–4497. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Cohan, D.S.; Lamsal, L.N.; Xiao, X.; Zhou, W. Inverse modeling of Texas NOx emissions using space-based and ground-based NO2 observations. Atmos. Chem. Phys. 2013, 13, 11005–11018. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Streets, D.G.; de Foy, B.; Lamsal, L.N.; Duncan, B.N.; Xing, J. Emissions of nitrogen oxides from US urban areas: Estimation from Ozone Monitoring Instrument retrievals for 2005–2014. Atmos. Chem. Phys. 2015, 15, 10367–10383. [Google Scholar] [CrossRef] [Green Version]
- Souri, A.H.; Choi, Y.; Jeon, W.; Li, X.; Pan, S.; Diao, L.; Westenbarger, D.A. Constraining NOx emissions using satellite NO2 measurements during 2013 DISCOVER-AQ campaign. Atmos. Environ. 2016, 131, 371–381. [Google Scholar] [CrossRef]
- Goldberg, D.L.; Saide, P.E.; Lamsal, L.N.; de Foy, B.; Lu, Z.; Woo, J.-H.; Kim, Y.; Kim, J.; Gao, M.; Carmichael, G.; et al. A top-down assessment using OMI NO2 suggests an underestimate in the NOx emissions inventory in Seoul, South Korea, during KORUS-AQ. Atmos. Chem. Phys. 2019, 19, 1801–1818. [Google Scholar] [CrossRef] [Green Version]
- Martin, R.V.; Jacob, D.J.; Chance, K.; Kurosu, T.P.; Palmer, P.I.; Evans, M.J. Global inventory of nitrogen oxide emissions constrained by space-based observations of NO2 columns. J. Geophys. Res. 2003, 108, 4537. [Google Scholar] [CrossRef] [Green Version]
- Martin, R.V.; Sioris, C.E.; Chance, K.; Ryerson, T.B.; Bertram, T.H.; Wooldridge, P.J.; Cohen, R.C.; Neuman, J.A.; Swanson, A.; Flocke, F.M. Evaluation of space-based constraints on global nitrogen oxide emissions with regional aircraft measurements over and downwind of eastern North America. J. Geophys. Res. 2006, 111, D15308. [Google Scholar] [CrossRef] [Green Version]
- Lamsal, L.N.; Martin, R.V.; van Donkelaar, A.; Celarier, E.A.; Bucsela, E.J.; Boersma, K.F.; Dirksen, R.; Luo, C.; Wang, Y. Indirect validation of tropospheric nitrogen dioxide retrieved from the OMI satellite instrument: Insight into the seasonal variation of nitrogen oxides at northern midlatitudes. J. Geophys. Res. 2010, 115, D05302. [Google Scholar] [CrossRef]
- Lamsal, L.N.; Martin, R.V.; Padmanabhan, A.; van Donkelaar, A.; Zhang, Q.; Sioris, C.E.; Chance, K.; Kurosu, T.P.; Newchurch, M.J. Application of satellite observations for timely updates to global anthropogenic NOx emission inventories. Geophys. Res. Lett. 2011, 38, L05810. [Google Scholar] [CrossRef]
- Miyazaki, K.; Eskes, H.J.; Sudo, K. Global NOx emission estimates derived from an assimilation of OMI tropospheric NO2 columns. Atmos. Chem. Phys. 2012, 12, 2263–2288. [Google Scholar] [CrossRef] [Green Version]
- Lamsal, L.N.; Krotkov, N.A.; Celarier, E.A.; Swartz, W.H.; Pickering, K.E.; Bucsela, E.J.; Gleason, J.F.; Martin, R.V.; Philip, S.; Irie, H.; et al. Evaluation of OMI operational standard NO2 column retrievals using in situ and surface-based NO2 observations. Atmos. Chem. Phys. 2014, 14, 11587–11609. [Google Scholar] [CrossRef] [Green Version]
- Miyazaki, K.; Eskes, H.; Sudo, K.; Boersma, K.F.; Bowman, K.; Kanaya, Y. Decadal changes in global surface NOx emissions from multi-constituent satellite data assimilation. Atmos. Chem. Phys. 2017, 17, 807–837. [Google Scholar] [CrossRef] [Green Version]
- Cooper, M.; Martin, R.V.; Padmanabhan, A.; Henze, D. Comparing mass balance and adjoint methods for inverse modeling of nitrogen dioxide column for global nitrogen oxide emissions. J. Geophys. Res. Atmos. 2017, 122, 4718–4734. [Google Scholar] [CrossRef]
- Kurokawa, J.; Yumimoto, K.; Uno, I.; Ohara, T. Adjoint inverse modeling of NOx emissions over eastern China using satellite observations of NO2 column densities. Atmos. Environ. 2007, 43, 1878–1887. [Google Scholar] [CrossRef]
- Qu, Z.; Henze, D.K.; Theys, N.; Wang, J.; Wang, W. Hybrid mass balance/4D-Var joint inversion of NOx and SO2 emissions in East Asia. J. Geophys. Res. Atmos. 2019, 124, 8203–8224. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, J.; Xu, X.; Henze, D.K.; Qu, Z. Inverse modeling of SO2 and NOx emissions over China from multi-sensor satellite data: 1. formulation and sensitivity analysis. Atmos. Chem. Phys. Discuss. 2019. in review. [Google Scholar]
- Mijling, B.; van der A, R.J. Using daily satellite observations to estimate emissions of short-lived air pollutants on a mesoscopic scale. J. Geophys. Res. Atmos. 2012, 117, D17302. [Google Scholar] [CrossRef]
- Ding, J.; van der A, R.J.; Mijling, B.; Levelt, P.F.; Hao, N. NOx emission estimates during the 2014 Youth Olympic Games in Nanjing. Atmos. Chem. Phys. 2015, 15, 9399–9412. [Google Scholar] [CrossRef] [Green Version]
- Leue, C.; Wenig, M.; Wagner, T.; Klimm, O.; Platt, U.; Jähne, B. Quantitative analysis of NOx emission from global ozone monitoring experiment satellite image sequences. J. Geophys. Res. 2001, 106, 5493–5505. [Google Scholar] [CrossRef] [Green Version]
- Toenges-Schuller, N.; Stein, O.; Rohrer, F.; Wahner, A.; Richter, A.; Burrows, J.P.; Beirle, S.; Wagner, T.; Platt, U.; Elvidge, C.D. Global distribution pattern of anthropogenic nitrogen oxide emissions: Correlation analysis of satellite measurements and model calculations. J. Geophys. Res. 2006, 111, D05312. [Google Scholar] [CrossRef] [Green Version]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Technical Note; National Center for Atmospheric Research (NCAR): Boulder, CO, USA, 2008; pp. 1–113.
- Stauffer, D.R.; Seaman, N.L. Use of four-dimensional data assimilation in a limited-area mesoscale model. Part I: Experiments with synoptic-scale data. Mon. Wea. Rev. 1990, 118, 1250–1277. [Google Scholar] [CrossRef] [Green Version]
- Stauffer, D.R.; Seaman, N.L. Multiscale four-dimensional data assimilation. J. Appl. Meteorol. 1994, 33, 416–434. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with and explicit treatment of entrainment processes. Mon. Wea. Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogenous atmosphere: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Kain, J.S. The Kain-Frisch convective parameterization: An update. J. Appl. Meteor. 2004, 43, 170–181. [Google Scholar] [CrossRef] [Green Version]
- Byun, D.W.; Schere, K.L. Review of the governing equations, computational algorithm, and other components of the models-3 community multi-scale air quality (CMAQ) modeling system. Appl. Mech. Rev. 2006, 59, 51–77. [Google Scholar] [CrossRef]
- Binkowski, F.S.; Roselle, S.J. Models-3 community multi-scale air quality (CMAQ) model aerosol components: 1. model description. J. Geophys. Res. 2003, 108, 4183. [Google Scholar] [CrossRef]
- Carter, W.P.L. Implementation of the SAPRC-99 Chemical Mechanism into the Models-3 Framework; United States Environmental Protection Agency (US-EPA): Washington, DC, USA, 2000; pp. 1–101. [Google Scholar]
- Han, K.M.; Park, R.S.; Kim, H.K.; Woo, J.H.; Kim, J.; Song, C.H. Uncertainty in biogenic isoprene emissions and its impacts on troposphric chemistry in East Asia. Sci. Total Environ. 2013, 463–464, 754–771. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Zhang, Q.; Kurokawa, J.-I.; Woo, J.-H.; He, K.; Lu, Z.; Ohara, T.; Song, Y.; Streets, D.G.; Carmichael, G.R.; et al. MIX: A mosaic Asian anthropogenic emission inventory under the international collaboration framework of the MICS-Asia and HTAP. Atmos. Chem. Phys. 2017, 17, 935–963. [Google Scholar] [CrossRef] [Green Version]
- Janssens-Maenhout, G.; Crippa, M.; Guizzardi, D.; Dentener, F.; Muntean, M.; Pouliot, G.; Keating, T.; Zhang, Q.; Kurokawa, J.; Wankmüller, R.; et al. HTAP_v2.2: A mosaic of regional and global emission grid maps for 2008 and 2010 to study hemispheric transport of air pollution. Atmos. Chem. Phys. 2015, 15, 11411–11432. [Google Scholar] [CrossRef] [Green Version]
- Sindelarova, K.; Granier, C.; Bouarar, I.; Guenther, A.; Tilmes, S.; Stavrakou, T.; Müller, J.-F.; Kuhn, U.; Stefani, P.; Knorr, W. Global data set of biogenic VOC emissions calculated by the MEGAN model over the last 30 years. Atmos. Chem. Phys. 2014, 14, 9317–9341. [Google Scholar] [CrossRef] [Green Version]
- Darmenov, A.; da Silva, A.M. The Quick Fire Emission Dataset (QFED)—Documentation of Versions 2.1, 2.2 and 2.4; National Aeronautics and Space Administration (NASA): Maryland, MD, USA, 2013; pp. 1–183.
- Leung, F.Y.T.; Logan, J.A.; Park, R.; Hyer, E.; Kasischke, E.; Streets, D.; Yurganov, L. Impacts of enhanced biomass burning in the boreal forests in 1998 on tropospheric chemistry and the sensitivity of model results to the injection height of emissions. J. Geophys. Res. 2007, 112, D10313. [Google Scholar] [CrossRef] [Green Version]
- Hyer, E.J.; Allen, D.J.; Kasischke, E.S. Examining injection properties of boreal forest fires using surface and satellite measurements of CO transport. J. Geophys. Res. 2007, 112, D18307. [Google Scholar] [CrossRef] [Green Version]
- Kurokawa, J.; Ohara, T.; Morikawa, T.; Hanayama, S.; Janssens-Maenhout, G.; Fukui, T.; Kawashima, K.; Akimoto, H. Emissions of air pollutants and greenhouse gases over Asian regions during 2000–2008: Regional Emission inventory in ASia (REAS) version 2. Atmos. Chem. Phys. 2013, 13, 11019–11058. [Google Scholar] [CrossRef] [Green Version]
- Boersma, K.F.; Braak, R.; van der A, R.J. Dutch OMI NO2 (DOMINO) Data Product v2.0 HE5 Data File User Mannual; Royal Netherlands Meteorological Institute (KNMI): De Bilt, The Netherlands, 2011; pp. 1–21. [Google Scholar]
- Boersma, K.F.; Eskes, H.J.; Dirksen, R.J.; van der A, R.J.; Veefkind, J.P.; Stammes, P.; Huijnen, V.; Kleipool, Q.L.; Sneep, M.; Claas, J.; et al. An improved tropospheric NO2 column retrieval algorithm for the Ozone Monitoring Instrument. Atmos. Meas. Tech. 2011, 4, 1905–1928. [Google Scholar] [CrossRef] [Green Version]
- Platt, U. Differential optial absorption spectroscopy (DOAS). Chem. Anal. Series 1994, 127, 27–83. [Google Scholar]
- Dirksen, R.J.; Boersma, K.F.; Eskes, H.J.; Ionov, D.V.; Bucsela, E.J.; Levelt, P.F.; Kelder, H.M. Evaluation of stratospheric NO2 retrieved from the ozone monitoring instrument: Intercomparison, diurnal cycle and trending. J. Geophys. Res. 2011, 116, D08305. [Google Scholar] [CrossRef] [Green Version]
- Irie, H.; Boersma, K.F.; Kanaya, Y.; Takashima, H.; Pan, X.; Wang, Z.F. Quantitative bias estimates for tropospheric NO2 columns retrieved from SCIAMACHY, OMI, and GOME-2 using a common standard for East Asia. Atmos. Meas. Tech. 2012, 5, 2403–2411. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.Z.; Beirle, S.; Jin, J.L.; Shaiganfar, R.; Yan, P.; Wagner, T. Tropospheric NO2 vertical column densities over Beijing: Results of the first three years of ground-based MAX-DOAS measurements (2008–2011) and satellite validation. Atmos. Chem. Phys. 2013, 13, 1547–1567. [Google Scholar] [CrossRef] [Green Version]
- McLinden, C.A.; Fioletov, V.; Boersma, K.F.; Kharol, S.K.; Krotkov, N.; Lamsal, L.; Makar, P.A.; Martin, R.V.; Veefkind, J.P.; Yang, K. Improved satellite retrievals of NO2 and SO2 over the Canadian oil sands and comparisons with surface measurements. Atmos. Chem. Phys. 2014, 14, 3637–3656. [Google Scholar] [CrossRef] [Green Version]
- Drosoglou, T.; Bais, A.F.; Zyrichidou, I.; Kouremeti, N.; Poupkou, A.; Liora, N.; Giannaros, C.; Koukouli, M.E.; Balis, D.; Melas, D. Comparisons of ground-based tropospheric NO2 MAX-DOAS measurements to satellite observations with the aid of an air quality model over the Thessaloniki area, Greece. Atmos. Chem. Phys. 2017, 17, 5829–5849. [Google Scholar] [CrossRef] [Green Version]
- Mak, H.W.L.; Laughner, J.L.; Fung, J.C.H.; Zhu, Q.; Cohen, R.C. Improved satellite retrieval of tropospheric NO2 column density via updating of air mass factor (AMF): Case study of Southern China. Remote Sens. 2018, 10, 1789. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Beirle, S.; Zhang, Q.; Dörner, S.; He, K.; Wagner, T. NOx lifetimes and emissions of cities and power plants in polluted background estimated by satellite observations. Atmos. Chem. Phys. 2016, 16, 5283–5298. [Google Scholar] [CrossRef] [Green Version]
- Kenagy, H.S.; Sparks, T.L.; Ebben, C.J.; Wooldrige, P.J.; Lopez-Hilfiker, F.D.; Lee, B.H.; Thornton, J.A.; McDuffie, E.E.; Fibiger, D.L.; Brown, S.S.; et al. NOx lifetime and NOy partitioning during WINTER. J. Geophys. Res. 2018, 123, 9813–9827. [Google Scholar]
- Laughner, J.; Cohen, R.C. Direct observation of changing NOx lifetime in North America cities. Science 2019, 366, 723–727. [Google Scholar] [CrossRef] [PubMed]
- Shah, V.; Jacob, D.J.; Li, K.; Silvern, R.F.; Zhai, S.; Liu, M.; Lin, J.; Zhang, Q. Effect of changing NOx lifetime on the seasonality and long-term trends of satellite-observed tropospheric NO2 columns over China. Atmos. Chem. Phys. 2020, 20, 1483–1495. [Google Scholar] [CrossRef] [Green Version]
- Han, K.M.; Song, C.H. A budget analysis of NOx column losses over the Korean peninsula. Asia Pac. J. Atmos. Sci. 2012, 48, 55–65. [Google Scholar] [CrossRef]
- Browne, E.C.; Cohen, R.C. Effects of biogenic nitrate chemistry on the NOx lifetime in remote continental regions. Atmos. Chem. Phys. 2012, 12, 11917–11932. [Google Scholar] [CrossRef] [Green Version]
- Han, K.M.; Lee, S.; Yoon, Y.J.; Lee, B.Y.; Song, C.H. A model investigation into the atmospheric NOy chemistry in remote continental Asia. Atmos. Environ. 2019, 214, 116817. [Google Scholar] [CrossRef]
- Heath, M.T. Scientific Computing: An Introductory Survey, 2nd ed.; McGraw-Hill: New York, NY, USA, 2002; pp. 1–563. [Google Scholar]
- Valin, L.C.; Russell, A.R.; Hudman, R.C.; Cohen, R.C. Effects of model resolution on the interpretation of satellite NO2 observations. Atmos. Chem. Phys. 2011, 11, 11647–11655. [Google Scholar] [CrossRef] [Green Version]
- Boersma, K.F.; Vinken, G.C.M.; Eskes, H.J. Representativeness errors in comparing chemistry transport and chemistry climate models with satellite UV/Vis tropospheric column retrievals. Geosci. Model Dev. 2016, 9, 875–898. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Jeong, U.; Ahn, M.; Kim, J.H.; Park, R.J.; Lee, H.; Song, C.H.; Choi, Y.S.; Lee, K.H.; Yoo, J.M.; et al. New era of air quality monitoring from space: Geostationary environment monitoring spectrometer (GEMS). Bull. Amer. Meteor. Soc. 2020, 101, E1–E22. [Google Scholar] [CrossRef] [Green Version]
- Chance, K.; Lui, X.; Suleiman, R.M.; Flittner, D.E.; Janz, S.J. Tropspheric emissions: Monitoring of pollution (TEMPO). In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 3–7 December 2012. [Google Scholar]
- Ingmann, P.; Veihelmann, B.; Langen, J.; Lamarre, D.; Stark, H.; Courreges-Lacoste, G.B. Requirements for the GMES atmosphere service and ESA’s implementation concept: Sentinels-4/-5 and-5p. Remote Sens. Environ. 2012, 120, 58–69. [Google Scholar] [CrossRef]
- Lamsal, L.N.; Duncan, B.N.; Yoshida, Y.; Krotkov, N.U.S. NO2 trends (2005–2013): EPA air quality system (AQS) data versus improved observations from the ozone monitoring instrument (OMI). Atmos. Environ. 2015, 110, 130–143. [Google Scholar] [CrossRef]
- Dunlea, E.J.; Herndon, S.C.; Nelson, D.D.; Volkamer, R.M.; San Martini, F.; Sheehy, P.M.; Zahniser, M.S.; Shorter, J.H.; Wormhoudt, J.; Lamb, B.K.; et al. Evaluation of nitrogen dioxide chemiluminescence monitors in a polluted urban environment. Atmos. Chem. Phys. 2007, 7, 2691–2704. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.-T. Satellite constraint for emissions of nitrogen oxides from anthropogenic, lightning and soil sources over East China on a high-resolution grid. Atmos. Chem. Phys. 2012, 12, 2881–2898. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.-T.; Liu, Z.; Zhang, Q.; Liu, H.; Mao, J.; Zhuang, G. Modeling uncertainties for tropospheric nitrogen dioxide columns affecting satellite-based inverse modeling of nitrogen oxides emissions. Atmos. Chem. Phys. 2012, 12, 12255–12275. [Google Scholar] [CrossRef]
- Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E.; Dentener, F.; van Aardenne, J.A.; Monni, S.; Doering, U.; Olivier, J.G.J.; Pagliari, V.; et al. Gridded emissions of air pollutants for the period 1970–2012 within EDGAR v4.3.2. Earth Syst. Sci. Data 2018, 10, 1987–2013. [Google Scholar] [CrossRef] [Green Version]


| References | Methodology | Target Region and Year | NOx Emission |
|---|---|---|---|
| Leue et al. [48] | - E: emission strength (top-down NOx); - Ωs: satellite-derived NOx columns; - τ: NOx lifetime (constant value of 27 ± 3 h) | Global/ 1997 | 43.5 Tg N yr−1 (for the globe) 2.7 Tg N yr−1 (for China) 0.5 Tg N yr−1 (for Japan) |
| Martin et al. [35,36] | (i) Top-down NOx (Et): - Et: top-down NOx; - Eb: bottom-up (a priori) NOx; - Ωs: satellite-derived NO2 columns; - Ωm: CTM-derived NO2 column; | Global/ Sep. 1996– Aug. 1997 | 38.0 Tg N yr−1 (for the globe) 5.4 Tg N yr−1 (for East Asia) |
| (ii) A posterior NOx (E, optimized NOx emissions) - εb: relative geometric error between a priori and EDGAR NOx emissions; - εt: relative geometric error between top-down and EDGAR NOx emissions | Global/Sep. 1996 − Aug. 1997 | 37.7 Tg N yr−1 (for the globe) 5.3 Tg N yr−1 (for East Asia) | |
| Boersma et al. [30] | Basic concept from Martin et al. [35] Here, K (kernel) matrix defined as K - k: smoothing parameter (k = 12 in the study) | Eastern US & Mexico/Mar. 2006 | 0.5 Tg N month−1 (for Eastern US) 0.1 Tg N month−1 (for Mexico) |
| Zhao and Wang [20] | Assimilated a posteriori based on Martin et al. [35] | East Asia/Jul. 2007 | 9.5 Tg N yr−1 (for East Asia) |
| Lamsal et al. [37,40] | Top-down NOx estimation from Martin et al. [35] and Boersma et al. [30] | N. America, Europe, and East Asia/2006–2007 | 7.6–8.9 Tg N yr−1 (for N. America) 3.9–5.2 Tg N yr−1 (for Europe) 10.9–13.1 Tg N yr−1 (for East Asia) |
| Lin et al. [21] | Concept based on study of Leue et al. [42], using multi-satellite data observed at different scanning time - Et: top-down NOx emission; - Ωs|n: satellite NOx columns at n-th hour; - Ωs|0: satellite NOx columns at 0-th hour; - τ: NOx lifetime; - Δt: time interval; - Ei: NOx emission at i-th hour; - Ē: daily mean of E | China/2008 | 6.8 Tg N yr−1 (best estimate for China) |
| Ghude et al. [22] | Basic concept from Martin et al. [35] - Ωm: model-predicted NO2 columns w/ consideration of averaging kernel | India/2005 | 1.9 Tg N yr−1 (for India) |
| Goldberg et al. [34] | Exponentially modified Gaussian fitting method [15] - E: top-down NOx emission; - Ωs: satellite-derived NO2 columns; - τ: effective NO2 lifetime; - 1.33: mean column-averaged NOx/NO2 ratio; - x0: e-fold distance downwind; - ω: mean zonal wind speed | South Korea/2016 (KORUS-AQ field campaign) | 0.353 ± 0.146 Tg NOx yr-1 (for Seoul Metropolitan areas) |
| Month | Region | Bottom-Up NOx | Best Top-Down NOx |
|---|---|---|---|
| Jan. (Gg N month−1) | Entire domain | 814.20 | 990.99 |
| China | 686.84 | 823.26 | |
| N. Korea | 6.29 | 8.16 | |
| S. Korea | 23.22 | 38.24 | |
| Japan | 41.26 | 50.11 | |
| Jul. (Gg N month−1) | Entire domain | 913.55 | 1346.10 |
| China | 780.72 | 1137.28 | |
| N. Korea | 6.71 | 12.95 | |
| S. Korea | 24.27 | 37.62 | |
| Japan | 36.07 | 63.41 | |
| Annual 1 (Tg N yr−1) | Entire domain | 10.37 | 14.02 |
| China | 8.81 | 11.76 | |
| N. Korea | 0.08 | 0.13 | |
| S. Korea | 0.28 | 0.46 | |
| Japan | 0.46 | 0.68 |
| Month | In-Situ | CMAQ w/Bottom-Up NOx | CMAQ w/Best Top-Down NOx |
|---|---|---|---|
| Jan. (ppb) | 41.80 ± 10.91 * | 24.05 ± 8.27 | 32.49 ± 13.19 |
| Jul. (ppb) | 23.78 ± 10.70 | 23.53 ± 8.18 | 22.43 ± 9.20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, K.M.; Kim, H.S.; Song, C.H. An Estimation of Top-Down NOx Emissions from OMI Sensor Over East Asia. Remote Sens. 2020, 12, 2004. https://doi.org/10.3390/rs12122004
Han KM, Kim HS, Song CH. An Estimation of Top-Down NOx Emissions from OMI Sensor Over East Asia. Remote Sensing. 2020; 12(12):2004. https://doi.org/10.3390/rs12122004
Chicago/Turabian StyleHan, Kyung M., Hyun S. Kim, and Chul H. Song. 2020. "An Estimation of Top-Down NOx Emissions from OMI Sensor Over East Asia" Remote Sensing 12, no. 12: 2004. https://doi.org/10.3390/rs12122004
APA StyleHan, K. M., Kim, H. S., & Song, C. H. (2020). An Estimation of Top-Down NOx Emissions from OMI Sensor Over East Asia. Remote Sensing, 12(12), 2004. https://doi.org/10.3390/rs12122004