Remote Sensing Support for the Gain-Loss Approach for Greenhouse Gas Inventories
Abstract
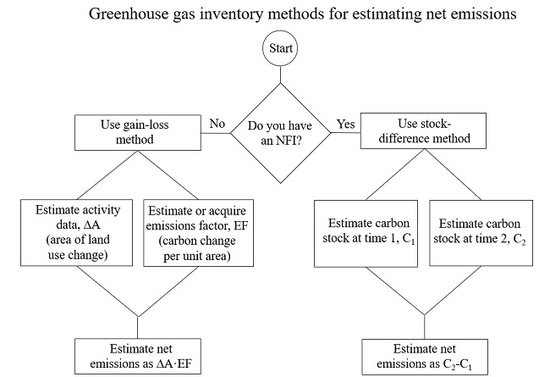
1. Introduction
2. Estimating Total Emissions
3. Activity Data
3.1. Data
3.1.1. Reference Data
3.1.2. Auxiliary Data
3.2. Statistical Estimators
3.2.1. Design-Based Inference
3.2.2. Simple Expansion Estimator
3.2.3. Stratified Estimators
3.2.4. Post-Stratified Estimators
3.2.5. Model-Assisted Estimators
3.3. Time Series Analyses
4. Emissions and Removals Factors
4.1. Probability Samples of Ground Reference Data
4.2. Non-Probability Samples of Ground Reference Data
4.2.1. Data-Related Challenges
4.2.2. Model-Based Inference
4.3. Remote Sensing-Based Maps as Sources of Reference Data
4.3.1. Reference Data Estimates
4.3.2. Map-Based Estimates
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- GFOI. Integration of Remote-Sensing and Ground-Based Observations for Estimation of Emissions and Removals of Greenhouse Gases in Forests: Methods and Guidance from the Global Forest Observations Initiative, Ed. 2.0; Food and Agriculture Organization: Rome, Italy, 2016; Available online: https://www.reddcompass.org/frontpage (accessed on 8 June 2020).
- Eggleston, H.S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. (Eds.) 2006 IPCC Guidelines for National Greenhouse Gas Inventories, Volume 4: Agriculture, Forestry and Other Land Use; Institute for Global Environmental Strategies: Hayama, Japan, 2006; Available online: http://www.ipcc-nggip.iges.or.jp/public/2006gl/index.html (accessed on 8 June 2020).
- Bucki, M.; Cuypers, D.; Mayaux, P.; Achard, F.; Estreguil, C.; Grassi, G. Assessing REDDC performance of countries with low monitoring capacities: The matrix approach. Environ. Res. Lett. 2012, 7, 014031. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Næsset, E.; McRoberts, R.E.; Ståhl, G.; Andersen, H.-E.; Gobakken, T.; Ene, L.; Nelson, R. Statistical rigor in lidar-assisted estimation of aboveground forest biomass. Remote Sens. Environ. 2016, 173, 98–108. [Google Scholar] [CrossRef]
- Birigazzi, L.; Gregoire, T.G.; Finegold, Y.; Golec, R.C.D.; Sandker, E.; Donegan, E.; Gamarra, J.G.P. Data quality reporting: Good practice for transparent estimates from forestand land cover surveys. Environ. Sci. Policy 2019, 96, 85–94. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Comparing the stock-change and gain–loss approaches for estimating forest carbon emissions for the aboveground biomass pool. Can. J. For. Res. 2018, 48, 1535–1542. [Google Scholar] [CrossRef]
- REDD+ Web Platform. Available online: https://redd.unfccc.int/fact-sheets.html (accessed on 8 June 2020).
- Olofsson, P.; Foody, G.M.; Stehman, S.V.; Woodcock, C.E. Making better use of accuracy data in land change studies: Estimating accuracy and area and quantifying uncertainty using stratified estimation. Remote Sens. Environ. 2013, 129, 122–131. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Foody, G.M. The impact of imperfect ground reference data on the accuracy of land cover change estimation. Int. J. Remote Sens. 2009, 30, 3275–3281. [Google Scholar] [CrossRef]
- Foody, G.M. Assessing the accuracy of land cover change with imperfect ground reference data. Remote Sens. Environ. 2010, 14, 2271–2285. [Google Scholar] [CrossRef]
- Foody, G.M. Ground reference data error and the mis-estimation of the area of land cover change as a function of its abundance. Remote Sens. Lett. 2013, 4, 8. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Stehman, S.V.; Liknes, G.C.; Næsset, E.; Sannier, C.; Walters, B.F. The effects of imperfect reference data on remote sensing-assisted estimators of land cover class proportions. Isprs J. Photogramm. Remote Sens. 2018, 142, 292–300. [Google Scholar] [CrossRef]
- Sun, B.; Chen, X.; Zhou, Q. Analyzing the uncertainties of ground validation for remote sensing land cover mapping in the era of big geographic data. In Spatial Data Handling in Big Data Era. Advances in Geographic Information Science; Zhou, C., Su, F., Harvey, F., Xu, J., Eds.; Springer: Singapore, 2017; pp. 31–38. [Google Scholar]
- Mannel, S.; Price, M.; Hua, D. A method to obtain large quantities of reference data. Int. J. Remote Sens. 2006, 27, 623–627. [Google Scholar] [CrossRef]
- Stehman, S.V. Model-assisted estimation as a unifying framework for estimating the area of land cover and land-cover change from remote sensing. Remote Sens. Environ. 2009, 113, 2455–2462. [Google Scholar] [CrossRef]
- Mowrer, H.T.; Congalton, R.G. (Eds.) Quantifying Spatial Uncertainty in Natural Resources: Theory and Applications for GIS and Remote Sensing; Sleeping Bear Press: Ann Arbor, MI, USA, 2000. [Google Scholar]
- Næsset, E. The effect of season upon registrations of stand mean height, crown closure and tree species on aerial photos. Commun. Skogforsk 1991, 44, 1–28. [Google Scholar]
- Næsset, E. The effect of scale, type of film and focal length upon interpretation of tree species mixture on aerial photos. Commun. Skogforsk 1992, 45, 1–28. [Google Scholar]
- Powell, R.L.; Matzke, N.; de Souza, D.; Clark, M.; Numata, I.; Hess, L.L.; Roberts, D.A. Sources of error in accuracy assessment of thematic land-cover maps in the Brazilian Amazon. Remote Sens. Environ. 2004, 90, 221–234. [Google Scholar] [CrossRef]
- Pengra, B.P.; Stehman, S.V.; Horton, J.A.; Dockter, D.J.; Schroeder, T.A.; Yang, Z.; Cohen, W.B.; Healey, S.P.; Loveland, T.R. Quality control and assessment of interpreter consistency of annual land cover reference data in an operational national monitoring program. Remote Sens. Environ. 2020, 238, 111261. [Google Scholar] [CrossRef]
- Guyana Forestry Commission. Guyana REDD+ Monitoring Reporting & Verification System (MRVS) Interim Measures Report 01 October 2010–31 December 2011 Version 1, 15 June 2012. Available online: http://occguyana.org/lcds/index.php/documents/reports/national/guyana-mrvs-interim-measures-reports-1/61-guyana-forestry-commission-guyana-redd-monitoring-reporting-verification-system-mrvs-interim-measures-report-01-october-2010-31-december-2011-version-3-26-july-2012/file (accessed on 8 June 2020).
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Sannier, C.; McRoberts, R.E.; Fichet, L.-V. Suitability of Global Forest Change data to report forest cover estimates at national level in Gabon. Remote Sens. Environ. 2016, 173, 326–338. [Google Scholar] [CrossRef]
- Næsset, E.; Ørka, H.O.; Solberg, S.; Bollandsås, O.M.; Hansen, E.H.; Mauya, E.; Zahabu, E.; Malimbwi, R.; Chamuya, N.; Olsson, H.; et al. Mapping and estimating forest area and aboveground biomass in miombo woodlands in Tanzania using data from airborne laser scanning, TanDEM-X, RapidEye, and global forest maps: A comparison of estimated precision. Remote Sens. Environ. 2016, 175, 282–300. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Vibrans, A.C.; Sannier, C.; Næsset, E.; Hansen, M.C.; Walters, B.F.; Lingner, D.V. Methods for evaluating the utilities of local and global maps for increasing the precision of estimates of subtropical forest area. Can. J. For. Res. 2016, 46, 924–932. [Google Scholar] [CrossRef]
- Mermoz, S.; Bouvet, A.; Le Toan, T.; Herold, M. Impacts of the forest definitions adopted by African countries on carbon conservation. Environ. Res. Lett. 2018, 13, 104014. [Google Scholar] [CrossRef]
- De Wasseige, C.; Flynn, J.; Louppe, D.; Hiol Hiol, F.; Mayaux, P. (Eds.) The Forests of the Congo Basin–State of the Forest; Weyrich: Neufchâateu, Belgium, 2013. [Google Scholar]
- Cochran, W.G. Sampling Techniques, 3rd ed.; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Särndal, C.-E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer: New York, NY, USA, 1992. [Google Scholar]
- Westfall, J.A.; Patterson, P.L.; Coulston, J.W. Post-stratified estimation: Within-strata and total sample size recommendations. Can. J. For. Res. 2011, 41, 1130–1139. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Wendt, D.G.; Nelson, M.D.; Hansen, M.H. Using a land cover classification based on satellite imagery to improve the precision of forest inventory area estimates. Remote Sens. Environ. 2002, 81, 36–44. [Google Scholar] [CrossRef]
- Olofsson, P.; Arévalo, A.; Espejo, A.B.; Green, C.; Lindquist, E.; McRoberts, R.E.; Sanz, M.J. Mitigating the effects of omission errors on area and area change estimates. Remote Sens. Environ. 2020, 236, 111492. [Google Scholar] [CrossRef]
- Gregoire, T.; Valentine, H. Sampling Strategies for Natural Resources and the Environment; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Ståhl, G.; Saarela, S.; Schnell, S.; Holm, S.; Breidenbach, J.; Healey, S.P.; Patterson, P.L.; Magnussen, S.; Næsset, E.; McRoberts, R.E.; et al. Use of models in large-area forest surveys: Comparing model-assisted, model-based and hybrid estimation. For. Ecosyst. 2016, 3, 5. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area from an accuracy assessment error matrix. Remote Sens. Environ. 2013, 132, 202–211. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Nasset, E.; Saatchi, S.; Liknes, G.C.; Walters, B.F.; Chen, Q. Local validation of global biomass maps. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101931. [Google Scholar] [CrossRef]
- McRoberts, R.E. Post-classification approaches to estimating change in forest area using remotely sensed auxiliary data. Remote Sens. Environ. 2014, 151, 149–156. [Google Scholar] [CrossRef]
- Khan, A.; Hansen, M.C.; Potapov, P.V.; Adusei, B.; Pickens, A.; Krylov, A.; Stehman, S.V. Evaluating Landsat and RapidEye data for winter wheat mapping and area estimation in Punjab, Pakistan. Remote Sens. 2018, 10, 489. [Google Scholar] [CrossRef]
- Gallego, F.J. Remote sensing and land cover area estimation. Int. J. Remote Sens. 2004, 25, 3019–3047. [Google Scholar] [CrossRef]
- Vibrans, A.C.; McRoberts, R.E.; Moser, P.; Nicoletti, A.L. Using satellite image-based maps and ground inventory data to estimate the area of the remaining Atlantic forest in the Brazilian state of Santa Catarina. Remote Sens. Environ. 2013, 130, 87–95. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area and map accuracy for stratified random sampling when the strata are different from the map classes. Int. J. Remote Sens. 2014, 35, 4923–4939. [Google Scholar] [CrossRef]
- McRoberts, R.E. Probability- and model-based approaches to inference for proportion forest using satellite imagery as ancillary data. Remote Sens. Environ. 2010, 114, 1017–1025. [Google Scholar] [CrossRef]
- Sannier, C.; McRoberts, R.E.; Fichet, L.-V.; Makaga, E.M.K. Using the regression estimator with Landsat data to estimate proportion forest cover and net proportion deforestation in Gabon. Remote Sens. Environ. 2014, 151, 138–148. [Google Scholar] [CrossRef]
- Ying, Q.; Hansen, M.C.; Potapov, P.V.; Tyukavina, A.; Wang, L.; Stehman, S.V.; Moore, R.; Hancher, M. Global bare ground gain from 2000 to 2012 using Landsat imagery. Remote Sens. Environ. 2017, 194, 161–176. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Gregoire, T.G.; Ståhl, G. Model-assisted estimation of change in forest biomass over an 11 year period in a sample survey supported by airborne LiDAR: A case study with post-stratification to provide “activity data”. Remote Sens. Environ. 2013, 128, 299–314. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Walters, B.F. Statistical inference for remote sensing-based estimates of net deforestation. Remote Sens. Environ. 2012, 124, 394–401. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. Indirect and direct estimation of forest biomass change using forest inventory and airborne laser scanning data. Remote Sens. Environ. 2015, 164, 36–42. [Google Scholar] [CrossRef]
- Claggett, P.R.; Okay, J.A.; Stehman, S.V. Monitoring regional riparian forest cover change using stratified sampling and multiresolution imagery. J. Am. Water Resour. Assoc. 2010, 46, 334–343. [Google Scholar] [CrossRef]
- Tyukavina, A.; Hansen, M.C.; Potapov, P.V.; Parker, D.; Okpa, C.; Stehman, S.V.; Kommareddy, I.; Turubanova, S. Congo Basin forest loss dominated by increasing smallholder clearing. Sci. Adv. 2018, 4, eaat2993. [Google Scholar] [CrossRef]
- Pickering, J.; Stehman, S.V.; Tyukavina, A.; Potapov, P.; Watt, P.; Jantz, S.M.; Bholanath, P.; Hansen, M.C. Quantifying the trade-off between cost and precision in estimating area of forest loss and degradation using probability sampling in Guyana. Remote Sens. Environ. 2019, 221, 122–135. [Google Scholar] [CrossRef]
- Zimmerman, P.L.; Housman, I.W.; Perry, C.H.; Chastain, R.A.; Webb, J.B.; Finco, M.V. An accuracy assessment of forest disturbance mapping in the western Great Lakes. Remote Sens. Environ. 2013, 128, 176–185. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Cohen, W.B.; Schroeder, T.A. Trajectory-based change detection for automated characterization of forest disturbance dynamics. Remote Sens. Environ. 2007, 110, 370–386. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Kennedy, R. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. TimeSync—Tools for calibration and validation. Remote Sens. Environ. 2010, 114, 2199–2924. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Olofsson, P. Continuous monitoring of forest disturbance using all available Landsat imagery. Remote Sens. Environ. 2012, 122, 75–91. [Google Scholar] [CrossRef]
- Reiche, J.; de Bruin, S.; Hoekman, D.; Verbesselt, J.; Herold, M. A Bayesian approach to combine Landsat and ALOS PALSAR time series for near real-time deforestation detection. Remote Sens. 2015, 7, 4973–4996. [Google Scholar] [CrossRef]
- Reiche, J.; Verbesselt, J.; Hoekman, D.; Herold, M. Fusing Landsat and SAR time series to detect deforestation in the tropics. Remote Sens. Environ. 2015, 156, 276–293. [Google Scholar] [CrossRef]
- Arevalo, P.; Woodcock, C.E.; Olofsson, P. Continuous monitoring of land change activities and post-disturbance dynamics from Landsat time series: A test methodology for REDD+ reporting. Remote Sens. Environ. 2019, 238, 111051. [Google Scholar] [CrossRef]
- Corona, P.; Fattorini, L.; Franceschi, S.; Scrinzi, G.; Torresan, C. Estimation of standing wood volume in forest compartments by exploiting airborne laser scanning information: Model-based, design-based, and hybrid perspectives. Can. J. For. Res. 2014, 4, 1303–1311. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Domke, G.M.; Ståhl, G.; Saarela, S.; Westfall, J.A. Hybrid estimators for mean aboveground carbon per unit area. For. Ecol. Manag. 2016, 378, 44–56. [Google Scholar] [CrossRef]
- Condés, S.; McRoberts, R.E. Updating national forest inventory estimates of growing stock volume using hybrid inference. For. Ecol. Manag. 2017, 400, 48–57. [Google Scholar] [CrossRef]
- IPCC. User Manual, Database on Greenhouse as Emission Factors. Version 3.0. 2018. Available online: https://www.ipcc-nggip.iges.or.jp/EFDB/documents/EFDB_User_Manual.pdf (accessed on 8 June 2020).
- Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R.; Hoppus, M.L.; Jacobs, D.M.; Lister, A.J.; Moisen, G.G.; Nelson, M.D.; Riemann, R.; et al. Mapping, U.S. forest biomass using national forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Mermoz, S.; Bouvet, A.; Le Toan, T.; Carvalhais, N.; Rozendaal, D.; Herold, M.; Avitabile, V.; Quegan, S.; et al. A detailed portrait of the forest aboveground biomass pool for the year 2010 obtained from multiple remote sensing observations. Geophys. Res. Abstr. 2018, 20, EGU2018-18932. [Google Scholar]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O. ESA Biomass Climate Change Initiative (Biomass_cci): Global datasets of forest above-ground biomass for the year 2017, v1. Cent. Environ. Data Anal. 2019. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Gobakken, T.; Næsset, E. Post-stratified estimation of forest area and growing stock volume using lidar-based stratifications. Remote Sens. Environ. 2012, 125, 157–166. [Google Scholar] [CrossRef]
- Särndal, C.E. The calibration approach in survey theory and practice. Surv. Methodol. 2007, 33, 99–119. [Google Scholar]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Inference for lidar-assisted estimation of forest growing stock volume. Remote Sens. Environ. 2013, 128, 268–275. [Google Scholar] [CrossRef]
- Poorazimy, M.; Shataee, S.; McRoberts, R.E.; Mohammadi, J. Integrating airborne laser scanning data, space-borne radar data and digital aerial imagery to estimate aboveground carbon stock in Hyrcanian forests, Iran. Remote Sens. Environ. 2020, in press. [Google Scholar] [CrossRef]
- Tomppo, E.; Haakana, M.; Katia, M.; Peräsaari, J. Multi-Source National Forest Inventory-Methods and Applications; Managing Forest Ecosystems; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Esteban, J.; McRoberts, R.E.; Fernández-Landa, A.; Tomé, J.L.; Næssset, E. Estimating forest volume and biomass and their changes Using random forests and remotely sensed data. Remote Sens. 2019, 11, 1994. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Solberg, S.; Gregoire, T.G.; Nelson, R.; Ståhl, G.; Weydahl, D. Model-assisted regional forest biomass estimation using LiDAR and InSAR as auxiliary data: A case study from a boreal forest area. Remote Sens. Environ. 2011, 115, 3599–3614. [Google Scholar] [CrossRef]
- Næsset, E.; McRoberts, R.E.; Pekkarinen, A.; Saatchi, S.; Santoro, M.; Trier, O.D.; Zahabu, E.; Gobakken, T. Use of local and global maps of forest canopy height and aboveground biomass to enhance local estimates of biomass in miombo woodlands in Tanzania. Int. J. Appl. Earth Obs. Geoinf. 2020, in press. [Google Scholar]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Solberg, S.; McRoberts, R.E. The effects of field plot size on model-assisted estimation of aboveground biomass change using multitemporal interferometric SAR and airborne laser scanning data. Remote Sens. Environ. 2015, 168, 252–264. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Ståhl, G.; Næsset, E.; Gobakken, T.; Nelson, R.; Holm, S. Model-assisted estimation of biomass in a LiDAR sample survey in Hedmark county, Norway. Can. J. For. Res. 2011, 41, 83–95. [Google Scholar] [CrossRef]
- Mauya, E.W.; Hansen, E.H.; Gobakken, T.; Bollandsås, O.M.; Malimbwi, R.E.; Næsset, E. Effects of field plot size on the prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rain forests of Tanzania. Carbon Balance Manag. 2015, 10, 10. [Google Scholar] [CrossRef]
- Tomppo, E.; Kuusinen, N.; Mäkisara, K.; Katila, M.; McRoberts, R.E. Effects of field plot configurations on the uncertainties of ALS-assisted forest resource estimates. Scand. J. For. Res. 2017, 32, 488–500. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Tomppo, T.; Schadauer, K.; Vidal, C.; Ståhl, G.; Chirici, G.; Lanz, A.; Cienciala, A.; Winter, S.; Smith, W.B. Harmonizing national forest inventories. J. For. 2009, 107, 179–187. [Google Scholar] [CrossRef]
- Tomppo, E.; Gschwantner, T.; Lawrence, M.; McRoberts, R.E. (Eds.) National Forest Inventories: Pathways to Common Reporting; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Saarela, S.; Schnell, S.; Tuominen, S.; Balázs, A.; Hyyppä, J.; Grafström, A. Effects of positional errors in model-assisted and model-based estimation of growing stock volume. Remote Sens. Environ. 2016, 172, 101–108. [Google Scholar] [CrossRef]
| Parameter | Response Variable | Estimator * | References |
|---|---|---|---|
| Area | Class | STR | Stehman [36] |
| PSTR | McRoberts et al. [6,26,32,38], Stehman [16,36] | ||
| DIF | Stehman [36], Khan et al. [39] | ||
| GREG | Gallego [40], Stehman [16], Vibrans et al. [41], McRoberts et al. [26,38] | ||
| Proportion | STR | Stehman [42] | |
| PSTR | McRoberts [43] | ||
| DIF | McRoberts [43] | ||
| GREG | Sannier et al. [24,44] | ||
| Area change | Class | STR | Olofsson et al. [8,9,33], Ying et al. [45] |
| PSTR | McRoberts et al. [6], Næsset et al. [46] | ||
| DIF | |||
| GREG | Stehman [16], Næsset et al. [46], McRoberts and Walters [47], McRoberts et al. [48] | ||
| Proportion | STR | Claggett et al. [49], Tyukavina et al. [50] | |
| PSTR | Pickering et al. [51] | ||
| DIF | Zimmerman et al. [52] | ||
| GREG | Stehman [16], Sannier et al. [24,44] |
| Parameter | Estimator * | References |
|---|---|---|
| Biomass (volume) | STR | Næsset et al. [76,77] |
| PSTR | McRoberts et al. [6,37,69], Tomppo et al. [74] (p. 56) | |
| DIF | McRoberts et al. [37], Næsset et al. [77] | |
| GREG | Næsset et al. [25,76,77], Poorazimy et al. [71] | |
| Biomass (volume) change | STR | Næsset et al. [78] |
| PSTR | McRoberts et al. [7,48], Næsset et al. [46] | |
| DIF | ||
| GREG | Gregoire et al. [79], McRoberts et al. [6,48], Næsset et al. [46,78], Esteban et al. [75] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McRoberts, R.E.; Næsset, E.; Sannier, C.; Stehman, S.V.; Tomppo, E.O. Remote Sensing Support for the Gain-Loss Approach for Greenhouse Gas Inventories. Remote Sens. 2020, 12, 1891. https://doi.org/10.3390/rs12111891
McRoberts RE, Næsset E, Sannier C, Stehman SV, Tomppo EO. Remote Sensing Support for the Gain-Loss Approach for Greenhouse Gas Inventories. Remote Sensing. 2020; 12(11):1891. https://doi.org/10.3390/rs12111891
Chicago/Turabian StyleMcRoberts, Ronald E., Erik Næsset, Christophe Sannier, Stephen V. Stehman, and Erkki O. Tomppo. 2020. "Remote Sensing Support for the Gain-Loss Approach for Greenhouse Gas Inventories" Remote Sensing 12, no. 11: 1891. https://doi.org/10.3390/rs12111891
APA StyleMcRoberts, R. E., Næsset, E., Sannier, C., Stehman, S. V., & Tomppo, E. O. (2020). Remote Sensing Support for the Gain-Loss Approach for Greenhouse Gas Inventories. Remote Sensing, 12(11), 1891. https://doi.org/10.3390/rs12111891