Deep Learning-Based Single Image Super-Resolution: An Investigation for Dense Scene Reconstruction with UAS Photogrammetry
Abstract
1. Introduction
- An overview of the SR problem and DCNN approaches for SISR is provided with emphasis on generative adversarial network (GAN) architecture. GAN-based models are fully reviewed including their specific loss functions. Additionally, different learning strategies and image quality measures (IQMs) typically employed for SISR tasks are reviewed.
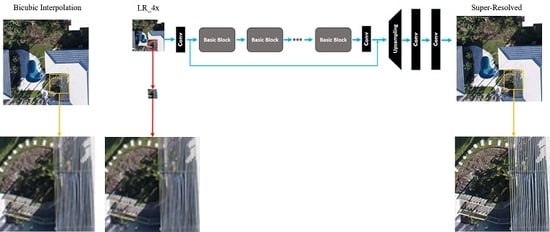
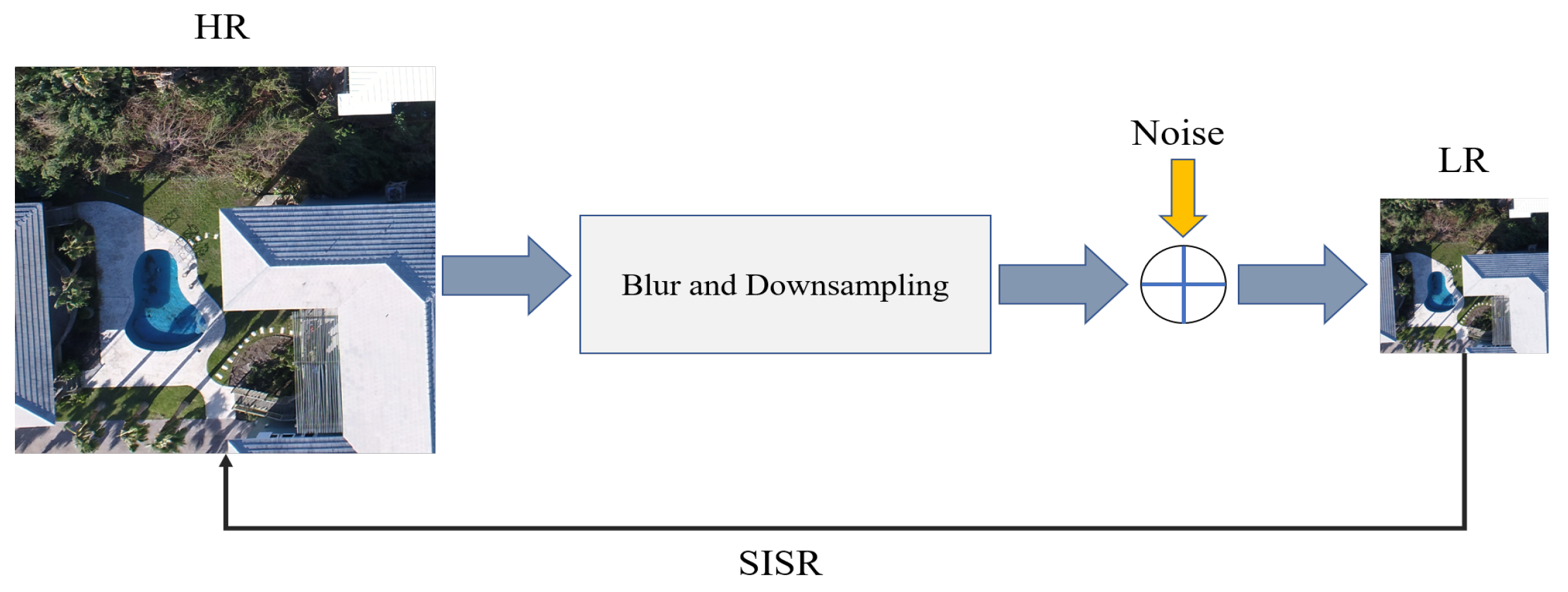
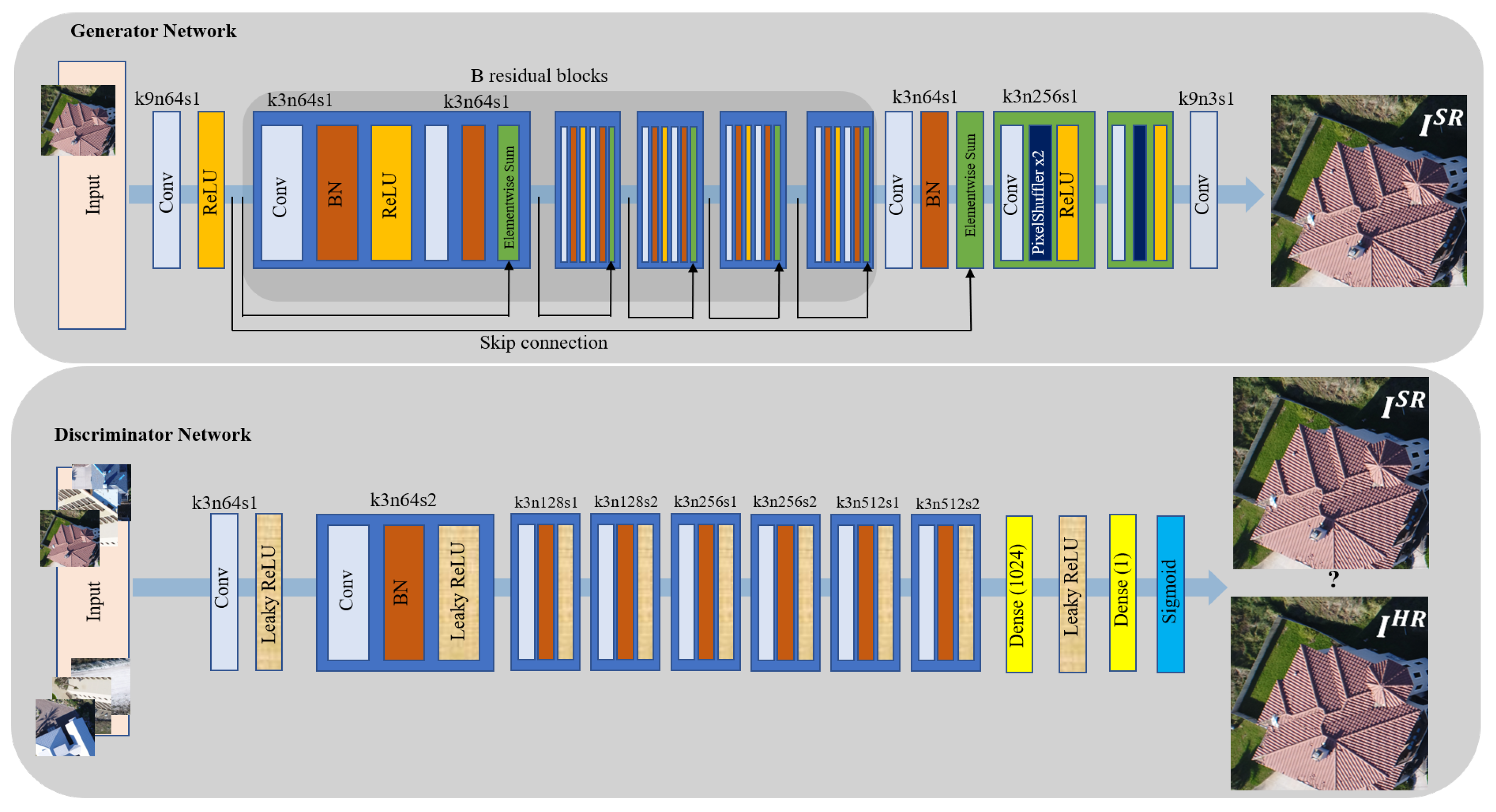
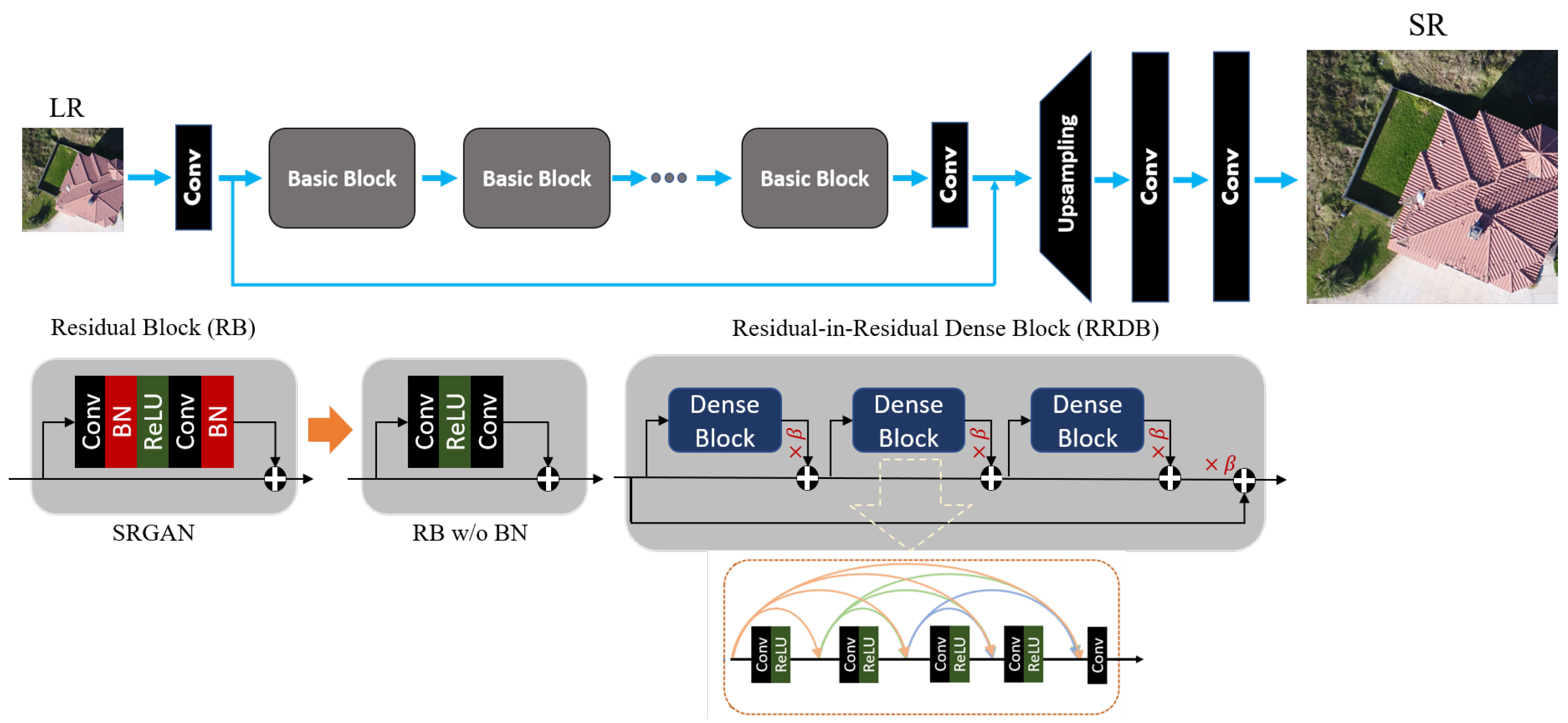
- A high performance DCNN-based SISR model based on GAN architecture [31], known as enhanced SRGAN (ESRGAN) [32], is adopted and trained on a set of LR UAS images virtually generated by downsampling the original HR image set by factor . Additive white Gaussian noise is applied to the LR imagery to make the SISR task more challenging. Such noise can always appear in any digital imaging and image transmission systems due to the electronics, imaging sensor quality, and the interaction of the digital imaging system with the natural environment, such as the level of illumination, temperature, etc [33]. Model performance in recovering the degraded or lost image details and noise reduction in the predicted super-resolved images is then carried out using standard IQMs. In this experiment, IQMs include peak signal-to-noise ratio (PSNR), structure similarity (SSIM) index, and a qualitative analysis through visually inspecting resulting SR images.
- A task-based IQM using Structure-from-Motion (SfM) photogrammetry is carried out on the predicted SR image set.
- A comprehensive comparative analysis of SfM derived photogrammetric data products, resulting from processing of the LR, HR, and SR UAS image sets, is carried out. Those products include: the camera calibration and camera pose information, densified 3D point clouds, and digital surface models (DSMs).
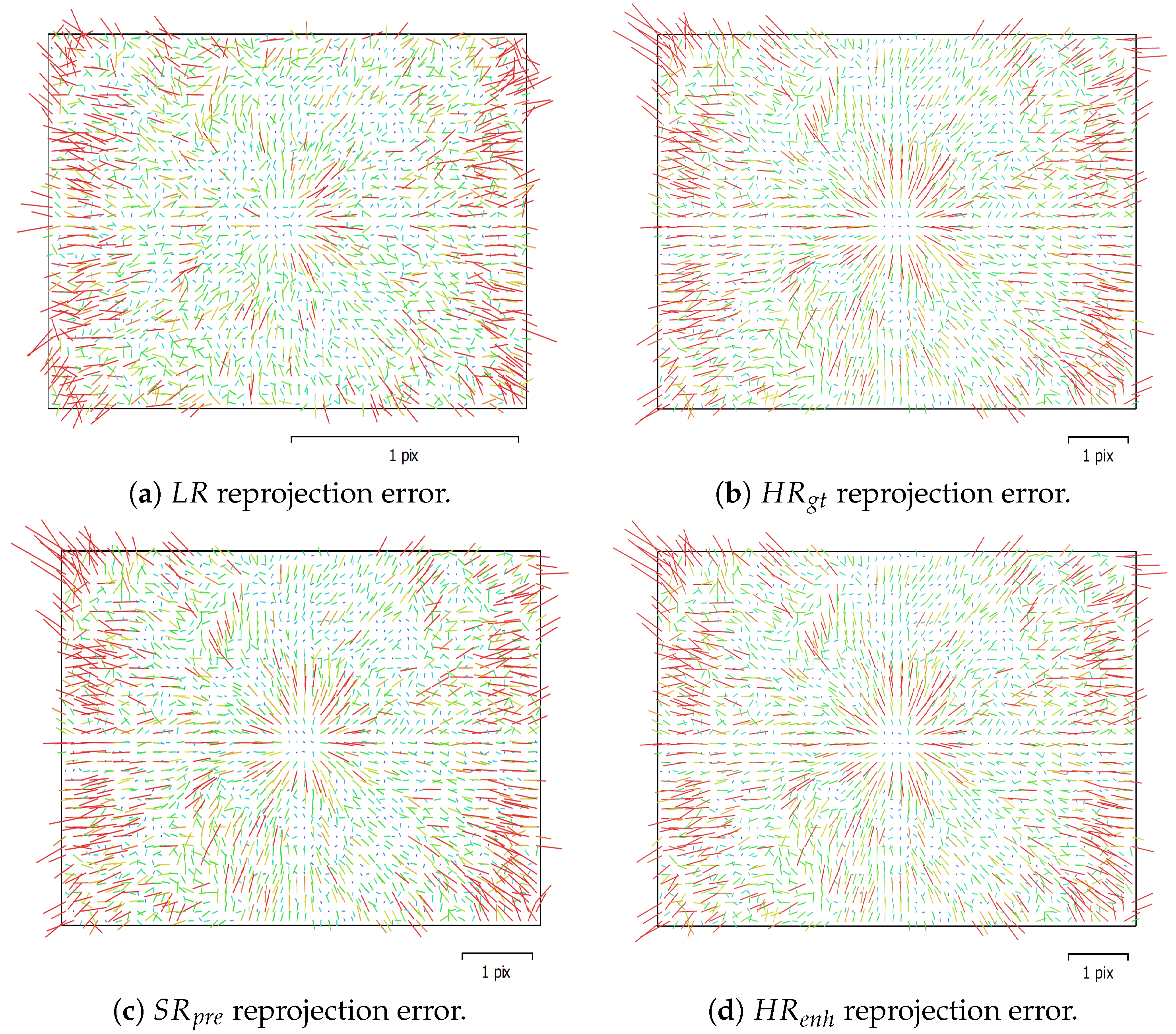
- The performance of the adopted DCNN-based SISR model on retrieving both the interior and exterior geometry of the UAS imagery is investigated. In SfM photogrammetry, the accuracy and reliability of all derived parameters, within the robust bundle adjustment (BA) computations, are closely related to the accuracy and reliability of extracted keypoint features from raw images. Any image distortions and artefacts introduced by adding noise or upsampling images can dramatically affect the reliability of derived parameters within BA computations.
- The potential of the employed DCNN-based SISR model to downgrade the level of inherent and additional noise introduced to the original HR images is investigated. In most image-based 3D reconstruction algorithms, including SfM photogrammetry, lower level of noise in the underlying image set results in estimating the imaging and scene geometry with higher accuracy. That is due to the fact that the feature detection operators, using sophisticated image processing algorithms, extract keypoints features with higher accuracy and lower uncertainty across multiple images in an UAS image set. To do this, the naive pre-trained ESRGAN model, with upscaling factor , is taken as an image restoration network. The idea is to explore the effectiveness of the ESRGAN model, trained on a large number of images within several standard image sets, to downgrade the inherent noise and restore the original UAS HR images.
2. Image Super-Resolution
3. Deep Learning for SISR
3.1. DCNN Architectures for SISR
3.2. GAN for SISR
4. Learning Strategies
4.1. Pixel Loss
4.2. Perceptual/Content Loss
4.3. Adversarial Loss
5. Image Quality Metrics
5.1. Peak Signal-to-Noise Ratio (PSNR)
5.2. Structural Similarity (SSIM) Index
5.3. Task-Based Evaluation
6. Methods and Materials
6.1. Methodology
6.2. IQMs for SR Images
6.2.1. Standard IQM methods
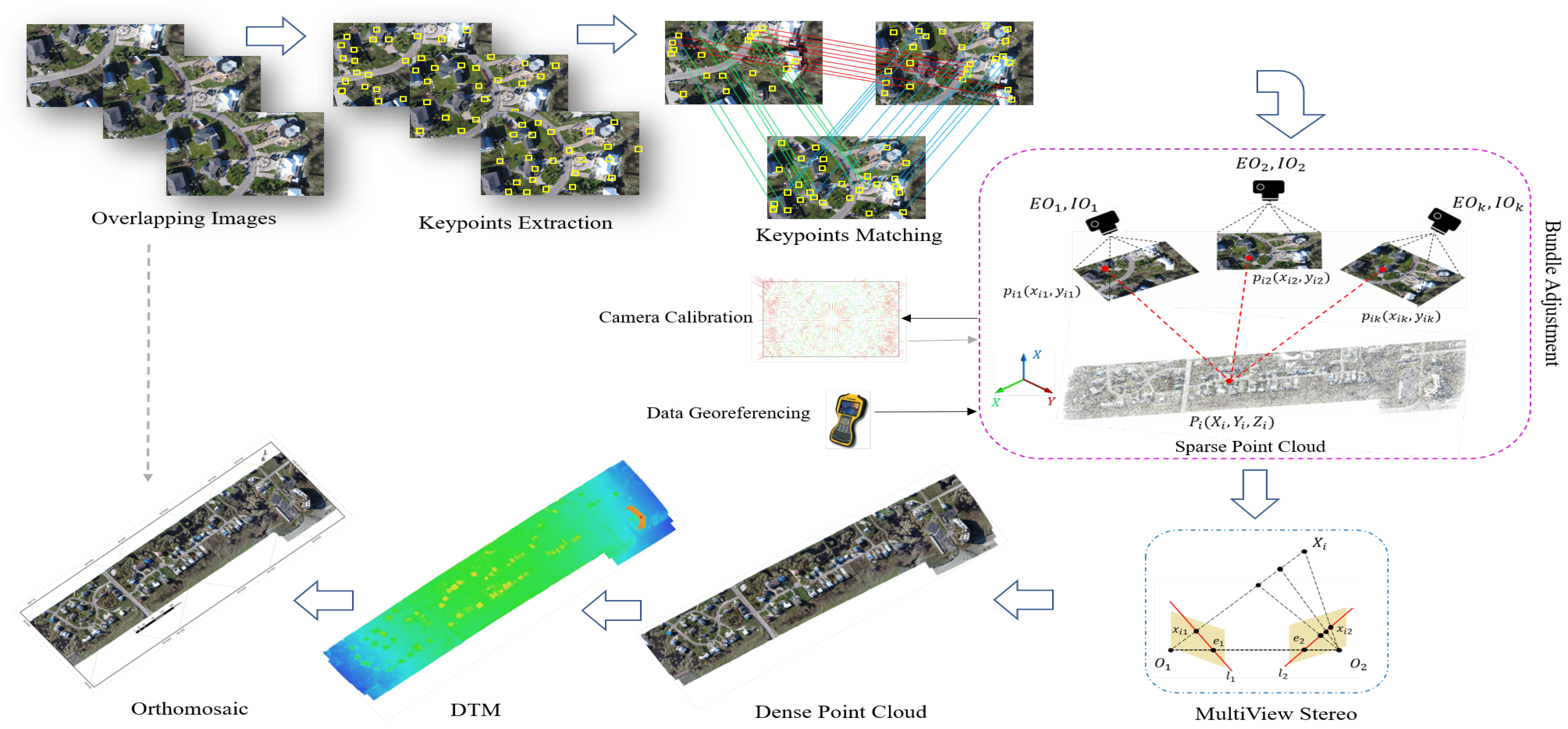
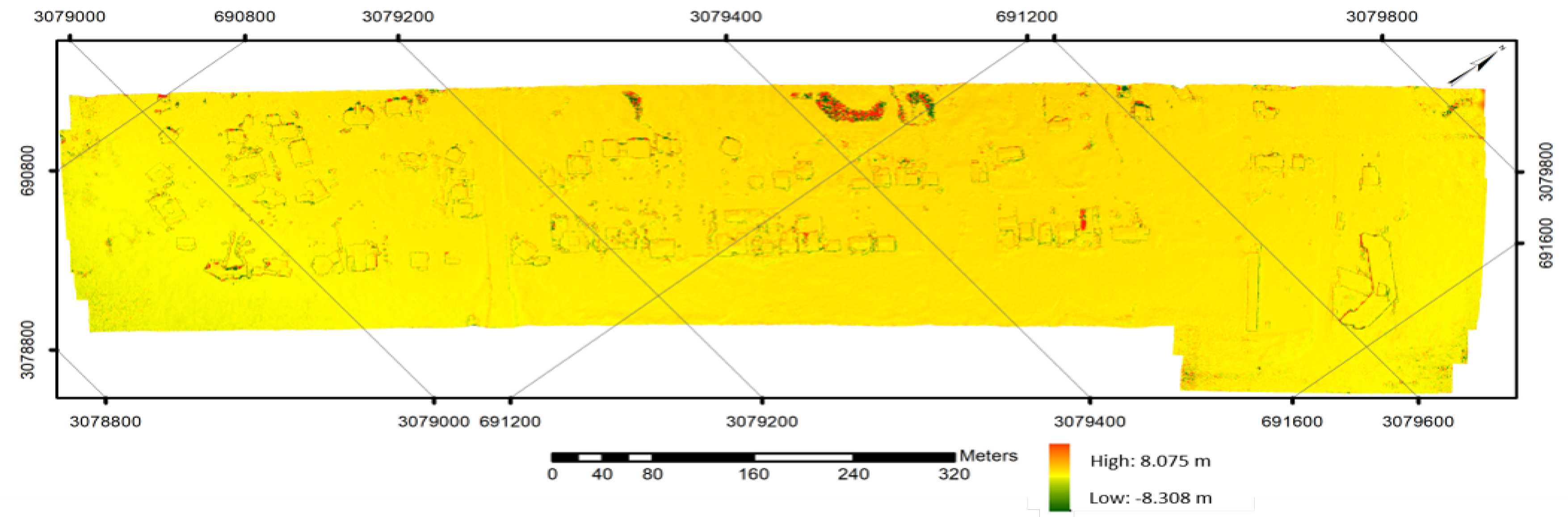
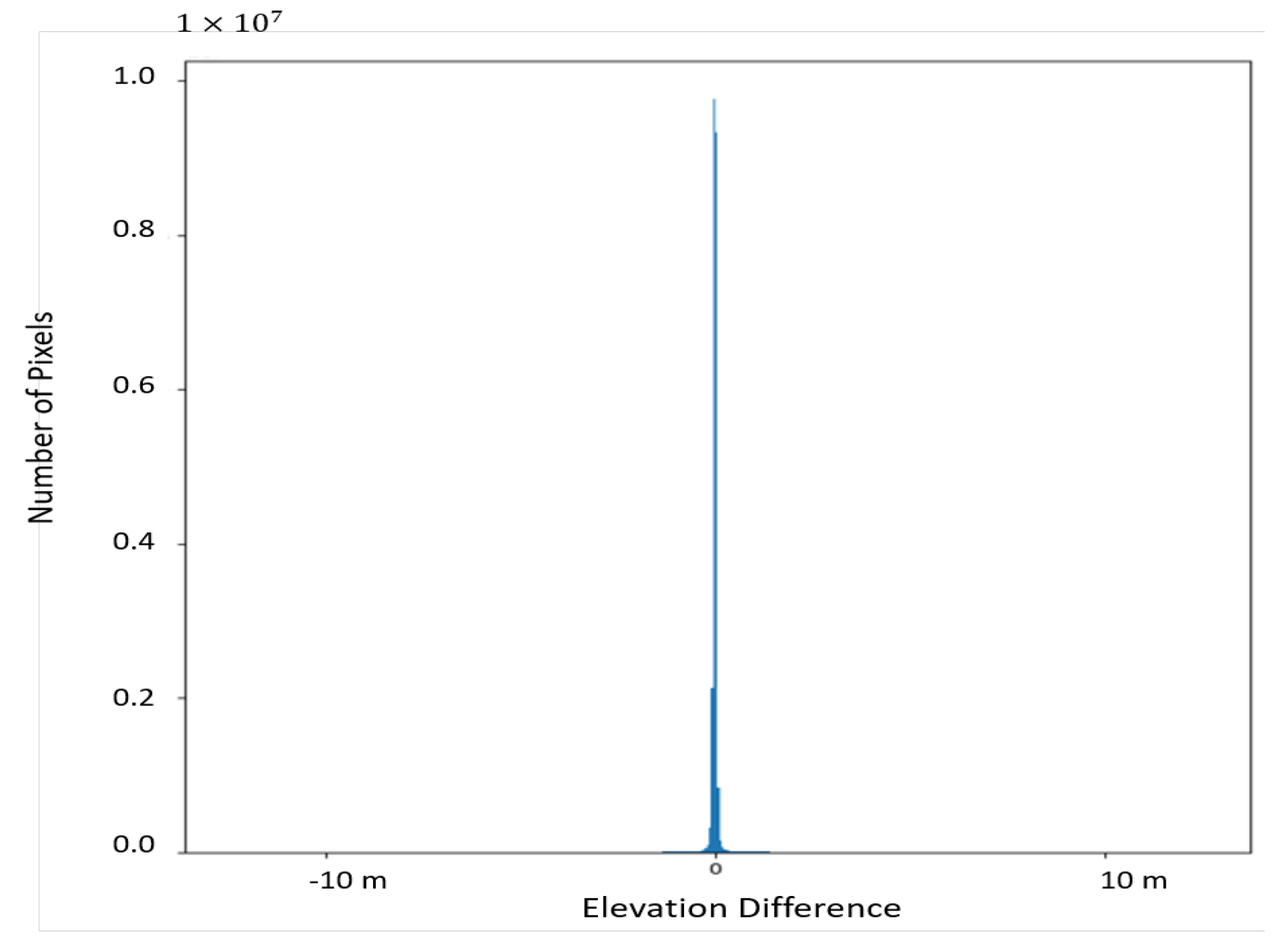
6.2.2. SfM Photogrammetry for Task-Based IQM
6.3. Study Site and Dataset
6.4. Data Preparation and Model Training
7. Results
7.1. Qualitative Assessment
7.2. Quantitative Results
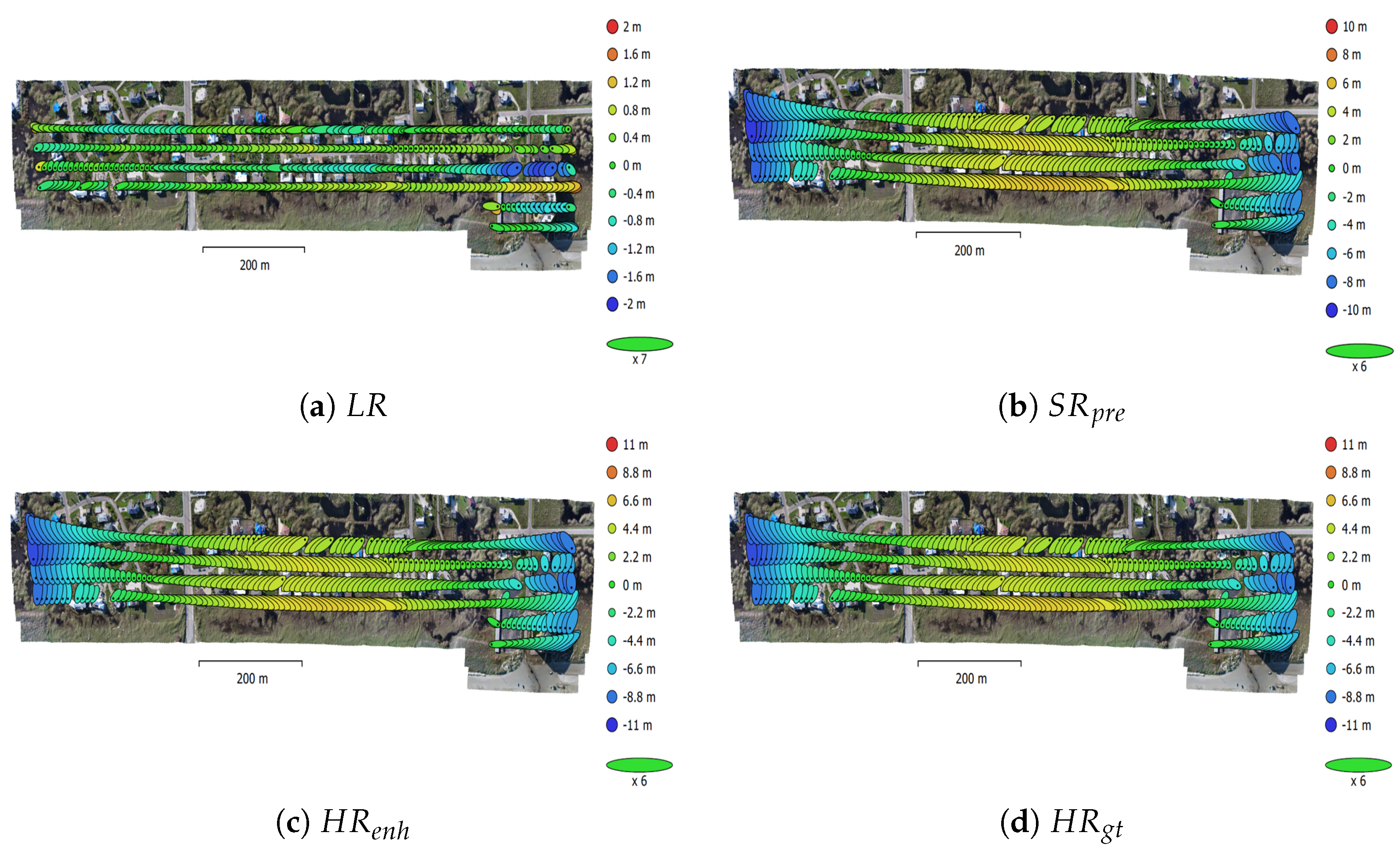
7.3. Task-based IQM and Related Results
8. Discussion
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Aizawa, K.; Komatsu, T.; Saito, T. Acquisition of very high resolution images using stereo cameras. In Proceedings of the Visual Communications and Image Processing’91: Visual Communication, Boston, MA, USA, 10 November 1991; International Society for Optics and Photonics; Volume 1605, pp. 318–328. [Google Scholar]
- Dare, P.M. Shadow analysis in high-resolution satellite imagery of urban areas. Photogramm. Eng. Remote Sens. 2005, 71, 169–177. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, S. Super-Resolution Imaging; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 632. [Google Scholar]
- Al-falluji, R.A.A.; Youssif, A.A.H.; Guirguis, S.K. Single Image Super Resolution Algorithms: A Survey and Evaluation. Int. Adv. Res. Comput. Eng. Technol. 2017, 6, 1445–1451. [Google Scholar]
- Vega, M.; Mateos, J.; Molina, R.; Katsaggelos, A.K. Super-resolution of multispectral images. Comput. J. 2009, 52, 153–167. [Google Scholar]
- Zhang, H.; Zhang, L.; Shen, H. A super-resolution reconstruction algorithm for hyperspectral images. Signal Process. 2012, 92, 2082–2096. [Google Scholar]
- Zhang, H.; Yang, Z.; Zhang, L.; Shen, H. Super-resolution reconstruction for multi-angle remote sensing images considering resolution differences. Remote Sens. 2014, 6, 637–657. [Google Scholar]
- Greenspan, H. Super-resolution in medical imaging. Comput. J. 2009, 52, 43–63. [Google Scholar] [CrossRef]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Task-driven super resolution: Object detection in low-resolution images. arXiv 2018, arXiv:1803.11316. [Google Scholar]
- Sajjadi, M.S.; Scholkopf, B.; Hirsch, M. Enhancenet: Single image super-resolution through automated texture synthesis. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 29 October 2017; pp. 4491–4500. [Google Scholar]
- Bai, Y.; Zhang, Y.; Ding, M.; Ghanem, B. Sod-mtgan: Small object detection via multi-task generative adversarial network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 206–221. [Google Scholar]
- Tuna, C.; Unal, G.; Sertel, E. Single-frame super resolution of remote-sensing images by convolutional neural networks. Int. J. Remote Sens. 2018, 39, 2463–2479. [Google Scholar]
- Yue, L.; Shen, H.; Li, J.; Yuan, Q.; Zhang, H.; Zhang, L. Image super-resolution: The techniques, applications, and future. Signal Process. 2016, 128, 389–408. [Google Scholar]
- Borman, S.; Stevenson, R.L. Super-resolution from image sequences-a review. In Proceedings of the 1998 Midwest Symposium on Circuits and Systems, Notre Dame, IN, USA, 12 August 1998; pp. 374–378. [Google Scholar]
- Hardie, R.C.; Barnard, K.J.; Armstrong, E.E. Joint MAP registration and high-resolution image estimation using a sequence of undersampled images. IEEE Trans. Image Process. 1997, 6, 1621–1633. [Google Scholar] [PubMed]
- Tipping, M.E.; Bishop, C.M. Bayesian image super-resolution. Adv. Neural Inf. Process. Syst. 2003, 15, 1303–1310. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27 June 2016; pp. 770–778. [Google Scholar]
- Pashaei, M.; Starek, M.J. Fully Convolutional Neural Network for Land Cover Mapping In A Coastal Wetland with Hyperspatial UAS Imagery. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 6106–6109. [Google Scholar]
- Pashaei, M.; Kamangir, H.; Starek, M.J.; Tissot, P. Review and Evaluation of Deep Learning Architectures for Efficient Land Cover Mapping with UAS Hyper-Spatial Imagery: A Case Study Over a Wetland. Remote Sens. 2020, 12, 959. [Google Scholar] [CrossRef]
- Kamangir, H.; Rahnemoonfar, M.; Dobbs, D.; Paden, J.; Fox, G. Deep hybrid wavelet network for ice boundary detection in radra imagery. In Proceedings of the 2018 the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 3449–3452. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.H.; Liao, Q. Deep learning for single image super-resolution: A brief review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef]
- Liebel, L.; Körner, M. Single-image super resolution for multispectral remote sensing data using convolutional neural networks. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 883–890. [Google Scholar]
- Wang, C.; Liu, Y.; Bai, X.; Tang, W.; Lei, P.; Zhou, J. Deep residual convolutional neural network for hyperspectral image super-resolution. In Proceedings of the International Conference on Image and Graphics, Shanghai, China, 2–4 July 2017; pp. 370–380. [Google Scholar]
- Haut, J.M.; Fernandez-Beltran, R.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Pla, F. A new deep generative network for unsupervised remote sensing single-image super-resolution. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6792–6810. [Google Scholar] [CrossRef]
- Arun, P.V.; Herrmann, I.; Budhiraju, K.M.; Karnieli, A. Convolutional network architectures for super-resolution/sub-pixel mapping of drone-derived images. Pattern Recognit. 2019, 88, 431–446. [Google Scholar] [CrossRef]
- Burdziakowski, P. Increasing the Geometrical and Interpretation Quality of Unmanned Aerial Vehicle Photogrammetry Products using Super-Resolution Algorithms. Remote Sens. 2020, 12, 810. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 2, 2672–2680. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Dougherty, G. Digital Image Processing for Medical Applications; Cambridge University Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Park, S.C.; Park, M.K.; Kang, M.G. Super-resolution image reconstruction: A technical overview. IEEE Signal Process. Mag. 2003, 20, 21–36. [Google Scholar] [CrossRef]
- Chang, H.; Yeung, D.Y.; Xiong, Y. Super-resolution through neighbor embedding. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 1. [Google Scholar]
- Goto, T.; Fukuoka, T.; Nagashima, F.; Hirano, S.; Sakurai, M. Super-resolution System for 4K-HDTV. In Proceedings of the 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; pp. 4453–4458. [Google Scholar]
- Peled, S.; Yeshurun, Y. Superresolution in MRI: Application to human white matter fiber tract visualization by diffusion tensor imaging. Magn. Reson. Med. Off. J. Int. Soc. Magn. Reson. Med. 2001, 45, 29–35. [Google Scholar]
- Shi, W.; Caballero, J.; Ledig, C.; Zhuang, X.; Bai, W.; Bhatia, K.; de Marvao, A.M.S.M.; Dawes, T.; O’Regan, D.; Rueckert, D. Cardiac image super-resolution with global correspondence using multi-atlas patchmatch. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Nagoya, Japan, 22–26 September 2013; pp. 9–16. [Google Scholar]
- Thornton, M.W.; Atkinson, P.M.; Holland, D. Sub-pixel mapping of rural land cover objects from fine spatial resolution satellite sensor imagery using super-resolution pixel-swapping. Int. J. Remote Sens. 2006, 27, 473–491. [Google Scholar] [CrossRef]
- Gunturk, B.K.; Batur, A.U.; Altunbasak, Y.; Hayes, M.H.; Mersereau, R.M. Eigenface-domain super-resolution for face recognition. IEEE Trans. Image Process. 2003, 12, 597–606. [Google Scholar] [PubMed]
- Zhang, L.; Zhang, H.; Shen, H.; Li, P. A super-resolution reconstruction algorithm for surveillance images. Signal Process. 2010, 90, 848–859. [Google Scholar]
- Yang, C.Y.; Huang, J.B.; Yang, M.H. Exploiting self-similarities for single frame super-resolution. In Proceedings of the Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010; pp. 497–510. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1874–1883. [Google Scholar]
- Wang, Z.; Chen, J.; Hoi, S.C. Deep learning for image super-resolution: A survey. arXiv 2019, arXiv:1902.06068. [Google Scholar] [CrossRef]
- Yang, C.Y.; Ma, C.; Yang, M.H. Single-image super-resolution: A benchmark. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 372–386. [Google Scholar]
- Baker, S.; Kanade, T. Limits on super-resolution and how to break them. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1167–1183. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi-Morel, M.L. Low-Complexity Single-Image Super-Resolution Based on Nonnegative Neighbor Embedding. 2012. Available online: http://people.rennes.inria.fr/Aline.Roumy/publi/12bmvc_Bevilacqua_lowComplexitySR.pdf (accessed on 24 April 2020).
- Yang, J.; Wang, Z.; Lin, Z.; Cohen, S.; Huang, T. Coupled dictionary training for image super-resolution. IEEE Trans. Image Process. 2012, 21, 3467–3478. [Google Scholar] [CrossRef]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European conference on computer vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European conference on computer vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 391–407. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image super-resolution using dense skip connections. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4799–4807. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–10 February 2017. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 624–632. [Google Scholar]
- Bruhn, A.; Weickert, J.; Schnörr, C. Lucas/Kanade meets Horn/Schunck: Combining local and global optic flow methods. Int. J. Comput. Vis. 2005, 61, 211–231. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 694–711. [Google Scholar]
- Bruna, J.; Sprechmann, P.; LeCun, Y. Super-resolution with deep convolutional sufficient statistics. arXiv 2015, arXiv:1511.05666. [Google Scholar]
- Gatys, L.; Ecker, A.S.; Bethge, M. Texture synthesis using convolutional neural networks. Adv. Neural Inf. Process. Syst. 2015, 1, 262–270. [Google Scholar]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. Image style transfer using convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2414–2423. [Google Scholar]
- Bulat, A.; Tzimiropoulos, G. Super-FAN: Integrated facial landmark localization and super-resolution of real-world low resolution faces in arbitrary poses with GANs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 109–117. [Google Scholar]
- Wang, X.; Yu, K.; Dong, C.; Change Loy, C. Recovering realistic texture in image super-resolution by deep spatial feature transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 606–615. [Google Scholar]
- Yuan, Y.; Liu, S.; Zhang, J.; Zhang, Y.; Dong, C.; Lin, L. Unsupervised image super-resolution using cycle-in-cycle generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 701–710. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Channappayya, S.S.; Bovik, A.C.; Caramanis, C.; Heath, R.W. SSIM-optimal linear image restoration. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 765–768. [Google Scholar]
- Sheikh, H.R.; Sabir, M.F.; Bovik, A.C. A statistical evaluation of recent full reference image quality assessment algorithms. IEEE Trans. Image Process. 2006, 15, 3440–3451. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at signal fidelity measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar]
- Dai, D.; Wang, Y.; Chen, Y.; Van Gool, L. Is image super-resolution helpful for other vision tasks? In Proceedings of the 2016 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Placid, NY, USA, 7–9 March 2016; pp. 1–9. [Google Scholar]
- Fookes, C.; Lin, F.; Chandran, V.; Sridharan, S. Evaluation of image resolution and super-resolution on face recognition performance. J. Vis. Commun. Image Represent. 2012, 23, 75–93. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Z.; Cheng, C.W.; Hsu, W.H.; Qiao, Y.; Liu, W.; Zhang, T. Super-identity convolutional neural network for face hallucination. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 183–198. [Google Scholar]
- Chen, Y.; Tai, Y.; Liu, X.; Shen, C.; Yang, J. Fsrnet: End-to-end learning face super-resolution with facial priors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2492–2501. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Jolicoeur-Martineau, A. The relativistic discriminator: A key element missing from standard GAN. arXiv 2018, arXiv:1807.00734. [Google Scholar]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar]
- Snavely, N. Scene reconstruction and visualization from internet photo collections: A survey. IPSJ Trans. Comput. Vis. Appl. 2011, 3, 44–66. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Furukawa, Y.; Hernández, C. Multi-view stereo: A tutorial. Found. Trends Comput. Graph. Vis. 2015, 9, 1–148. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? Adv. Neural Inf. Process. Syst. 2014, 2, 3320–3328. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in PyTorch. 2017. Available online: https://openreview.net/pdf?id=BJJsrmfCZ (accessed on 24 April 2020).
- Agustsson, E.; Timofte, R. Ntire 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 126–135. [Google Scholar]
- Timofte, R.; Agustsson, E.; Van Gool, L.; Yang, M.H.; Zhang, L. Ntire 2017 challenge on single image super-resolution: Methods and results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 114–125. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Iccv Vancouver, Vancouver, BC, Canada, 7–14 July 2001. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Blau, Y.; Mechrez, R.; Timofte, R.; Michaeli, T.; Zelnik-Manor, L. The 2018 PIRM challenge on perceptual image super-resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Agisoft. Metashape—Photogrammetric Processing of Digital Images and 3D Spatial Data Generation. 2019. Available online: https://www.agisoft.com/ (accessed on 24 April 2020).
- Fraser, C.S. Digital camera self-calibration. ISPRS J. Photogramm. Remote Sens. 1997, 52, 149–159. [Google Scholar] [CrossRef]
- Remondino, F.; Fraser, C. Digital camera calibration methods: Considerations and comparisons. Int. Arch. Photogramm. Remote Sens. 2006, 36, 266–272. [Google Scholar]

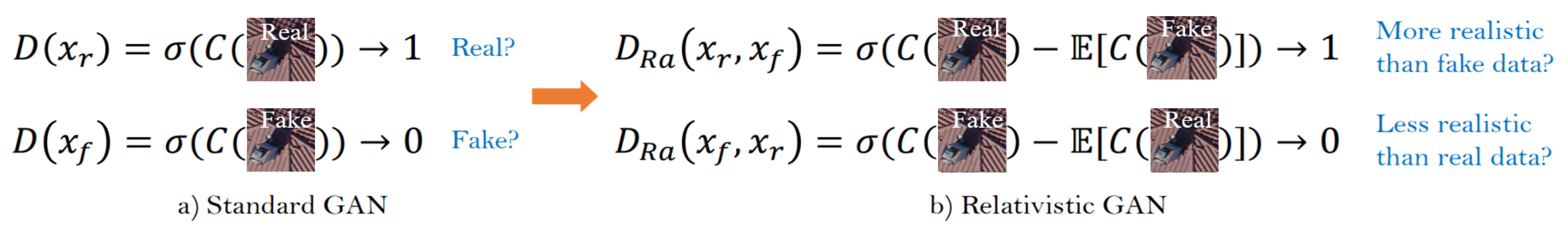




| Dense Block | RRDB | Learning Rate | Adam Optimization Parameters |
|---|---|---|---|
| 23 | , , |
| Image Set | Lowest PSNR/SSIM | Highest PSNR/SSIM | Mean PSNR/SSIM |
|---|---|---|---|
| Parameters | ||||
|---|---|---|---|---|
| −1.7070 | −2.8148 | −1.6030 | ||
| −1.0218 | −1.4783 | −1.0199 | ||
| Image Set | ||||
|---|---|---|---|---|
| Max reprojection error (pix) | ||||
| Reprojection error (pix) | ||||
| X error (m) | ||||
| Y error (m) | ||||
| Z error (m) | ||||
| error (m) | ||||
| Total error (m) |
| Parameters | to | to | ||||
|---|---|---|---|---|---|---|
| Num. of images | 440 | 440 | 440 | 440 | ||
| Flying altitude (m) | 106 | 106 | 107 | 106 | ||
| Tie points (points) | 1,398,877 | 11,051,665 | 8,268,475 | 11,630,227 | ||
| Dense cloud (points) | 1,805,966 | 31,041604 | 31,052,606 | 31,940,817 | ||
| Point density (points/m) | ||||||
| DSM resolution (cm/pix) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pashaei, M.; Starek, M.J.; Kamangir, H.; Berryhill, J. Deep Learning-Based Single Image Super-Resolution: An Investigation for Dense Scene Reconstruction with UAS Photogrammetry. Remote Sens. 2020, 12, 1757. https://doi.org/10.3390/rs12111757
Pashaei M, Starek MJ, Kamangir H, Berryhill J. Deep Learning-Based Single Image Super-Resolution: An Investigation for Dense Scene Reconstruction with UAS Photogrammetry. Remote Sensing. 2020; 12(11):1757. https://doi.org/10.3390/rs12111757
Chicago/Turabian StylePashaei, Mohammad, Michael J. Starek, Hamid Kamangir, and Jacob Berryhill. 2020. "Deep Learning-Based Single Image Super-Resolution: An Investigation for Dense Scene Reconstruction with UAS Photogrammetry" Remote Sensing 12, no. 11: 1757. https://doi.org/10.3390/rs12111757
APA StylePashaei, M., Starek, M. J., Kamangir, H., & Berryhill, J. (2020). Deep Learning-Based Single Image Super-Resolution: An Investigation for Dense Scene Reconstruction with UAS Photogrammetry. Remote Sensing, 12(11), 1757. https://doi.org/10.3390/rs12111757