A Hierarchical Clustering Method for Land Cover Change Detection and Identification

Abstract

A method to detect abrupt land cover changes using hierarchical clustering of multi-temporal satellite imagery was developed. The Autochange method outputs the pre-change land cover class, the change magnitude, and the change type. Pre-change land cover information is transferred to post-change imagery based on classes derived by unsupervised clustering, enabling using data from different instruments for pre- and post-change. The change magnitude and change types are computed by unsupervised clustering of the post-change image within each cluster, and by comparing the mean intensity values of the lower level clusters with their parent cluster means. A computational approach to determine the change magnitude threshold for the abrupt change was developed. The method was demonstrated with three summer image pairs Sentinel-2/Sentinel-2, Landsat 8/Sentinel-2, and Sentinel-2/ALOS 2 PALSAR in a study area of 12,372 km² in southern Finland for the detection of forest clear cuts and tested with independent data. The Sentinel-2 classification produced an omission error of 5.6% for the cut class and 0.4% for the uncut class. Commission errors were 4.9% for the cut class and 0.4% for the uncut class. For the Landsat 8/Sentinel-2 classifications the equivalent figures were 20.8%, 0.2%, 3.4%, and 1.6% and for the Sentinel-2/ALOS PALSAR classification 16.7%, 1.4%, 17.8%, and 1.3%, respectively. The Autochange algorithm and its software implementation was considered applicable for the mapping of abrupt land cover changes using multi-temporal satellite data. It allowed mixing of images even from the optical and synthetic aperture radar (SAR) sensors in the same change analysis.

1. Introduction

A major benefit of space-borne observations compared to other data collection methods is the possibility to acquire information at frequent intervals without dedicated data collection campaigns. Repeated data acquisition enables monitoring of change. The recognized benefit of satellite observations in detecting and monitoring change is even more evident now that the European Sentinel satellites of the Copernicus Program provide global imagery with spatial resolution up to 10 m and higher than weekly image acquisition frequencies. The identical Sentinel 2A and Sentinel 2B acquire images at five-day intervals at the equator and at even higher frequency at higher latitudes [1].

Remote sensing applications for land cover change monitoring cover a wide variety of uses. Examples taken from the large number of published papers include land cover [2], forest cover [3], forest pest damage [4], forest cutting and deforestation [5,6,7], forest fire, [8,9,10], urban change [11], flood [12], and crop monitoring [13].

The simplest way to monitor change is to compare individual maps [3,7,14]. The benefit of the map comparison approach is its simplicity. With this approach, it is possible to utilize different input data to produce maps for different purposes. Monitoring complicated change combinations, such as changes between several land cover classes, is also possible. A drawback of the approach is the accumulation of map errors, leading to loss of statistical significance of derived change information [15]. However, map comparison is a commonly used method in Earth observation based change detection. In the activity data reporting of the REDD+ (Reduction of Emissions from Deforestation and forest Degradation), changes between land use classes are reported as a matrix [16]. Use of individual maps from different points of time to generate the matrices is a realistic alternative for REDD+ for practical reasons. However, the risk for accumulated errors is emphasized when the number of classes is high.

Alternatively, the change can be detected by applying direct change detection to remote sensing data using spectral or backscattering features of bi-temporal or time series data [5,17,18,19,20,21]. These approaches have also been combined [22]. The direct change detection methods can also be divided into pixel and object-based categories [23].

Direct change detection methods can be further divided into composite analyses in which the multi-temporal data set is merged for change detection, either to make a classification or to apply image transformation to extract the change, to image differencing and rationing, or to identify changes in the residuals of a regression model that shows the general trend [5,19]. Spectral transformations of multi-temporal data have been shown to be a feasible approach for visual interpretation of change. Methods that apply transformations include principal component analysis, Kauth-Thomas transformation, Gramm-Schmidt orthogonalization, and MAD (Multivariate Alteration Detection) transformation [5,24,25,26].

Direct classification of merged bi- or multi-temporal images can principally be used to output the change classes and the thematic classes representing the target area in general. The drawback of the method is that the actual change can be obscured by other variability in the images. For direct classification of merged multi-date imagery and some other approaches using merged multi-temporal data, such as MAD transformation, principal component analysis may be most applicable to bi-temporal imagery or a low number of multi-temporal images because interpretation of the results can become difficult with long time ranges and large numbers of images.

Time series approaches have become common for change monitoring due to increased image repositories and computing power in the cloud. These methods include TimeSAT, BFAST (Breaks for Additive Seasonal and Trend), LandTrendr, CCDC (Continuous Change Detection and Classification) and COLD (COntinuous monitoring of Land Disturbance) [20,27,28,29,30,31]. Anomalies in the modeled long-term trajectory of spectral reflectance or another feature indicate an abrupt land cover change such as fire or cutting. These methods can be applicable to additionally monitoring general trends in vegetation greenness and biomass, but simultaneous vegetative succession, noise in the multi-temporal data and disturbances can lead to results with no clear information content, which appears as increasing omission and commission errors in predicting the variable of interest [31].

A complex CCDC change detection method for Landsat data based on modeling the annual trajectory of reflectance for each multi-temporal pixel using a sinusoidal model was presented in [20]. The method required at least 15 reflectance-calibrated multi-temporal images, of which the three most recent are used for change detection. Change was identified by analyzing deviations from the modeled spectral trajectory. The method was further developed to reduce commission error [31].

Sentinel-1 time series data supported by multi-temporal Landsat and ALOS-2 PALSAR-2 (Advanced Land Observing Satellite; Phased Array type L-band Synthetic Aperture Radar) imagery were applied to detect forest clear cuttings on a flat terrain using a supervised method. Probability density functions for one feature representing each image type were computed for the two classes based on forest and non-forest reference data sites. The probability for a pixel membership to the two classes was computed using all three image types when they were available. The final change likelihood was computed from the results of all three image data sources without merging different image types. Although longer time series were used, actual change detection was based on bi-temporal data [32].

The time series methods referred to above require radiometric image calibration through a spectral index or atmospherically corrected data [30]. They often apply a single feature, such as Normalized Difference Vegetation Index (NDVI). Furthermore, deviation from the modeled trajectory may have to be substantial compared to normal noise before it can be designated as a true change.

The most commonly used approaches require that the input features for change detection represent the same wavelength area and that either absolute or relative calibration has been conducted for multi-temporal spectral features. Even a relatively small mismatch in the calibration can cause changed areas to appear unchanged and stable areas to appear changed [5]. Mechanical image standardization easily leads to unsuccessful matching as one of the images may have some remaining clouds even after cloud masking, or the images can represent different seasons, which affects the reflectance.

A clustering method called Autochange attempted to combine change detection, change type identification and land cover classification using bi-temporal data [33]. The method required availability of bi-temporal data with same wavelength bands and same spatial resolution. The corresponding bands with the bi-temporal data had to be inter-calibrated. This method gave good results if no clouds or seasonal aspect affected calibration. If the calibration was unsuccessful, even the most dramatic changes such as clear cuts could remain undetected but unchanged areas could appear as changes. The problems with the method were similar to those with using difference bands for change mapping.

The method presented in this paper aims at removing the serious problems with the original method. It also attempts to consider undesirable characteristics that are associated with other methods discussed above; particularly the need to restrict to the same sensor in time series and the accuracy decrease resulting from the noise in the absolute image calibration of multi-temporal data. Our objective was to develop a method that could:

• Combine data from different bands and sensors in the same classification including optical and radar data;
• Be insensitive to the relative or absolute calibration of multi-temporal data or compressing images into vegetation indices or other single spectral features;
• Provide information on the type of change;
• Restrict the change analysis to selected land cover types.

The paper focuses on the description of the algorithm that is meant for the detection of abrupt changes in general. Its application is demonstrated for clear-cut classifications between bi-temporal Sentinel-2, Landsat 8 and Sentinel-2, and Sentinel-2 and ALOS PALSAR data. Forest clear cuts were selected for the demonstration because reliable data were available for the assessment of classification performance. We kept the Autochange name for the method although the logic of the algorithm is different.

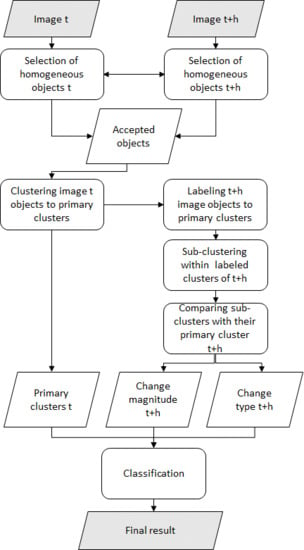
2. Algorithm

2.1. Computation of Change Features

It is assumed that the majority of the image area does not include changes of interest to the user. The algorithm is described in this paper for bi-temporal data, but it can also be applied to time series by applying it continuously to image pairs, as shown in [34].

A sample of pixel groups is selected for the clustering to reduce computation time (Figure 1). The sample consists of mean spectral vectors of groups of pixels representing relatively homogeneous ground targets. The homogeneity is tested by computing the standard deviation vector (alternatively coefficient of variation) of each n x n pixel group in both images. A sample of m groups with lowest non-zero deviations is selected for the clustering. The zero deviation groups are rejected because they can represent a multiplied single pixel due to resampling. Use of the standard deviation as a criterion favors low-reflectance groups that typically represent mature forests. They are over-represented in the sample, which has increased the performance of the algorithm in the detection of forest cuts. The homogeneity test has to be passed in both images before a pixel group is accepted to the clustering process.

Clustering is performed by k-means on the selected homogeneous pixel groups (later observations) of the pre-change image to compose primary clusters (image representing the state at the start of monitoring). The image spectral bands are standardized before clustering because the k-means algorithm uses the Euclidean distance and is thus sensitive to the dynamic range of a spectral band (Figure 1). The cluster seeds that initiate the clustering are selected automatically in an iterative process so that they represent the whole spectral domain. The first observation on the observation list is taken as a seed. The next observation is accepted as a seed if its Euclidean distance to the selected seed is larger than a parameter that is automatically defined by the number of spectral bands applied for change detection. The distance of a seed candidate has to exceed the distance criterion to all already selected seeds.

The clusters from the pre-change image are sorted by their ‘biomass’ index (BM). We have used as the index the reflectance of the red band that has a relatively high correlation with the biomass (Equation (1)) [35]. After the operation, the cluster with the highest BM value has the smallest cluster number and the lowest index has the highest cluster number.

$$\begin{array}{c}a\left[i\right]=\frac{1}{{\sigma }_i},i=1\dots n\\ b\left[i\right]=-\frac{{\mu }_i}{{\sigma }_i},i=1\dots n\\ y_k=x_k\ast a\left[k\right]+b\left[k\right]=\frac{x_k}{{\sigma }_k}-\frac{{\mu }_k}{{\sigma }_k}\\ y_k=scaledintensityofapixelinchannelk\\ x_k=intensityofapixeltobescaledinchannelk\\ {\mu }_k=intensitymeaninchannelk\\ {\sigma }_k=standarddeviationinchannelk\end{array}$$

(1)

$$\begin{array}{c}bmi\\ \mathrm{BM}=\{\begin{array}{cc}\hfill \mathrm{integer}\left(100\ast \frac{maxv-re{d}_e}{maxv-minv}\right),& re{d}_e\le maxv\hfill \\ \hfill 0,& re{d}_e>maxv\hfill \end{array}\\ Limitsforscaledredintensity,\pm 3standarddeviations:\\ maxv=3.0\\ minv=-3.0\\ re{d}_e=scaledredintensityofpixelinearlierimage\end{array}$$

(2)

The clustering result for the primary clusters from the pre-change image is used for two purposes: to acquire general information about the land cover before the changes, and to set the initial state for the second level clustering of the post-change image (image representing the state at the end of monitoring).

The observations of the post-change image are labeled with the cluster numbers of the primary clusters without performing a new clustering. The spectral intensity distribution of a primary cluster will consequently become heterogeneous if a change has occurred between the moments of acquisition of the two images.

A secondary clustering to n sub-clusters is performed within each labeled primary cluster of the post-change image. This extracts the observations that represent change to specific secondary clusters.

The Euclidean distance between each secondary cluster and its post-change primary cluster is computed as the length of the spectral mean vector and represents the magnitude of change (Equation (3)). The change magnitude does not consider the type of change, i.e., whether the reflectance has increased or decreased due to change.

Change magnitude (CM):

$$\begin{array}{c}CM=\Vert x^P-x^S\Vert \ast \frac{100}{\sqrt{n}}\\ x^P=meanvectorofthepost-changeimageprimarycluster\\ x^S=meanvectorofthepost-changeimagesecondarycluster\\ n=numberofbandsinthelaterimage\end{array}$$

(3)

A post-change image primary cluster is heterogeneous as it also includes observations that represent change, as discussed above. Although the change is assumed to represent only a small fraction of all the cluster observations, it affects the mean of the primary cluster. The change magnitude is therefore computed iteratively. The observations that represent a secondary cluster with the greatest change magnitude are removed from its primary cluster and the change magnitudes between the secondary clusters and the primary clusters are re-computed.

The CM gets a value of 100 if the Euclidean distance of a secondary cluster to its primary cluster of each spectral band is as large as the standard deviation of the CM band. The CM value is also 100 if the post-change image has two bands and the distance is zero on one band and as large as two standard deviations on the other band, for instance.

The change type is computed using two spectral features. One feature is the BM, i.e., the intensity of a spectral feature that is considered to correlate with biomass change.

The other feature is the Normalized Difference Vegetation Index or NDVI. The near infrared band of the NDVI is sensitive to the existence of green vegetation and exposed soil. In addition, particularly in boreal forest, the near-infrared reflectance of broadleaved trees is typically 1.5 to 2 times higher than conifer reflectance [36] making NDVI a good indicator of the proportion of broadleaf cover. The NDVI is effective to characterize the type of change, particularly removal of broadleaved trees. Its value also usually decreases in a clear cutting even if bare soil is not exposed.

The red and NDVI differences between the primary cluster and secondary clusters produce four change types (Figure 2):

• BM decrease (red increase) & NDVI increase: can indicate, e.g., conifer tree removal with remaining broad-leaved trees and grasses
• BM decrease & NDVI decrease: typical change due to clear-cuts
• BM increase & NDVI increase: biomass growth
• BM increase & NDVI decrease: biomass growth with associated decrease in broadleaved trees or shrubs and grasses. Such change can be associated with silvicultural operations on conifer regeneration sites, for instance.

The above change type definitions apply best in the boreal forest zone. However, NDVI change and red reflectance change should also characterize changes in other global locations. The change types do not take into consideration the magnitude of change, but any observation involved in the clustering is allocated to one of the four possible change types.

The outputs from processing the sampled observations are:

• Primary cluster mean intensity vector from the pre-change image;
• Primary and secondary cluster mean intensity vectors from the post-change image, enabling computation of change magnitude;
• Primary and secondary cluster BM and NDVI means from the post-change image, enabling computation of change type.

Using these statistics, each pixel of the pre-change image is classified based on the primary clusters. From the post-change image, the change magnitude and type are computed. Thus, the principal output is a three-band image.

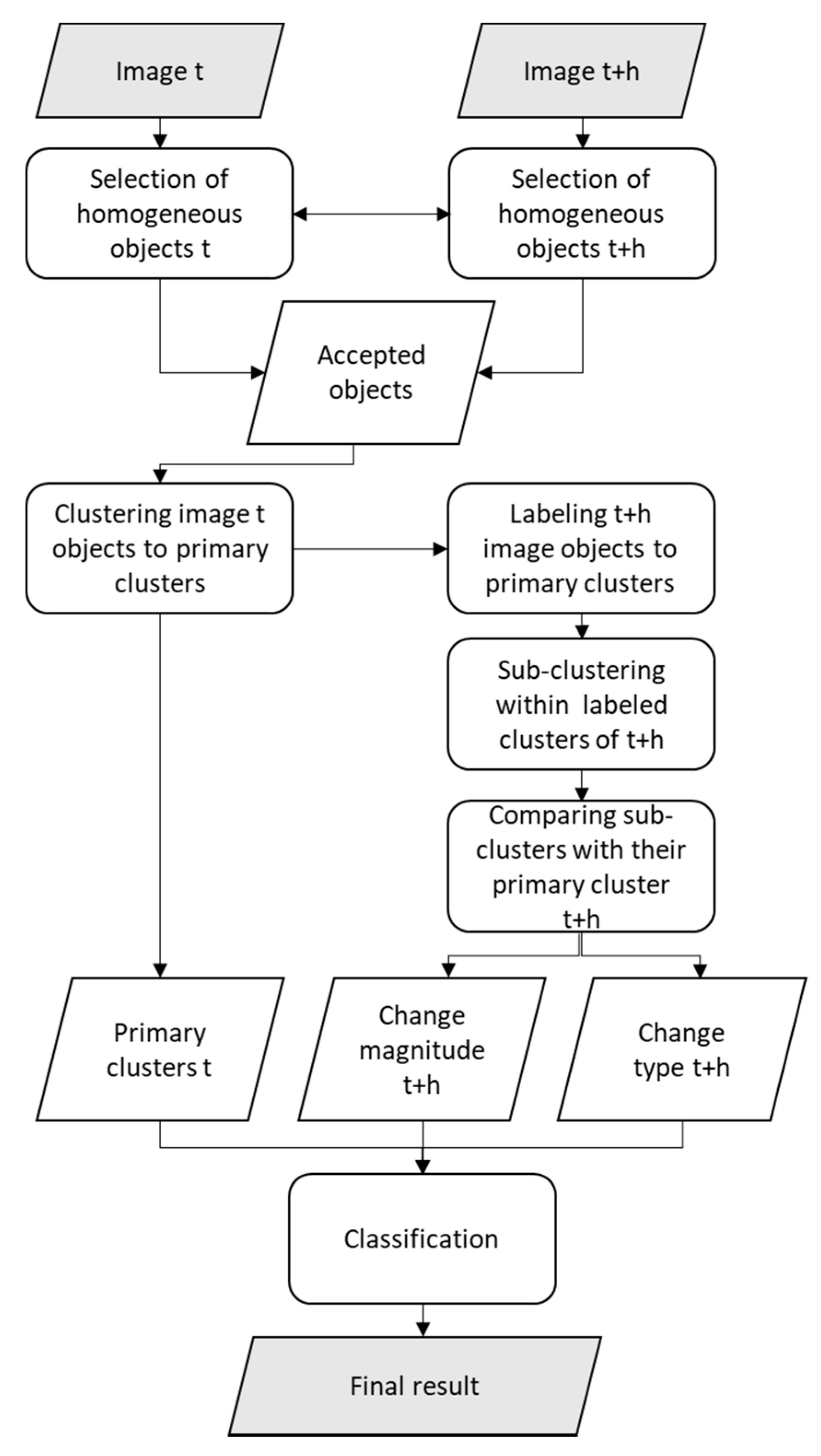
2.2. Compilation of Change Classification Output

The final change classification is compiled by applying simple logical operations to the three-band output image. For instance, accepting only primary clusters from the pre-change image that reflect mature forest, change types that indicate biomass decrease, and selecting a threshold for change magnitude produces mapping of clear cuts.

For the definition of a threshold for change magnitude, we developed an automatic approach. This method is based on analyzing change magnitude histogram. For the practical reasons the histogram was transformed to cumulative format.

The histograms of Change Magnitude ($CM$) output features are multimodal. $CM$ = 0 is not possible as this would mean that the mean vector of the labeled primary cluster at t+h would be identical to its sub-cluster. Thus, values $CM>0$ are used for defining the threshold for cuttings.

The first mode with low $CM$ values typically represents the ‘unchanged’ class, whereas the last mode represents a clearly ‘changed’ class. Somewhere between the first and last mode is an optimal threshold, $C{M}_0$, which is optimal in the sense that the pixels with smaller magnitudes practically belong to the unchanged class, pixels with larger magnitudes represent the changed classes, and mixing of these classes is minimal. The threshold may not be unique due to the multimodality of $CM$.

We defined an algorithm to identify candidates for the thresholds based on the slopes $s_i$ of the standardized cumulative histogram $F$ of change magnitudes (Equation (4)). Cumulative histograms were computed because analysis of the slopes was more convenient to perform with these than with the original histograms. The function $F$ is considered to be a piece-wise linear function between the change magnitude values $c{m}_i$, $i=1,\dots ,N$, which occur in the pixel data. If the standardized frequencies at $c{m}_i$ are denoted as $f_i$, $i=1,\dots ,N$, the linearly interpolated cumulative histogram $F$ is defined at all values $cm$ as

$$\begin{array}{c}F\left(0\right)=0,\\ F\left(cm\right)=\left(\frac{cm}{c{m}_1}\right)f_1,\mathrm{if}cm\le c{m}_1,\\ F\left(cm\right)=f_1+\cdots +f_{i-1}+\left(\frac{cm-c{m}_{i-1}}{c{m}_i-c{m}_{i-1}}\right)f_i,\mathrm{if}c{m}_{i-1}\le cm\le c{m}_i,\\ \mathrm{and}F\left(cm\right)=1,\mathrm{if}cm>c{m}_N.\mathrm{With}\mathrm{a}\mathrm{shorthand}\mathrm{notation}{F}_i=F\left(c{m}_i\right)\mathrm{the}\mathrm{slopes}{s}_i\mathrm{are}\mathrm{then}\mathrm{defined}\mathrm{as}\\ s_i=\frac{F_{i+1}-F_i}{c{m}_{i+1}-c{m}_i},\end{array}$$

(4)

where $c{m}_{i+1}$ is the $\left(i+1\right)$ ^th change magnitude value in which $f_{i+1}=F_{i+1}-F_i>0$. Low CM frequencies between the local modes of the original histogram make the slope of the cumulative histogram relatively flat. When the change is very distinct, the frequency at some intensity levels of $CM$ can be 0, which results in completely flat local parts in the cumulative histogram $F$. We search for the flat or relatively flat locations of the histogram (Figure 3).

Since the slopes are positive with highly variable values, we made a logarithmic transformation of the slope values to facilitate their comparison. Even if $C{M}_0>100$ at the optimal threshold for change and no change, the side-effects of the standardization and the presence of noise in the data can provide a candidate estimate of the optimal threshold $C{M}_0$ with value $<100$. Thus, we focused on the limited interval $A\le CM\le B$, where $A\mathrm{and} B$ are lower and upper bound parameters, and considered points where $log\left(s_i\right)$ dropped to a local minimum. These points were our first candidates for the threshold. The parameter $B>100$ was needed since $log\left(s_i\right)$ achieves a global minimum at the right end of the $CM$ range. The other parameter $A$ is chosen to satisfy $0<A<100$ but it should be relatively close to $CM$ = 100 to avoid consideration of insignificantly low values of $CM$. We expect to see a ‘gap’ (large difference $c{m}_{i+1}-c{m}_i$) or a ‘drop’ (small $f_{i+1}=F_{i+1}-F_i$ after a large $f_i$) or both between the local modes of unchanged and changed pixels. We search for the shallowest slopes.

The algorithm to find threshold candidates is as follows:

• Select the subset of pairs $\left(c{m}_i+1,\log (s_i)\right)$ where $A\le c{m}_i+1\le B$.
• Sort these pairs $\left(c{m}_i+1,\log (s_i)\right)$ according to the values of $\log \left(s_i\right)$.
• Discard the pairs $\left(c{m}_i+1,\log (s_i)\right)$ in which the values $\log \left(s_i\right)$ are larger than the 25^th percentile of all $\log \left(s_i\right)$ values within $A\le CM\le B$. This reduces the number of pairs to ¼ of the original pairs.
• Sort the remaining pairs according to the values of $\log \left(s_i\right)$ and output their respective $c{m}_i$ values.
• Select the threshold value $c{m}_c$ among the n lowest slope values. The selection of the threshold from the candidates depends on whether avoiding commission or omission error is more desirable or if it is most important to aim at equal magnitudes of the error types.

3. Demonstration of the Algorithm

3.1. Data

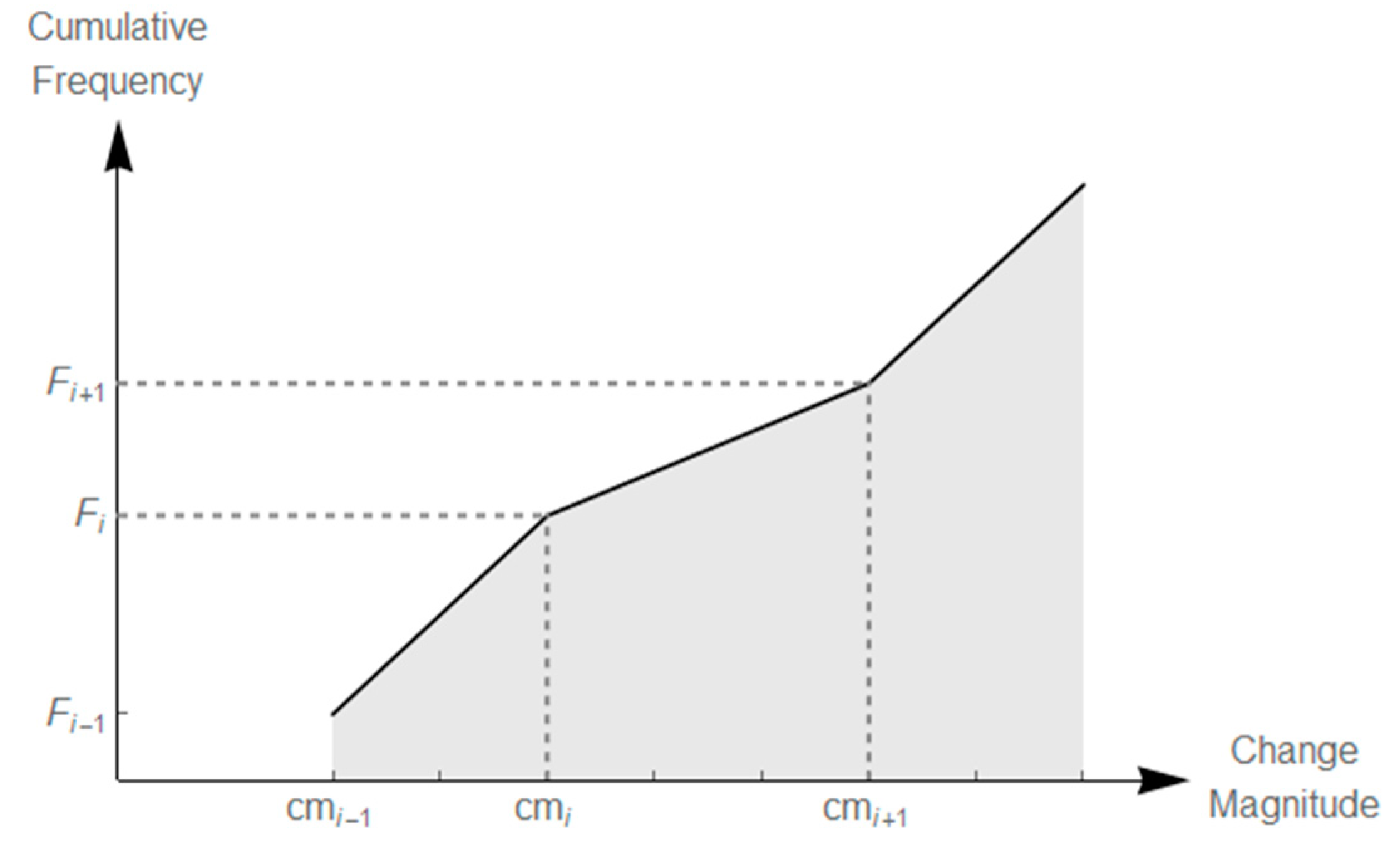
3.1.1. Study Area

The study area in southern Finland represented a mixture of conifer-dominated forest in addition to agricultural and residential land (Figure 4). The proportion of agricultural land was higher than in most boreal forest in Finland. The main tree species in the southern boreal area with relatively rich soil types was Norway spruce (Picea abies Karst.) and the other common conifer species was Scots pine (Pinus sylvestris L.). Within the region of the study area, the proportion of spruce was 48% of the growing stock volume, whereas the proportions of pine and broadleaved trees, mainly birch (Betula sp.) were 28% and 24%, respectively [37].

The mainstream forest management practice in Finland is the growth of even-aged stands in which two to three thinning cuts are performed during a 60–100 year rotation. More than 80% of the regenerated area is clear cut, after which the soil is partly cultivated and new seedlings are planted [38]. National legislation requires leaving residual tree groups on clear-cut stands to maintain biodiversity. The proportion of naturally generated trees is a significant addition to the planted trees. We focused on the detection of final felling through clear cuts in the demonstration. Typical growing stock volume of stands to be clear-cut varies from 200 m³/ha to 400 m³/ha in Finnish forests. In the harvester data used as the reference, the average stem volume was 244 m³/ha.

3.1.2. Satellite Imagery

Two Sentinel-2 images from the study area were acquired on 17 August 2015 and 31 August 2016. Visible bands 2, 3, 4 and near-infrared band 8 with 10 m spatial resolution and band 5 and two short-wave infrared bands with 20 m resolution were selected for the demonstration. Sentinel-2 bands with 20 m resolution were resampled as four 10 m pixels. Later in the text, we refer with Sentinel-2 as 10 m resolution imagery although this is literally somewhat inaccurate because of inclusion of the 20 m bands. The Landsat 8 image was acquired on 3 July 2015. From Landsat, 30 m resolution visible bands 2, 3, 4, near infrared band 5, and shortwave infrared bands 6 and 7 were used. The Landsat 8 image was converted from Universal Transverse Mercator (UTM) zone 34 to 35 using nearest neighbor resampling aligning the 30 m resolution pixels with the pixels of the Sentinel-2 image.

A cloud mask for the Sentinel-2 image from 2016 was computed by first applying an automated method [39]. The result was enhanced interactively. The Sentinel-2 and Landsat images from 2015 were cloudless. Water masks were computed by applying a ToA value of 5% for near infrared bands. The masking was done for the earlier images of the three image pairs with a parameter of Autochange. The threshold was the same for the Sentinel-2 and the Landsat images. The Landsat pixel values were converted to Top of Atmosphere (ToA) reflectances using in-house software. Sentinel-2 data did not require any conversion as the pixel values of the level 1C Sentinel-2 images were already ToA reflectances.

Five tiles of Global ALOS2 PALSAR mosaic [40] for year 2016 that covered the study area we were downloaded from https://www.eorc.jaxa.jp/ALOS/en/palsar_fnf/fnf_index.htm. The data included backscattering coefficients in horizontal-horizontal (HH) and horizontal-vertical (HV) polarizations and they had been ortho-rectified and slope corrected. The pixel size of the mosaic was 25 m. The data included the acquisition date, either September 4, September 22, September 27, October 2, or October 6, 2016 for every pixel. The wavelength of the L-band SAR onboard ALOS-2 is 22.9 cm, which makes the leaf layer of boreal forest transparent for the sensor. The data were applicable because the color changes and partial loss of leaf mass did not affect the backscattered signal.

3.1.3. Reference Data

The reference data for clear cuts to assess the performance of change classification were compiled from forest harvester measurements. A harvester measures the volume and other characteristics of the logged wood and a GPS receiver on the harvester records its location. We used information on clear cuts only without considering the harvested growing stock volume. The harvester locations were used to compute the stand borders taking into consideration the length of the boom of the cutting device. However, the location of the cutting device was unknown. The harvester data included the starting date of the cut and the type of cut. The cutting type data was subsequently collected manually from forest companies. The clear-cut areas were converted to polygon format.

Stands reported as clear-cut between the acquisition times of the images with a margin of 7 days were selected as the reference for clear cuts. Stands in which harvesting took place before acquisition of the first image or after acquisition of the latest image represented uncut forest. Stands smaller than 0.5 ha and any stands fully or partially covered by cloud and cloud shadow mask were excluded. This selection produced 141 stands of cut and 19 stands of uncut forest from Sentinel-2/Sentinel-2 (hereafter S2-S2) and 154 and 6 stands from Landsat 8/Sentinel-2 (hereafter L8-S2), respectively. The number of cut stands was slightly larger for Landsat because the Landsat image had been acquired earlier than the Sentinel-2 image for 2015. However, for the performance assessment we selected the 141 clear-cut stand set to ensure unambiguous testing for S2-S2 and L8-S2 classifications. The same test set was used to assess the performance of the Sentinel-2/ALOS2 PALSAR (hereafter S2-P) classification. The stand size varied from 0.5 ha to 12.2 ha with a median of 1.7 ha.

The annual proportion of clear cuts in the study area is in the order of one to two percent of forest area, which meant that the number of uncut stands in the harvester data was far too low. We selected additional stands for which forest use notifications had been submitted after the acquisition date of the later S2 image to represent uncut forest. Notifications submitted in 2017–2018 in the Uusimaa region and whose size was over 0.5 ha were included. For this set, we also selected stands for intended selective thinning cuts. Those stands usually have lower growing stock volume starting from less than 100 m³/ha, which also means higher reflectance values than mature stands, whose volume is usually more than 200 m³/ha. This ensured a more realistic assessment of the success of the detection of uncut forest than if only mature stands were included. The number of selected uncut additional stands was 1825 (

Table 1. Stands used in testing the method.

Change Class	Number of Stands	Minimum Area (ha)	Median Area (ha)	Maximum Area (ha)
Clear-cut	141 *	0.5	1.8	12.2
Uncut	6 * 1825 **	0.5	1.8	41.0

* From harvester data; ** From notifications of forest use.

).

The test data from forest harvesters and notifications of forest use were not selected using random sampling. Therefore, we defined the performance of the classifications according to overall agreement and omission and commission errors. In addition, we computed the F1-score (Equation (5)) [41]. Value 100 of the F1 index would mean complete agreement and value 0 complete disagreement with the reference data.

$$\begin{array}{c}F1score=\frac{\left(1-\mathrm{CE}\right)\ast \left(1-OE\right)}{2-\mathrm{CE}-\mathrm{OE}}\ast 200\%,where\\ \mathrm{CE}\mathrm{is}\mathrm{Commission}\mathrm{error}\left(\mathrm{scaled}\mathrm{between}0\text{-}1\right)\\ \mathrm{OE}\mathrm{is}\mathrm{Omission}\mathrm{error}\left(\mathrm{scaled}\mathrm{between}0\text{-}1\right)\end{array}$$

(5)

Our set for cut forest can be considered representative of southern Finnish forest. From the reference data for uncut forest only the lowest growing stock forests were missing. Autochange excluded these forests from the classification based on their primary cluster values. The proportion of cut stands in the set for accuracy assessment was more than 7%, which is much higher than the typical 1.5–2% annual proportion of clear cuts of total forest area.

The pixels for the change classification were extracted from a reference stand polygon. The change classification was considered correct if at least 50% of the classification result belonged to the same cut or uncut class as the reference. All reference data were used for the assessment of classification performance given that, for change classification, no specific training data were utilized.

3.1.4. Running the Demonstration with Autochange Software

Change classifications were made for the S2-S2, L8-S2, and S2-P image pairs using the Autochange software. Autochange was run over a subarea of approximately 100 × 100 km² in the northern part of the study area which had the lowest cloud frequency in the Sentinel-2 image from 2016. The same area was used in all classifications. The cluster statistics from the Autochange run were then applied to the images of the whole study area to output the primary cluster, change magnitude and change type output channels (Figure 1).

3.1.5. Test with ALOS2 PALSAR

S2-P classification was performed to determine whether Autochange is applicable when optical and microwave data are combined in the same analysis. The PALSAR mosaic was fairly homogeneous. However, minor differences could be observed in contrast and level of backscattering between mosaic parts acquired on different dates. Analysis of weather statistics suggested this to be due to higher surface moisture in images with lower contrast and slightly increased backscattering level. This apparent cause of contrast decrease was verified by checking the weather records in the study area. After the trials, the final change detection model was computed using mosaic parts of images from September 22 and October 6, 2016 that were acquired during dryer conditions in neighboring tracks. The change mapping result was better for the whole study area with this approach than when the higher moisture parts of the mosaic were included in the computation of the model. After preliminary testing we computed the Autochange model for S2-P using the HV polarization data only. Preliminary analysis did not encourage inclusion of the HH polarization band.

The Autochange method was originally developed for optical data, with change type based on the computation of NDVI and BM. With the PALSAR data, however, computation of NDVI was naturally not possible. We assigned the same HV band to represent both the ‘red’ and ‘near infrared’ bands. As a result, the change type indicated only lower or higher backscattering of a sub-cluster compared to its parent cluster.

Unlike with the optical data, automated definition of change magnitude threshold appeared unfeasible because the magnitude output did not have any distinct drops in its frequency histogram. After experimenting with manual definitions of the change magnitude thresholds, it was decided to base the change only on change type. All cases where sub-cluster backscattering was lower than the backscattering of its parent cluster were accepted as candidate clear cuts for accuracy assessment. However, the land cover information from the S2 image from before the change was considered in the same manner as with the S2-S2 and S2-L8 classifications.

3.2. Results

Those primary clusters from the pre-change image whose BM represented relatively high biomass with a red band ToA reflectance of 5% or lower were considered potentially clear-cut. The purpose of this division was to roughly exclude the majority of agricultural lands and young forests from the change analysis. The division was easy to do by thresholding the intensity values of the earlier-image cluster output since the intensity of a pixel indicated the cluster number and the clusters were sorted by their BM.

In the classifications based on optical data, the actual clear cuts were defined by thresholding the output feature for the CM of Autochange. Two preliminary assumptions were applied for the threshold definition. The lower limit of CM was $A=60,$ which corresponded to 90% of CM. The upper limit $B$ corresponded to 99.9% of CM values, i.e., we assumed that the proportion of clear-cut area within the investigated time range was higher than 0.1% and lower than 10% of the changed pixels of the area of interest. In addition, pixels whose CM was above the selected threshold had to represent a biomass decrease change type (Figure 2).

Table 2. The first five candidate thresholds for change magnitude for defining cut and un-cut forest.

Image Pair	1	2	3	4	5
S2-S2	84	89	137	221	239
L8-S2	76	163	211	221	232

shows the result of automated selection of thresholds that divide CM to represent cut and uncut forest. The threshold candidates that represent the smallest values of CM were almost the same for S2-S2 and L8-S2 and the two largest values were similar. Values #2 and #3 were, in contrast, dissimilar. After a general visual inspection of the results, we selected values that represented the smallest CM value, i.e., #1 in Table 2 for the final division. Figure 5 demonstrates the threshold locations in the original histogram of CM, in the cumulative histogram, and in the slope output.

Figure 6 shows a detail of Autochange output for S2-S2 and Figure 7. the same area in the final classification.

Table 3. Confusion matrix of S2-S2 change classification, higher than 50% agreement. Numbers in parentheses show the original result before manual checking of errors.

Prediction	Reference
	Un-cut	Clear-cut	Total
Uncut (50%)	1817 (1810)	8 (15)	1825
Clear-cut (50%)	7 (17)	136 (126)	143
Total	1824 (1827)	144 (141)	1968
Overall agreement %	99.2
OE for cut class %	5.6
OE for uncut class %	0.4
CE for cut class %	4.9
CE for uncut class %	0.4
F1 score for cut class %	94.8

and

Table 4. Confusion matrix of L8-S2 change classification, higher than 50% agreement. Numbers in parentheses show the original result before manual checking of errors.

Prediction	Reference
	Un-cut	Clear-cut	Total
Uncut (50%)	1820 (1815)	30 (35)	1850
Clear-cut (50%)	4 (12)	114 (106)	118
Total	1824 (1827)	144 (141)	1968
Overall agreement %	98.3
OE for cut class %	20.8
OE for uncut class %	0.2
CE for cut class %	3.4
CE for uncut class %	0.2
F1 score for cut class %	87.0

present the confusion matrices of S2-S2 and L8-S2 classifications that were based on CM threshold 84 for S2-S2 and 76 for L8-S2. The figures without parenthesis indicate the agreement (i.e., minimum 50% of reference stand area classified correctly) after all the mismatches in the original assessment that was done without human interaction were inspected visually with the help of ArcGIS software. The figures in parentheses represent the result before visual inspection. The visual inspection was done because the reference data were not completely reliable. The set for the visual inspection was selected from the mismatches of the S2-S2 classification. If the visual assessment indicated a borderline case, the classification result was interpreted as an error.

The agreement with reference data for uncut and cut forest was high in the S2-S2 classification. Commission and omission errors were very similar, which suggests unbiased estimation, although this conclusion should be interpreted with care due to the non-randomness of the reference. With L8-S2, the classification appeared too conservative, resulting in underestimation of clear-cut stands. The agreement with reference data for uncut forest was high also with the L8-S2 classification.

In the S2-S2 classification, seven of the 15 original reference clear cuts classified as uncut were in reality uncut and they were transferred to the uncut class. Of the seven apparent reference data errors, three were strip roads without any major removal of trees, three only partial cuttings, and one a misplaced reference stand (Figure 6). The strip road issue has been mitigated in further automation of the stand delineation process [42].

According to the visual inspection, the eight stands that were kept in the cut reference class included a significant number of remaining trees. The 50% criterion for cutting was consequently not met, although groups of changed pixels could be visually observed within the stands.

In the uncut reference class for the S2-S2 classification, ten of the 17 assessed stands were clear cut in reality and they were transferred to the class of cuts. The remaining seven stands were covered by cloud that was not considered in cloud masking of the 2016 image, which led to classification errors as cut stands.

The result of visual assessment of the L8-S2 classification was similar to the S2-S2 assessment (Table 4). The obvious error source in the L8-S2 classification was the coarser 30-m resolution of L8 compared to the 10-m resolution of S2. In addition, the lowest change magnitude value of 60, which was the starting point for automatically determining the threshold for cuttings, may have been too high. However, we wanted to have the same starting value for both optical classifications.

The demonstration in this study focused on forest lands. Agricultural areas were masked out only superficially and conservatively using a simple threshold for ToA reflectance of red band in the pre-change images. This resulted in changes similar to clear cuts on the agricultural land.

The result of the S2-P classification was poorer than the S2-S2 classification, but it can be considered better than the L8-S2 result for locating the clear cuts because the omission error with the L8-S2 classification was substantial (

Table 5. Confusion matrix of S2-PALSAR change classification, higher than 50% agreement with lower threshold.

Prediction	Reference
	Un-cut	Clear-cut	Total
Uncut (50%)	1798 (1791)	24 (31)	1822
Clear-cut (50%)	26 (36)	120 (110)	146
Total	1824 (1827)	144 (141)	1968
Overall agreement %	97.5
OE for cut class %	16.7
OE for uncut class %	1.4
CE for cut class %	17.8
CE for uncut class %	1.3
F1 score for cut class %	82.8

). However, as can be seen in Figure 9, the S2-P classification result was noisy compared to the optical classifications. The approach in the testing, in which the test object was a clear-cut stand, favored the S2-P classification since the scattered noise usually did not cover more than 50% of the uncut reference stand area.

4. Discussion

The results showed that the Autochange algorithm, in which lower-level clustering was done within the post-change image without considering the spectral intensities of the pre-change image, resolved the severe issues that can result from spectral mismatching of multi-temporal data. Seasonal or atmospheric differences between images did not affect the result because the information from the pre-change image was transferred to the post-change image based on cluster labels as opposed to spectral intensities. This also made it possible to use Sentinel-2 and ALOS PALSAR data in the same classification.

However, as with any change detection method, Autochange is not immune to seasonal effects. For instance, the result may be unsatisfactory if the season of the pre-change image is not compatible with the reasonable separation of land cover clusters. Such a situation could occur during winter due to snow on trees or very low sun angle [43]. In this study, cloud cover in the post-change image caused some commission errors. Clouds in the pre-change image would not cause such errors in felling mapping as cloudy pixels with high reflectance values would be ignored as having zero cutting potential. Omission errors could, however, result in such a case. The cloud and cloud shadow issue cannot be considered fully resolved despite cloud-screened data are routinely provided e.g., by the Copernicus program [44].

With SAR data, high surface moisture reduces the separability of biomass differences [45]. The effect of moisture was also observed in this study as slightly increased backscattering with decreasing contrast in parts of the PALSAR-2 mosaic and it was considered in the computation of the model.

A change affects the spectral mean of the labeled later-image parent or primary cluster. This potential error source was reduced by performing computation of change magnitude in an iterative manner. The mean vector of the parent cluster was re-computed after ignoring the observations of a sub-cluster whose mean was furthest from the parent cluster, i.e. the change magnitude was largest. This re-computed mean was used to compute the final change magnitudes and change types.

The automated definition of change magnitude threshold to extract cut and uncut forest was successful in the S2-S2 classification and led to near perfect separation of true clear cuts and only a few commission errors when the distinct mistakes in the reference data were taken into consideration. The commission errors in the uncut category were due to cloud in the 2016 Sentinel-2 image. The lowest change magnitude threshold candidate for cut forest led to best results since the result with higher thresholds was too conservative, resulting in omission errors with respect to clear cut area. Commission errors were still negligible with the applied lowest thresholds.

We chose the 90% point of the cumulative histogram of change magnitude at the lower end, and the 99.9% at the high end for the search window of the thresholds for change due to clear cuts. This meant that the maximum area of change could be 10% and the minimum area 0.1%. Automated selection of the lowest thresholds within the window resulted in a threshold at 94% of the cumulative histogram, meaning 6% changed area in the S2-S2 classification. With the L8-S2 classification, the threshold was at 93%, meaning a change proportion of 7%, respectively.

After taking into consideration the pre-change image primary cluster and the change type, the change proportions decreased to 2% in the S2-S2 classification which is compatible with the of 1.5% to 2% annual proportion of clear cuts of forest area in southern Finland. In the L8-S2 classification the change proportion was 4%. The difference is explained by the earlier phenological phase in early July of the Landsat 8 image in which agricultural fields were in their main growing stage. The broad thresholding of the primary clusters did not exclude all fields from the actual change classification, which resulted in extra changes to the agricultural land. In our experiment, the extra changes on agricultural land were insignificant because the forest location was known. Therefore a loose and simple rule for selecting pre-change-image primary clusters for change analysis could be applied. During the acquisition of the 2015 Sentinel-2 image in August, field greenness was reduced, resulting in increased intensities. The thresholding of the primary clusters thus excluded most fields from the change classification.

With the S2-P classification the area of predicted clear-cut pixels was higher, at 6.6% of land area, than with the optical classifications. This was due to the relatively high proportion of scattered change pixels. Thus, although the stand-based assessment of the classification performance suggested low bias with the PALSAR classification, pixel-based assessment would have led to overestimation of the cut area.

Inspection of the harvester-based reference data revealed that the harvester operator had made some mistakes in coding the cutting type. However, these errors in the reference data were easy to identify visually and did not affect the assessment of the performance of the Autochange method. The main error source in harvester data was that the cut type was registered incorrectly or based on the dominant cutting type. In future, the harvester operator should register the cutting type at the sub-stand level. In some cases the harvester data based clear-cut area may have been too large, particularly for the small clear cuts, since the position of the harvester arm was not known, but it had to be computed. It is also possible that the satellite image based mapping could systematically underestimate the cut area due to shadows at stand edges, for instance. There were also a few geometric shifts in the harvester data, likely due to GPS issues.

The L8-S2 classification demonstrated successful use of different data types with different spatial resolutions by Autochange. However, the coarser resolution of L8 decreased the accuracy of the results to some extent. With an L8-S2 image pair, nearly all test stands included pixel groups that represented change, but the area extents could be less than 50% of the reference stand area, resulting in an error in testing. If a cut was next to a high reflectance object, such as an agricultural field, the mixed pixels affected the primary clustering of the 2015 image, which weakened the change classification result.

Also, in the S2-P classification the coarser spatial resolution of ALOS PALSAR affected the results. It was not possible to compute the change type in the same manner as with the optical data, rather only the lower HV backscattering of the sub-cluster compared to its parent cluster indicated the change. The best result was achieved when only the direction of the change was considered but not the level of change magnitude. The result was relatively noisy, producing many wrong change alerts of few pixel extents. Trials with determining the change magnitude by thresholding it reduced the noise but resulted in omission errors.

The 10-m pixel of Sentinel-2 was ideal for a pixel-based approach since a pixel represented a large enough area for not including trees and spaces between trees in separate pixels, yet the pixel coverage was small enough to locate the cuts well. Autochange could also be applied to very high-resolution data for which image segmentation as a pre-processing step is preferred. The 30-m Landsat pixel was relatively coarse for the typical size of a clear cut stand in the study area.

In the S2-S2 classification, a 5.6% omission error and 4.9% commission error for clear cuts and 0.4% omission and commission errors for the stable class were achieved. In [20] these errors were 2.3% and 14.4% for abrupt land cover changes and 12.8% and 2.0% for the stable class, respectively. This classification consequently overestimated the change. In the improved version of the method the bias was significantly reduced with an omission error of 27% and commission error of 28% including all disturbance types [31]. In a study with Bolivian dry forests, the user’s and producer’s accuracies were 93.3% and 87.5% for forest clear cutting and close to 100% for the large stable class [32].

The results of different studies conducted in variable conditions and geographic regions are difficult to compare in an objective manner. Time series approaches may not automatically provide higher accuracies than bi-temporal imagery. Many time series methods actually contain additional potential error sources caused by the modeling of the time series for the stable situation and from radiometric calibration of the multi-temporal data. Furthermore, time series approaches may require more than ten images for definition of the stable situation, making the approach computationally heavy. On the other hand, the effect of the random variability of the pixel values that can cause errors in the bi-temporal approach is reduced.

Autochange is not only suitable for analyzing one pair of images because change features can be computed from successive images and a time series can be compiled from them. [34] studied a time series approach with Autochange using a series of four images for the detection of clear cuts and selective thinning cuts with Sentinel-2 data. Accuracy assessment was carried out by independently interpreting sample plots from very high resolution satellite imagery. Different thresholds for the change magnitude were applied. For the result with the highest F1 score, the omission and commission errors for the clear cuts were 19.8% and 8.3% and 2.9% and 9.2% for the uncut class. The classification was thus conservative, which was partly due to an atmospheric disturbance in the Sentinel-2 data in one of the three study sites. For the selective thinning cuts, the errors were 79.6% and 56.1%. Some thinning cuts were so light that they were hardly detectable by the visual interpreter of very high resolution data and thus not likely to be practically detectable in Sentinel-2 images.

5. Conclusions and Future Development Needs

The Autochange algorithm and its software implementation is considered applicable for the mapping of abrupt land cover changes using multi-temporal satellite data. It allows mixing of images even from the optical and SAR sensors in the same change analysis. Consequently, no absolute image calibration is required. The software has already been implemented as a service in the Forestry Thematic Exploitation Platform (Forestry TEP) [46].

The further development needs include application of Autochange for continuous change monitoring using longer time series, further adaption for using SAR data, and testing the method for several change types including gradual changes such as increases in biomass.