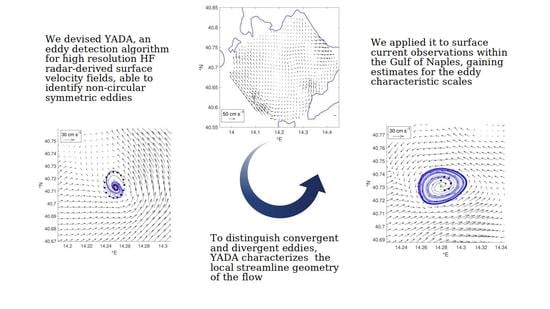
Eddy Detection in HF Radar-Derived Surface Currents in the Gulf of Naples
Abstract
1. Introduction
2. Materials
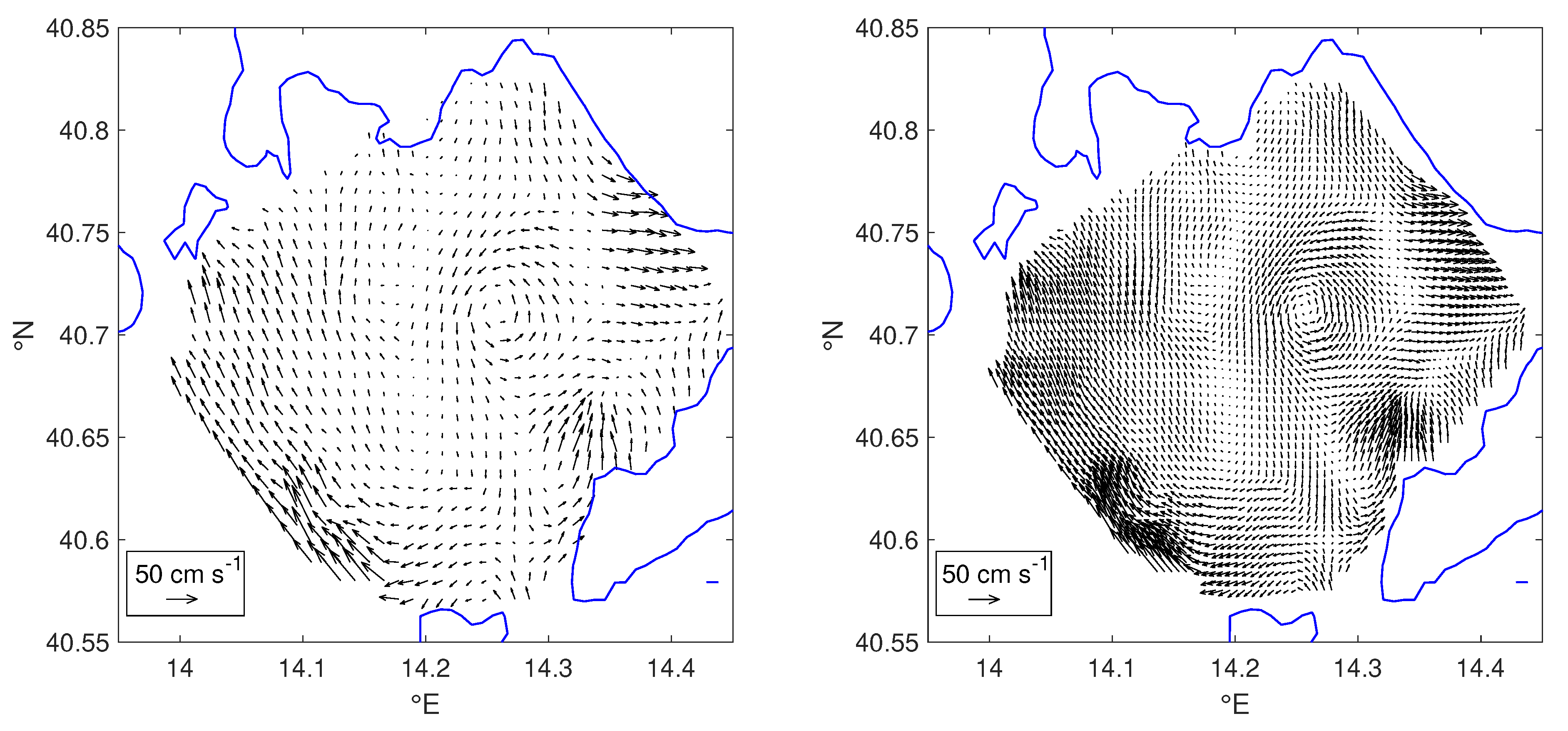
2.1. Dataset
2.2. Dynamical Parameters Characterizing Recirculations
2.2.1. Okubo–Weiss and Local Okubo–Weiss Parameters
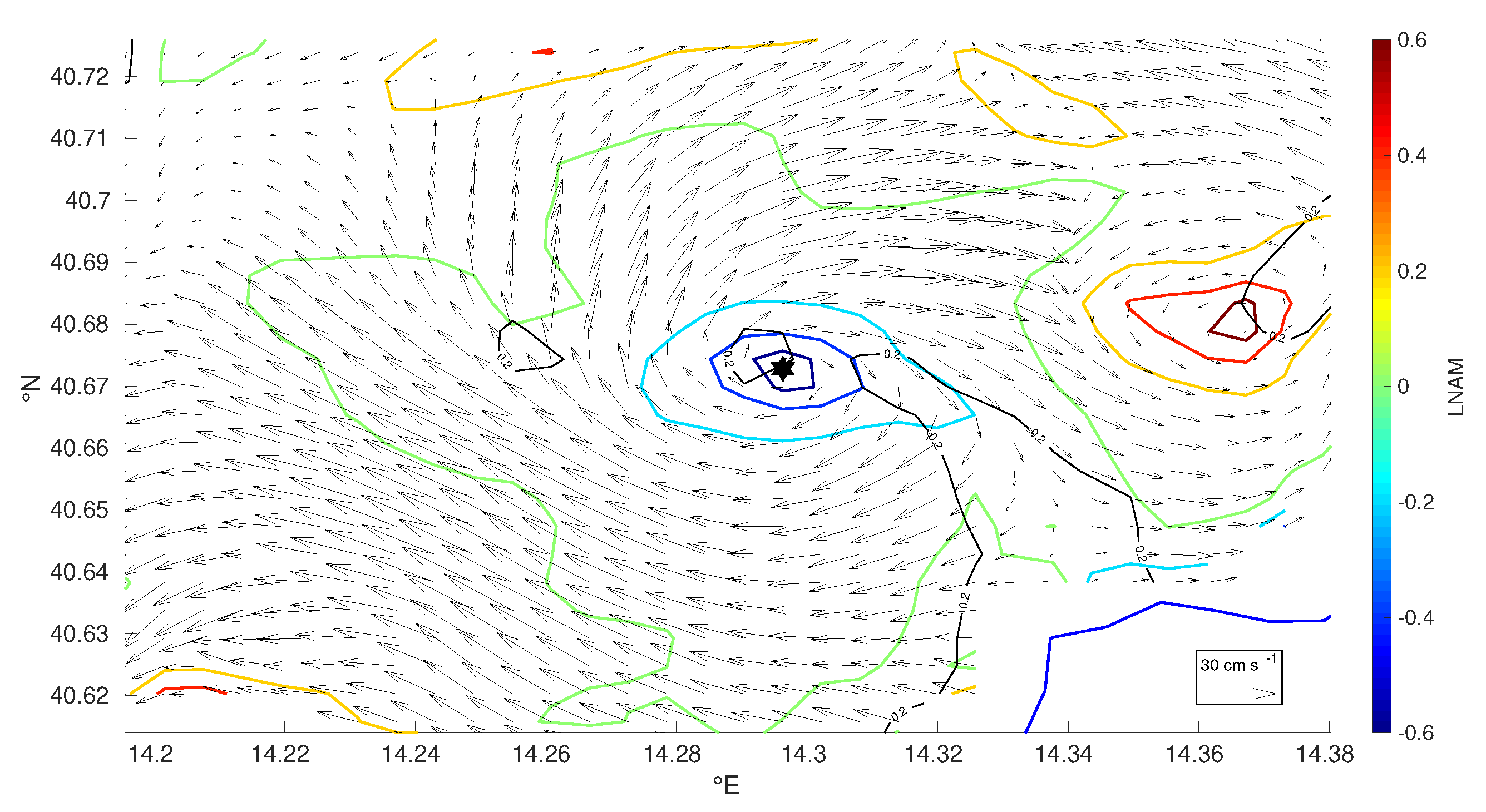
2.2.2. Local Normalized Angular Momentum and Momentum Flux Fields
3. Methods
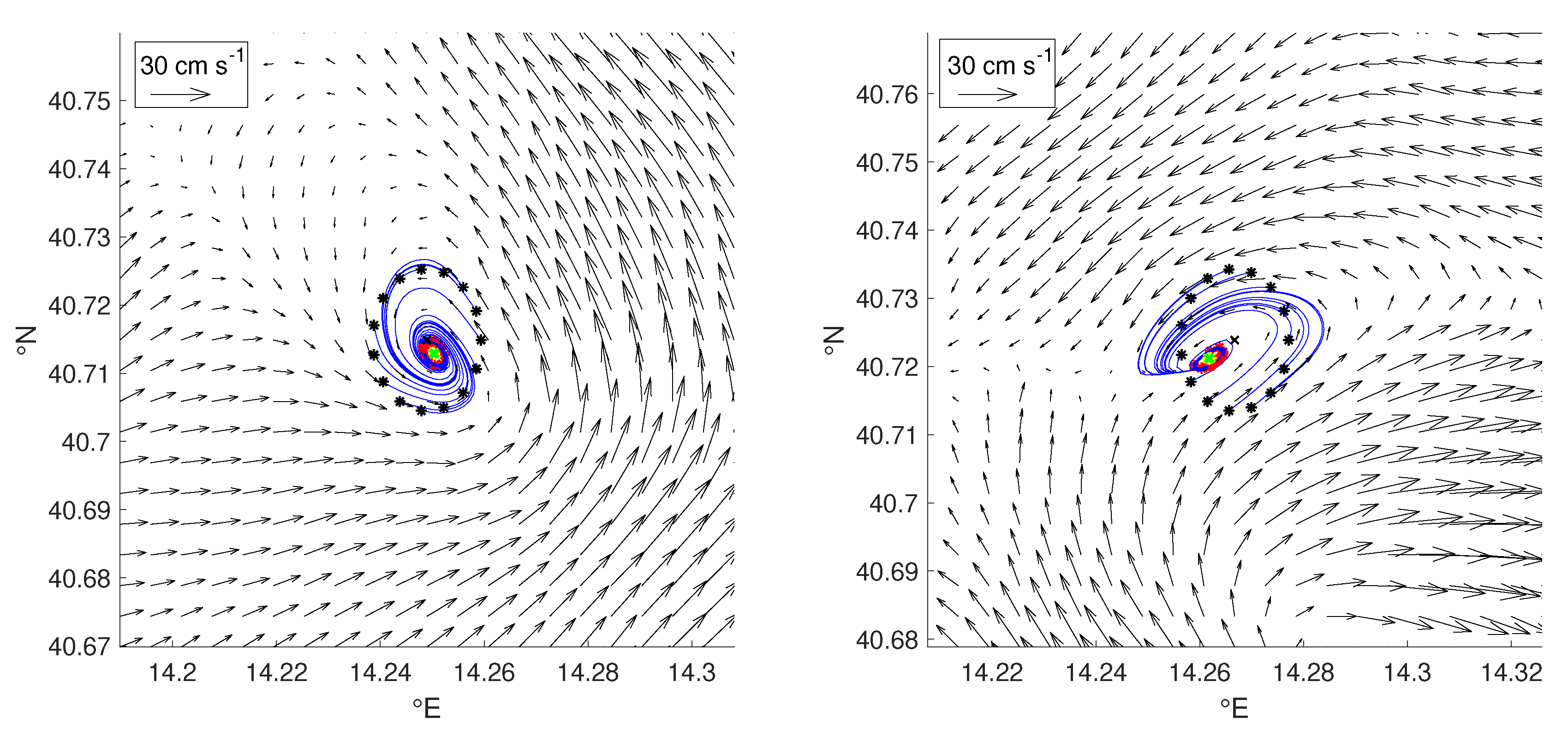
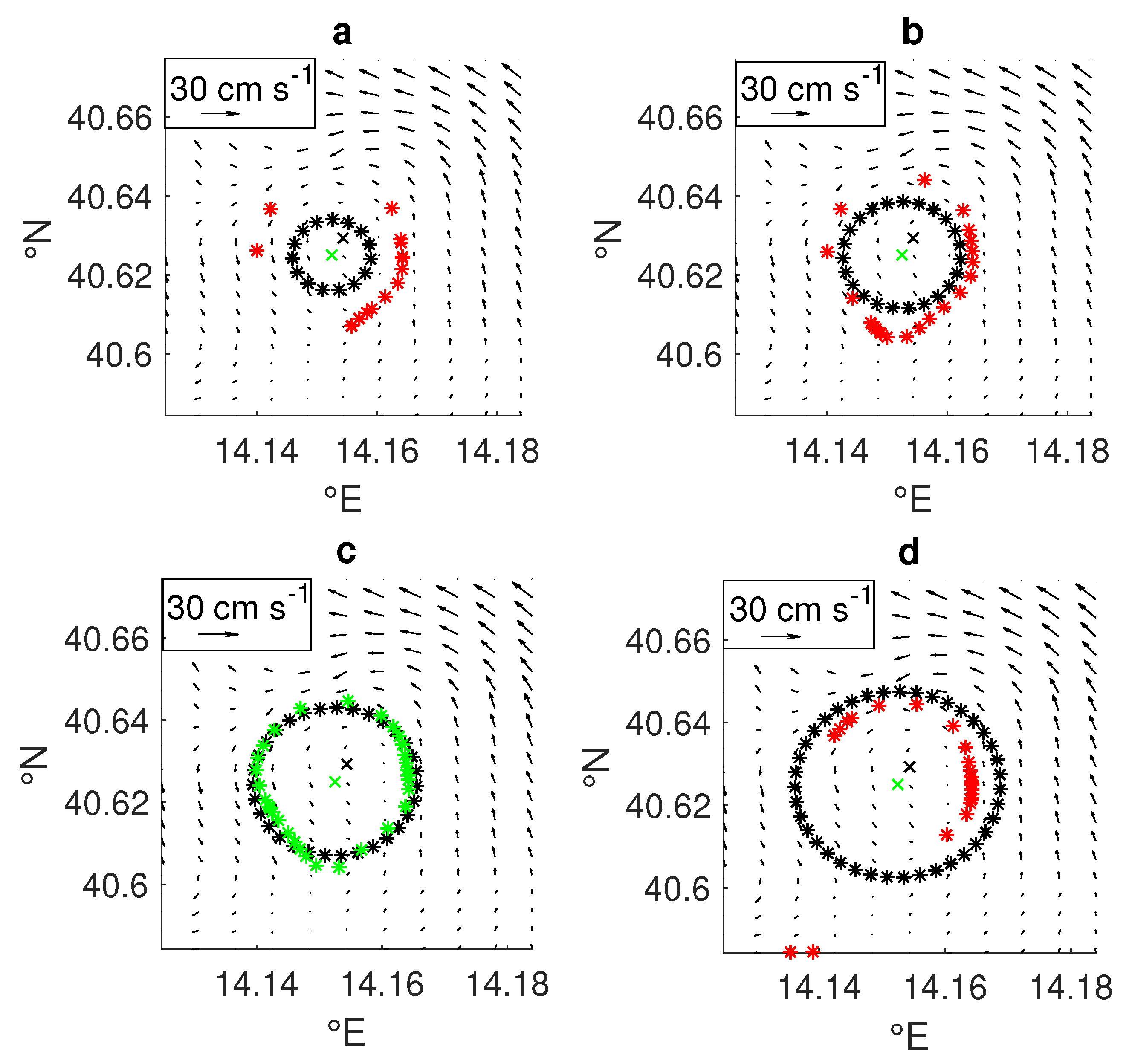
3.1. Eddy Detection Algorithms
3.2. Ameda
- 1.
- Identifies grid points which are local extrema of satisfying and , for a chosen threshold ;
- 2.
- Verifies the existence of at least one closed streamline around each extremum.
- 2’.
- Confirms that the velocity field constantly rotates along the perimeter of the square domain of edge and centered at the extremum, for a chosen distance b.
3.3. Neal
- 1.
- Identifies couples of adjacent grid points such that the meridional component of the velocity field changes sign going westward along the zonal segment of length , centered at , and increases its magnitude away from this point. This computation also provides the expected sign of rotation;
- 2.
- Verifies that, at any such grid point , the zonal component of the velocity field changes sign going northward along the meridional segment of length , centered at , and increases its magnitude away from this point. This change must be compatible with the expected rotation;
- 3.
- Identifies the (kinetic energy) local minima inside a square domain of edge , centered at , which are global minima in a square neighborhood of the same size;
- 4.
- Confirms that the velocity field constantly rotates along the perimeter .
3.4. Yada
- 1.
- Identifies the local extrema of a dynamical field like , or ;
- 2.
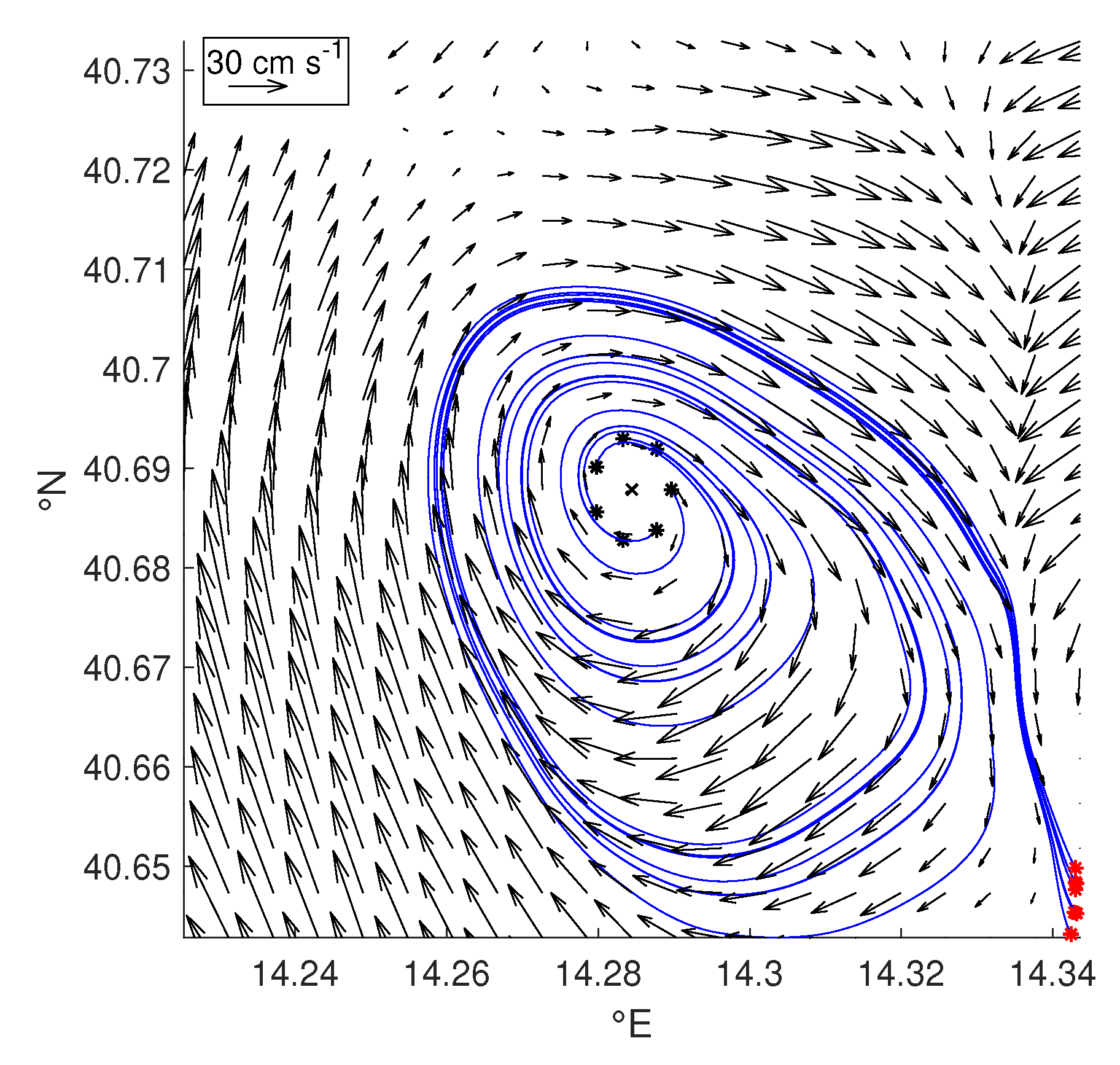
- Analyzes the streamline geometry within some neighborhood of each extremum, ensuring the existence of either bounded hyperbolic orbits (characterizing eddies with sink-like cores) or elliptic orbits (in presence of eddies having stable orbits).
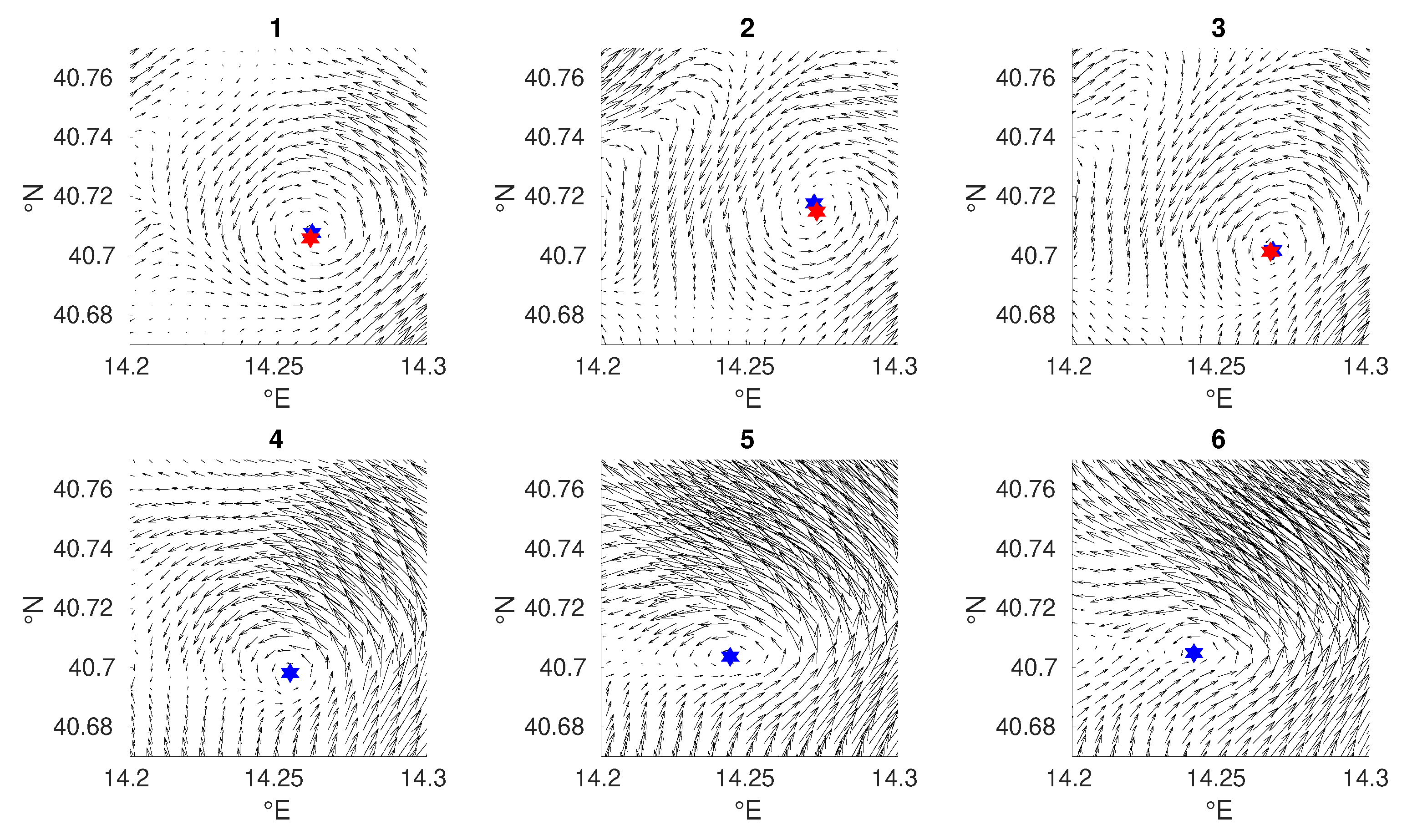
3.5. Tuning Strategy
4. Results
4.1. Ameda Tuning and Results
- 3.
- Discards those extrema satisfying .
4.2. Neal Tuning and Results
4.3. Yada Tuning and Results
- (1)
- The end points belong to the square domain (that is: they stay away from the boundary of the reference domain);
- (2)
- Each streamline completes at least one revolution.
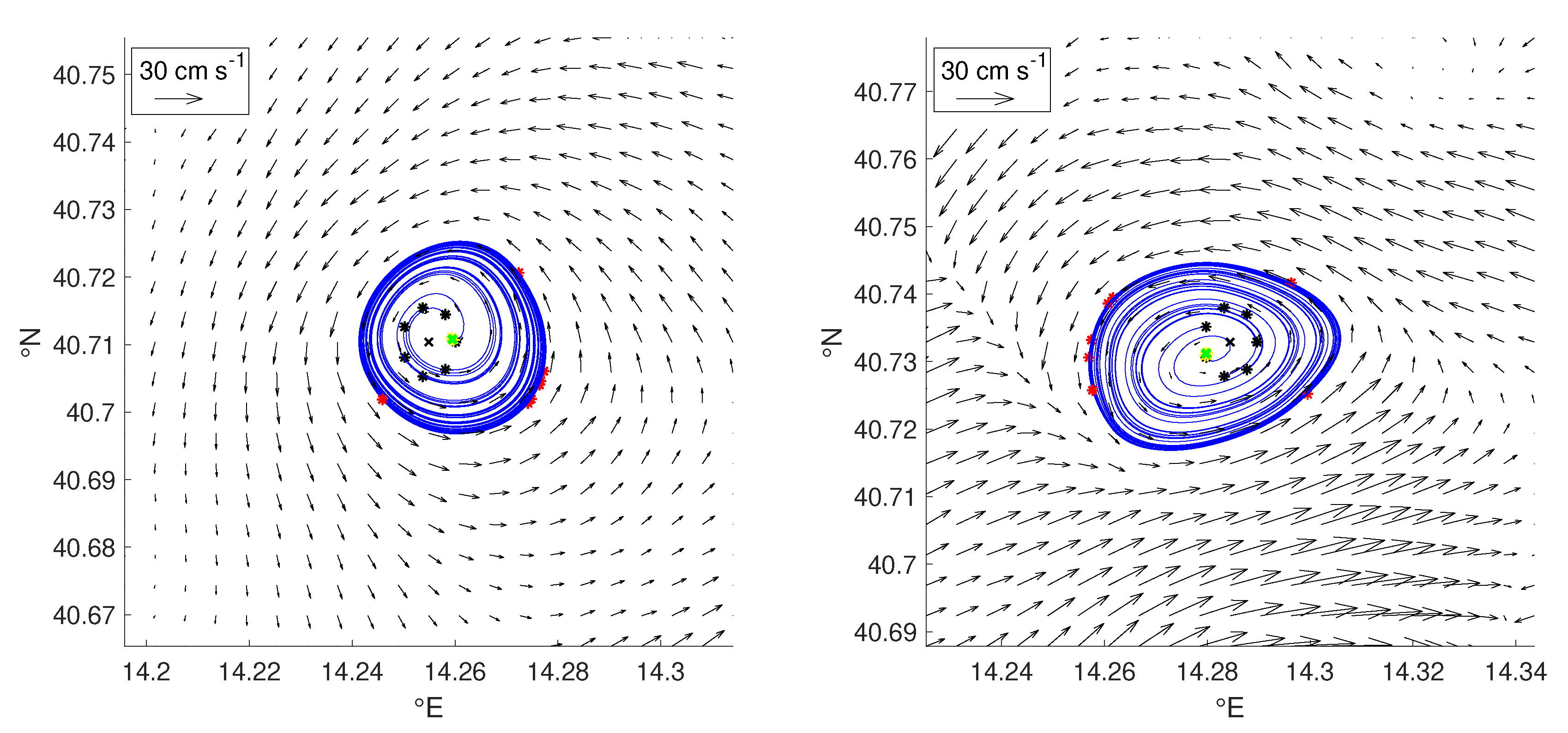
4.4. Eddy Boundaries
4.4.1. Sink-Like Cores
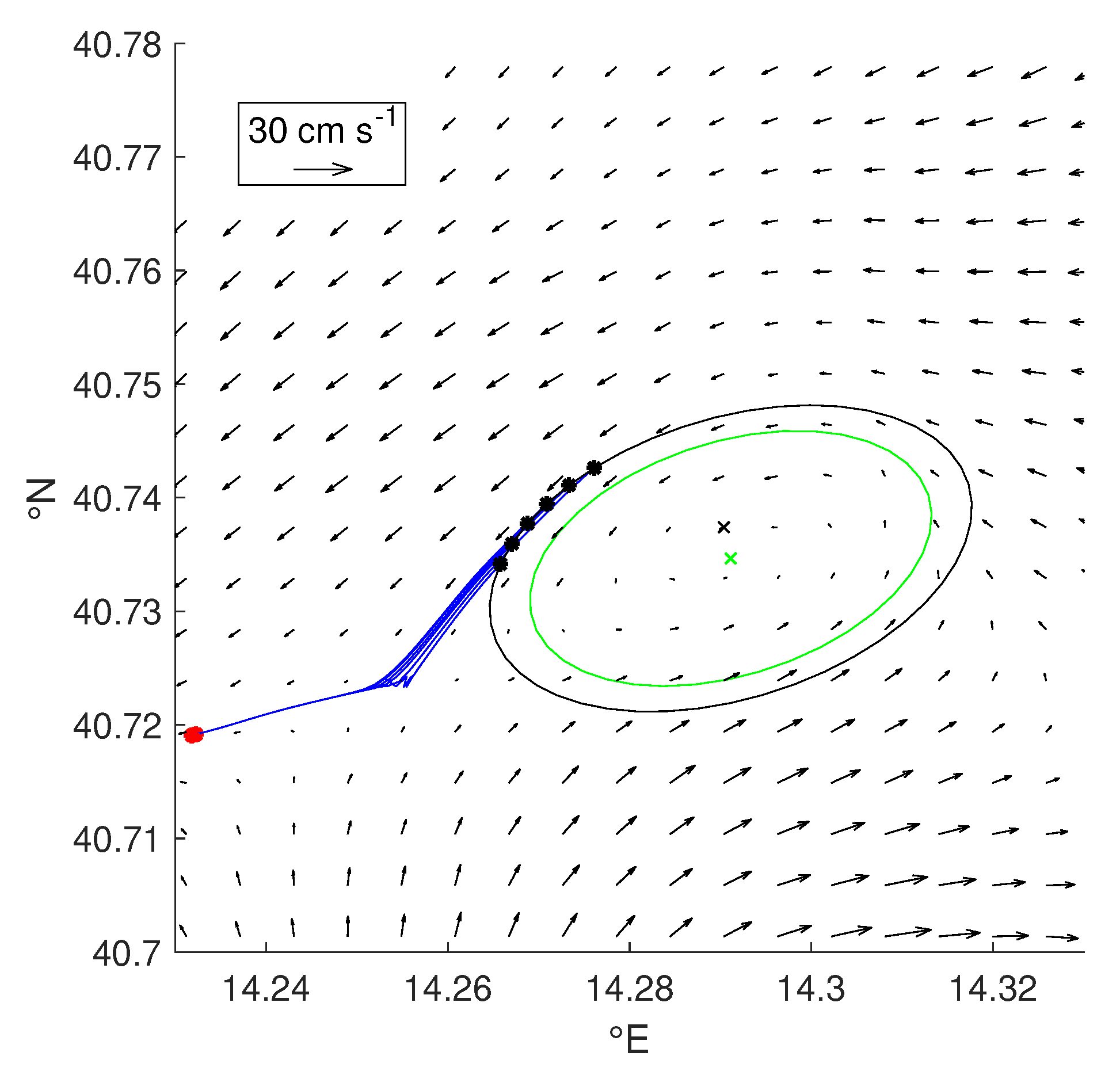
4.4.2. Eddies Having Elliptic Orbits
5. Discussion
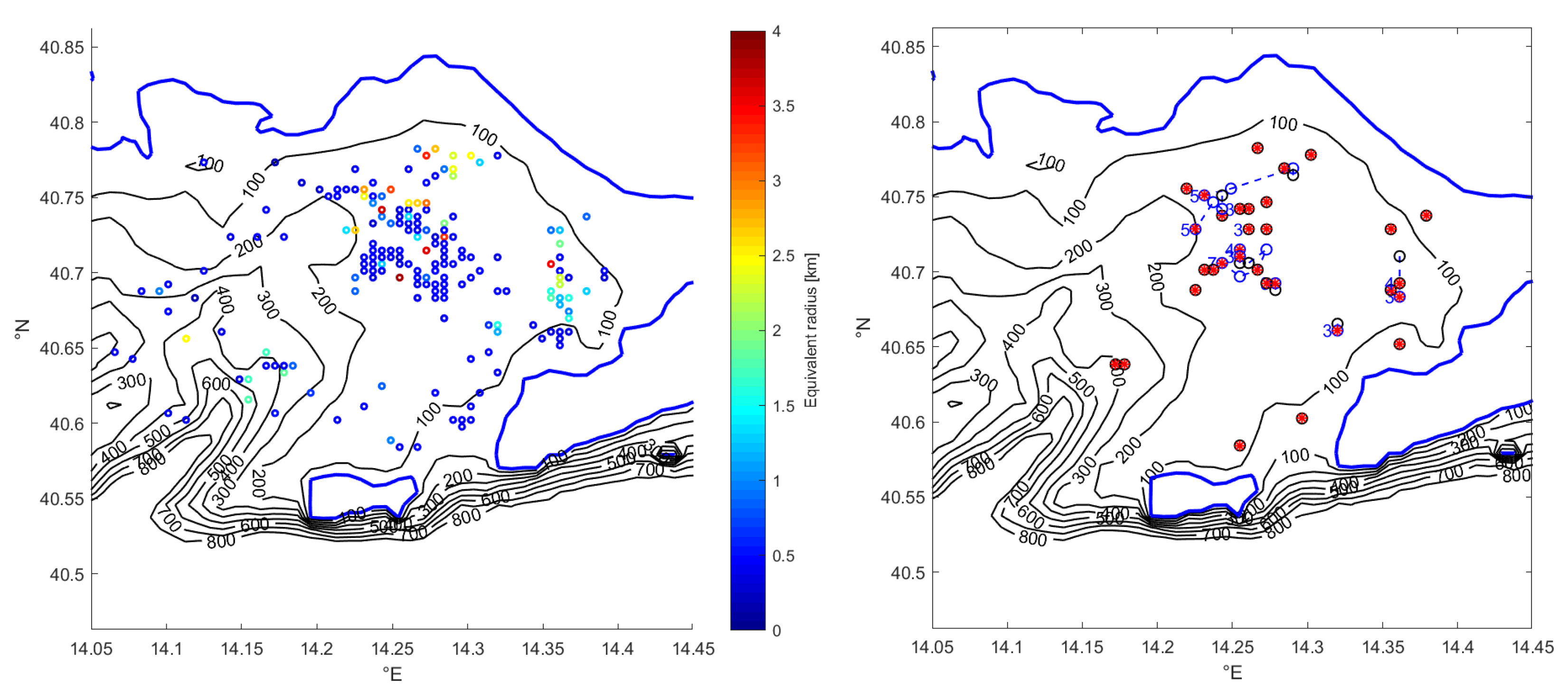
5.1. Detected Eddies
5.2. Equivalent Radii
5.3. Spatial Distribution
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. the Hausdorff Distance
References
- Cushman-Roisin, B.; Gualtieri, C.; Mihailovic, D.T. Environmental Fluid Mechanics: Current issues and future outlook. In Fluid Mechanics of Environmental Interfaces; Taylor & Francis: Abingdon UK, 2008; pp. 17–30. [Google Scholar]
- Zambianchi, E.; Griffa, A. Effects of finite scales of turbulence on dispersion estimates. J. Mar. Res. 1994, 52, 129–148. [Google Scholar] [CrossRef]
- Haza, A.C.; Özgökmen, T.M.; Griffa, A.; Garraffo, Z.D.; Piterbarg, L. Parameterization of particle transport at submesoscales in the Gulf Stream region using Lagrangian subgridscale models. Ocean. Model. 2012, 42, 31–49. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale, coherent vortices in the ocean. Rev. Geophys. 1985, 23, 165–182. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale currents in the ocean. Proc. R. Soc. A 2016. [Google Scholar] [CrossRef] [PubMed]
- Lévy, M.; Franks, P.J.; Smith, K.S. The role of submesoscale currents in structuring marine ecosystems. Nat. Commun. 2018, 9, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Mahadevan, A. The impact of submesoscale physics on primary productivity of plankton. Annu. Rev. Mar. Sci. 2016, 8, 161–184. [Google Scholar] [CrossRef]
- Poje, A.C.; Özgökmen, T.M.; Lipphardt, B.L.; Haus, B.K.; Ryan, E.H.; Haza, A.C.; Jacobs, G.A.; Reniers, A.; Olascoaga, M.J.; Novelli, G.; et al. Submesoscale dispersion in the vicinity of the Deepwater Horizon spill. Proc. Natl. Acad. Sci. USA 2014, 111, 12693–12698. [Google Scholar] [CrossRef]
- Doglioli, A.M.; Blanke, B.; Speich, S.; Lapeyre, G. Tracking coherent structures in a regional ocean model with wavelet analysis: Application to Cape Basin eddies. J. Geophys. Res. Ocean. 2007, 112, C5. [Google Scholar] [CrossRef]
- Le Vu, B.; Stegner, A.; Arsouzea, T. Angular Momentum Eddy Detection and tracking Algorithm (AMEDA) and its application to coastal eddy formation. Atmos. Ocean. Technol. 2017, 35, 739–762. [Google Scholar] [CrossRef]
- Nencioli, F.; Dong, C.; Duckey, T.; Washburn, L.; McWilliams, J.C. A Vector Geometry Based Eddy Detection Algorithm and Its Application to a High-Resolution Numerical Model Product and High-Frequency Radar Surface Velocities in the Southern California Bight. Atmos. Ocean. Technol. 2008, 27, 564–579. [Google Scholar] [CrossRef]
- Post, F.H.; Sadarjoen, I.A. Detection, quantification, and tracking of vortices using streamline geometry. Comput. Graph. 2000, 24, 333–341. [Google Scholar]
- Pessini, F.; Olita, A.; Cotroneo, Y.; Perilli, A. Mesoscale eddies in the Algerian Basin: do they differ as a function of their formation site? Ocean. Sci. 2018, 14, 5. [Google Scholar] [CrossRef]
- Chelton, D.B.; DeSzoeke, R.A.; Schlax, M.G.; El Naggar, K.; Siwertz, N. Geographical variability of the first baroclinic Rossby radius of deformation. J. Phys. Oceanogr. 1998, 28, 433–460. [Google Scholar] [CrossRef]
- Lévy, M.; Klein, P.; Treguier, A.M. Impact of sub-mesoscale physics on production and subduction of phytoplankton in an oligotrophic regime. J. Mar. Res. 2001, 59, 535–565. [Google Scholar] [CrossRef]
- Grilli, F.; Pinardi, N. The computation of Rossby radii of deformation for the Mediterranean Sea. MTP News 1998, 6, 4–5. [Google Scholar]
- Pinardi, N.; Masetti, E. Variability of the large scale general circulation of the Mediterranean Sea from observations and modelling: a review. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2000, 158, 153–173. [Google Scholar] [CrossRef]
- Corrado, R.; Lacorata, G.; Palatella, L.; Santoleri, R.; Zambianchi, E. General characteristics of relative dispersion in the ocean. Sci. Rep. 2017, 7, 46291. [Google Scholar] [CrossRef]
- Rubio, A.; Mader, J.; Corgnati, L.; Mantovani, C.; Griffa, A.; Novellino, A.; Quentin, C.; Wyatt, L.; Schulz-Stellenfleth, J.; Horstmann, J.; et al. HF radar activity in European coastal seas: next steps toward a pan-European HF radar network. Front. Mar. Sci. 2017, 4, 8. [Google Scholar] [CrossRef]
- Paduan, J.D.; Washburn, L. High-Frequency Radar Observations of Ocean Surface Currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef]
- Karimova, S.; Gade, M. Eddies in the Western Mediterranean seen by spaceborne radar. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3997–4000. [Google Scholar]
- Karimova, S.; Gade, M. Improved statistics of sub-mesoscale eddies in the Baltic Sea retrieved from SAR imagery. Int. J. Remote. Sens. 2016, 37, 2394–2414. [Google Scholar] [CrossRef]
- Karimova, S.S.; Gade, M. Eddies in the Red Sea as seen by satellite SAR imagery. In Remote Sensing of the African Seas; Springer: Berlin/Heidelberg, Germany, 2014; pp. 357–378. [Google Scholar]
- Menna, M.; Mercatini, A.; Uttieri, M.; Buonocore, B.; Zambianchi, E. Wintertime transport processes in the Gulf of Naples investigated by HF radar measurements of surface currents. Nuovo Cimento C 2007, 30, 605–622. [Google Scholar]
- Cianelli, D.; Falco, P.; Iermano, I.; Mozzillo, P.; Uttieri, M.; Buonocore, B.; Zambardino, G.; Zambianchi, E. Inshore/offshore water exchange in the Gulf of Naples. J. Mar. Syst. 2015, 145, 37–52. [Google Scholar] [CrossRef]
- Carrada, G.C.; Hopkins, T.S.; Bonaduce, G.; Ianora, A.; Marino, D.; Modigh, M.; Ribera D’Alcalà, M.; di Scotto, C.B. Variability in the hydrographic and biological features of the Gulf of Naples. Mar. Ecol. 1980, 1, 105–120. [Google Scholar] [CrossRef]
- Cianelli, D.; Uttieri, M.; Buonocore, B.; Falco, P.; Zambardino, G.; Zambianchi, E. Dynamics of a very special Mediterranean coastal area: the Gulf of Naples. In Mediterranean Ecosystems: Dynamics, Management and Conservation; Nova Science: Hauppauge, NY, USA, 2012; pp. 129–150. [Google Scholar]
- Moretti, M.; Sansone, E.; Spezie, G.; Vultaggio, M.; De Maio, A. Alcuni aspetti del movimento delle acque del Golfo di Napoli. Annali Ist Univ Nav XLV-XLVI 1976, 207–217. [Google Scholar]
- De Maio, A.; Moretti, M.; Sansone, E.; Spezie, G.; Vultaggio, M. Outline of marine currents in the Bay of Naples and some considerations on pollutant transport. Il Nuovo Cimento C 1985, 8, 955–969. [Google Scholar] [CrossRef]
- Uttieri, M.; Cianelli, D.; Nardelli, B.B.; Buonocore, B.; Falco, P.; Colella, S.; Zambianchi, E. Multiplatform observation of the surface circulation in the Gulf of Naples (Southern Tyrrhenian Sea). Ocean. Dyn. 2011, 61, 779–796. [Google Scholar] [CrossRef]
- De Ruggiero, P.; Esposito, G.; Napolitano, E.; Iacono, R.; Pierini, S.; Zambianchi, E. Modelling the marine circulation of the Campania Coastal System (Tyrrhenian Sea) for the year 2016: Analysis of the dynamics. J. Mar. Syst. 2019. Submitted. [Google Scholar]
- D’Alelio, D.; Mazzocchi, M.G.; Montresor, M.; Sarno, D.; Zingone, A.; Di Capua, I.; Franzè, G.; Margiotta, F.; Saggiomo, V.; Ribera d’Alcalà, M. The green-blue swing: plasticity of plankton food-webs in response to coastal oceanographic dynamics. Mar. Ecol. 2015, 36, 1155–1170. [Google Scholar] [CrossRef]
- Cianelli, D.; D’Alelio, D.; Uttieri, M.; Sarno, D.; Zingone, A.; Zambianchi, E.; d’Alcalà, M.R. Disentangling physical and biological drivers of phytoplankton dynamics in a coastal system. Sci. Rep. 2017, 7, 15868. [Google Scholar] [CrossRef]
- Sciascia, R.; Berta, M.; Carlson, D.F.; Griffa, A.; Panfili, M.; Mesa, M.L.; Corgnati, L.; Mantovani, C.; Domenella, E.; Fredj, E.; et al. Linking sardine recruitment in coastal areas to ocean currents using surface drifters and HF radar: A case study in the Gulf of Manfredonia, Adriatic Sea. Ocean. Sci. 2018, 14, 1461–1482. [Google Scholar] [CrossRef]
- Iermano, I.; Moore, A.; Zambianchi, E. Impacts of a 4-dimensional variational data assimilation in a coastal ocean model of southern Tyrrhenian Sea. J. Mar. Syst. 2016, 154, 157–171. [Google Scholar] [CrossRef]
- Kalampokis, A.; Uttieri, M.; Poulain, P.M.; Zambianchi, E. Validation of HF radar-derived currents in the Gulf of Naples with Lagrangian data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1452–1456. [Google Scholar] [CrossRef]
- Ranalli, M.; Lagona, F.; Picone, M.; Zambianchi, E. Segmentation of sea current fields by cylindrical hidden Markov models: a composite likelihood approach. J. R. Stat. Soc. Ser. Appl. Stat. 2018, 67, 575–598. [Google Scholar] [CrossRef]
- Saviano, S.; Kalampokis, A.; Zambianchi, E.; Uttieri, M. A year-long assessment of wave measurements retrieved from an HF radar network in the Gulf of Naples (Tyrrhenian Sea, Western Mediterranean Sea). J. Oper. Oceanogr. 2019, 12, 1–15. [Google Scholar] [CrossRef]
- Okubo, A. Horizontal dispersion of floatable trajectories in the vicinity of velocity singularities such as convergencies. Deep-Sea Res. 1970, 17, 445–454. [Google Scholar]
- Weiss, J. The dynamics of enstrophy transfer in 2-dimensional hydrodynamics. Phys. D 1991, 48, 273–294. [Google Scholar] [CrossRef]
- Mkhinini, N.; Coimbra, A.L.S.; Stegner, A.; Arsouze, T.; Taupier-Letage, I.; Béranger, K. Long-lived mesoscale eddies in the eastern Mediterranean Sea: Analysis of 20 years of AVISO geostrophic velocities. J. Geophys. Res. Oceans 2014, 119, 8603–8626. [Google Scholar] [CrossRef]
- Ferrari, R.; Wunsch, C. Ocean circulation kinetic energy: Reservoirs, sources, and sinks. Annu. Rev. Fluid Mech. 2009, 41, 253–282. [Google Scholar] [CrossRef]
- Lévy, M.; Ferrari, R.; Franks, P.J.; Martin, A.P.; Rivière, P. Bringing physics to life at the submesoscale. Geophys. Res. Lett. 2012, 39, 14. [Google Scholar] [CrossRef]
- Smith, K.M.; Hamlington, P.E.; Fox-Kemper, B. Effects of submesoscale turbulence on ocean tracers. J. Geophys. Res. Ocean. 2016, 121, 908–933. [Google Scholar] [CrossRef]
- Schroeder, K.; Chiggiato, J.; Haza, A.; Griffa, A.; Özgökmen, T.; Zanasca, P.; Molcard, A.; Borghini, M.; Poulain, P.M.; Gerin, R.; et al. Targeted Lagrangian sampling of submesoscale dispersion at a coastal frontal zone. Geophys. Res. Lett. 2012, 39, 11. [Google Scholar] [CrossRef]
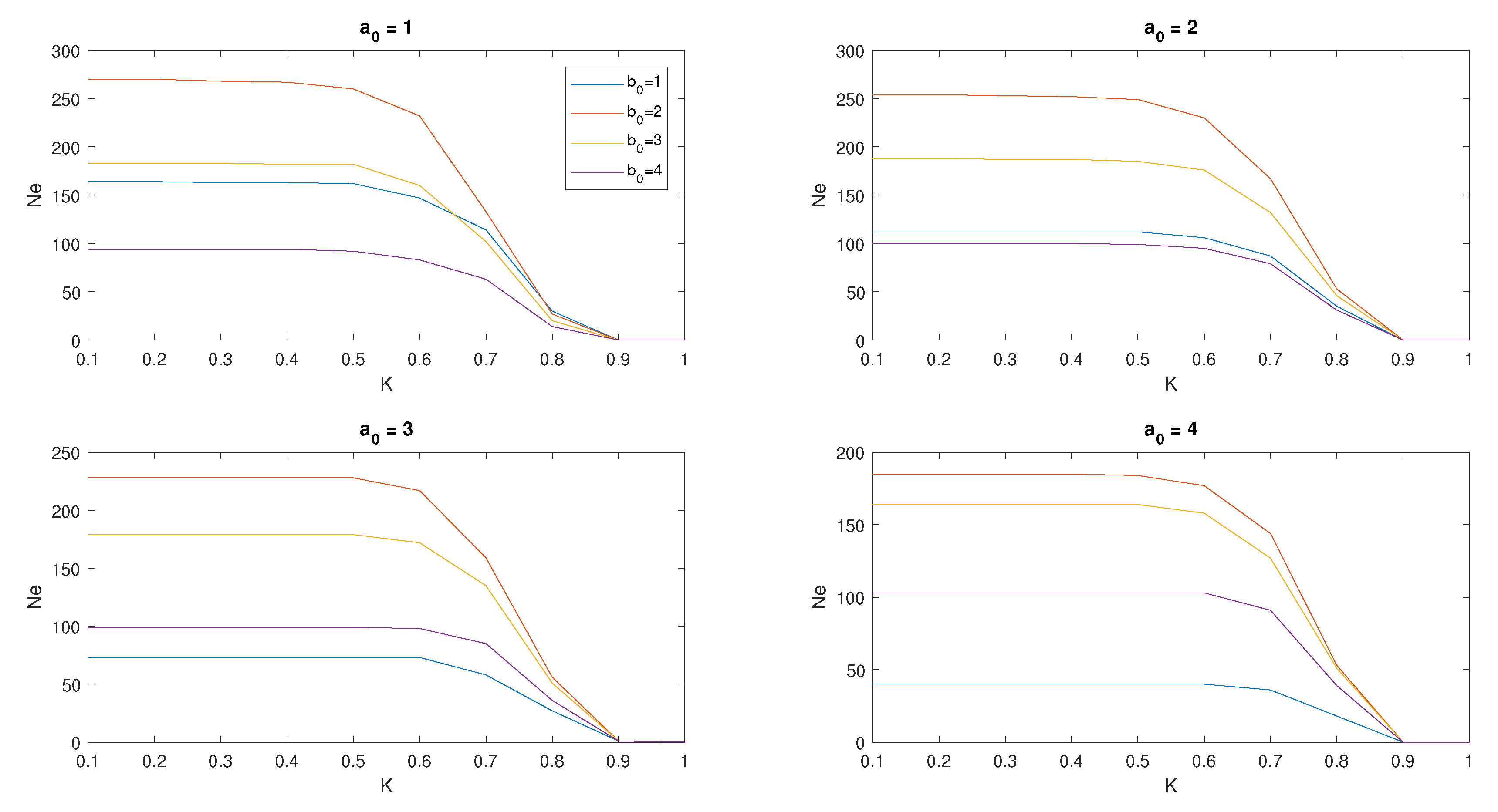
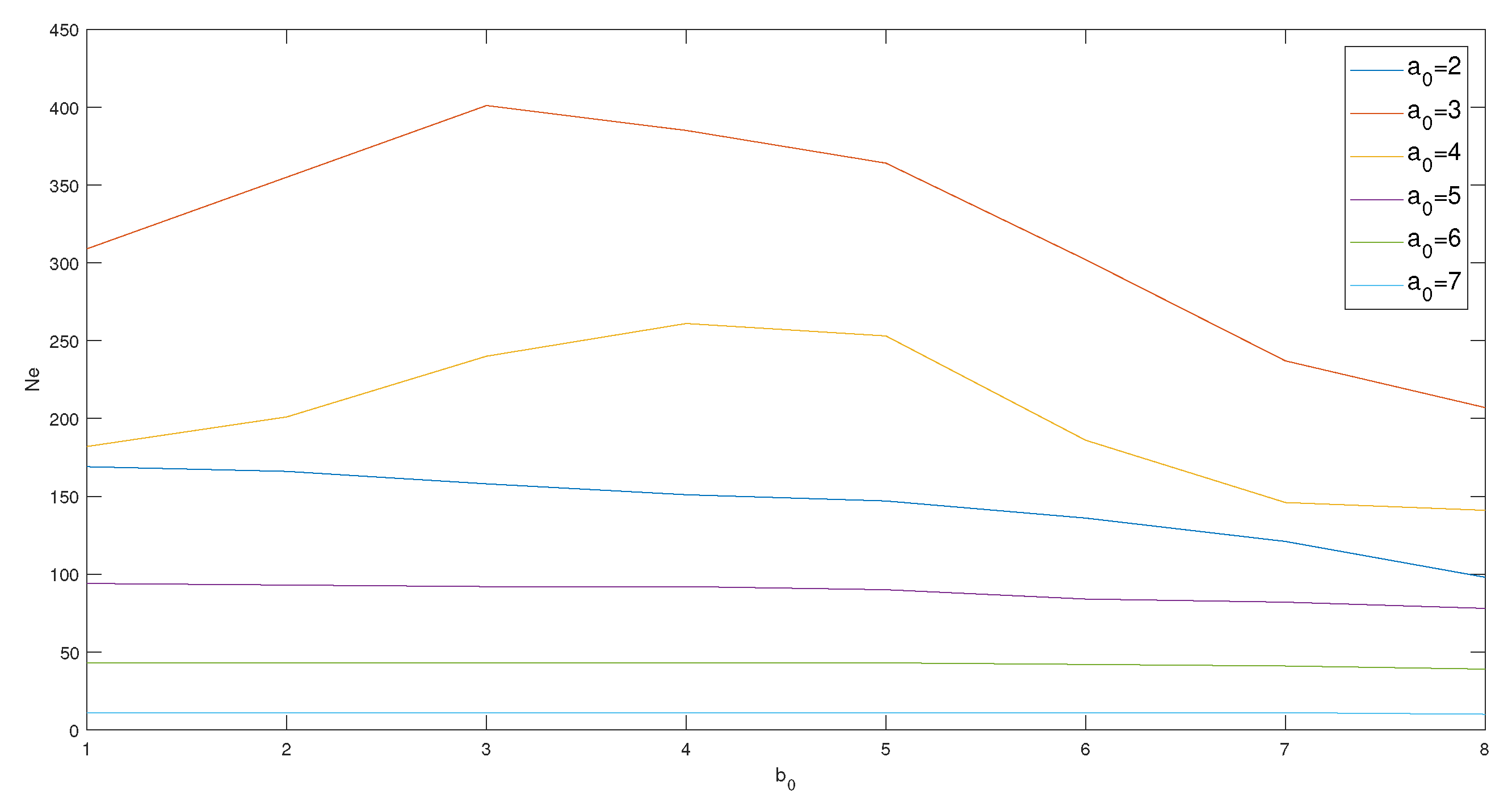
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagaglini, L.; Falco, P.; Zambianchi, E. Eddy Detection in HF Radar-Derived Surface Currents in the Gulf of Naples. Remote Sens. 2020, 12, 97. https://doi.org/10.3390/rs12010097
Bagaglini L, Falco P, Zambianchi E. Eddy Detection in HF Radar-Derived Surface Currents in the Gulf of Naples. Remote Sensing. 2020; 12(1):97. https://doi.org/10.3390/rs12010097
Chicago/Turabian StyleBagaglini, Leonardo, Pierpaolo Falco, and Enrico Zambianchi. 2020. "Eddy Detection in HF Radar-Derived Surface Currents in the Gulf of Naples" Remote Sensing 12, no. 1: 97. https://doi.org/10.3390/rs12010097
APA StyleBagaglini, L., Falco, P., & Zambianchi, E. (2020). Eddy Detection in HF Radar-Derived Surface Currents in the Gulf of Naples. Remote Sensing, 12(1), 97. https://doi.org/10.3390/rs12010097