Comparison of Vegetation Indices for Leaf Area Index Estimation in Vertical Shoot Positioned Vine Canopies with and without Grenbiule Hail-Protection Netting
Abstract
1. Introduction
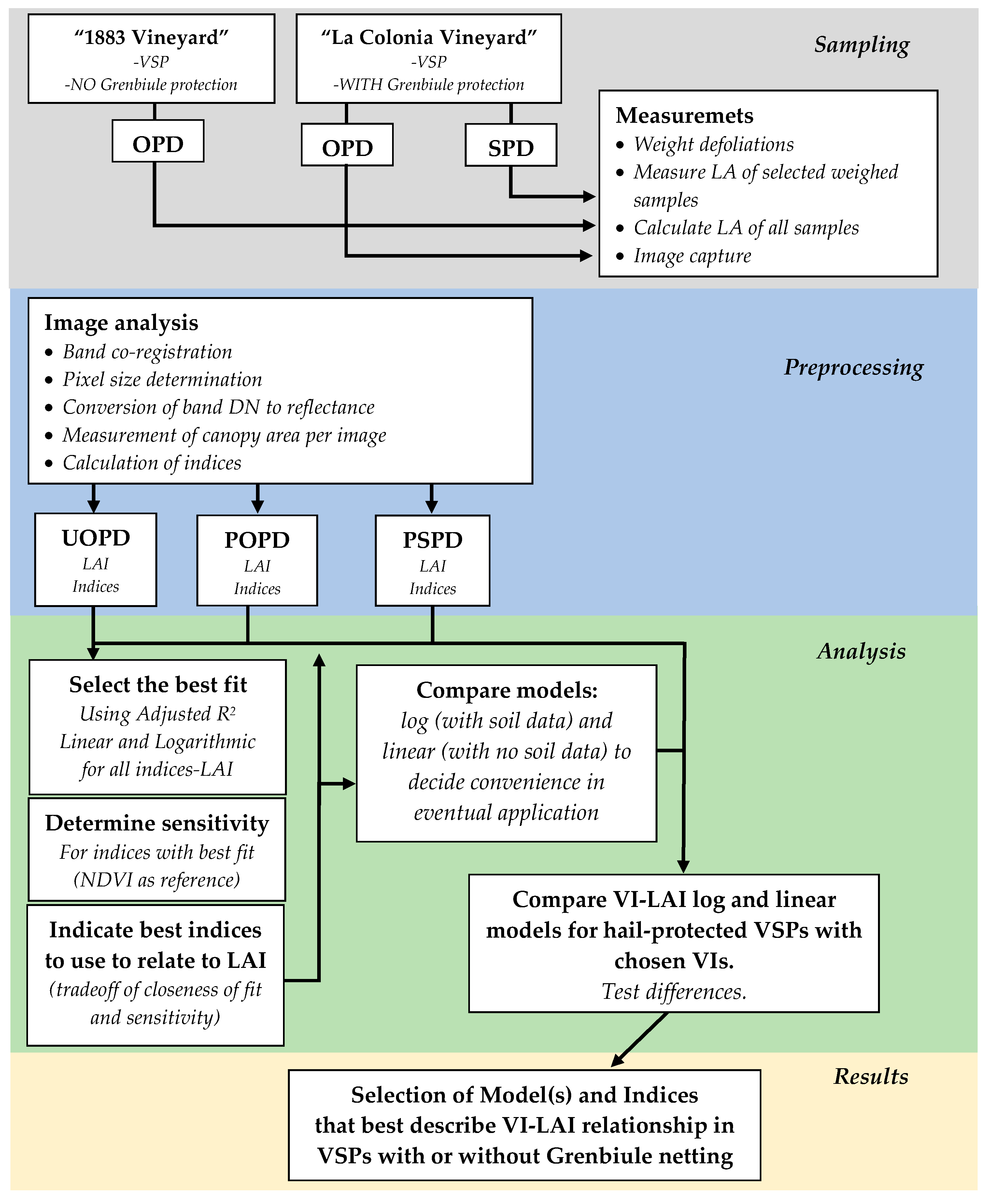
2. Materials and Methods
2.1. Description of the Study Sites
2.2. Canopy Leaf Distributions Generated with and without Hail Protection
2.3. LAI Estimation
2.4. Spectral Data Acquisition
2.5. Multispectral Image Analysis
2.6. Vegetation Indices
2.7. Data Analysis
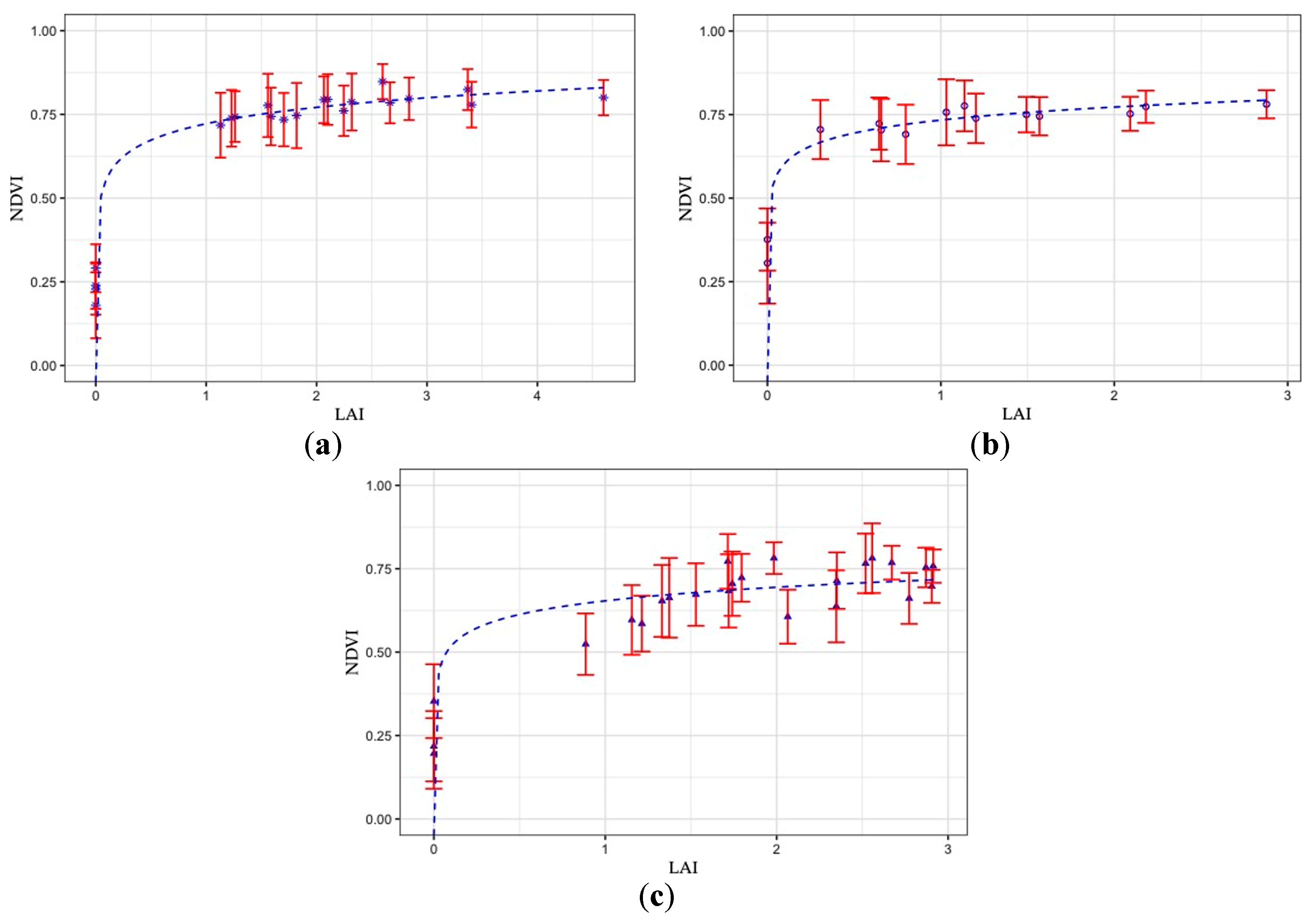
3. Results
3.1. VI Accuracy Comparison
3.2. VI Sensitivity to LAI Changes
3.3. Effect of Grenbiule Hail-Protection Netting on the VI–LAI Relationship
4. Discussion
4.1. VI Accuracy Comparison
4.2. VI Sensitivity to LAI Changes
4.3. Effect of Grenbiule Hail-Protection Netting on the VI–LAI Relationship
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ravaz, M.L. L’effeuillage de la vigne. Annales de L’Ecole Nationale d’agriculture de Montpellier 1911, 11, 216–244. [Google Scholar]
- Watson, D.J. Comparative Physiological Studies on the Growth of Field Crops: I. Variation in Net Assimilation Rate and Leaf Area between Species and Varieties, and within and between Years. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Milthorpe, F.L.; Moorby, J. An Introduction to Crop Physiology; Cambridge University Press: Cambridge, UK, 1974. [Google Scholar]
- Hall, A.; Lamb, D.W.; Holzapfel, B.; Louis, J. Optical remote sensing applications in viticulture—A Review. Aust. J. Grape Wine Res. 2002, 8, 36–47. [Google Scholar] [CrossRef]
- Johnson, L.F. Temporal stability of an NDVI-LAI relationship in a Napa Valley vineyard. Aust. J. Grape Wine Res. 2003, 9, 96–101. [Google Scholar] [CrossRef]
- Hall, A.; Lamb, D.; Holzapfel, B.P.; Louis, J.P. Within-season temporal variation in correlations between vineyard canopy and winegrape composition and yield. Precis. Agric. 2011, 12, 103–117. [Google Scholar] [CrossRef]
- Towers, P.C.; Strever, A.; Poblete-Echeverría, C. Estimation of Vine Pruning Weight using Remote Sensing Data: Relative Contribution of Variables. In Proceedings of the 20th GiESCO International Meeting, Mendoza, Argentina, 5–10 November 2017. [Google Scholar]
- Howell, G.S. Sustainable Grape Productivity and Growth-Yield Relationship: A Review. Am. J. Enol. Vitic. 2001, 52, 165–174. [Google Scholar]
- Kliewer, W.M.; Dokoozlian, N.K. Leaf area/crop Weight ratios of grapevines: Influence on fruit composition and wine quality. Am. J. Enol. Vitic. 2005, 56, 170–181. [Google Scholar]
- Bramley, R.G.V. Understanding variability in winegrape production systems-2. Within vineyard variation in quality over several vintages. Aust. J. Grape Wine Res. 2005, 11, 33–42. [Google Scholar] [CrossRef]
- Rydberg, A.M. Potential Crop Growth Assessment from Remotely Sensed Images Compared to Ordinary Yield Maps. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]
- Machado, S.; Bynum, E.D., Jr.; Archer, T.L.; Lascano, R.J.; Bordovsky, J.; Bronson, K.; Nesmith, D.M.; Segarra, E.; Rosenow, D.T.; Peterson, G.C.; et al. Spatial and temporal variability of sorghum and corn yield: Interactions of biotic and abiotic factors. In Proceedings of the Fifth International Conference on Precision Agriculture, American Society of Agronomy, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]
- Kravchenko, A.N.; Robertson, G.P.; Thelen, K.D.; Harwood, R.R. Management, Topographical, and Weather Effects on Spatial Variability of Crop Grain Yields. Agron. J. 2005, 97, 515–523. [Google Scholar] [CrossRef]
- Hall, A.; Louis, J.P.; Lamb, D.W. Low-resolution remotely sensed images of winegrape vineyards map spatial variability in planimetric canopy area instead of leaf area index. Aust. J. Grape Wine Res. 2008, 14, 9–17. [Google Scholar] [CrossRef]
- Walthall, C.L.; Pachepsky, Y.; Dulaney, W.P.; Timlin, D.J.; Daughtry, C.S.T. Exploitation of spatial information in high resolution digital imagery to map leaf area index. Precis. Agric. 2007, 8, 311–321. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.; Olmedo, G.F.; Ingram, B.; Bardeen, M. Detection and Segmentation of Vine Canopy in Ultra-High Spatial Resolution RGB Imagery Obtained from Unmanned Aerial Vehicle (UAV): A Case Study in a Commercial Vineyard. Remote Sens. 2017, 9, 268. [Google Scholar] [CrossRef]
- Jackson, R.D.; Huete, A.R. Interpreting Vegetation Indices. Prev. Vet. Med. 1991, 11, 185–200. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Qi, J.; Kerr, Y.; Chehbouni, A. External factor consideration in vegetation index development. In Proceedings of the 6th International Symposium on Physical Measurements and Signatures in Remote Sensing, Val D’Isere, France, 17–22 January 1994; pp. 723–730. [Google Scholar]
- Ray, T.W. A FAQ on Vegetation in Remote Sensing. Division of Geological and Planetary Sciences, California Institute of Technology. 1994. Available online: http://www.yale.edu/ceo/Documentation/rsvegfaq.html (accessed on 15 August 2018).
- Proffitt, T.; Pearse, B. Adding value to the wine business precisely: Using precision viticulture technology in Margaret River. Managing vineyard variation—Precision viticulture workshop. In Proceedings of the 12th Australian Wine Industry Technical Conference; The Australian and New Zealand Grapegrower and Winemaker: Broadview, Australia, 2004; pp. 40–44. [Google Scholar]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A Modified Soil Adjusted Vegetation Index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Arkebauer, T.J.; Rundquist, D.C.; Keydan, G.P.; Leavitt, B. Remote estimation of leaf area index and green leaf biomass in maize canopies. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Steele, M.R.; Gitelson, A.A.; Rundquist, D. Nondestructive Estimation of Leaf Chlorophyll Content in Grapes. Am. J. Enol. Vitic. 2008, 59, 299–305. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Viña, A.; Henebry, G.M.; Gitelson, A.A. Satellite monitoring of vegetation dynamics: Sensitivity enhancement by the wide dynamic range vegetation index. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Keller, M. The Science of Grapevines. Anatomy and Physiology; Academic Press: London, UK, 2010; pp. 125–158. [Google Scholar]
- Hatfield, J.L.; Gitelson, A.A.; Schepers, J.S.; Walthall, C.L. Application of Spectral Remote Sensing for Agronomic Decisions. Agron. J. 2008, 100, S-117–S-131. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Lobos, G.A.; Poblete Echeverría, C. Spectral Knowledge (SK-UTALCA): Software for Exploratory Analysis of High-Resolution Spectral Reflectance Data on Plant Breeding. Front. Plant Sci. 2017, 7, 1996. [Google Scholar] [CrossRef] [PubMed]
- Chanda, S.V.; Singh, Y.D. Estimation of Leaf Area in Wheat Using Linear Measurements. Plant Breed. Seed Sci. 2002, 46, 75–79. [Google Scholar]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2000, 76, 156–172. [Google Scholar] [CrossRef]
- Wiegand, C.L.; Richardson, A.J.; Escobar, D.E.; Gerbermann, A.H. Vegetation Indices in Crop Assessments. Remote Sens. Environ. 1991, 35, 105–119. [Google Scholar] [CrossRef]
- Peng, Y.; Gitelson, A.A.; Keydan, G.; Rundquist, D.C.; Moses, W. Remote estimation of gross primary production in maize and support for a new paradigm based on total crop chlorophyll content. Remote Sens. Environ. 2011, 115, 978–989. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Nelson, S.G. Relationship Between Remotely-sensed Vegetation Indices, Canopy Attributes and Plant Physiological Processes: What Vegetation Indices Can and Cannot Tell Us About the Landscape. Sensors 2008, 8, 2136. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Johnson, L.F.; Roczen, D.; Youkhana, S. Vineyard Canopy Density Mapping with IKONOS Satellite Imagery. In Proceedings of the Third International Conference on Geospatial Information in Agriculture and Forestry, Denver, CO, USA, 5–7 November 2001. [Google Scholar]
- Perry, A.; Weber, K. Land Cover Change Analysis Using MSAVI2 for Orchard Project; Orchard LCC Project 2015; Idaho State University: Pocatello, ID, USA, 2015. [Google Scholar]
- Laosuwan, T.; Uttaruk, Y. Estimating Tree Biomass via Remote Sensing, MSAVI 2, and Fractional Cover Model. IETE Tech. Rev. 2014, 31, 362–368. [Google Scholar] [CrossRef]
- Ahmad, F. Spectral vegetation indices performance evaluated for Cholistan Desert. J. Geogr. Reg. Plan. 2012, 5, 165–172. [Google Scholar]




| Index | Formula | Features |
|---|---|---|
| NDVI—Normalized difference vegetation index | Robust but insensitive at high leaf area index (LAI) values | |
| RVI—Ratio vegetation index | Sensitive over a broad range | |
| WDRVI—Wide dynamic range veg. index [6] | Sensitive at high LAI | |
| MSAVI—Modified soil-adjusted vegetation index [24] | (1) | Corrects influence of soil and provides a variable value for L |
| MSAVI2—Second modified soil-adjusted vegetation index [24] | Corrects influence of soil and provides and does not require L (1) | |
| PVI —Perpendicular vegetation index [23] | (2) | Affected by atmospheric attenuation and soil dampness |
| CIrededge—Red edge chlorophyll index [25] | Sensitive in corn, good gross primary productivity estimator | |
| SAVI2—Soil-adjusted vegetation index 2 [35] | (3) | Sensitive in corn, good gross primary productivity estimator |
| Vegetation Index | Logarithmic Regression Model | Adjusted R2 | RMSE | Linear Regression Model | Adjusted R2 | RMSE |
|---|---|---|---|---|---|---|
| NDVI | 0.069 ln(LAI) – 0.72 | 0.98 | 0.59 | 0.03 LAI + 0.71 | 0.48 | 0.61 |
| WDRVI (1) | 0.098 ln(LAI) + 0.33 | 0.97 | 0.87 | 0.06 LAI + 0.27 | 0.48 | 0.69 |
| MSAVI2 | 0.064 ln(LAI) + 0.67 | 0.96 | 1.10 | 0.04 LAI + 0.63 | 0.36 | 0.71 |
| WDRVI (2) | 0.056 ln(LAI) – 0.47 | 0.91 | 2.71 | 0.05 LAI – 0.56 | 0.47 | 0.80 |
| RVI | 0.866 ln(LAI) + 7.48 | 0.83 | 5.63 | 1.02 LAI + 5.55 | 0.46 | 0.91 |
| SAVI2 | 2.886 ln(LAI) + 21.10 | 0.73 | 10.04 | 4.93 LAI + 11.96 | 0.45 | 0.55 |
| MSAVI | 0.106 ln(LAI)+ 0.95 | 0.69 | 2.63 | 0.21 LAI + 0.58 | 0.33 | 0.80 |
| PVI | 0.027 ln(LAI) + 0.52 | 0.67 | 7.10 | 0.03 LAI + 0.46 | 0.15 | 0.89 |
| CIrededge | 0.056 ln(LAI) – 1.05 | 0.41 | 5.40 | - | - | - |
| Vegetation Index | Relative Sensitivity (Sr) |
|---|---|
| NDVI (Reference) | 1.0 |
| RVI | 2.74 |
| WDRVI (α = 0.05) | 2.07 |
| MSAVI2 | 1.45 |
| WDRVI (α = 0.3) | 1.42 |
| NDVI | WDRVI (α = 0.05) | RVI | ||||
|---|---|---|---|---|---|---|
| Coefficient | Estimation | p-Value | Estimation | p-Value | Estimation | p-Value |
| Constant | 0.72 | <0.0001 | −0.48 | <0.0001 | 7.26 | <0.0001 |
| lnLAI | 0.07 | <0.001 | 0.05 | <0.0001 | 0.83 | <0.0001 |
| POPD | 0.01 | 0.3265 | −0.02 | 0.3435 | −0.5 | 0.1888 |
| PSPD | −0.06 | <0.0001 | −0.01 | <0.0001 | −1.73 | <0.0001 |
| POPD_lnLAI | −0.01 | 0.0112 | −0.01 | 0.2878 | −0.13 | 0.3308 |
| PSPD_lnLAI | 0.0036 | 0.4518 | −0.01 | 0.1026 | −0.22 | 0.0874 |
| NDVI | WDRVI (α = 0.05) | RVI | ||||
|---|---|---|---|---|---|---|
| Coefficient | Estimation | p-Value | Estimation | p-Value | Estimation | p-Value |
| Constant | 0.72 | <0.0001 | −0.54 | <0.0001 | 5.78 | <0.0001 |
| LAI | 0.02 | 0.0212 | 0.05 | 0.0014 | 0.92 | 0.0004 |
| POPD | −0.02 | 0.6117 | −0.02 | 0.7242 | −0.18 | 0.8194 |
| PSPD | −0.19 | <0.0001 | −0.21 | 0.0001 | −3.32 | 0.0005 |
| POPD_LAI | 0.01 | 0.6887 | −0.0042 | 0.8640 | 0.0045 | 0.9916 |
| PSPD_LAI | 0.05 | 0.0021 | −0.05 | 0.0443 | 0.61 | 0.1269 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Towers, P.C.; Strever, A.; Poblete-Echeverría, C. Comparison of Vegetation Indices for Leaf Area Index Estimation in Vertical Shoot Positioned Vine Canopies with and without Grenbiule Hail-Protection Netting. Remote Sens. 2019, 11, 1073. https://doi.org/10.3390/rs11091073
Towers PC, Strever A, Poblete-Echeverría C. Comparison of Vegetation Indices for Leaf Area Index Estimation in Vertical Shoot Positioned Vine Canopies with and without Grenbiule Hail-Protection Netting. Remote Sensing. 2019; 11(9):1073. https://doi.org/10.3390/rs11091073
Chicago/Turabian StyleTowers, Pedro C., Albert Strever, and Carlos Poblete-Echeverría. 2019. "Comparison of Vegetation Indices for Leaf Area Index Estimation in Vertical Shoot Positioned Vine Canopies with and without Grenbiule Hail-Protection Netting" Remote Sensing 11, no. 9: 1073. https://doi.org/10.3390/rs11091073
APA StyleTowers, P. C., Strever, A., & Poblete-Echeverría, C. (2019). Comparison of Vegetation Indices for Leaf Area Index Estimation in Vertical Shoot Positioned Vine Canopies with and without Grenbiule Hail-Protection Netting. Remote Sensing, 11(9), 1073. https://doi.org/10.3390/rs11091073








