Evaluation and Validation of CryoSat-2-Derived Water Levels Using In Situ Lake Data from China
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. CryoSat-2
2.1.2. Hydrological Databases
2.1.3. In Situ Data
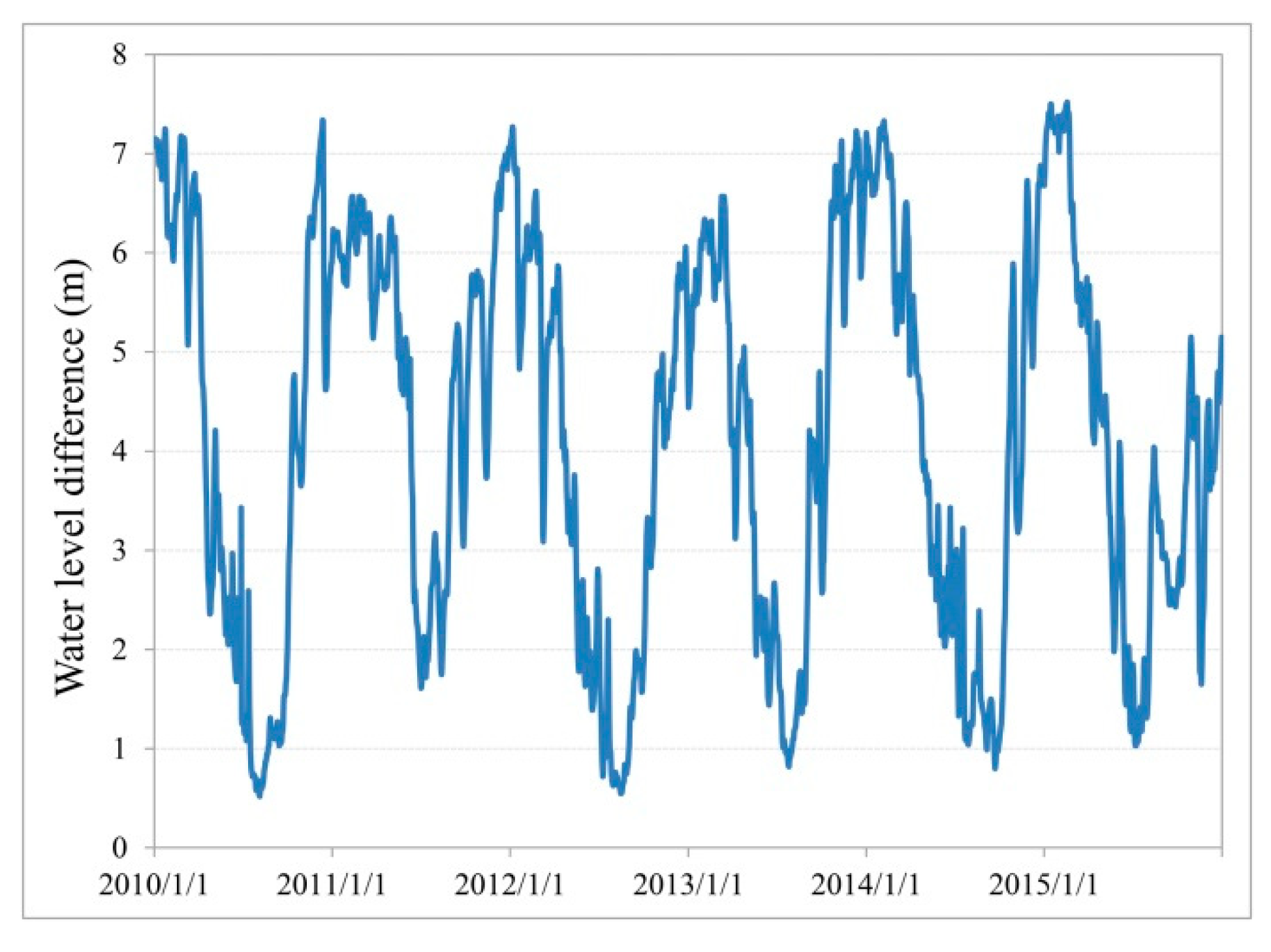
2.1.4. Study Area
2.2. Method
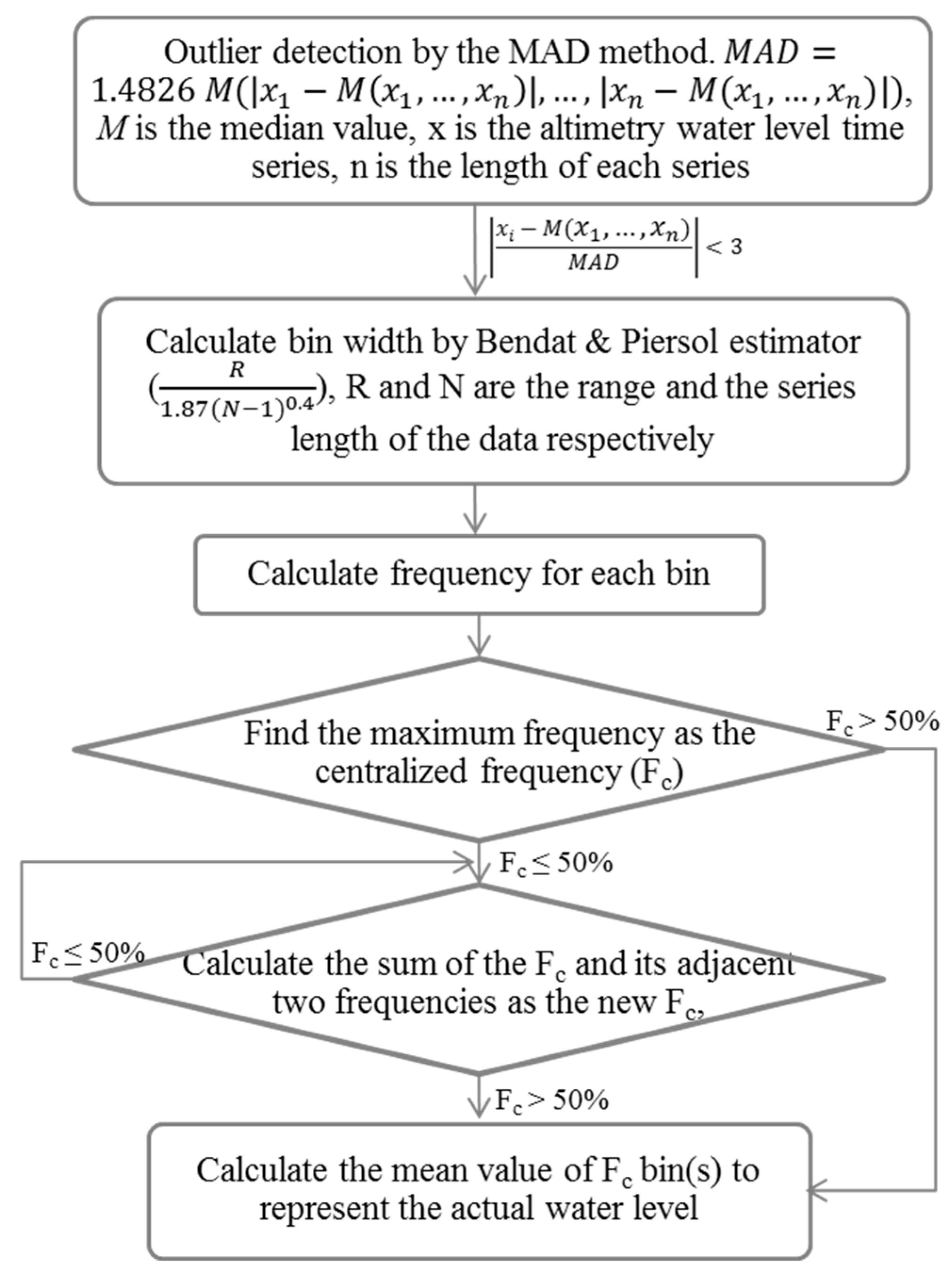
2.2.1. The Concentrated Probability Density Function (PDF) Method for Each Along-Track Geophysical Data Record (GDR)
- Outlier detection for each along-track by the MAD method. MAD is calculated by Equation (1) according to [26].where M is the median value of a series, x is the altimetry water level time series, and n is the length of each series. If , or , then these GDR points were deleted as outliers.
- For the remaining GDR heights, if the number of GDR heights in the along-track segment was larger than 5, then we calculated the bin width using the Bendat and Piersol estimator [33]. If the number of heights was less than or equal to 5, the along-track data were abandoned.
- Calculate the frequency (F) for each bin. , in which nb is the number of heights in a bin, and N is the number of heights in an along-track segment.
- Find the maximum frequency as the concentrated frequency (Fc). If Fc > 50%, then go to step 6, otherwise, go to step 5. This step aimed to detect the majority of “correct” altimetry water levels.
- Calculate the sum of the Fc and its adjacent two frequencies as the new Fc. If the new Fc > 50% then go to step 6, otherwise repeat step 5 until the new Fc > 50%.
- Calculate the mean value of the Fc bin(s) to represent the actual water level.
2.2.2. Evaluation Criteria
3. Results
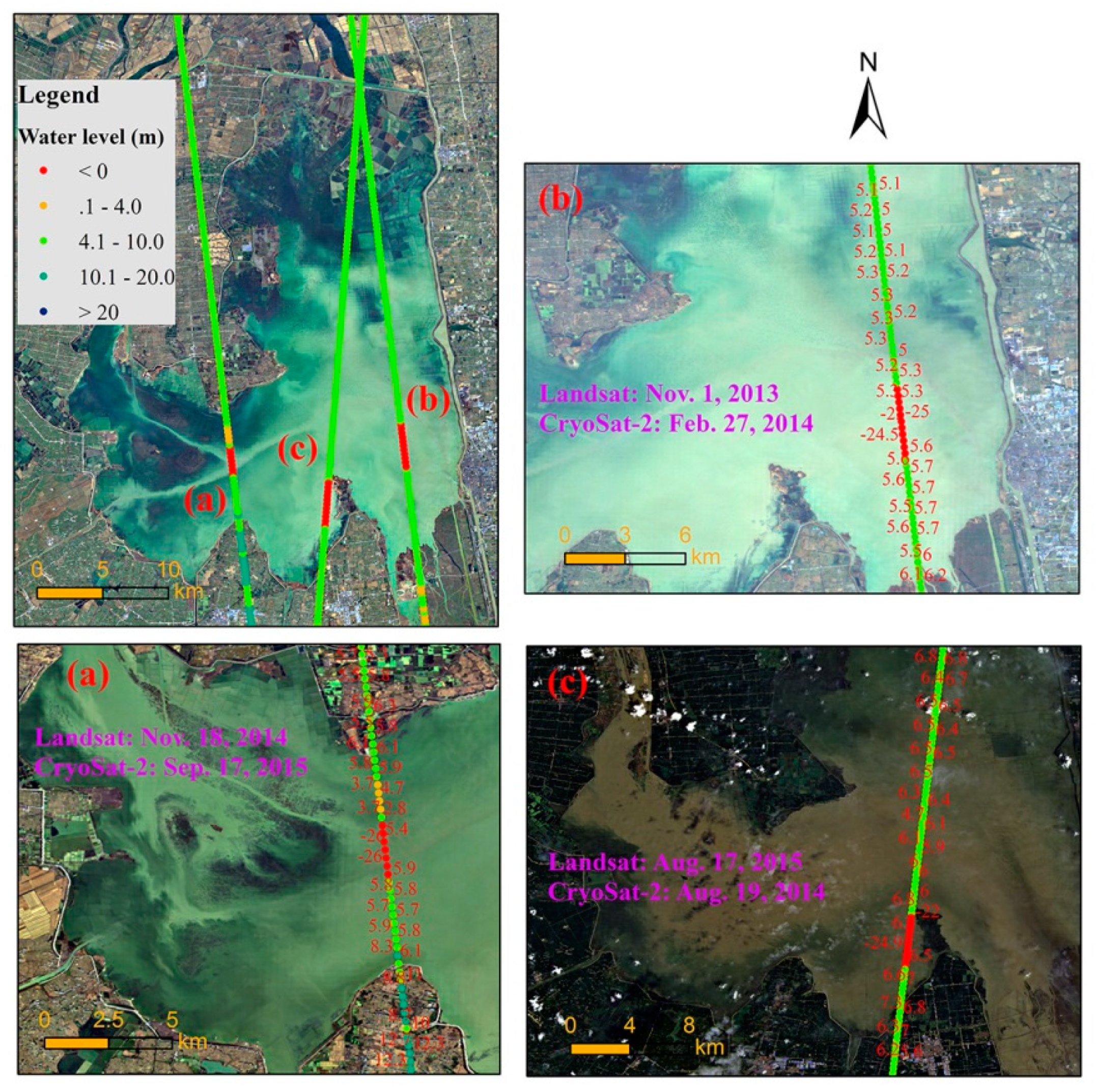
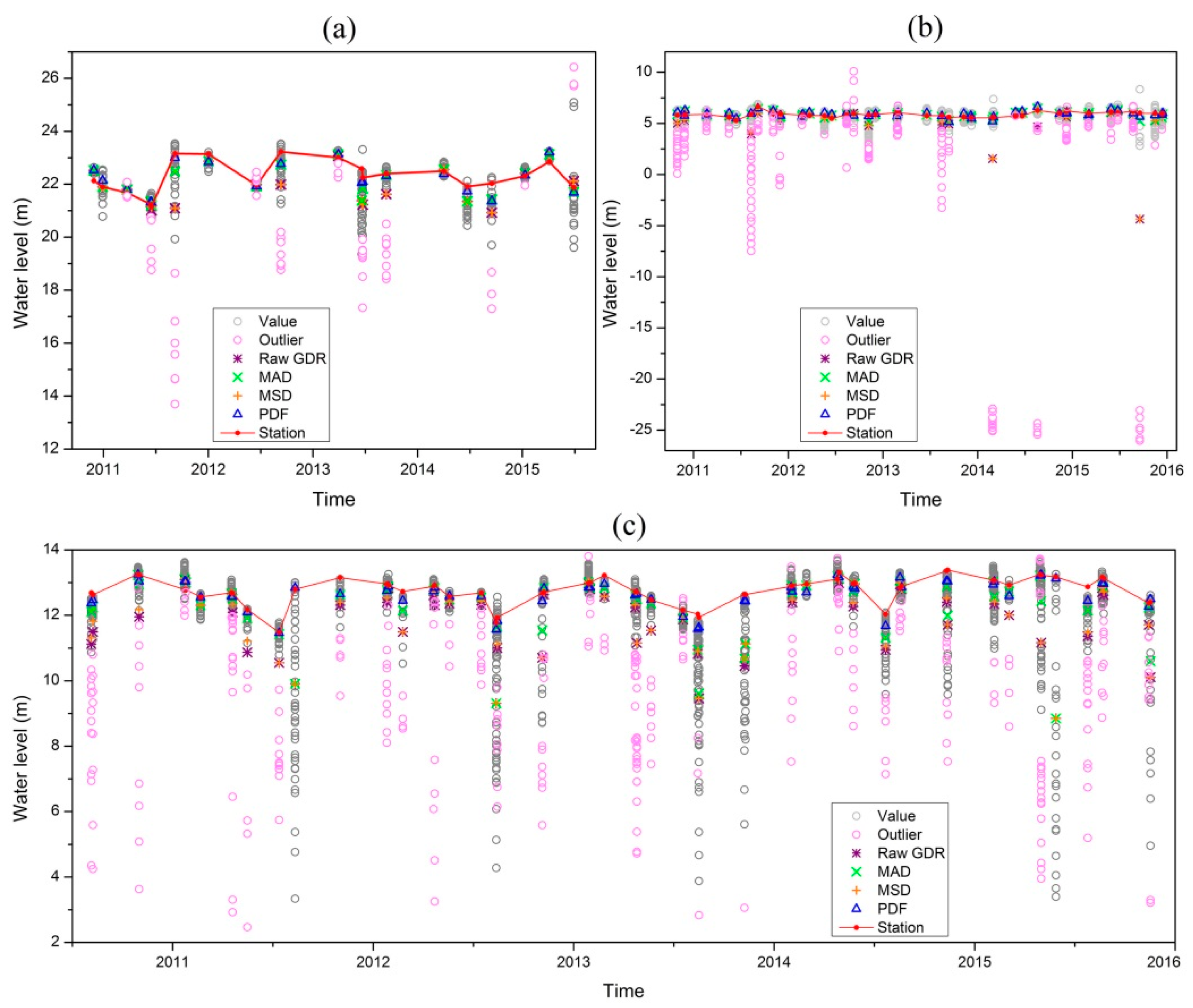
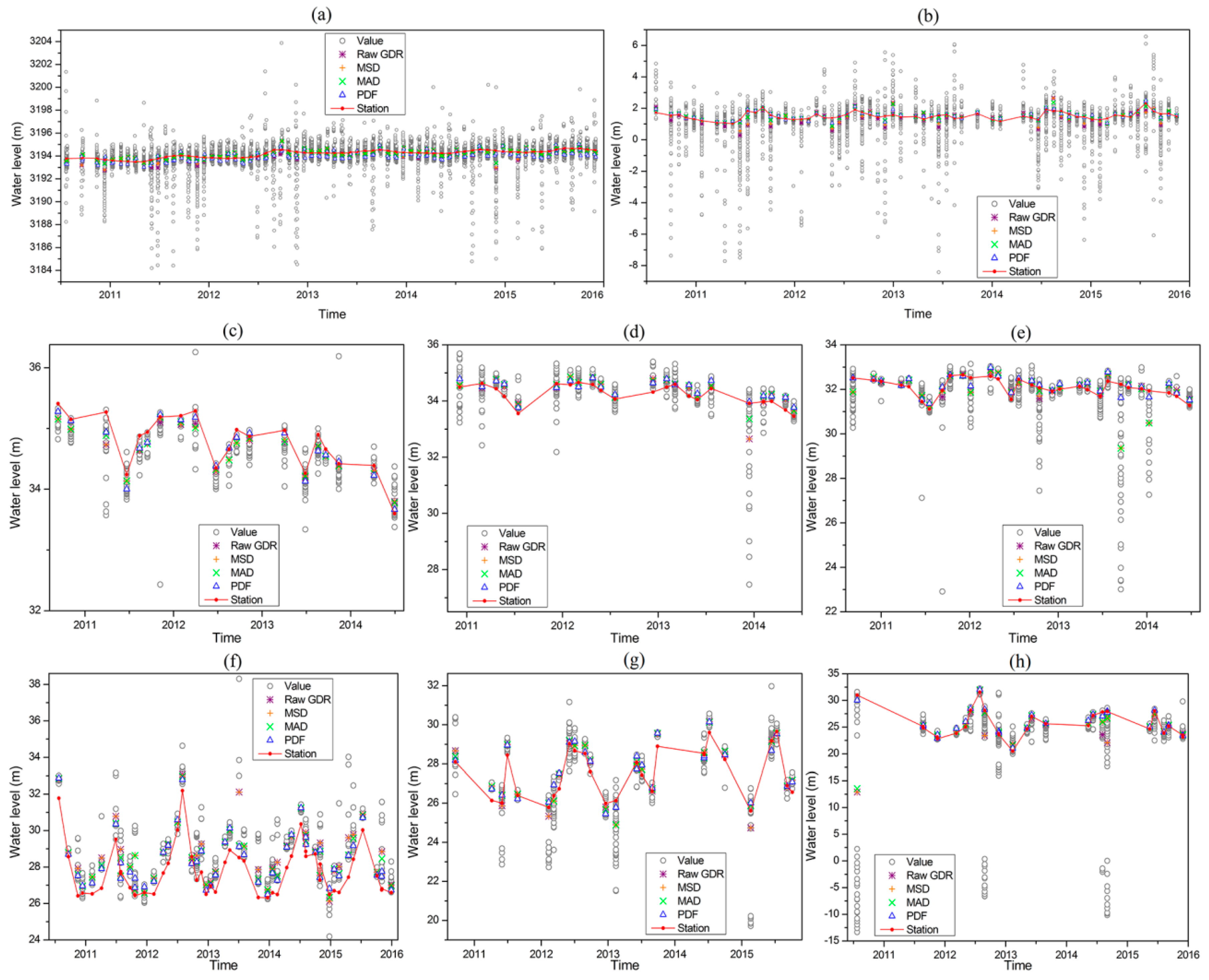
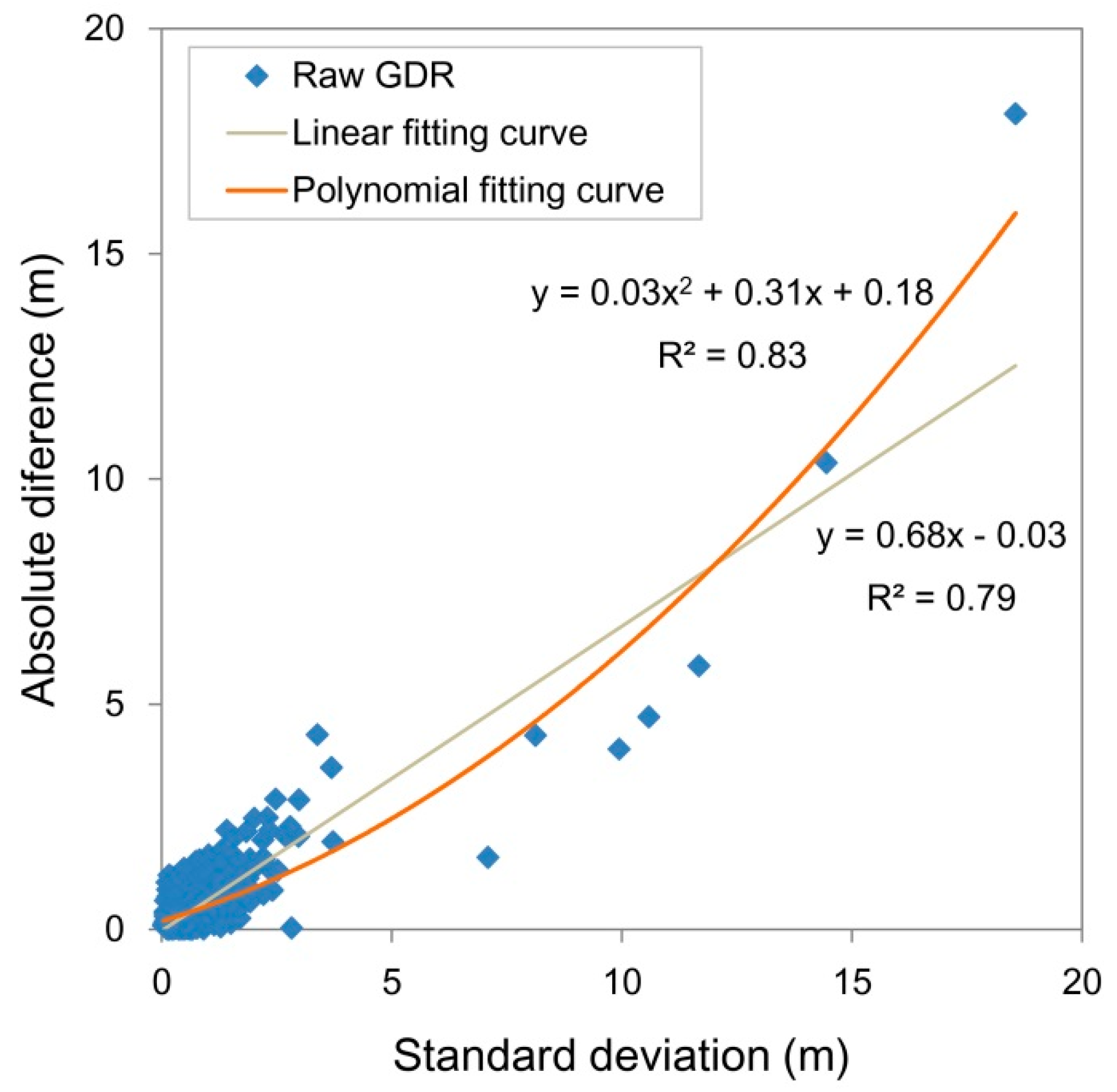
3.1. Evaluation of Different Pre-Processing Methods of the CryoSat-2 GDR Water Levels
3.2. Validation of the CryoSat-2 GDR Water Levels
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kleinherenbrink, M.; Ditmar, P.G.; Lindenbergh, R.C. Retracking Cryosat data in the SARIn mode and robust lake level extraction. Remote Sens. Environ. 2014, 152, 38–50. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Jiang, L.; Schneider, R.; Andersen, O.B.; Bauer-Gottwein, P. CryoSat-2 altimetry applications over rivers and lakes. Water 2017, 9, 211. [Google Scholar] [CrossRef]
- Ricker, R.; Hendricks, S.; Helm, V.; Gerdes, R. Classification of CryoSat-2 radar echoes. In Towards an Interdisciplinary Approach in Earth System Science; Lohmann, G., Meggers, H., Unnithan, V., Wolf-Gladrow, D., Notholt, J., Bracher, A., Eds.; Springer: Cham, Switzerland, 2015; pp. 149–158. [Google Scholar]
- Raney, R.K. The delay/doppler radar altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Bergé-Nguyen, M.; Calmant, S.; Romanovski, V.V.; Meyssignac, B.; Perosanz, F.; Tashbaeva, S.; Arsen, A.; Fund, F.; Martignago, N.; et al. Calibration of envisat radar altimeter over Lake Issykkul. Adv. Space Res. 2013, 51, 1523–1541. [Google Scholar] [CrossRef]
- Nielsen, K.; Stenseng, L.; Andersen, O.B.; Villadsen, H.; Knudsen, P. Validation of CryoSat-2 SAR mode based lake levels. Remote Sens. Environ. 2015, 171, 162–170. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef]
- Birkett, C.M.; Beckley, B. Investigating the performance of the Jason-2/OSTM radar altimeter over lakes and reservoirs. Mar. Geod. 2010, 33, 204–238. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Calmant, S.; Del-Rio, R.A.; Kouraev, A.; Bergé-Nguyen, M.; Maisongrande, P. Lakes studies from satellite altimetry. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 509–533. [Google Scholar]
- Dettmering, D.; Schwatke, C.; Boergens, E.; Seitz, F. Potential of ENVISAT radar altimetry for water level monitoring in the pantanal wetland. Remote Sens. 2016, 8, 596. [Google Scholar] [CrossRef]
- Fernandes, M.J.; Lázaro, C.; Nunes, A.L.; Scharroo, R. Atmospheric corrections for altimetry studies over inland water. Remote Sens. 2014, 6, 4952–4997. [Google Scholar] [CrossRef]
- Sridevi, T.; Sharma, R.; Mehra, P.; Prasad, K.V.S.R. Estimating discharge from the Godavari River using ENVISAT, Jason-2, and SARAL/AltiKa radar altimeters. Geophys. Res. Lett. 2016, 7, 348–357. [Google Scholar] [CrossRef]
- Frappart, F.; Biancamaria, S.; Normandin, C.; Blarel, F.; Bourrel, L.; Aumont, M.; Azemar, P.; Vu, P.L.; Toan, T.L.; Lubac, B.; et al. Influence of recent climatic events on the surface water storage of the Tonle Sap Lake. Sci. Total Environ. 2018, 636, 1520–1533. [Google Scholar] [CrossRef]
- Boergens, E.; Dettmering, D.; Schwatke, C.; Seitz, F. Treating the hooking effect in satellite altimetry data: A case study along the Mekong River and its tributaries. Remote Sens. 2016, 8, 91. [Google Scholar] [CrossRef]
- Hossain, F.; Siddique-E-Akbor, A.; Mazumder, L.C.; ShahNewaz, S.M.; Biancamaria, S.; Lee, H.; Shum, C. Proof of concept of an altimeter-based river forecasting system for transboundary flow inside Bangladesh. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 587–601. [Google Scholar] [CrossRef]
- Passaro, M.; Rose, S.K.; Andersen, O.B.; Boergens, E.; Calafat, F.M.; Dettmering, D.; Benveniste, J. ALES+: Adapting a homogenous ocean retracker for satellite altimetry to sea ice leads, coastal and inland waters. Remote Sens. Environ. 2018, 211, 456–471. [Google Scholar] [CrossRef]
- Frappart, F.; Calmant, S.; Cauhopé, M.; Seyler, F.; Cazenave, A. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon basin. Remote Sens. Environ. 2006, 100, 252–264. [Google Scholar] [CrossRef]
- Göttl, F.; Dettmering, D.; Müller, F.L.; Schwatke, C. Lake level estimation based on CryoSat-2 SAR altimetry and multi-looked waveform classification. Remote Sens. 2016, 8, 885. [Google Scholar] [CrossRef]
- Bogning, S.; Frappart, F.; Blarel, F.; Niño, F.; Mahé, G.; Bricquet, J.P.; Seyler, F.; Onguéné, R.; Etamé, J.; Paiz, M.C.; et al. Monitoring water levels and discharges using radar altimetry in an ungauged river basin: The case of the Ogooué. Remote Sens. 2018, 10, 350. [Google Scholar] [CrossRef]
- Song, C.; Ye, Q.; Cheng, X. Shifts in water-level variation of Namco in the central Tibetan Plateau from ICESat and CryoSat-2 altimetry and station observations. Sci. Bull. 2015, 60, 1287–1297. [Google Scholar] [CrossRef]
- Boergens, E.; Nielsen, K.; Andersen, O.B.; Dettmering, D.; Seitz, F. River levels derived with CryoSat-2 SAR data classification—A case study in the Mekong River Basin. Remote Sens. 2017, 9, 1238. [Google Scholar] [CrossRef]
- Sheese, P.E.; Boone, C.D.; Walker, K.A. Detecting physically unrealistic outliers in ACE-FTS atmospheric measurements. Atmos. Meas. Tech. 2015, 8, 741–750. [Google Scholar] [CrossRef]
- Kleinherenbrink, M.; Lindenbergh, R.C.; Ditmar, P.G. Monitoring of lake level changes on the Tibetan Plateau and Tian Shan by retracking Cryosat SARIn waveforms. J. Hydrol. 2015, 521, 119–131. [Google Scholar] [CrossRef]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Benveniste, J. Annual sea level variability of the coastal ocean: The Baltic Sea-North Sea transition zone. J. Geophys. Res. Oceans 2015, 120, 3061–3078. [Google Scholar] [CrossRef]
- Bouzinac, C. CryoSat Product Handbook. Available online: https://earth.esa.int/documents/10174/125272/CryoSat_Product_Handbook (accessed on 20 February 2019).
- Liu, Z.; Yao, Z.; Wang, R. Automatic identification of the lake area at Qinghai–Tibetan Plateau using remote sensing images. Quat. Int. 2019, 503, 136–145. [Google Scholar] [CrossRef]
- Cretaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.V.; Vuglinski, V.V.; Bergé-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca-Del-Rio, R.; Cazenave, A.; et al. SOLS: A lake database to monitor in near real time water level and storage variations from remote sensing data. J. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Guo, H.R.; Jiao, W.H.; Yang, Y.X. The systematic difference and its distribution between the 1985 national height datum and the global quasigeoid. Acta Geod. Cartogr. Sin. 2004, 33, 100–104, (In Chinese but with English Abstract). [Google Scholar]
- Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Measurements and Analysis of Random Data; John Wiley and Sons: New York, NY, USA, 1966. [Google Scholar]
- Doane, D.P. Aesthetic frequency classifications. Am. Stat. 1976, 30, 181–183. [Google Scholar]
- Sturges, H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926, 21, 65–66. [Google Scholar] [CrossRef]
- Nielsen, K.; Stenseng, L.; Andersen, O.B.; Knudsen, P. The performance and potentials of the CryoSat-2 SAR and SARIn modes for lake level estimation. Water 2017, 9, 374. [Google Scholar] [CrossRef]
- Ma, R.H.; Yang, G.S.; Duan, H.T.; Jiang, J.H.; Wang, S.M.; Feng, X.Z.; Li, A.N.; Kong, F.X.; Xue, B.; Wu, J.L.; et al. China’s lakes at present: Number, area and spatial distribution. Sci. China Earth Sci. 2011, 54, 283–289. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Andersen, O.B.; Bauer-Gottwein, P. CryoSat-2 radar altimetry for monitoring freshwater resources of China. Remote Sens. Environ. 2017, 200, 125–139. [Google Scholar] [CrossRef]
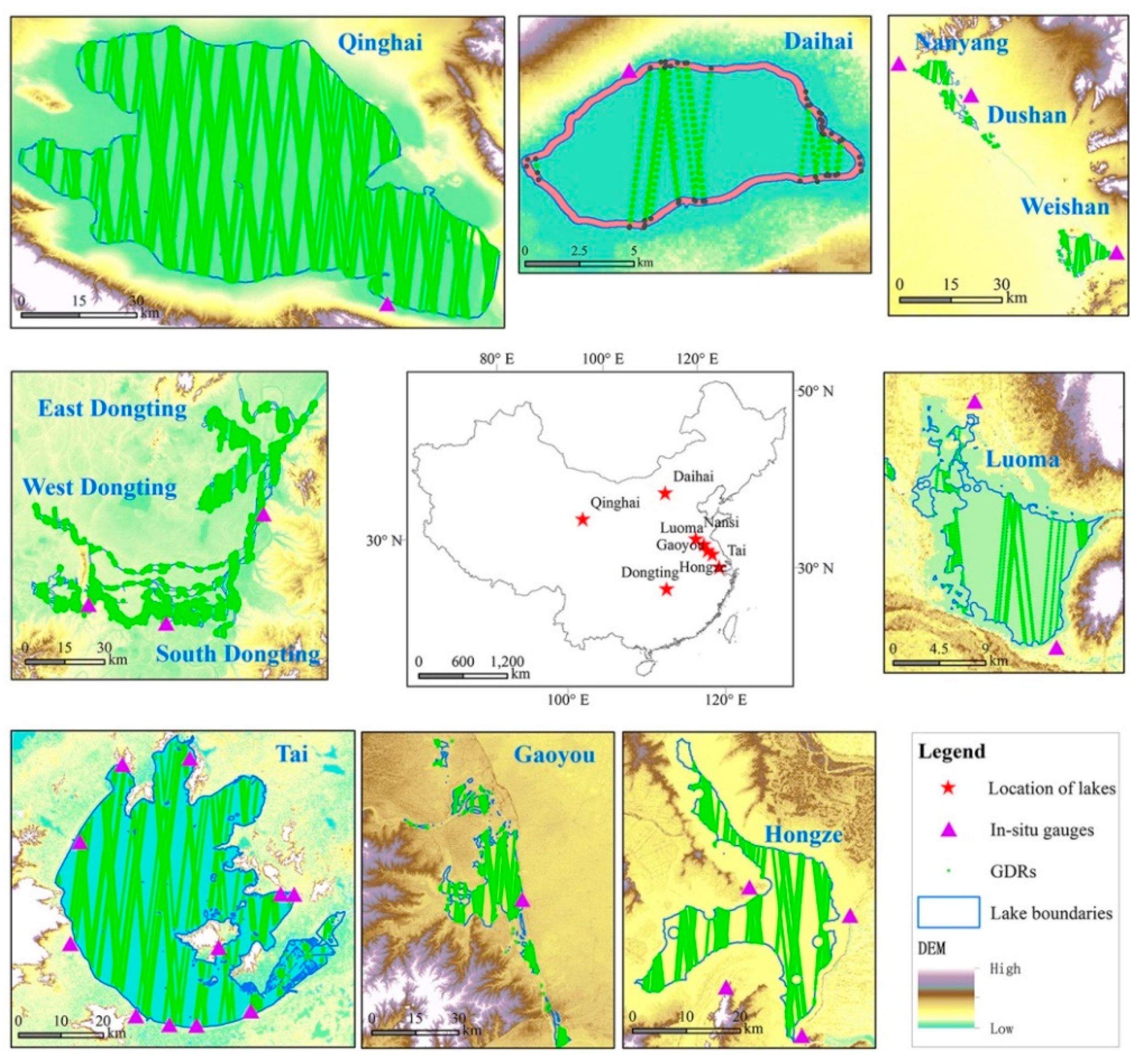
| Name of Lakes | Luoma | Gaoyou | Hongze | Qinghai | Tai | Nanyang | Dushan | Weishan | West Dongting | South Dongting | East Dongting | Daihai | Mean Absolute Means | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean of in situ data | 22.28 | 5.87 | 2.77 | 3194.2 | 1.54 | 34.78 | 34.24 | 32.08 | 27.76 | 27.57 | 25.67 | (--) | ||
| Standard Deviation (SD) of in situ data | 0.61 | 0.24 | 0.42 | 0.32 | 0.25 | 0.46 | 0.36 | 0.4 | 1.4 | 1.26 | 2.51 | 0.61 | ||
| Mean difference | −0.07 | 0.03 | −0.19 | −0.03 | 0.03 | −0.09 | 0.18 | 0.1 | 0.67 | 0.19 | 0.19 | (--) | 0.16 | |
| MAD | −0.17 | −0.06 | −0.52 | −0.04 | 0.03 | −0.13 | 0.17 | −0.07 | 0.8 | 0.18 | −0.53 | (--) | 0.25 | |
| MSD | −0.36 | −0.47 | −0.78 | −0.05 | −0.03 | −0.15 | 0.11 | −0.08 | 0.98 | 0.09 | −0.93 | (--) | 0.37 | |
| GDR | −0.37 | −0.53 | −0.85 | −0.07 | −0.08 | −0.15 | 0.11 | −0.09 | 0.98 | 0.09 | −1.04 | (--) | 0.4 | |
| SD difference | −0.02 | 0.05 | 0.1 | 0.05 | 0.04 | −0.02 | −0.04 | 0 | 0.09 | 0.02 | −0.15 | 0.1 | 0.06 | |
| MAD | 0.01 | 0.06 | 0.59 | 0.08 | 0.05 | −0.08 | 0.03 | 0.29 | 0.07 | 0.12 | 0.53 | 0.42 | 0.19 | |
| MSD | 0.08 | 1.41 | 0.66 | 0.1 | 0.13 | −0.09 | 0.14 | 0.29 | 0.15 | 0.24 | 0.56 | 0.44 | 0.36 | |
| GDR | 0.08 | 1.41 | 0.65 | 0.11 | 0.17 | −0.09 | 0.13 | 0.29 | 0.16 | 0.25 | 0.53 | 0.45 | 0.36 | |
| Root Mean Square Error (RMSE) | 0.29 | 0.25 | 0.27 | 0.25 | 0.14 | 0.11 | 0.17 | 0.22 | 0.41 | 0.36 | 0.37 | 0.29 | 0.27 | |
| MAD | 0.62 | 0.38 | 0.4 | 0.28 | 0.18 | 0.12 | 0.21 | 0.62 | 0.47 | 0.4 | 0.56 | 0.48 | 0.39 | |
| MSD | 0.61 | 1.61 | 0.51 | 0.30 | 0.29 | 0.13 | 0.33 | 0.63 | 0.69 | 0.45 | 1.48 | 0.49 | 0.63 | |
| GDR | 0.69 | 1.62 | 0.86 | 0.31 | 0.34 | 0.13 | 0.34 | 0.63 | 0.89 | 0.45 | 1.63 | 0.51 | 0.70 | |
| Correlation Coefficient (CC) | 0.89 | 0.58 | 0.89 | 0.75 | 0.88 | 0.97 | 0.88 | 0.84 | 0.96 | 0.96 | 0.99 | 0.78 | 0.86 | |
| MAD | 0.79 | 0.55 | 0.55 | 0.73 | 0.8 | 0.98 | 0.83 | 0.4 | 0.95 | 0.95 | 0.28 | 0.48 | 0.69 | |
| MSD | 0.46 | 0.08 | 0.57 | 0.7 | 0.62 | 0.97 | 0.72 | 0.38 | 0.89 | 0.96 | 0.13 | 0.47 | 0.58 | |
| GDR | 0.47 | 0.04 | 0.57 | 0.68 | 0.6 | 0.97 | 0.71 | 0.39 | 0.89 | 0.96 | 0.1 | 0.46 | 0.57 | |
| Number of altimetry heights | 541 | 2291 | 2766 | 19,202 | 9517 | 521 | 787 | 1042 | 732 | 579 | 1467 | 175 | ||
| Number of tracks | 32 | 48 | 64 | 167 | 91 | 23 | 26 | 37 | 62 | 51 | 43 | 20 | ||
| Lake area (km2) | 263.4 | 612.3 | 879.1 | 4149.8 | 1968.5 | 44.5 | 31.6 | 97.1 | 153 | 317.2 | 457.8 | 49.3 | ||
| HYDROWEB | DAHITI | ||||
|---|---|---|---|---|---|
| Hongze | East Dongting | Qinghai | Tai | South Dongting | |
| Mean difference | 0.48 | −1.89 | 0.00 | −0.27 | −1.43 |
| SD difference | 0.03 | 0.47 | −0.01 | −0.03 | 0.1 |
| RMSE | 0.25 | 0.84 | 0.11 | 0.16 | 0.35 |
| CC | 0.86 | 0.52 | 0.91 | 0.81 | 0.97 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Yao, Z.; Wang, R. Evaluation and Validation of CryoSat-2-Derived Water Levels Using In Situ Lake Data from China. Remote Sens. 2019, 11, 899. https://doi.org/10.3390/rs11080899
Liu Z, Yao Z, Wang R. Evaluation and Validation of CryoSat-2-Derived Water Levels Using In Situ Lake Data from China. Remote Sensing. 2019; 11(8):899. https://doi.org/10.3390/rs11080899
Chicago/Turabian StyleLiu, Zhaofei, Zhijun Yao, and Rui Wang. 2019. "Evaluation and Validation of CryoSat-2-Derived Water Levels Using In Situ Lake Data from China" Remote Sensing 11, no. 8: 899. https://doi.org/10.3390/rs11080899
APA StyleLiu, Z., Yao, Z., & Wang, R. (2019). Evaluation and Validation of CryoSat-2-Derived Water Levels Using In Situ Lake Data from China. Remote Sensing, 11(8), 899. https://doi.org/10.3390/rs11080899





