Impact of Soil Reflectance Variation Correction on Woody Cover Estimation in Kruger National Park Using MODIS Data
Abstract
:1. Introduction
2. Materials and Methods
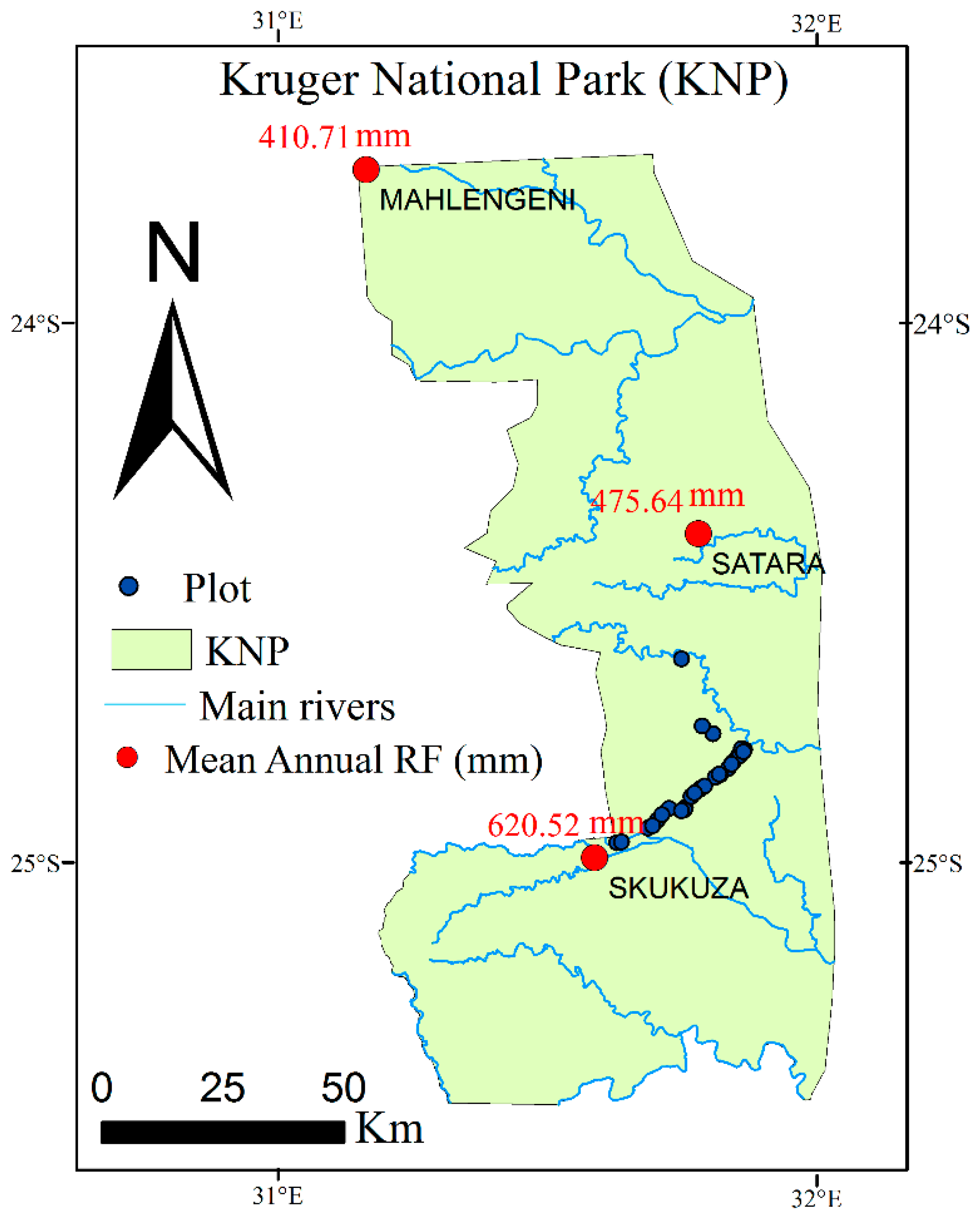
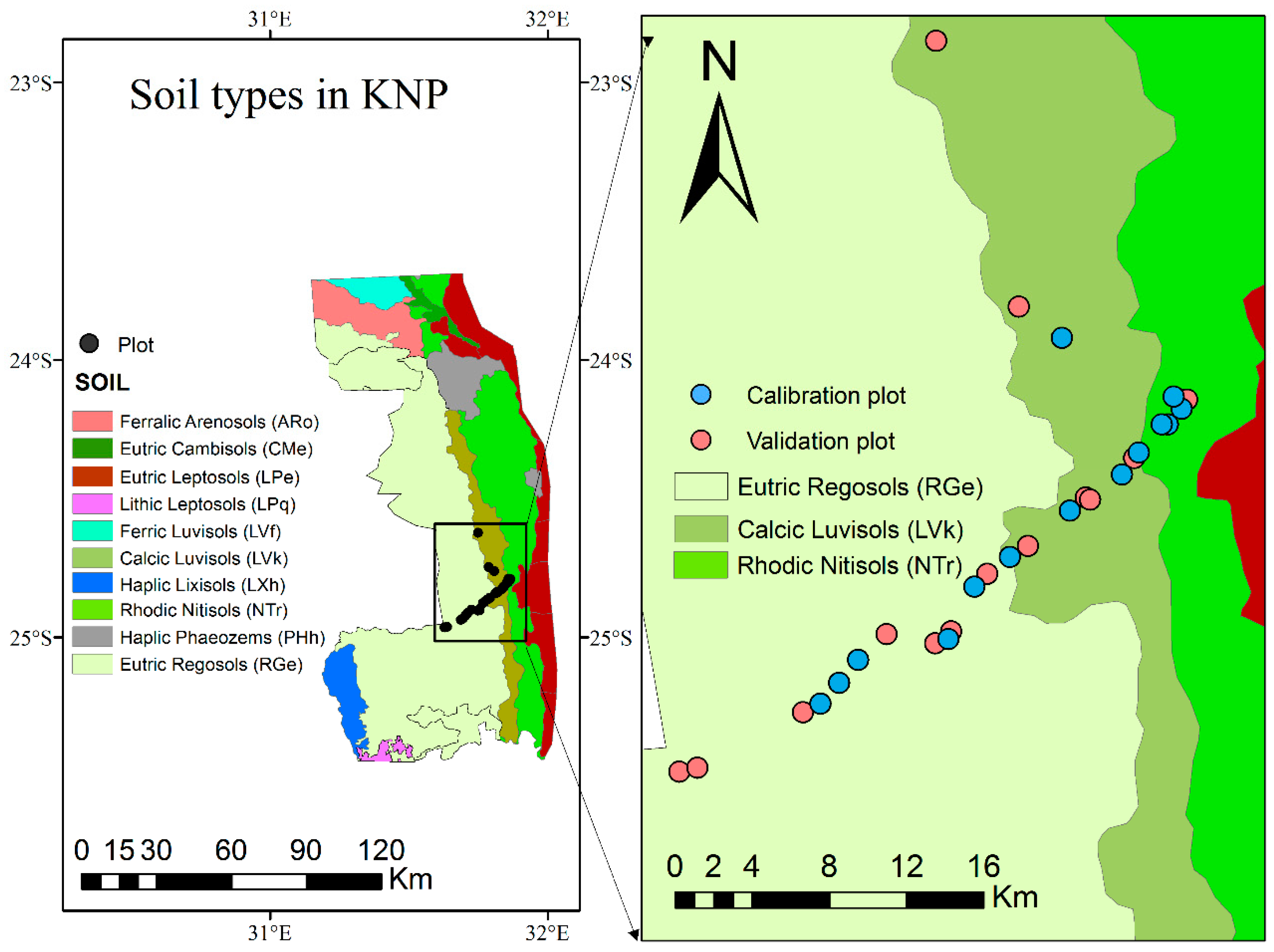
2.1. The Study Area
2.2. Data
2.2.1. Field Data
2.2.2. MODIS NDVI Data
2.2.3. MODIS SAVI Data
2.2.4. MODIS Vegetation Continuous Field (VCF)
2.2.5. Validation Datasets
2.3. Woody Cover Estimation
2.3.1. Woody Cover Estimate Using NDVIpixel and SAVIpixel
2.3.2. Woody Cover Estimation Using NDVIsoil Determination Methods
2.4. Regression Analyses
2.5. Assessment of Model Performance
2.6. Comparison of Woody Cover Estimates with LiDAR/SAR and Bucini Woody Cover Maps
3. Results
3.1. Model Calibration
3.1.1. NDVIpixel and SAVIpixel for Woody Cover Estimate
3.1.2. NDVI and SAVI for Woody Cover Estimation with NDVIsoil Determination Using a Modified Procedure by Zeng et al. [34] and Wu et al. [35]
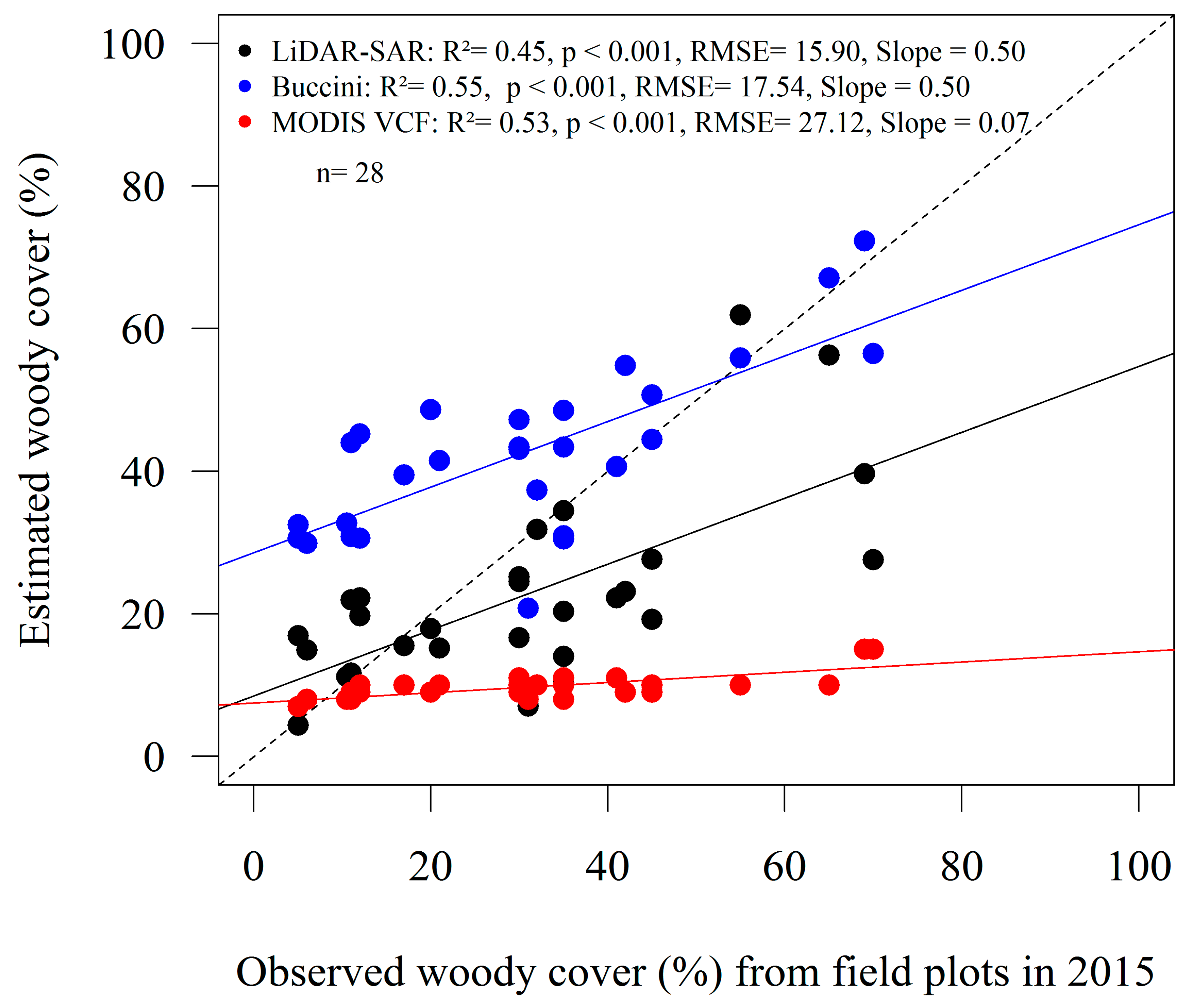
3.2. Comparison of LiDAR/SAR, Bucini and MODIS VCF Woody Cover with Field Data at Plot Level
3.3. Validation of Woody Cover Estimates
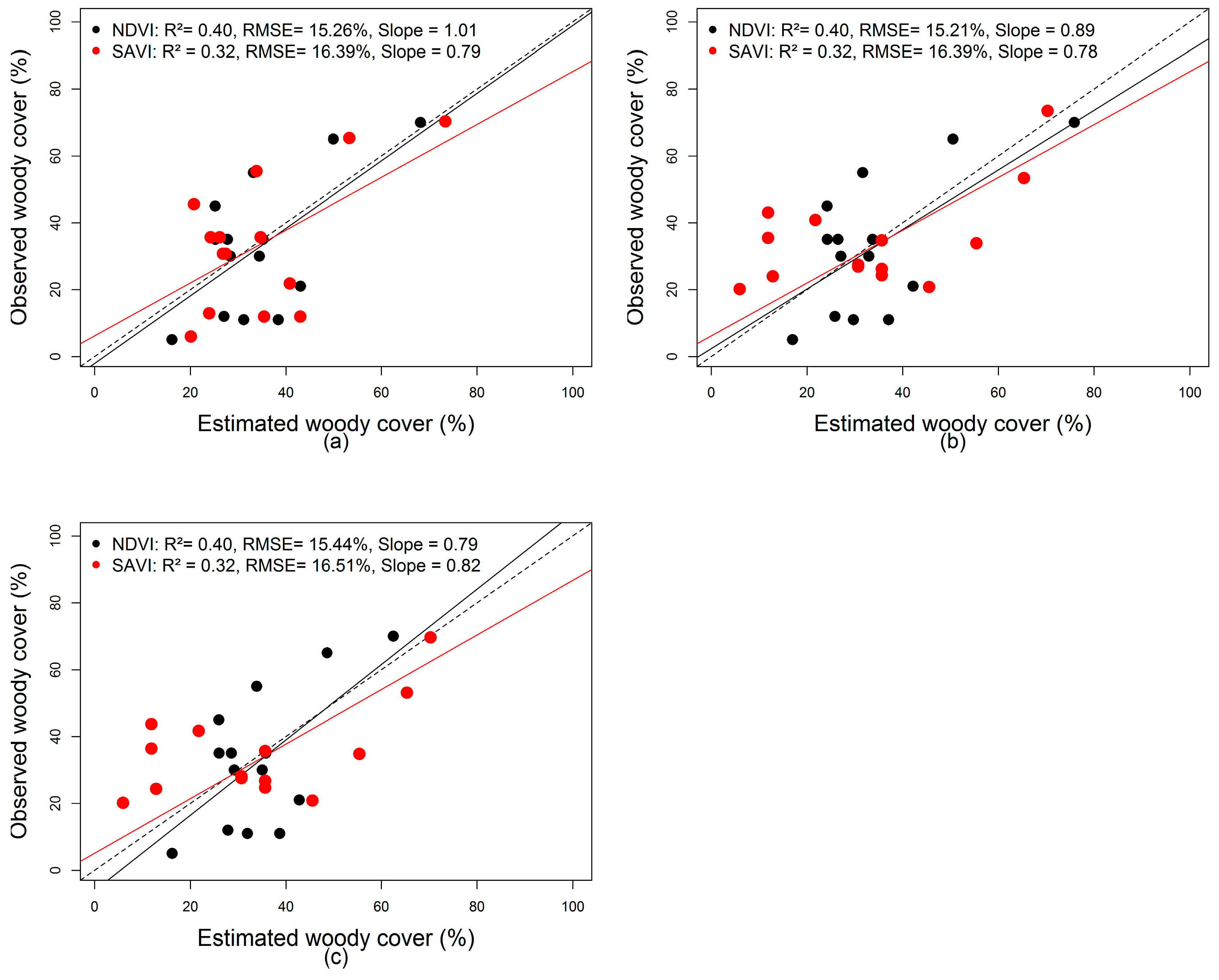
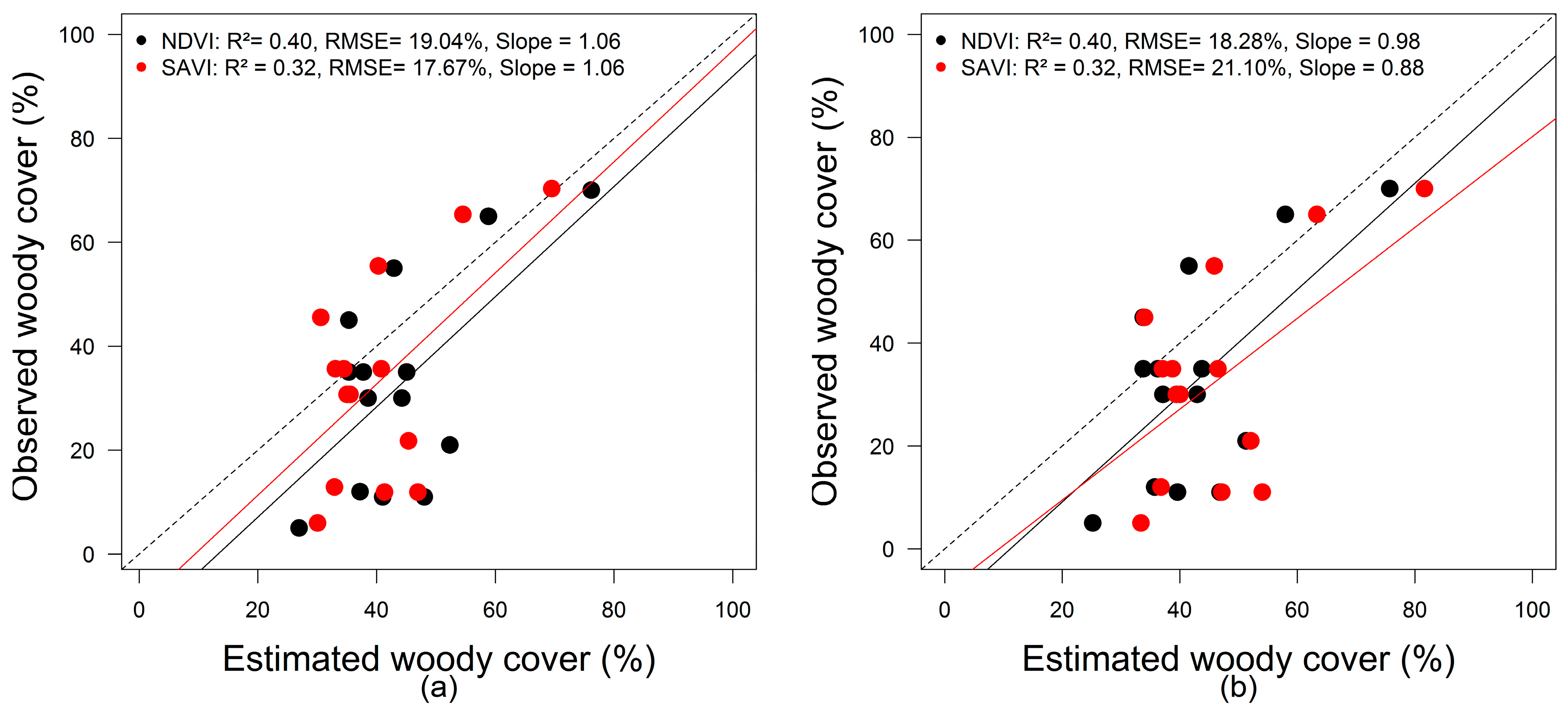
3.3.1. MODIS NDVIpixel and SAVIpixel Woody Cover Maps
3.3.2. NDVI and SAVI Woody Cover Estimation from the NDVIsoil Determination Methods by Zeng et al. [34] and Wu et al. [35]
3.3.3. Comparison of Estimated Woody Cover with LiDAR/SAR-Derived and Bucini’s Woody Cover Estimates Using Pearson Correlation Analysis and RMSE
4. Discussion
4.1. Comparison of LiDAR/SAR, Bucini and MODIS VCF Data
4.2. The NDVIpixel and SAVIpixel
4.3. Woody Cover Estimated Using Two NDVIsoil and SAVIsoil Determination Methods
4.4. The Uncertainties and Sources of Errors and Proposed Improvements
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- House, J.I.; Archer, S.; Breshears, D.D.; Scholes, R.J. Conundrums in mixed woody-herbaceous plant systems. J. Biogeogr. 2003, 30, 1763–1777. [Google Scholar] [CrossRef]
- Gill, T.K.; Phinn, S.R.; Armston, J.D.; Pailthorpe, B.A. Estimating tree-cover change in Australia: Challenges of using the MODIS vegetation index product. Int. J. Remote Sens. 2009, 30, 1547–1565. [Google Scholar] [CrossRef]
- Brandt, M.; Hiernaux, P.; Tagesson, T.; Verger, A.; Rasmussen, K.; Diouf, A.A.; Mbow, C.; Mougin, E.; Fensholt, R. Woody plant cover estimation in drylands from Earth Observation based seasonal metrics. Remote Sens. Environ. 2016, 172, 28–38. [Google Scholar] [CrossRef]
- Montandon, L.; Small, E. The impact of soil reflectance on the quantification of the green vegetation fraction from NDVI. Remote Sens. Environ. 2008, 112, 1835–1845. [Google Scholar] [CrossRef]
- Guan, K.; Wood, E.F.; Caylor, K.K. Multi-sensor derivation of regional vegetation fractional cover in Africa. Remote Sens. Environ. 2012, 124, 653–665. [Google Scholar] [CrossRef]
- Mathieu, R.; Naidoo, L.; Cho, M.A.; Leblon, B.; Main, R.; Wessels, K.; Asner, G.P.; Buckley, J.; Van Aardt, J.; Erasmus, B.F. Toward structural assessment of semi-arid African savannahs and woodlands: The potential of multitemporal polarimetric RADARSAT-2 fine beam images. Remote Sens. Environ. 2013, 138, 215–231. [Google Scholar] [CrossRef]
- Gessner, U.; Machwitz, M.; Conrad, C.; Dech, S. Estimating the fractional cover of growth forms and bare surface in savannas. A multi-resolution approach based on regression tree ensembles. Remote Sens. Environ. 2013, 129, 90–102. [Google Scholar] [CrossRef]
- Villegas, J.C.; Dominguez, F.; Barron-Gafford, G.A.; Adams, H.D.; Guardiola-Claramonte, M.; Sommer, E.D.; Selvey, A.W.; Espeleta, J.F.; Zou, C.B.; Breshears, D.D. Sensitivity of regional evapotranspiration partitioning to variation in woody plant cover: Insights from experimental dryland tree mosaics. Glob. Ecol. Biogeogr. 2015, 24, 1040–1048. [Google Scholar] [CrossRef]
- Giglio, L.; Van der Werf, G.; Randerson, J.; Collatz, G.; Kasibhatla, P. Global estimation of burned area using MODIS active fire observations. Atmos. Chem. Phys. 2006, 6, 957–974. [Google Scholar] [CrossRef]
- DeFries, R.; Achard, F.; Brown, S.; Herold, M.; Murdiyarso, D.; Schlamadinger, B.; de Souza, C. Earth observations for estimating greenhouse gas emissions from deforestation in developing countries. Environ. Sci. Policy 2007, 10, 385–394. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical modeling of a conifer forest canopy. IEEE Trans. Geosci. Remote Sens. 1985, 705–721. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gamon, J.A. Remote sensing of plant functional types. New Phytol. 2010, 186, 795–816. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Muñoz, J.C.; Sobrino, J.A.; Plaza, A.; Guanter, L.; Moreno, J.; Martínez, P. Comparison between fractional vegetation cover retrievals from vegetation indices and spectral mixture analysis: Case study of PROBA/CHRIS data over an agricultural area. Sensors 2009, 9, 768–793. [Google Scholar] [CrossRef] [PubMed]
- Hill, M.J.; Hanan, N.P. Ecosystem Function in Savannas: Measurement and Modeling at Landscape to Global Scales; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Verger, A.; Martínez, B.; Camacho-de Coca, F.; García-Haro, F. Accuracy assessment of fraction of vegetation cover and leaf area index estimates from pragmatic methods in a cropland area. Int. J. Remote Sens. 2009, 30, 2685–2704. [Google Scholar] [CrossRef]
- Gessner, U.; Conrad, C.; Huttich, C.; Keil, M.; Schmidt, M.; Schramm, M.; Dech, S. A Multi-Scale Approch for Retreiving Proportional Cover of Life Forms. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; pp. III-700–III-703. [Google Scholar]
- Cho, M.A.; Debba, P.; Mathieu, R.; Naidoo, L.; Van Aardt, J.; Asner, G.P. Improving discrimination of savanna tree species through a multiple-endmember spectral angle mapper approach: Canopy-level analysis. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4133–4142. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. J. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Smith, A.M.S.; Falkowski, M.J.; Greenberg, J.A.; Tinkham, W.T. Remote sensing of vegetation structure, function, and condition: Special issue. Remote Sens. Environ. 2014, 154, 319–321. [Google Scholar] [CrossRef]
- Smith, A.M.S.; Kolden, C.A.; Tinkham, W.T.; Talhelm, A.F.; Marshall, J.D.; Hudak, A.T.; Boschetti, L.; Falkowski, M.J.; Greenberg, J.A.; Anderson, J.W.; et al. Remote sensing the vulnerability of vegetation in natural terrestrial ecosystems. Remote Sens. Environ. 2014, 154, 322–337. [Google Scholar] [CrossRef]
- Hansen, M.; DeFries, R.; Townshend, J.; Carroll, M.; Dimiceli, C.; Sohlberg, R. Global percent tree cover at a spatial resolution of 500 meters: First results of the MODIS vegetation continuous fields algorithm. Earth Interact. 2003, 7, 1–15. [Google Scholar] [CrossRef]
- Heiskanen, J. Evaluation of global land cover data sets over the tundra-taiga transition zone in northernmost Finland. Int. J. Remote Sens. 2008, 29, 3727–3751. [Google Scholar] [CrossRef]
- Herold, M.; Mayaux, P.; Woodcock, C.; Baccini, A.; Schmullius, C. Some challenges in global land cover mapping: An assessment of agreement and accuracy in existing 1 km datasets. Remote Sens. Environ. 2008, 112, 2538–2556. [Google Scholar] [CrossRef]
- Gitelson, A.A. Remote estimation of crop fractional vegetation cover: The use of noise equivalent as an indicator of performance of vegetation indices. Int. J. Remote Sens. 2013, 34, 6054–6066. [Google Scholar] [CrossRef]
- White, M.A.; Shaw, J.D.; Ramsey, R.D. Accuracy assessment of the vegetation continuous field tree cover product using 3954 ground plots in the south-western USA. Int. J. Remote Sens. 2005, 26, 2699–2704. [Google Scholar] [CrossRef]
- Ibrahim, S.A.; Balzter, H.; Tansey, K.; Tsutsumida, N.; Mathieu, R. Estimating fractional cover of plant functional types in African savanna from harmonic analysis of MODIS time-series. Int. J. Remote Sens. 2018, 39, 2718–2745. [Google Scholar] [CrossRef]
- Eckhardt, H.; Van Wilgen, B.; Biggs, H. Trends in woody vegetation cover in the Kruger National Park, South Africa, between 1940 and 1998. 2000. [Google Scholar] [CrossRef]
- Archibald, S.; Scholes, R.J. Leaf green-up in a semi-arid African savanna separating tree and grass responses to environmental cues. J. Veg. Sci. 2007, 18, 583–594. [Google Scholar] [CrossRef]
- Khalefa, E.; Smit, I.P.J.; Nickless, A.; Archibald, S.; Comber, A.; Balzter, H. Retrieval of savanna vegetation canopy height from ICESat-GLAS spaceborne LiDAR with terrain correction. 2013, 10, 1439–1443. 2013, 10, 1439–1443. [Google Scholar]
- Venter, F.J. “A Classification of Land for Management Planning in the Kruger National Park”, A Classification of Land for Management Planning in the Kruger National Park. Ph.D. Thesis, University of South Africa, Pretoria, South Africa, 1990. [Google Scholar]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens. 2000, 21, 353–366. [Google Scholar] [CrossRef]
- Los, S.; Pollack, N.; Parris, M.; Collatz, G.; Tucker, C.; Sellers, P.; Malmström, C.; DeFries, R.; Bounoua, L.; Dazlich, D. A global 9-yr biophysical land surface dataset from NOAA AVHRR data. J. Hydrometeorol. 2000, 1, 183–199. [Google Scholar] [CrossRef]
- Zeng, X.; Dickinson, R.E.; Walker, A.; Shaikh, M.; DeFries, R.S.; Qi, J. Derivation and evaluation of global 1-km fractional vegetation cover data for land modeling. J. Appl. Meteorol. 2000, 39, 826–839. [Google Scholar] [CrossRef]
- Wu, D.; Wu, H.; Zhao, X.; Zhou, T.; Tang, B.; Zhao, W.; Jia, K. Evaluation of spatiotemporal variations of global fractional vegetation cover based on GIMMS NDVI data from 1982 to 2011. Remote Sens. 2014, 6, 4217–4239. [Google Scholar] [CrossRef]
- Ding, Y.; Zheng, X.; Zhao, K.; Xin, X.; Liu, H. Quantifying the Impact of NDVIsoil Determination Methods and NDVIsoil Variability on the Estimation of Fractional Vegetation Cover in Northeast China. Remote Sens. 2016, 8, 29. [Google Scholar] [CrossRef]
- van Engelen, V.; Hartemink, A. The global soils and terrain database (SOTER). ACLEP Newsl. 2000, 9, 22–27. [Google Scholar]
- Law, B.E.; Arkebauer, T.; Campbell, J.L.; Chen, J.; Sun, O.; Schwartz, M.; van Ingen, C.; Verma, S. Terrestrial Carbon Observations: Protocols for Vegetation Sampling and Data Submission; FAO: Rome, Italy, 2008. [Google Scholar]
- Strahler, A.H.; Muller, J.; Lucht, W.; Schaaf, C.; Tsang, T.; Gao, F.; Li, X.; Lewis, P.; Barnsley, M.J. MODIS BRDF/albedo product: Algorithm theoretical basis document version 5.0. MODIS Doc. 1999, 23, 42–47. [Google Scholar]
- Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V006. NASA EOSDIS Land Processes DAAC. 2015. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/products/vegetation-indices/MOD13Q1/ (accessed on 5 November 2016).
- Los, S.O.; North, P.R.J.; Grey, W.M.F.; Barnsley, M.J. A method to convert AVHRR Normalized Difference Vegetation Index time series to a standard viewing and illumination geometry. Remote Sens. Environ. 2005, 99, 400–411. [Google Scholar] [CrossRef]
- Moreno-de las Heras, M.; Díaz-Sierra, R.; Turnbull, L.; Wainwright, J. Assessing vegetation structure and ANPP dynamics in a grassland-shrubland Chihuahuan ecotone using NDVI-rainfall relationships. Biogeosci. Discuss. 2015, 12, 51–92. [Google Scholar] [CrossRef]
- Foody, G.M. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI–rainfall relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Chamaille-Jammes, S.; Fritz, H. Precipitation-NDVI relationships in eastern and southern African savannas vary along a precipitation gradient. Int. J. Remote Sens. 2009, 30, 3409–3422. [Google Scholar] [CrossRef]
- Los, S. Analysis of trends in fused AVHRR and MODIS NDVI data for 1982–2006: Indication for a CO2 fertilization effect in global vegetation. Glob. Biogeochem. Cycles 2013, 27, 318–330. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global primary production: A remote sensing approach. J. Biogeogr. 1995, 815–835. [Google Scholar] [CrossRef]
- Zhu, L.; Southworth, J. Disentangling the relationships between net primary production and precipitation in southern Africa savannas using satellite observations from 1982 to 2010. Remote Sens. 2013, 5, 3803–3825. [Google Scholar] [CrossRef]
- Mbow, C.; Fensholt, R.; Nielsen, T.T.; Rasmussen, K. Advances in monitoring vegetation and land use dynamics in the Sahel. Geogr. Tidsskr.-Dan. J. Geogr. 2014, 114, 84–91. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Bucini, G.; Saatchi, S.; Hanan, N.; Boone, R.B.; Smit, I. Woody cover and heterogeneity in the savannas of the Kruger National Park, South Africa. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. IV-334–IV-337. [Google Scholar]
- Bucini, G.; Hanan, N.; Boone, R.; Smit, I.; Saatchi, S.; Lefsky, M.; Asner, G. Woody fractional cover in Kruger National Park, South Africa: Remote-sensing-based maps and ecological insights. In Ecosystem Function in Savannas: Measurement and Modeling at Landscape to Global Scales; CRC Press: Boca Raton, FL, USA, 2010; pp. 219–238. [Google Scholar]
- Gilabert, M.; González-Piqueras, J.; Garcıa-Haro, F.; Meliá, J. A generalized soil-adjusted vegetation index. Remote Sens. Environ. 2002, 82, 303–310. [Google Scholar] [CrossRef]
- Townshend, J.; Carroll, M.; Dimiceli, C.; Sohlberg, R.; Hansen, M.; DeFries, R. Vegetation Continuous Fields MOD44B, 2000 Percent Tree Cover, Collection 5; University of Maryland: College Park, MD, USA, 2011. [Google Scholar]
- Hansen, M.; DeFries, R.; Townshend, J.R.; Sohlberg, R. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Wessels, K.; Mathieu, R.; Erasmus, B.; Asner, G.; Smit, I.; Van Aardt, J.; Main, R.; Fisher, J. Impact of communal land use and conservation on woody vegetation structure in the Lowveld savannas of South Africa–LiDAR results. In Proceedings of the 34th International Symposium for Remote Sensing of Environment, Sydney, Australia, 10–15 April 2011. [Google Scholar]
- Naidoo, L.; Mathieu, R.; Main, R.; Kleynhans, W.; Wessels, K.; Asner, G.; Leblon, B. Savannah woody structure modelling and mapping using multi-frequency (X-, C-and L-band) Synthetic Aperture Radar data. ISPRS J. Photogramm. Remote Sens. 2015, 105, 234–250. [Google Scholar] [CrossRef]
- Urbazaev, M.; Thiel, C.; Mathieu, R.; Naidoo, L.; Levick, S.R.; Smit, I.P.; Asner, G.P.; Schmullius, C. Assessment of the mapping of fractional woody cover in southern African savannas using multi-temporal and polarimetric ALOS PALSAR L-band images. Remote Sens. Environ. 2015, 166, 138–153. [Google Scholar] [CrossRef]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Jiang, Z.; Huete, A.R.; Chen, J.; Chen, Y.; Li, J.; Yan, G.; Zhang, X. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sens. Environ. 2006, 101, 366–378. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Penuelas, J.; Valentini, R. Relationships between NDVI, canopy structure, and photosynthesis in three Californian vegetation types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef]
- Scanlon, T.M.; Albertson, J.D.; Caylor, K.K.; Williams, C.A. Determining land surface fractional cover from NDVI and rainfall time series for a savanna ecosystem. Remote Sens. Environ. 2002, 82, 376–388. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Hill, M.J.; Renzullo, L.J.; Barrett, D.J.; Marks, A.S.; Botha, E.J. Estimating fractional cover of photosynthetic vegetation, non-photosynthetic vegetation and bare soil in the Australian tropical savanna region upscaling the EO-1 Hyperion and MODIS sensors. Remote Sens. Environ. 2009, 113, 928–945. [Google Scholar] [CrossRef]
- Ramsey, E., 3rd; Meyer, B.M.; Rangoonwala, A.; Overton, E.; Jones, C.E.; Bannister, T. Oil source-fingerprinting in support of polarimetric radar mapping of Macondo-252 oil in Gulf Coast marshes. Mar. Pollut. Bull. 2014, 89, 85–95. [Google Scholar] [CrossRef] [PubMed]
- WRB, I.W.G. World Reference Base for Soil Resources 2014, Update 2015 International Soil Classification System for Naming Soils and Creating Legends for Soil Maps. World Soil Resources; Reports No. 106; FAO: Rome, Italy, 2015. [Google Scholar]
- Dupont, W.D.; Plummer, W.D., Jr. Power and sample size calculations for studies involving linear regression. Control Clin. Trials 1998, 19, 589–601. [Google Scholar] [CrossRef]
- Sellers, P. Canopy reflectance, photosynthesis, and transpiration, II. The role of biophysics in the linearity of their interdependence. Remote Sens. Environ. 1987, 21, 143–183. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A.; Montgomery, R.A.; Townsend, P.A.; Zygielbaum, A.I.; Bitan, K.; Tilman, D.; Cavender-Bares, J. Seasonal variation in the NDVI-species richness relationship in a prairie grassland experiment (Cedar Creek). Remote Sens. 2016, 8, 128. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Los, S.; Rosette, J.; Kljun, N.; North, P.; Chasmer, L.; Suárez, J.; Hopkinson, C.; Hill, R.; Gorsel, E.v.; Mahoney, C. Vegetation height and cover fraction between 60 S and 60 N from ICESat GLAS data. Geosci. Model Dev. 2012, 5, 413–432. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.-P.; Feng, M.; Noojipady, P.; Anand, A.; Huang, C.; Kim, D.-H.; Collins, K.M.; Channan, S.; DiMiceli, C. Global, 30-m resolution continuous fields of tree cover: Landsat-based rescaling of MODIS vegetation continuous fields with lidar-based estimates of error. Int. J. Digit. Earth 2013, 6, 427–448. [Google Scholar] [CrossRef]
- Hansen, M.C.; Townshend, J.R.G.; DeFries, R.S.; Carroll, M. Estimation of tree cover using MODIS data at global, continental and regional/local scales. Int. J. Remote Sens. 2005, 26, 4359–4380. [Google Scholar] [CrossRef]
- Herrmann, S.M.; Wickhorst, A.J.; Marsh, S.E. Estimation of tree cover in an agricultural parkland of Senegal using rule-based regression tree modeling. Remote Sens. 2013, 5, 4900–4918. [Google Scholar] [CrossRef]
- Hansen, M.C.; DeFries, R.S.; Townshend, J.R.G.; Sohlberg, R.; Dimiceli, C.; Carroll, M. Towards an operational MODIS continuous field of percent tree cover algorithm: Examples using AVHRR and MODIS data. Remote Sens. Environ. 2002, 83, 303–319. [Google Scholar] [CrossRef]
- Venter, F.J.; Scholes, R.J.; Eckhardt, H.C.; Du Toit, J.; Rogers, K.; Biggs, H. The abiotic template and its associated vegetation pattern. Kruger Exp. Ecol. Manag. Savanna Heterog. 2003, 21, 83–129. [Google Scholar]
- Su, L.; Huang, Y.; Chopping, M.; Rango, A.; Martonchik, J. An empirical study on the utility of BRDF model parameters and topographic parameters for mapping vegetation in a semi-arid region with MISR imagery. Int. J. Remote Sens. 2009, 30, 3463–3483. [Google Scholar] [CrossRef]
- Sousa, D.; Small, C. Global cross-calibration of Landsat spectral mixture models. Remote Sens. Environ. 2017, 192, 139–149. [Google Scholar] [CrossRef]
- Fuller, D.O.; Prince, S.D.; Astle, W.L. The influence of canopy strata on remotely sensed observations of savanna-woodlands. Int. J. Remote Sens. 1997, 18, 2985–3009. [Google Scholar] [CrossRef]
- Price, J.C. On the information content of soil reflectance spectra. Remote Sens. Environ. 1990, 33, 113–121. [Google Scholar] [CrossRef]
- Baumgardner, M.F.; Silva, L.F.; Biehl, L.L.; Stoner, E.R. Reflectance Properties of Soils. In Advances in Agronomy, Brady, N.C., Ed.; Academic Press: Cambridge, MA, USA, 1986; Volume 38, pp. 1–44. [Google Scholar]
- Walter-Shea, E.; Blad, B.; Hays, C.; Mesarch, M.; Deering, D.; Middleton, E. Biophysical properties affecting vegetative canopy reflectance and absorbed photosynthetically active radiation at the FIFE site. J. Geophys. Res. Atmos. 1992, 97, 18925–18934. [Google Scholar] [CrossRef]
- Muller, E.; Décamps, H. Modeling soil moisture–reflectance. Remote Sens. Environ. 2001, 76, 173–180. [Google Scholar] [CrossRef]
- Huete, A.; Jackson, R.; Post, D. Spectral response of a plant canopy with different soil backgrounds. Remote Sens. Environ. 1985, 17, 37–53. [Google Scholar] [CrossRef]
- Prins, H. Plant phenology patterns in Lake Manyara National Park, Tanzania. J. Biogeogr. 1988, 15, 465–480. [Google Scholar] [CrossRef]
- Chidumayo, E.N. Climate and Phenology of Savanna Vegetation in Southern Africa. J. Veg. Sci. 2001, 12, 347–354. [Google Scholar] [CrossRef]
- February, E.C.; Frost, P.G.H.; Sankaran, M.; Diouf, A.; Feral, C.J.; Cade, B.S.; Prins, H.H.T.; Bicini, G.; Hrabar, H.; Coughenour, M.B.; et al. Determinants of woody cover in African savannas. Nature 2005, 438, 846–849. [Google Scholar] [CrossRef]
- Scholes, R.; Archer, S. Tree-grass interactions in savannas. Annu. Rev. Ecol. Syst. 1997, 517–544. [Google Scholar] [CrossRef]
- Scholes, R. Convex relationships in ecosystems containing mixtures of trees and grass. Environ. Resour. Econ. 2003, 26, 559–574. [Google Scholar] [CrossRef]
- Smit, I.P.; Asner, G.P.; Govender, N.; Kennedy-Bowdoin, T.; Knapp, D.E.; Jacobson, J. Effects of fire on woody vegetation structure in African savanna. Ecol. Appl. 2010, 20, 1865–1875. [Google Scholar] [CrossRef]
- Stoner, E.R.; Baumgardner, M. Characteristic variations in reflectance of surface soils. Soil Sci. Soc. Am. J. 1981, 45, 1161–1165. [Google Scholar] [CrossRef]
- Smallman, T.; Exbrayat, J.F.; Mencuccini, M.; Bloom, A.; Williams, M. Assimilation of repeated woody biomass observations constrains decadal ecosystem carbon cycle uncertainty in aggrading forests. J. Geophys. Res. Biogeosci. 2017, 122, 528–545. [Google Scholar] [CrossRef]
- Kaduk, J.D.; Los, S.O. Predicting the time of green up in temperate and boreal biomes. Clim. Chang. 2011, 107, 277–304. [Google Scholar] [CrossRef]



| Plot | Woody Cover | Grass Cover | Bare Soil | NDVIpixel | SAVIpixel |
|---|---|---|---|---|---|
| 1 | 5 | 85 | 10 | 0.336 | 0.485 |
| 3 | 6 | 85 | 9 | 0.289 | 0.454 |
| 4 | 10.5 | 45 | 44.5 | 0.264 | 0.434 |
| 7 | 12 | 67 | 21 | 0.3492 | 0.544 |
| 9 | 17 | 78 | 5 | 0.349 | 0.499 |
| 10 | 20 | 70 | 10 | 0.3547 | 0.520 |
| 12 | 30 | 45 | 25 | 0.352 | 0.511 |
| 15 | 31 | 55 | 14 | 0.335 | 0.498 |
| 16 | 32 | 35 | 33 | 0.375 | 0.557 |
| 19 | 35 | 22 | 43 | 0.341 | 0.502 |
| 21 | 41 | 35 | 24 | 0.389 | 0.551 |
| 22 | 42 | 30 | 28 | 0.346 | 0.515 |
| 24 | 45 | 45 | 10 | 0.330 | 0.562 |
| 27 | 69 | 20 | 11 | 0.471 | 0.691 |
| Plot | Woody Cover | Grass Cover | Bare Soil | Grass & Bare Soil | Soil Types | NDVIpixel | NDVIZeng | NDVIWu | SAVIpixel | NDVIZeng | NDVIWu |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 85 | 10 | 95 | Nitisols | 0.336 | 0.290 | 0.290 | 0.485 | 0.404 | 0.384 |
| 3 | 6 | 85 | 9 | 94 | Nitisols | 0.289 | 0.244 | 0.244 | 0.454 | 0.469 | 0.354 |
| 4 | 10.5 | 45 | 44.5 | 89.5 | Regosols | 0.263 | 0.220 | 0.231 | 0.434 | 0.504 | 0.371 |
| 7 | 12 | 67 | 21 | 88 | Luvisols | 0.349 | 0.306 | 0.306 | 0.544 | 0.426 | 0.466 |
| 9 | 17 | 78 | 5 | 83 | Regosols | 0.349 | 0.310 | 0.320 | 0.499 | 0.501 | 0.440 |
| 10 | 20 | 70 | 10 | 80 | Regosols | 0.354 | 0.316 | 0.326 | 0.520 | 0.447 | 0.463 |
| 12 | 30 | 45 | 25 | 70 | Regosols | 0.352 | 0.318 | 0.327 | 0.511 | 0.454 | 0.461 |
| 15 | 31 | 55 | 14 | 69 | Luvisols | 0.335 | 0.302 | 0.302 | 0.498 | 0.451 | 0.437 |
| 16 | 32 | 35 | 33 | 68 | Luvisols | 0.375 | 0.342 | 0.342 | 0.557 | 0.488 | 0.497 |
| 19 | 35 | 22 | 43 | 65 | Regosols | 0.340 | 0.309 | 0.317 | 0.502 | 0.447 | 0.456 |
| 21 | 41 | 35 | 24 | 59 | Luvisols | 0.389 | 0.361 | 0.361 | 0.551 | 0.438 | 0.499 |
| 22 | 42 | 30 | 28 | 58 | Regosols | 0.346 | 0.319 | 0.326 | 0.515 | 0.493 | 0.474 |
| 24 | 45 | 45 | 10 | 55 | Nitisols | 0.330 | 0.304 | 0.304 | 0.562 | 0.578 | 0.504 |
| 27 | 69 | 20 | 11 | 31 | Luvisols | 0.471 | 0.457 | 0.457 | 0.691 | 0.683 | 0.664 |
| Plot No. | Woody Cover (%) | NDVIpixel | SAVIpixel | NDVIpixel Estimated Woody Cover | SAVIpixel Estimated Woody Cover | ||||
|---|---|---|---|---|---|---|---|---|---|
| Linear | Polynomial | Logarithmic | Linear | Polynomial | Logarithmic | ||||
| 2 | 5 | 0.307 | 0.486 | 16.17 | 16.99 | 16.24 | 19.35 | 19.35 | 19.32 |
| 5 | 11 | 0.359 | 0.550 | 31.21 | 29.74 | 31.98 | 34.80 | 34.78 | 35.73 |
| 6 | 11 | 0.385 | 0.582 | 38.42 | 37.07 | 38.71 | 42.43 | 42.41 | 43.14 |
| 8 | 12 | 0.345 | 0.502 | 27.08 | 25.88 | 27.89 | 23.19 | 23.19 | 23.59 |
| 11 | 21 | 0.401 | 0.573 | 43.04 | 42.20 | 42.80 | 40.23 | 40.21 | 41.04 |
| 13 | 30 | 0.371 | 0.517 | 34.47 | 32.95 | 35.08 | 26.69 | 26.68 | 27.37 |
| 14 | 30 | 0.350 | 0.514 | 28.41 | 27.10 | 29.23 | 26.13 | 26.12 | 26.77 |
| 17 | 35 | 0.347 | 0.511 | 27.78 | 26.52 | 28.60 | 25.41 | 25.40 | 26.00 |
| 18 | 35 | 0.374 | 0.547 | 35.24 | 33.74 | 35.80 | 34.08 | 34.06 | 35.00 |
| 20 | 35 | 0.338 | 0.503 | 25.26 | 24.27 | 26.04 | 23.50 | 23.50 | 23.93 |
| 23 | 45 | 0.338 | 0.489 | 25.22 | 24.24 | 26.01 | 19.99 | 19.99 | 20.03 |
| 25 | 55 | 0.366 | 0.544 | 33.20 | 31.68 | 33.88 | 33.19 | 33.17 | 34.11 |
| 26 | 65 | 0.425 | 0.625 | 49.99 | 50.53 | 48.65 | 52.84 | 52.84 | 52.62 |
| 28 | 70 | 0.489 | 0.710 | 68.22 | 75.92 | 62.53 | 73.12 | 73.17 | 69.35 |
| Plot No. | Observe Woody Cover (%) | NDVIpixel | SAVIpixel | Estimated Woody Cover (%) (Zeng et al.) | Estimated Woody Cover (%) (Wu et al.) | Estimated Woody Cover (%) (Zeng et al.) | Estimated Eoody Cover (%) (Wu et al.) |
|---|---|---|---|---|---|---|---|
| 2.00 | 5.00 | 0.307 | 0.486 | 28.52 | 28.99 | 29.382 | 33.39 |
| 5.00 | 11.00 | 0.359 | 0.550 | 39.94 | 43.83 | 40.757 | 47.17 |
| 6.00 | 11.00 | 0.385 | 0.582 | 45.57 | 51.16 | 46.445 | 54.06 |
| 8.00 | 12.00 | 0.345 | 0.502 | 31.36 | 32.68 | 32.225 | 36.83 |
| 11.00 | 21.00 | 0.401 | 0.573 | 43.95 | 49.05 | 44.845 | 52.12 |
| 13.00 | 30.00 | 0.371 | 0.517 | 33.94 | 36.04 | 34.892 | 40.06 |
| 14.00 | 30.00 | 0.350 | 0.514 | 33.53 | 35.50 | 34.358 | 39.42 |
| 17.00 | 35.00 | 0.347 | 0.511 | 33.00 | 34.81 | 33.825 | 38.77 |
| 18.00 | 35.00 | 0.374 | 0.547 | 39.40 | 43.14 | 40.224 | 46.52 |
| 20.00 | 35.00 | 0.338 | 0.503 | 31.59 | 32.98 | 32.403 | 37.05 |
| 23.00 | 45.00 | 0.338 | 0.489 | 28.99 | 29.60 | 29.915 | 34.03 |
| 25.00 | 55.00 | 0.366 | 0.544 | 38.75 | 42.29 | 39.691 | 45.88 |
| 26.00 | 65.00 | 0.425 | 0.625 | 53.27 | 61.17 | 54.088 | 63.32 |
| 28.00 | 70.00 | 0.489 | 0.710 | 68.25 | 80.65 | 69.195 | 81.63 |
| Woody Cover Estimates | LiDAR/SAR 2008 | Bucini 2001 | ||||
|---|---|---|---|---|---|---|
| r | p-Value | RMSE (%) | r | p-Value | RMSE | |
| NDVIpixel (Linear) | 0.52 | 0.05 | 16.46 | 0.63 | 0.014 | 15.15 |
| NDVIpixel (Polynomial) | 0.49 | 0.07 | 17.14 | 0.62 | 0.016 | 15.98 |
| NDVIpixel (Logarithmic) | 0.52 | 0.05 | 15.99 | 0.63 | 0.014 | 14.93 |
| NDVI (Zeng’s et al.) | 0.52 | 0.05 | 19.28 | 0.59 | 0.02 | 12.85 |
| NDVI (Wu et al.) | 0.52 | 0.05 | 22.85 | 0.59 | 0.02 | 12.78 |
| SAVIpixel (Linear) | 0.53 | 0.05 | 16.74 | 0.59 | 0.02 | 16.66 |
| SAVIpixel (Polynomial) | 0.53 | 0.05 | 16.74 | 0.59 | 0.02 | 16.67 |
| SAVIpixel (Logarithmic) | 0.53 | 0.05 | 16.42 | 0.58 | 0.02 | 16.28 |
| SAVI (Zeng’s et al.) | 0.52 | 0.05 | 19.94 | 0.59 | 0.02 | 12.51 |
| SAVI (Wu et al.) | 0.52 | 0.05 | 25.49 | 0.59 | 0.02 | 12.50 |
| MODIS VCF | 0.39 | 0.16 | 23.36 | 0.40 | 0.17 | 40.83 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, S.; Balzter, H.; Tansey, K.; Mathieu, R.; Tsutsumida, N. Impact of Soil Reflectance Variation Correction on Woody Cover Estimation in Kruger National Park Using MODIS Data. Remote Sens. 2019, 11, 898. https://doi.org/10.3390/rs11080898
Ibrahim S, Balzter H, Tansey K, Mathieu R, Tsutsumida N. Impact of Soil Reflectance Variation Correction on Woody Cover Estimation in Kruger National Park Using MODIS Data. Remote Sensing. 2019; 11(8):898. https://doi.org/10.3390/rs11080898
Chicago/Turabian StyleIbrahim, Sa’ad, Heiko Balzter, Kevin Tansey, Renaud Mathieu, and Narumasa Tsutsumida. 2019. "Impact of Soil Reflectance Variation Correction on Woody Cover Estimation in Kruger National Park Using MODIS Data" Remote Sensing 11, no. 8: 898. https://doi.org/10.3390/rs11080898
APA StyleIbrahim, S., Balzter, H., Tansey, K., Mathieu, R., & Tsutsumida, N. (2019). Impact of Soil Reflectance Variation Correction on Woody Cover Estimation in Kruger National Park Using MODIS Data. Remote Sensing, 11(8), 898. https://doi.org/10.3390/rs11080898








