Predicting Forest Inventory Attributes Using Airborne Laser Scanning, Aerial Imagery, and Harvester Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Remotely Sensed Data
2.3. Data Retrieved from the Harvesters’ Information Systems
2.3.1. Tree and Location Measurements
2.3.2. Deriving Tree and Stand Attributes from Harvester Data
2.4. Selection of Modeling and Validation Data
2.5. Generation of Modeling Plots
2.6. Extraction of Predictors from Remote Sensing Data
2.7. Building Prediction Models for Forest Inventory Attributes
2.8. Aggregation of Forest Inventory Attributes for Validation Stands and Accuracy Evaluations
3. Results
3.1. Features Selected for the Prediction Models
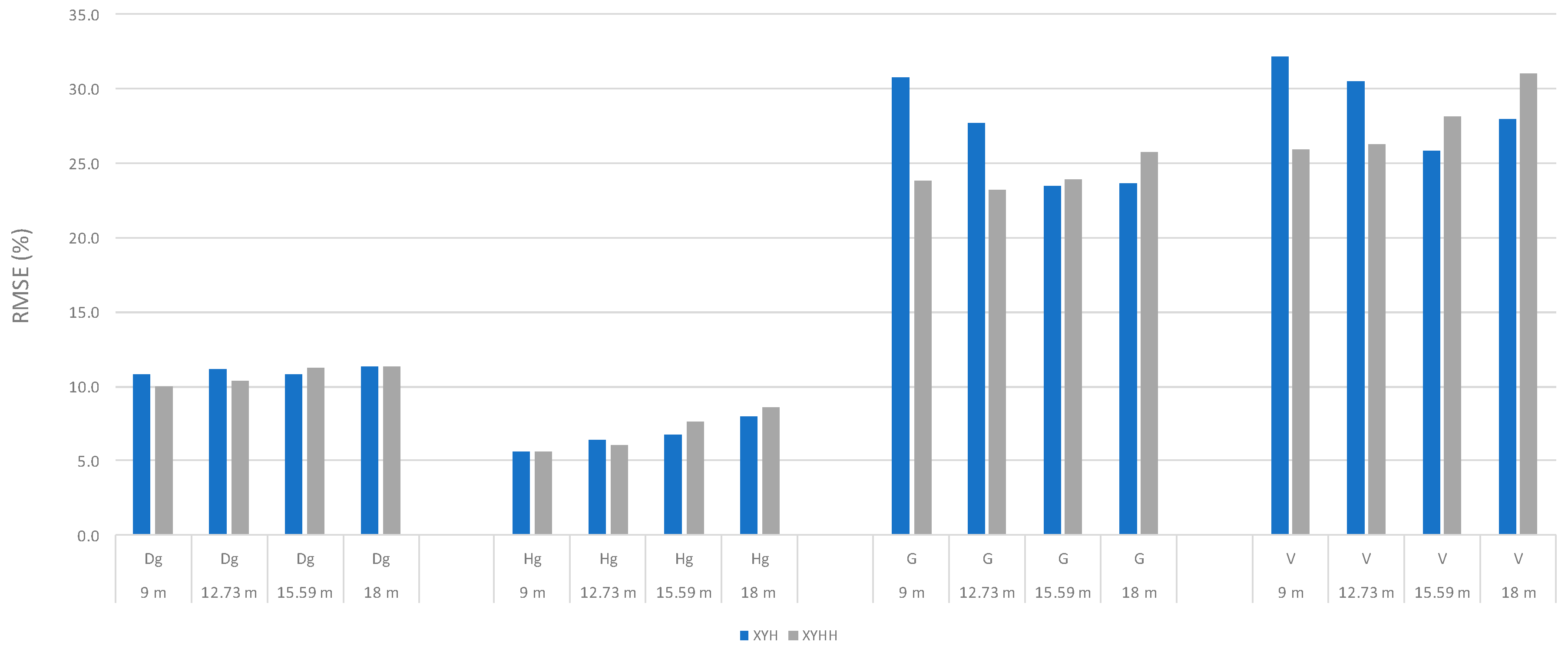
3.2. Accuracy of the Stand-Level Predictions
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Holopainen, M.; Vastaranta, M.; Hyyppä, J. Outlook for the next generation’s precision forestry in Finland. Forests 2014, 5, 1682–1694. [Google Scholar] [CrossRef]
- Siipilehto, J.; Lindeman, H.; Vastaranta, M.; Yu, X.; Uusitalo, J. Reliability of the predicted stand structure for clear-cut stands using optional methods: Airborne laser scanning-based methods, smartphone-based forest inventory application Trestima and pre-harvest measurement tool EMO. Silva Fenn. 2016, 50, 1568. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å.; Söderman, U. Laser scanning of forest resources: The Nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Wulder, M.A.; Coops, N.C.; Hudak, A.T.; Morsdorf, F.; Nelson, R.; Newnham, G.; Vastaranta, M. Status and prospects for LiDAR remote sensing of forested ecosystems. Can. J. Remote Sens. 2013, 39, S1–S5. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinen, K.; Packalén, P.; Hyyppä, J. Estimation of stem volume using laser scanning-based canopy height metrics. Forestry 2006, 79, 217–229. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A.; Haapanen, R.; Melkas, T.; Yu, X.; Hyyppä, J. Uncertainty in timber assortment estimates predicted from forest inventory data. Eur. J. For. Res. 2010, 129, 1131–1142. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E. Assessing effects of positioning errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Maltamo, M.; Bollandsås, O.M.; Næsset, E.; Gobakken, T.; Packalén, P. Different plot selection strategies for field training data in ALS-assisted forest inventory. Forestry 2010, 84, 23–31. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Kotivuori, E.; Korhonen, L.; Packalen, P. Nationwide airborne laser scanning based models for volume, biomass and dominant height in Finland. Silva Fenn. 2016, 50, 1567. [Google Scholar] [CrossRef]
- Holopainen, M.H.; Hyyppä, J.; Vastaranta, M.; Hyyppä, H. Laserkeilaus metsävarojen hallinnassa [Laser Scanning in Forest Resources Management]; University of Helsinki Department of Forest Sciences: Helsinki, Finland, 2013; Volume 5. [Google Scholar]
- Kangas, A.; Astrup, R.; Breidenbach, J.; Fridman, J.; Gobakken, T.; Korhonen, K.T.; Maltamo, M.; Nilsson, M.; Nord-Larsen, T.; Næsset, E.; Olsson, H.l. Remote sensing and forest inventories in Nordic countries–roadmap for the future. Scand. J. For. Res. 2017, 33, 397–412. [Google Scholar] [CrossRef]
- Melkas, T.; Vastaranta, M.; Haapanen, R.; Holopainen, M.; Yu, X.; Hyyppä, J.; Hyyppä, H. Updating forest resource data by using ALS measurements and information collected with a harvester. In Proceedings of the SILVILASER; The 9th International Conference on Lidar Applications for Assessing Forest Ecosystems, Texas A&M University, College Station, TX, USA, 14–16 October 2009; pp. 128–136. [Google Scholar]
- Lindroos, O.; Ringdahl, O.; La Hera, P.; Hohnloser, P.; Hellström, T.H. Estimating the Position of the Harvester Head–a Key Step towards the Precision Forestry of the Future? Croat. J. For. Eng. 2015, 36, 147–164. [Google Scholar]
- Hauglin, M.; Hansen, E.H.; Næsset, E.; Busterud, B.E.; Gjevestad, J.G.O.; Gobakken, T. Accurate single-tree positions from a harvester: A test of two global satellite-based positioning systems. Scand. J. For. Res. 2017, 32, 774–781. [Google Scholar] [CrossRef]
- Skogforsk 2018. StanForD/StanForD 2010—Standard for Forest Machine Data and Communication. Available online: http://www.skogforsk.se/english/projects/stanford/ (accessed on 25 January 2018).
- Rasinmäki, J.; Melkas, T. A Method for estimating tree composition and volume using harvester data. Scand. J. For. Res. 2005, 20, 85–95. [Google Scholar] [CrossRef]
- Stendahl, J.; Dahlin, B. Possibilities for Harvester-based Forest Inventory in Thinnings. Scand. J. For. Res. 2002, 17, 548–555. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Vastaranta, M.; Kukko, A.; Jaakkola, A.; Yu, X.; Pyörälä, J.; Liang, X.; Liu, J.; Wang, Y.; Kaijaluoto, R. Accuracy of kinematic positioning using global satellite navigation systems under forest canopies. Forests 2002, 6, 3218–3236. [Google Scholar] [CrossRef]
- Melkas, T.; Riekki, K. The Positioning Accuracy of Trees Based on Harvester Location and Harvester Head Position Measurements—A Computational Algorithm for Improving the Estimate for Harvester Head Position; Metsätehon Tuloskalvosarja 9b/2017; Metsäteho Oy: Vantaa, Finland, 2017; Available online: http://www.metsateho.fi/the-positioning-accuracy-of-trees-based-on-harvester-location/ (accessed on 15 December 2018).
- Yu, X.; Hyyppä, J.; Karjalainen, M.; Nurminen, K.; Karila, K.; Vastaranta, M.; Kankare, V.; Kaartinen, H.; Holopainen, M.; Honkavaara, E.; et al. Comparison of Laser and Stereo Optical, SAR and InSAR Point Clouds from Air- and Space-Borne Sources in the Retrieval of Forest Inventory Attributes. Remote Sens. 2015, 7, 15933–15954. [Google Scholar] [CrossRef]
- Wallenius, T.; Laamanen, R.; Peuhkurinen, J.; Mehtätalo, L.; Kangas, A. Analysing the agreement between an airborne laser scanning based forest inventory and a control inventory—a case study in the state owned forests in Finland. Silva Fenn. 2012, 46, 111–129. [Google Scholar] [CrossRef]
- Hyyppa, J.; Hyyppa, H.; Yu, X.; Kaartinen, H.; Kukko, H.; Holopainen, M. Forest inventory using small-footprint airborne lidar. In Topographic Laser Ranging and Scanning: Principles and Processing, 2nd ed.; Shan, J., Toth, C., Eds.; CRC Press. Taylor & Francis: Group Boca Raton, FL, USA, 2009; pp. 335–370. [Google Scholar]
- Melkas, T.; Riekki, K.; Sorsa, J.-A. Automated Stand Delineation Based on Harvester Location Data; Metsätehon tuloskalvosarja 7b/2018; Metsäteho Oy: Vantaa, Finland, 2018; Available online: http://www.metsateho.fi/automated-stand-delineation-based-on-harvester-location-data/ (accessed on 15 December 2018).
- Act on Measuring Timber Volumes Using Harvester; Act number 15/06. Dnro 926/01/2006; Ministry of Agriculture and Forestry: Helsinki, Finland, 2006. Available online: http://puuhuolto.fi/mittaus-ja-laatu/wp-content/uploads/sites/9/2017/04/Hakkuukonemittaus_MMM_asetus_18042006_FI.pdf (accessed on 15 December 2018).
- Laasasenaho, J. Taper Curve and Volume Functions for Pine, Spruce and Birch; Communicationes Instituti Forestalis Fenniae: Helsinki, Finland, 1982; Volume 108, pp. 1–74. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Corfu, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Packalen, P.; Suvanto, A.; Maltamo, M. A Two Stage Method to Estimate Species-specific Growing Stock. Photogramm. Eng. Remote Sens. 2009, 75, 1451–1460. [Google Scholar] [CrossRef]
- Junttila, V.; Maltamo, M.; Kauranne, T. Sparse Bayesian Estimation of Forest Stand Characteristics from Airborne Laser Scanning. For. Sci. 2008, 54, 543–552. [Google Scholar]
- Junttila, V.; Kauranne, T.; Leppänen, V. Estimation of Forest Stand Parameters from Airborne Laser Scanning Using Calibrated Plot Databases. For. Sci. 2010, 56, 257–270. [Google Scholar]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- Vastaranta, M.; Yu, X.; Luoma, V.; Karjalainen, M.; Saarinen, N.; Wulder, M.A.; White, J.C.; Persson, H.J.; Hollaus, M.; Yrttimaa, T.; et al. Aboveground forest biomass derived using multiple dates of WorldView-2 stereo-imagery: Quantifying the improvement in estimation accuracy. Int. J. Remote Sens. 2018, 1–18. [Google Scholar] [CrossRef]
- Crookston, N.L.; Finley, A.O. yaImpute: An R Package for kNN Imputation. J. Stat. Softw. 2008, 23, 1–16. [Google Scholar] [CrossRef]
- Saukkola, A. Hakkuukoneen paikannetulla hakkuulaitteella kerätynpuutiedon hyödyntäminen lentolaserkeilaukseen perustuvan puustotulkinnan aputietona. [Utilising Location and Stem Data Collected by Harvesters as an Auxiliary Data in ALS—Based Forest Inventories]. Master’s Thesis, University of Helsinki, Department of Forest Science, Helsinki, Finland, 2017. [Google Scholar]
- Söderberg, J. A Method for Using Harvester Data in Airborne Laser Prediction of Forest Variables in Mature Coniferous Stands. Master’s Thesis, Sveriges lantbruksuniversitet, Umeå, Sweden, 2015. [Google Scholar]
- Holmgren, J.; Barth, A.; Larsson, H.; Olsson, H. Prediction of stem attributes by combining airborne laser scanning and measurements from harvesters. Silva Fenn. 2012, 46, 227–239. [Google Scholar] [CrossRef]
- Næsset, E. Airborne laser scanning as a method in operational forest inventory: Status of accuracy assessments accomplished in Scandinavia. Scand. J. For. Res. 2007, 22, 433–442. [Google Scholar] [CrossRef]
- Andersen, H.; Clarkin, T.; Winterberger, K.; Strunk, J. An Accuracy Assessment of Positions Obtained Using Survey- and Recreational-Grade Global Positioning System Receivers across a Range of Forest Conditions within the Tanana Valley of Interior Alaska. West. J. Appl. For. 2009, 24, 128–136. [Google Scholar]
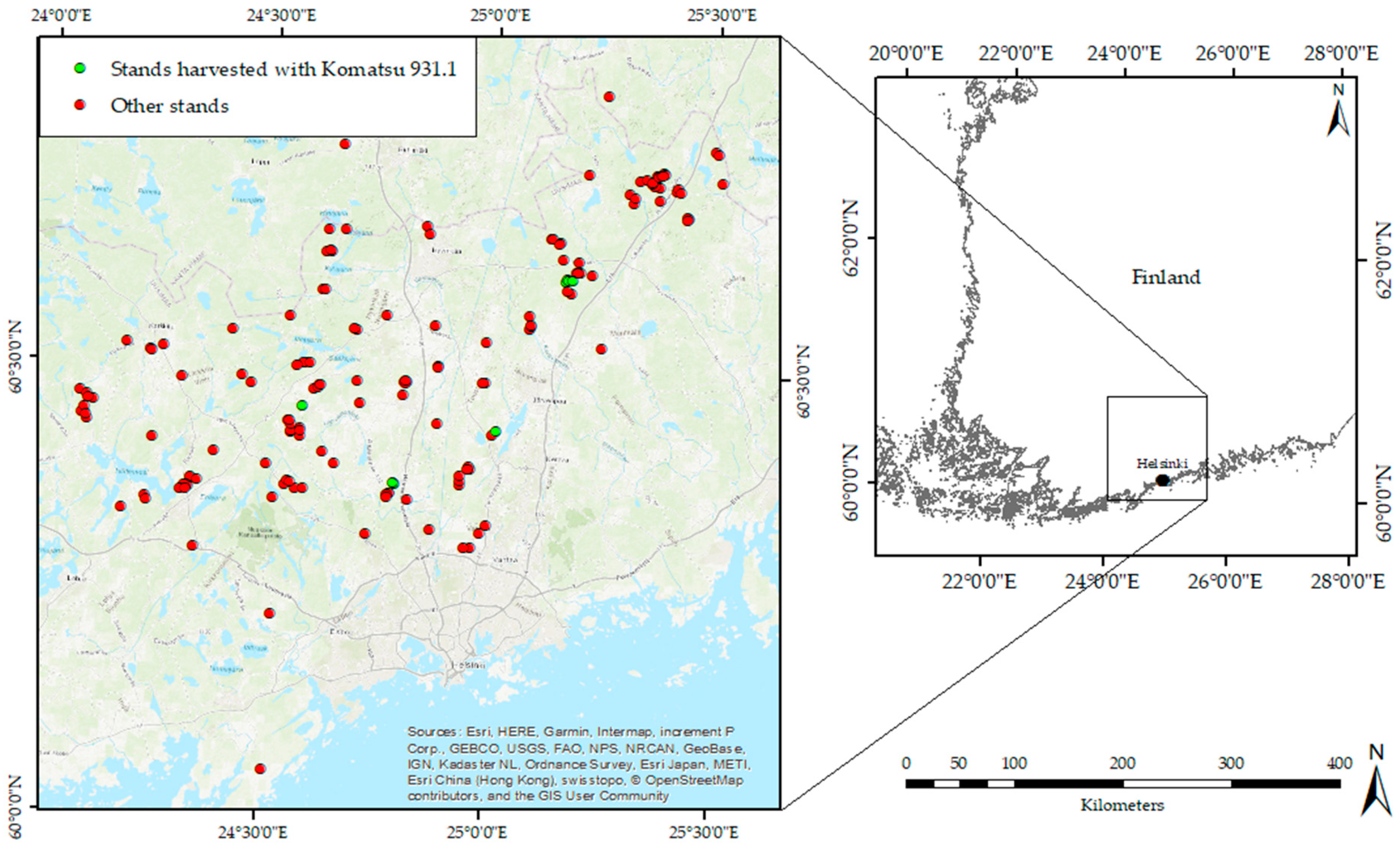
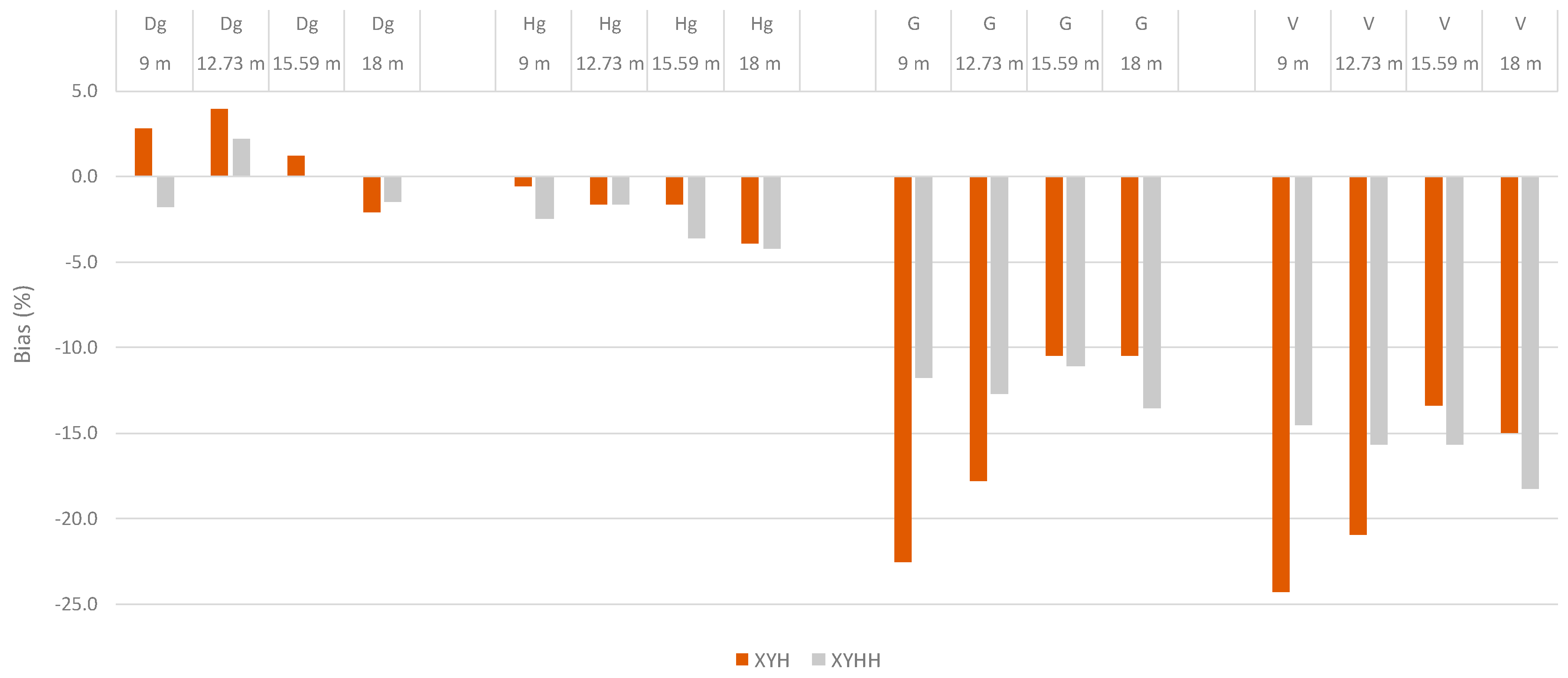
| Stand | Dg (cm) | Hg (m) | G (m2/ha) | V (m3/ha) | |
|---|---|---|---|---|---|
| Modeling (n = 8) | Minimum | 19.3 | 16.1 | 11.2 | 89.4 |
| Mean | 28.4 | 22.8 | 25.2 | 286.2 | |
| Maximum | 37.4 | 26.1 | 32.0 | 397.9 | |
| Standard deviation | 6.1 | 3.3 | 6.4 | 92.4 | |
| Validation (n = 150) | Minimum | 14.9 | 12.8 | 1.2 | 12.9 |
| Mean | 28.5 | 22.6 | 24.4 | 270.1 | |
| Maximum | 46.8 | 29.5 | 41.3 | 552.0 | |
| Standard deviation | 4.8 | 2.6 | 6.2 | 83.0 |
| Forest Inventory Attribute | Sample Plot Size, m2 | Bias XYH | Relative Bias, XYH (%) | Bias XYHH | Relative Bias, XYHH (%) | RMSE XYH | Relative RMSE, XYH (%) | RMSE XYHH | Relative RMSE, XYHH (%) |
|---|---|---|---|---|---|---|---|---|---|
| Dg, cm | 254 | 0.8 | 2.8 | −0.5 | −1.8 | 3.1 | 10.8 | 2.9 | 10.0 |
| 509 | 0.9 | 3.9 | 0.6 | 2.2 | 3.2 | 11.2 | 2.9 | 10.3 | |
| 761 | 0.3 | 1.2 | 0.0 | 0.0 | 3.1 | 10.8 | 3.2 | 11.2 | |
| 1018 | −0.6 | −2.1 | −0.4 | −1.5 | 3.2 | 11.3 | 3.2 | 11.4 | |
| Hg, m | 254 | −0.1 | −0.6 | −0.6 | −2.5 | 1.3 | 5.6 | 1.3 | 5.6 |
| 509 | −0.4 | −1.6 | −0.4 | −1.6 | 1.5 | 6.4 | 1.4 | 6.0 | |
| 761 | −0.4 | −1.6 | −0.8 | −3.6 | 1.5 | 6.8 | 1.7 | 7.6 | |
| 1018 | −0.9 | −3.9 | −1 | −4.2 | 1.8 | 8.0 | 1.9 | 8.6 | |
| G, m2/ha | 254 | −5.5 | −22.5 | −2.9 | −11.8 | 7.5 | 30.8 | 5.8 | 23.8 |
| 509 | −4.3 | −17.8 | −3.1 | −12.7 | 6.8 | 27.7 | 5.7 | 23.2 | |
| 761 | −2.6 | −10.5 | −2.7 | −11.1 | 5.7 | 23.5 | 5.8 | 23.9 | |
| 1018 | −2.6 | −10.5 | −3.3 | −13.5 | 5.8 | 23.6 | 6.3 | 25.8 | |
| V, m3/ha | 254 | −65.6 | −24.3 | −39.1 | −14.5 | 87.0 | 32.2 | 70.0 | 25.9 |
| 509 | −56.5 | −20.9 | −42.4 | −15.7 | 82.3 | 30.5 | 70.9 | 26.3 | |
| 761 | −36.1 | −13.4 | −42.4 | −15.7 | 69.9 | 25.9 | 76.0 | 28.2 | |
| 1018 | −40.5 | −15 | −49.5 | −18.3 | 75.4 | 27.9 | 83.9 | 31.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saukkola, A.; Melkas, T.; Riekki, K.; Sirparanta, S.; Peuhkurinen, J.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Predicting Forest Inventory Attributes Using Airborne Laser Scanning, Aerial Imagery, and Harvester Data. Remote Sens. 2019, 11, 797. https://doi.org/10.3390/rs11070797
Saukkola A, Melkas T, Riekki K, Sirparanta S, Peuhkurinen J, Holopainen M, Hyyppä J, Vastaranta M. Predicting Forest Inventory Attributes Using Airborne Laser Scanning, Aerial Imagery, and Harvester Data. Remote Sensing. 2019; 11(7):797. https://doi.org/10.3390/rs11070797
Chicago/Turabian StyleSaukkola, Atte, Timo Melkas, Kirsi Riekki, Sanna Sirparanta, Jussi Peuhkurinen, Markus Holopainen, Juha Hyyppä, and Mikko Vastaranta. 2019. "Predicting Forest Inventory Attributes Using Airborne Laser Scanning, Aerial Imagery, and Harvester Data" Remote Sensing 11, no. 7: 797. https://doi.org/10.3390/rs11070797
APA StyleSaukkola, A., Melkas, T., Riekki, K., Sirparanta, S., Peuhkurinen, J., Holopainen, M., Hyyppä, J., & Vastaranta, M. (2019). Predicting Forest Inventory Attributes Using Airborne Laser Scanning, Aerial Imagery, and Harvester Data. Remote Sensing, 11(7), 797. https://doi.org/10.3390/rs11070797








