A Method for Landsat and Sentinel 2 (HLS) BRDF Normalization
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. HLS Data
2.1.2. MODIS Data
2.1.3. Homogeneous Sites
2.1.4. SURFRAD Data
2.1.5. OzFlux Data
2.2. Methods
2.2.1. Current HLS BRDF Normalization
2.2.2. Proposed BRDF Normalization Method
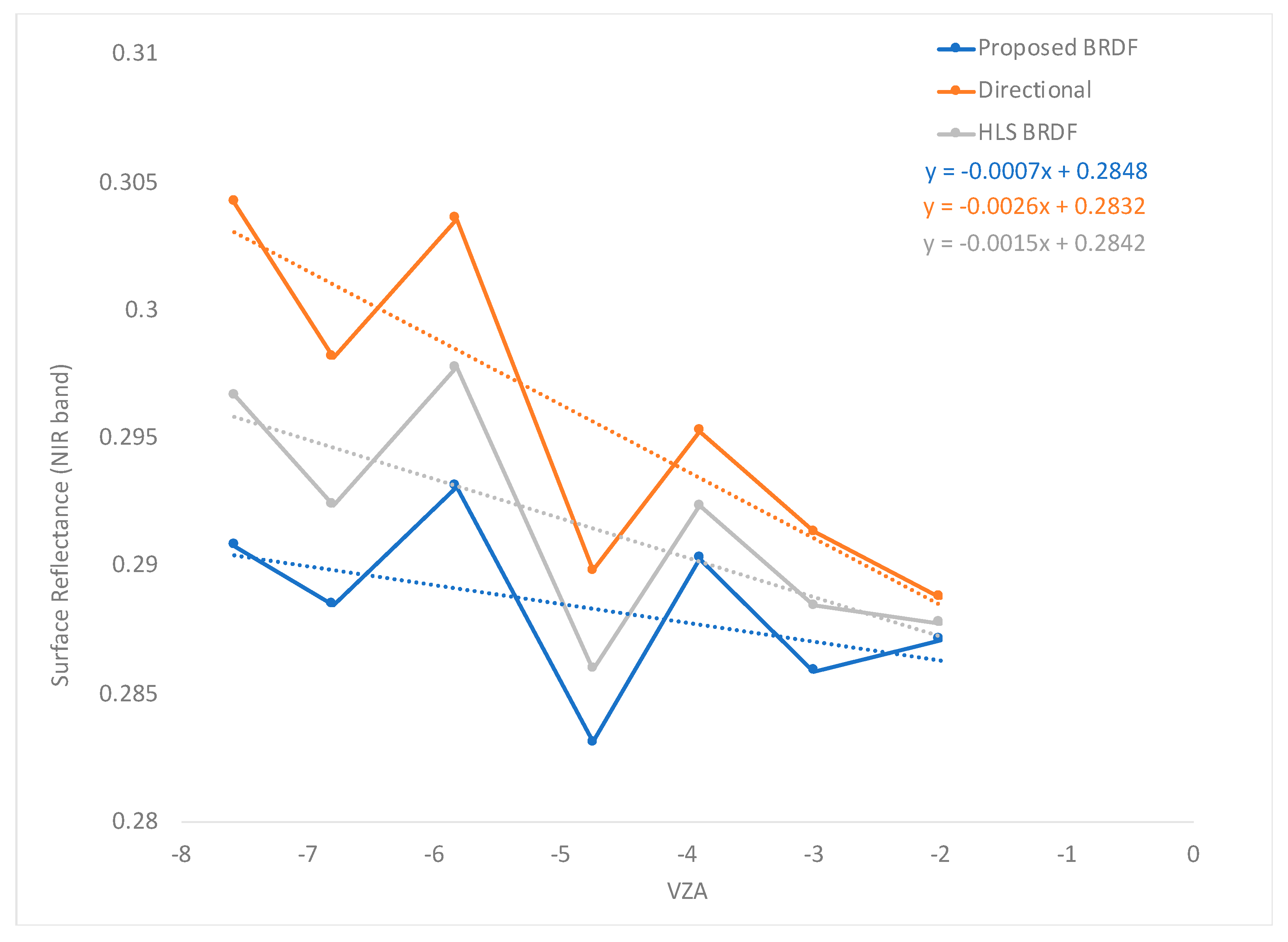
2.2.3. Temporal Evaluation of Homogeneous Sites
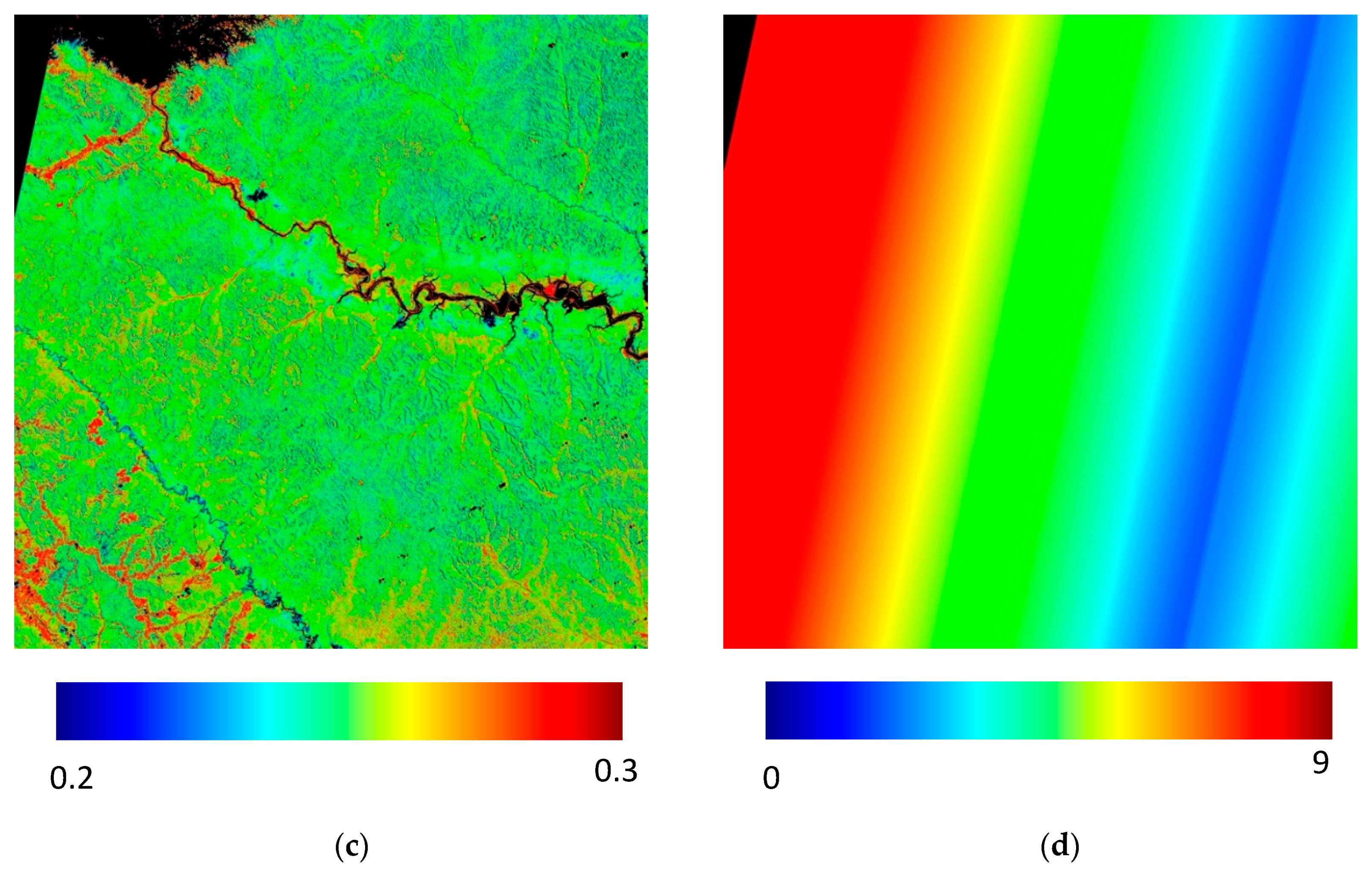
2.2.4. Spatial Evaluation of an Equatorial Region
2.2.5. Albedo Validation
3. Results
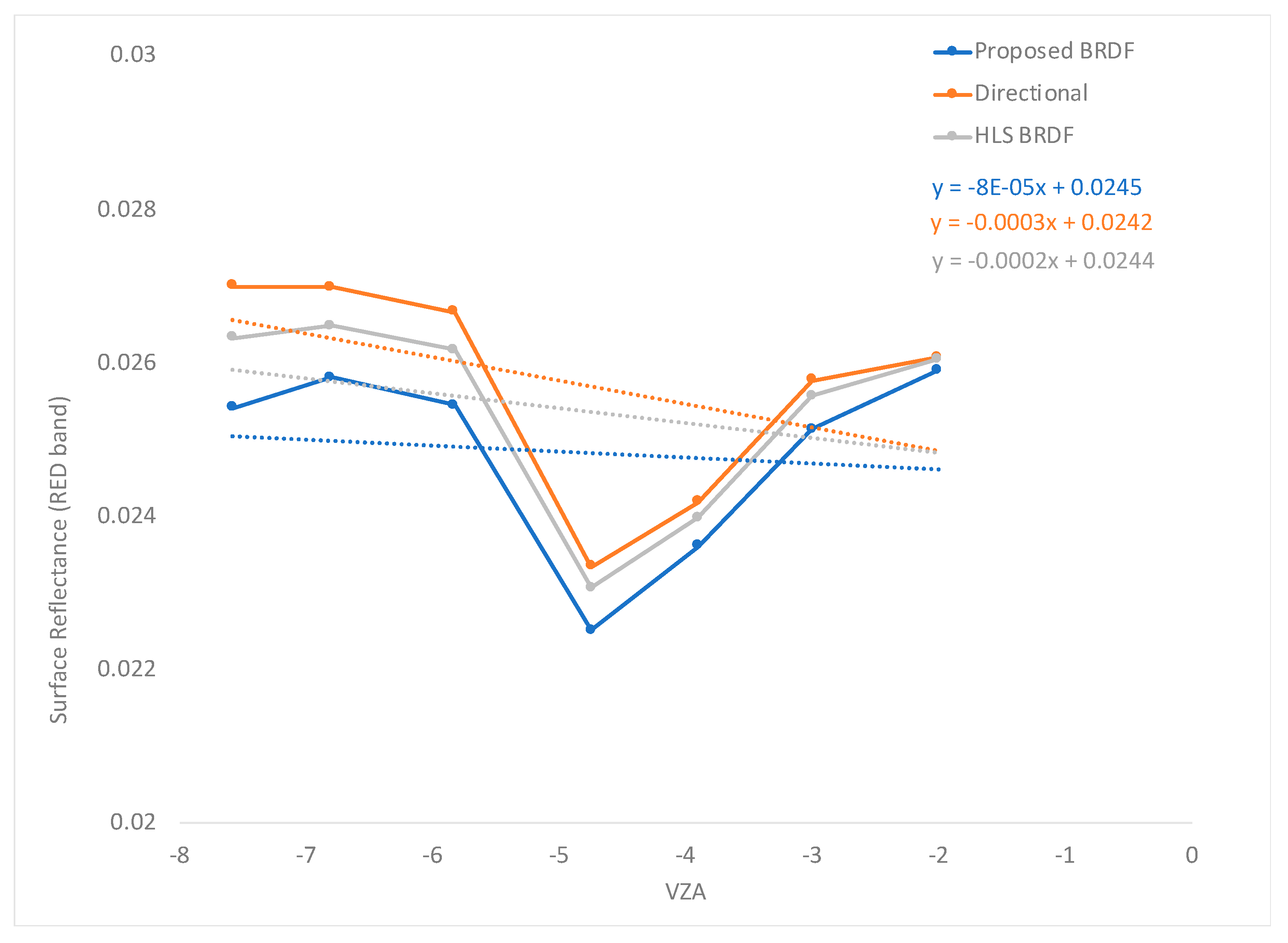
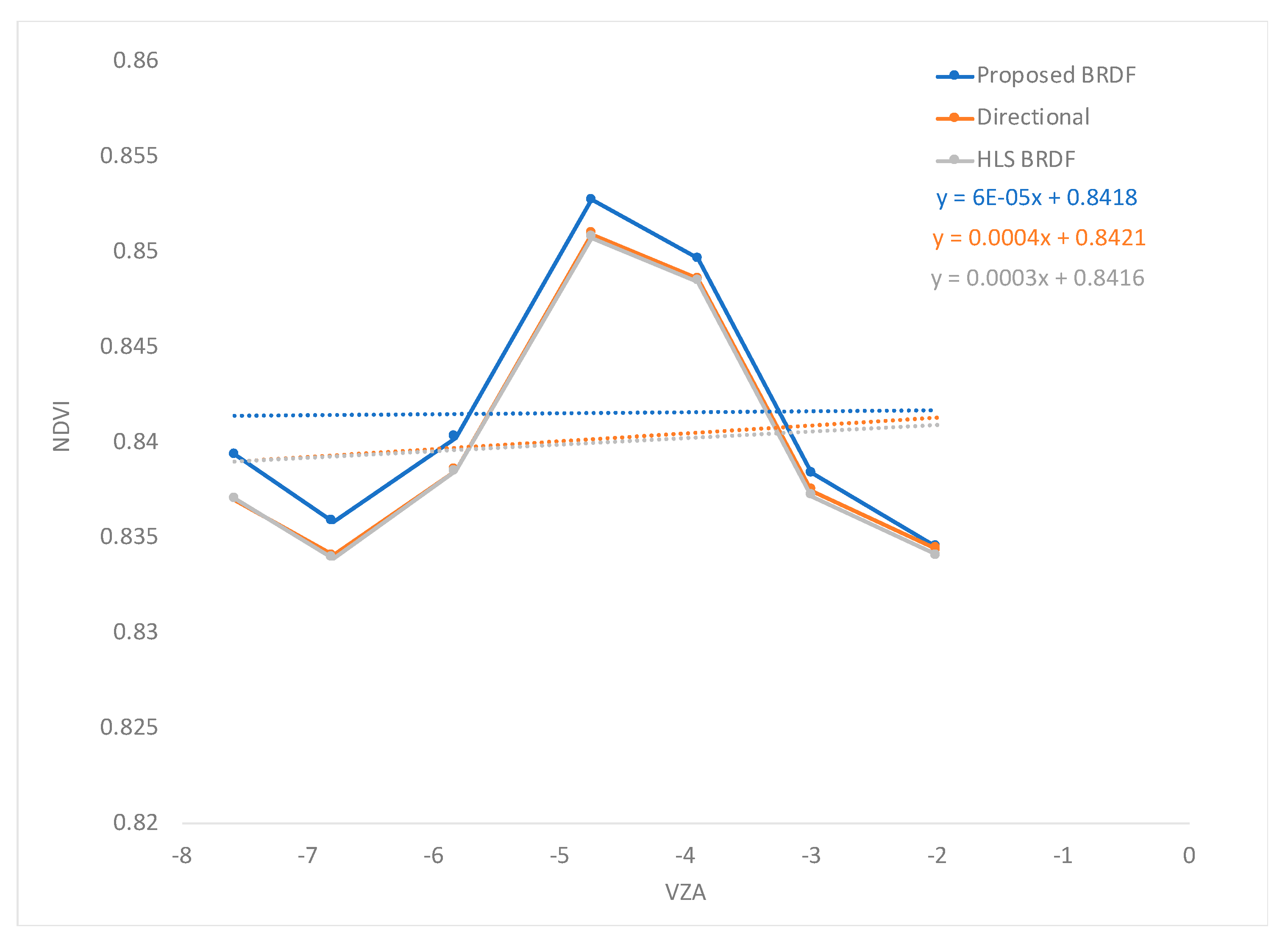
3.1. Temporal Evaluation of Homogeneous Sites
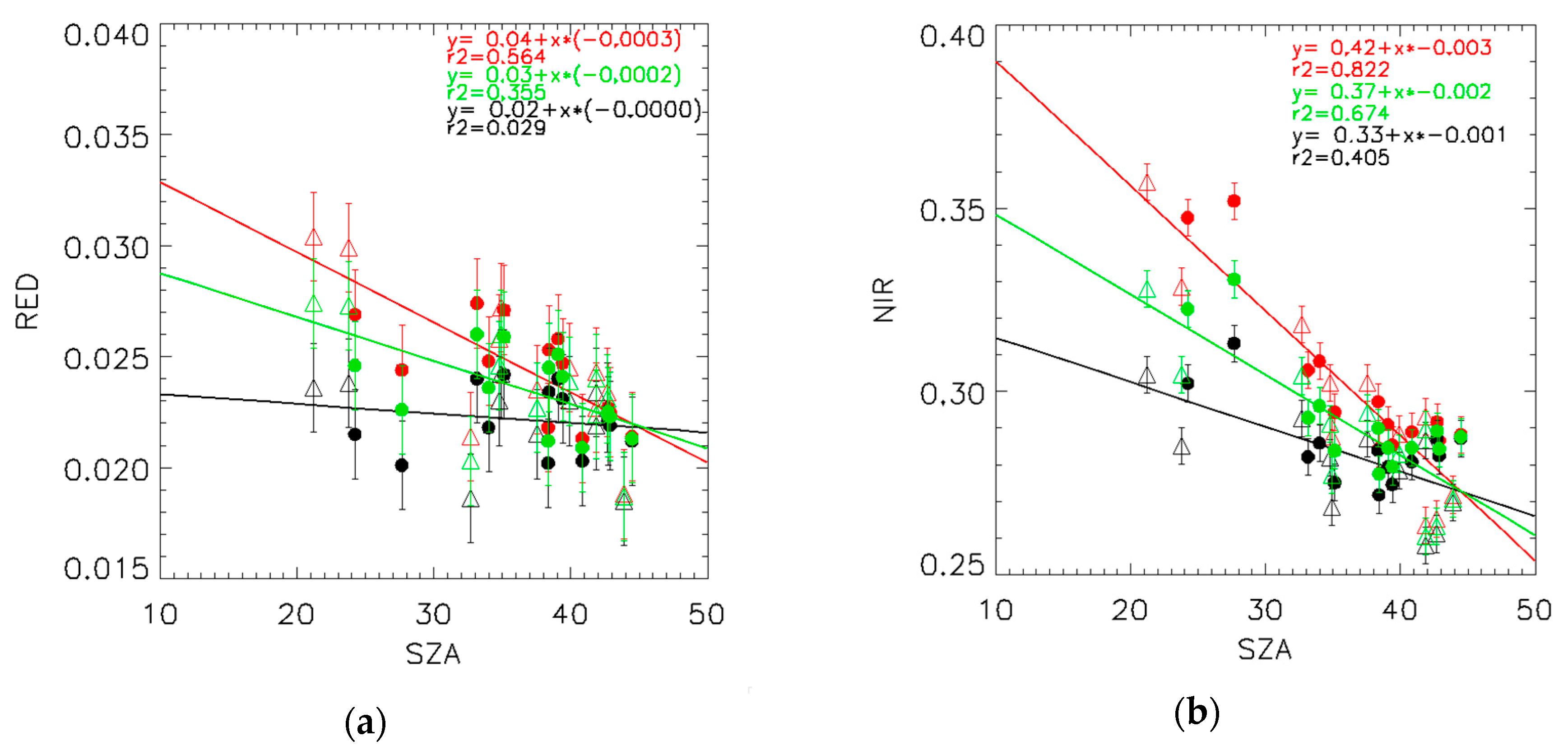
3.2. Spatial Evaluation of an Equatorial Region
3.3. Surface Albedo Validation
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Villaescusa-Nadal, J.L.; Franch, B.; Roger, J.; Vermote, E.F.; Skakun, S.; Justice, C. Spectral Adjustment Model’s Analysis and Application to Remote Sensing Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 1–12. [Google Scholar] [CrossRef]
- Gao, F.; He, T.; Masek, J.G.; Shuai, Y.; Schaaf, C.B.; Wang, Z. Angular Effects and Correction for Medium Resolution Sensors to Support Crop Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4480–4489. [Google Scholar] [CrossRef]
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Schaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A general method to normalize Landsat reflectance data to nadir BRDF adjusted reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.G.; Gao, F.; Schaaf, C.B. An algorithm for the retrieval of 30-m snow-free albedo from Landsat surface reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.G.; Gao, F.; Schaaf, C.B.; He, T. An approach for the long-term 30-m land surface snow-free albedo retrieval from historic Landsat surface reflectance and MODIS-based a priori anisotropy knowledge. Remote Sens. Environ. 2014, 152, 467–479. [Google Scholar] [CrossRef]
- Flood, N.; Danaher, T.; Gill, T.; Gillingham, S. An Operational Scheme for Deriving Standardised Surface Reflectance from Landsat TM/ETM+ and SPOT HRG Imagery for Eastern Australia. Remote Sens. 2013, 5, 83–109. [Google Scholar] [CrossRef]
- Van doninck, J.; Tuomisto, H. Evaluation of directional normalization methods for Landsat TM/ETM+ over primary Amazonian lowland forests. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 249–263. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Claverie, M. Intercomparison of Landsat albedo retrieval techniques and evaluation against in situ measurements across the US SURFRAD network. Remote Sens. Environ. 2014, 152. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.O.; Breon, F.M. Towards a Generalized Approach for Correction of the BRDF Effect in MODIS Directional Reflectances. IEEE Trans. Geosci. Remote Sens. 2009, 47, 898–908. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Sobrino, J.A.; Julien, Y. Retrieval of Surface Albedo on a Daily Basis: Application to MODIS Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7549–7558. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.; Skakun, S.; Roger, J.-C.; Santamaria-Artigas, A.; Villaescusa-Nadal, J.L.; Masek, J. Toward Landsat and Sentinel-2 BRDF Normalization and Albedo Estimation: A Case Study in the Peruvian Amazon Forest. Front. Earth Sci. 2018, 6, 185. [Google Scholar] [CrossRef]
- Vihermaa, L.E.; Waldron, S.; Domingues, T.; Grace, J.; Cosio, E.G.; Limonchi, F.; Hopkinson, C.; Rocha, H.R.; Gloor, E. Fluvial carbon export from a lowland Amazonian rainforest in relation to atmospheric fluxes. J. Geophys. Res. Biogeosciences 2016, 121, 3001–3018. [Google Scholar] [CrossRef]
- Nagol, J.R.; Sexton, J.O.; Kim, D.-H.; Anand, A.; Morton, D.; Vermote, E.; Townshend, J.R. Bidirectional effects in Landsat reflectance estimates: Is there a problem to solve? ISPRS J. Photogramm. Remote Sens. 2015, 103, 129–135. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Leroy, M.; Deschamps, P.-Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical bidirectional reflectance modeling of a conifer forest canopy. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 906–919. [Google Scholar] [CrossRef]
- Lucht, W. Expected retrieval accuracies of bidirectional reflectance and albedo from EOS-MODIS and MISR angular sampling. J. Geophys. Res. Atmos. 1998, 103, 8763–8778. [Google Scholar] [CrossRef]
- Maignan, F.; Bréon, F.-M.; Lacaze, R. Bidirectional reflectance of Earth targets: Evaluation of analytical models using a large set of spaceborne measurements with emphasis on the Hot Spot. Remote Sens. Environ. 2004, 90, 210–220. [Google Scholar] [CrossRef]
- Skakun, S.; Vermote, E.F.; Roger, J.-C.; Justice, C.O.; Masek, J.G. Validation of the LaSRC cloud detection algorithm for Landsat 8 images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Stenberg, P.; Rautiainen, M.; Manninen, T.; Voipio, P.; Smolander, H. Reduced simple ratio better than NDVI for estimating LAI in Finnish pine and spruce stands. Silva Fennica 2004, 38, 431. [Google Scholar] [CrossRef]
- Bréon, F.-M.; Vermote, E. Correction of MODIS surface reflectance time series for BRDF effects. Remote Sens. Environ. 2012, 125, 1–9. [Google Scholar] [CrossRef]
- Muro, J.; Tuomisto, H.; Higgins, M.A.; Moulatlet, G.M.; Ruokolainen, K. Floristic composition and across-track reflectance gradient in Landsat images over Amazonian forests. ISPRS J. Photogramm. Remote Sens. 2016, 119, 361–372. [Google Scholar] [CrossRef]
- Higgins, M.A.; Asner, G.P.; Perez, E.; Elespuru, N.; Tuomisto, H.; Ruokolainen, K.; Alonso, A. Use of Landsat and SRTM data to detect broad-scale biodiversity patterns in Northwestern Amazonia. Remote Sens. 2012, 4, 2401–2418. [Google Scholar] [CrossRef]
- Van doninck, J.; Tuomisto, H. A Landsat composite covering all Amazonia for applications in ecology and conservation. Remote Sens. Ecol. Conserv. 2018, 4, 197–210. [Google Scholar] [CrossRef]

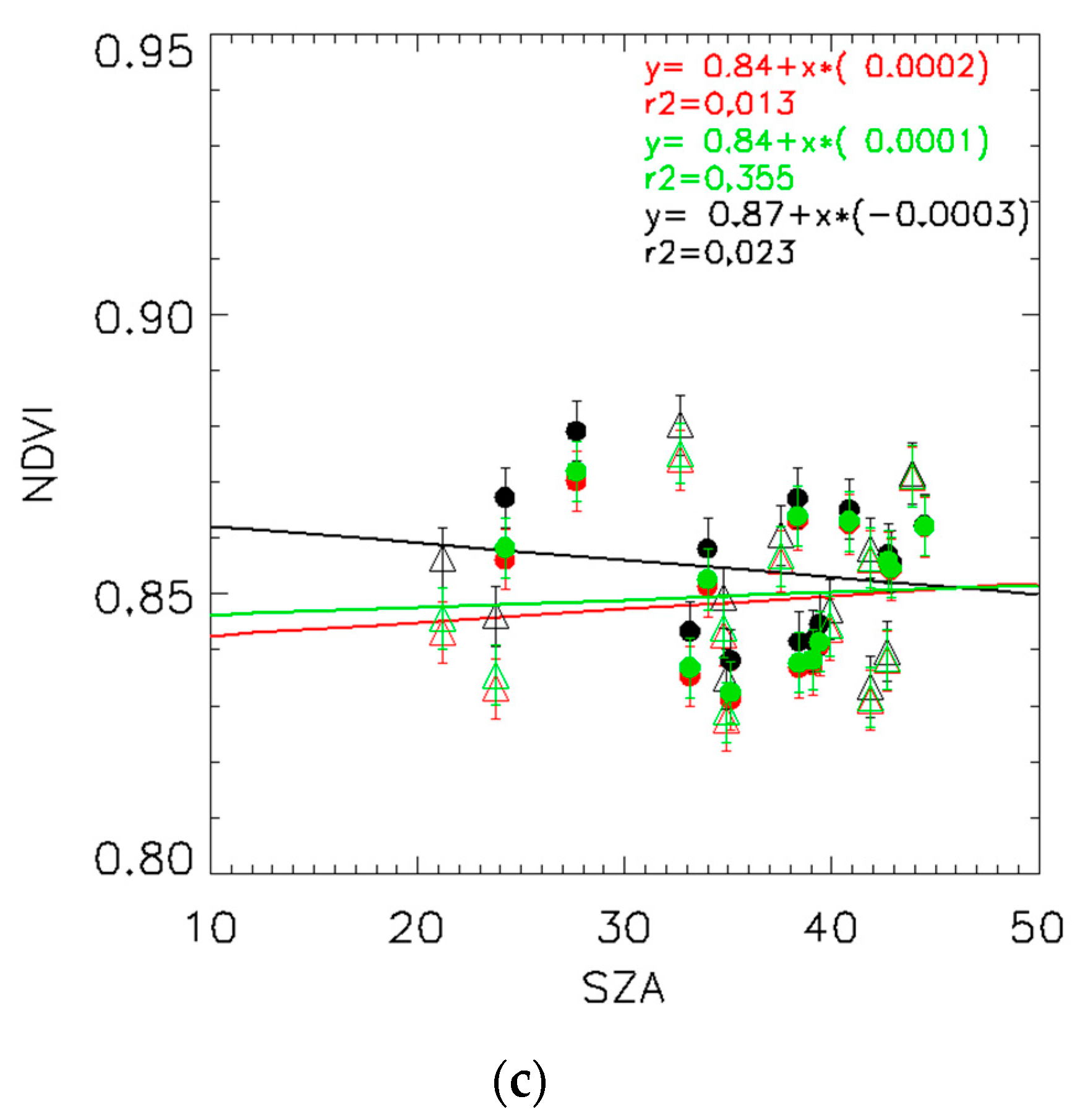
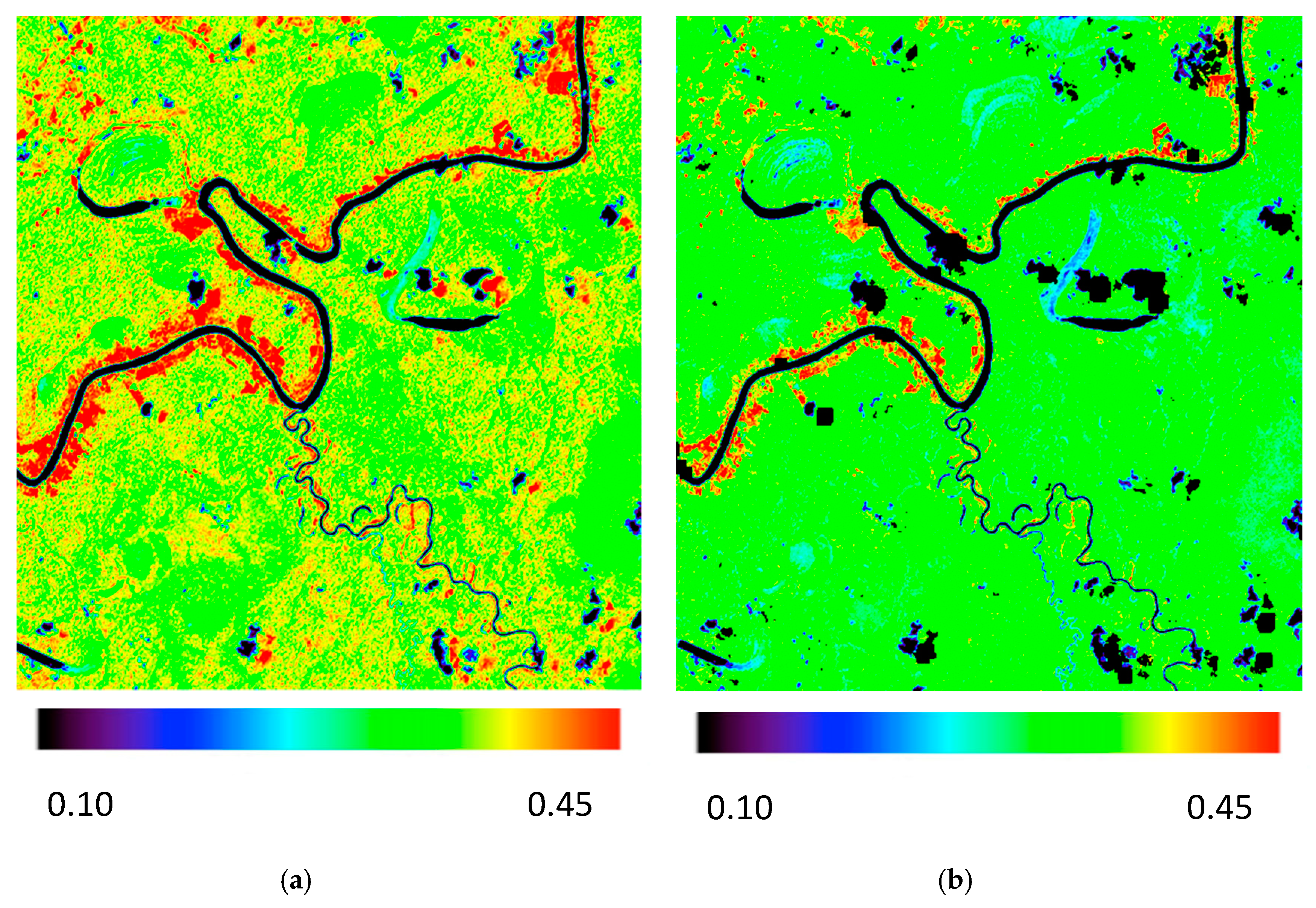
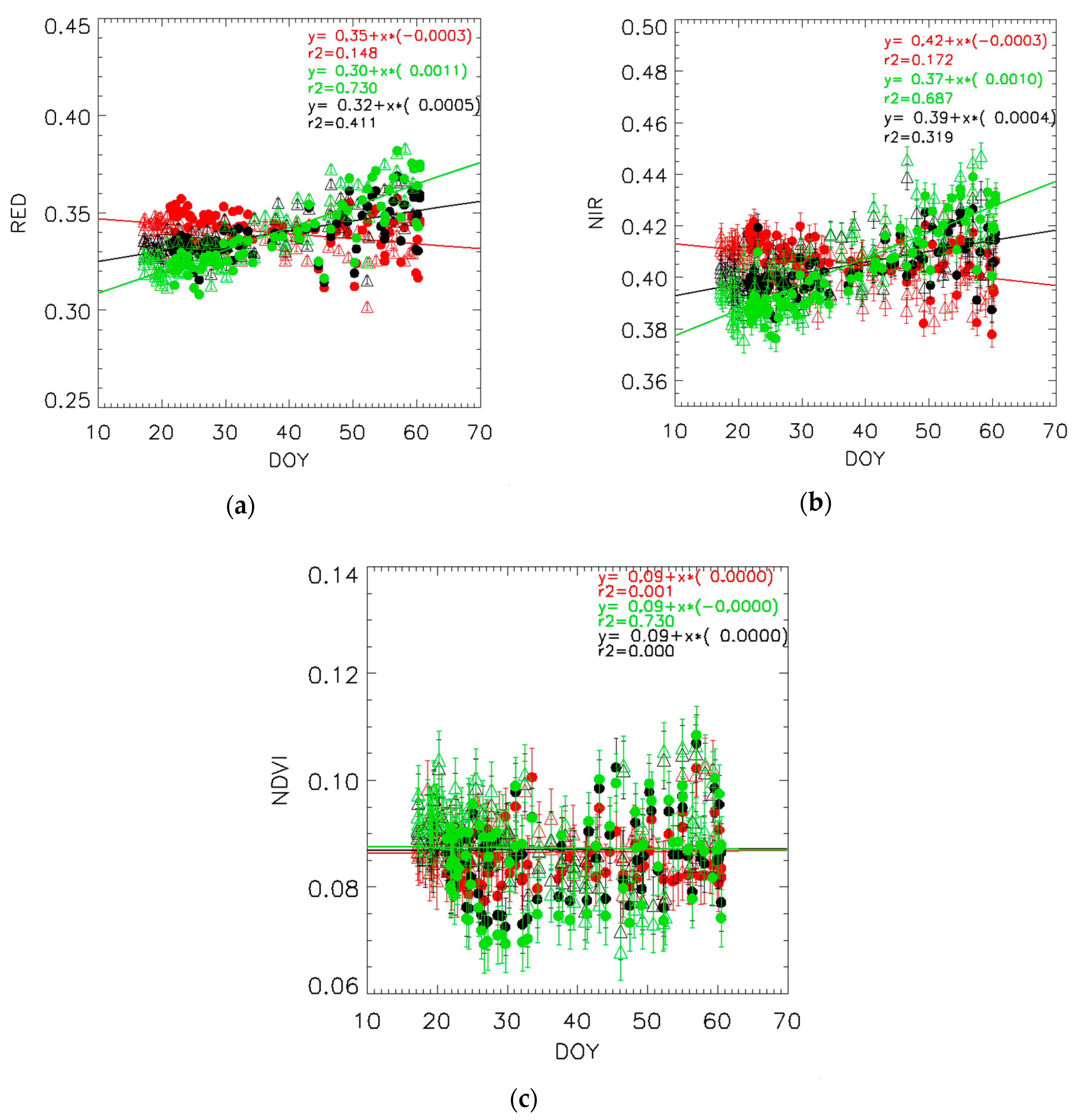

| Station Name | Network | Location Latitude, Longitude | Land cover Type | HLS Tile | Tower Height above Target |
|---|---|---|---|---|---|
| Desert Rock Station | SURFRAD | 36.6232N, 116.0196W | Sparse vegetation | 11SNA | 10 m |
| Table Mountain | SURFRAD | 40.1256N, 105.2378W | Sandy with exposed rocks, sparse grasses and shrubs | 13TDE | 10 m |
| Bondville | SURFRAD | 40.0516N, 88.3733W | Agriculture | 16TCK | 10 m |
| Goodwin creek | SURFRAD | 34.2547N, 89.8729W | Pasture grass and sparsely distributed deciduous trees | 16SBD | 10 m |
| Penn state university | SURFRAD | 40.7203N, 77.9310W | Agriculture Research field | 18TTL | 10 m |
| Fort Peck | SURFRAD | 48.3078N, 105.1017W | Sparse vegetation | 13UDP | 10 m |
| Sioux Falls | SURFRAD | 43.7340N, 96.62328W | Prairie grasses | 14TPP | 10 m |
| Station Name | Network | Location Latitude, Longitude | Land cover Type | HLS Tile | Tower Height above Target |
|---|---|---|---|---|---|
| Calperum | OzFlux | 34.0027S, 140.5877E | Sand dunes with trees and shrubs | 54HVH | 20 m |
| Cumberland Plain | OzFlux | 33.6152S, 150.7236E | Dry sclerophyll forest | 56HKH | 29 m (~6 m above canopy) |
| Whroo | OzFlux | 36.6732S, 145.0294E | Eucalyptus forest | 55HCV | 36 m (~10 m above canopy) |
| Wombat | OzFlux | 37.4222S, 144.0944E | Eucalyptus forest | 55HBU | 30 m (~5 m above canopy) |
| Yanco | OzFlux | 34.9893S, 146.2907E | Grassland | 55HDB | 2 m |
| CV (%) | RED | NIR | NDVI |
|---|---|---|---|
| Directional reflectance | 11.4 | 8.3 | 1.6 |
| Current HLS BRDF normalization | 9.3 | 6.0 | 1.6 |
| Proposed BRDF normalization | 7.6 | 4.5 | 1.6 |
| CV (%) | RED | NIR | NDVI |
|---|---|---|---|
| Directional reflectance | 2.8 | 2.3 | 6.8 |
| Current HLS BRDF normalization | 5.4 | 4.2 | 10.1 |
| Proposed BRDF normalization | 3.3 | 2.5 | 8.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franch, B.; Vermote, E.; Skakun, S.; Roger, J.-C.; Masek, J.; Ju, J.; Villaescusa-Nadal, J.L.; Santamaria-Artigas, A. A Method for Landsat and Sentinel 2 (HLS) BRDF Normalization. Remote Sens. 2019, 11, 632. https://doi.org/10.3390/rs11060632
Franch B, Vermote E, Skakun S, Roger J-C, Masek J, Ju J, Villaescusa-Nadal JL, Santamaria-Artigas A. A Method for Landsat and Sentinel 2 (HLS) BRDF Normalization. Remote Sensing. 2019; 11(6):632. https://doi.org/10.3390/rs11060632
Chicago/Turabian StyleFranch, Belen, Eric Vermote, Sergii Skakun, Jean-Claude Roger, Jeffrey Masek, Junchang Ju, Jose Luis Villaescusa-Nadal, and Andres Santamaria-Artigas. 2019. "A Method for Landsat and Sentinel 2 (HLS) BRDF Normalization" Remote Sensing 11, no. 6: 632. https://doi.org/10.3390/rs11060632
APA StyleFranch, B., Vermote, E., Skakun, S., Roger, J.-C., Masek, J., Ju, J., Villaescusa-Nadal, J. L., & Santamaria-Artigas, A. (2019). A Method for Landsat and Sentinel 2 (HLS) BRDF Normalization. Remote Sensing, 11(6), 632. https://doi.org/10.3390/rs11060632









