Combining Electrical Resistivity Tomography and Satellite Images for Improving Evapotranspiration Estimates of Citrus Orchards
Abstract
1. Introduction
2. Materials and Methods
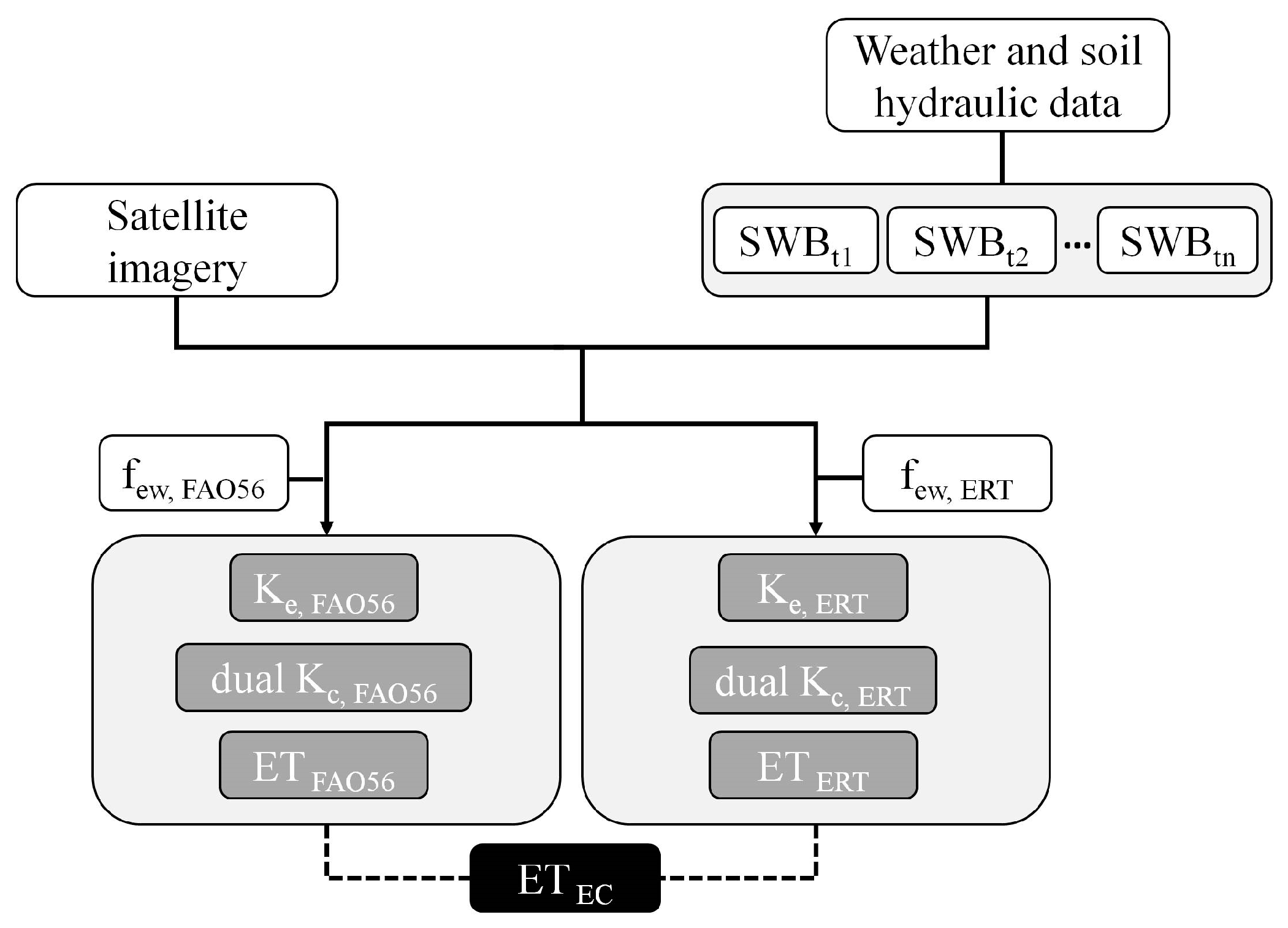
2.1. Original Model Description
2.2. ERT-Adjusted Model Parameter
2.3. Satellite-Based Dual Kc Approach
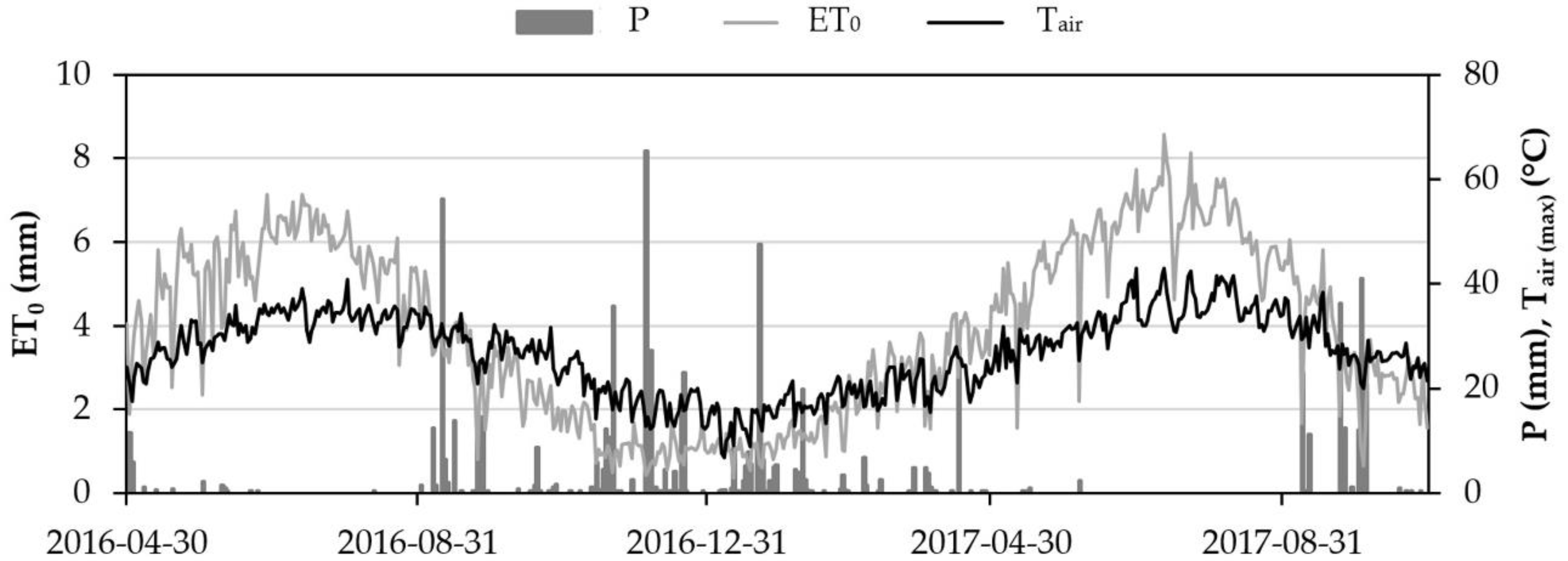
2.4. Ancillary Weather and Soil Data
2.5. Evapotranspiration Validation Using EC
2.6. Water Stress Coefficient Determination
3. Results
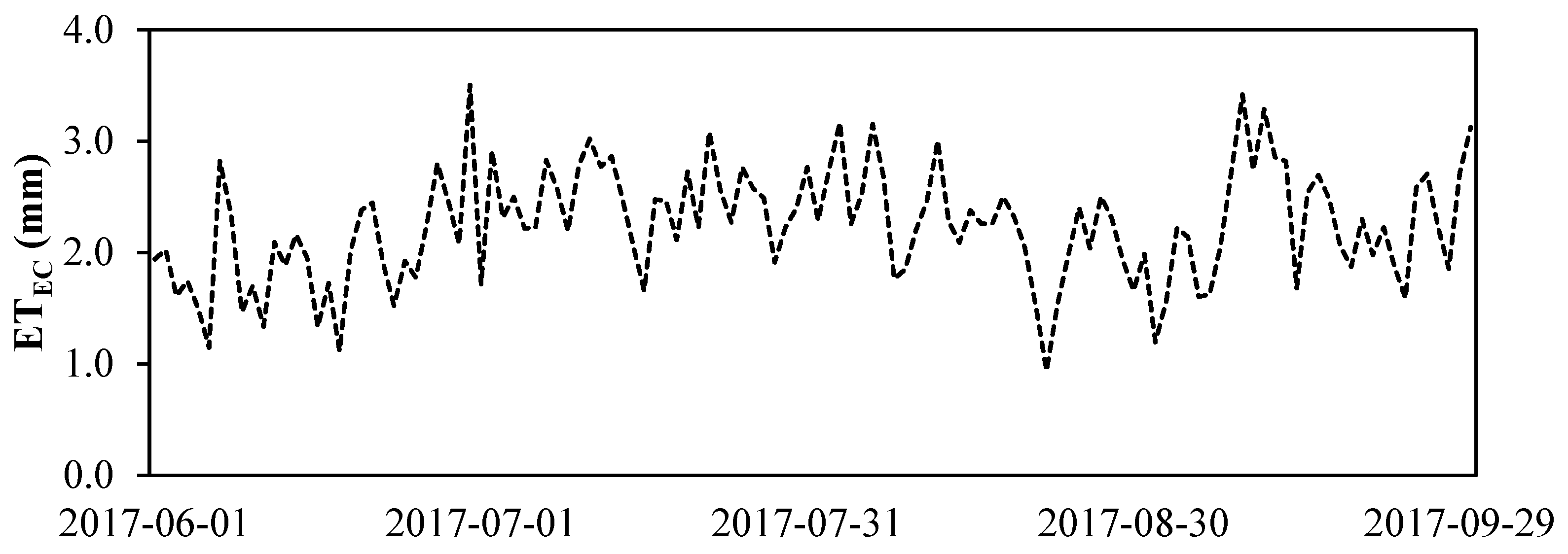
3.1. Evapotranspiration Rates using EC
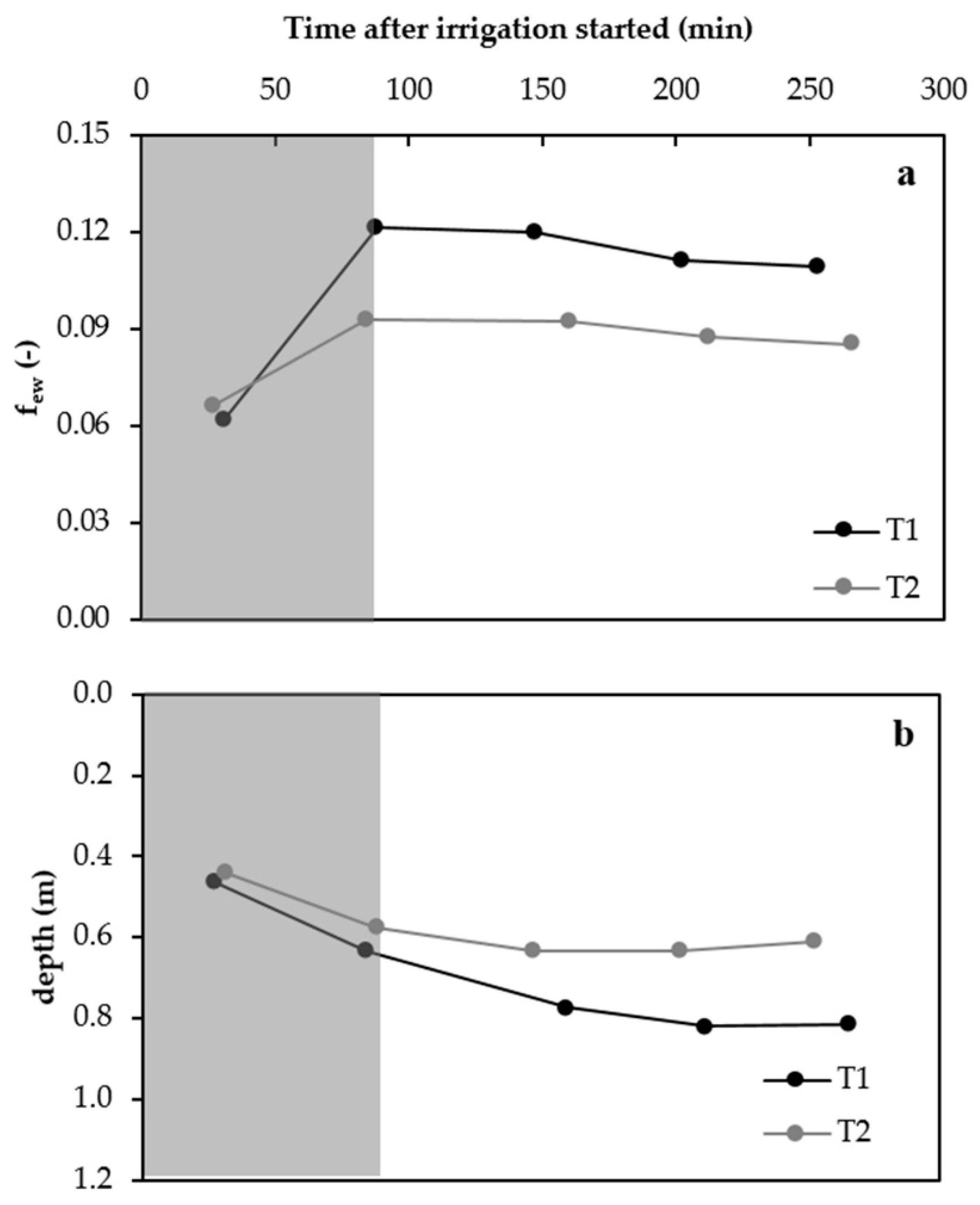
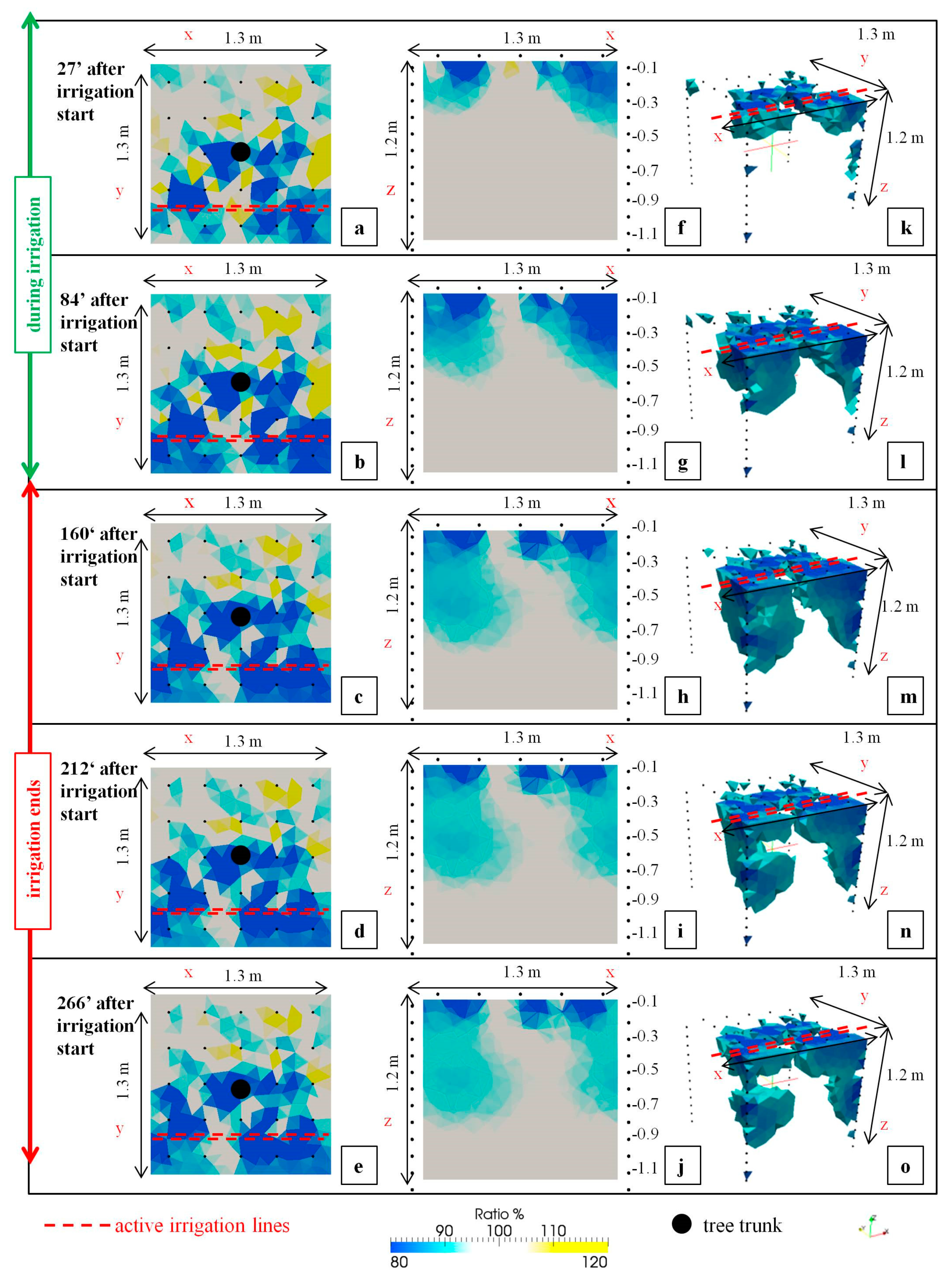
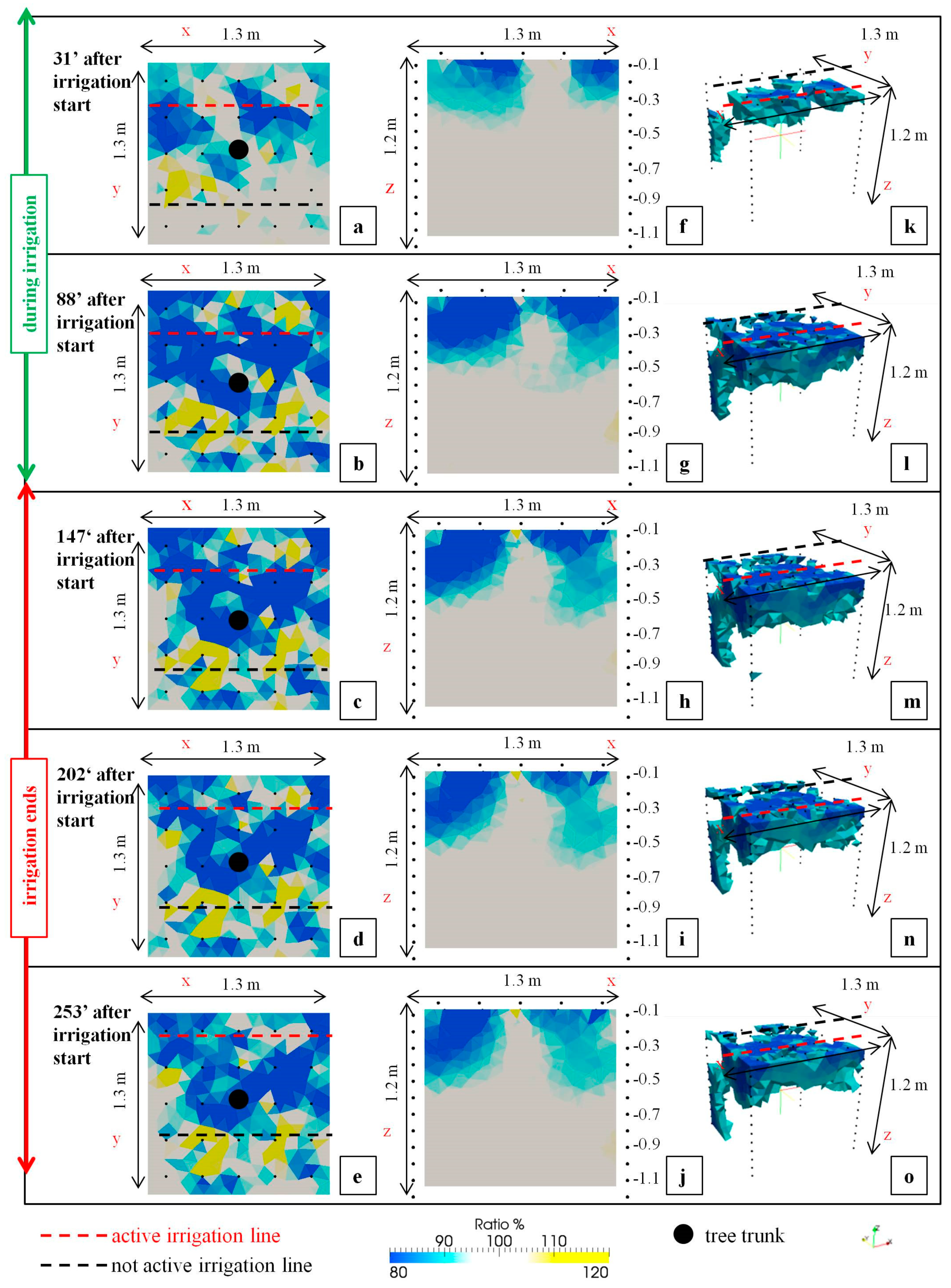
3.2. Soil Wetting Distribution Patterns Using ERT
3.3. Satellite dual Kc Approach
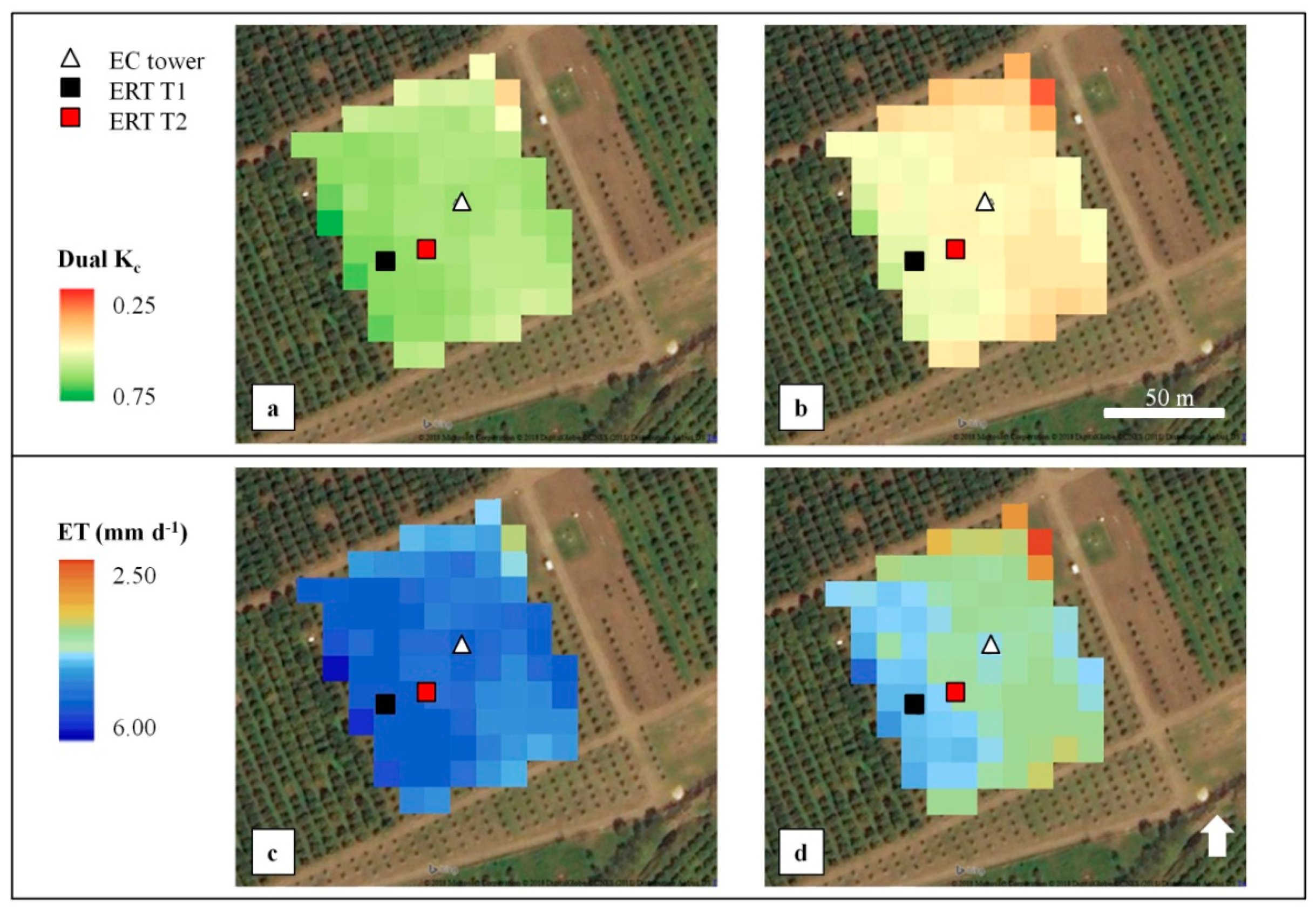
3.3.1. Maps of original and ERT-adjusted dual Kc FAO-56
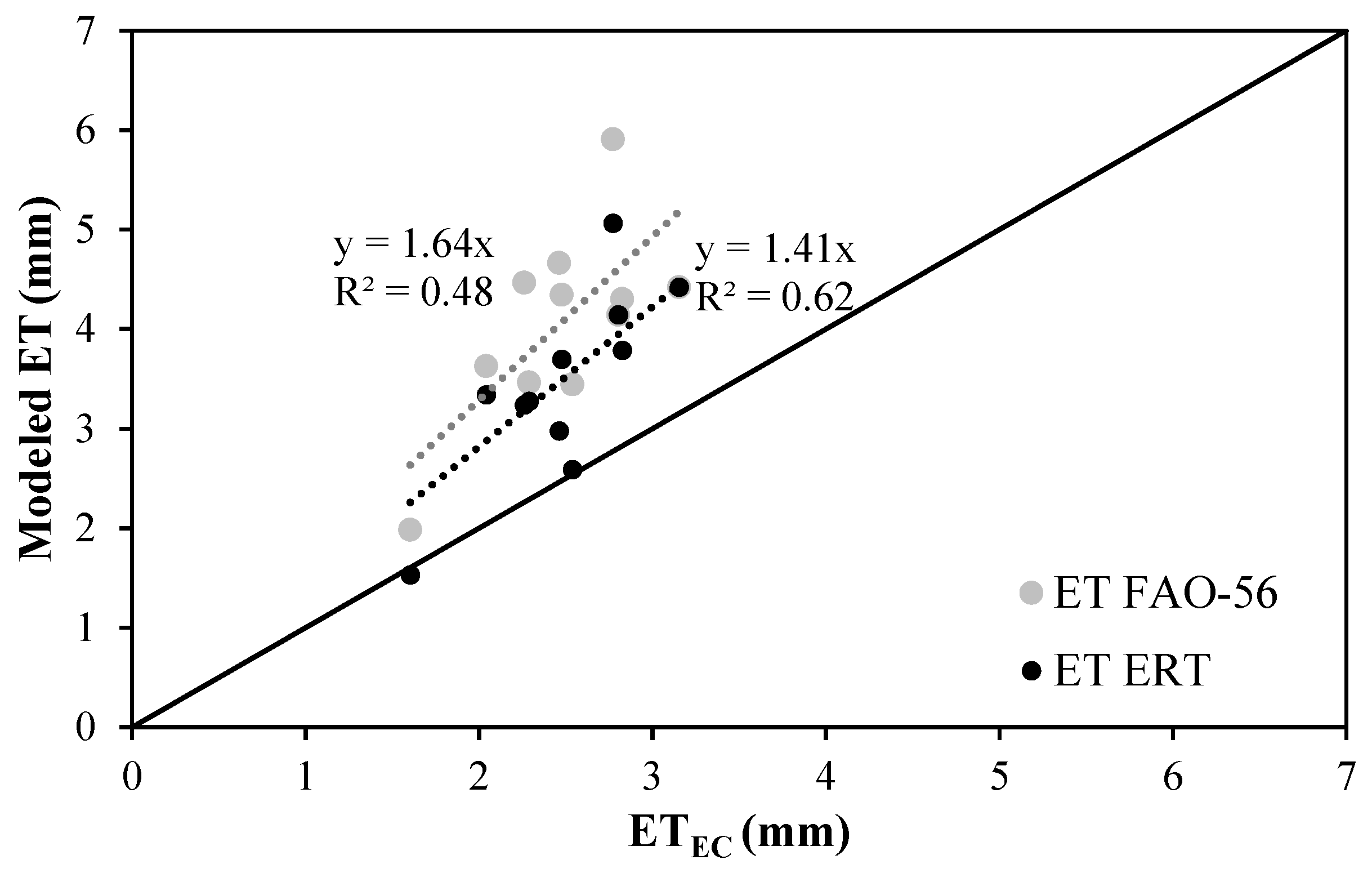
3.3.2. ET Comparison: Original and ERT-Adjusted Dual Kc FAO-56 vs EC
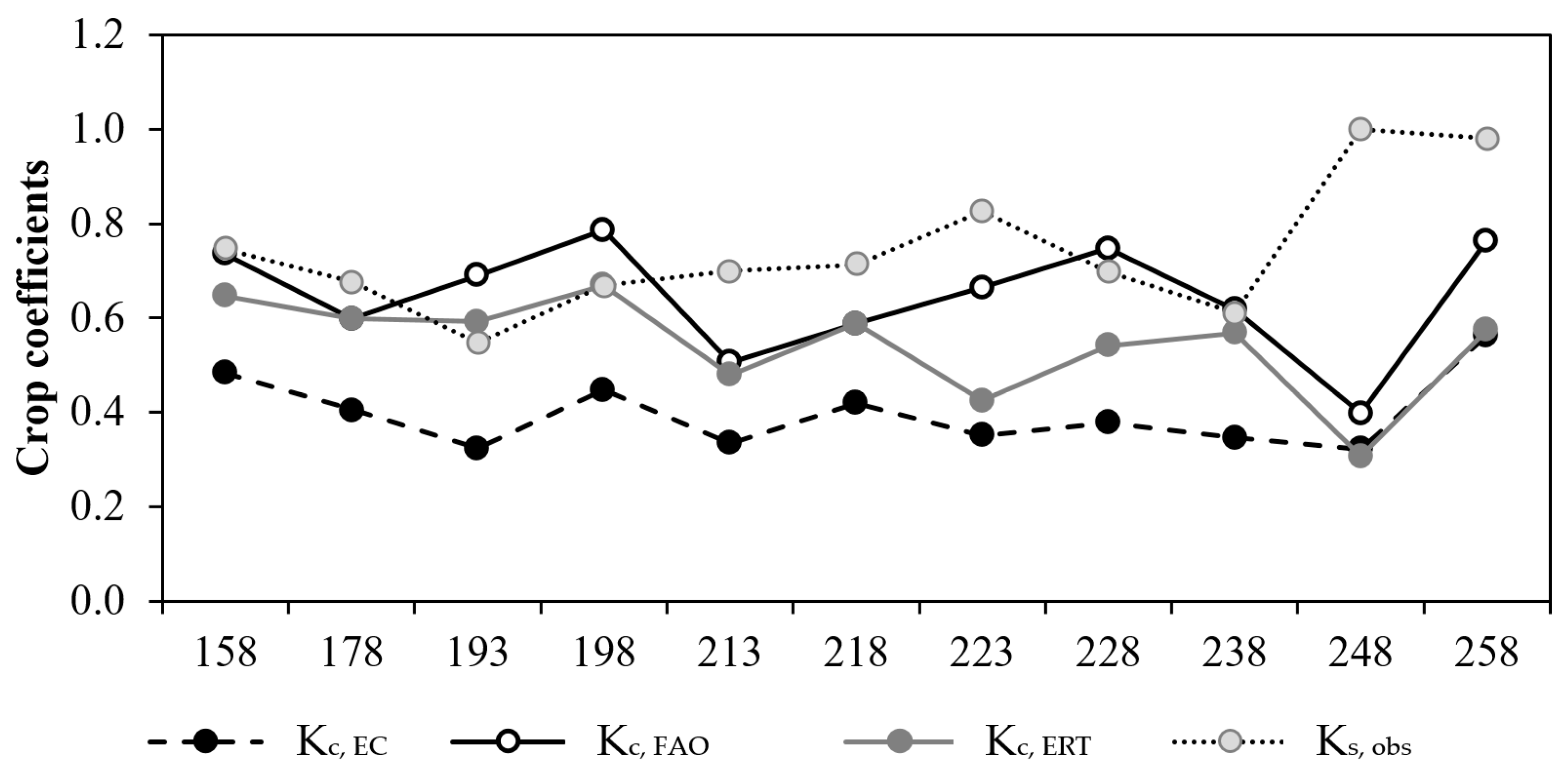
3.3.3. Crop Coefficients Comparison and Ks Estimation
4. Discussion
5. Conclusions
- Spatially distributed ET rates can be obtained by incorporating VIs computed using remote sensing technologies into the dual Kc FAO-56 approach.
- The integration of 3-D ERT methodology into the dual Kc FAO-56 approach considerably reduced errors in ET estimates. This technology allowed the tracking of the wetting distribution patterns, helping to accurately estimate few and therefore the water evaporated from the soil surface.
- The dual Kc FAO-56 approach determines ET under standard conditions where no limitations are placed on crop growth or ET, whereas EC measures ET even for non-standard conditions (e.g., under soil water stress conditions). From the comparison between the ET measured from the EC tower and the ET estimated from the ERT-adjusted dual Kc FAO-56 approach, the Ks term can be experimentally derived.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- French, R.J.; Schultz, J.E. Water use efficiency of wheat in a Mediterranean type environment. I. The relation between yield, water use and climate. Aust. J. Agric. Res. 1984, 35, 743–764. [Google Scholar] [CrossRef]
- French, R.J.; Schultz, J.E. Water use efficiency of wheat in a mediterranean-type environment. II. Some limitations to efficiency. Aust. J. Agric. Res. 1984, 35, 765–775. [Google Scholar] [CrossRef]
- Capra, A.; Consoli, S.; Russo, A.; Scicolone, B. Integrated agro-economic approach to deficit irrigation on lettuce crops in Sicily (Italy). J. Irrig. Drain. Eng. 2008, 134, 437–445. [Google Scholar] [CrossRef]
- Consoli, S.; Papa, R. Corrected surface energy balance to measure and model the evapotranspiration of irrigated orange orchards in semi-arid Mediterranean conditions. Irrig. Sci. 2013, 31, 1159–1171. [Google Scholar] [CrossRef]
- Zhao, P.; Kang, S.; Li, S.; Ding, R.; Tong, L.; Du, T. Seasonal variations in vineyard ET partitioning and dual crop coefficients correlate with canopy development and surface soil moisture. Agric. Water Manag. 2018, 197, 19–33. [Google Scholar] [CrossRef]
- Yau, S.K.; Nimah, M.; Farran, M. Early sowing and irrigation to increase barley yields and water use efficiency in Mediterranean conditions. Agric. Water Manag. 2011, 98, 1776–1781. [Google Scholar] [CrossRef]
- Yan, A.; Gao, C.; Ren, Y.; Zong, R.; Ma, Y.; Li, Q. Effects of pre-sowing irrigation and straw mulching on the grain yield and water use efficiency of summer maize in the North China Plain. Agric. Water Manag. 2017, 186, 21–28. [Google Scholar] [CrossRef]
- Eastham, J.; Gregory, P.J.; Williamson, D.R.; Watson, G.D. The influence of early seeding of wheat and lupin crops on evapotranspiration and evaporation from the soil surface in a Mediterranean climate. Agric. Water Manag. 1999, 42, 205–218. [Google Scholar] [CrossRef]
- Liu, C.M.; Zhang, X.Y.; Zhang, Y.Q. Determination of daily evaporation and evapotranspiration of winter wheat and maize by large-scale weighing lysimeter and micro-lysimeter. Agric. For. Meteorol. 2002, 111, 109–120. [Google Scholar] [CrossRef]
- Photiades, A.; Hadjichristodoulou, A. Sowing date, sowing depth, seed rate and row spacing of wheat and barley under dryland conditions. Field Crops Res. 1984, 9, 151–162. [Google Scholar] [CrossRef]
- Lascano, R.J.; Baumhardt, R.L.; Hicks, S.K.; Heilman, J.L. Soil and plant water evaporation from strip-tillage control, measurement and simulation. Agron. J. 1994, 86, 987–994. [Google Scholar] [CrossRef]
- Stagnari, F.; Galieni, A.; Speca, S.; Cafiero, G.; Pisante, M. Effects of straw mulch on growth and yield of durum wheat during transition to Conservation Agriculture in Mediterranean environment. Field Crops Res. 2014, 167, 51–63. [Google Scholar] [CrossRef]
- Prosdocimi, M.; Jordan, A.; Tarolli, P.; Keesstra, S.; Novara, A.; Cerda, A. The immediate effectiveness of barley straw mulch in reducing soil erodibility and surface runoff generation in Mediterranean vineyards. Sci. Total Environ. 2016, 547, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- González-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models forestimating crop evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- Subbaiah, R. A review of models for predicting soil water dynamics during trickle irrigation. Irrig. Sci. 2013, 31, 225–258. [Google Scholar] [CrossRef]
- Jarvis, N.; Koestel, J.; Larsbo, M. Understanding preferential flow in the vadose zone: Recent advances and future prospects. Vadose Zone J. 2016, 15, 15. [Google Scholar] [CrossRef]
- Hardie, M.; Ridges, J.; Swarts, N.; Close, D. Drip irrigation wetting patterns and nitrate distribution: Comparison between electrical resistivity (ERI), dye tracer, and 2D soil–water modelling approaches. Irrig. Sci. 2018, 36, 97–110. [Google Scholar] [CrossRef]
- Cassiani, G.; Boaga, J.; Vanella, D.; Perri, M.T.; Consoli, S. Monitoring and modelling of soil–plant interactions: The joint use of ERT, sap flow and eddy covariance data to characterize the volume of an orange tree root zone. Hydrol. Earth Syst. Sci. 2015, 19, 2213–2225. [Google Scholar] [CrossRef]
- Cassiani, G.; Boaga, J.; Rossi, M.; Putti, M.; Fadda, G.; Majone, B.; Bellin, A. Soil–plant interaction monitoring: Small scale example of an apple orchard in Trentino, North-eastern Italy. Sci. Total Environ. 2016, 543, 851–861. [Google Scholar] [CrossRef]
- Consoli, S.; Stagno, F.; Vanella, D.; Boaga, J.; Cassiani, G.; Roccuzzo, G. Partial root-zone drying irrigation in orange orchards: Effects on water use and crop production characteristics. Eur. J. Agron. 2017, 82, 190–202. [Google Scholar] [CrossRef]
- Vanella, D.; Cassiani, G.; Busato, L.; Boaga, J.; Barbagallo, S.; Binley, A.; Consoli, S. Use of small scale electrical resistivity tomography to identify soil-root interactions during deficit irrigation. J. Hydrol. 2018, 556, 310–324. [Google Scholar] [CrossRef]
- Binley, A.M.; Kemna, A. DC resistivity and induced polarization methods. In Hydrogeophysics; Rubin, Y., Hubbard, S.S., Eds.; Springer: Dordrecht, The Netherlands, 2005; Volume 50, pp. 129–156. [Google Scholar] [CrossRef]
- Binley, A. Tools and techniques: DC electrical methods. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 11, pp. 233–259. [Google Scholar] [CrossRef]
- Consoli, S.; Vanella, D. Comparisons of satellite-based models for estimating evapotranspiration fluxes. J. Hydrol. 2014, 513, 475–489. [Google Scholar] [CrossRef]
- Consoli, S.; Vanella, D. Mapping crop evapotranspiration by integrating vegetation indices into a soil water balance model. Agric. Water Manag. 2014, 143, 71–81. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoringthe Vernal Advancement and Retrogradation of Natural Vegetation; Type III, Final Report; NASA/GSFC: Greenbelt, MD, USA, 1974; pp. 1–371.
- Consoli, S.; Stagno, F.; Roccuzzo, G.; Cirelli, G.; Intrigliolo, F. Sustainable management of limited water resources in a young orange orchard. Agric. Water Manag. 2014, 132, 60–68. [Google Scholar] [CrossRef]
- Vanella, D.; Consoli, S. Eddy Covariance fluxes versus satellite-based modelisation in a deficit irrigated orchard. Ital. J. Agrometeorol. 2018, 2, 41–52. [Google Scholar] [CrossRef]
- Aiello, R.; Bagarello, V.; Barbagallo, S.; Consoli, S.; Di Prima, S.; Giordano, G.; Iovino, M. An assessment of the Beerkan method for determining the hydraulic properties of a sandy loam soil. Geoderma 2014, 235, 300–307. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Aubinet, M.; Grelle, A.; Ibrom, A.; Rannik, U.; Moncrieff, J.; Foken, T.; Kowalski, A.S.; Martin, P.H.; Berbigier, P.; Bernhofer, C.; et al. Estimates of the annual net carbon and water exchange of European forests: The EUROFLUX methodology. Adv. Ecol. Res. 2000, 30, 113–175. [Google Scholar]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary-Layer Flows: Their Structure and Measurement; Oxford University Press: Oxford, UK, 1994; 289p. [Google Scholar]
- Prueger, J.H.; Hatfield, J.L.; Kustas, W.P.; Hipps, L.E.; MacPherson, J.I.; Parkin, T.B. Tower and aircraft eddy covariance measurements of water vapor, energy and carbon dioxide fluxes during SMACEX. J. Hydrometeorol. 2005, 6, 954–960. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.; Meyers, T.P.; Prueger, J.H.; Starksh, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. An improved method for estimating global evapotranspiration based on satellite determination of surface net radiation, vegetation index, temperature, and soil moisture. J. Hydrometeorol. 2008, 9, 712–727. [Google Scholar] [CrossRef]
- Knipper, K.; Hogue, T.; Scott, R.; Franz, K. Evapotranspiration estimates derived using multi-platform remote sensing in a semiarid region. Remote Sens. 2017, 9, 184. [Google Scholar] [CrossRef]
- Sun, G.; Alstad, K.; Chen, J.; Chen, S.; Ford, C.R.; Lin, G.; Liu, C.; Lu, N.; McNulty, S.G.; Miao, H.; et al. A general predictive model for estimating monthly ecosystem evapotranspiration. Ecohydrology 2011, 4, 245–255. [Google Scholar] [CrossRef]
- Consoli, S.; Licciardello, F.; Vanella, D.; Pasotti, L.; Villani, G.; Tomei, F. Testing the water balance model criteria using TDR measurements, micrometeorological data and satellite-based information. Agric. Water Manag. 2016, 170, 68–80. [Google Scholar] [CrossRef]
- Kim, J.H.; Yi, M.J.; Park, S.G.; Kim, J.G. 4-D inversion of DC resistivity monitoring data acquired over a dynamically changing earth model. J. Appl. Geophys. 2009, 68, 522–532. [Google Scholar] [CrossRef]
- Busato, L.; Boaga, J.; Perri, M.T.; Majone, B.; Bellin, A.; Cassiani, G. Hydrogeophysical characterization and monitoring of the hyporheic and riparian zones: The Vermigliana Creek case study. Sci. Total Environ. 2018, 648, 1105–1120. [Google Scholar] [CrossRef]
- Paço, T.A.; Ferreira, M.I.; Conceição, N. Peach orchard evapotranspiration in a sandy soil: Comparison between eddy covariance measurements and estimates by the FAO 56 approach. Agric. Water Manag. 2006, 85, 305–313. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Guemouria, J.; Ezzahar, J.; Khabba, S.; Boulet, G.; Hanich, L. Citrus orchard evapotranspiration: Comparison between eddy covariance measurements and the FAO-56 approach estimates. Plant Biosyst. 2009, 143, 201–208. [Google Scholar] [CrossRef]
- Maestre-Valero, J.F.; Testi, L.; Jiménez-Bello, M.A.; Castel, J.R.; Intrigliolo, D.S. Evapotranspiration and carbon exchange in a citrus orchard using eddy covariance. Irrig. Sci. 2017, 35, 397–408. [Google Scholar] [CrossRef]
| T1 | T2 | ||||
|---|---|---|---|---|---|
| Time Id | State | Starting Time | Ending Time | Starting Time | Ending Time |
| 00 | no irrigation | 9.17 | 9.46 | 9.29 | 10.02 |
| 01 | during the irrigation phase | 10.42 | 11.11 | 11.01 | 11.35 |
| 02 | 11.39 | 12.09 | 11.58 | 12.30 | |
| 03 | after the irrigation phase | 12.55 | 13.24 | 12.57 | 13.30 |
| 04 | 13.47 | 14.16 | 13.52 | 14.24 | |
| 05 | 14.41 | 15.09 | 14.43 | 15.17 | |
| Acquisition Dates | Day of the Year (DOY) |
|---|---|
| 7 June 2017 | 158 |
| 27 June 2017 | 178 |
| 12 July 2017 | 193 |
| 17 July 2017 | 198 |
| 1 August 2017 | 213 |
| 6 August 2017 | 218 |
| 11 August 2017 | 223 |
| 16 August 2017 | 228 |
| 26 August 2017 | 238 |
| 5 September 2017 | 248 |
| 15 September 2017 | 258 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanella, D.; Ramírez-Cuesta, J.M.; Intrigliolo, D.S.; Consoli, S. Combining Electrical Resistivity Tomography and Satellite Images for Improving Evapotranspiration Estimates of Citrus Orchards. Remote Sens. 2019, 11, 373. https://doi.org/10.3390/rs11040373
Vanella D, Ramírez-Cuesta JM, Intrigliolo DS, Consoli S. Combining Electrical Resistivity Tomography and Satellite Images for Improving Evapotranspiration Estimates of Citrus Orchards. Remote Sensing. 2019; 11(4):373. https://doi.org/10.3390/rs11040373
Chicago/Turabian StyleVanella, Daniela, Juan Miguel Ramírez-Cuesta, Diego S. Intrigliolo, and Simona Consoli. 2019. "Combining Electrical Resistivity Tomography and Satellite Images for Improving Evapotranspiration Estimates of Citrus Orchards" Remote Sensing 11, no. 4: 373. https://doi.org/10.3390/rs11040373
APA StyleVanella, D., Ramírez-Cuesta, J. M., Intrigliolo, D. S., & Consoli, S. (2019). Combining Electrical Resistivity Tomography and Satellite Images for Improving Evapotranspiration Estimates of Citrus Orchards. Remote Sensing, 11(4), 373. https://doi.org/10.3390/rs11040373









