Identification of Linear Vegetation Elements in a Rural Landscape Using LiDAR Point Clouds
Abstract
1. Introduction
2. Data and study area
2.1. LiDAR and Orthophoto Data
2.2. Study Area
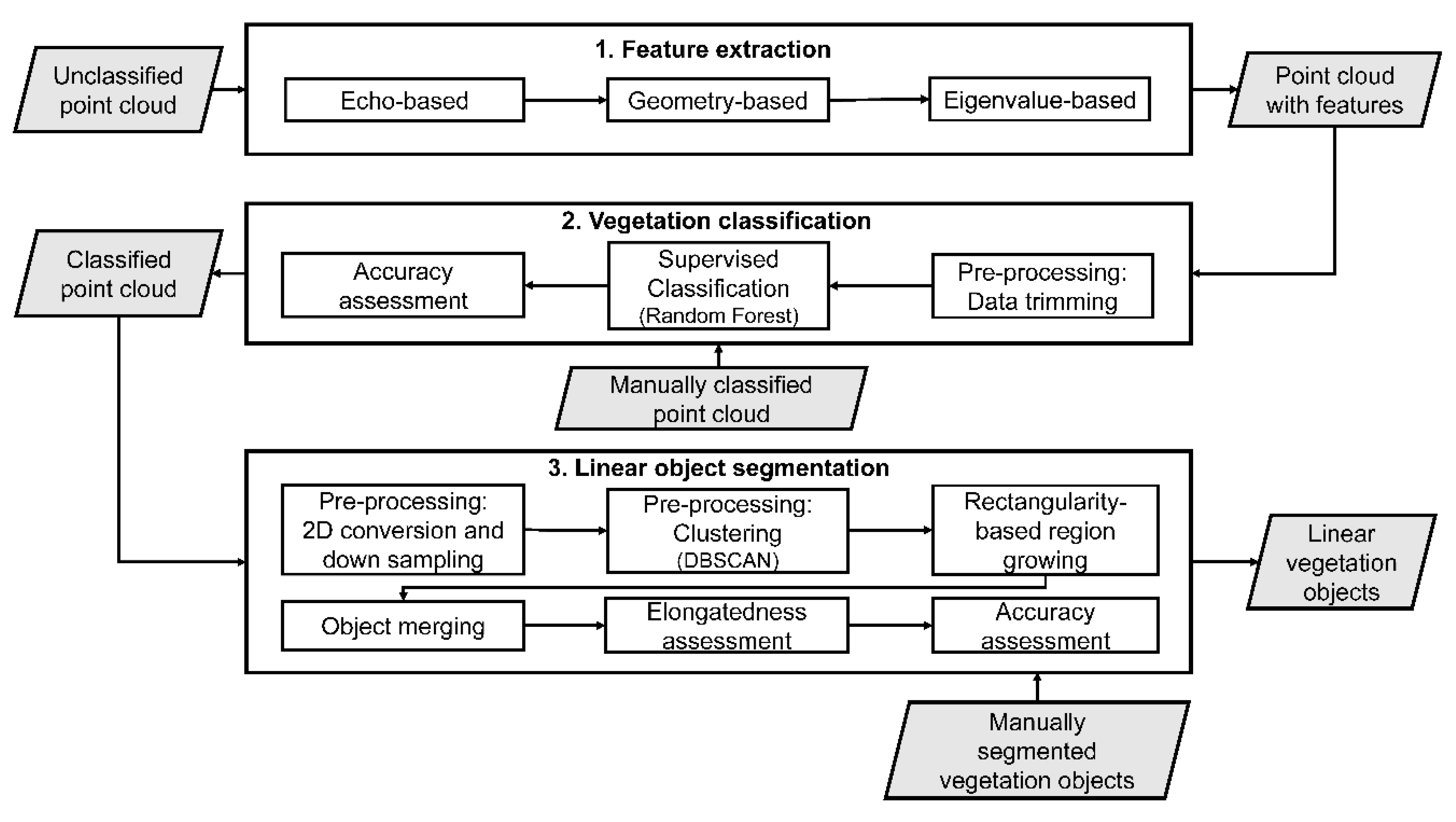
3. Method
3.1. Feature Extraction
3.1.1. Point-Based Features
3.1.2. Neighborhood-Based Features
3.2. Vegetation Classification
3.2.1. Preprocessing
3.2.2. Supervised Classification
3.2.3. Accuracy Assessment
3.3. Linear Object Segmentation
3.3.1. Preprocessing
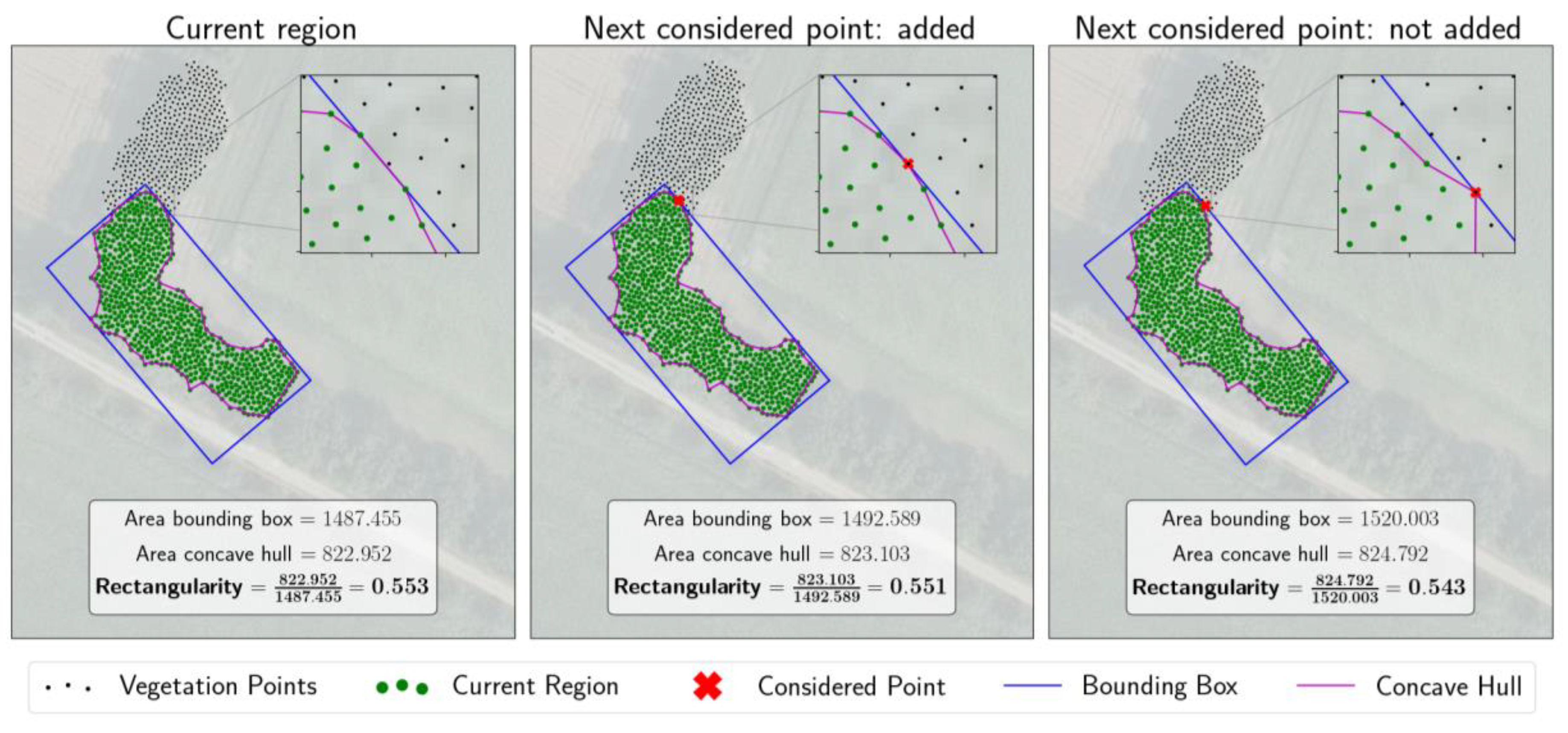
3.3.2. Rectangularity-Based Region Growing
3.3.3. Object Merging
3.3.4. Elongatedness
3.3.5. Accuracy Assessment
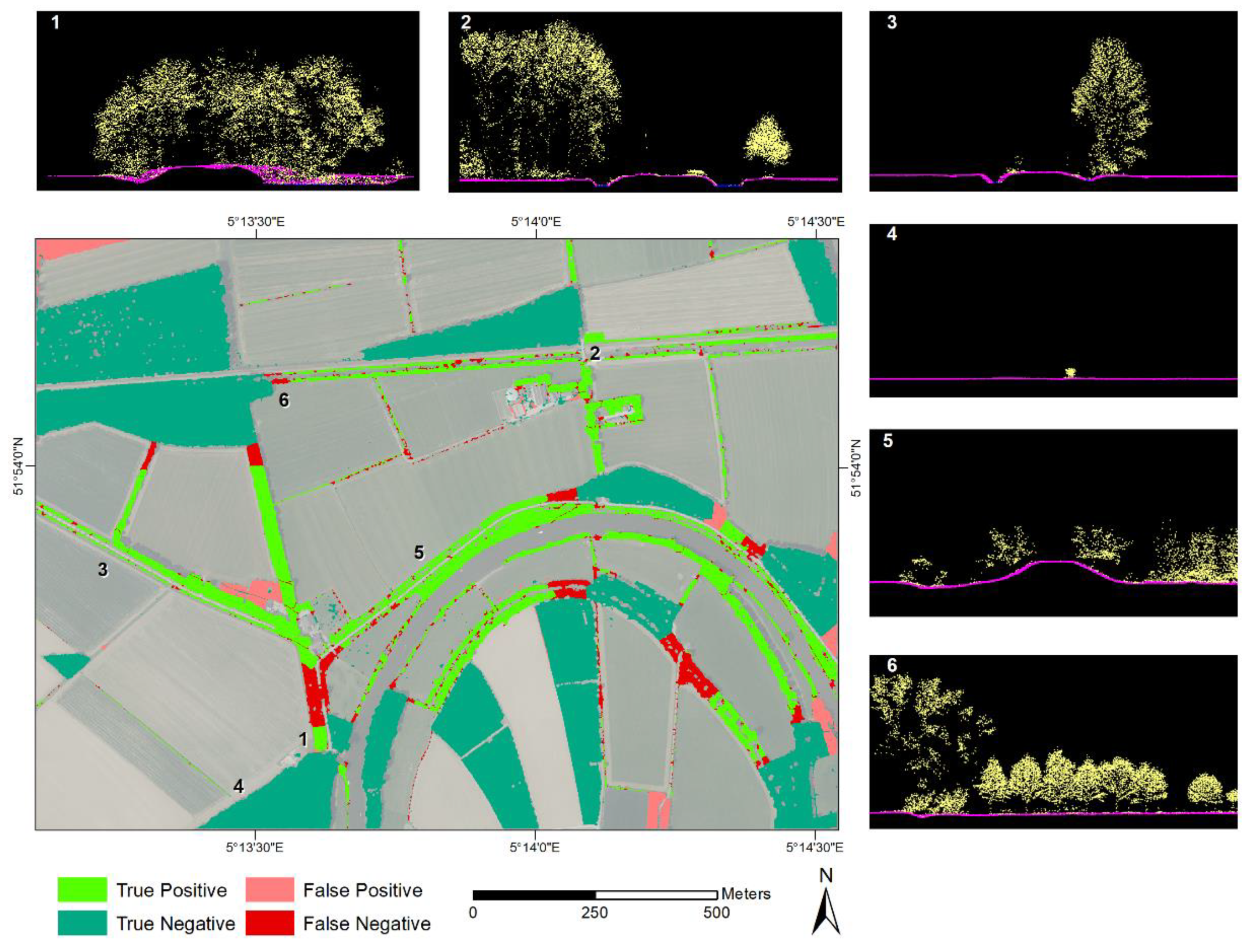
4. Results
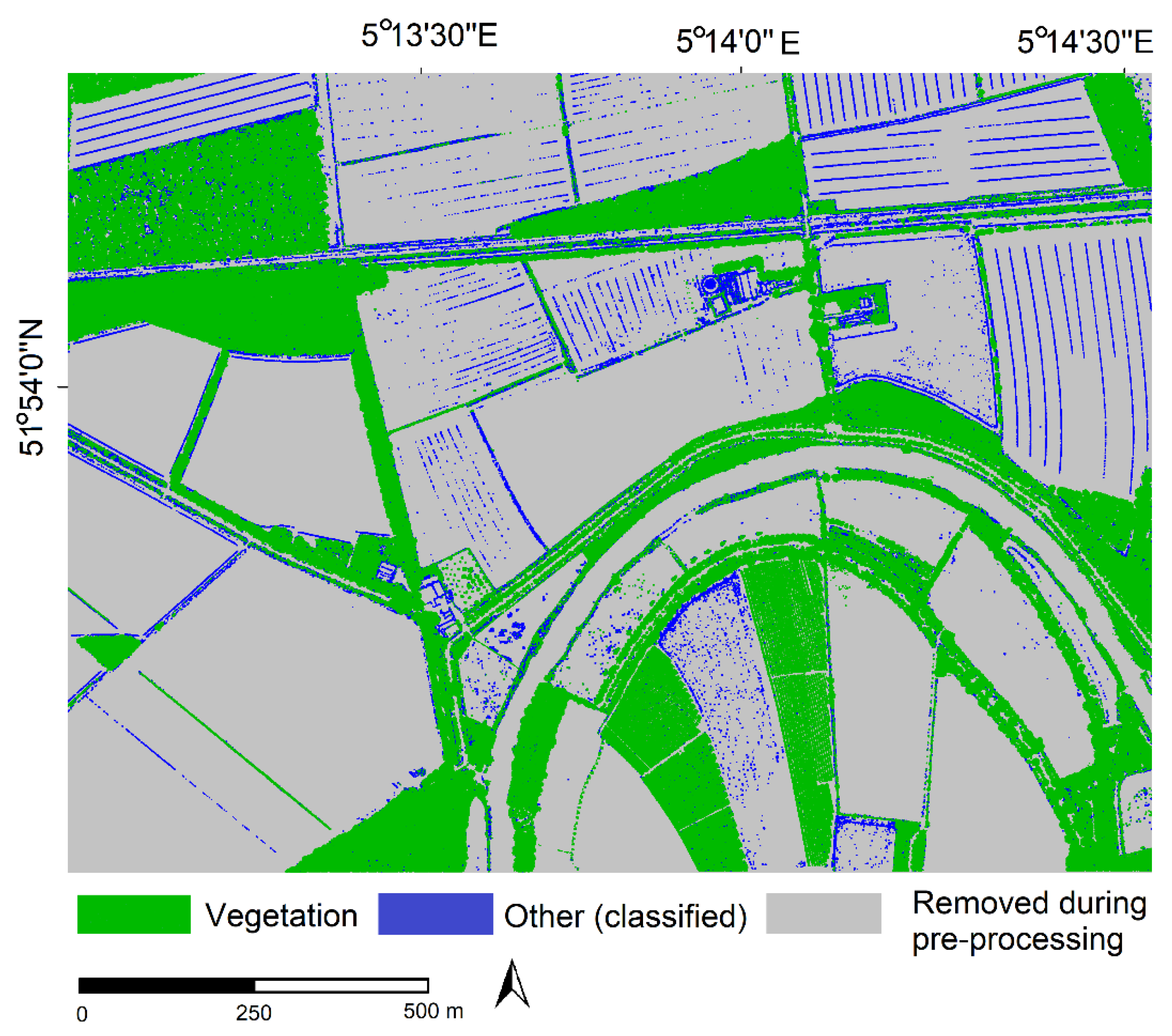
4.1. Vegetation Classification
4.2. Linear Object Segmentation
5. Discussion
5.1. Feature Extraction
5.2. Vegetation Classification
5.3. Linear Object Segmentation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Turner, M.G. Landscape ecology: The effect of pattern on process. Annu. Rev. Ecol. Syst. 1989, 20, 171–197. [Google Scholar] [CrossRef]
- Marquer, L.; Gaillard, M.-J.; Sugita, S.; Poska, A.; Trondman, A.-K.; Mazier, F.; Nielsen, A.B.; Fyfe, R.M.; Jöhnsson, A.M.; Smith, B.; et al. Quantifying the effects of land use and climate on Holocene vegetation in Europe. Quat. Sci. Rev. 2017, 171, 20–37. [Google Scholar] [CrossRef]
- Bailly, J.S.; Lagacherie, P.; Millier, C.; Puech, C.; Kosuth, P. Agrarian landscapes linear features detection from lidar: Application to artificial drainage networks. Int. J. Remote Sens. 2008, 29, 3489–3508. [Google Scholar] [CrossRef]
- Meyer, B.C.; Wolf, T.; Grabaum, R. A multifunctional assessment method for compromise optimisation of linear landscape elements. Ecol. Indic. 2012, 22, 53–63. [Google Scholar] [CrossRef]
- Van der Zanden, E.H.; Verburg, P.H.; Mücher, C.A. Modelling the spatial distribution of linear landscape elements in Europe. Ecol. Indic. 2013, 27, 125–136. [Google Scholar] [CrossRef]
- Aguirre-Gutiérrez, J.; Kissling, W.D.; Carvalheiro, L.G.; WallisDeVries, M.F.; Franzén, M.; Biesmeijer, J.C. Functional traits help to explain half-century long shifts in pollinator distributions. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Spellerberg, I.F.; Sawyer, J.W. An Introduction to Applied Biogeography; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Croxton, P.; Hann, J.; Greatorex-Davies, J.; Sparks, T. Linear hotspots? The floral and butterfly diversity of green lanes. Biol. Conserv. 2005, 121, 579–584. [Google Scholar] [CrossRef]
- Burel, F. Hedgerows and their role in agricultural landscapes. Crit. Rev. Plant Sci. 1996, 15, 169–190. [Google Scholar] [CrossRef]
- Jongman, R.G.H. Landscape linkages and biodiversity in Europe. In The New Dimensions of the European Landscape; Jongman, R.G.H., Ed.; Springer: Dordrecht, The Netherlands, 1996; pp. 179–189. [Google Scholar]
- Gobster, P.H.; Nassauer, J.I.; Daniel, T.C.; Fry, G. The shared landscape: What does aesthetics have to do with ecology? Landsc. Ecol. 2007, 22, 959–972. [Google Scholar] [CrossRef]
- Boutin, C.; Jobin, B.; Bélanger, L.; Baril, A.; Freemark, K. Hedgerows in the Farming Landscapes of Canada. Hedgerows of the World: Their Ecological Functions in Different Landscapes. Available online: https://www.researchgate.net/publication/264670164_Hedgerows_in_the_farming_landscapes_of_Canada (accessed on 31 January 2019).
- Stoate, C.; Boatman, N.; Borralho, R.; Carvalho, C.R.; De Snoo, G.; Eden, P. Ecological impacts of arable intensification in Europe. J. Environ. Manag. 2001, 63, 337–365. [Google Scholar] [CrossRef]
- Aksoy, S.; Akcay, H.G.; Wassenaar, T. Automatic mapping of linear woody vegetation features in agricultural landscapes using very high resolution imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 511–522. [Google Scholar] [CrossRef]
- Thornton, M.W.; Atkinson, P.M.; Holland, D. Sub-pixel mapping of rural land cover objects from fine spatial resolution satellite sensor imagery using super-resolution pixel-swapping. Int. J. Remote Sens. 2006, 27, 473–491. [Google Scholar] [CrossRef]
- Vannier, C.; Hubert-Moy, L. Multiscale comparison of remote-sensing data for linear woody vegetation mapping. Int. J. Remote Sens. 2014, 35, 7376–7399. [Google Scholar] [CrossRef]
- Tansey, K.; Chambers, I.; Anstee, A.; Denniss, A.; Lamb, A. Object-oriented classification of very high resolution airborne imagery for the extraction of hedgerows and field margin cover in agricultural areas. Appl. Geogr. 2009, 29, 145–157. [Google Scholar] [CrossRef]
- Kissling, W.D.; Seijmonsbergen, A.C.; Foppen, R.; Bouten, W. eEcolidar, eScience infrastructure for ecological applications of LiDAR point clouds: Reconstructing the 3d ecosystem structure for animals at regional to continental scales. Res. Ideas Outcomes 2017, 3, e14939. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. Lidar remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies: Lidar, an emerging remote sensing technology that directly measures the three-dimensional distribution of plant canopies, can accurately estimate vegetation structural attributes and should be of particular interest to forest, landscape, and global ecologists. AIBS Bull. 2002, 52, 19–30. [Google Scholar]
- Eitel, J.U.; Höfle, B.; Vierling, L.A.; Abellán, A.; Asner, G.P.; Deems, J.S.; Glennie, C.L.; Joerg, P.C.; LeWinter, A.L.; Magney, T.S.; et al. Beyond 3-d: The new spectrum of lidar applications for earth and ecological sciences. Remote Sens. Environ. 2016, 186, 372–392. [Google Scholar] [CrossRef]
- Song, J.-H.; Han, S.-H.; Yu, K.; Kim, Y.-I. Assessing the possibility of land-cover classification using lidar intensity data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 259–262. [Google Scholar]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- PDOK. Available online: https://www.pdok.nl/viewer/ (accessed on 12 July 2018).
- AHN Inwinjaren AHN2 & AHN3. Available online: http://www.ahn.nl/common-nlm/inwinjaren-ahn2--ahn3.html (accessed on 12 July 2018).
- Yan, W.Y.; Shaker, A.; El-Ashmawy, N. Urban land cover classification using airborne LiDAR data: A review. Remote Sens. Environ. 2015, 158, 295–310. [Google Scholar] [CrossRef]
- Van der Walt, S.; Colbert, S.C.; Varoquaux, G. The numpy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- SciPy: Open source scientific tools for Python. Available online: http://www.scipy.org/ (accessed on 12 July 2018).
- McKinney, W. Data structures for statistical computing in python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 51–56. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- CGAL Project. CGAL User and Reference Manual, 4.13th ed.; CGAL Editorial Board, 2018; Available online: https://doc.cgal.org/latest/Manual/packages.html (acceseed on 1 February 2019).
- PDAL. Available online: https://pdal.io/ (accessed on 12 July 2018).
- Cloud Compare. Available online: http://www.cloudcompare.org/ (accessed on 12 July 2018).
- Chehata, N.; Guo, L.; Mallet, C. Airborne lidar feature selection for urban classification using random forests. Remote Sens. Spat. Inf. Sci. 2009, 38, 207–2012. [Google Scholar]
- Guo, L.; Chehata, N.; Mallet, C.; Boukir, S. Relevance of airborne LiDAR and multispectral image data for urban scene classification using random forests. ISPRS J. Photogramm. Remote Sens. 2011, 66, 56–66. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F.; Roux, M.; Soergel, U.; Heipke, C. Relevance assessment of full-waveform lidar data for urban area classification. ISPRS J. Photogramm. Remote Sens. 2011, 66, S71–S84. [Google Scholar] [CrossRef]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Contextual classification of LiDAR data and building object detection in urban areas. SPRS J. Photogramm. Remote Sens. 2018, 87, 152–165. [Google Scholar] [CrossRef]
- Pauly, M.; Gross, M.; Kobbelt, L.P. Efficient simplification of point-sampled surfaces. In Proceedings of the Conference on Visualization, IEEE Visualization, Boston, MA, USA, 27 October–1 November 2002; pp. 163–170. [Google Scholar]
- West, K.F.; Webb, B.N.; Lersch, J.R.; Pothier, S.; Triscari, J.M.; Iverson, A.E. Context-driven automated target detection in 3d data. In Proceedings of the SPIE 5426, Automatic Target Recognition XIX, Orlando, FL, USA, 21 September 2004; pp. 133–143. [Google Scholar] [CrossRef]
- Kashani, A.G.; Olsen, M.J.; Parrish, C.E.; Wilson, N. A review of LiDAR radiometric processing: From ad hoc intensity correction to rigorous radiometric calibration. Sensors 2015, 15, 28099–28128. [Google Scholar] [CrossRef]
- Hoppe, H.; DeRose, T.; Duchampt, T.; McDonald, J.; Stuetzle, W. Surface reconstruction from unorganized points. Comp. Graph. 1992, 26, 2. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Int. 1998, 20, 832–844. [Google Scholar]
- Hsu, C.; Chang, C.; Lin, C. A Practical Guide to Support Vector Classification. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 12 July 2018).
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to Learn Imbalanced Data; Technik Report 666; Department of Statistics, UC Berkeley: Berkeley, CA, USA, 2004. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Bradley, A.P. The use of the area under the roc curve in the evaluation of machine learning algorithms. Pattern Recogn. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of t4 phage lysozyme. Biochim. Biophys. Acta (BBA) Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Kubat, M.; Holte, R.C.; Matwin, S. Machine learning for the detection of oil spills in satellite radar images. Mach. Learn. 1998, 30, 195–215. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1145. [Google Scholar]
- Sun, Y.; Wong, A.K.; Kamel, M.S. Classification of imbalanced data: A review. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 687–719. [Google Scholar] [CrossRef]
- López, V.; Fernandez, A.; García, S.; Palade, V.; Herrera, F. An insight into classification with imbalanced data: Empirical results and current trends on using data intrinsic characteristics. Inf. Sci. 2013, 250, 113–141. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Kdd-96 Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Rabbani, T.; Van Den Heuvel, F.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Vosselman, G. Point cloud segmentation for urban scene classification. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 1, 257–262. [Google Scholar] [CrossRef]
- Rosin, P.L. Measuring rectangularity. Mach. Vis. Appl. 1999, 11, 191–196. [Google Scholar] [CrossRef]
- Toussaint, G.T. Solving geometric problems with the rotating calipers. In Proceedings of the IEEE Melecon’83, Athens, Greece, 24–26 May 1983; pp. 1–8. [Google Scholar]
- Preparata, F.P.; Shamos, M. Computational Geometry: An Introduction; Springer-Verlag: New York, NY, USA, 1985; ISBN 978-0-387-96131-6. [Google Scholar]
- Freeman, H.; Shapira, R. Determining the minimum-area encasing rectangle for an arbitrary closed curve. Commun. ACM 1975, 18, 409–413. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
- Delaunay, B. Sur la sphere vide. Izv. Akad. Nauk SSSR. Otdelenie Matematicheskii i Estestvennyka Nauk 7 1934, 1–2, 793–800. [Google Scholar]
- Nagao, M.; Matsuyama, T. A Structural Analysis of Complex Aerial Photographs; Springer-Verlag: New York, NY, USA, 1980; ISBN13 9781461582960. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; ISBN 9781420055139. [Google Scholar]
- Eysn, L.; Hollaus, M.; Schadauer, K.; Pfeifer, N. Forest Delineation Based on Airborne LiDAR Data. Remote Sens. 2012, 4, 762–783. [Google Scholar] [CrossRef]
- Yang, H.; Chen, W.; Qian, T.; Shen, D.; Wang, J. The Extraction of Vegetation Points from LiDAR Using 3D Fractal Dimension Analyses. Remote Sens. 2015, 7, 10815–10831. [Google Scholar] [CrossRef]
- Pfeiffer, N.; Mandlburger, G.; Otepka, J.; Karel, W. OPALS—A framework for Airborne Laser Scanning data analysis. Comput. Environ. Urban Syst. 2014, 45, 125–136. [Google Scholar] [CrossRef]
- Maes, J.; Teller, A.; Erhard, M.; Liquete, C.; Braat, L.; Berry, P.; Egoh, B.; Puydarrieux, P.; Fiorina, C.; Santos, F.; et al. Mapping and Assessment of Ecosystems and Their Services; Tech. Rep. EUR 27143 EN. Joint Research Center—Institute for Environment and Sustainability, 2013. Available online: http://ec.europa.eu/environment/nature/knowledge/ecosystem_assessment/pdf/102.pdf (accessed on 10 December 2018).
- Biała, K.; Condé, S.; Delbaere, B.; Jones-Walters, L.; Torre-Marín, A. Streamlining European Biodiversity Indicators 2020; Tech. Rep. 11/2012. European Environment Agency, 2012. Available online: https://www.eea.europa.eu/publications/streamlining-european-biodiversity-indicators-2020 (accessed on 10 December 2018).
- Paracchini, M.L.; Petersen, J.-E.; Hoogeveen, Y.; Bamps, C.; Burfield, I.; van Swaay, C. High Nature Value Farmland in Europe; Tech. Rep. EUR 23480 EN. Joint Research Center—Institute for Environment and Sustainability, 2008. Available online: http://agrienv.jrc.ec.europa.eu/publications/pdfs/HNV_Final_Report.pdf (accessed on 10 December 2018).
- Bouwma, I.; Sanders, M.; Op Akkerhuis, G.J.; Onno Knol, J.V.; de Wit, B.; Wiertz, J.; van Hinsber, A. Biodiversiteit Bekeken: Hoe Evalueert en Verkent Het PBL het Natuurbeleid? 2014. Available online: https://www.pbl.nl/sites/default/files/cms/publicaties/PBL_2014_Biodiversiteit%20bekeken_924.pdf (accessed on 10 December 2018).
| Feature Group | Feature | Symbol | Formula | Reference |
|---|---|---|---|---|
| Point | ||||
| Echo | Number of returns | Rt | - | - |
| Normalized return number | Rn | R/Rt | [35] | |
| Neighborhood | ||||
| Geometric | Height difference | ∆z | [23] | |
| Height standard deviation | σz | [23] | ||
| Local radius | rl | [23] | ||
| Local point density | D | [23] | ||
| Eigenvalue | Normal vector Z | Nz | [38] | |
| Linearity | Lλ | [39] | ||
| Planarity | Pλ | [39] | ||
| Scatter | Sλ | [39] | ||
| Omnivariance | Oλ | [39] | ||
| Eigentropy | Eλ | [39] | ||
| Sum of eigenvalues | ∑λ | [36] | ||
| Curvature | Cλ | [38] |
| Actual | ||||
|---|---|---|---|---|
| Vegetation | Other | User’s Accuracy | ||
| Predicted | Vegetation | 974,177 | 8171 | 0.99 |
| Other | 22,908 | 47,999 | 0.68 | |
| Producer’s accuracy | 0.98 | 0.85 | Overall accuracy: 0.97 | |
| Actual | ||||
|---|---|---|---|---|
| Linear | Non-Linear | Producer’s Accuracy | ||
| Predicted | Linear | 116,483.76 | 20,201.53 | 0.85 |
| Non-linear | 28,385.56 | 33,6754.65 | 0.92 | |
| User’s accuracy | 0.80 | 0.94 | Overall accuracy: 0.90 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucas, C.; Bouten, W.; Koma, Z.; Kissling, W.D.; Seijmonsbergen, A.C. Identification of Linear Vegetation Elements in a Rural Landscape Using LiDAR Point Clouds. Remote Sens. 2019, 11, 292. https://doi.org/10.3390/rs11030292
Lucas C, Bouten W, Koma Z, Kissling WD, Seijmonsbergen AC. Identification of Linear Vegetation Elements in a Rural Landscape Using LiDAR Point Clouds. Remote Sensing. 2019; 11(3):292. https://doi.org/10.3390/rs11030292
Chicago/Turabian StyleLucas, Chris, Willem Bouten, Zsófia Koma, W. Daniel Kissling, and Arie C. Seijmonsbergen. 2019. "Identification of Linear Vegetation Elements in a Rural Landscape Using LiDAR Point Clouds" Remote Sensing 11, no. 3: 292. https://doi.org/10.3390/rs11030292
APA StyleLucas, C., Bouten, W., Koma, Z., Kissling, W. D., & Seijmonsbergen, A. C. (2019). Identification of Linear Vegetation Elements in a Rural Landscape Using LiDAR Point Clouds. Remote Sensing, 11(3), 292. https://doi.org/10.3390/rs11030292





