Interoperability of Direction-Finding and Beam-Forming High-Frequency Radar Systems: An Example from the Australian High-Frequency Ocean Radar Network
Abstract
1. Introduction
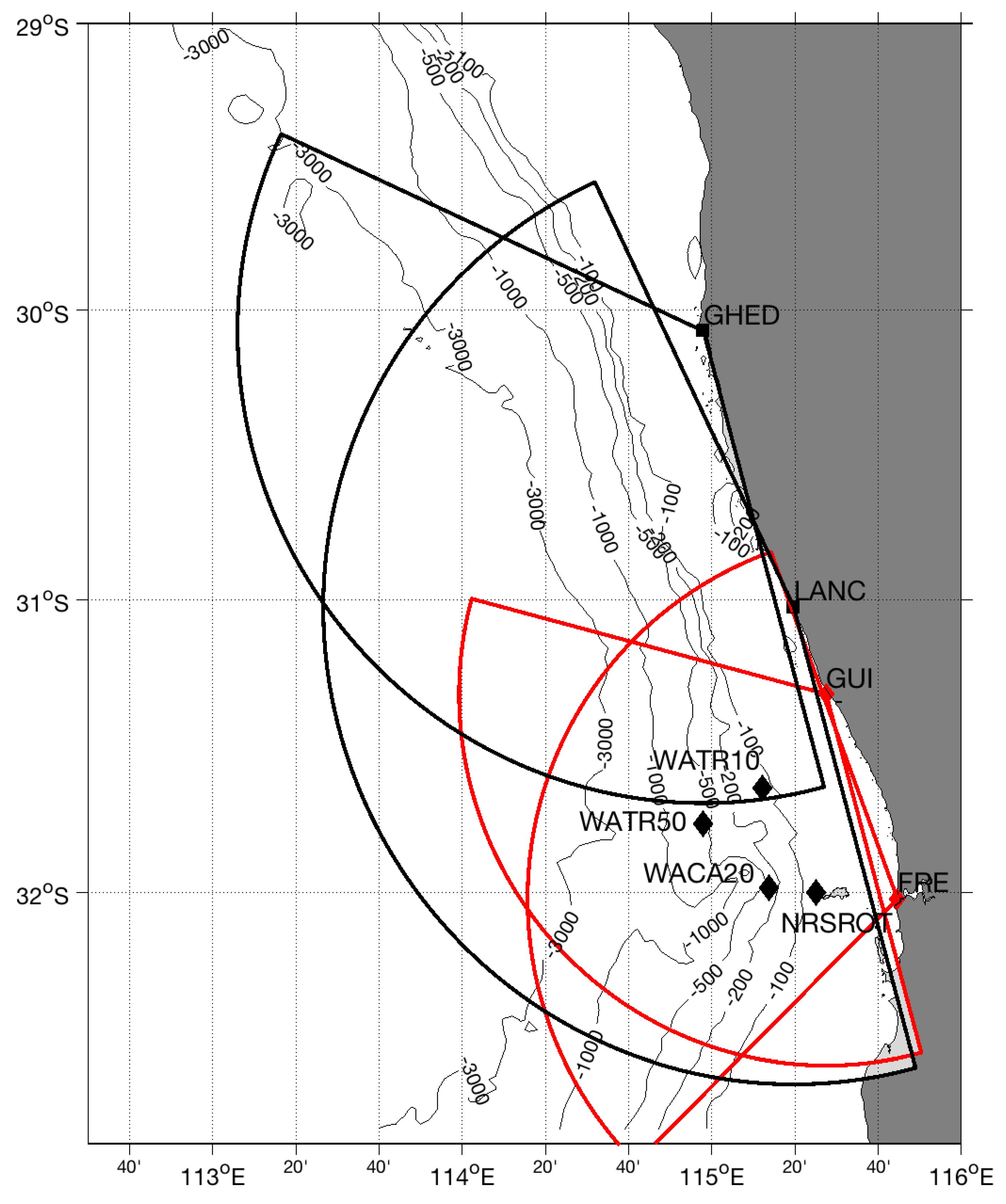
2. Materials and Methods
3. Results
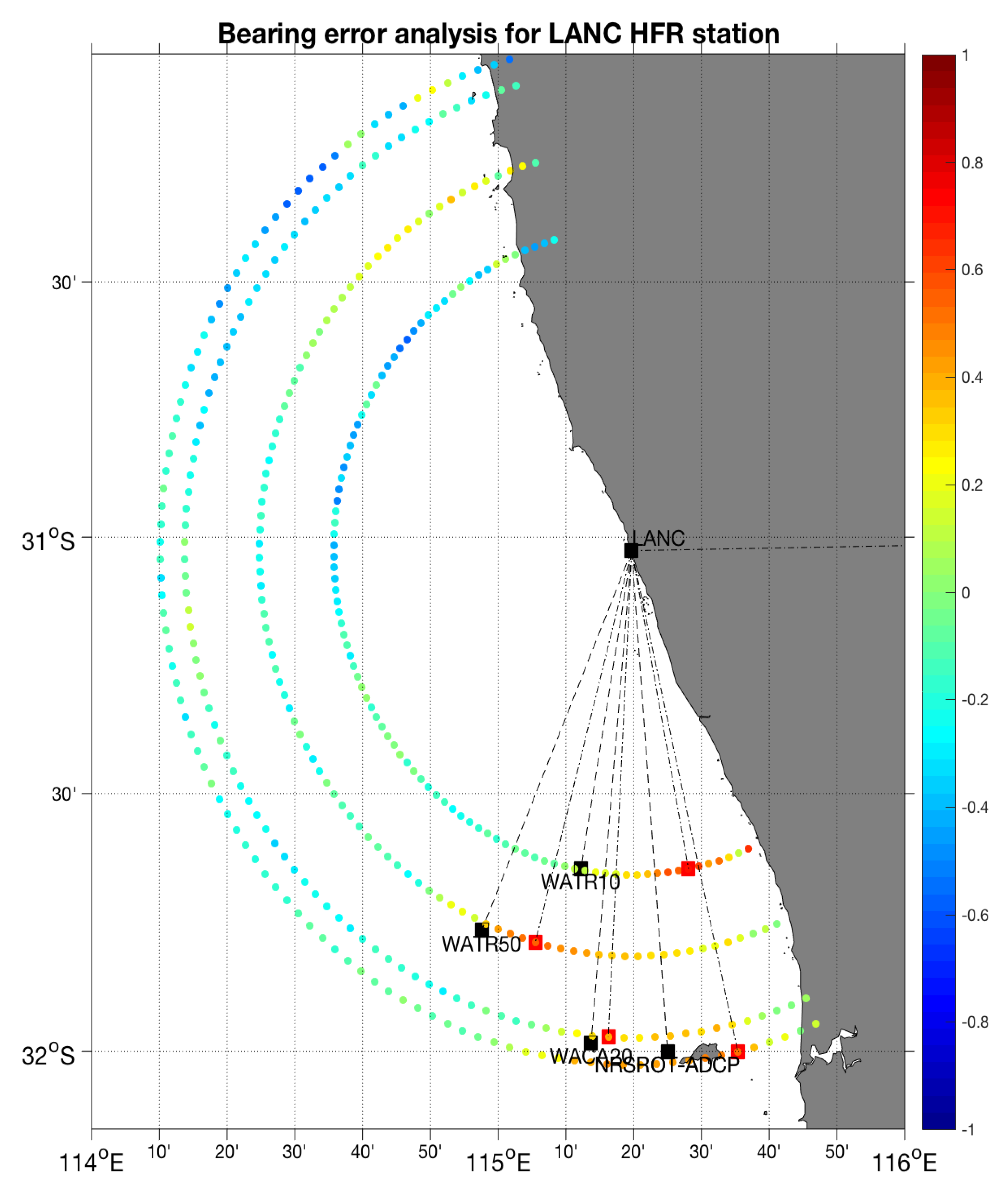
3.1. Accuracy of WERA and SeaSonde Radial Data
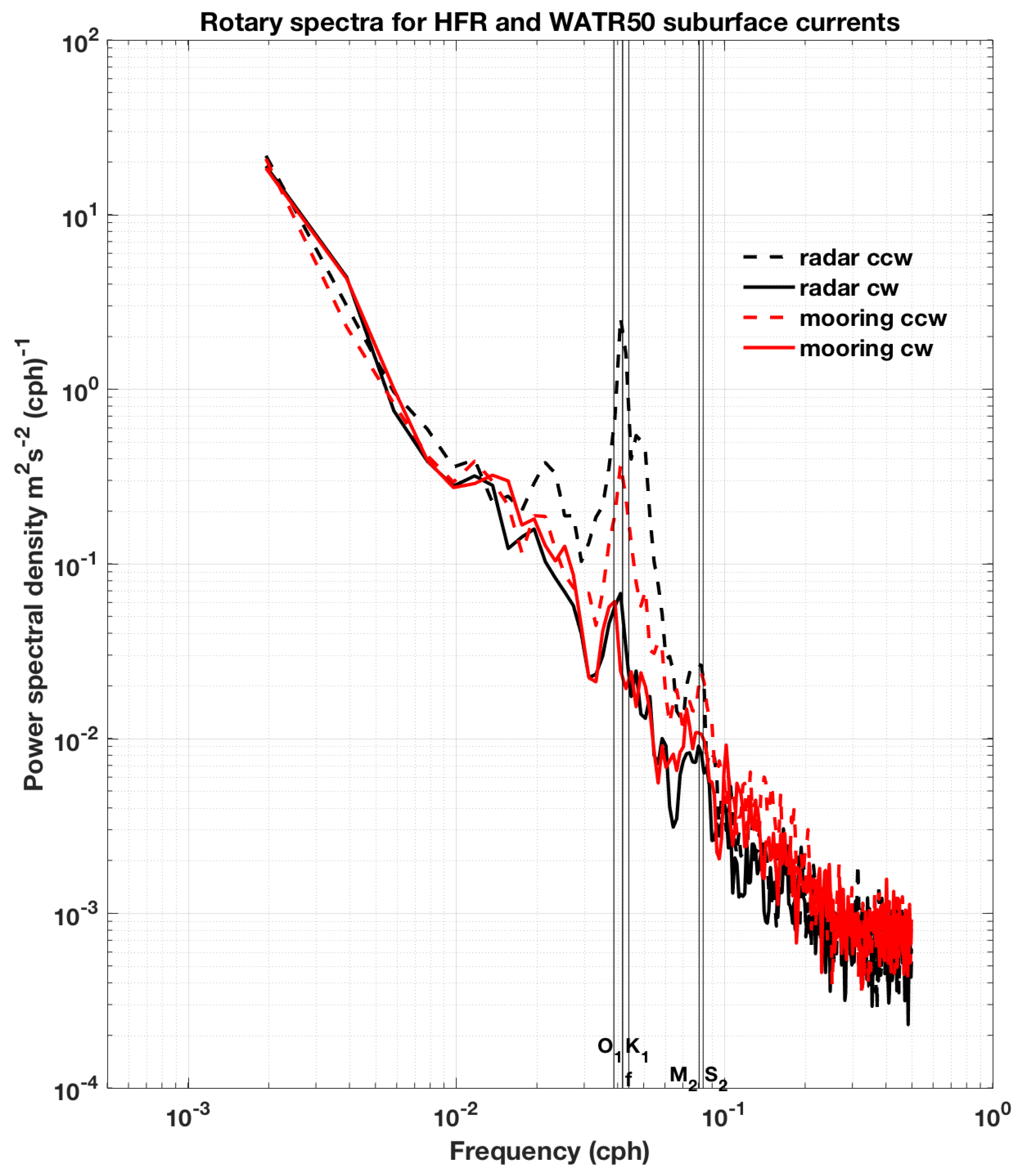
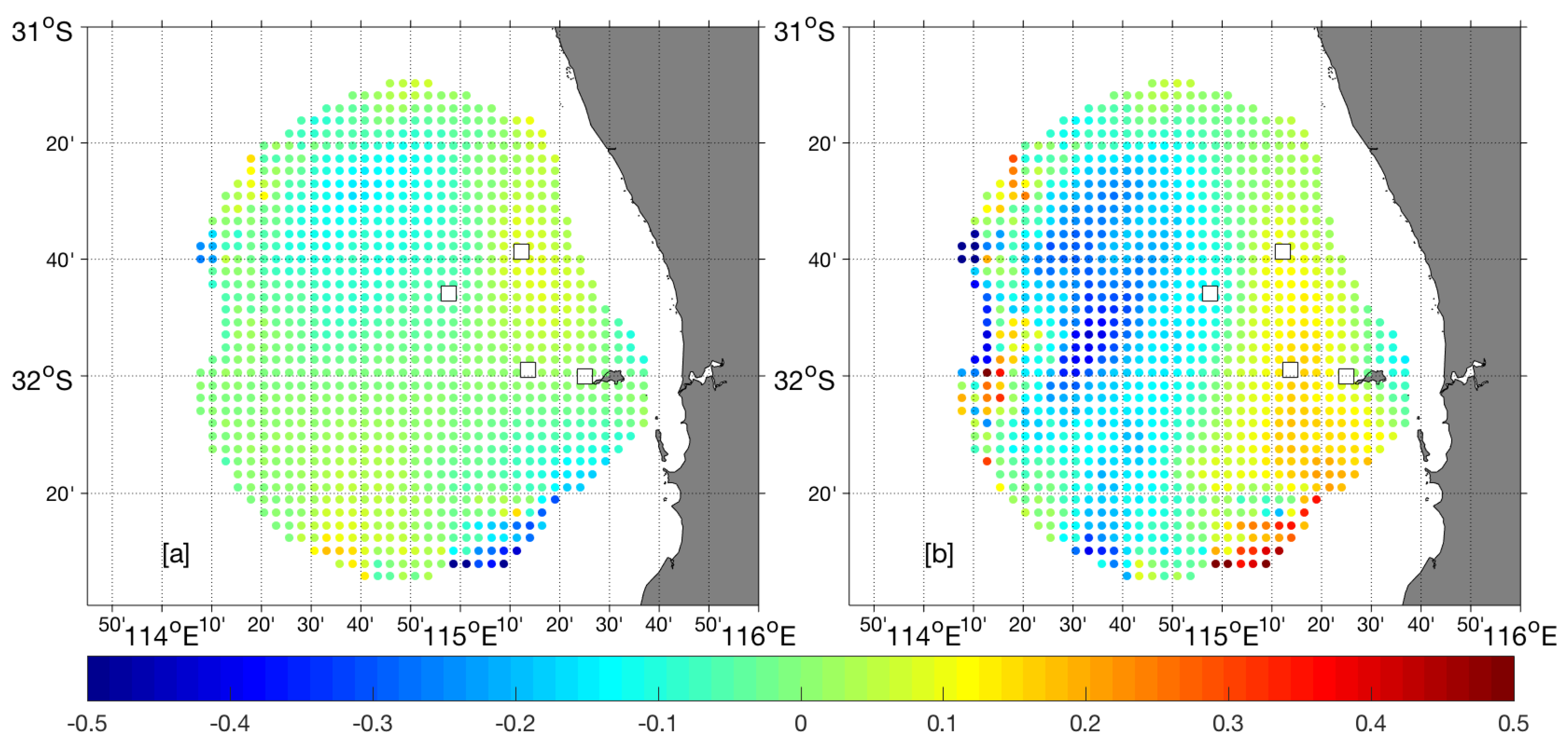
3.2. Comparison of WERA and SeaSonde Vector Maps
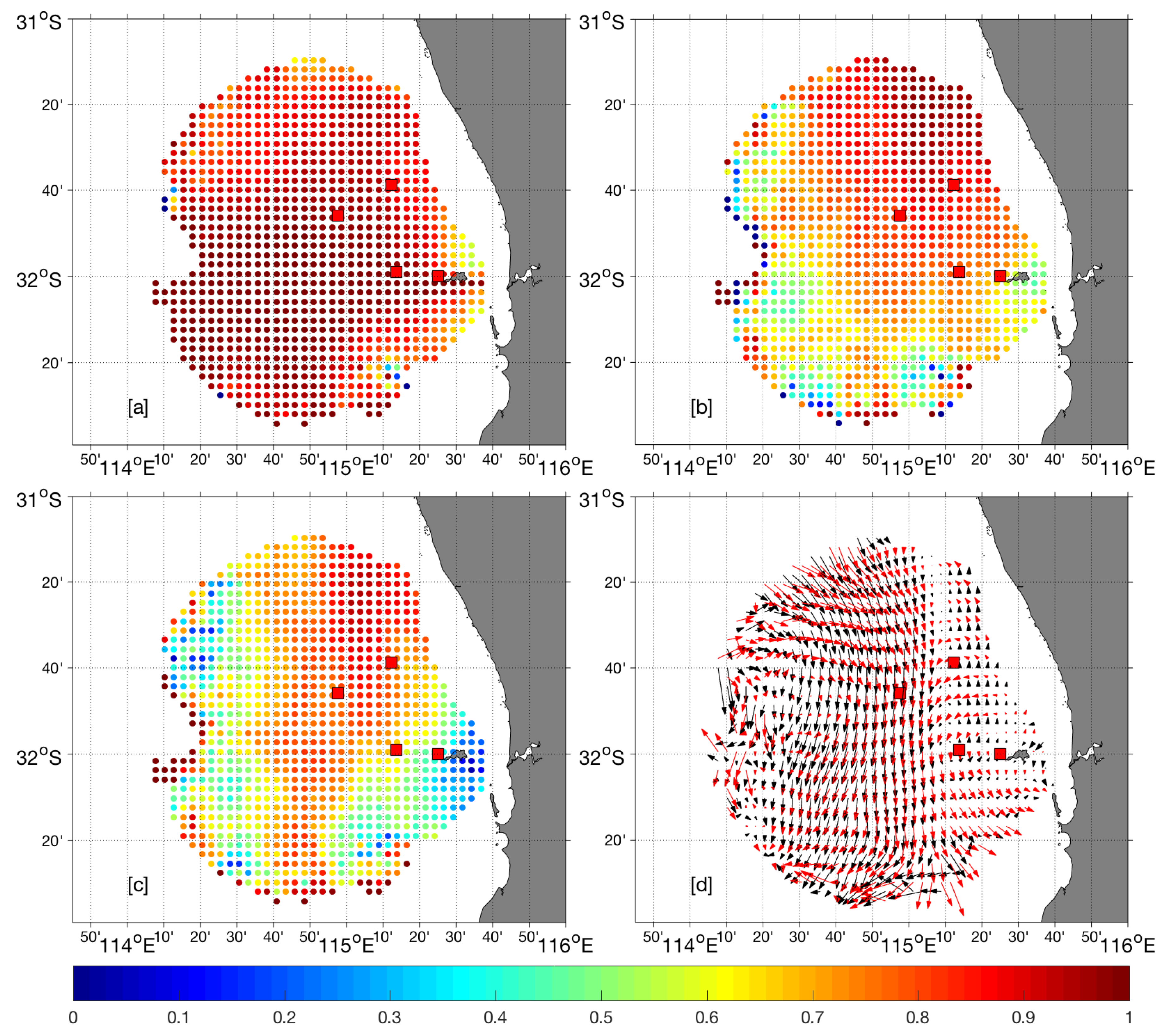
3.3. Comparison of Merged WERA–SeaSonde Merged Vector Maps
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Paduan, J.D.; Washburn, L. High-frequency radar observations of ocean surface currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef] [PubMed]
- Paduan, J.D.; Kosro, P.M.; Glenn, S.M. A national coastal ocean surface current mapping system for the United States. Mar. Technol. Soc. J. 2004, 38, 102–108. [Google Scholar] [CrossRef]
- Fujii, S.; Heron, M.L.; Kim, K.; Lai, J.-W.; Lee, S.-H.; Wu, X.; Wu, X.; Wyatt, L.R.; Yang, W. An overview of developments and applications of oceanographic radar networks in Asia and Oceania countries. Ocean Sci. J. 2013, 48, 69–97. [Google Scholar] [CrossRef]
- Wyatt, L.R. High frequency radar applications in coastal monitoring, planning and engineering. Aust. J. Civ. Eng. 2014, 12, 1–15. [Google Scholar] [CrossRef]
- Bellomo, L.; Griffa, A.; Cosoli, S.; Falco, P.; Gerin, R.; Iermano, I.; Kalampokis, A.; Kokkini, Z.; Lana, A.; Magaldi, M.G.; et al. Toward an integrated HF radar network in the Mediterranean Sea to improve search and rescue and oil spill response: The TOSCA project experience. J. Oper. Oceanogr. 2015, 8, 1–13. [Google Scholar] [CrossRef]
- Rubio, A.; Mader, J.; Corgnati, L.; Mantovani, C.; Griffa, A.; Novellino, A.; Quentin, C.; Wyatt, L.; Schulz-Stellenfleth, J.; Horstmann, J.; et al. HF Radar activity in European coastal seas: Next steps toward a Pan-European HF Radar Network. Front. Mar. Sci. 2017, 4, 8. [Google Scholar] [CrossRef]
- Chapman, R.D.; Shay, L.K.; Graber, H.C.; Edson, J.B.; Karachintsev, A.; Trump, C.L.; Ross, D.B. On the accuracy of HF radar surface current measurements: Intercomparisons with ship-based sensors. J. Geophys. Res. Oceans 1997, 102, 18737–18748. [Google Scholar] [CrossRef]
- Kohut, J.T.; Glenn, S.M. Improving HF radar surface current measurements with measured antenna beam patterns. J. Atmos. Ocean. Technol. 2003, 20, 1303–1316. [Google Scholar] [CrossRef]
- Emery, B.M.; Washburn, L.; Harlan, J.A. Evaluating radial current measurements from CODAR high-frequency radars with moored current meters. J. Atmos. Ocean. Technol. 2004, 21, 1259–1271. [Google Scholar] [CrossRef]
- Davies, A.M.; Hall, P.; Howarth, M.J.; Knight, P.J.; Player, R.J. Comparison of observed (HF radar and ADCP measurements) and computed tides in the North channel of the Irish sea. J. Phys. Oceanogr. 2001, 31, 1764–1785. [Google Scholar] [CrossRef]
- Erofeeva, S.Y.; Egbert, G.D.; Kosro, P.M. Tidal currents on the central Oregon shelf: Models, data, and assimilation. J. Geophys. Res. Oceans 2003, 108. [Google Scholar] [CrossRef]
- Mau, J.-C.; Wang, D.-P.; Ullman, D.S.; Codiga, D.L. Comparison of observed (HF radar, ADCP) and model barotropic tidal currents in the New York Bight and Block Island Sound. Estuar. Coast. Shelf Sci. 2007, 72, 129–137. [Google Scholar] [CrossRef]
- Shay, L.K.; Lentz, S.J.; Graber, H.C.; Haus, B.K. Current structure variations detected by high-frequency radar and vector-measuring current meters. J. Atmos. Ocean. Technol. 1998, 15, 237–256. [Google Scholar] [CrossRef]
- Rosenfeld, L.; Shulman, I.; Cook, M.; Paduan, J.D.; Shulman, L. Methodology for a regional tidal model evaluation, with application to central California. Deep Sea Res. Part II Top. Stud. Oceanogr. 2009, 56, 199–218. [Google Scholar] [CrossRef]
- Bjorkstedt, E.; Roughgarden, J. Larval transport and coastal upwelling: An application of HF radar in ecological research. Oceanography 1997, 10, 64–67. [Google Scholar] [CrossRef]
- Graber, H.C.; Limouzy-Paris, C.B. Transport patterns of tropical reef fish larvae by spin-off eddies in the straits of Florida. Oceanography 1997, 10, 68–71. [Google Scholar] [CrossRef]
- Cosoli, S.; Ličer, M.; Vodopivec, M.; Malačič, V. Surface circulation in the Gulf of Trieste (northern Adriatic Sea) from radar, model, and ADCP comparisons. J. Geophys. Res. Oceans 2013, 118, 6183–6200. [Google Scholar] [CrossRef]
- Barrick, D.; Lipa, B.J.; Crissman, R.D. Mapping surface currents with CODAR. Sea Technol. 1985, 26, 43–48. [Google Scholar]
- Gurgel, K.-W.; Essen, H.-H.; Schlick, T. Wellen Radar (WERA): A new ground-wave HF radar for ocean remote sensing. Coast. Eng. 1999, 37, 219–234. [Google Scholar] [CrossRef]
- Wyatt, L.R.; Green, J.J.; Middleditch, A.; Moorhead, M.D.; Howarth, J.; Holt, M.; Keogh, S. Operational wave, current, and wind measurements with the Pisces HF Radar. IEEE J. Ocean. Eng. 2006, 31, 819–834. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Helzel, T.; Petersen, L. WERA: Remote ocean sensing for current, wave, and wind direction: Introduction to the principle of operation. In Proceedings of the 2006 IEEE US/EU Baltic International Symposium, Klaipeda, Lithuania, 23–26 May 2006; Available online: http://www.helzel.com/ files/432/upload/Papers/WERA-Basics-Paper-6605.pdf (accessed on 22 October 2018).
- Liu, Y.; Weisberg, R.H.; Merz, C. Assessment of Codar SeaSonde HF Radars in mapping surface currents on the West Florida Shelf. J. Atmos. Ocean. Technol. 2014, 31, 1363–1382. [Google Scholar] [CrossRef]
- Fernandez, D.M.; Paduan, J.D. Simultaneous CODAR and OSCR measurements of ocean surface currents in Monterey Bay. In Proceedings of the IGARSSʼ96: IEEE 1996 International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31–31 May 1996; Volume 3, pp. 1749–1752. [Google Scholar] [CrossRef]
- Teague, C.C.; Fernandez, D.M.; Laws, K.E.; Paduan, J.D.; Vesecky, J.F. Comparison of multifrequency phased-array and direction-finding HF radar systems during COPE-3. In Proceedings of the IGARSS ʼ98: 1998 IEEE International Geoscience and Remote Sensing Symposium, Seattle, WA, USA, 6–10 July 1998; Volume 1, pp. 201–203. [Google Scholar] [CrossRef]
- Teague, C.C.; Vesecky, J.F.; Hallock, Z.R. A comparison of multifrequency HF radar and ADCP measurements of near-surface currents during COPE-3. IEEE J. Ocean. Eng. 2001, 26, 399–405. [Google Scholar] [CrossRef]
- Gurgel, K.-W.; Antonischki, G.; Schlick, T. A comparison of surface current fields derived by beam forming and direction finding techniques as applied by the HF radar WERA. In Proceedings of the IGARSSʼ97: 1997 International Geoscience and Remote Sensing Symposium, Singapore, 3–8 August 1997; Volume 4, pp. 1805–1807. [Google Scholar] [CrossRef]
- Essen, H.-H.; Gurgel, K.-W.; Schlick, T. On the accuracy of current measurements by means of HF radar. IEEE J. Ocean. Eng. 2000, 25, 472–480. [Google Scholar] [CrossRef]
- Kim, S.Y.; Terrill, E.; Cornuelle, B.D.; Jones, B.; Washburn, L.; Moline, M.A.; Paduan, J.D.; Garfield, N.; Largier, J.L.; Crawford, G.; et al. Mapping the U.S. West Coast surface circulation: A multiyear analysis of high-frequency radar observations. J. Geophys. Res. 2011, 116, C03011. [Google Scholar] [CrossRef]
- Gurgel, K.W.; Barbin, Y.; Schlick, T. Radio frequency interference suppression techniques in FMCW modulated HF radars. In Proceedings of the IEEE/Oceans’07 Europe 2007, Aberdeen, UK, 18–21 June 2007. [Google Scholar]
- Gomez, R.; Helzel, T.; Merz, C.R.; Liu, Y.; Weisberg, R.H.; Thomas, N. Improvements in ocean surface radar applications through real-time data quality-control. In Proceedings of the 2015 IEEE/OES Eleventh Current, Waves and Turbulence Measurement (CWTM), St. Petersburg, FL, USA, 2–6 March 2015. [Google Scholar] [CrossRef]
- Dzvonkovskaya, A.; Petersen, L.; Helzel, T. HF Ocean Radar with a triangle waveform implementation. In Proceedings of the 19th International Radar Symposium IRS 2018, Bonn, Germany, 20–22 June 2018; ISBN 978-3-7369-9545-1. [Google Scholar]
- Yoshikawa, Y.; Masuda, A.; Marubayashi, K.; Ishibashi, M.; Okuno, A. On the accuracy of HF radar measurement in the Tsushima Strait. J. Geophys. Res. 2006, 111, C04009. [Google Scholar] [CrossRef]
- Cosoli, S.; Grcic, B.; de Vos, S.; Hetzel, Y. Improving data quality for the Australian high frequency ocean radar network through real-time and delayed-mode quality-control procedures. Remote Sens. 2018, 10, 1476. [Google Scholar] [CrossRef]
- Middleditch, A.; Cosoli, S. Operational data management procedures for the Australian Coastal Ocean Radar Network. In Proceedings of the OCEANS 2016 MTS/IEEE, Monterey, CA, USA, 19–23 September 2016. [Google Scholar] [CrossRef]
- Archer, M.R.; Keating, S.R.; Roughan, M.; Johns, W.E.; Lumpkin, R.; Beron-Vera, F.; Shay, L.K. The kinematic similarity of two western boundary currents revealed by sustained high-resolution observations. Geophys. Res. Lett. 2018, 45, 6176–6185. [Google Scholar] [CrossRef]
- Archer, M.R.; Roughan, M.; Keating, S.; Schaeffer, A. On the Variability of the East Australian Current: Jet Structure, Meandering, and Influence on Shelf Circulation. J. Geophys. Res. Oceans 2017, 122, 8464–8481. [Google Scholar] [CrossRef]
- Kerry, C.; Powell, B.; Roughan, M.; Oke, P. Development and evaluation of a high-resolution reanalysis of the East Australian Current region using the Regional Ocean Modelling System (ROMS 3.4) and Incremental Strong-Constraint 4-Dimensional Variational (IS4D-Var) data assimilation. Geosci. Model Dev. 2016, 9, 3779–3801. [Google Scholar] [CrossRef]
- Mantovanelli, A.; Keating, S.; Wyatt, L.R.; Roughan, M.; Schaeffer, A. Lagrangian and Eulerian characterization of two counterrotating submesoscale eddies in a western boundary current. J. Geophys. Res. Oceans 2018, 122, 4902–4921. [Google Scholar] [CrossRef]
- Mihanovic, H.; Pattiaratchi, C.; Verspecht, F. Diurnal Sea Breezes Force Near-Inertial Waves along Rottnest Continental Shelf, Southwestern Australia. J. Phys. Oceanogr. 2016, 46, 3487–3508. [Google Scholar] [CrossRef]
- Schaeffer, A.; Gramoulle, A.; Roughan, M.; Mantovanelli, A. Characterizing frontal eddies along the East Australian Current from HF radar observations. J. Geophys. Res. Oceans 2017, 122, 3964–3980. [Google Scholar] [CrossRef]
- Wandres, M.; Wijeratne, E.M.S.; Cosoli, S.; Pattiaratchi, C. The effect of the Leeuwin Current on offshore surface gravity waves in southwestwestern Australia. J. Geophys. Res. Oceans 2017, 122, 9047–9067. [Google Scholar] [CrossRef]
- Heron, M.L.; Atwater, D.P. Temporal and spatial resolution of HF ocean radars. Ocean Sci. J. 2013, 48, 99–103. [Google Scholar] [CrossRef]
- Integrated Marine Observing System (IMOS). 2018. NRSROT July 2017. Available online: http://data.aodn.org.au/IMOS/ANMN/NRS/NRSROT/Velocity/IMOS_ANMN-NRS_AETVZ_20170724T080000Z_NRSROT-ADCP_FV01_NRSROT-ADCP-1707-Sentinel-or-Monitor-Workhorse-ADCP-44_END-20171123T234000Z_C-20171124T012415Z.nc (accessed on 16 April 2018).
- Integrated Marine Observing System (IMOS). 2018. NRSROT November 2017. Available online: http://data.aodn.org.au/IMOS/ANMN/WA/WACA20/Velocity/IMOS_ANMN-WA_AETVZ_20170915T080000Z_WACA20_FV01_WACA20-1709-Continental-194_END-20180301T233000Z_C-20180302T042339Z.nc (accessed on 16 April 2018).
- Integrated Marine Observing System (IMOS). 2018. WATR50 March 2017. Available online: http://data.aodn.org.au/IMOS/ANMN/NRS/NRSROT/Velocity/IMOS_ANMN-NRS_AETVZ_20171123T080000Z_NRSROT-ADCP_FV01_NRSROT-ADCP-1711-Sentinel-or-Monitor-Workhorse-ADCP-44_END-20180409T002000Z_C-20180413T052411Z.nc (accessed on 16 April 2018).
- Integrated Marine Observing System (IMOS). 2018. WATR10 May 2017. Available online: http://data.aodn.org.au/IMOS/ANMN/WA/WATR50/Velocity/IMOS_ANMN-WA_AETVZ_20170308T000000Z_WATR50_FV01_WATR50-1703-Long-Ranger-Workhorse-ADCP-496_END-20171109T010000Z_C-20171117T055142Z.nc (accessed on 16 April 2018).
- Integrated Marine Observing System (IMOS). 2018. WACA20 September 2017. Available online: http://data.aodn.org.au/IMOS/ANMN/WA/WATR10/Velocity/IMOS_ANMN-WA_AETVZ_20170525T080000Z_WATR10_FV01_WATR10-1705-Aquadopp-Profiler-98_END-20171025T233000Z_C-20171129T052225Z.nc (accessed on 16 April 2018).
- Morello, E.B.; Galibert, G.; Smith, D.; Ridgwayd, K.R.; Howell, B.; Slawinskie, D.; Timms, G.P.; Evans, K.; Lynch, T.P. Quality Control (QC) procedures for Australia’s National Reference Station’s sensor data—Comparing semi-autonomous systems to an expert oceanographer. Methods Oceanogr. 2014, 9, 17–33. [Google Scholar] [CrossRef]
- Kundu, P.K. Ekman veering observed near the ocean bottom. J. Phys. Oceanogr. 1976, 6, 238–242. [Google Scholar] [CrossRef]
- Breaker, L.C.; Gemmill, W.H.; Crosby, D.S. The application of a technique for vector correlation to problems in meteorology and oceanography. J. Appl. Meteorol. 1994, 33, 1354–1365. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1986, 1, 54–77. [Google Scholar] [CrossRef]
- Cosoli, S.; Gacic, M.; Mazzoldi, A. Variability of currents in front of the Venice Lagoon, Northern Adriatic Sea. Ann. Geophys. 2008, 26, 731–746. [Google Scholar] [CrossRef]
- Cosoli, S.; Gacic, M.; Mazzoldi, A. Surface current variability and wind influence in the northeastern Adriatic Sea as observed from high-frequency (HF) radar measurements. Cont. Shelf Res. 2012, 33, 1–13. [Google Scholar] [CrossRef]
- Welch, P.D. The use of fast-Fourier transform for the estimation of power spectra: A method based on time-averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Paduan, J.D.; Rosenfeld, L.K. Remotely sensed surface currents in Monterey Bay from shore-based HF radar (CODAR). J. Geophys. Res. 1996, 101, 20669–20686. [Google Scholar] [CrossRef]
- Cosoli, S.; Bolzon, G. Accuracy of surface current mapping from High-Frequency (HF) ocean radars. Bollettino di Geofisica Teorica ed Applicata 2014, 55. [Google Scholar] [CrossRef]

| Mooring Name | Instrument Type | Upwards/Downwards Looking | Seafloor Depth (m) | Deployment Depth (m) | Blanking Distance (m) | Bin Resolution (m) | Temporal Resolution (min) |
|---|---|---|---|---|---|---|---|
| NRSROT | RDI WorkHorse | Upwards | 47 | 44 | 3 | 2 | 20 |
| NRSROT | RDI WorkHorse | Upwards | 47 | 44 | 3 | 2 | 20 |
| WATR50 | RDI Long Ranger | Upwards | 500 | 496 | 24.5 | 16 | 30 |
| WATR10 | Nortek Aquadopp Pro | Upwards | 104 | 98 | 3.5 | 2.5 | 30 |
| WACA20 | Nortek 190 KHz Continental | Upwards | 200 | 194 | 7 | 5 | 30 |
| Mooring | Distance from Surface (m) | FRE Radar−look Angle/% Data | FRE R (95% CL)/RMSD (bias) | GUI Radar−look Angle/% Data | GUI R (95% CL)/RMSD (bias) | LANC Radar−look Angle/% Data | LANC R (95% CL)/RMSD (bias) | GHED Radar−look Angle/% Data | GHED R (95% CL)/RMSD (bias) |
|---|---|---|---|---|---|---|---|---|---|
| NRSROT | 15 | 87/96 | 0.14 (0.09, 0.18)/10.3 (1.3) | 175/98 | 0.31 (0.26, 0.34)/27.6 (2.9) | 184/41 | 0.42 (0.49)/31.0 (0.04) | −/− | −/− |
| NRSROT | 15 | 87/55 | −0.03 (−0.11, 0.05)/9.2 (0.5) | 175/71 | 0.18 (0.10, 0.24)/30.3 (−4.6) | −/− | −/− | −/− | −/− |
| WATR50 | 56 | 68/95 | 0.74 (0.71, 0.75)/19.3 (1.5) | 133/98 | 0.44 (0.40, 0.48)/24.2 (2.7) | 157/69 | 0.33 (0.26, 0.40)/27.5 (−0.11) | 180/11 | 0.39 (0.20, 0.54))/33.6 (0.22) |
| WATR10 | 43 | 40/92 | 0.57 (0.53, 0.61)/17.8 (−5.2) | 141/96 | 0.48 (0.43, 0.51)/12.2 (5.2) | 170/51 | 0.1 (−0.01, 0.20)/26.2 (0.03) | 187/2 | 0.38 (−0.24, 0.78)/37.2 (0.2) |
| WACA20 | 32 | 96/92 | 0.25 (0.20, 0.29)/14.2 (−3.5) | 161/99 | 0.61 (0.58, 0.63)/20.5 (4.1) | 175/53 | 0.29 (0.21, 0.36)/34.8 (0.09) | −/− | −/− |
| Mooring | Distance from Surface (m) | FRE Max Angle/% Data | FRE R (95% CL)/RMSD (bias) | GUI max Angle/% Data | GUI R (95% CL)/RMSD (bias) | LANC Max Angle/% Data | LANC R (95% CL)/RMSD (bias) | GHED Max Angle/% Data | GHED R (95% CL)/RMSD (bias) |
|---|---|---|---|---|---|---|---|---|---|
| NRSROT | 15 | 89/96 | 0.14 (0.09, 0.18)/10.3 (1.3) | 170/98 | 0.42 (0.38, 0.45)/25.8 (3.3) | 193/18 | 0.52 (0.40, 0.61)/29.8 (−0.05) | 195/0.2 | 1 (1, 1)/10.9 (0) |
| NRSROT | 15 | 44/55 | 0.07 (−0.016, 0.15)/ 9.6 (0.2) | 167/72 | 0.31 (0.23, 0.37)/29.6 (−2.8) | −/− | −/− | −/− | −/− |
| WATR50 | 56 | 73/95 | 0.78 (0.76, 0.79)/ 18.2 (−3.5) | 130/98 | 0.56 (0.53, 0.59)/21.4 (5.9) | 165/65 | 0.53 (0.47, 0.59)/21.4 (−0.07) | 193/1.8 | 0.68 (0.28, 0.87)/41.6 (0.36) |
| WATR10 | 43 | 43/92 | 0.58 (0.54, 0.32)/ 20.3 (0.1) | 145/96 | 0.48 (0.43, 0.51)/12.2 (5.2) | 191/14 | 0.72 (0.59, 0.80)/17.5 (−0.06) | 195/9.5 | 0.42 (0.17, 0.61)/26.7 (0.1) |
| WACA20 | 32 | 87/92 | 0.31 (0.27, 0.34)/ 14.3 (−2.5) | 161/99 | 0.61 (0.58, 0.63)/20.6 (4.1) | 177/45 | 0.38 (0.31, 0.45)/33.1 (0.07) | 169/0.2% | 0.91 (1, 1)/ 19.4 (0.2) |
| Mooring | Distance from Surface (m) | N | RU (95% CL)/RMSDU (biasU) | RV (95% CL)/RMSDV (biasV) | ρ (95% CL)/φ |
|---|---|---|---|---|---|
| NRSROT | 15 | 663 | −0.12 (−0.19, −0.04)/13.5 (−0.5) | 0.61 (0.56, 0.65)/20.7 (3.3) | 0.58 (0.05, 0.64/ −28° |
| NRSROT | 15 | 250 | 0.31 (0.19, 0.42)/12.3 (−4.9) | 0.69 (0.62, 0.75)/21.1 (−0.5) | 0.66 (0.05, 0.70)/−10° |
| WATR50 | 56 | 761 | 0.83 (0.82, 0.86)/13.2 (−2.3) | 0.86 (0.85, 0.88)/15.4 (6.5) | 0.86 (0.06, 0.92)/−6° |
| WATR10 | 43 | 411 | 0.34 (0.26,0.43)/15.7 (−1.9) | 0.70 (0.65, 0.75)/15.9 (8.3) | 0.65 (0.05, 0.68)/ 28° |
| WACA20 | 32 | 1450 | 0.34 (0.29, 0.38)/14.5 (−5.1) | 0.78 (0.77, 0.81)/17.3 (9.6) | 0.68 (0.06, 0.73)/−9° |
| Mooring | Distance from Surface (m) | N | RU (95% CL)/RMSDU (biasU) | RV (95% CL)/RMSDV (biasV) | ρ (95% CL)/φ |
|---|---|---|---|---|---|
| NRSROT | 15 | 499 | 0.89 (0.87 0.90)/3.5 (−0.9) | 0.40 (0.33, 0.47)/24.1 (−6.4) | 0.45 (0.05, 0.62)/−5° |
| NRSROT | 15 | − | − /− | − /− | − /− |
| WATR50 | 56 | 988 | 0.93 (0.92, 0.94)/9.1 (4.4) | 0.65 (0.62, 0.65)/23.0 (11.1) | 0.78 (0.10, 0.82)/ 8° |
| WATR10 | 43 | 1057 | 0.81 (0.79, 0.83)/13.9 (−8.3) | 0.78 (0.76, 0.80)/16.4 (−9.8) | 0.79 (0.26, 0.89)/22° |
| WACA20 | 32 | 800 | 0.98 (0.98, 0.99)/2.9 (−1.6) | 0.54 (0.49, 0.59)/29.7 (−16.5) | 0.63/1.5° |
| Mooring | Distance from Surface (m) | N | RU (95% CL)/RMSDU (biasU) | RV (95% CL)/RMSDV (biasV) | ρ (95% CL)/φ |
|---|---|---|---|---|---|
| NRSROT | 15 | 732 | −0.20 (−0.27, −0.13)/14.6 (1.6) | 0.51 (0.45, 0.56)/26.2 (−1.3) | 0.47 (0.04, 0.64)/25° |
| NRSROT | 15 | − | −/− | −/− | −/− |
| WATR50 | 56 | 634 | 0.83 (0.81, 0.85)/14.3 (1.1) | 0.63 (0.58, 0.63)/22.5 (12.8) | 0.72 (0.15, 0.73)/ 7° |
| WATR10 | 43 | 368 | 0.23 (0.14, 0.33)/24.2 (−9.5) | 0.39 (0.31, 0.48)/19.9 (−0.4) | 0.50 (0.07, 0.61)/51° |
| WACA20 | 32 | 1450 | 0.34 (0.29, 0.38)/ 14.6 (−5.1) | 0.79 (0.77, 0.81)/17.3 (9.6) | 0.68 (0.06, 0.73)/3° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cosoli, S.; de Vos, S. Interoperability of Direction-Finding and Beam-Forming High-Frequency Radar Systems: An Example from the Australian High-Frequency Ocean Radar Network. Remote Sens. 2019, 11, 291. https://doi.org/10.3390/rs11030291
Cosoli S, de Vos S. Interoperability of Direction-Finding and Beam-Forming High-Frequency Radar Systems: An Example from the Australian High-Frequency Ocean Radar Network. Remote Sensing. 2019; 11(3):291. https://doi.org/10.3390/rs11030291
Chicago/Turabian StyleCosoli, Simone, and Stuart de Vos. 2019. "Interoperability of Direction-Finding and Beam-Forming High-Frequency Radar Systems: An Example from the Australian High-Frequency Ocean Radar Network" Remote Sensing 11, no. 3: 291. https://doi.org/10.3390/rs11030291
APA StyleCosoli, S., & de Vos, S. (2019). Interoperability of Direction-Finding and Beam-Forming High-Frequency Radar Systems: An Example from the Australian High-Frequency Ocean Radar Network. Remote Sensing, 11(3), 291. https://doi.org/10.3390/rs11030291






