On the Optimal Design of Doppler Scatterometers
Abstract
1. Introduction
2. Optimizing Doppler Scatterometer Parameters Given SNR
2.1. Error Models
2.1.1. Measurement Noise and Wind Speed Error
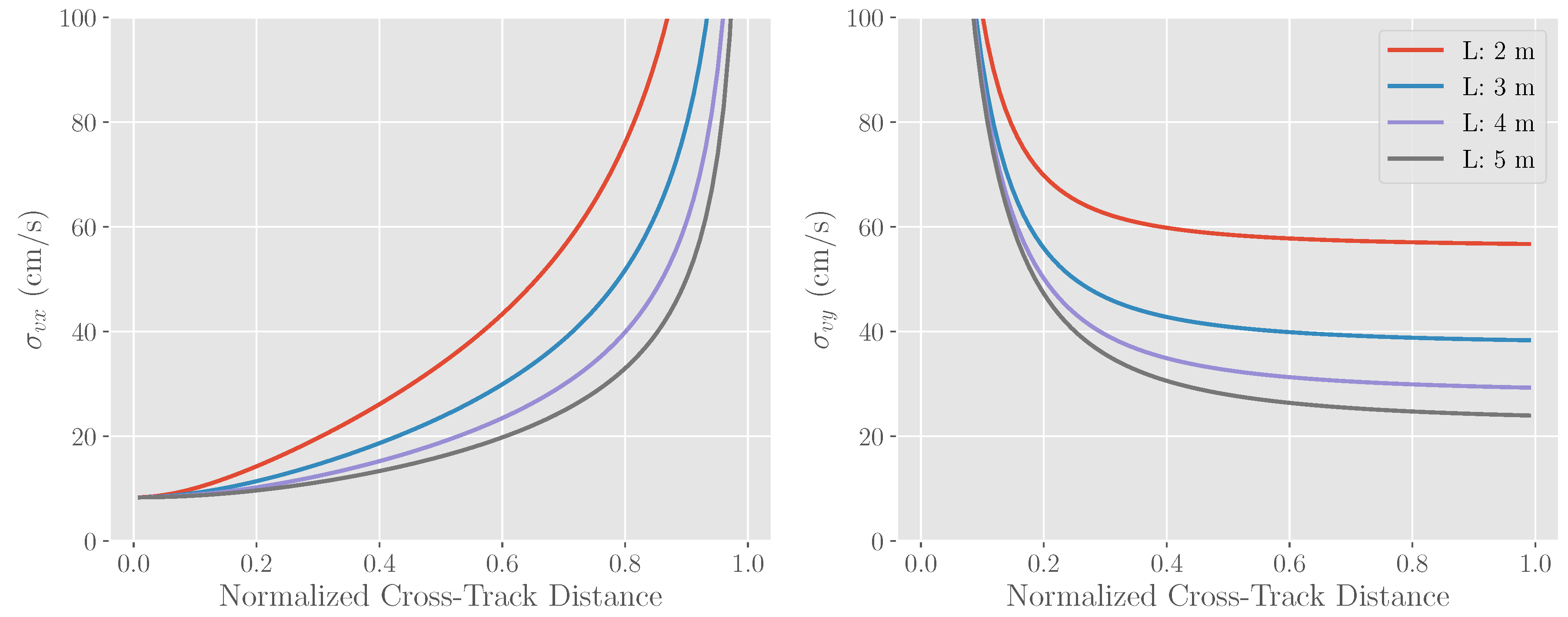
2.1.2. Radial Velocity Errors
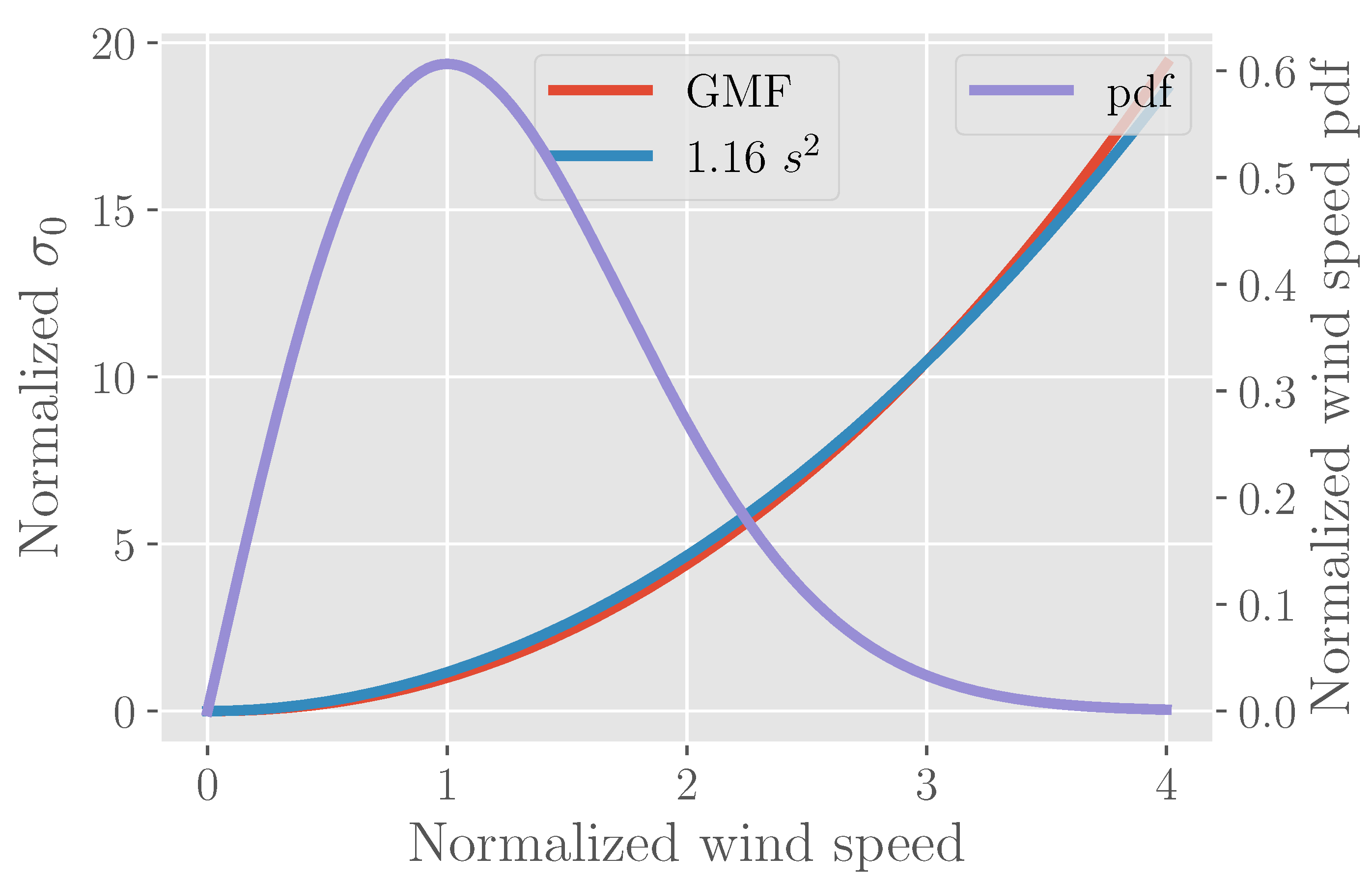
2.2. Optimizing
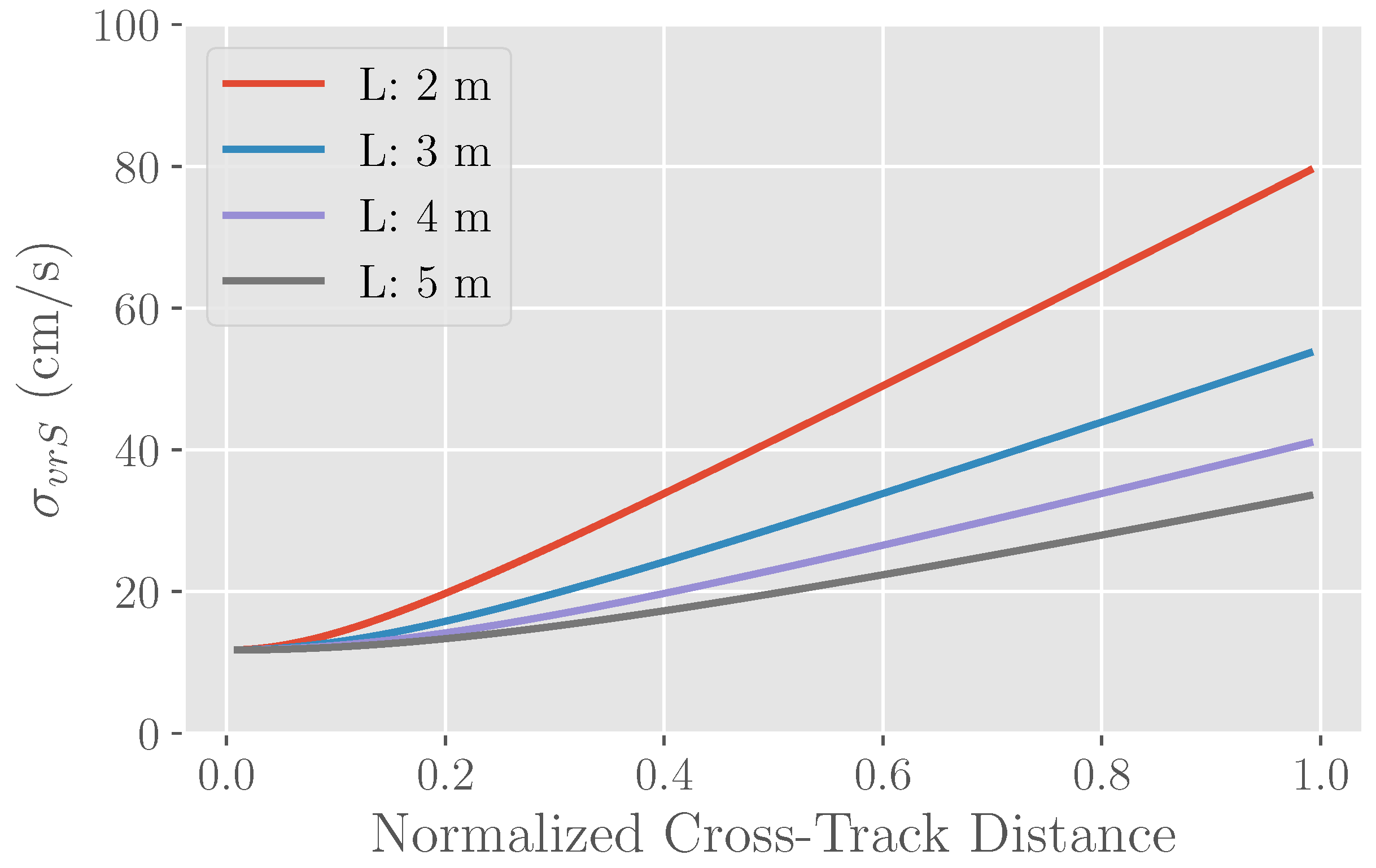
2.3. Optimizing Radial Velocity Variance
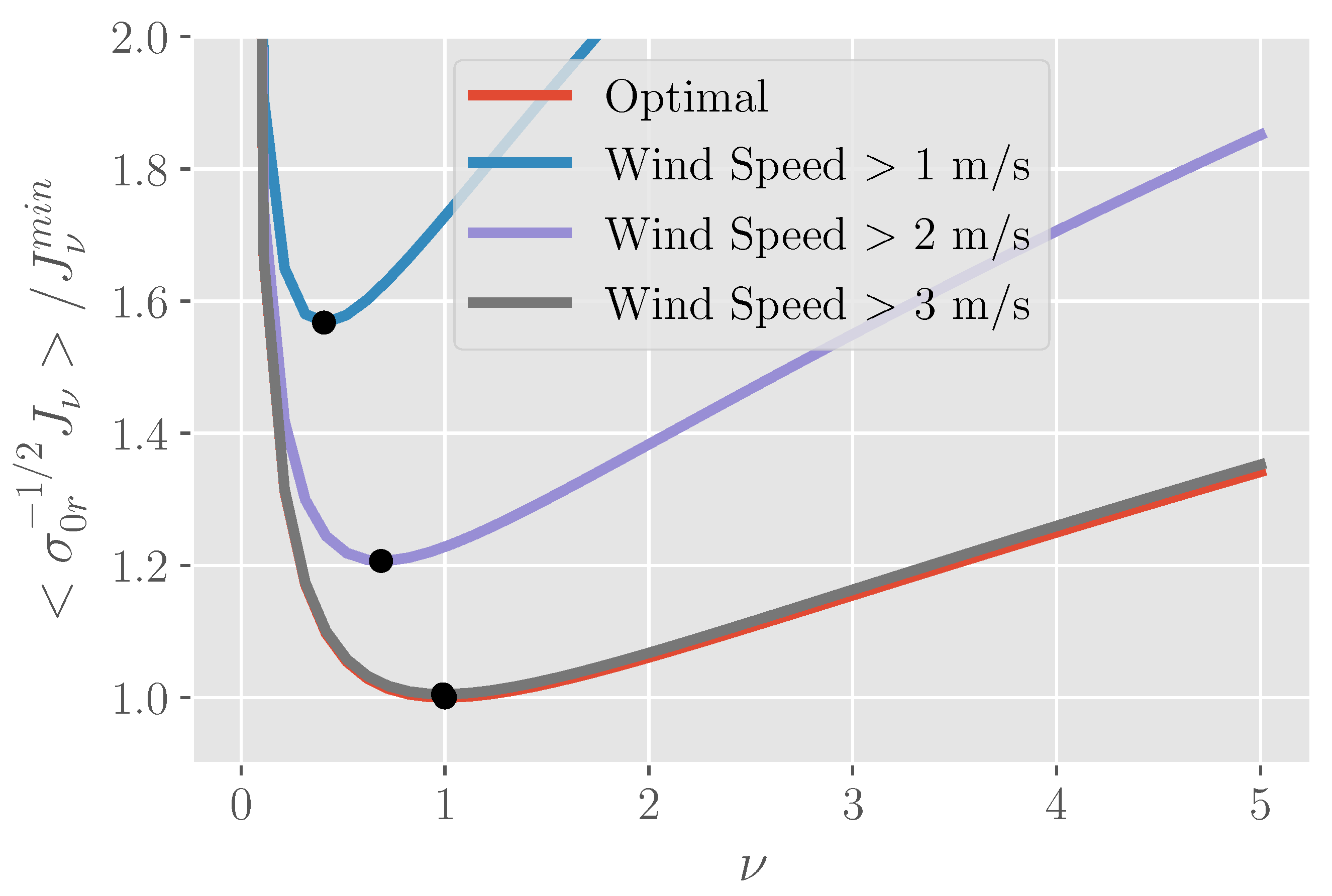
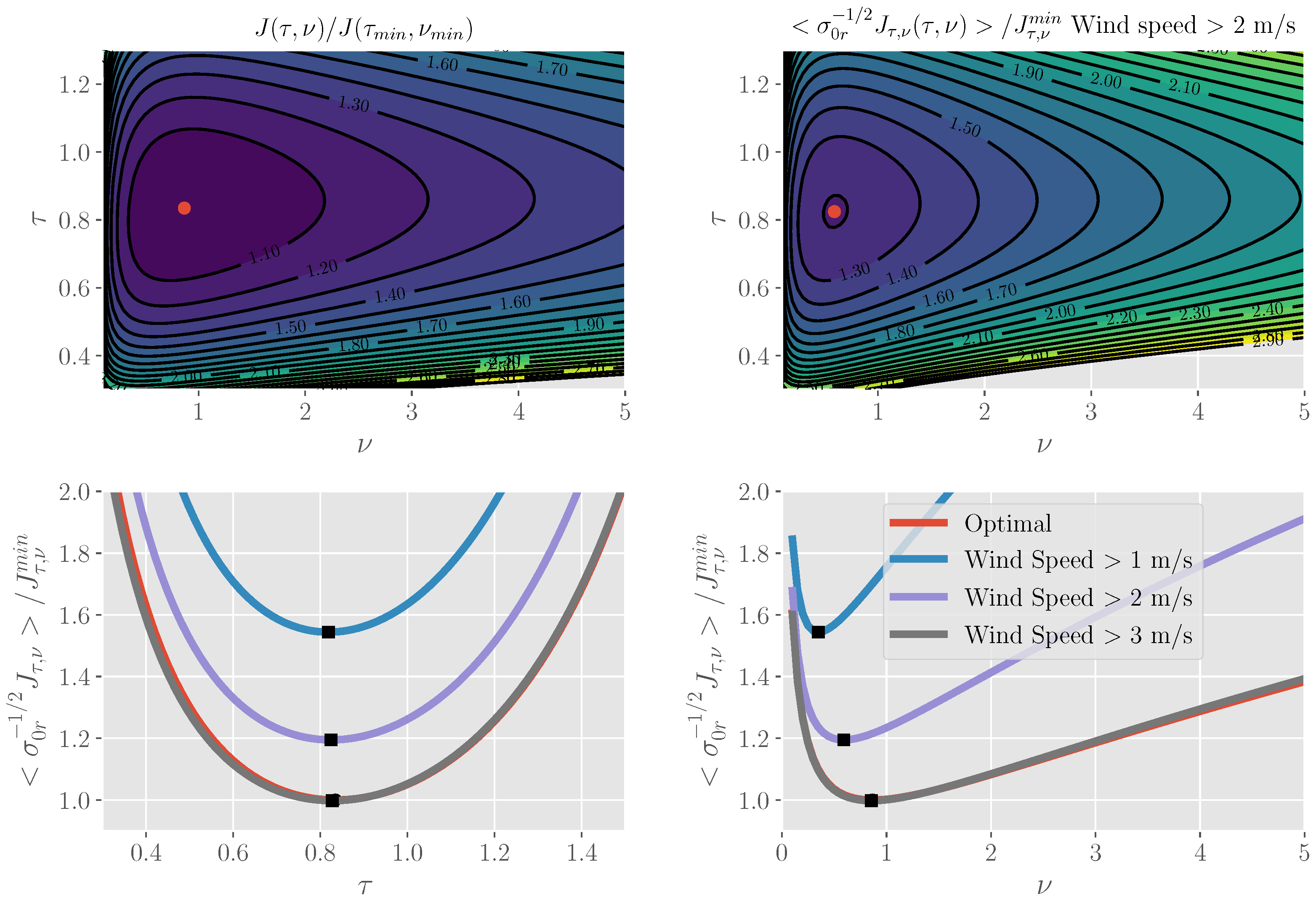
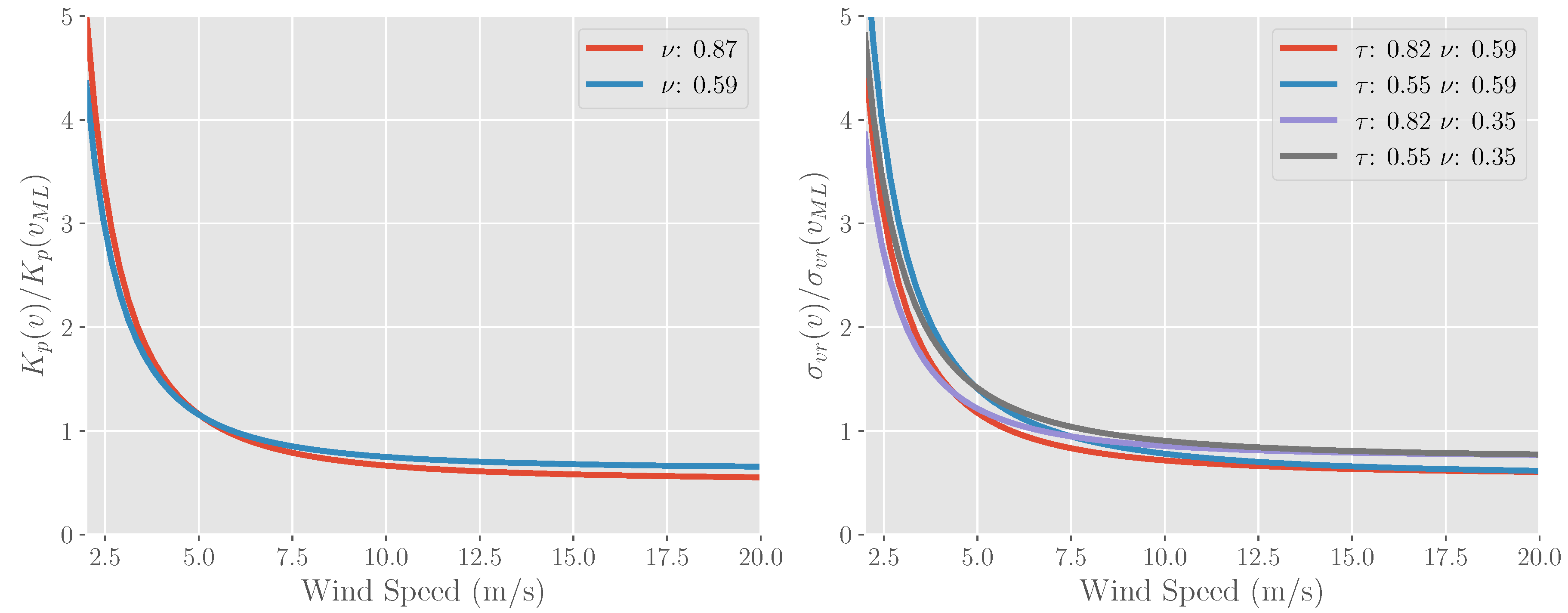
3. Optimizing Doppler Scatterometer Parameters over Winds
Optimizing Wind Estimates
4. Other Design Considerations
4.1. Frequency and Polarization
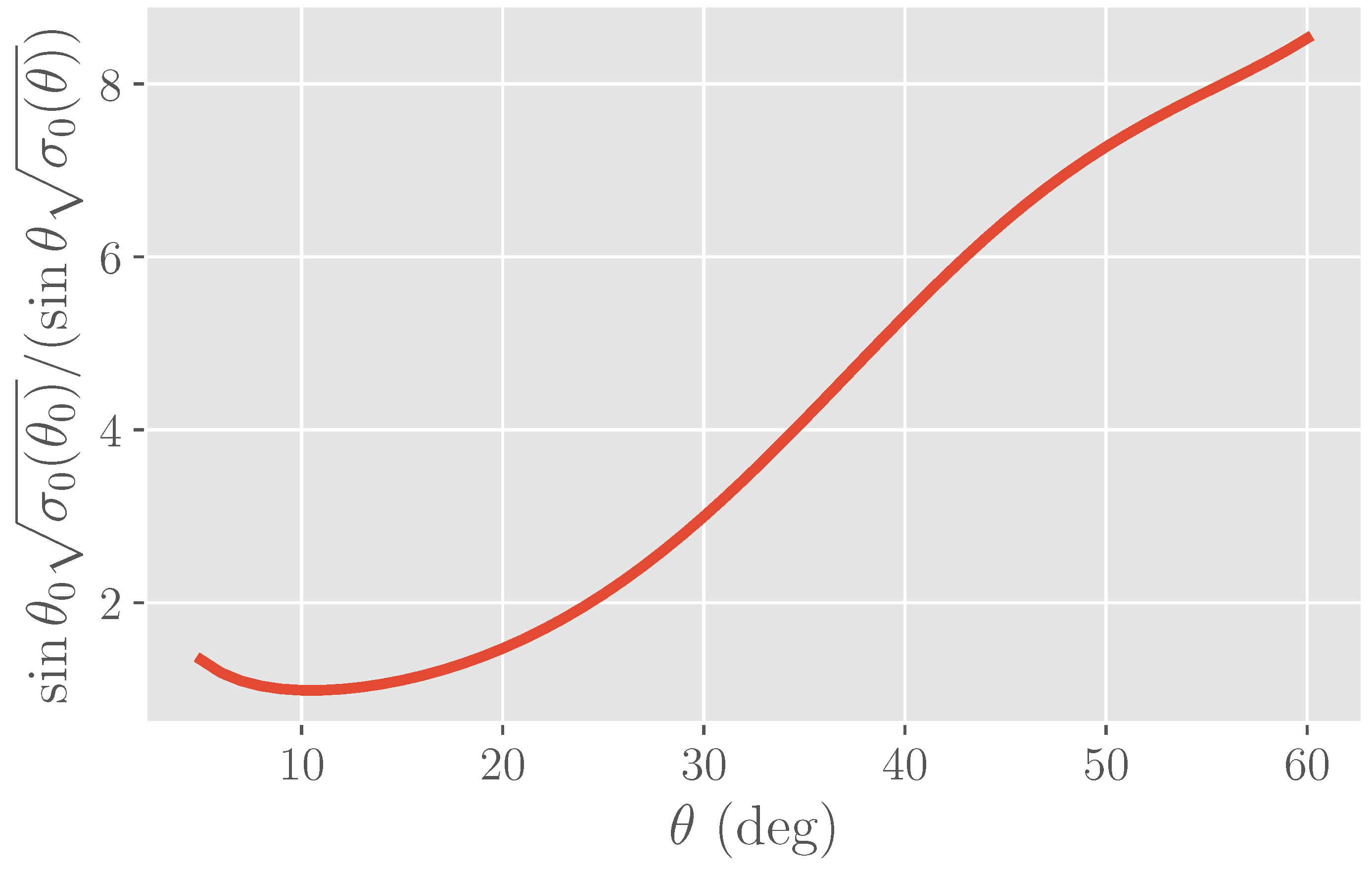
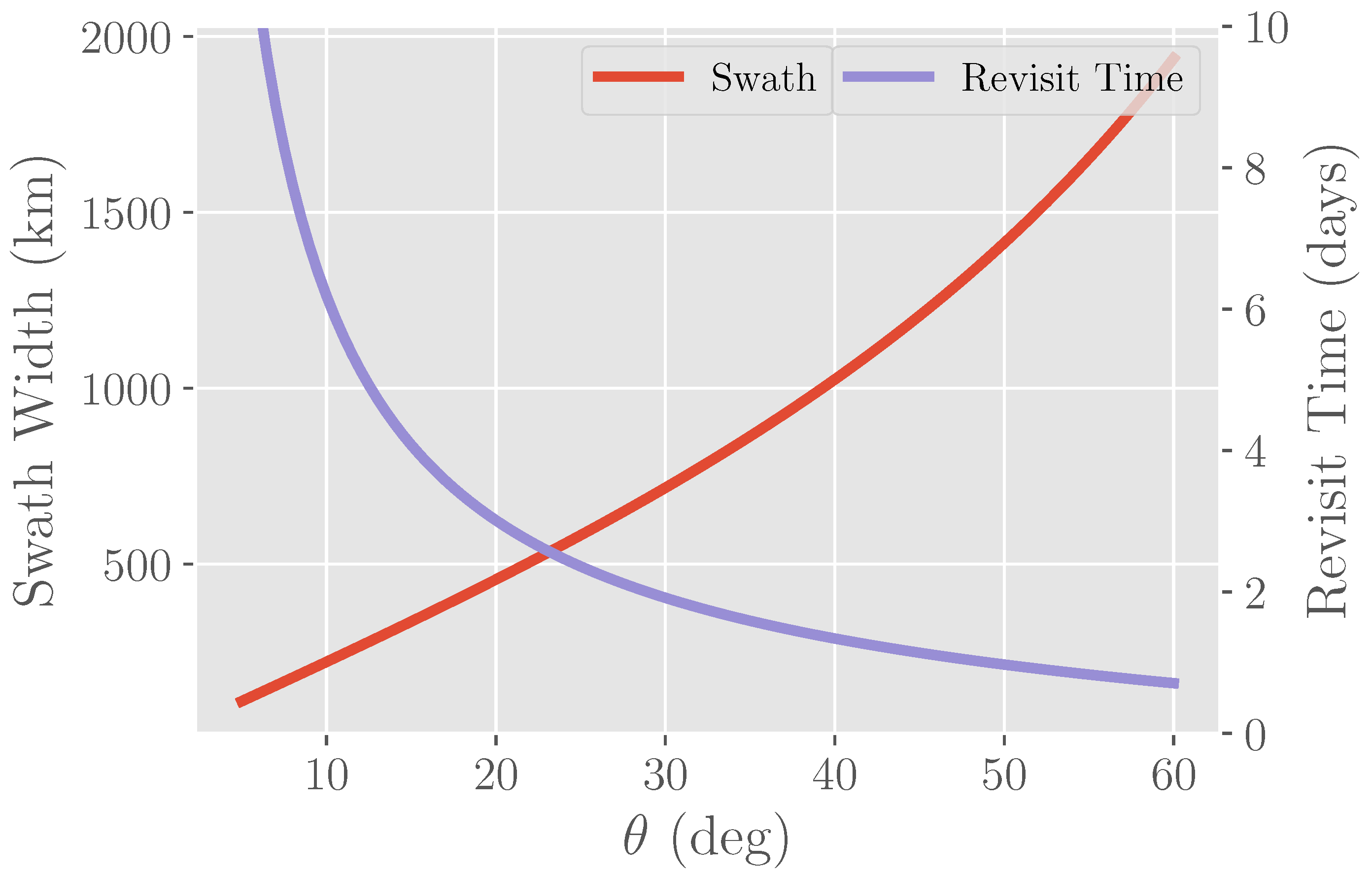
4.2. Incidence Angle
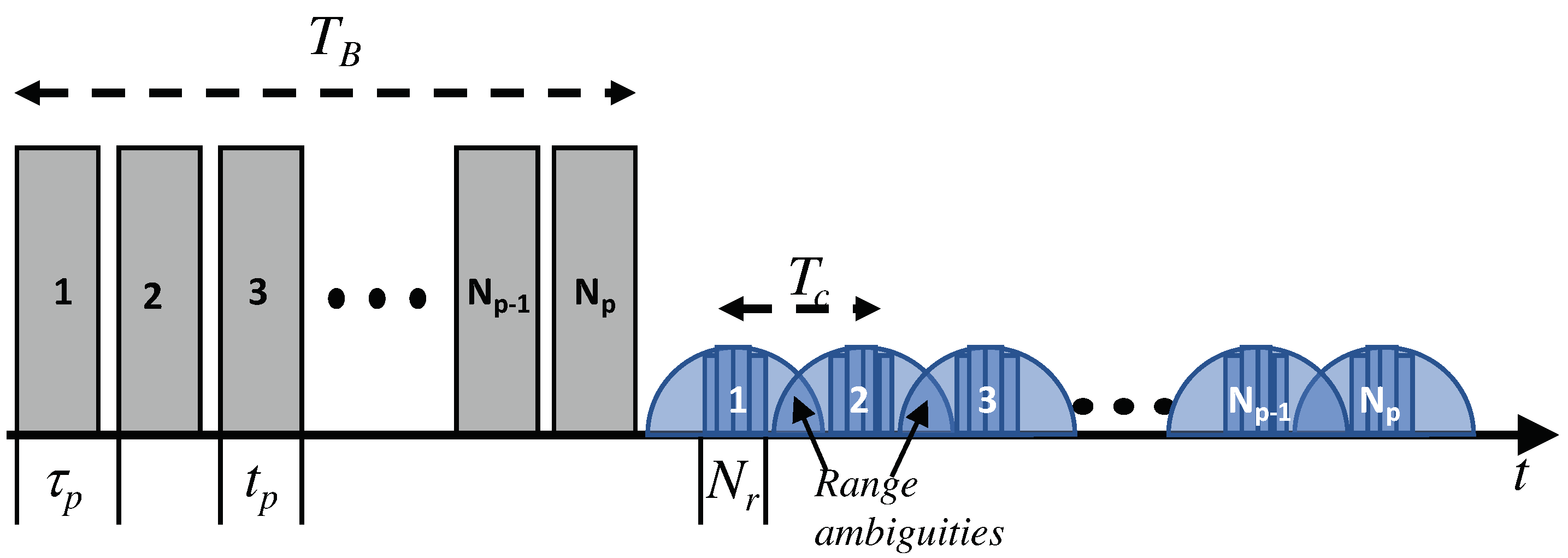
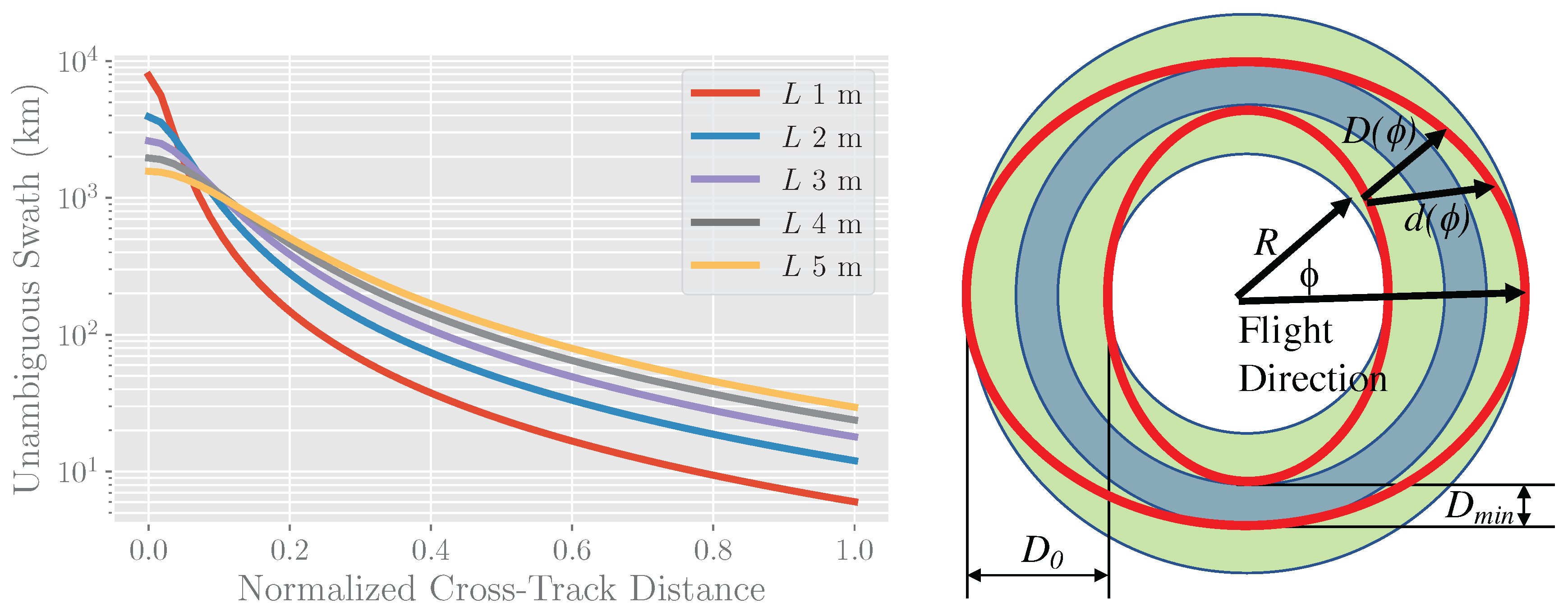
4.3. Range Ambiguities and Contiguous Scans
4.4. System Spatial Resolution
5. Design Examples
6. Conclusions
- The system bandwidth should be chosen so that the signal-to-noise ratio is approximately 1. This somewhat counterintuitive result can be understood as balancing the number of looks and the SNR in the equation, and will typically lead to higher bandwidths than in historical designs (e.g., QuikSCAT).
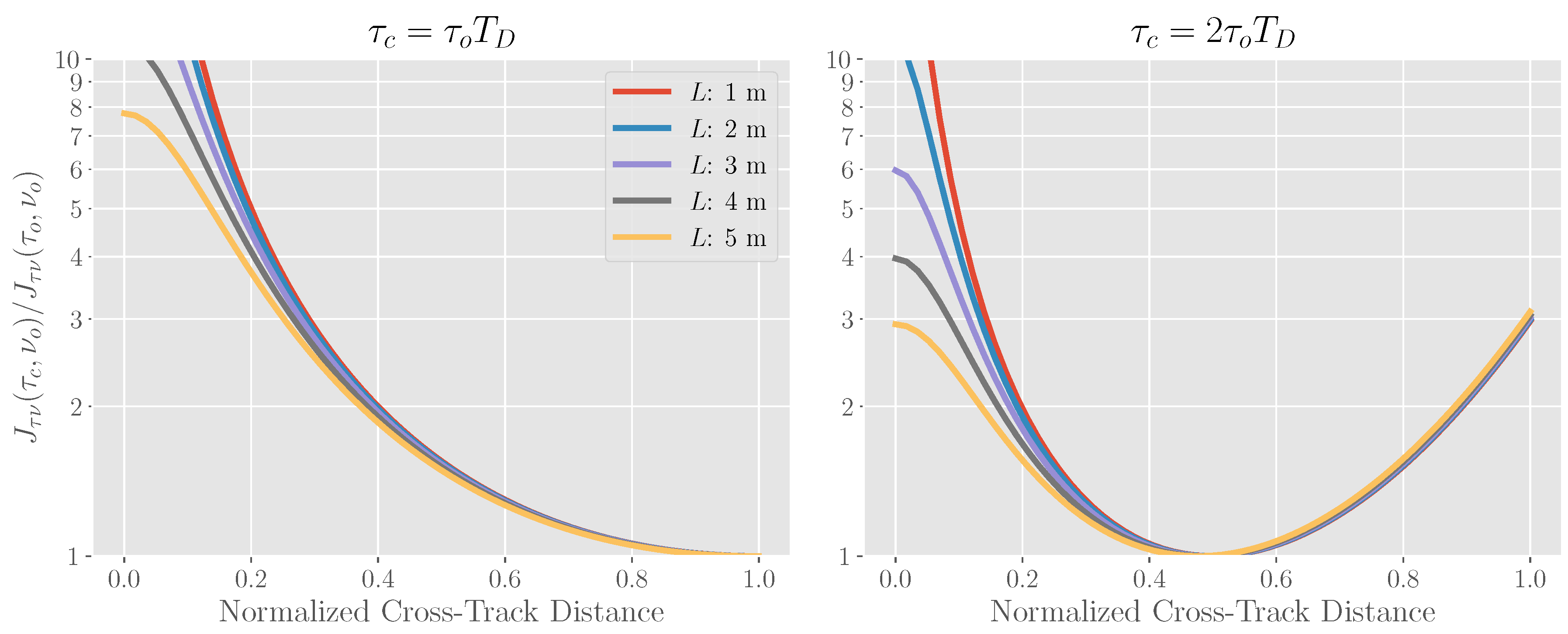
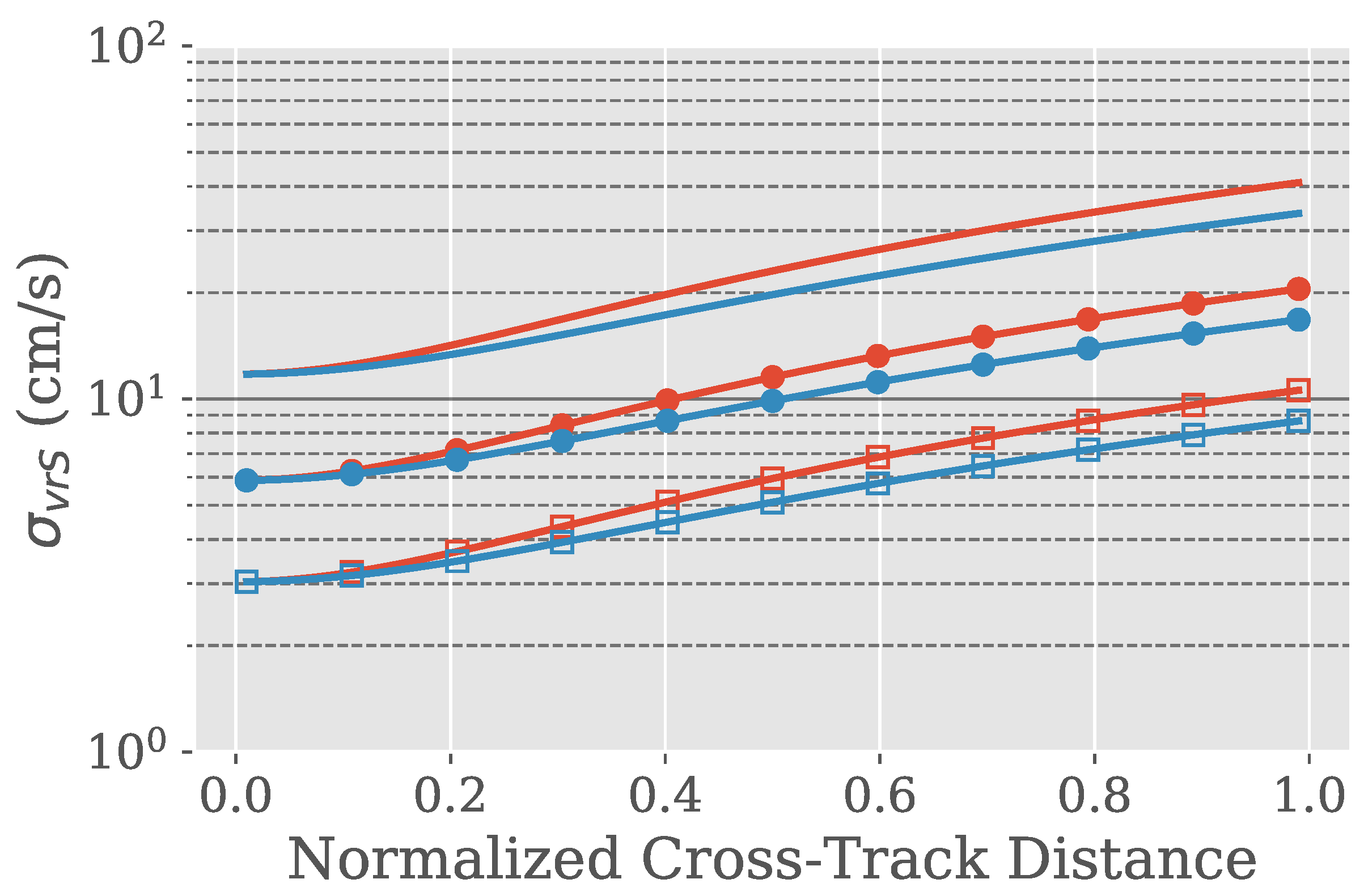
- Varying the inter-pulse period as a function of scan angle so that the Doppler bandwidth is appropriately sampled (but not over-sampled) can have significant benefits in the radial velocity performance. One should use the opportunity presented by longer pulse correlation times to separate the pulses as much as possible, while lengthening them to improve the SNR per pulse.
- As high a frequency should be chosen as possible, all other things being equal.
- The fast change in brightness with incidence angle strongly suggests that near-nadir incidence angles be used, as in SKIM. However, increasing the antenna length can mitigate this significantly. Near-nadir incidence angles have additional disadvantages in terms of temporal revisit and mapping errors, due to the reduced swath. The incidence angle is probably the parameter that needs most optimization to balance random measurement errors and interpolation mapping errors.
- Varying the PRF has significant advantages for the continuity of the along-track coverage and minimizing range ambiguities.
- It is possible, with systems that are at the present state of the art, to achieve the performance goals outlined by Chelton et al. [2]. A high-power system will exceed these requirements, but may have greater engineering challenges.
- By varying the spacing between the pulses while keeping the total burst energy constant, one can expect significant improvements (up to an order of magnitude in the along-track direction) for the radial velocity error, as shown in Figure 5.
- By varying the PRF, one can increase substantially (up to two orders of magnitude in the along-track direction) the unambiguous footprint, as shown in Figure 9. This allows ground coverage without gaps with a moderate-sized antenna at antenna realizable spin-rates. This is beneficial in the mission mechanical design.
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Symbol | Description |
|---|---|
| Normalized radar cross section. | |
| Error in parameter x | |
| Coefficient of variation | |
| v | Speed |
| Azimuth angle. | |
| Radial velocity. | |
| Pulse-pair phase. | |
| Radial velocity | |
| EM wavelength | |
| k | EM wavenumber |
| Inter-pulse period. | |
| Standard deviation of parameter x. | |
| Number of range samples. | |
| Number of independent pulse pair samples | |
| Total correlation coefficient. | |
| Thermal noise correlation. | |
| Temporal correlation. | |
| Doppler correlation. | |
| Burst time. | |
| Pulse-pair correlation time. | |
| Water correlation time. | |
| Platform speed | |
| SNR | Signal-to-noise ratio. |
| Noise-to-signal ratio | |
| Gaussian azimuth antenna pattern standard deviation. | |
| L | Antenna length |
| Azimuth beamwidth factor. | |
| B | System bandwidth |
| X | Desired range resolution. |
| Incidence angle | |
| c | Speed of light. |
| Minimum bandwidth | |
| Noise-only minimization function (Equation (20)) | |
| Optimal number of range looks | |
| Optimum | |
| Temporal and noise minimization function (Equation (25)) | |
| Optimal | |
| Optimal | |
| Optimal radial velocity | |
| Most likely wind speed. | |
| s | Wind speed normalized by most likely wind speed. |
| Wind speed probability density function. | |
| for most likely wind speed | |
| Noise-equivalent | |
| for most likely wind speed | |
| relative to most likely wind | |
| Average over wind speeds | |
| Antenna azimuth resolution | |
| Final azimuth resolution after averaging | |
| Number of contiguous range-direction footprints | |
| D | Size of range footprint |
| Rotation period | |
| R | Inner radius of the scanned annulus |
| Width of the annulus (i.e., the along-track swath) | |
| Along-track direction in order to ensure along-track continuity |
References
- The National Academy of Sciences, Engineering, and Medicine. Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; The National Academy Press: Washington, DC, USA, 2018. [Google Scholar]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; Farrar, J.T.; Molemaker, M.J.; McWilliams, J.C.; Gula, J. Prospects for Future Satellite Estimation of Small-Scale Variability of Ocean Surface Velocity and Vorticity. Prog. Oceanogr. 2018, in press. [Google Scholar] [CrossRef]
- Spencer, M.; Tsai, W.; Long, D. High-Resolution Measurements with a Spaceborne Pencil-Beam Scatterometer Using Combined Range/Doppler Discrimination Techniques. IEEE Trans. Geosci. Remote Rens. 2003, 41, 567–581. [Google Scholar] [CrossRef]
- Bao, Q.; Dong, X.; Zhu, D.; Lang, S.; Xu, X. The Feasibility of Ocean Surface Current Measurement Using Pencil-Beam Rotating Scatterometer. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 3441–3451. [Google Scholar] [CrossRef]
- Miao, Y.; Dong, X.; Bao, Q.; Zhu, D. Perspective of a Ku-Ka Dual-Frequency Scatterometer for Simultaneous Wide-Swath Ocean Surface Wind and Current Measurement. Remote Sens. 2018, 10, 1042. [Google Scholar] [CrossRef]
- Bourassa, M.; Rodriguez, E.; Chelton, D. Winds and currents mission: Ability to observe mesoscale AIR/SEA coupling. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016. [Google Scholar]
- Ardhuin, F.; Aksenov, Y.; Benetazzo, A.; Bertino, L.; Brandt, P.; Caubet, E.; Chapron, B.; Collard, F.; Cravatte, S.; Dias, F.; et al. Measuring currents, ice drift, and waves from space: The Sea Surface KInematics Multiscale monitoring (SKIM) concept. Ocean Sci. 2018, 14, 337–354. [Google Scholar] [CrossRef]
- Jackson, F.C.; Walton, T.W.; Baker, P.L. Aircraft and satellite measurement of ocean wave directional spectra using scanning-beam microwave radars. J. Geophys. Res. 1985, 90, 987–1004. [Google Scholar] [CrossRef]
- Gommenginger, C.; Chapron, B.; Martin, A.; Marquez, J.; Brownsword, C.; Buck, C. SEASTAR: A new mission for high-resolution imaging of ocean surface current and wind vectors from space. In Proceedings of the 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 4–7 June 2018. [Google Scholar]
- Fois, F.; Hoogeboom, P.; Chevalier, F.; Stoffelen, A.; Mouche, A. DopSCAT: A mission concept for simultaneous measurements of marine winds and surface currents. J. Geophys. Res. Oceans 2015, 120, 7857–7879. [Google Scholar] [CrossRef]
- Stoffelen, A.; Aaboe, S.; Calvet, J.C.; Cotton, J.; Chiara, G.; Saldaa, J.; Mouche, A.; Portabella, M.; Scipal, K.; Wagner, W. Scientific Developments and the EPS-SG Scatterometer. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 2086–2097. [Google Scholar] [CrossRef]
- Hoogeboom, P.; Stoffelen, A.; Lopez Dekker, P. Ocean Current with DopSCA. In Proceedings of the 2018 Doppler Oceanography from Space Symposium, Brest, France, 10–12 October 2018. [Google Scholar]
- Rodriguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gal, T.; Stiles, B.; Niamsuwan, N.; Monje, R. Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer. Remote Sens. 2018, 10, 576. [Google Scholar] [CrossRef]
- Long, D.G.; Spencer, M.W. Radar backscatter measurement accuracy for a spaceborne pencil-beam wind scatterometer with transmit modulation. IEEE Trans. Geosci. Remote Sens. 1997, 35, 102–114. [Google Scholar] [CrossRef]
- Spencer, M.W.; Wu, C.; Long, D.G. Tradeoffs in the design of a spaceborne scanning pencil beam scatterometer: Application to SeaWinds. IEEE Trans. Geosci. Remote Sens. 1997, 35, 115–126. [Google Scholar] [CrossRef]
- Oliphant, T.E.; Long, D.G. Accuracy of scatterometer-derived winds using the Cramer-Rao bound. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2642–2652. [Google Scholar] [CrossRef]
- Wentz, F.; Smith, D. A model function for the ocean-normalized radar cross section at 14 GHz derived from NSCAT observations. J. Geophys. Res. Oceans 1999, 104, 11499–11514. [Google Scholar] [CrossRef]
- Ricciardulli, L.; Wentz, F. A Scatterometer Geophysical Model Function for Climate-Quality Winds: QuikSCAT Ku-2011. J. Atmos. Ocean. Technol. 2015, 32, 1829–1846. [Google Scholar] [CrossRef]
- Yurovsky, Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Ka-Band Dual Copolarized Empirical Model for the Sea Surface Radar Cross Section. IEEE Geosci. Remote Sens. 2016, 55, 1629–1647. [Google Scholar] [CrossRef]
- Spencer, M.; Wu, C.; Long, D. Improved Resolution Backscatter Measurements with the SeaWinds Pencil-Beam Scatterometer. IEEE Trans. Geosci. Remote Sens. 2000, 38, 89–104. [Google Scholar] [CrossRef]
- Freilich, M.; Challenor, P. A New Approach for Determining Fully Empirical Altimeter Wind Speed Model Functions. J. Geophys. Res. Oceans 1994, 99, 25051–25062. [Google Scholar] [CrossRef]
- Shankaranarayanan, K.; Donelan, M. A probabilistic approach to scatterometer model function verification. J. Geophys. Res. Oceans 2001, 106, 19969–19990. [Google Scholar] [CrossRef]

| L | 2 m | 3 m | 4 m | 5 m |
|---|---|---|---|---|
| Transmit Power | ||||
| Altitude | 700 km | 700 km | 700 km | 700 km |
| Total Swath | 1706 km | 1706 km | 1706 km | 1706 km |
| m | m | m | m | |
| Polarization | VV | VV | VV | VV |
| Antenna Width | 0.88 m | 0.58 m | 0.44 m | 0.35 m |
| 2-way Gain | 104.5 dB | 104.5 dB | 104.5 dB | 104.5 dB |
| Azimuth Beamwidth | ||||
| Azimuth Resolution | 5.5 km | 3.6 km | 2.7 km | km |
| Elevation Beamwidth | ||||
| Range Footprint | 22.3 km | 33.5 km | 44.7 km | 55.9 km |
| 1-look Bandwidth | 36 kHz | 36 kHz | 36 kHz | 36 kHz |
| 1-look Elevation Resolution | 5.0 km | 5.0 km | 5.0 km | 5.0 km |
| Antenna Efficiency | 70% | 70% | 70% | 70% |
| Transmit Loss | –1.4 dB | –1.4 dB | –1.4 dB | –1.4 dB |
| Burst Length | 1.5 ms | 1.5 ms | 1.5 ms | 1.5 m |
| System Temperature | K | K | K | K |
| 1-look Noise Equivalent |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez, E. On the Optimal Design of Doppler Scatterometers. Remote Sens. 2018, 10, 1765. https://doi.org/10.3390/rs10111765
Rodriguez E. On the Optimal Design of Doppler Scatterometers. Remote Sensing. 2018; 10(11):1765. https://doi.org/10.3390/rs10111765
Chicago/Turabian StyleRodriguez, Ernesto. 2018. "On the Optimal Design of Doppler Scatterometers" Remote Sensing 10, no. 11: 1765. https://doi.org/10.3390/rs10111765
APA StyleRodriguez, E. (2018). On the Optimal Design of Doppler Scatterometers. Remote Sensing, 10(11), 1765. https://doi.org/10.3390/rs10111765






