Improved Faraday Rotation Estimation in Spaceborne PolSAR Data Using Total Variation Denoising
Abstract
1. Introduction
2. Materials and Methods
2.1. FR Estimation
2.2. TV Denoising
3. Experimental Results and Discussion
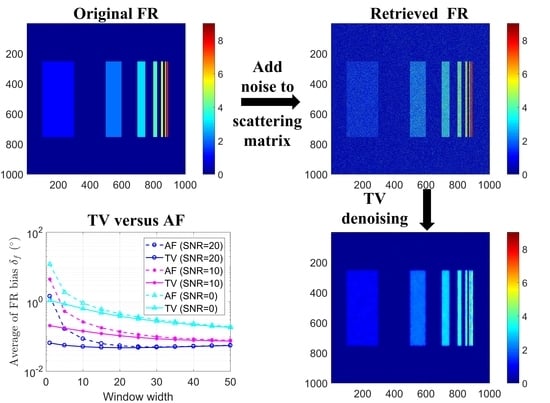
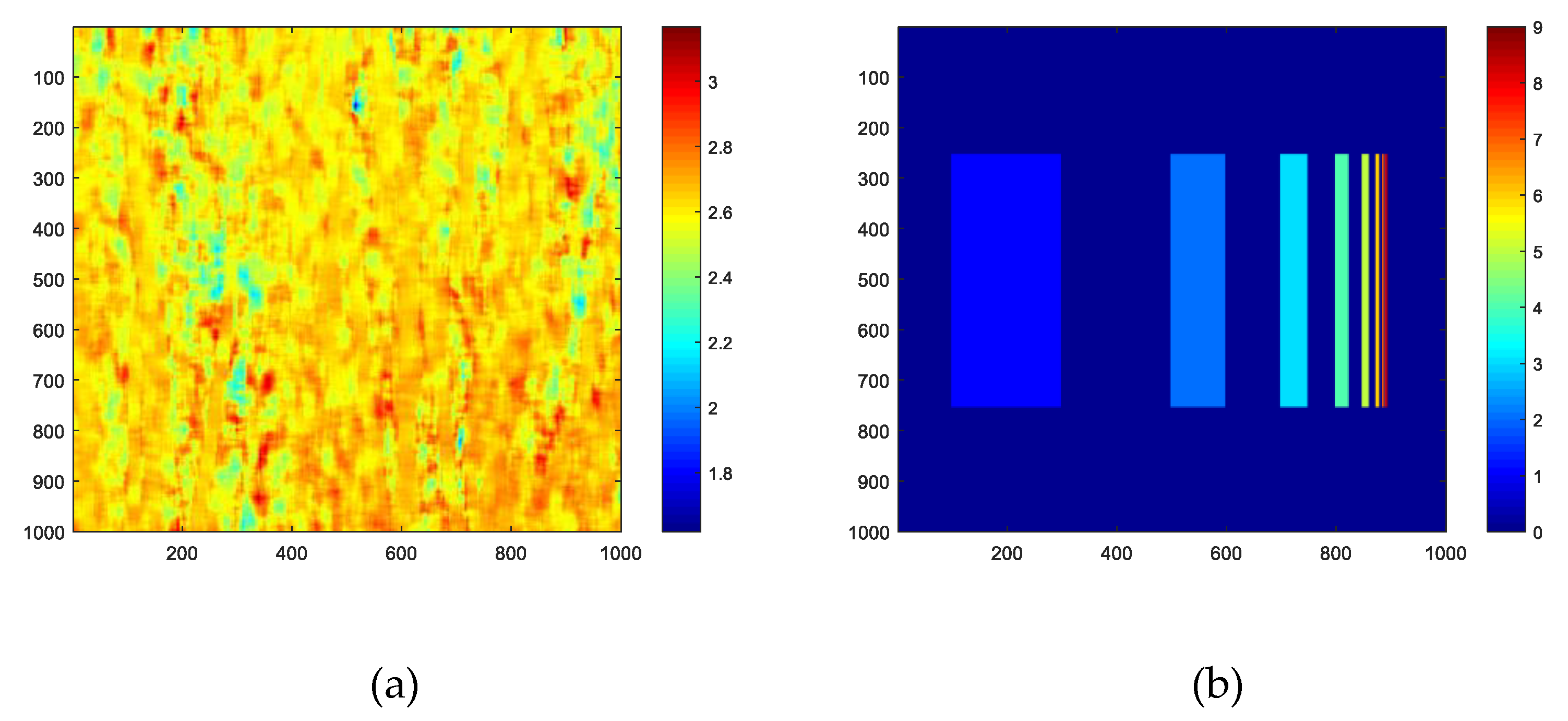
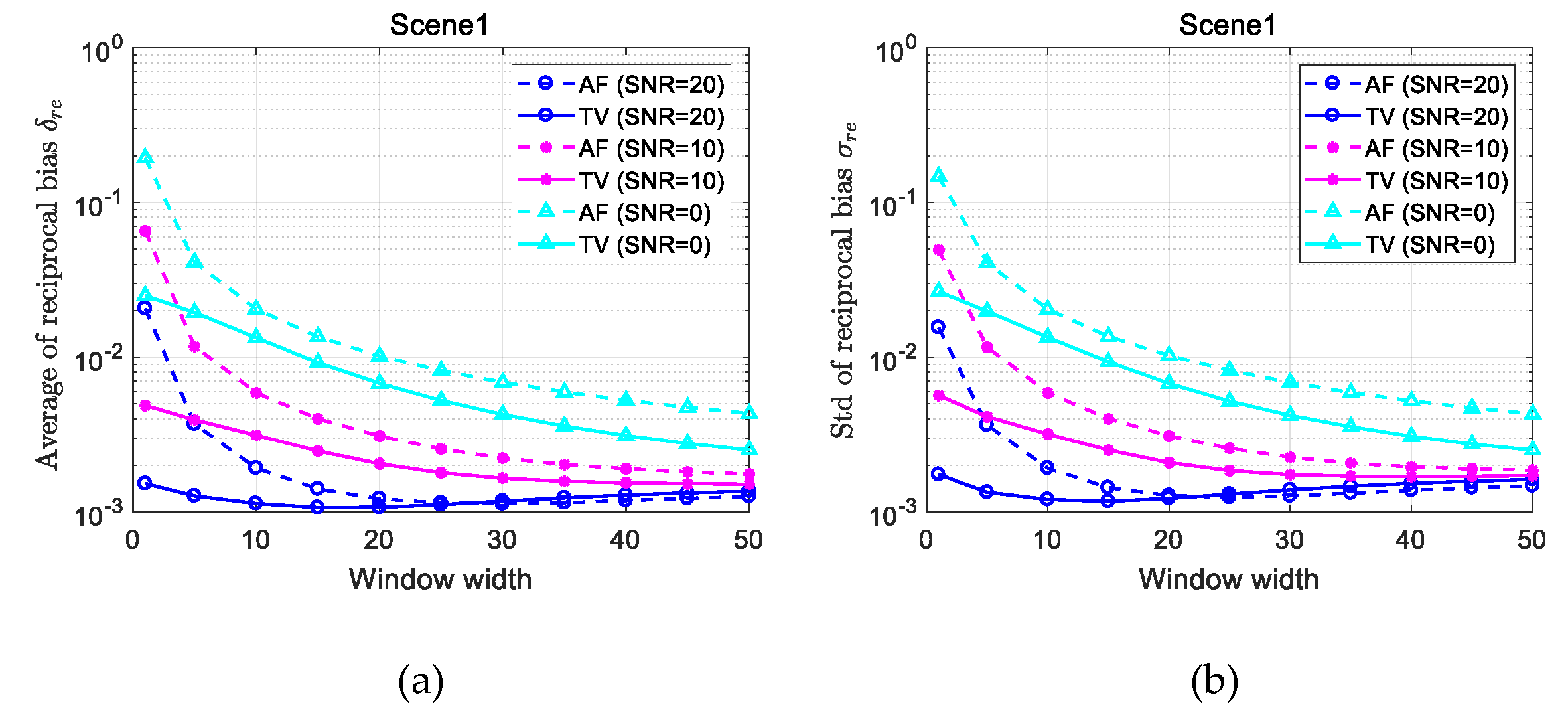
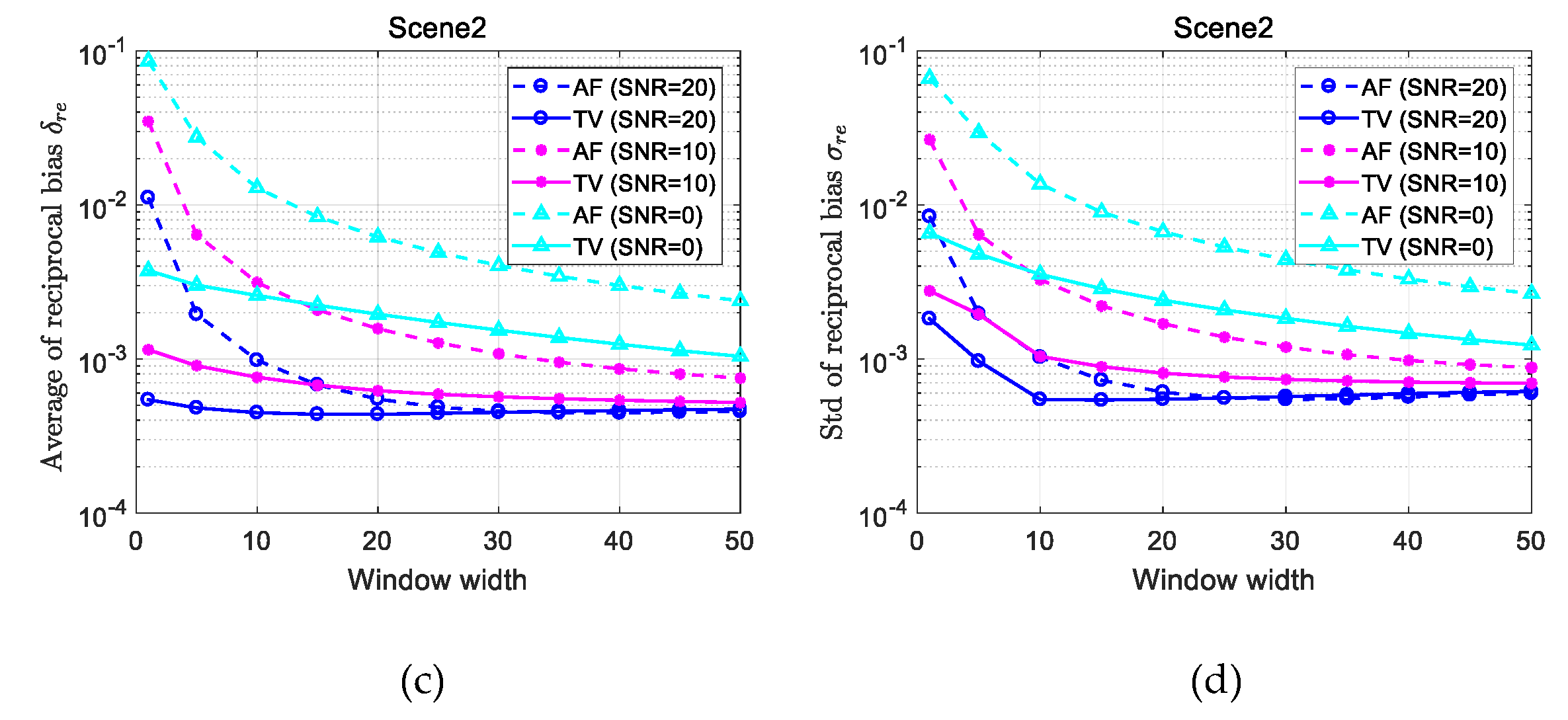
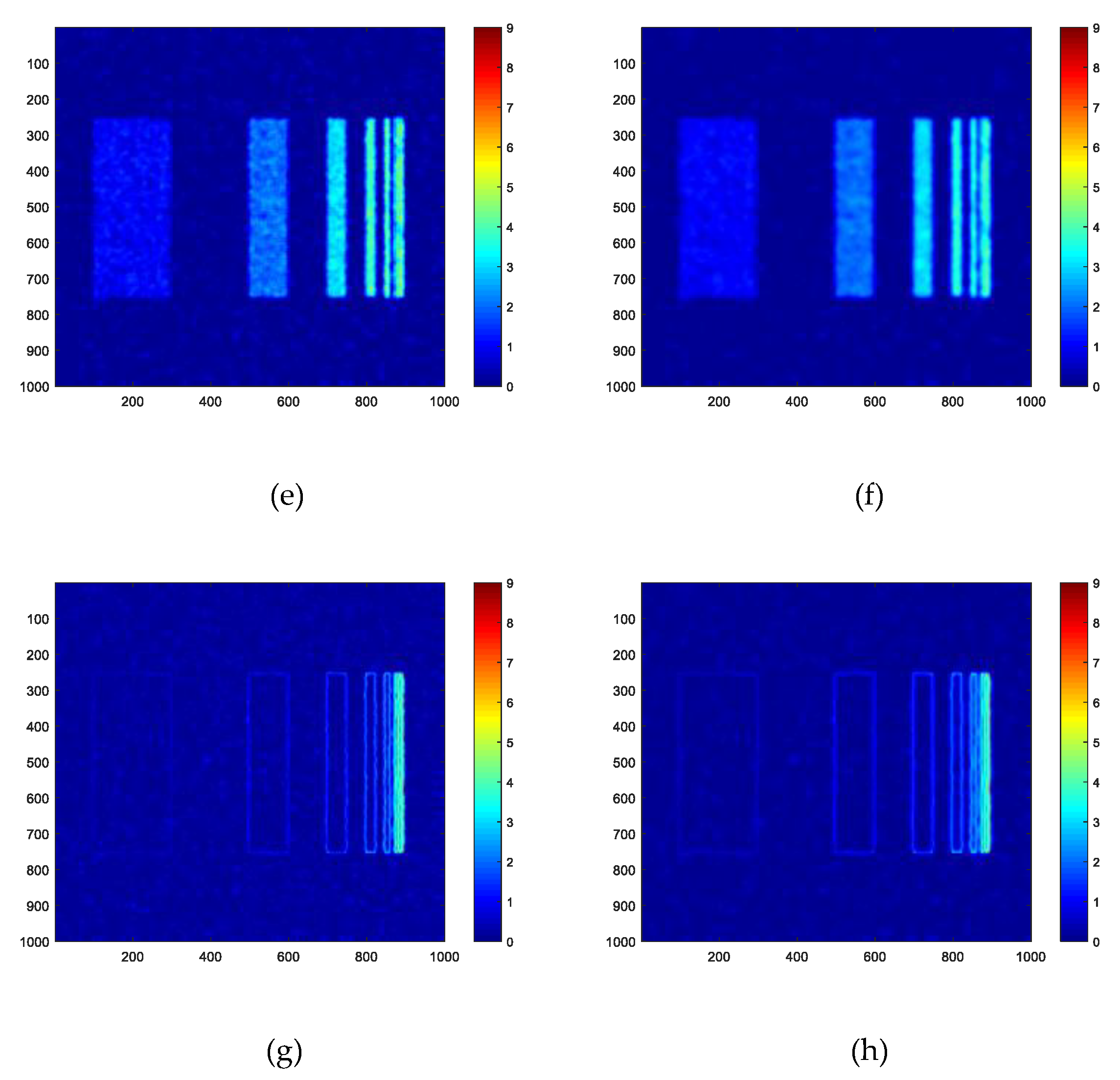
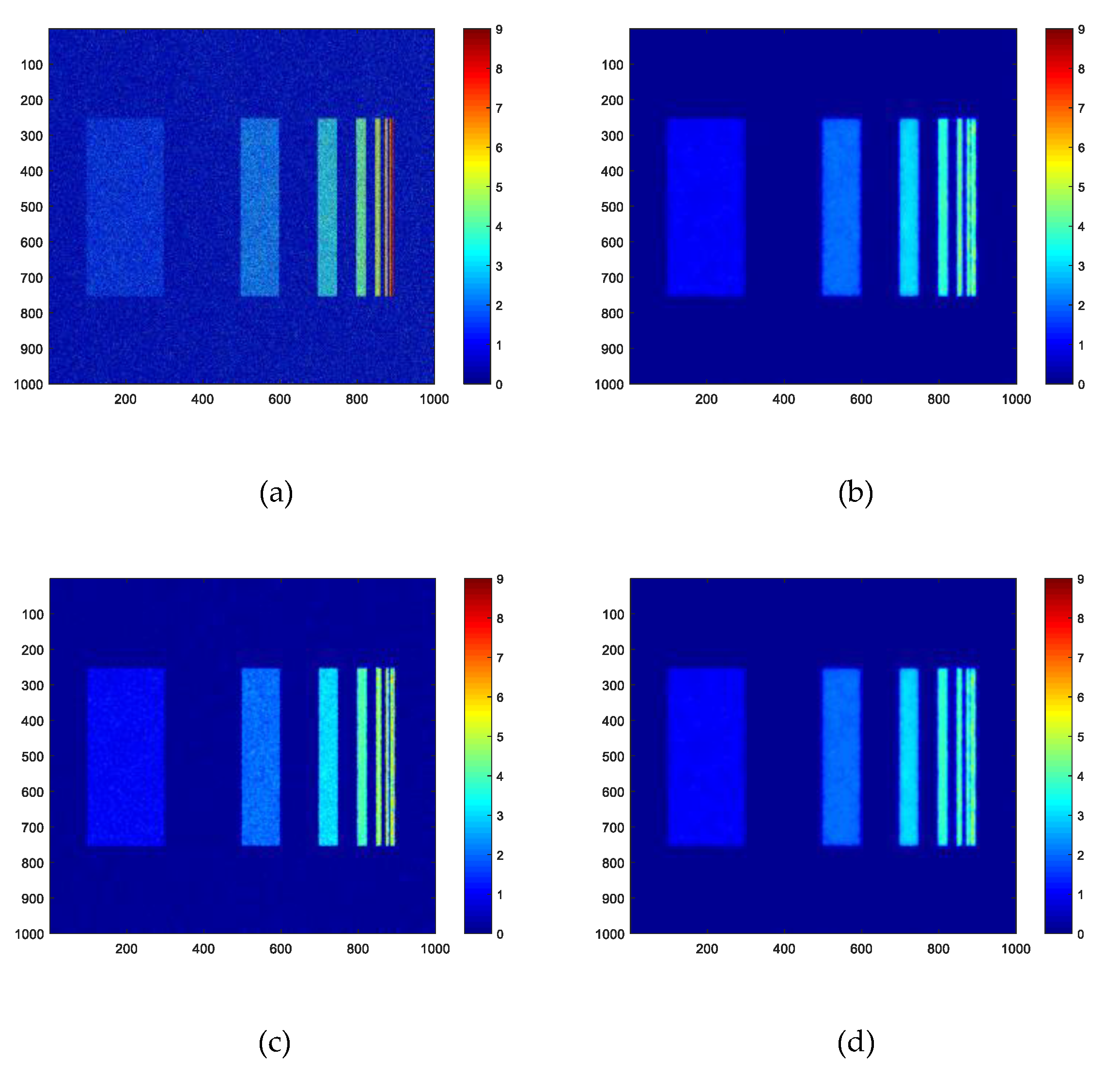
3.1. Synthetic Experiment
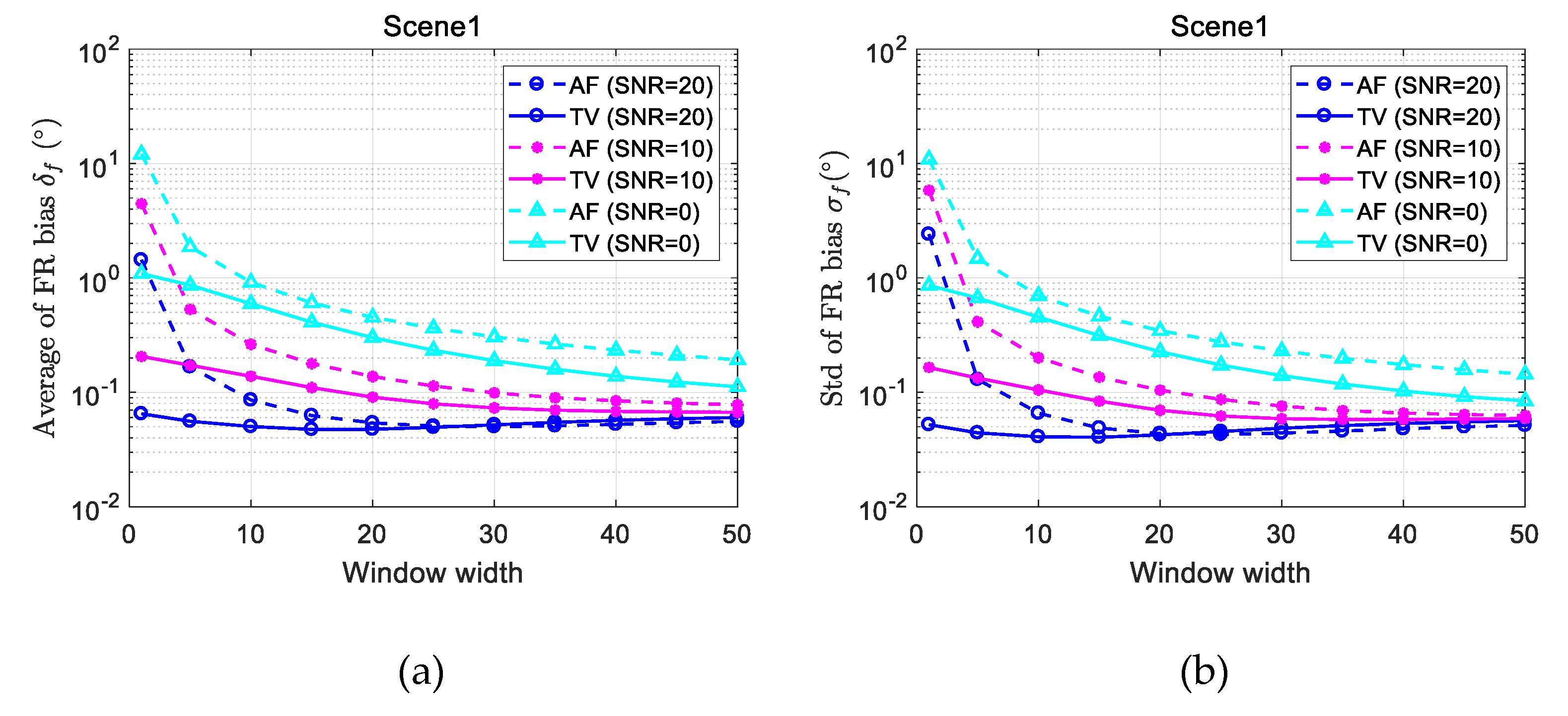
3.1.1. Result on the First FR Image
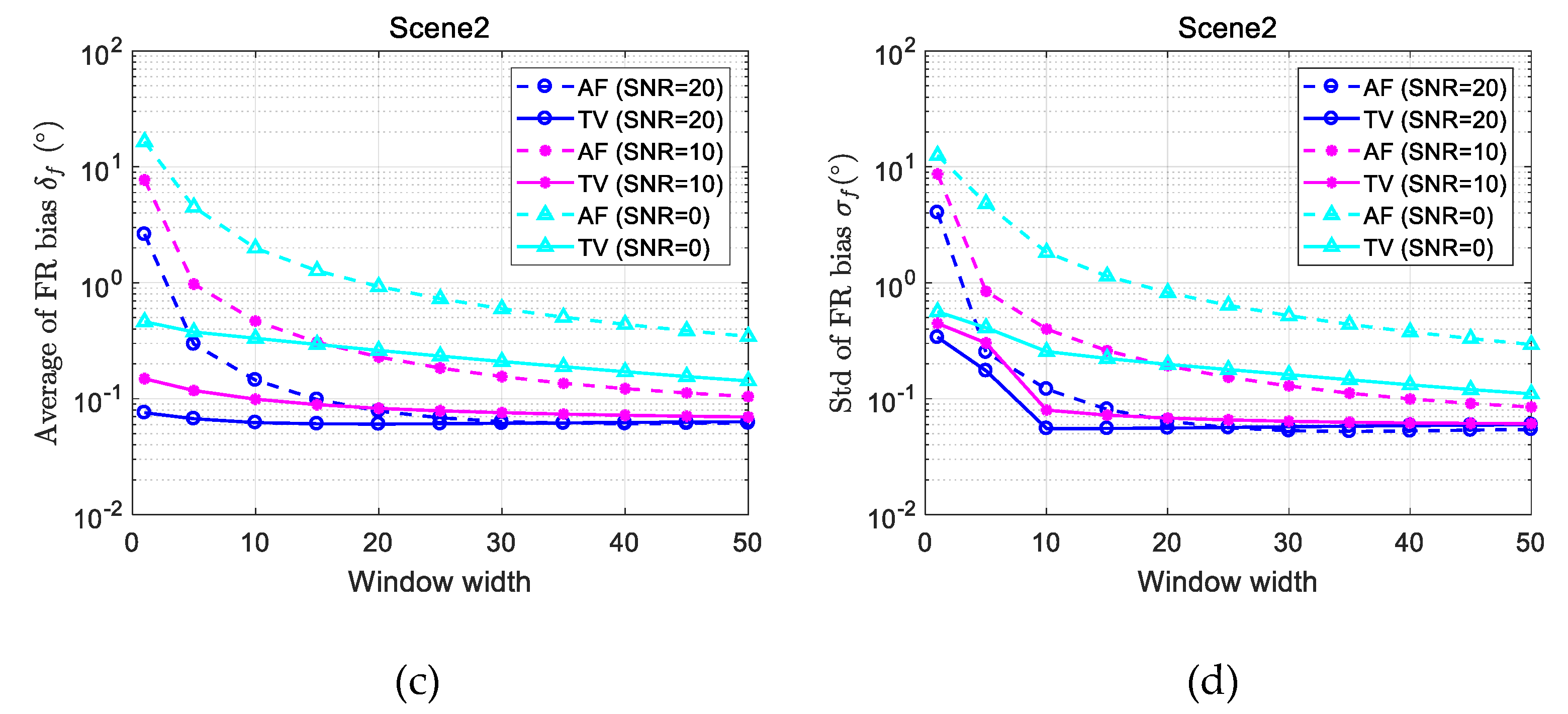
3.1.2. Result on the Second FR Image
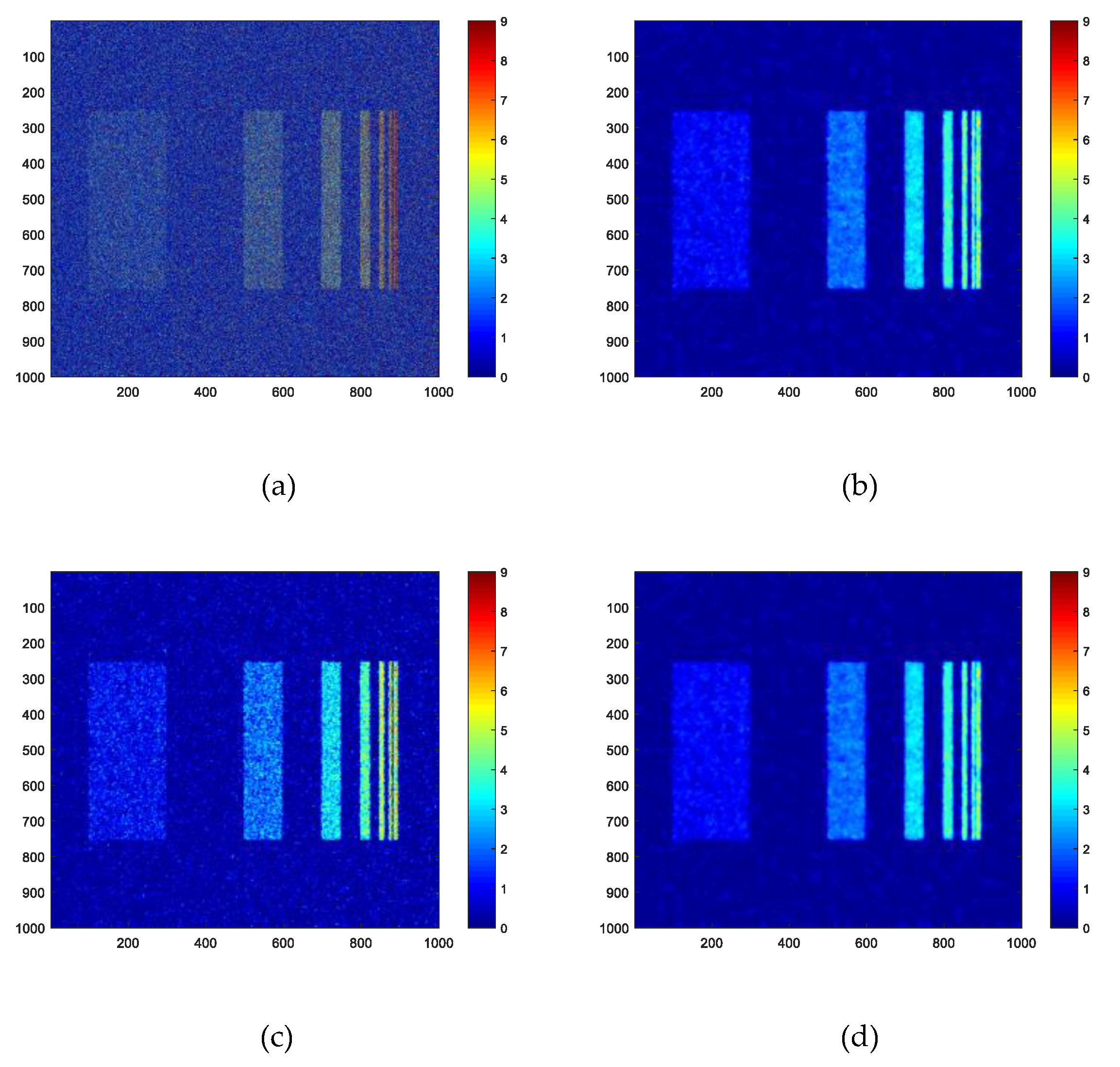
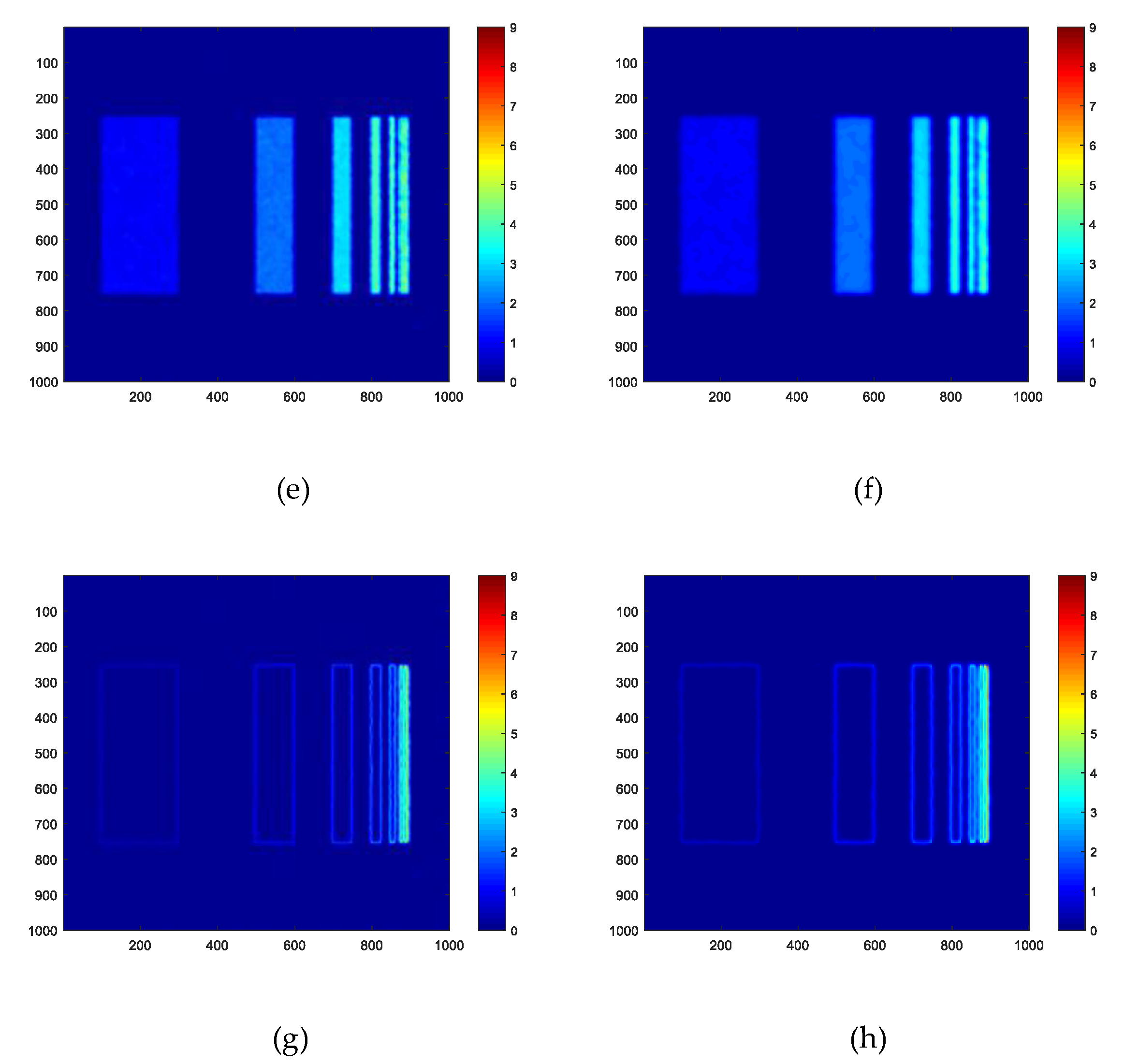
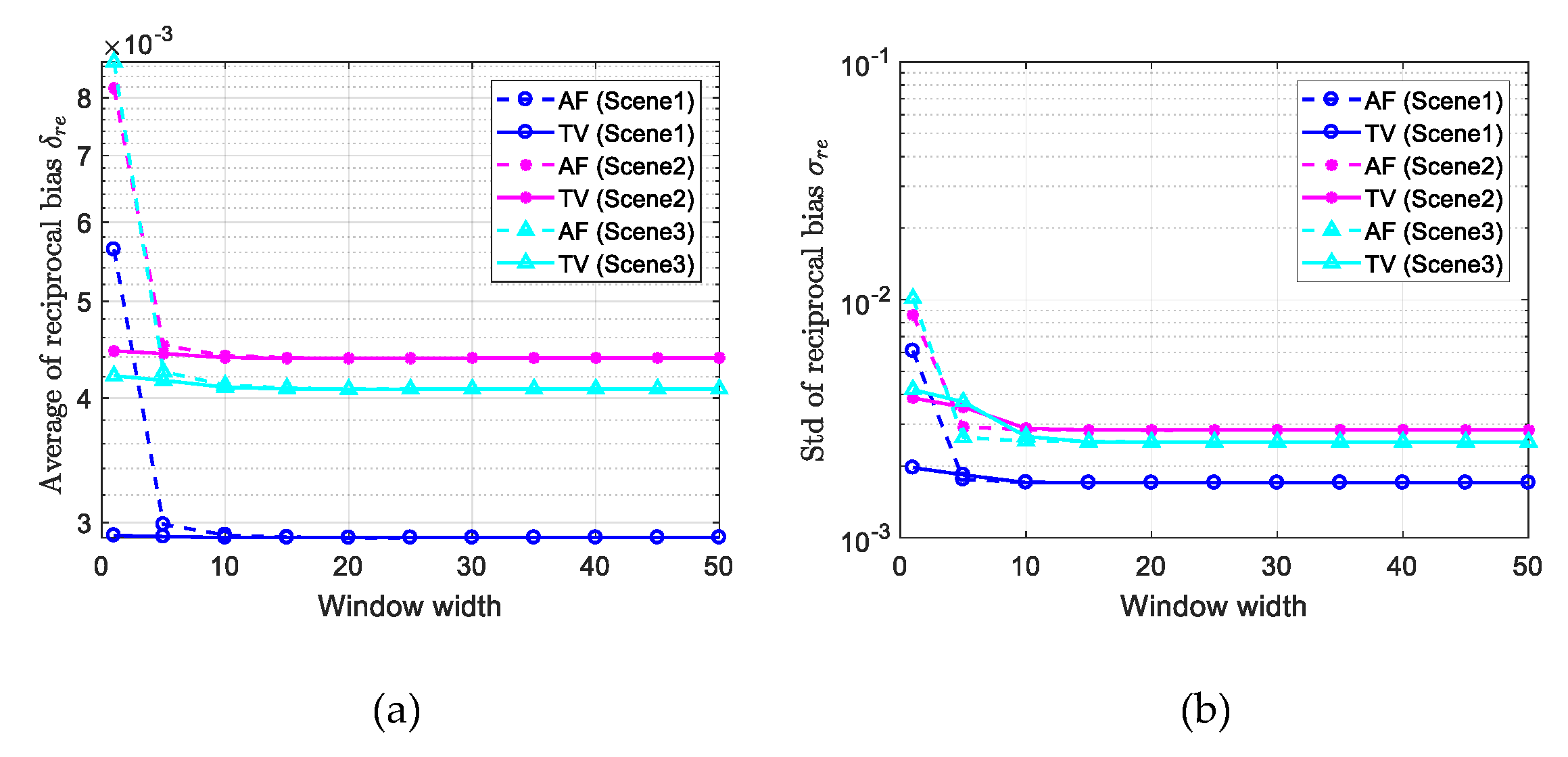
3.2. Real Experiment
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Meyer, F.J. Performance Requirements for Ionospheric Correction of Low-Frequency SAR Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3694–3702. [Google Scholar] [CrossRef]
- Dong, X.; Hu, J.; Hu, C.; Li, Y.; Sun, S. Modeling and Analyzing Impacts of Drifting Anisotropic Ionospheric Irregularities on Inclined Geosynchronous SAR. IEEE Access 2019, 7, 143090–143096. [Google Scholar] [CrossRef]
- Wang, C.; Chen, L.; Zhao, H.; Lu, Z.; Bian, M.; Zhang, R.; Feng, J. Ionospheric Reconstructions Using Faraday Rotation in Spaceborne Polarimetric SAR Data. Remote Sens. 2017, 9, 1169. [Google Scholar] [CrossRef]
- Wang, C.; Guo, W.; Zhao, H.; Chen, L.; Wei, Y.; Zhang, Y. Improving the Topside Profile of Ionosonde with TEC Retrieved from Spaceborne Polarimetric SAR. Sensors 2019, 19, 516. [Google Scholar] [CrossRef] [PubMed]
- Bickel, S.H.; Bates, R.H.T. Effects of magneto-ionic propagation on the polarization scattering matrix. Proc. IEEE 1965, 53, 1089–1091. [Google Scholar] [CrossRef]
- Freeman, A. Calibration of linearly polarized polarimetric SAR data subject to Faraday rotation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1617–1624. [Google Scholar] [CrossRef]
- Chen, J.; Quegan, S. Improved Estimators of Faraday Rotation in Spaceborne Polarimetric SAR Data. IEEE Geosci. Remote Sens. Lett. 2010, 7, 846–850. [Google Scholar] [CrossRef]
- Wang, C.; Liu, L.; Chen, L.; Feng, J.; Zhao, H.-S. Improved TEC retrieval based on spaceborne PolSAR data. Radio Sci. 2017, 52. [Google Scholar] [CrossRef]
- Borner, T.; Papathanassiou, K.P.; Marquart, N.; Zink, M.; Meadows, P.J.; Rye, A.J.; Wright, P.; Meininger, M.; Tell, B.R.; Traver, I.N. ALOS PALSAR products verification. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 5214–5217. [Google Scholar]
- Eriksson, L.E.B.; Sandberg, G.; Ulander, L.M.H.; Smith-Jonforsen, G.; Hallberg, B.; Folkesson, K.; Fransson, J.E.S.; Magnusson, M.; Olsson, H.; Gustavsson, A.; et al. ALOS PALSAR Calibration and Validation Results from Sweden. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1589–1592. [Google Scholar]
- Kim, J.S.; Papathanassiou, K.P.; Scheiber, R.; Quegan, S. Correcting Distortion of Polarimetric SAR Data Induced by Ionospheric Scintillation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6319–6335. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The Split Bregman Method for L1 Regularized Problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Qi, R.; Jin, Y. Analysis of the Effects of Faraday Rotation on Spaceborne Polarimetric SAR Observations at P-Band. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1115–1122. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Dong, Z.; Liang, D. New Faraday Rotation Estimators Based on Polarimetric Covariance Matrix. IEEE Geosci. Remote Sens. Lett. 2014, 11, 133–137. [Google Scholar] [CrossRef]
- Pi, X.; Freeman, A.; Chapman, B.; Rosen, P.; Li, Z. Imaging ionospheric inhomogeneities using spaceborne synthetic aperture radar. J. Geophys. Res. Space Phys. 2011, 116, A04303. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, Y.; Zhang, Q.; Dong, Z.; Yao, B. Retrieval of Ionospheric Faraday Rotation Angle in Low-Frequency Polarimetric SAR Data. IEEE Access 2019, 7, 3181–3193. [Google Scholar] [CrossRef]
- Rudin, L.I. Images, Numerical Analysis of Singularities and Shock Filters; Report TR:5250:87; California Institute of Techonology, Computer Science Department: Pasadena, CA, USA, 1987. [Google Scholar]
- Wang, Y.; Yin, W.; Zhang, Y. A Fast Algorithm for Image Deblurring with Total Variation Regularization; CAAM technical reports; Department of Computational and Applied Mathematics, Rice University: Houston, TX, USA, 2007. [Google Scholar]
- Zhao, Y.; Liu, J.G.; Zhang, B.; Hong, W.; Wu, Y. Adaptive Total Variation Regularization Based SAR Image Despeckling and Despeckling Evaluation Index. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2765–2774. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, T.; Zhu, Y.; Lv, Z. Sar Image Despeckling Based on a Novel Total Variation Regularization Model and Gf-3 Data. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2018), Munich, Germany, 22–27 July 2018; pp. 2362–2365. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Vogel, C.R.; Oman, M.E. Iterative Methods for Total Variation Denoising. SIAM J. Imaging Sci. 1996, 17, 227–238. [Google Scholar] [CrossRef]
- Osher, S.; Burger, M.; Goldfarb, D.; Xu, J.; Yin, W. An Iterative Regularization Method for Total Variation-Based Image Restoration. Multiscale Model. Simul. 2005, 4, 460–489. [Google Scholar] [CrossRef]
- Bregman, L.M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. Ussr Comput. Math. Math. Phys. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Alaska Satellite Facility. Available online: https://vertex.daac.asf.alaska.edu/ (accessed on 25 January 2019).
- Meyer, F.J.; Nicoll, J.B. Prediction, Detection, and Correction of Faraday Rotation in Full-Polarimetric L-Band SAR Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3076–3086. [Google Scholar] [CrossRef]
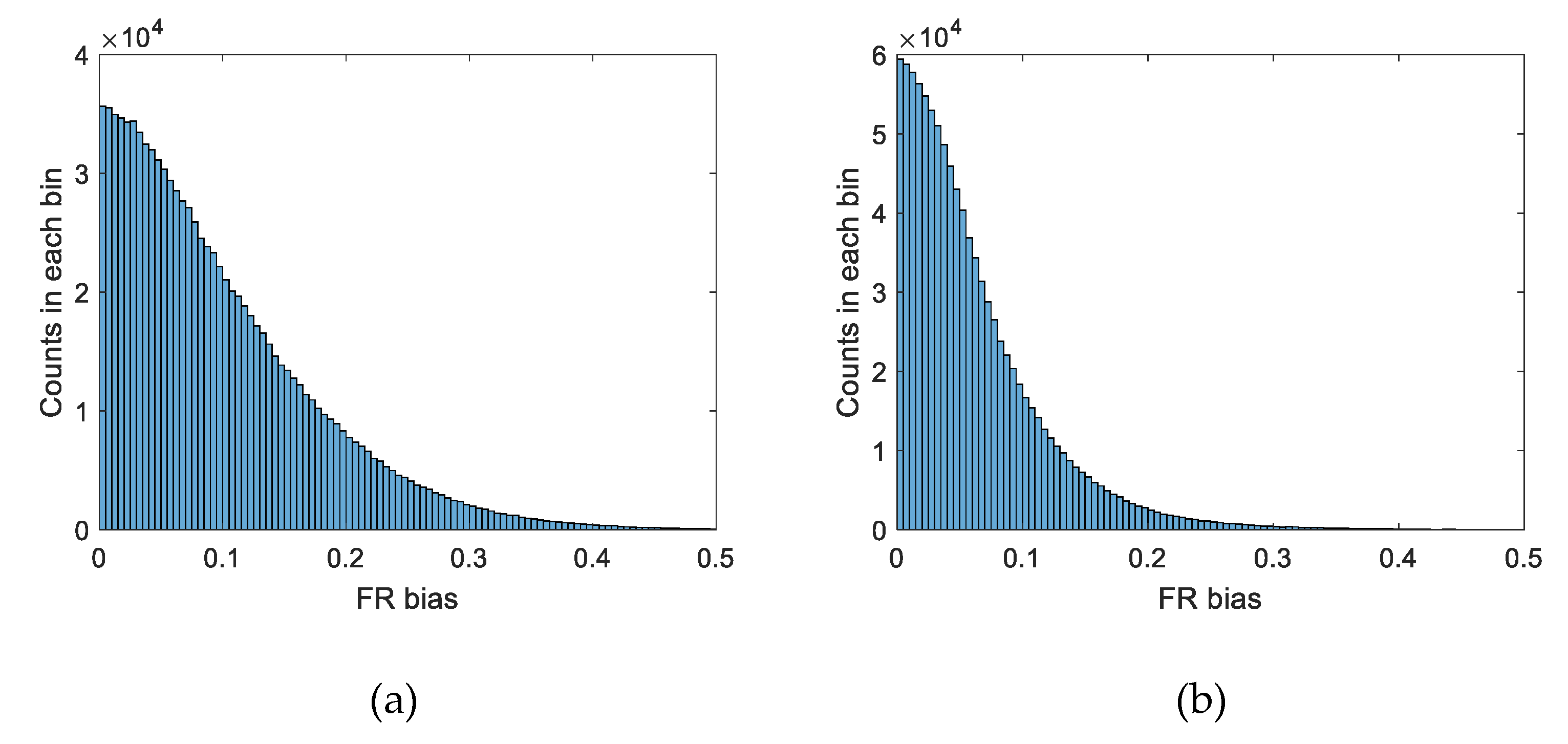
| Calculate the of each scene according to Equation (2). |
| Let , and . |
| Define the maximum number of iterations as , |
| and initial the number of iterations . |
| While and |
| Calculate from Equation (14), |
| update , using Equation (15), |
| update , with Equation (11), |
| update the number of iterations . |
| end |
| Scene No. | Locations | Observation Time |
|---|---|---|
| Scene 1 | (56.456N, -161.598W) | 20110328 08:41 |
| Scene 2 | (49.578N, 118.250E) | 20070428 14:13 |
| Scene No. | Locations | Observation Time |
|---|---|---|
| Scene 1 | (65.193N, -148.439W) | 20110319 07:32 |
| Scene 2 | (65.194N, -147.369W) | 20110331 07:28 |
| Scene 3 | (65.183N, -147.450W) | 20100806 21:06 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Liu, L.; Liu, B.; Chen, L.; Zhao, H.; Wang, C. Improved Faraday Rotation Estimation in Spaceborne PolSAR Data Using Total Variation Denoising. Remote Sens. 2019, 11, 2943. https://doi.org/10.3390/rs11242943
Guo W, Liu L, Liu B, Chen L, Zhao H, Wang C. Improved Faraday Rotation Estimation in Spaceborne PolSAR Data Using Total Variation Denoising. Remote Sensing. 2019; 11(24):2943. https://doi.org/10.3390/rs11242943
Chicago/Turabian StyleGuo, Wulong, Lu Liu, Bo Liu, Liang Chen, Haisheng Zhao, and Cheng Wang. 2019. "Improved Faraday Rotation Estimation in Spaceborne PolSAR Data Using Total Variation Denoising" Remote Sensing 11, no. 24: 2943. https://doi.org/10.3390/rs11242943
APA StyleGuo, W., Liu, L., Liu, B., Chen, L., Zhao, H., & Wang, C. (2019). Improved Faraday Rotation Estimation in Spaceborne PolSAR Data Using Total Variation Denoising. Remote Sensing, 11(24), 2943. https://doi.org/10.3390/rs11242943