Hyperspectral Image Super-Resolution via Adaptive Dictionary Learning and Double
ℓ
1
Constraint
Abstract
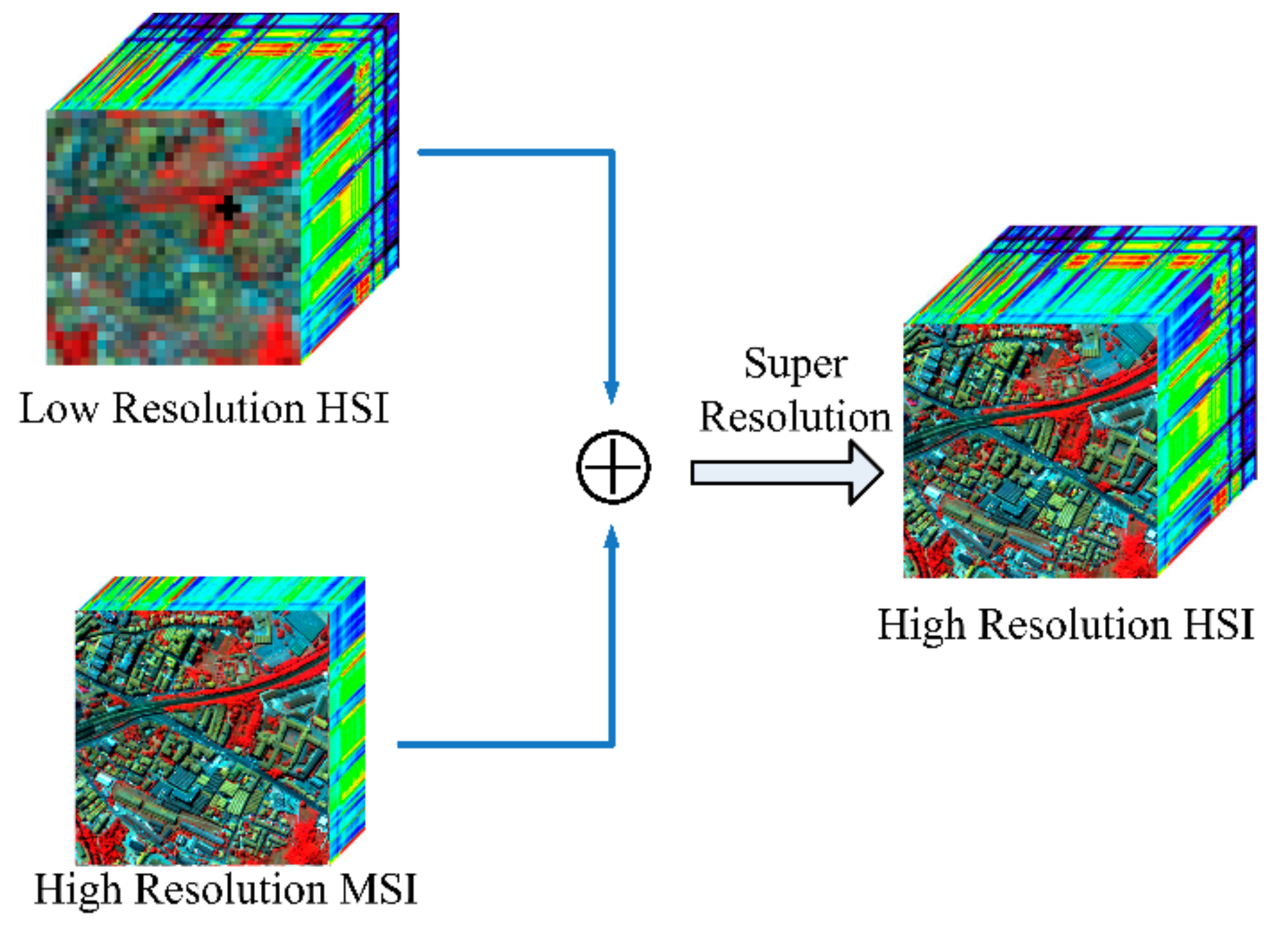
1. Introduction
1.1. Related Work
1.1.1. Spectral Unmixing Based Methods
1.1.2. Sparse Representation-Based Methods
1.2. Motivation and Contributions
2. Mothodology (or Materials and Methods)
2.1. The Traditional Sparse-Representation Method
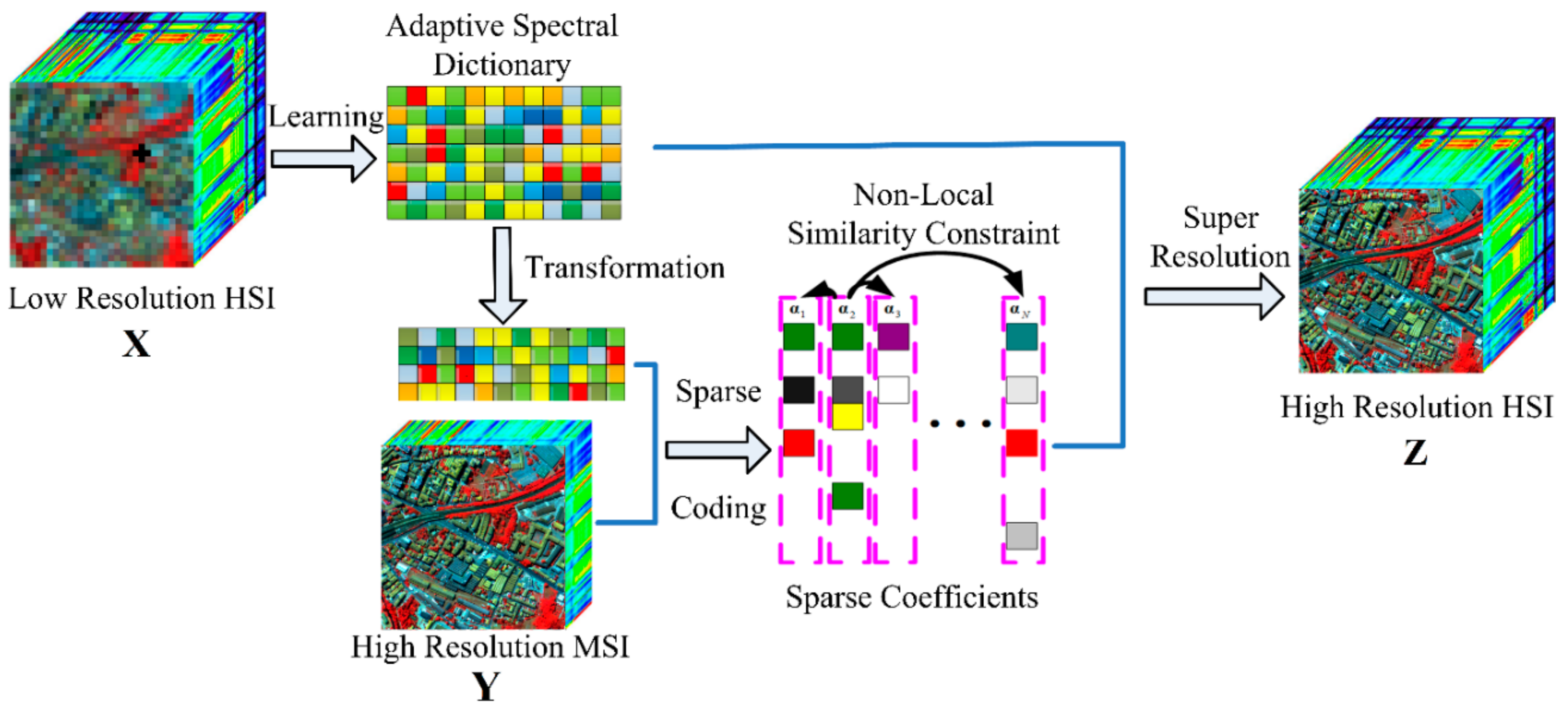
2.2. The Proposed Method
2.2.1. Adaptive Spectral Dictionary Learning
| Algorithm 1: Adaptive Spectral Dictionary Learning |
| Input: the training examples , the regularization parameters , . Initialize , , , while do Input , , update by (17); Input , update by (20); Input and , update by (13); ; end while Output: the spectral dictionary |
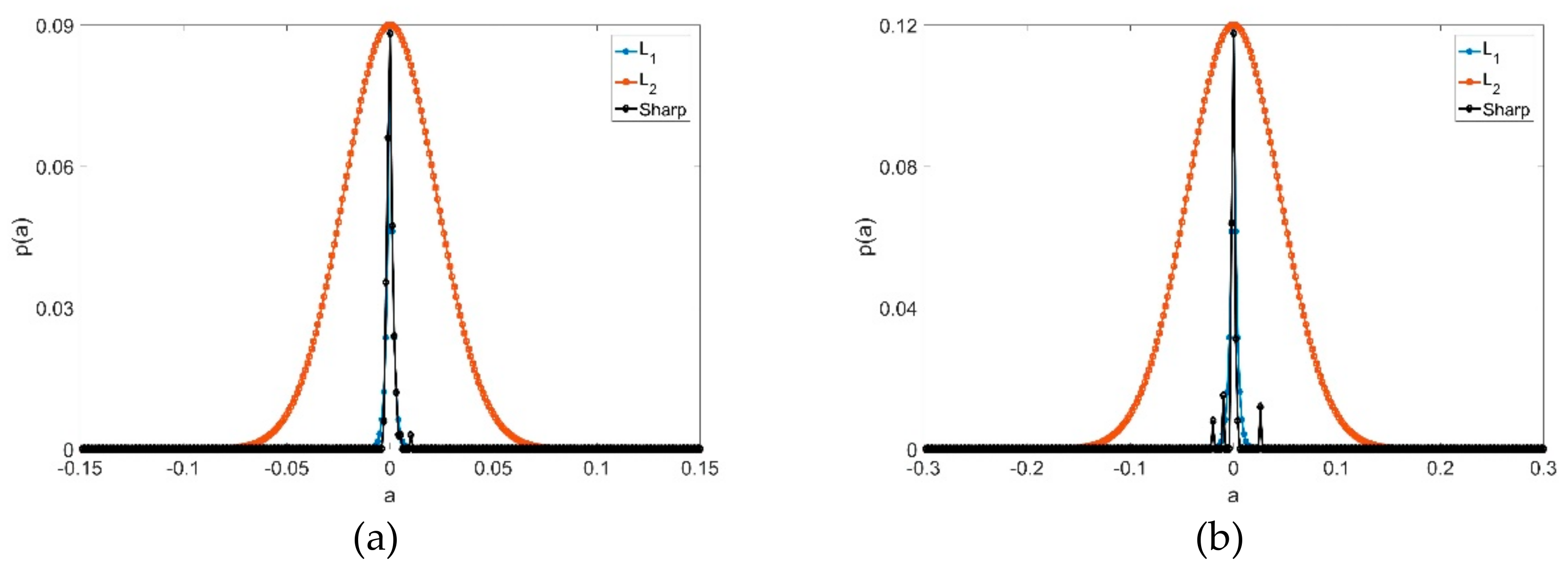
2.2.2. Double Regularization
| Algorithm 2:DoubleRegularized Sparse Coding |
| Input: the pixel set , the spectral dictionary (), the transform matrix (), the regularization parameters ( and ), and the number of iterations (). For do Initialize ; For do End For End For Output: the sparse coefficients . |
| Algorithm 3:HSI SR by Adaptive Dictionary Learning and DoubleRegularized Sparse Representation |
| Input: LR HSI (), HR MSI (), and the regularization parameters ( and ). (1) Learn the spectral dictionary, , from by using Algorithm 1; (2) Obtain the sparse representation, , from and by using Algorithm 2. Output: the HR HSI . |
3. Experimental Results and Analysis
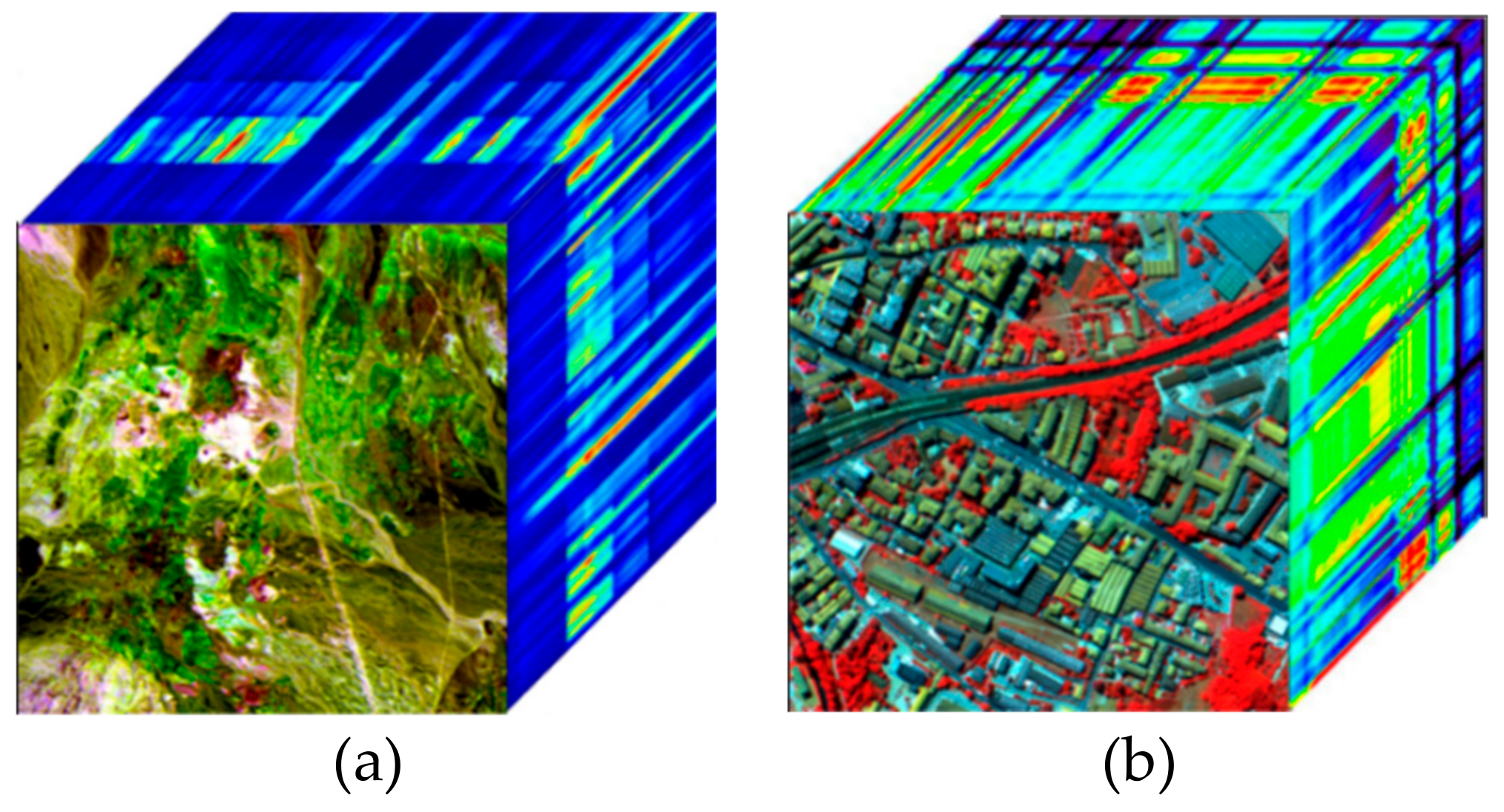
3.1. Datasets and Experimental Setup
3.2. Quality Metrics
3.3. Performance Comparison of Different Methods
3.4. Effects of the Adaptive Size Dictionary
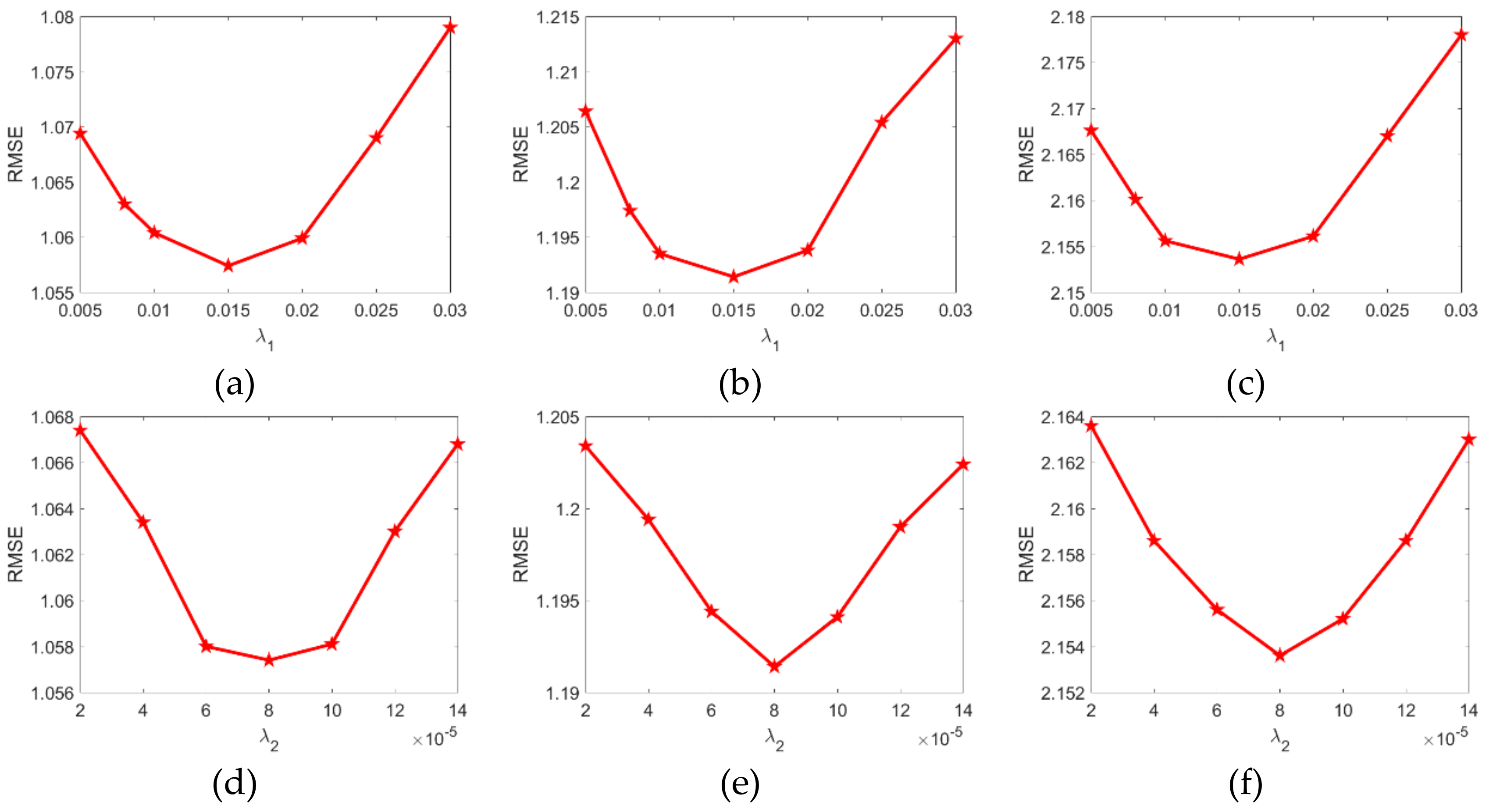
3.5. Parameters Analysis
3.6. Discussion on Computational Complexity
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, L.; Zhan, T.; Wu, Z.; Xiao, L.; Jeon, B. Hyperspectral mixed denoising via spectral difference-induced total variation and low-rank approximation. Remote Sens. 2018, 10, 1956. [Google Scholar] [CrossRef]
- Sun, L.; Jeon, B.; Bushra, N.S.; Zheng, Y.H.; Wu, Z.B.; Xiao, L. Fast superpixel based subspace low rank learning method for hyperspectral denoising. IEEE Access. 2018, 6, 12031–12043. [Google Scholar] [CrossRef]
- Gao, H.; Yang, Y.; Li, C.; Zhou, H.; Qu, X. Joint Alternate Small Convolution and Feature Reuse for Hyperspectral Image Classification. ISPRS Int. J. Geo Inf. 2018, 7, 349. [Google Scholar] [CrossRef]
- Sun, L.; Ma, C.; Chen, Y.; Zheng, Y.; Shim, H.J.; Wu, Z.; Jeon, B. Low Rank Component Induced Spatial-spectral Kernel Method for Hyperspectral Image Classification; IEEE: New York, NY, USA, 2019; pp. 1–14. [Google Scholar]
- Van Nguyen, H.; Banerjee, A.; Chellappa, R. Tracking via Object Reflectance Using a Hyperspectral Video Camera. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition—Workshops, San Francisco, CA, USA, 13–18 June 2010; pp. 44–51. [Google Scholar]
- Uzair, M.; Mahmood, A.; Mian, A. Hyperspectral Face Recognition using 3D-DCT and Partial Least Squares. In Proceedings of the British Machine Vision Conference, Bristol, UK, 9–13 September 2013; p. 57. [Google Scholar]
- Yang, J.; Jiang, Z.; Hao, S.; Zhang, H. Higher Order Support Vector Random Fields for Hyperspectral Image Classification. ISPRS Int. J. Geo Inf. 2018, 7, 19. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Han, Z.; He, S. Hyperspectral Image Super-Resolution via Nonlocal Low-Rank Tensor Approximation and Total Variation Regularization. Remote. Sens. 2017, 9, 1286. [Google Scholar] [CrossRef]
- Tang, S.; Xiao, L.; Huang, W.; Liu, P.; Wu, H. Pan-sharpening using 2D CCA. Remote Sens. Lett. 2015, 6, 341–350. [Google Scholar] [CrossRef]
- Tu, T.-M.; Huang, P.; Hung, C.-L.; Chang, C.-P. A Fast Intensity–Hue–Saturation Fusion Technique With Spectral Adjustment for IKONOS Imagery. IEEE Geosci. Remote. Sens. Lett. 2004, 1, 309–312. [Google Scholar] [CrossRef]
- Liu, P.; Xiao, L. A Novel Generalized Intensity-Hue-Saturation (GIHS) Based Pan-Sharpening Method With Variational Hessian Transferring. IEEE Access 2018, 6, 46751–46761. [Google Scholar] [CrossRef]
- El-Mezouar, M.C.; Kpalma, K.; Taleb, N.; Ronsin, J. A pan-sharpening based on the non-subsampled contourlet transform: application to WorldView-2 imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1806–1815. [Google Scholar] [CrossRef]
- Garzelli, A.; Aiazzi, B.; Alparone, L.; Lolli, S.; Vivone, G. Multispectral pansharpening with radiative transfer-based detail-injection modeling for preserving changes in vegetation cover by Andrea. Remote Sens. 2018, 10, 1308. [Google Scholar] [CrossRef]
- Li, S.; Yang, B. A new pan-sharpening method using a compressed sensing technique. IEEE Trans. Geosci. Remote Sens. 2010, 49, 738–746. [Google Scholar] [CrossRef]
- Liu, P.; Xiao, L.; Li, T. A Variational Pan-Sharpening Method Based on Spatial Fractional-Order Geometry and Spectral–Spatial Low-Rank Priors. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 1788–1802. [Google Scholar] [CrossRef]
- Tang, S. Pansharpening via sparse regression. Opt. Eng. 2017, 56, 1. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote. Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Veganzones, M.A.; Simoes, M.; Licciardi, G.; Yokoya, N.; Bioucas-Dias, J.M.; Chanussot, J. Hyperspectral super-resolution of locally low rank images from complementary multisource data. IEEE Trans. Image Proc. 2015, 25, 274–288. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Geosci. Remote Sens. 2011, 50, 528–537. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Algorithms for Non-Negative Matrix Factorization. In Advances in Neural Information Processing Systems; Michael, I.J., Yann, L.C., Sara, A.S., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 556–562. [Google Scholar]
- Bendoumi, M.A.; He, M.; Mei, S. Hyperspectral Image Resolution Enhancement Using High-Resolution Multispectral Image Based on Spectral Unmixing. IEEE Trans. Geosci. Remote. Sens. 2014, 52, 6574–6583. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process Mag. 2002, 19, 44–57. [Google Scholar]
- Iordache, M.-D.; Bioucas-Dias, J.M.; Plaza, A. Sparse Unmixing of Hyperspectral Data. IEEE Trans. Geosci. Remote. Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef]
- Kawakami, R.; Matsushita, Y.; Wright, J.; Ben-Ezra, M.; Tai, Y.-W.; Ikeuchi, K. High-Resolution Hyperspectral Imaging via Matrix Factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2329–2336. [Google Scholar]
- Li, S.; Dian, R.; Fang, L.; Bioucas-Dias, J.M. Fusing Hyperspectral and Multispectral Images via Coupled Sparse Tensor Factorization. IEEE Trans. Image Process. 2018, 27, 4118–4130. [Google Scholar] [CrossRef] [PubMed]
- Dian, R.; Fang, L.; Li, S. Hyperspectral Image Super-Resolution via Non-local Sparse Tensor Factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017 ; pp. 3862–3871. [Google Scholar]
- Wei, Q.; Bioucas-Dias, J.; Dobigeon, N.; Tourneret, J.Y. Hyperspectral and multispectral image fusion based on a sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3658–3668. [Google Scholar] [CrossRef]
- Akhtar, N.; Shafait, F.; Mian, A. Bayesian Sparse Representation for Hyperspectral Image Super Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–12 June 2015; pp. 3631–3640. [Google Scholar]
- Yi, C.; Zhao, Y.Q.; Chan, J.C.W. Hyperspectral image super-resolution based on spatial and spectral correlation rusion. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4165–4177. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Bai, C.; Gao, Y.; Zhang, Y. Exploiting Clustering Manifold Structure for Hyperspectral Imagery Super-Resolution. IEEE Trans. Image Process. 2018, 27, 5969–5982. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Song, H.; Cui, H.; Peng, J.; Xu, Z. Spatial and spectral image fusion using sparse matrix factorization. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1693–1704. [Google Scholar] [CrossRef]
- Grohnfeldt, C.; Zhu, X.X.; Bamler, R. Jointly Sparse Fusion of Hyperspectral and Multispectral Imagery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium, Melbourne, Australia, 21–26 July 2013; pp. 4090–4093. [Google Scholar]
- Akhtar, N.; Shafait, F.; Mian, A. Sparse Spatio-Spectral Representation for Hyper-Spectral Image Super-Resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 63–78. [Google Scholar]
- Liang, J.; Zhang, Y.; Mei, S. Hyperspectral and Multispectral Image Fusion using Dual-Source Localized Dictionary Pair. In Proceedings of the International Symposium on Intelligent Signal Processing and Communication Systems, Xiamen, Fujian, China, 6–9 November 2017; pp. 261–264. [Google Scholar]
- Lanaras, C.; Baltsavias, E.; Schindler, K.; Charis, L.; Emmanuel, B.; Konrad, S. Hyperspectral Super-Resolution by Coupled Spectral Unmixing. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2015; pp. 3586–3594. [Google Scholar]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral Super-Resolution with Spectral Unmixing Constraints. Remote. Sens. 2017, 9, 1196. [Google Scholar] [CrossRef]
- Dong, W.; Fu, F.; Shi, G.; Cao, X.; Wu, J.; Li, G.; Li, X. Hyperspectral Image Super-Resolution via Non-Negative Structured Sparse Representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef]
- Han, X.-H.; Shi, B.; Zheng, Y. Self-Similarity Constrained Sparse Representation for Hyperspectral Image Super-Resolution. IEEE Trans. Image Process. 2018, 27, 5625–5637. [Google Scholar] [CrossRef]
- Fang, L.Y.; Zhuo, H.J.; Li, S.T. Super-resolution of hyperspectral image via superpixel-based sparse representation. Neurocomputing 2018, 273, 171–177. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.-M. A Non-Local Algorithm for Image Denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 05), San Diego, CA, USA, 20–25 June 2005; 2, pp. 60–65. [Google Scholar]
- Glasner, D.; Bagon, S.; Irani, M. Super-resolution from a single image. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 349–356. [Google Scholar]
- Cotter, S.; Rao, B.; Engan, K.; Kreutz-Delgado, K. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE Trans. Signal Process. 2005, 53, 2477–2488. [Google Scholar] [CrossRef]
- Lu, C.; Shi, J.; Jia, J. Scale adaptive dictionary learning. IEEE Trans. Image Process. 2013, 23, 837–847. [Google Scholar] [CrossRef] [PubMed]
- Aharon, M.; Elad, M. Sparse and redundant modeling of image content using an image-signature-dictionary. SIAM J. Imaging Sci. 2008, 1, 228–247. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Tang, S.; Zhou, N. Local Similarity Regularized Sparse Representation for Hyperspectral Image Super-Resolution. IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 21–29 July 2018; pp. 5120–5123. [Google Scholar]
- Daubechies, I.; Defrise, M.; De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L. Comparison of Pansharpening Algorithms: Outcome of the 2006 GRS-S Data-Fusion Contest. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, Y. K-SVD: An algorithm for designing of overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal Matching Pursuit: Recursive Function Approximation with Applications to Wavelet Decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Jiang, Y.; Zhao, M.; Hu, C.; He, L.; Bai, H.; Wang, J. A parallel FP-growth algorithm on World Ocean Atlas data with multi-core CPU. J. Supercomput. 2019, 75, 732–745. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor Decompositions and Applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Foi, A.; Katkovnik, V.; Egiazarian, K. Pointwise shape-adaptive DCT for high-quality denoising and deblocking of grayscale and color images. IEEE Trans. Image Process. 2007, 16, 1395–1411. [Google Scholar] [CrossRef]
- Müller, H.-G.; Fan, J.; Gijbels, I. Local Polynomial Modeling and Its Applications. J. Am. Stat. Assoc. 1998, 93, 835. [Google Scholar] [CrossRef]
- Tu, Y.; Lin, Y.; Wang, J.; Kim, J.U. Semi-supervised learning with generative adversarial networks on digital signal modulation classification. Comput. Mater. Contin. 2018, 55, 243–254. [Google Scholar]
- Meng, R.; Rice, S.G.; Wang, J.; Sun, X. A fusion steganographic algorithm based on faster R-CNN. Comput. Mater. Contin. 2018, 55, 1–16. [Google Scholar]
- Long, M.; Zeng, Y. Detecting Iris Liveness with Batch Normalized Convolutional Neural Network. Comput. Mater. Contin. 2019, 58, 493–504. [Google Scholar] [CrossRef]
- He, S.; Li, Z.; Tang, Y.; Liao, Z.; Wang, J.; Kim, H.J. Parameters compressing in deep learning. Comput. Mater. Contin. 2019, 62, 1–16. [Google Scholar]
- Song, Y.; Yang, G.; Xie, H.; Zhang, D.; Xingming, S. Residual domain dictionary learning for compressed sensing video recovery. Multimed. Tools Appl. 2017, 76, 10083–10096. [Google Scholar] [CrossRef]
- Zeng, D.; Dai, Y.; Li, F.; Wang, J.; Sangaiah, A.K. Aspect based sentiment analysis by a linguistically regularized CNN with gated mechanism. J. Intell. Fuzzy Syst. 2019, 36, 3971–3980. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, X.; Sun, J.; Wang, J.; Sangaiah, A.K. Spatial and semantic convolutional features for robust visual object tracking. Multimedia Tools Appl. 2018, 1, 1–21. [Google Scholar] [CrossRef]
- Zhou, S.; Ke, M.; Luo, P. Multi-camera transfer GAN for person re-dentification. J. Vis. Commun. Image R. 2019, 59, 393–400. [Google Scholar] [CrossRef]







| Downsampling Factor | Methods | Cuprite | Pavia Center | ||||
|---|---|---|---|---|---|---|---|
| RMSE | ERGAS | SAM | RMSE | ERGAS | SAM | ||
| SASFM | 1.0065 | 0.5987 | 2.1624 | 1.8734 | 0.7003 | 2.3561 | |
| G-SOMP+ | 0. 8410 | 0.5683 | 1.8999 | 1.5552 | 0.5826 | 1.9708 | |
| SSR | 0.7627 | 0.5511 | 1.8239 | 1.2390 | 0.5747 | 1.9089 | |
| NNSR | 0.6373 | 0.4562 | 1.6120 | 1.1537 | 0.5521 | 1.8295 | |
| SSCSR | 0.5663 | 0.3318 | 1.2278 | 0.0990 | 0.5159 | 1.7566 | |
| Proposed | 0.4852 | 0.2961 | 0.9088 | 1.0574 | 0.4975 | 1.6388 | |
| SASFM | 1.1818 | 0.3136 | 1.9852 | 2.1621 | 0.3519 | 2.4395 | |
| G-SOMP+ | 0.9109 | 0.2796 | 1.7674 | 1.7861 | 0.3009 | 2.1477 | |
| SSR | 0.8567 | 0.2788 | 1.7585 | 1.3697 | 0.2978 | 2.1344 | |
| NNSR | 0.7629 | 0.2005 | 1.5662 | 1.2790 | 0.2977 | 1.9591 | |
| SSCSR | 0.6937 | 0.1811 | 1.3039 | 1.2190 | 0.2891 | 1.8889 | |
| Proposed | 0.5474 | 0.1695 | 1.0157 | 1.1904 | 0.2837 | 1.8650 | |
| SASFM | 1.4076 | 0.1629 | 2.0011 | 4.2323 | 0.3002 | 4.0387 | |
| G-SOMP+ | 1.1267 | 0.1436 | 1.8117 | 3.8084 | 0.2511 | 3.3054 | |
| SSR | 0.9845 | 0.1397 | 1.7546 | 3.4486 | 0.2332 | 2.9203 | |
| NNSR | 0.8393 | 0.1128 | 1.4658 | 2.8099 | 0.2008 | 2.5580 | |
| SSCSR | 0.7654 | 0.1095 | 1.3267 | 2.2790 | 1.1744 | 2.3016 | |
| Proposed | 0.6826 | 0.1015 | 1.1990 | 2.1847 | 0.1575 | 2.0664 | |
| Downsampling Factor | Cuprite | Pavia Center | ||
|---|---|---|---|---|
| Traditional | Adaptive | Traditional | Adaptive | |
| 11.1233 | 2.1488 | 19.0409 | 6.3434 | |
| 2.1488 | 1.9752 | 15.5154 | 2.9938 | |
| 0.6115 | 0.5165 | 10.3444 | 0.7820 | |
| Method | RMSE | ERGAS | SAM |
|---|---|---|---|
| K-SVD | 1.0451 3.2085 | 0.1322 0.2288 | 1.6000 3.0525 |
| Adaptive dictionary | 0.6826 2.18747 | 0.1015 0.1575 | 1.1900 2.0664 |
| Method | SASFM | G-SOMP+ | SSR | NNSR | SSCSR | Proposed |
|---|---|---|---|---|---|---|
| Time | 11 | 235 | 579 | 146 | 723 | 276 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, S.; Xu, Y.; Huang, L.; Sun, L.
Hyperspectral Image Super-Resolution via Adaptive Dictionary Learning and Double
Tang S, Xu Y, Huang L, Sun L.
Hyperspectral Image Super-Resolution via Adaptive Dictionary Learning and Double
Tang, Songze, Yang Xu, Lili Huang, and Le Sun.
2019. "Hyperspectral Image Super-Resolution via Adaptive Dictionary Learning and Double
Tang, S., Xu, Y., Huang, L., & Sun, L.
(2019). Hyperspectral Image Super-Resolution via Adaptive Dictionary Learning and Double







