Analysis of Parameters for the Accurate and Fast Estimation of Tree Diameter at Breast Height Based on Simulated Point Cloud
Abstract
:1. Introduction
2. Materials and Methods
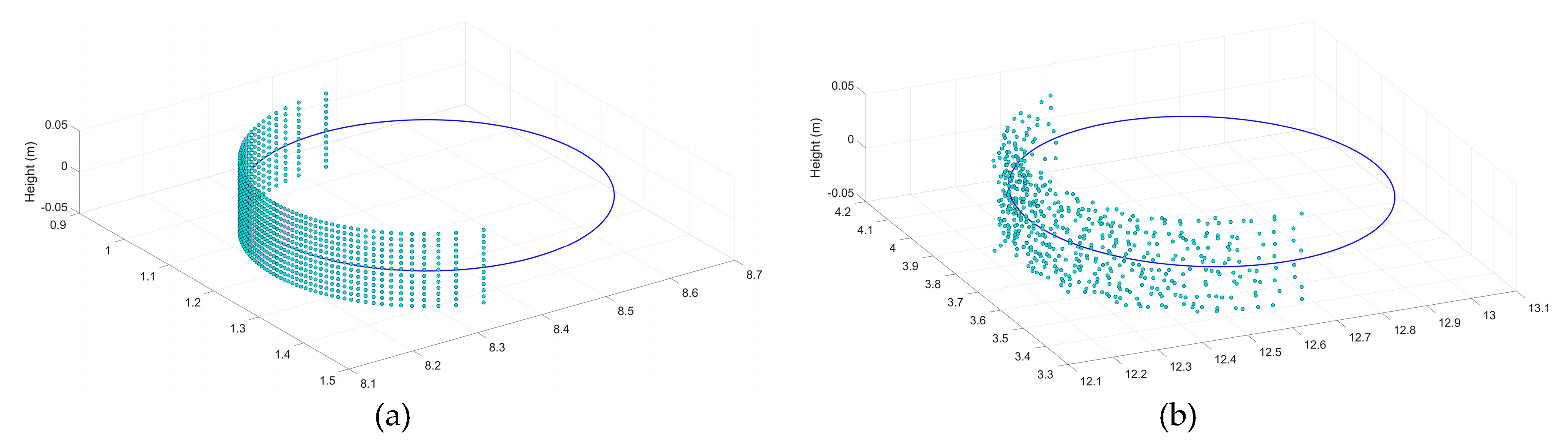
2.1. In-Situ TLS and Simulation Data
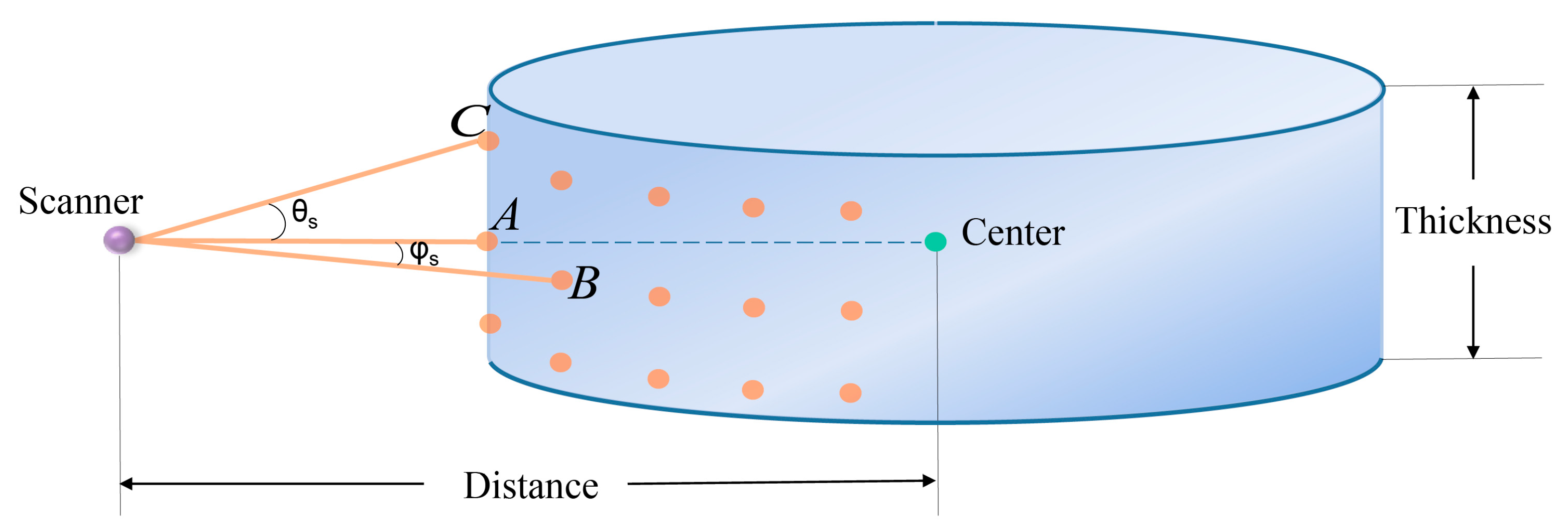
2.2. DBH Model Construction
- (a)
- Each trunk was a cylinder that was perpendicular to the horizontal ground.
- (b)
- The virtual TLS scanner was placed at a height of 1.3 m, which is the exact height where the breast diameter was measured.
- (c)
- The position of the virtual TLS scanner was the origin (0, 0, 0) of the local coordinate system.
2.3. DBH Model Simulations
- The range of DBH values was 0.1 m 0.4 m. The diameter of a slice was randomly chosen from this range.
- The distance between the scanner and the real center of a slice was a random value in the range of 0.1 m 30 m.
- The thickness of the slices was 0.1 m.
2.4. DBH Model Estimations
2.5. Accuracy Assessment
3. Results
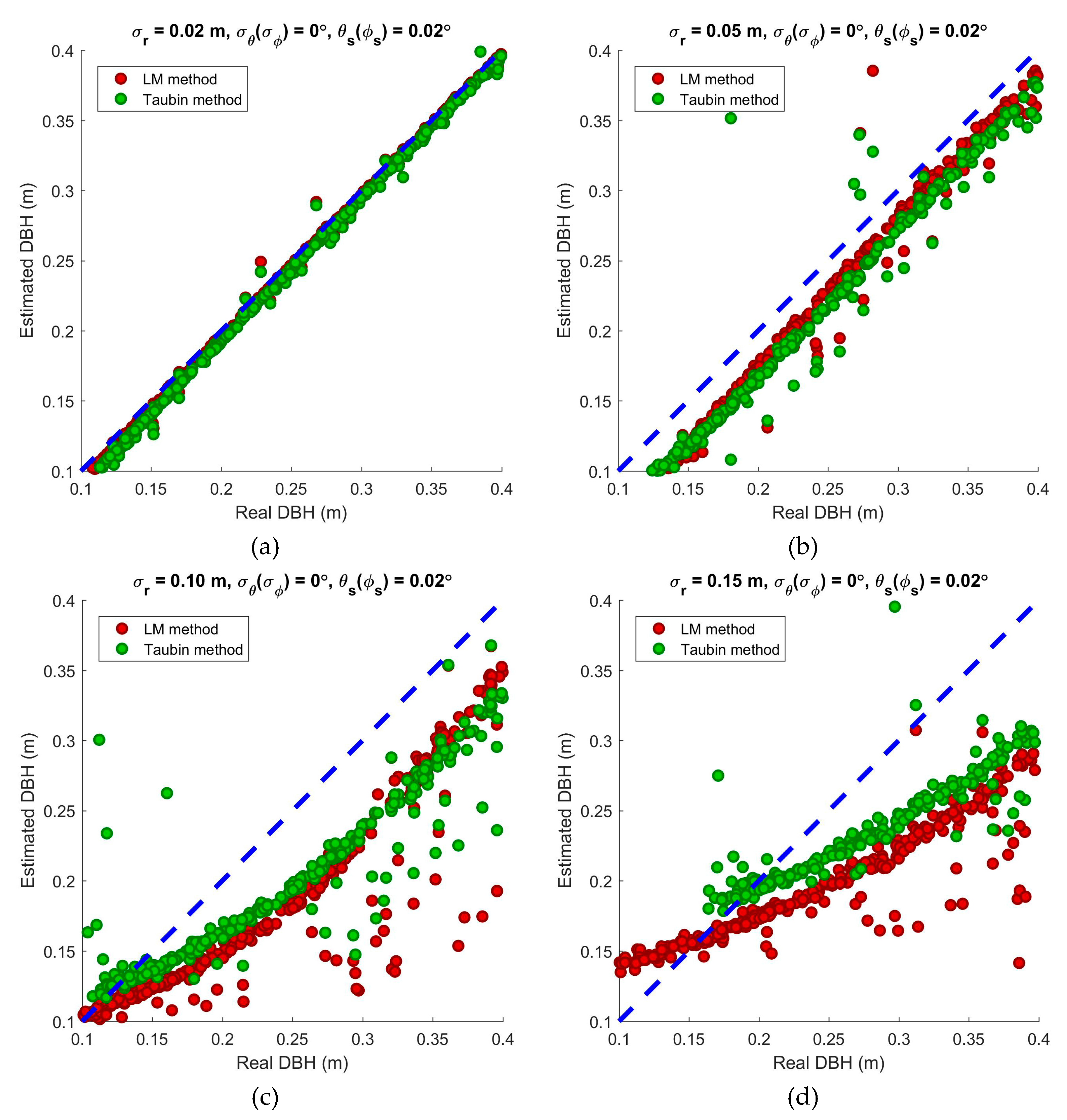
3.1. Performances of the Two Circle Fitting Methods
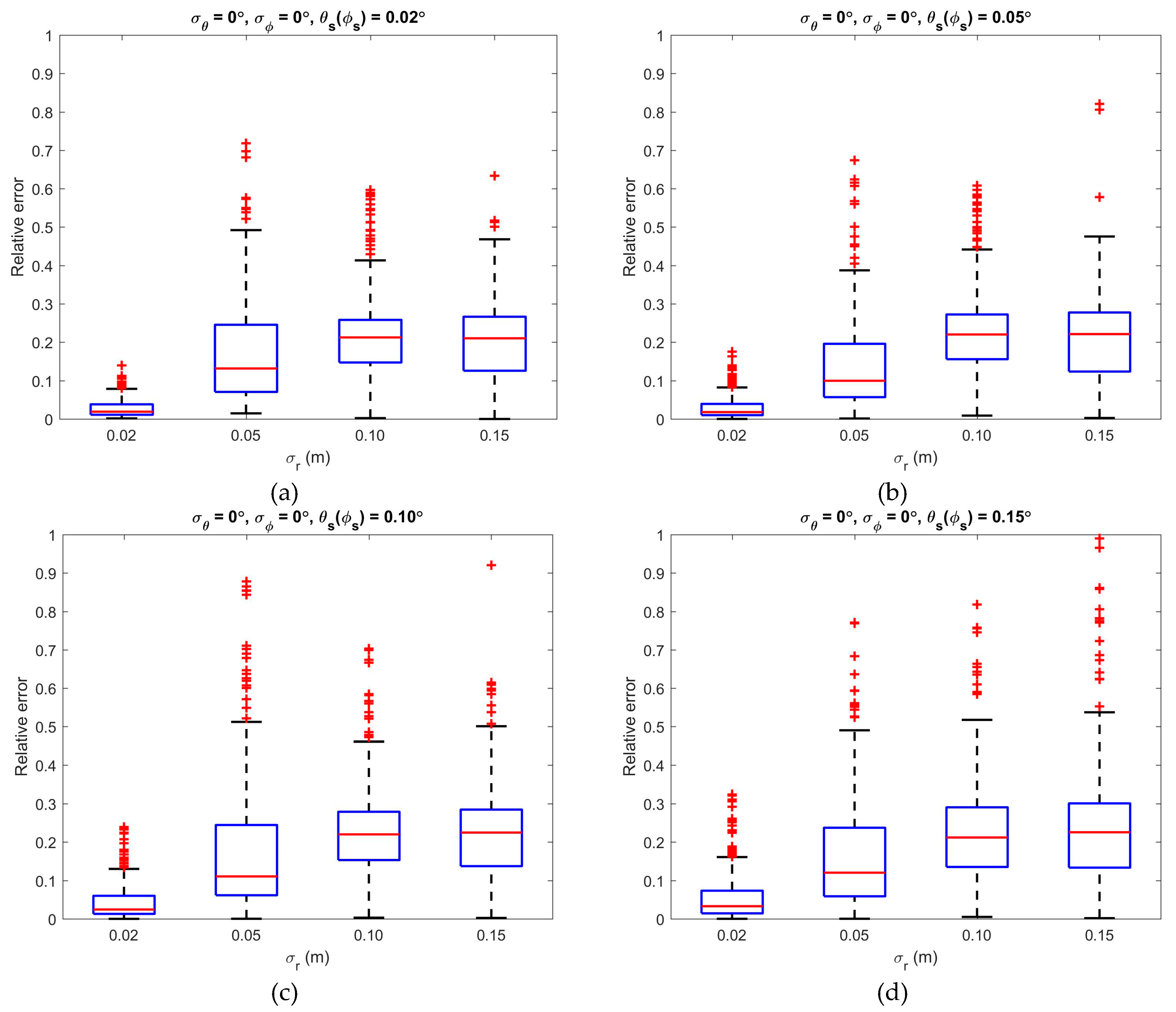
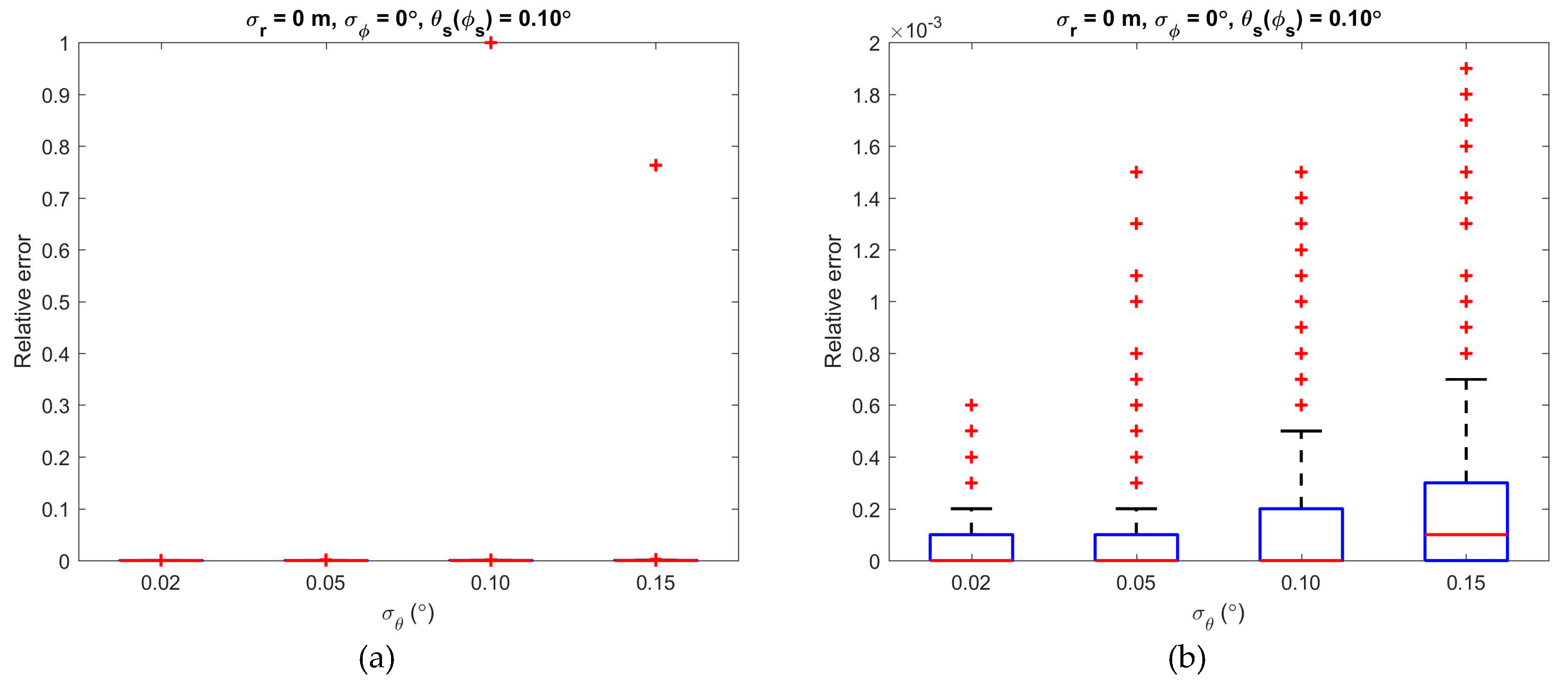
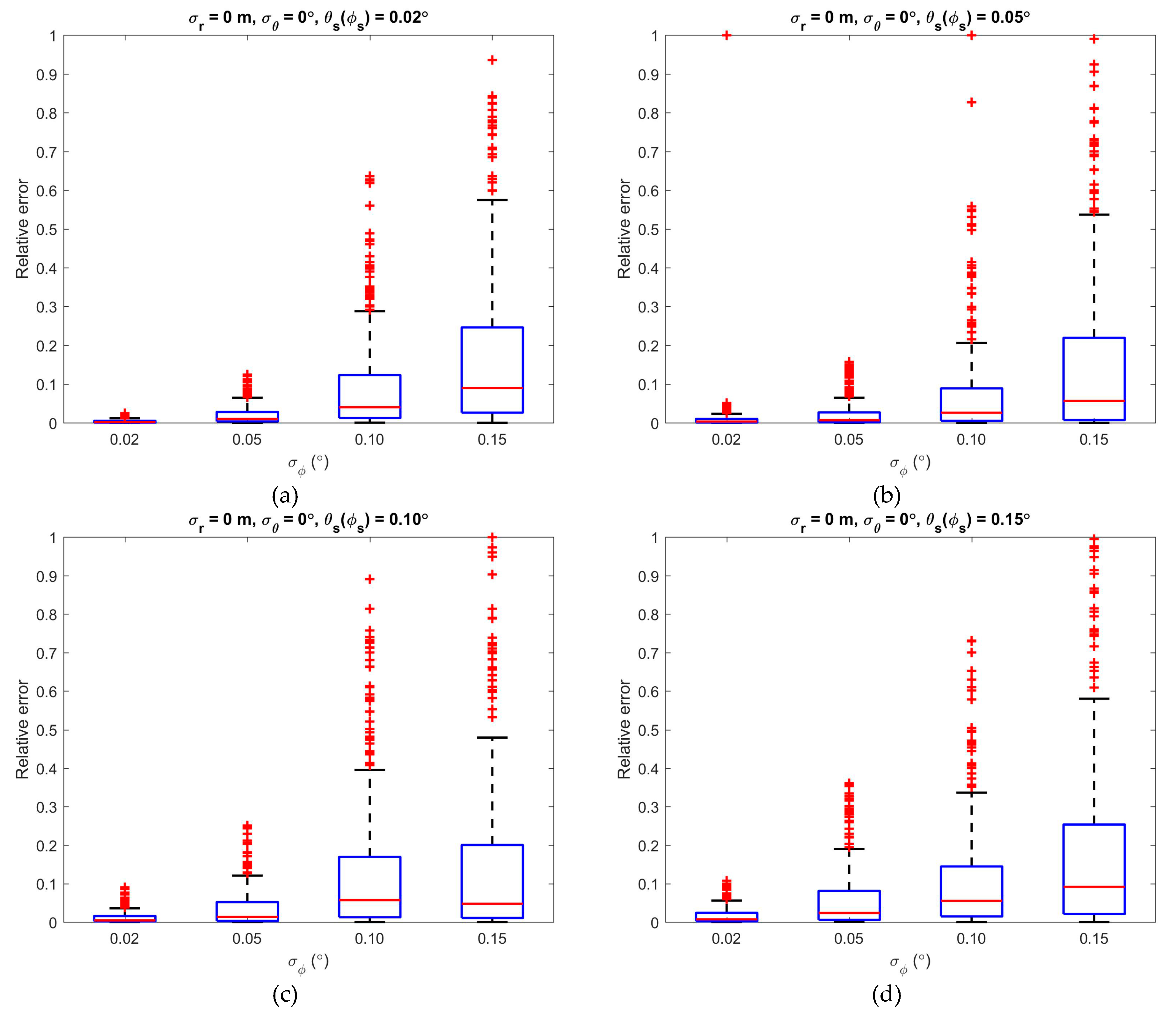
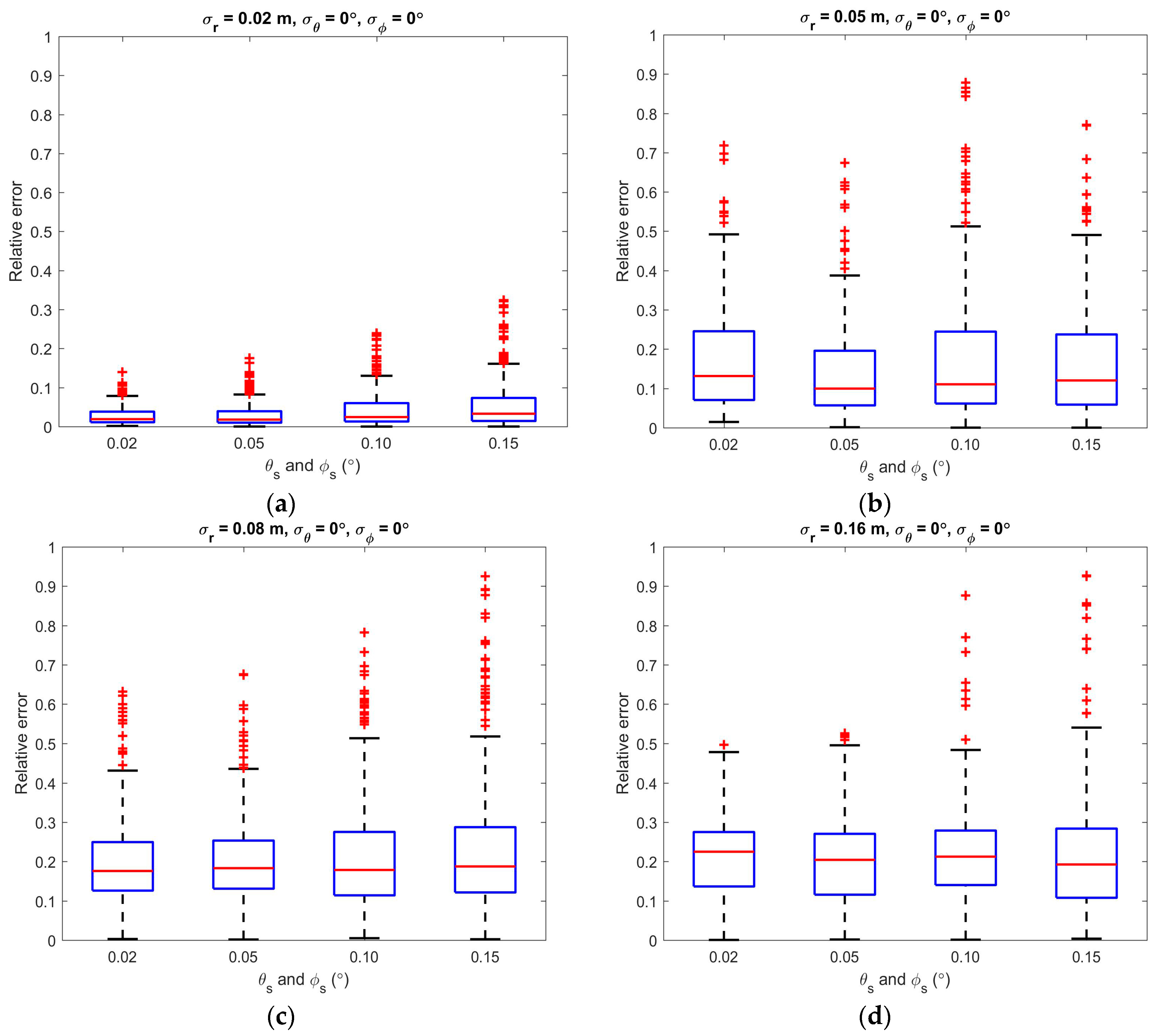
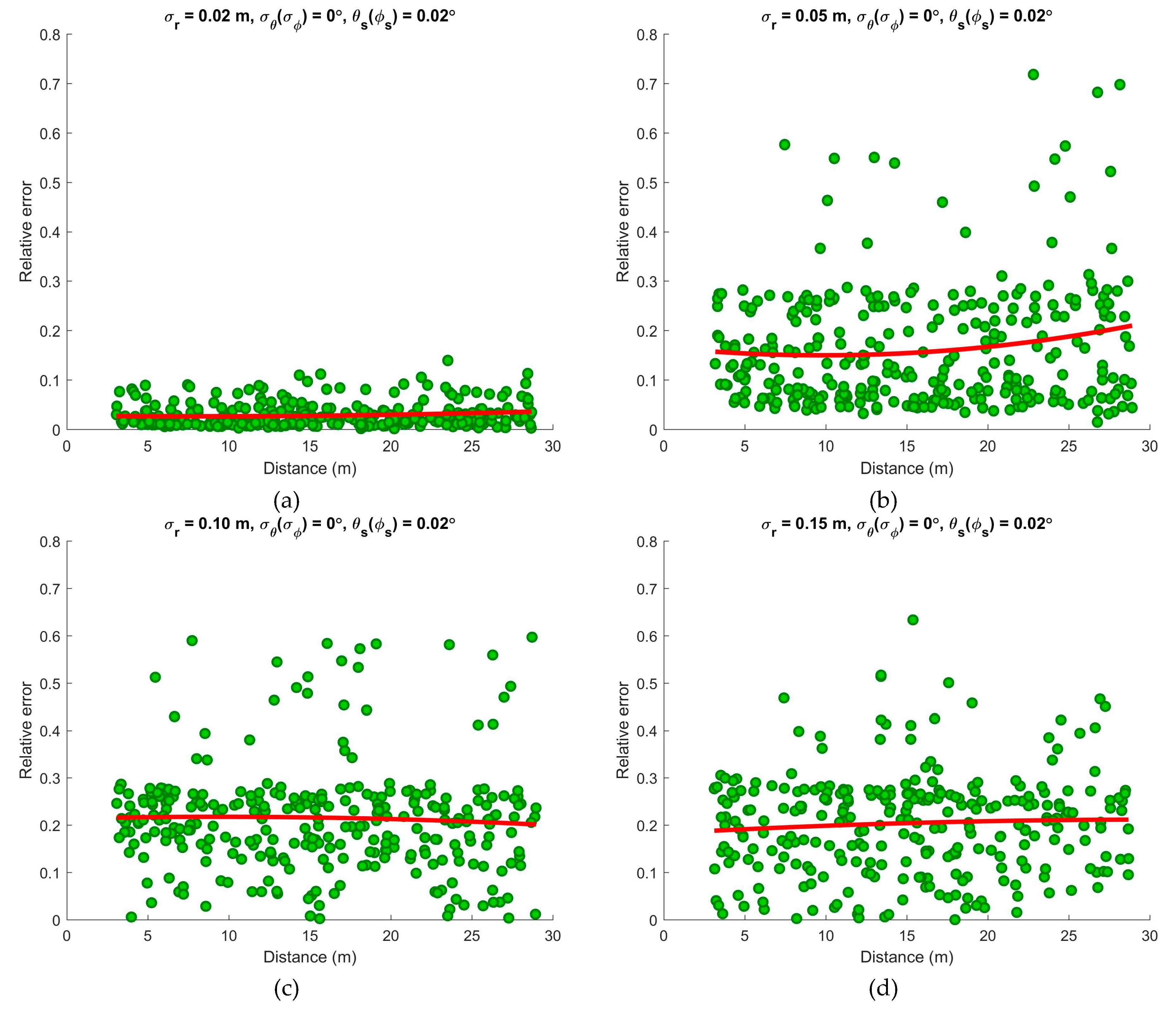
3.2. Impacts of the Error Parameters
3.3. Impacts of the Angular Step Widths
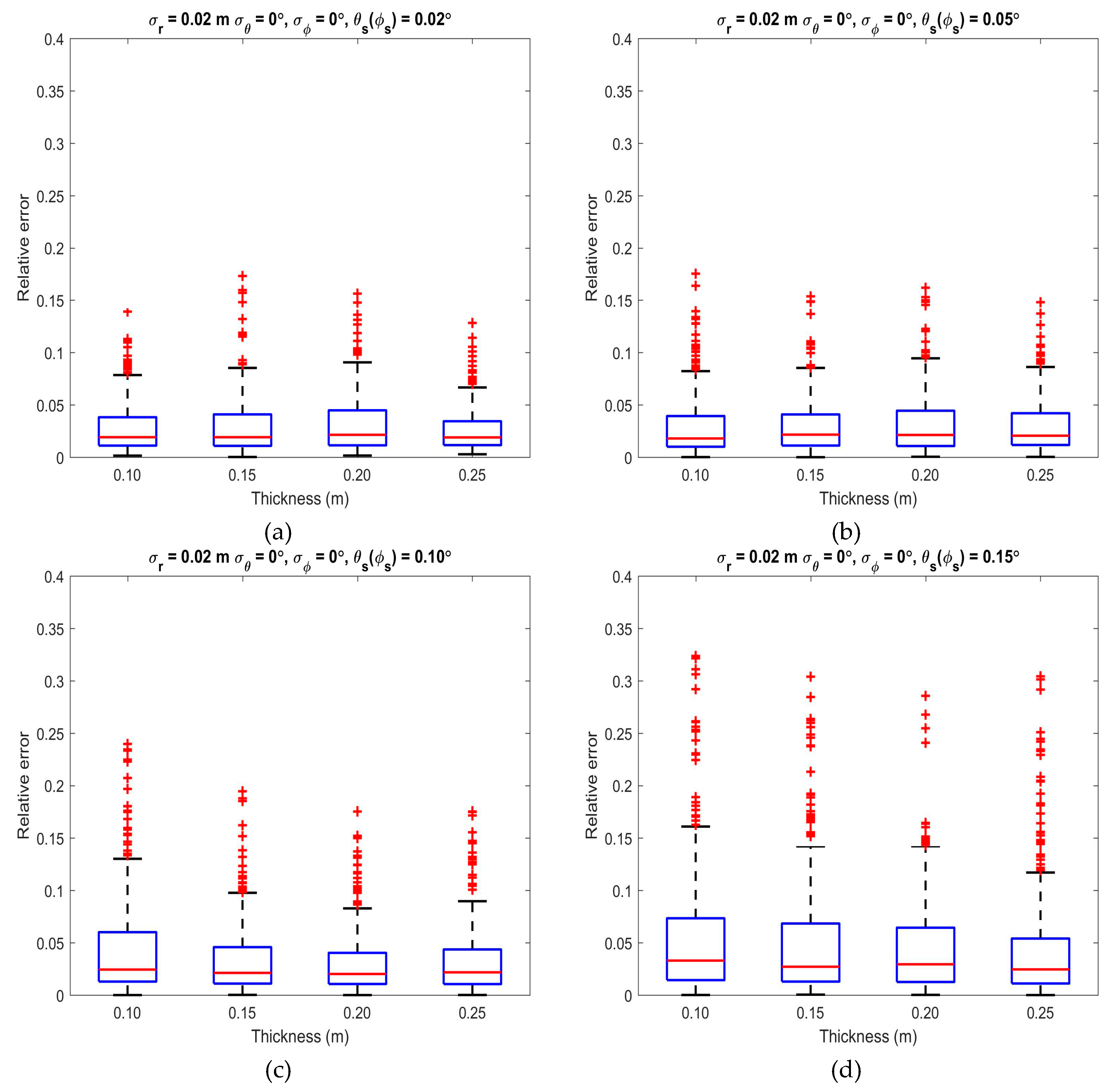
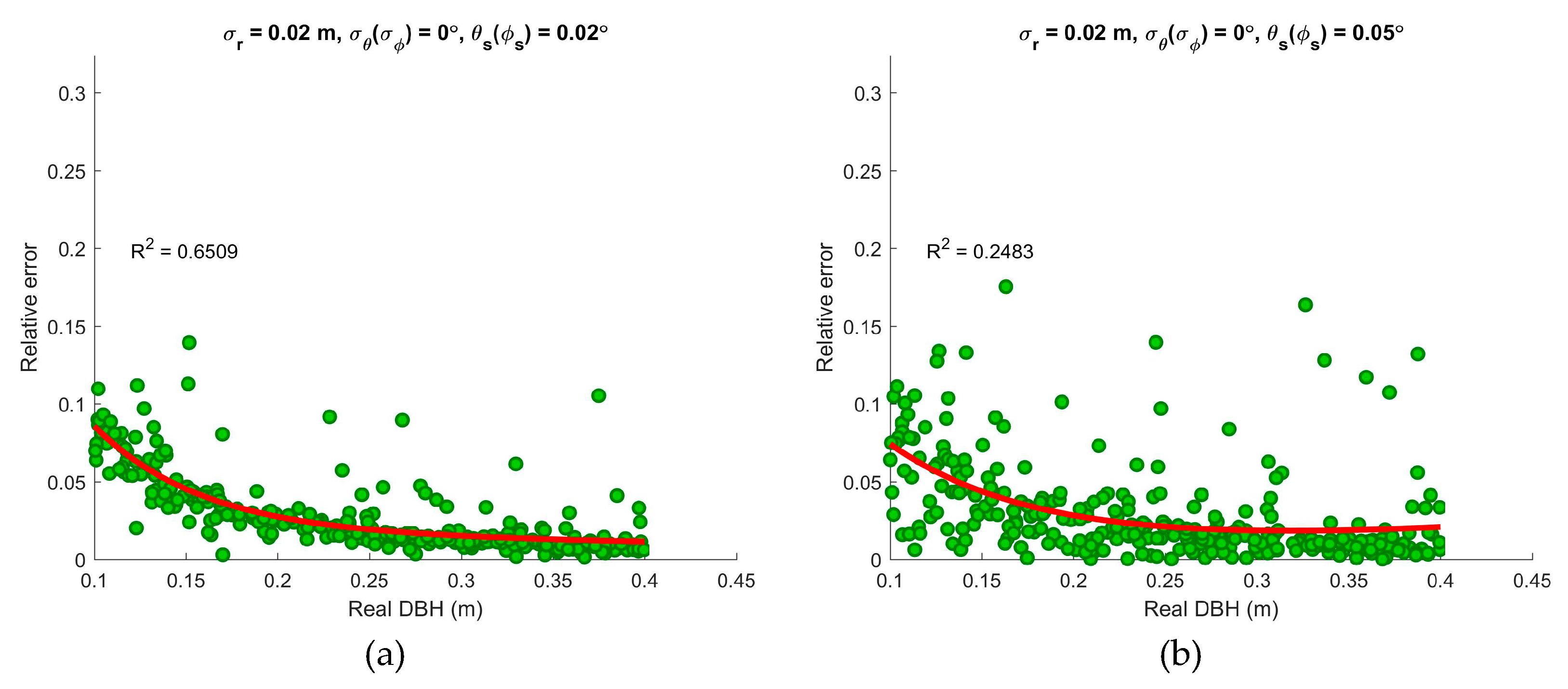
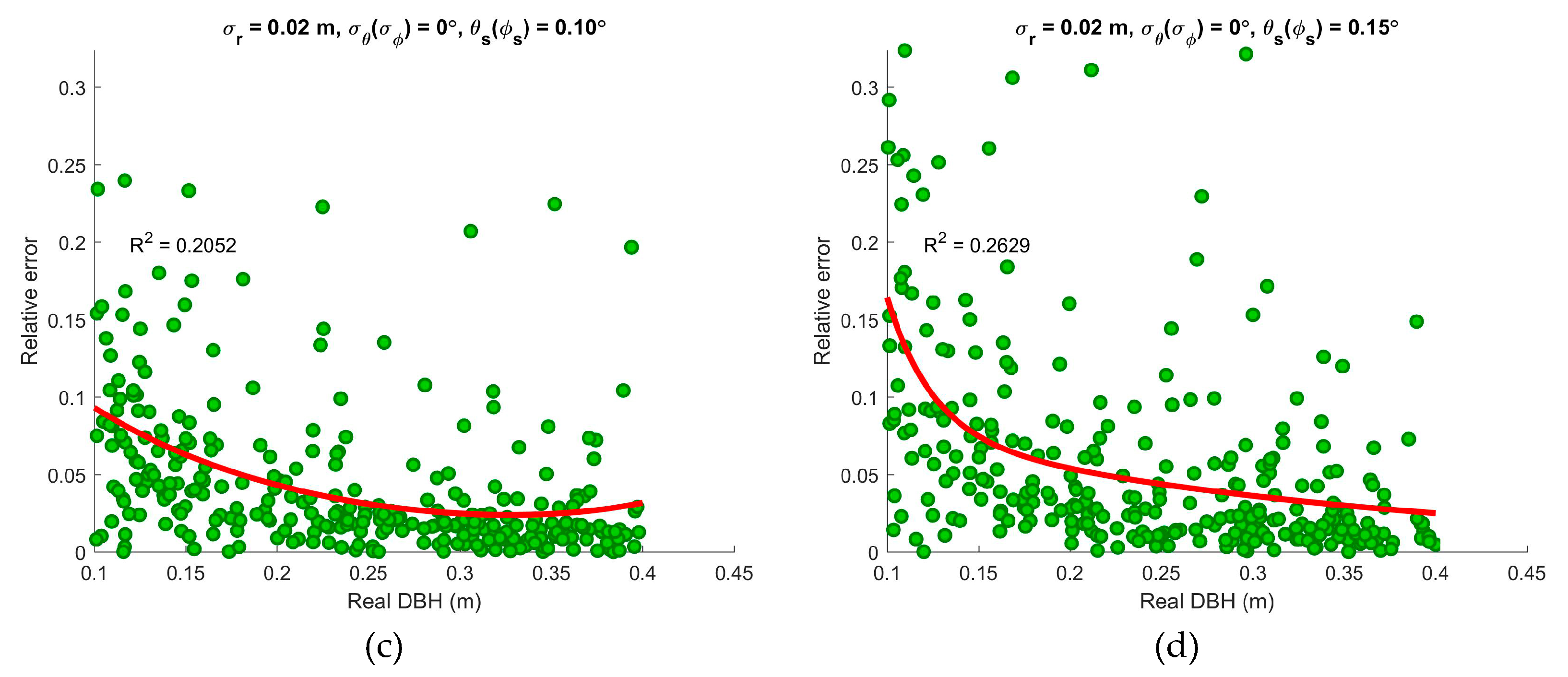
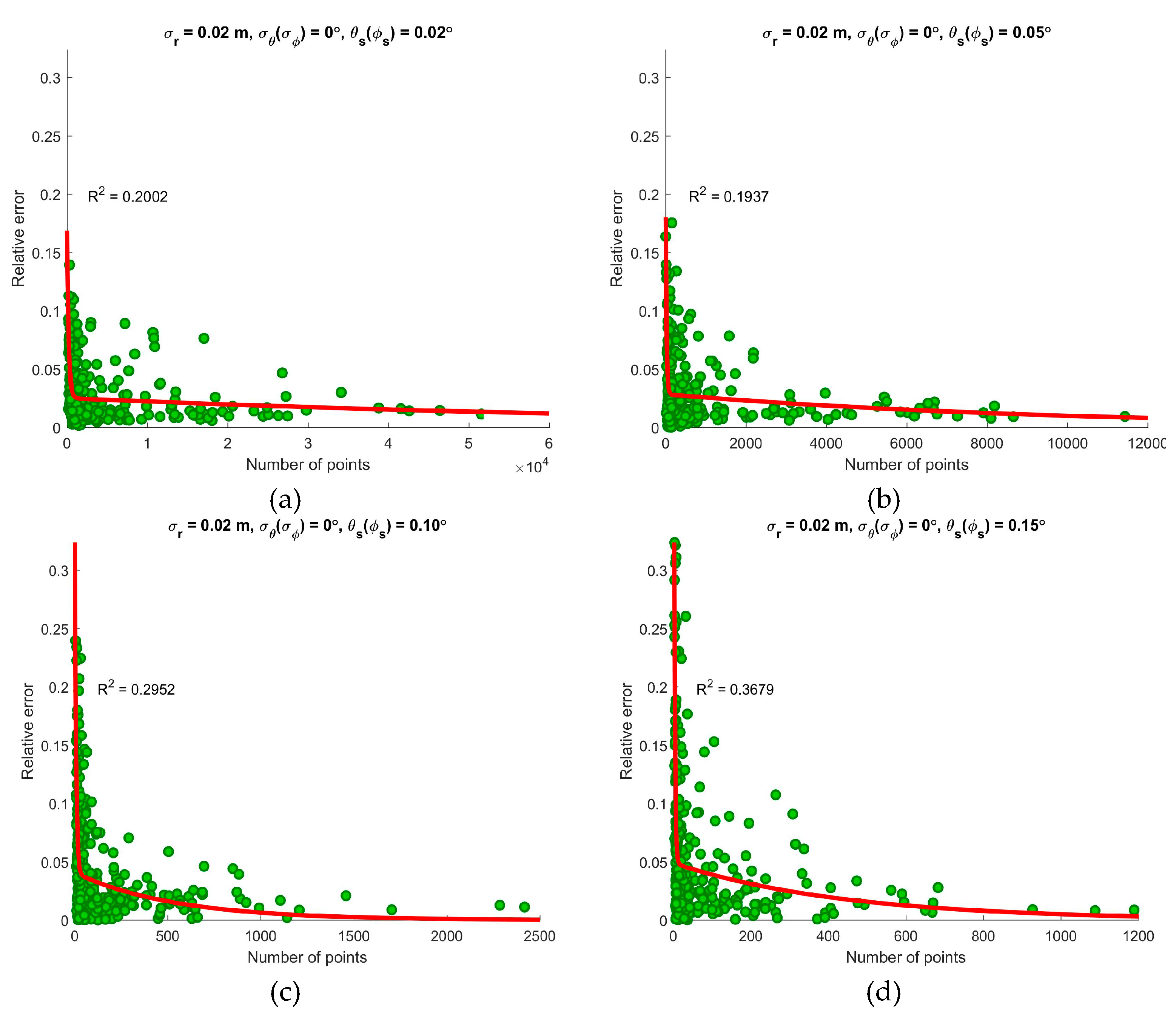
3.4. Impacts of the Slice Parameters
4. Discussion
4.1. Circle Fitting Methods
4.2. Error Parameters
4.3. Scanning Parameters
4.4. Slice Parameters
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Phillips, O.L.; Jackson, R.B. The Structure, Distribution, and Biomass of the World’s Forests. Annu. Rev. Ecol. Evol. Syst. 2013, 44, 593–622. [Google Scholar] [CrossRef]
- Maas, H.-G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Telenius, B.F. A software tool for standardised non-destructive biomass estimation in short rotation forestry. Bioresour. Technol. 1997, 60, 267–268. [Google Scholar] [CrossRef]
- Liang, X.; Litkey, P.; Hyyppa, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic Stem Mapping Using Single-Scan Terrestrial Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Lovell, J.L.; Jupp, D.L.B.; Newnham, G.J.; Culvenor, D.S. Measuring tree stem diameters using intensity profiles from ground-based scanning lidar from a fixed viewpoint. ISPRS J. Photogramm. Remote Sens. 2011, 66, 46–55. [Google Scholar] [CrossRef]
- Strahler, A.H.; Jupp, D.L.B.; Woodcock, C.E.; Schaaf, C.B.; Yao, T.; Zhao, F.; Yang, X.; Lovell, J.; Culvenor, D.; Newnham, G.; et al. Retrieval of forest structural parameters using a ground-based lidar instrument (Echidna®). Can. J. Remote Sens. 2008, 34, S426–S440. [Google Scholar] [CrossRef]
- Yao, T.; Yang, X.; Zhao, F.; Wang, Z.; Zhang, Q.; Jupp, D.; Lovell, J.; Culvenor, D.; Newnham, G.; Ni-Meister, W.; et al. Measuring forest structure and biomass in New England forest stands using Echidna ground-based lidar. Remote Sens. Environ. 2011, 115, 2965–2974. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing forest metrics with a ground-based scanning lidar. Can. J. For. Res. 2004, 34, 573–583. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree Stem and Height Measurements using Terrestrial Laser Scanning and the RANSAC Algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- De Tanago, J.G.; Lau, A.; Bartholomeus, H.; Herold, M.; Avitabile, V.; Raumonen, P.; Martius, C.; Goodman, R.C.; Disney, M.; Manuri, S.; et al. Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR. Methods Ecol. Evol. 2018, 9, 223–234. [Google Scholar] [CrossRef]
- Hansen, E.; Gobakken, T.; Bollandsås, O.; Zahabu, E.; Næsset, E. Modeling Aboveground Biomass in Dense Tropical Submontane Rainforest Using Airborne Laser Scanner Data. Remote Sens. 2015, 7, 788–807. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.-L.; Fournier, R.A.; Côté, J.-F.; Verstraete, M.M. Estimating leaf area distribution in savanna trees from terrestrial LiDAR measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Leaf Orientation Retrieval From Terrestrial Laser Scanning (TLS) Data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3970–3979. [Google Scholar] [CrossRef]
- Pesci, A.; Teza, G.; Bonali, E. Terrestrial Laser Scanner Resolution: Numerical Simulations and Experiments on Spatial Sampling Optimization. Remote Sens. 2011, 3, 167–184. [Google Scholar] [CrossRef]
- Bailey, B.N.; Ochoa, M.H. Semi-direct tree reconstruction using terrestrial LiDAR point cloud data. Remote Sens. Environ. 2018, 208, 133–144. [Google Scholar] [CrossRef]
- Forsman, M.; Börlin, N.; Olofsson, K.; Reese, H.; Holmgren, J. Bias of cylinder diameter estimation from ground-based laser scanners with different beam widths: A simulation study. ISPRS J. Photogramm. Remote Sens. 2018, 135, 84–92. [Google Scholar] [CrossRef]
- Kankare, V.; Liang, X.; Vastaranta, M.; Yu, X.; Holopainen, M.; Hyyppä, J. Diameter distribution estimation with laser scanning based multisource single tree inventory. ISPRS J. Photogramm. Remote Sens. 2015, 108, 161–171. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Pueschel, P.; Newnham, G.; Rock, G.; Udelhoven, T.; Werner, W.; Hill, J. The influence of scan mode and circle fitting on tree stem detection, stem diameter and volume extraction from terrestrial laser scans. ISPRS J. Photogramm. Remote Sens. 2013, 77, 44–56. [Google Scholar] [CrossRef]
- Pueschel, P. The influence of scanner parameters on the extraction of tree metrics from FARO Photon 120 terrestrial laser scans. ISPRS J. Photogramm. Remote Sens. 2013, 78, 58–68. [Google Scholar] [CrossRef]
- Bu, G.; Wang, P. Adaptive circle-ellipse fitting method for estimating tree diameter based on single terrestrial laser scanning. J. Appl. Remote Sens. 2016, 10, 026040. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Watt, P.J.; Donoghue, D.N.M. Measuring forest structure with terrestrial laser scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
- Kelbe, D.; Romanczyk, P.; van Aardt, J.; Cawse-Nicholson, K. Reconstruction of 3D Tree Stem Models from Low-Cost Terrestrial Laser Scanner Data; SPIE Defense, Security, and Sensing; Rochester Institute of Technology: Baltimore, MD, USA, 2013; p. 873106. [Google Scholar]
- Liang, X.; Kukko, A.; Kaartinen, H.; Hyyppä, J.; Yu, X.; Jaakkola, A.; Wang, Y. Possibilities of a Personal Laser Scanning System for Forest Mapping and Ecosystem Services. Sensors 2014, 14, 1228–1248. [Google Scholar] [CrossRef]
- Wang, P.; Li, R.; Bu, G.; Zhao, R. Automated low-cost terrestrial laser scanner for measuring diameters at breast height and heights of plantation trees. PLoS ONE 2019, 14, e0209888. [Google Scholar] [CrossRef]
- Chernov, N. Circular and Linear Regression: Fitting Circles and Lines by Least Squares; Taylor & Francis: Boca Raton, FL, USA, 2010; ISBN 978-0-429-15141-5. [Google Scholar]
- Lichti, D.D.; Jamtsho, S. Angular resolution of terrestrial laser scanners. Photogramm. Rec. 2006, 21, 141–160. [Google Scholar] [CrossRef]
- Lichti, D.D. A review of geometric models and self-calibration methods for terrestrial laser scanners. Bol. Ciênc. Geod. 2010, 16, 17. [Google Scholar]
- Product_Information_LMS5xx_Laser_Measurement_Technology_En_IM0038166.PDF. Available online: https://cdn.sick.com/media/docs/6/66/166/Product_information_LMS5xx_Laser_Measurement_Technology_en_IM0038166.PDF (accessed on 8 October 2019).



| Group No. | Purposes | ||||
|---|---|---|---|---|---|
| 1 | 0.02, 0.05, 0.10, 0.15 | 0 | 0 | 0.02 | Circle fitting methods, distance |
| 2 | 0.02, 0.05, 0.10, 0.15 | 0 | 0 | 0.02, 0.05, 0.10, 0.15 | Range error, angular step width |
| 3 | 0 | 0.02, 0.05, 0.10, 0.15 | 0 | 0.10 | Vertical angular errors |
| 4 | 0 | 0 | 0.02, 0.05, 0.10, 0.15 | 0.02, 0.05, 0.10, 0.15 | Horizontal angular errors |
| 5 | 0.02 | 0 | 0 | 0.02, 0.05, 0.10, 0.15 | Number of points, real diameters at breast height (DBH), scanning angular width |
| 6 | 0.02 | 0 | 0 | 0.02, 0.05, 0.10, 0.15 | Thickness |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Gan, X.; Zhang, Q.; Bu, G.; Li, L.; Xu, X.; Li, Y.; Liu, Z.; Xiao, X. Analysis of Parameters for the Accurate and Fast Estimation of Tree Diameter at Breast Height Based on Simulated Point Cloud. Remote Sens. 2019, 11, 2707. https://doi.org/10.3390/rs11222707
Wang P, Gan X, Zhang Q, Bu G, Li L, Xu X, Li Y, Liu Z, Xiao X. Analysis of Parameters for the Accurate and Fast Estimation of Tree Diameter at Breast Height Based on Simulated Point Cloud. Remote Sensing. 2019; 11(22):2707. https://doi.org/10.3390/rs11222707
Chicago/Turabian StyleWang, Pei, Xiaozheng Gan, Qing Zhang, Guochao Bu, Li Li, Xiuxian Xu, Yaxin Li, Zichu Liu, and Xiangming Xiao. 2019. "Analysis of Parameters for the Accurate and Fast Estimation of Tree Diameter at Breast Height Based on Simulated Point Cloud" Remote Sensing 11, no. 22: 2707. https://doi.org/10.3390/rs11222707
APA StyleWang, P., Gan, X., Zhang, Q., Bu, G., Li, L., Xu, X., Li, Y., Liu, Z., & Xiao, X. (2019). Analysis of Parameters for the Accurate and Fast Estimation of Tree Diameter at Breast Height Based on Simulated Point Cloud. Remote Sensing, 11(22), 2707. https://doi.org/10.3390/rs11222707







