In this section, the equivalence between the lifting scheme and the convolution in CNNs is first proven, extending the few wavelet bases that can be replaced with the lifting scheme to convolution kernels with random-valued parameters. With that, the relative lifting scheme is derived for a 1 × 3 convolution kernel as an example. Finally, we propose a novel lifting scheme-based deep neural network (LSNet), substituting the linear convolutional layers in CNNs with the nonlinear lifting scheme, demonstrating the superiority of the lifting scheme to introduce nonlinearity into the feature extraction module. The datasets used in the experiment are also described in this section.
2.1. Equivalence between the Lifting Scheme and Convolution
In the two-channel filter bank representation of the traditional wavelet transform, a low-pass digital filter
and a high-pass digital filter
are used to process the input signal
, followed by a downsampling operation with base 2, as shown in Equations (
1) and (
2).
The filter bank is elaborately designed according to requirements such as compact support and perfect reconstruction, while downsampling is used for redundancy removal. The low-pass filter is highly contacted with the high-pass filter. In other words, with the low-pass filter designed, the high-pass filter is consequently generated. Therefore, the wavelet bases of the first-generation wavelets are finite, restricted, and prefixed. In contrast, parameters of convolution kernels in CNNs are changing ceaselessly during backpropagation, which makes it necessary to expand the lifting scheme to be equivalent to a random-valued filter. In addition, to fit the structure of the convolutional layer, the detailed component generated by the lifting scheme is removed while the coarse component is retained in the following proof.
Consider a 1D convolution kernel represented by
. It is a finite impulse response (FIR) filter from the signal processing perspective, as only a finite number of filter coefficients are non-zero. The
z-transform of the FIR filter
is a Laurent polynomial given by
The degree of the Laurent polynomial
H(
z) is
In contrast to the convolution in the signal processing field [
32,
33], convolution in the CNN omits the reverse operation. The convolution between the input signal
and the convolution kernel
can be written as
where
represents the matrix of output feature maps. Operators “⊙” and “*” represent the cross-correlation and the convolution in the spotlight of digital signal processing, respectively, while
is the reversal signal of
. The
z-transform of Equation (
5) is
where
is the
z-transform of the reversal sequence
.
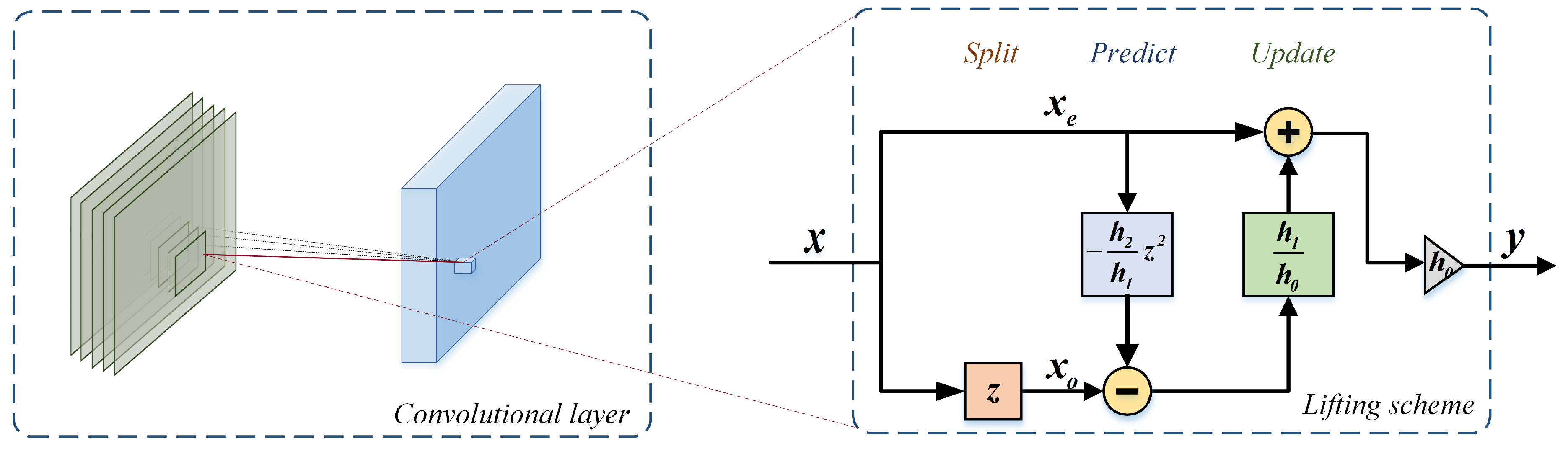
In the lifting scheme implementation of traditional wavelets, a common method in the split stage is splitting the original signal
into an even subset
and an odd subset
. Transforming the signal space to the
z-domain, the two-channel filter bank representation shown in Equations (
1) and (
2) is equivalent to Equation (
7), with
and
to represent the
z-transform of
and
.
and
are the
z-transform of
and
, which are the even subset and odd subset of
, respectively.
is the polynomial matrix of
and
:
where
and
are the
z-transform of the even subset
and the odd subset
of
, respectively, while
and
are the
z-transform of the even subset
and the odd subset
of
, respectively.
Different from the DWT in Equations (
1) and (
2), there is only one branch in the convolution in CNN, as shown in Equation (
6). To adapt to the particular form of the convolution in CNN, we maintain the low-pass filter
while discarding the high-pass filter
, and modify the polynomial matrix to preserve only the relative part of
, as in Equation (
9).
Instead of the lazy wavelet transform, we use the original signal
and a time-shift signal
as
and
in the first stage to obtain the same form as Equation (
6), as shown in Equation (
10).
Furthermore, the polynomial matrix
can be decomposed into a multiplication form of finite matrices and thus is completed by finite prediction and update steps. As mentioned above, both
and
are Laurent polynomials. If the following conditions are satisfied:
There always exists a Laurent polynomial
(the quotient) with
, and a Laurent polynomial
(the remainder) with
so that
Iterating the above step,
is then decomposed. As convolution kernels frequently used in CNN are commonly oddly size, such as 1 × 3, 3 × 1 [
34], 3 × 3, 5 × 5, the above conditions are generally satisfied. Comparing Equation (
6) with (
10), we reach a conclusion that convolution in CNN, which is with random-valued parameters, has equivalent lifting scheme implementation.
2.3. Lifting Scheme-Based Deep Neural Network
In this section, the lifting scheme is introduced into the deep learning field, and a lifting scheme-based deep neural network (LSNet) method is proposed to enhance network performance. From
Section 2.1 and
Section 2.2, the lifting scheme can substitute the convolutional layer because it can perform convolution and utilize backpropagation to update parameters. Specifically, operators in the lifting scheme are flexible, which can be designed not only to make the lifting scheme equivalent to vanilla convolutional layers but also extended to meet other requirements. Thus, we develop the LSNet with nonlinear feature extractors utilizing the ability of nonlinear transformation of the lifting scheme.
2.3.1. Basic Block in LSNet
Nonlinearity enables neural networks to fit complex functions and thus strengthens their representation ability. As the lifting scheme is capable of constructing nonlinear wavelets, we introduce nonlinearity into the feature extraction module to build the LSNet. It is realized by designing nonlinear predict and update operators in the lifting scheme, which demonstrates the enormous potential of the lifting scheme to perform nonlinear transformation and enhance the nonlinear representation of the neural network.
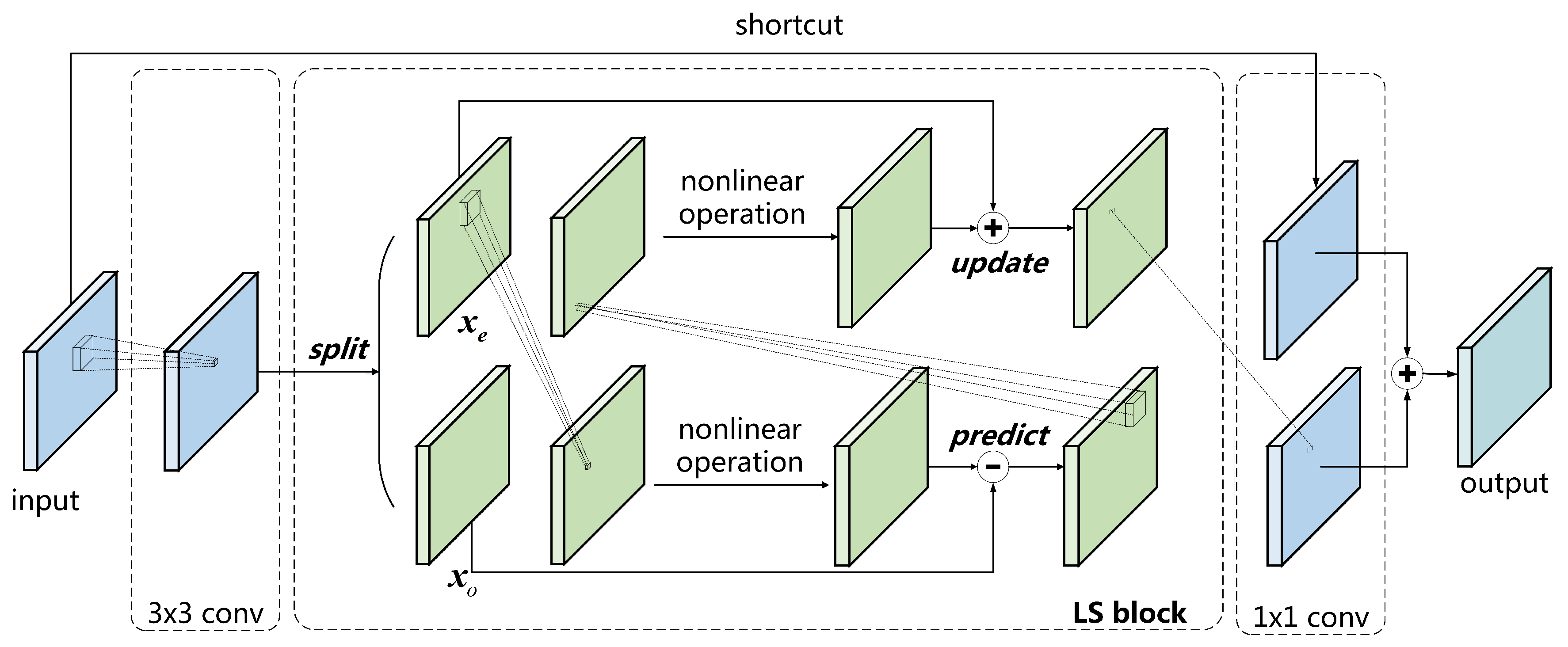
We construct the basic block in LSNet based on ResNet34 [
35], as shown in
Figure 3. The first layer in the basic block is a 3 × 3 convolutional layer, which is used to change the number of channels and downsampling. The middle layer is the LS block, mainly for feature extraction, with the same number of channels between the input and the output. The plug-and-play LS block is used to substitute the vanilla convolutional layer without any other alterations. In the LS block, the input is split into two parts, including
and
. The nonlinear predict operator and update operator are constructed by a vanilla convolution kernel followed by a nonlinear function.
is then predicted by
to gain the detailed component, which is discarded after the update step.
is updated by the detailed component, the outcome of which is the coarse component and used as the final output of the LS block. Finally, we add a 1 × 1 convolutional layer as the third layer to enhance channel-wise communication. Batch normalization and ReLU are followed by the first two layers for overfitting avoidance and activation, respectively. The identity of the input through a shortcut is added to the output of the third layer, followed by batch normalization. The addition outcome is again activated by ReLU, which is the final output of the basic block.
As both the 1D and 2D convolutional layers are widely used, we propose the 1D and 2D LS block, named the LS1D block and LS2D block, respectively. The specific processes of which are illustrated in
Table 2.
Note that and denote the nonlinear transformation in the predict step and the update step, respectively. PconvnD and UconvnD represent the vanilla nD convolution operation in the predict and the update step, respectively. The operators {PconvnD} and {UconvnD} are the prediction and update operators, respectively, which are changeable to meet other requirements.
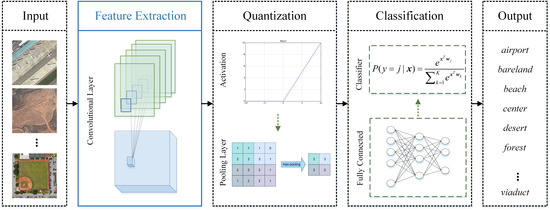
2.3.2. Network Architecture and Settings
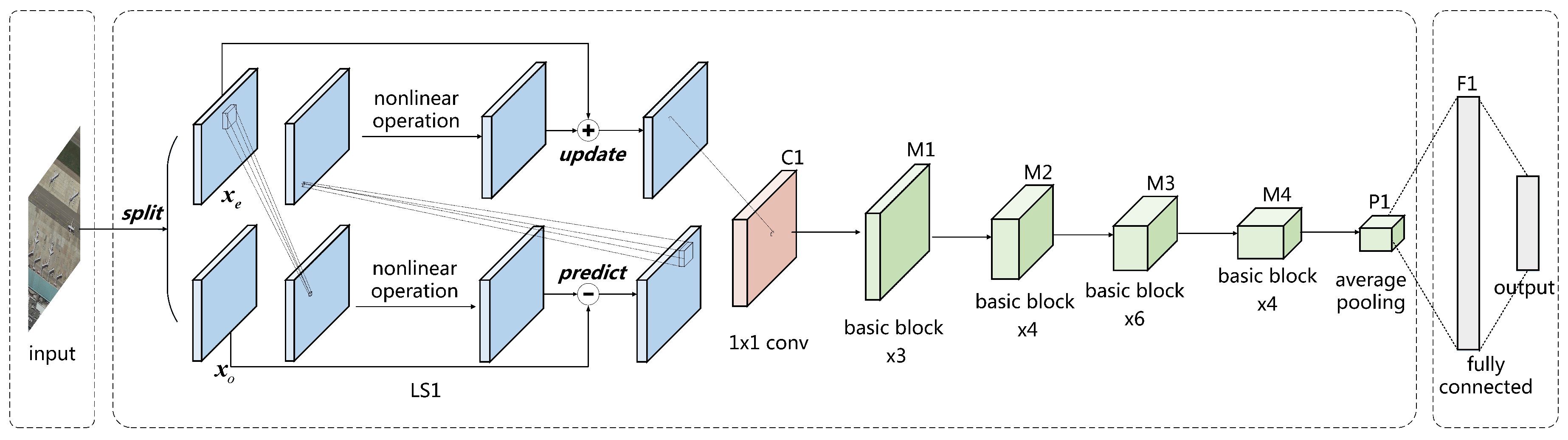
The network architecture of LSNet is shown in
Figure 4. The input of LSNet passes through a single LS block and a 1 × 1 convolutional layer for initial feature extraction. The feature maps are then processed by stacked basic blocks to obtain low dimension image representation, which is followed by an average pooling for dimension reduction. Finally, the representation is unfolded as a 1D vector, and processed by a fully connected layer and a softmax function to obtain the output.
The modified ResNet34 is chosen as the baseline model to evaluate the performance of LSNet. Experiments are separately conducted for the 1D convolution and the 2D convolution, as both are widely used. The setups of each network are listed in
Table 3.
In
Table 3, the size and the number of convolution kernels in vanilla convolutional layers are listed. For LSNet, the structure of the LS1D block and LS2D block are shown in
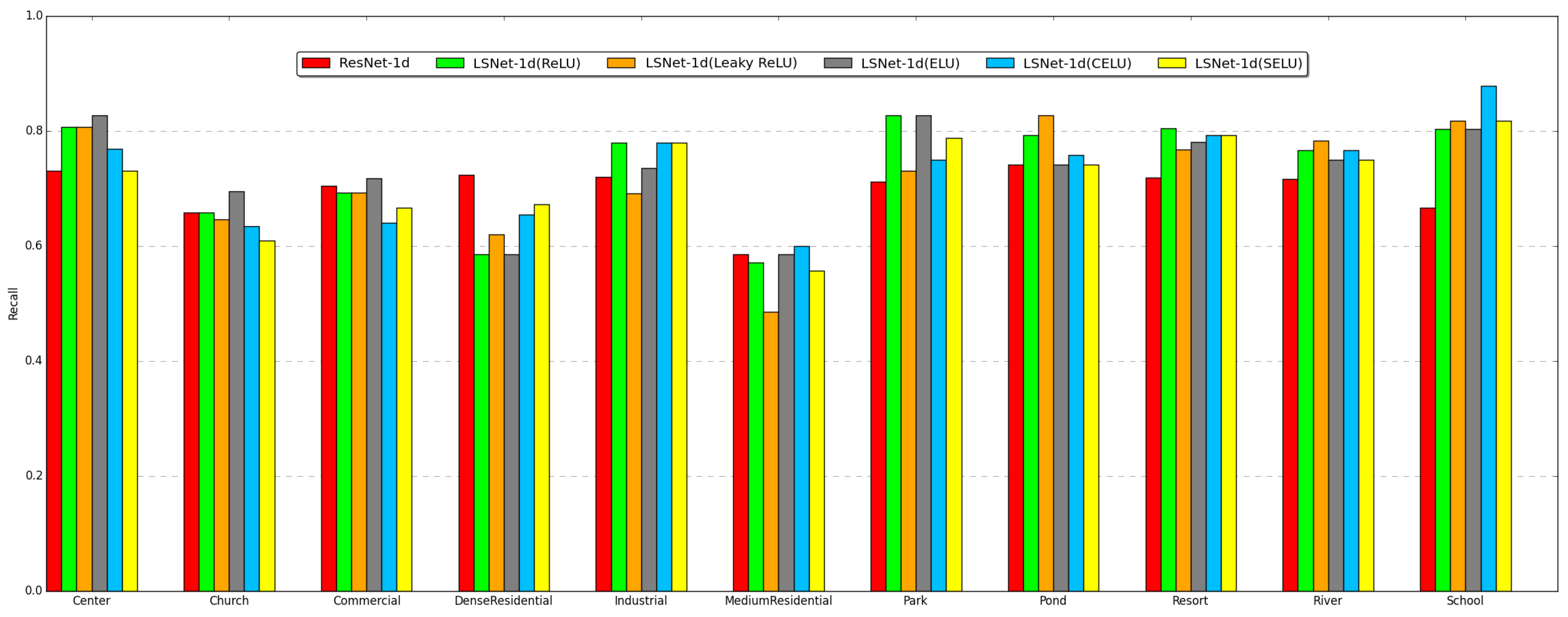
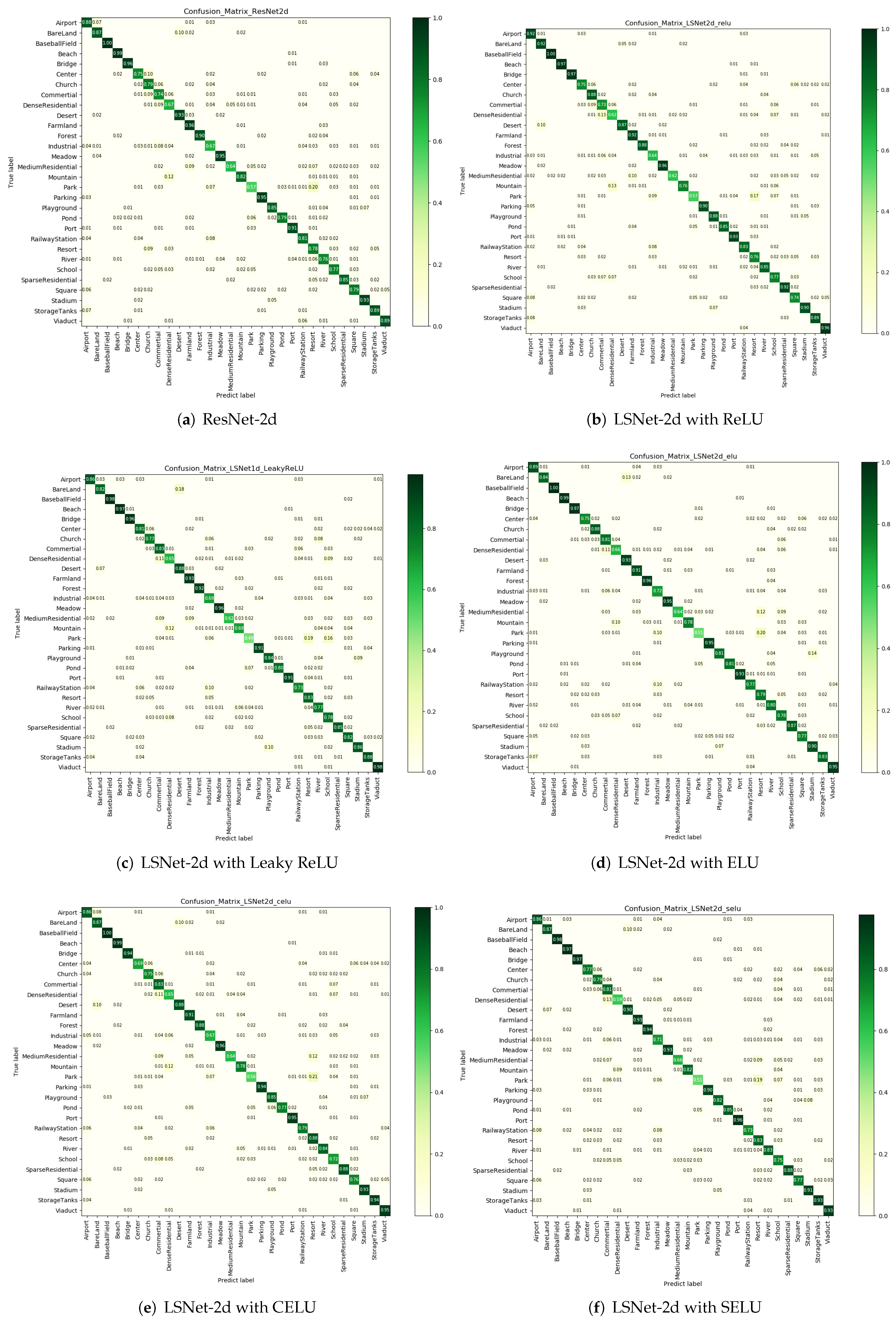
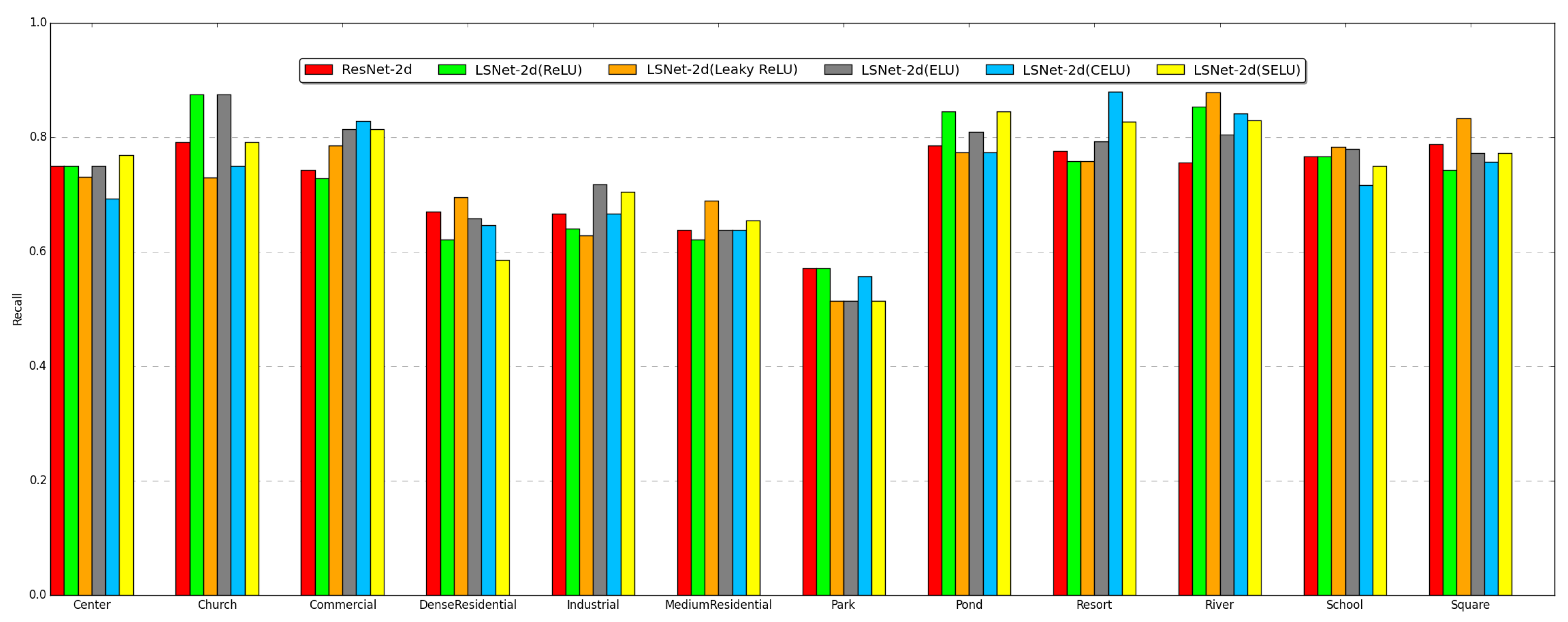
Table 2, while the number represents the depth of the output. To demonstrate the effect of nonlinearity, we use five different nonlinear functions to construct different LS blocks to compare the performance, which are ReLU [
3], leaky ReLU [
4], ELU [
5], and CELU and SELU [
6].
In the experiment on the AID dataset, we use the stochastic gradient descent (SGD) as an optimizer, with a momentum of 0.9 and a weight decay of . We train the training set for 100 epochs, setting the mini-batch size as 32. The learning rate is 0.01 initially, which decreases by 5 times every 25 epochs. For the CIFAR-100 dataset, all the settings are the same except that the mini-batch size is 128, and the initial learning rate is 0.1.
2.4. Materials
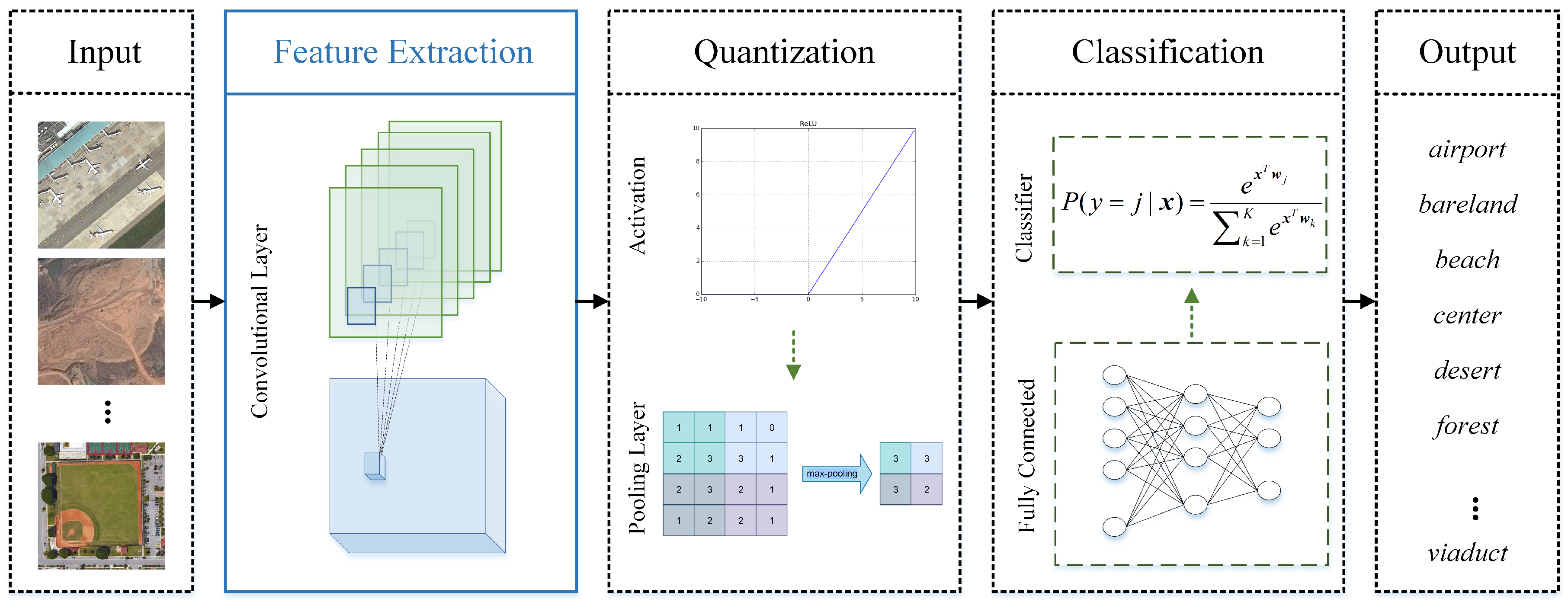
LSNet is firstly validated using the CIFAR-100 dataset [
36], which is one of the most widely used datasets for deep learning reaches. Then, we conduct experiments on the AID dataset [
37] to demonstrate the effectiveness of LSNet on the scene classification task.
CIFAR-100 dataset: This dataset contains 60,000 images, which are grouped into 100 classes. Each class contains 600 32 × 32 colored images, which are further divided into 500 training images and 100 testing images. The 100 classes in the CIFAR-100 dataset are grouped into 20 superclasses. In this dataset, a “fine” label indicates the class to which the image belongs, while a “coarse” label indicates the superclass to which the image belongs.
AID dataset: The AID dataset is a large-scale high-resolution remote sensing dataset proposed by Xia et al. [
37] for aerial scene classification. With high intra-class diversity and low inter-class dissimilarity, the AID dataset is suitable as the benchmark for aerial scene classification models. Thirty classes are included, each with 220 up to 420 600 × 600 images. In our experiment,
images of each class are chosen as the training data, while the rest
are chosen as testing data. Each image is resized to 64 × 64. Some samples of the AID dataset are shown in
Figure 5.