1. Introduction
Transmission line inspection and maintenance are crucial aspects of power resource management [
1]. A power transmission corridor generally includes high-voltage (HV) towers, attachments (e.g., insulators), and transmission wire, as well as vegetation, buildings, and other environmental objects on the ground. As an important part of the transmission system, HV towers not only play a mechanical supporting role for the long-distance conductor, but also serve as the nodes of connections or turning points, realizing large-scale deployment of power resources over a long distance. Similarly, as the pipeline for electric power, transmission wires are important carriers of power resources. Key power transmission elements like HV power pylons and wires are joined together and connected with isolators. They are mostly located in remote environments with harsh terrains, e.g., deep forests, which require great effort to maintain. To guarantee the safety and reliability of power transmission systems, power companies have to ensure that these components maintain sufficient safety margins from the surroundings. One routine risk-management job is power corridor inspection. Traditionally, inspections of the HV transmission corridors have mainly relied on laborious and dangerous human work using aerial- and ground-based devices (e.g., telescopes and video/infrared cameras) [
2]. Corridor inspections by these traditional techniques are neither efficient nor effective, as the subjective judgements rely heavily on experience.
As an important part of remote sensing, airborne remote sensing is an efficient and flexible technology to obtain large-coverage, high-precision measurements compared to ground-based techniques. The up-to-date airborne remote-sensing data mainly include synthetic aperture radar images, optical images, thermal images, and laser scanning point clouds [
3]. Compared to aerial images, light detection and ranging (Lidar), or laser scanning data, in the form of point clouds, provide the spatial coordinates of objects in 3D with higher accuracy [
4,
5]. Information on intensity and multi-return echoes is often available. By using Lidar, the 3D surface information of observed objects, such as their geometric structure and semantic information, can be effectively derived [
6,
7]. Airborne Lidar inspection of the transmission corridor at close range enables the detection of detailed condition information of the power corridor in 3D, such as the accurate geometry of power lines and spatial distribution of pylons [
8]. Their risk states can then be analyzed by a series of construction, modeling, and assessment, which contributes to the corridor’s safety maintenance [
9].
The use of unmanned aerial vehicles (UAVs) carrying new sensors for electric power inspection has been developed largely since the end of the 20th century [
10]. Given that the HV power line (PL) facilities in remote or harsh environments are generally difficult to reach, UAV mapping presents huge advantages by saving manpower and producing more reliable results. UAV systems have been increasingly used by communities due to their low cost, less strict requirements for take-off and landing, and their ability to load different types of sensors (e.g., camera and Lidar) [
11]. As a light-weight and close-range airborne laser scanning (ALS) technology, UAV Lidar, usually equipped with middle-sized or small laser sensors, has been rapidly developed for transmission line inspection as a time-saving and cost-friendly solution. It can directly generate dense point clouds in 3D with a higher level of precision compared to aerial optical imagery and video [
5,
12,
13], because image-based techniques can produce noisy results from the stereo-matching stage [
14]. According to comparative studies of power line monitoring, the accuracy of height estimation for poles and trees is clearly better when using UAV Lidar data than aerial images [
4,
15]. Compared to robotic inspection [
16], UAVs have higher flexibility and larger coverage. UAV Lidar is also used for monitoring the vegetation around PLs, which has generally not been paid as much attention as direct monitoring of the power line components [
3]. Some other studies have concentrated on the integration of ALS data and aerial images [
17,
18].
Nevertheless, the irregular distribution and complexity of Lidar data make it challenging to detect anomalies in power transmission objects and their surroundings without knowing their spatial relationships [
19,
20]. Therefore, one must first extract transmission wires and HV pylons from the rest of the point cloud and distinguish them from the environmental elements. To provide comprehensive guidance for facility maintenance, a thorough UAV Lidar processing method of UAV Lidar inspction data was demonstrated in this paper, including the precise extraction of transmission lines, the 3D localization of pylons, the accurate detection of insulators, and the modeling of power transmission components.
2. Related Work
Research in transmission circumstance analysis involves both the classification of point clouds to extract transmission elements [
16,
21,
22,
23,
24,
25,
26] and their reconstruction for safety analysis [
27,
28,
29,
30,
31]. Methods and algorithms aiming at processing power transmission inspection data have bloomed in recent years, including both image and Lidar data acquired from various types of platforms, e.g., terrestrial laser scanning (TLS), ALS [
32], and inspection robots [
16].
The image-based methods mainly focus on the extraction of PLs. Song et al. [
33] proposed a sequential local-to-global power line detection algorithm using morphological filtering and a graph-cut model to detect PLs. Zhu et al. [
22] proposed a method based on statistical analysis and two-dimensional (2D) image processing to automatically extract PLs from ALS data. Fryskowska [
34] presented a wavelet-based method to improve the extraction of PLs from low-cost imagery. However, image-based techniques can sometimes produce noisy results [
35]. Instead of PL extraction using imagery data, methods of extracting 3D objects from point clouds have obtained more comprehensive spatial contents, e.g., coordinate, shape, and spatial distribution properties of power transmission elements [
36,
37].
Many researchers have studied the extraction of power transmission objects from point cloud data. Melzer and Briese [
27] proposed a Hough transform (HT)-based automatic transmission conductor extraction method. Lidar points were separated by a rule-based classification considering HT. Nasseri et al. [
38] combined HT with a particle filter to detect PLs. Liu and Liang [
39] proposed an automatic PL extraction method based on space-domain segmentation. Jwa and Sohn [
40] used a voxel-based piece-wise line detector method and detected the PL orientation to identify the PL points. The above-mentioned methods extract the candidate PL points in the beginning, so the final detection quality is greatly influenced by the candidate PL extraction. Kim and Sohn [
41] developed a supervised classification using a random forest classifier. Guo et al. [
42] designed a classification method using the joint boost classifier. Zhou et al. [
43] combined the joint boost method with some multiscale features to classify HV-bundled conductors. These knowledge-based classifications were sensitive to the scene diversity and the success rate was affected by factors such as data gaps, despite the high classification rate. Cheng and Tong [
25] extracted transmission lines through the connectivity analysis of 3D hierarchical voxels. Chen et al. [
2] segmented the PL points based on dimensional features, utilizing a height histogram to obtain a relatively accurate separation interface. However, most of these methods require the filtering terrain points in the preprocessing stage, so they can be limited by terrain-filtering algorithms.
On the other hand, a range of results have been presented for the detection and modeling of pylons. Araar et al. [
44] employed monocular depth estimation to recognize and reconstruct pylons. Tilawat et al. [
45] utilized serialized images to detect the locations of pylons. In this method, non-electric-transmission objects were separated by a global threshold, which cannot be easily applied to data covering large scenes with topographic fluctuations or with a wide range of mountainous areas in complex natural environments. Sohn et al. [
31] proposed a detection method that provided individual pylon locations by Markov random field. Awrangjeb et al. [
46] and Ortega et al. [
47] proposed unsupervised extraction methods based on 2D-mask and linear rectification of PLs and pylons. However, tall, highly dense trees in the environment affected the recognition of power towers. Li et al. [
48] and Guo et al. [
49] constructed pylons from a library of 3D parametric models using polyhedrons based on stochastic geometry. Zhou et al. [
50] used a heuristic method to reconstruct pylons for power pylons widely used in high-voltage transmission systems from an airborne Lidar point cloud, which combined both data-driven and model-driven strategies. Lin and Zhang [
51] identified the exact position of each pylon by providing accurate 2D information of all pylons as a priori knowledge. Basically, different types of a priori knowledge (e.g., horizontal coordinates, PL structure types with respect to power voltage, multiple echoes over the PLs) of the approximate positions were used to classify pylon points from ALS data. However, due to the irregular distribution of PL points, some proposed approaches have been limited in applicability to other cases [
52,
53].
Overall, the most widely used strategy in the classification and extraction of power elements is to first remove ground points by filtering, so the remained non-ground points are mainly from PLs, towers, poles, and other ground objects, such as vegetation, buildings, etc. To identify the target of power elements from the filtered data, it is necessary to identify each single target from the group of non-ground points, mainly using linear features or features like large local height difference and high point density. Graphical segmentation has also been used for improvement in some methods [
25,
54].
In consideration of the existing limitations, an automatic method is proposed herein to extract transmission corridor objects from UAV Lidar point clouds and reconstruct 3D models for corridor safety maintenance. First, after noise removal without ground-point filtering, a 5 × 5 m 2D gridding in the horizontal plane was processed to calculate grid-level features. The point cloud was then subdivided into numerous blocks of 3D grids (i.e., voxels) using an improved spatial hash structure to facilitate subsequent steps. Using features of grid points in 3D blocks, the preliminary extractions of HV PLs and pylons were carried out. The extraction results were then optimized and refined according to the connectivity between the transmission components. Next, vector curves were fitted with the extracted PL points, and towers and their insulators were reconstructed after calculating the precise center point of each HV pylon. The final reconstructions could be used to determine the areas of potential hazard points, and to provide data support for the subsequent safety analysis.
The advantages of the proposed method include the following: (1) a sparse grid method is used to store and manage accumulated points in the spatial hashing matrix, which subdivides space effectively, allowing quick access; (2) there is no need for precise and complex ground-point filtering in the preprocessing, as the data after removing noise points by a statistical method are directly fed into the following steps; (3) the extractions of pylons and lines do not need any priori information; (4) the extraction precision is high in both plain and mountainous areas; (5) each pylon is reconstructed as a whole model and detailed by the modeling of insulators.
3. Method
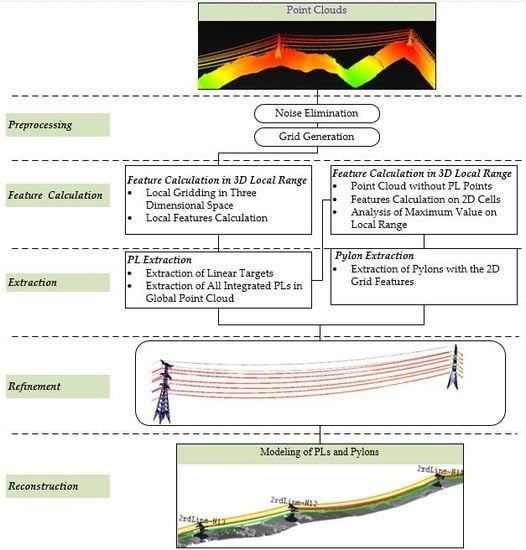
Figure 1 illustrates the whole workflow of the proposed method, which consists of five steps: data preprocessing, feature calculation, object extraction, optimization, and reconstruction.
Preprocessing. The first step is to remove the sparse noisy points and divide the data into grids at different levels. First, 5 × 5 m2 grids were constructed in the 2D horizontal plane considering the horizontal diameter of HV pylons, then were further divided into 0.5 m3 voxels for detailed analysis. The grid structure contains not only the point set within its range, but also grid features including the values of height difference, inclination, and point density within the grid.
Dimensional feature generation. Based on the analysis of several geometrical distribution features of transmission lines locally (linear, parallel, consistent) and globally (elongate), PLs were extracted using 3D grid features; four further features were then extracted based on 2D grids, i.e., large height difference, continuous height distribution, local extremely high value, and limited range in planar projection map, were calculated to differentiate pylons and poles from the other objects.
Extraction of individual lines and towers. First, PL segments were labeled based on the local linear geometric distribution in 3D. Consecutive PL segments were then merged as PL candidates. Next, the HV pylons were detected using the 2D grid features calculated above within the whole strip of the scanned transmission corridor.
Optimization. The preliminary result was optimized by a feature of positional relationship between the HV towers and PLs in the 3D space, on the basis that they successively connect to each other around individual lines at the point of attachment (POA) [
40].
Reconstruction. The 3D PL was modeled using a 2D line in a projected ground plane and a catenary curve in the vertical plane that is perpendicular to the projection plane. The pylons were constructed by fitting with models from an existing library.
3.1. Preprocessing
Traditional point cloud data management and search methods are often computationally costly [
55,
56]. Therefore, in this paper, PLs were segmented by means of data partitioning based on a memory- and computing-efficient data structure.
Planar compression and hash storage scheme: The voxel grid was set as the unit to organize by the hashing storing scheme, which contains the index of all voxels. The spatial hash [
57,
58,
59,
60,
61,
62,
63] data structure dealt with the voxels of observed space by marking them in the hash table with a pointer stored in it. Additionally, structured data can be read and written effectively, allowing for faster calculation of features [
64]. The grid blocks were stored using this scheme, combined with the sparse matrix. Unlike conventional or hierarchical grid data structure, this 3D hashing matrix can substitute memory intensively and can compactly deal with sparse grids (grids that contain few points). In fact, many grids did not contain laser points; they conformed to sparse matrix logic [
65], and thus were stored in the spatial hashing structure which sparsely and efficiently managed compressed point clouds in grid blocks. Consequently, a large number of data-free grids were eliminated to save memory. The processing with 3D grid as the unit improved the efficiency of the subsequent clustering for local PL segmentation.
2D grid generation: Due to the high volume, high density, and unordered distribution of the point cloud data, planar 2D gridding was exploited to manage the contextual features. Local grid features (the density and height at the level of individual grid) were calculated during the process of planar gridding, which facilitated the rapid identification of HV pylons candidate areas. First, the distribution range of the original points was computed to estimate the number of grids [
66]. Each point was re-calculated with regard to the new planar coordinate system to allocate it to its grid. The process iterated until all points were allocated. The formula used is as follows:
where (x, y) refers to the candidate horizontal coordinates,
represents the minimum value of the x-coordinate in the overall point cloud data,
refers to the minimum y-coordinate,
represents the size of the planar grid, and m and n are the row and column numbers corresponding to the grid where the point is located.
Voxel Hashing: The 3D hashing scheme stores 2D grids in the beginning. Subsequently, in each 2D grid, new coordinates of each point are calculated during the dynamic update of voxels with regard to hashing voxels, as follows:
where
represents the 3D coordinate;
represents the minimum value of x-coordinate within the grid;
represents the minimum y-coordinate within the grid;
refers to the local minimum z-coordinate within the grid; d3 refers to the 3D voxel grid size; and
and
are the row, column, and height corresponding to the points in the 3D grid, respectively. The voxel was built based on the planar grid as a parent unit, and the size of the voxel grid was determined by the 3D spatial distribution and the voltage level of the HV wires (e.g., the offset of adjacent lines or voltage classes should be taken into account). To balance computation efficiency and feature accuracy, 0.5 m was set empirically as the size of voxel.
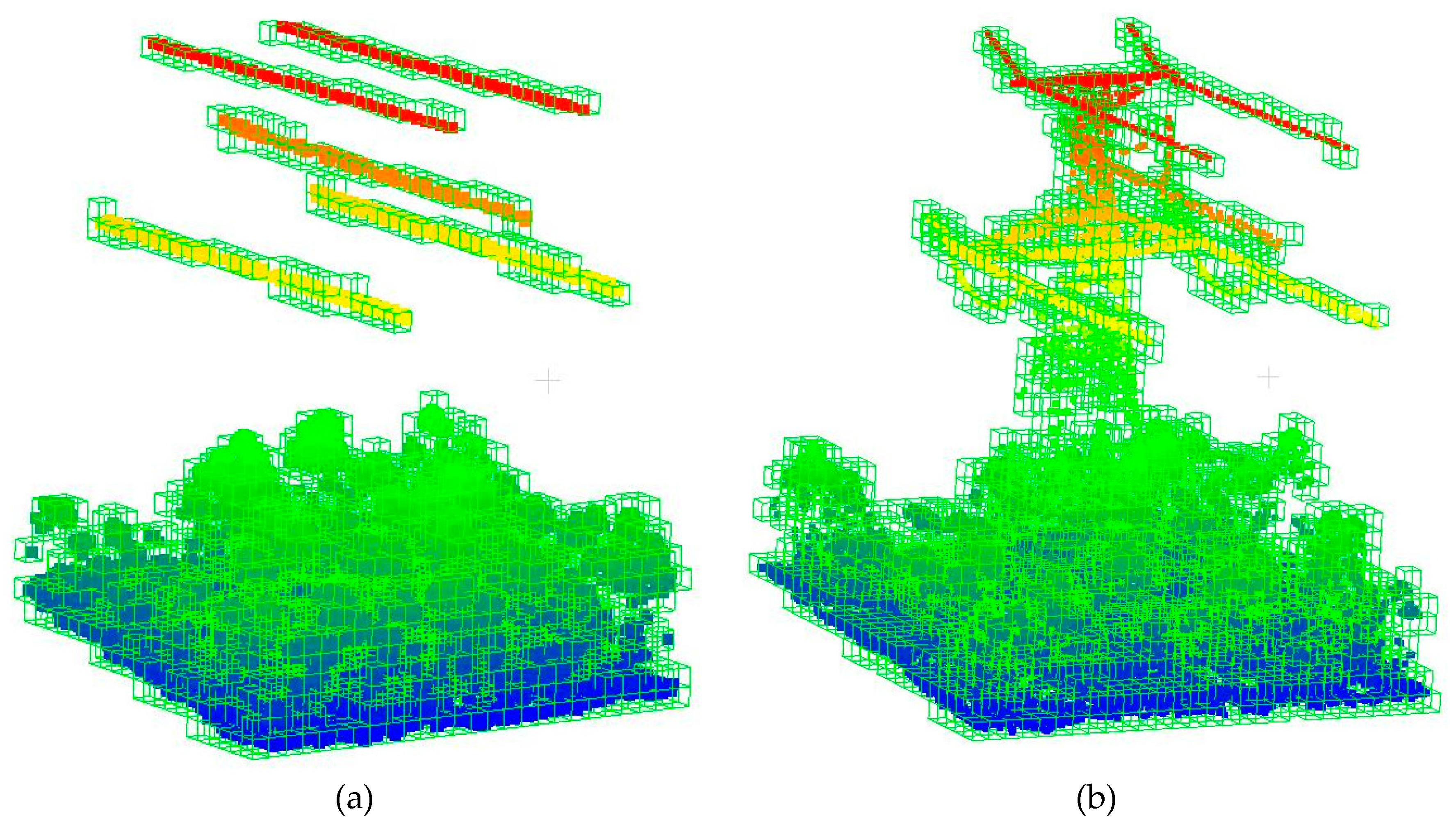
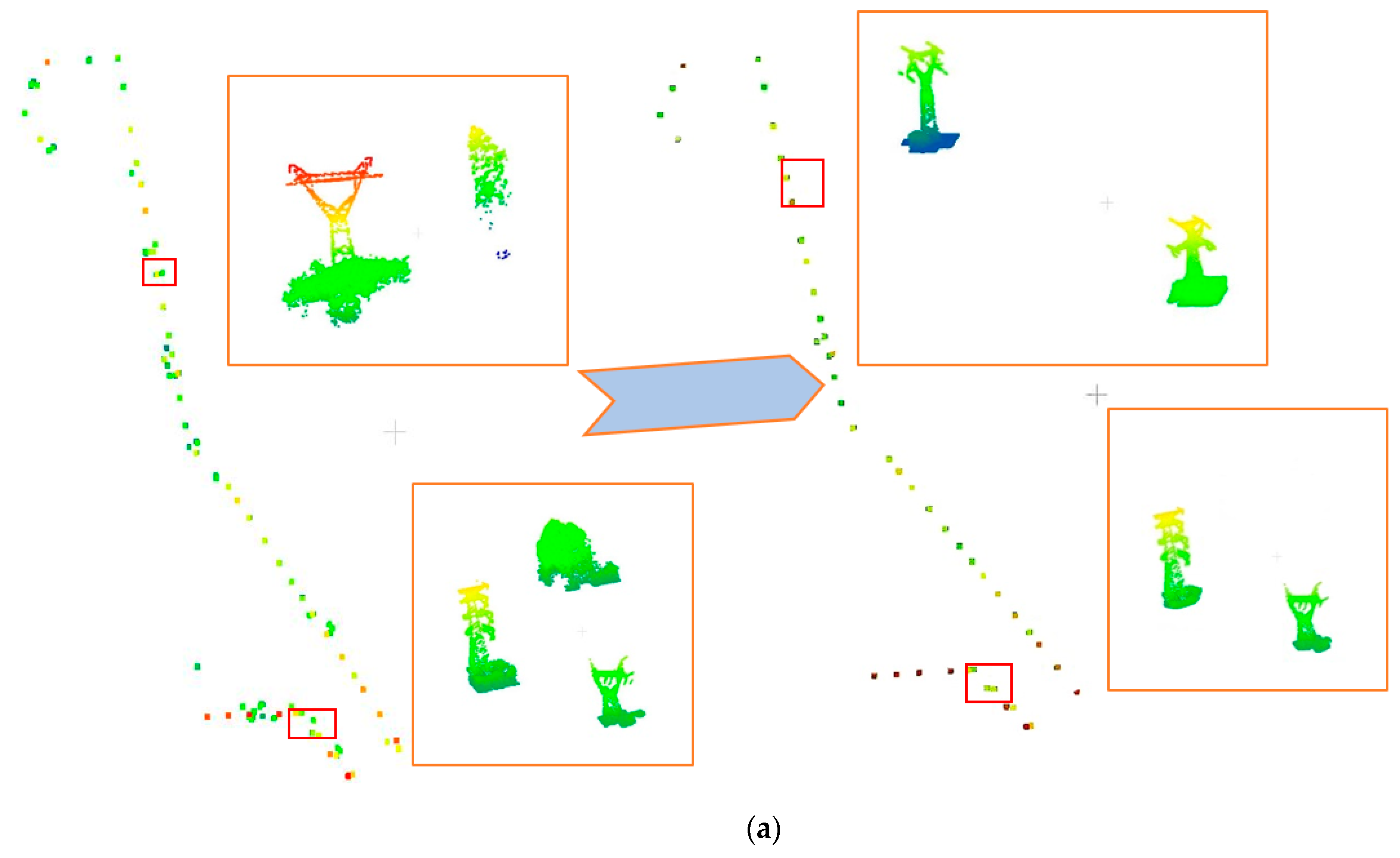
Figure 2 shows the results of the PL and pylon voxel blocks and blocks without power transmission objects.
3.2. Feature Calculation
In order to extract the transmission objects, different features of PLs and pylons, i.e., dimensional features (eigenvalue-based) and distribution features (point-based) of the point clusters were utilized. The distribution features consisted of height features (e.g., local digital elevation model (DEM), digital surface model (DSM), and height difference) and density features.
Feature calculationin 2D grids: The terrain where power transmission lines are constructed is generally uneven. Nevertheless, power pylon points normally have large height differences and continuous vertical distributions, and their height values tend to be high [
67]. These properties of distribution are not affected by the terrain and surrounding objects, providing a strong basis for pylon identification.
Considering a grid as a unit, features of point data in each grid were calculated, including DEM, DSM, and height-difference. Among them, DEM and DSM were obtained directly through statistical analysis of the point cloud. The height difference was calculated by subtracting DEM from DSM. Notice that the PL points extracted earlier from the corresponding point cloud data should be separated out when the grid-based DSM features are computed.
DEM reflects the distribution of topographic relief in the mapping area. The adverse impact of topography fluctuation on pylon extraction can be suppressed by normalizing the DSM using DEM. Normalized DSM (nDSM) reflects the local height differences within the point cloud data. Because of the large height difference of HV towers, the pylons are easily visible in nDSM.
3D feature calculation: According to Kim et al. [
41] and Melzer et al. [
27], PL points have the properties of local linearity and consistency of local convergence, which can be used to distinguish PLs from other objects. In
Figure 3, these dimensional features can be intuitively observed. Points in each 2D grid were first clustered based on Euclidean distance, then the voxels in each cluster were taken as a basic unit to calculate the dimensional features of points. By computing the covariance matrix [
7] and the eigenvalues of all points in the clustered voxels, the linear, planar, and spherical features were derived. The linear structure of a point set was determined by comparing the three values
,
, and
, calculated as:
where
,
,
(
>
>
) [
68] refer to the eigenvalues of the covariance matrix of each point set.
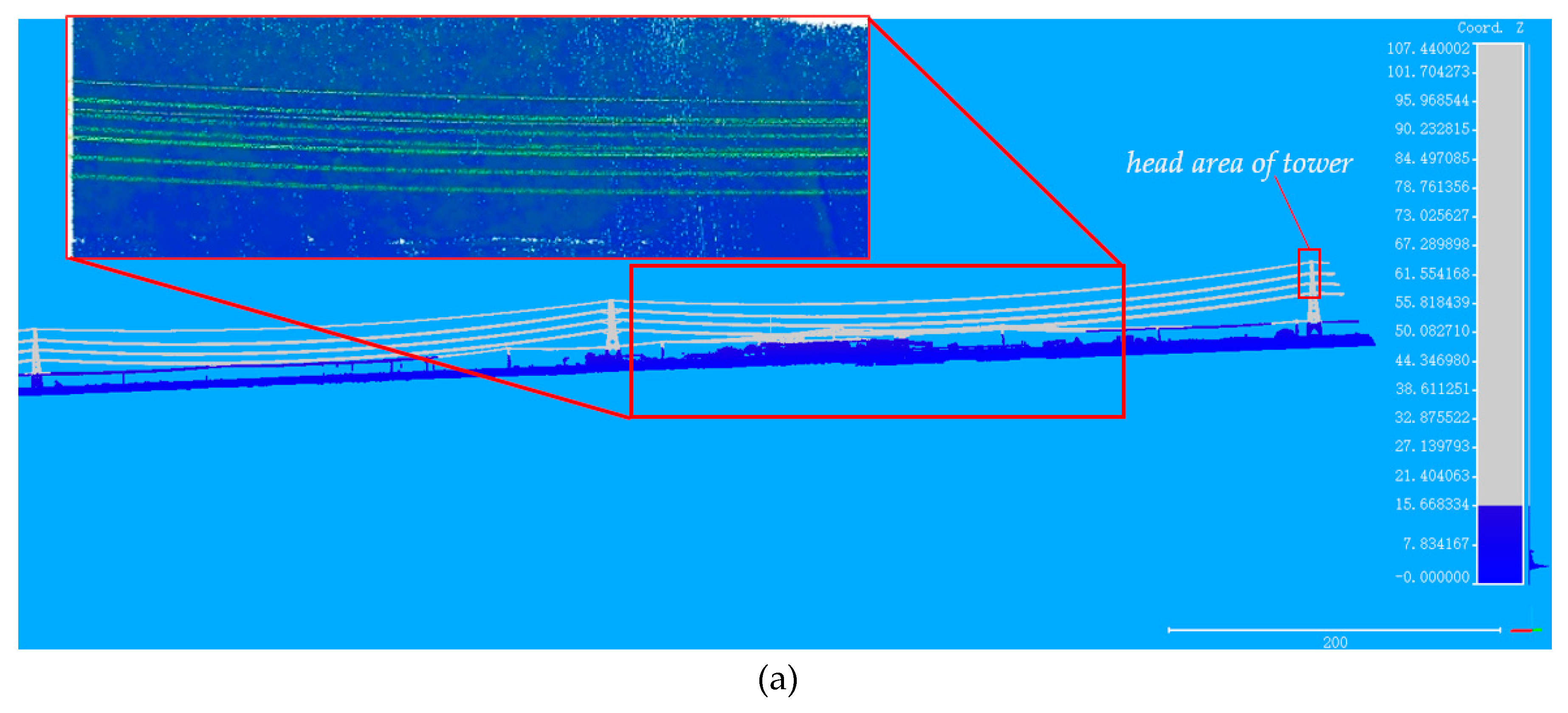
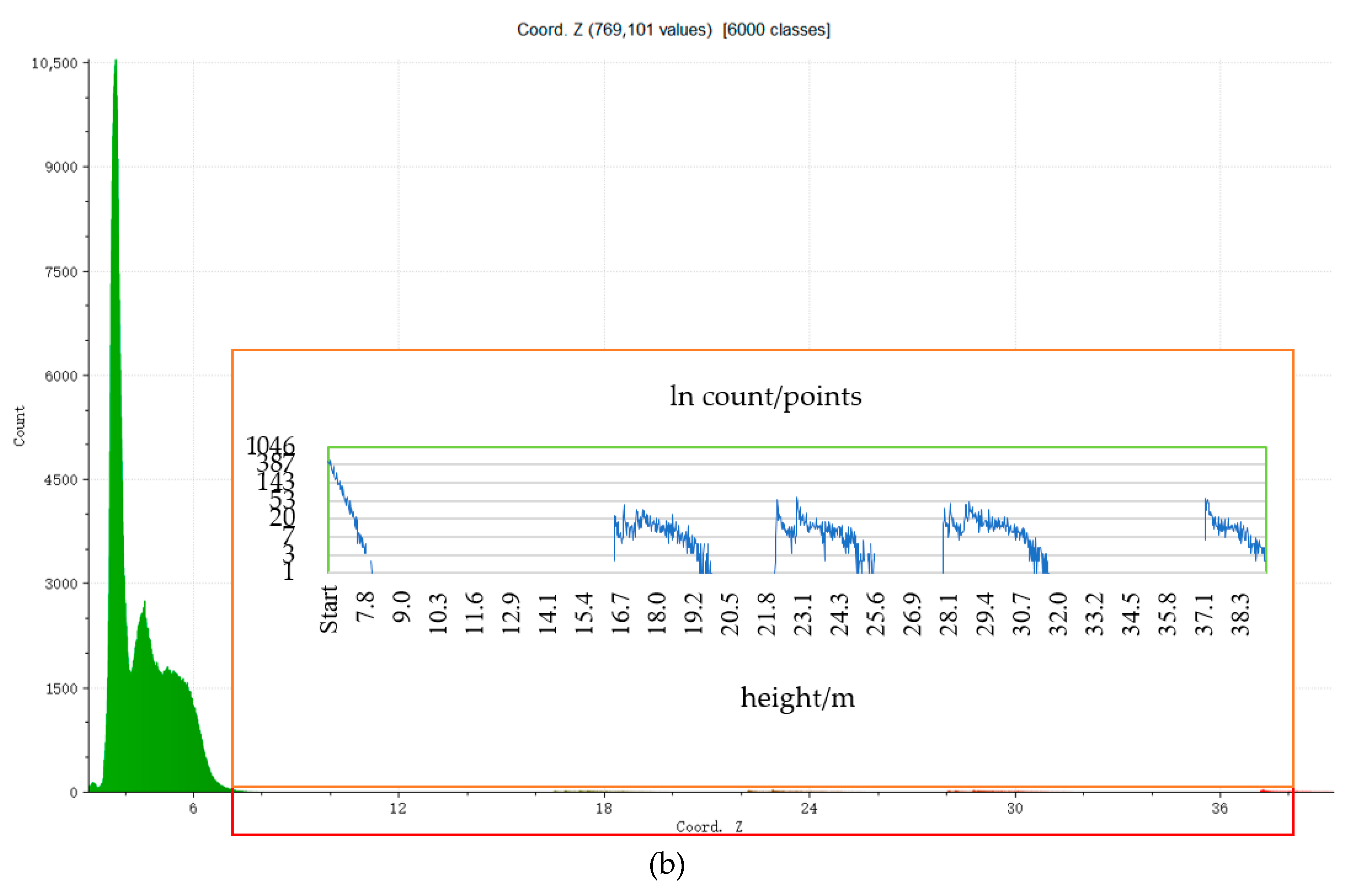
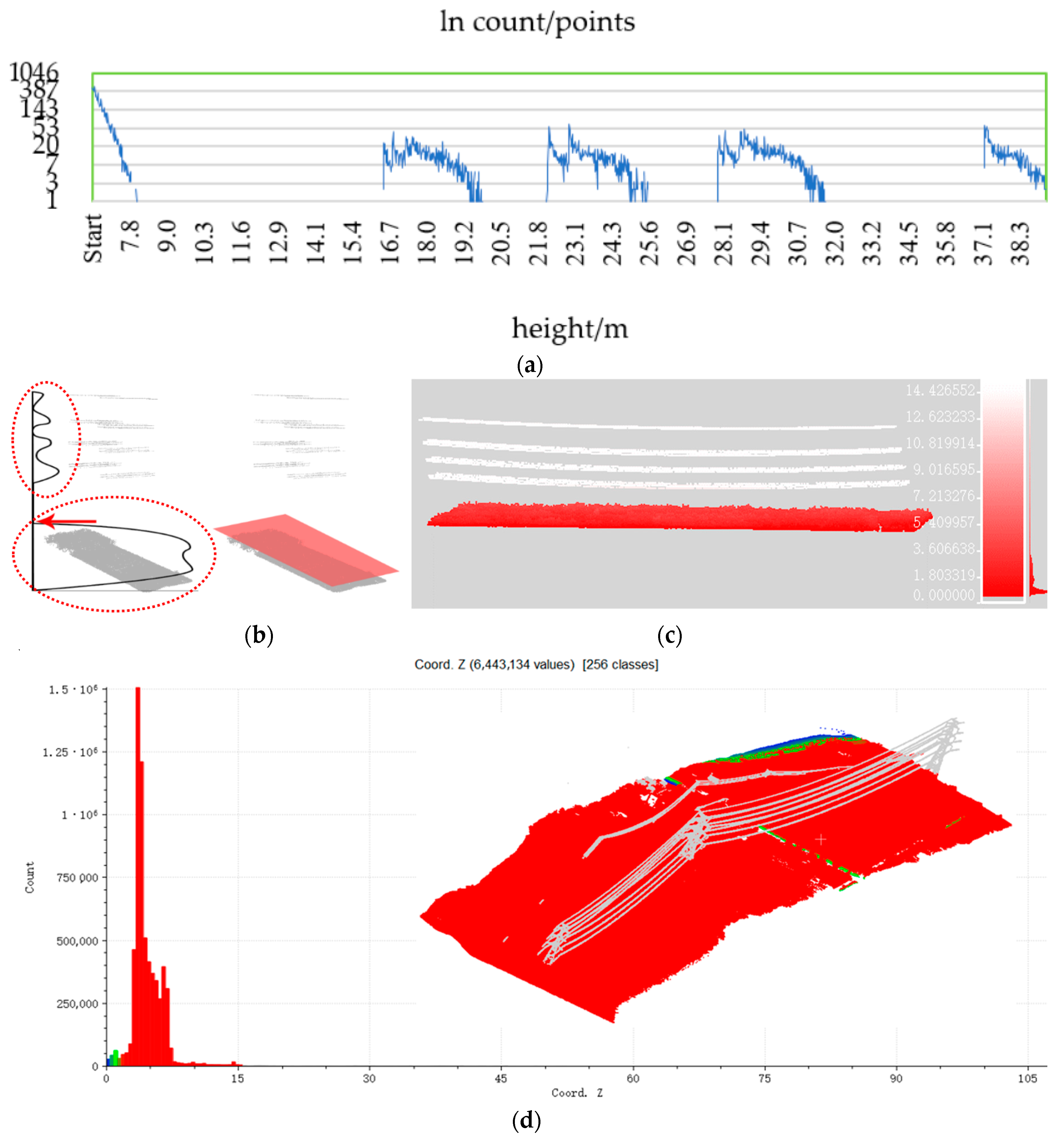
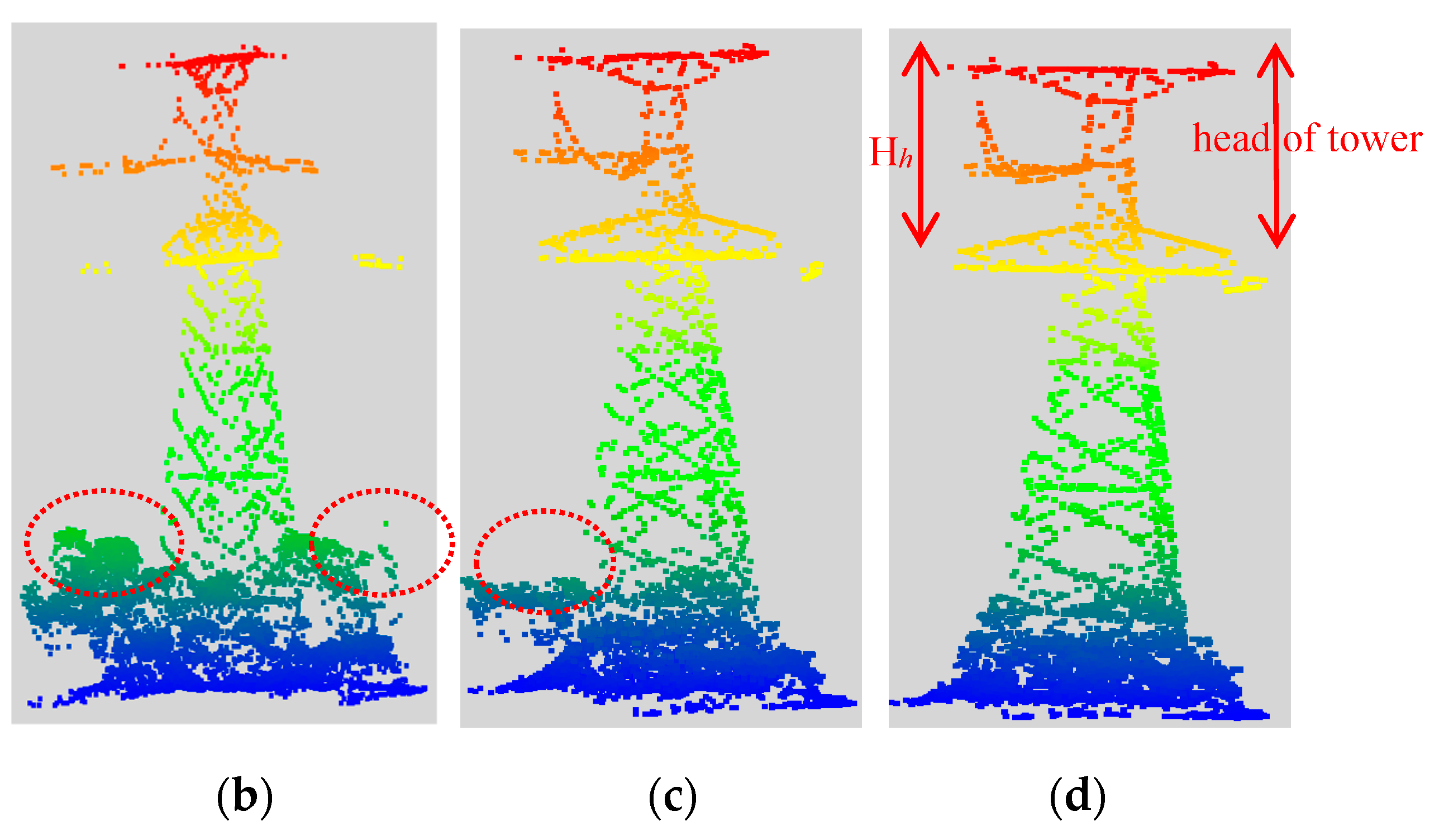
Height distribution: By analyzing the patterns shown in
Figure 4, it can be obviously seen that the relative height and local linearity are features able to distinguish PLs from other objects. The clustering distance is indicated by the distance calculated by the height distribution feature. The value is the minimum height gap from an overhead PL to the ground objects in a span (the space between two adjacent pylons). Using the height distribution histogram (
Figure 4b) of a test dataset in
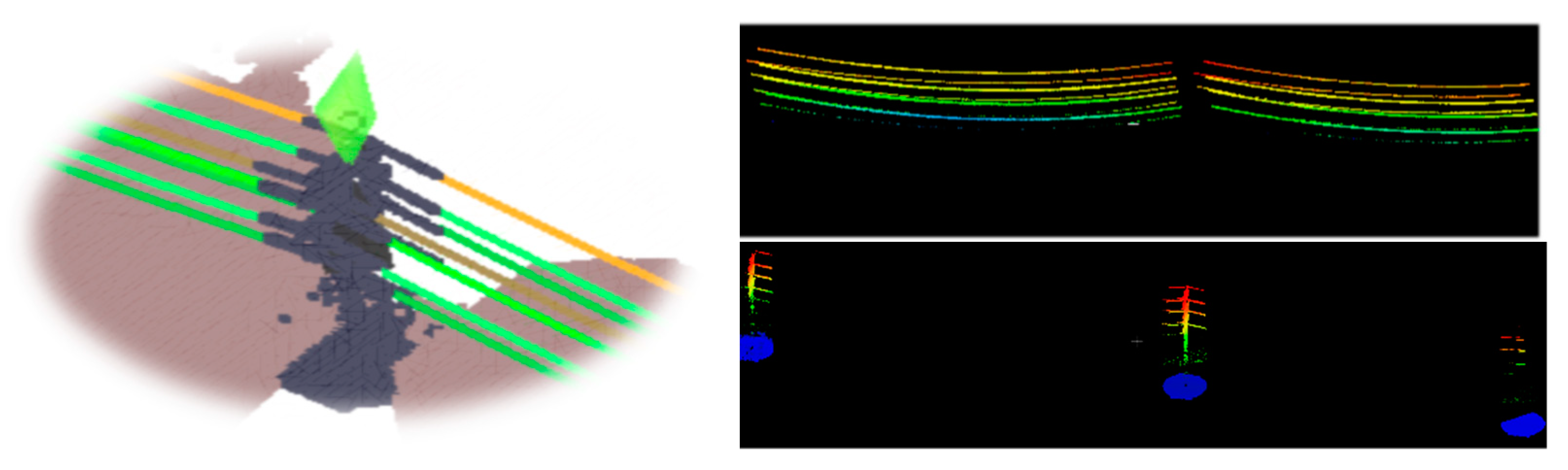
Figure 4a, where the points above 13 m are highlighted, the gap was fixed at the height of about 8 m. The gap between the first and the last peak was considered similar to the height of the top area of a tower, named as the head of the tower.
3.3. Segmentation of Power Lines and Pylons
The main components of HV power transmission corridors include PLs, pylon insulators, fixed accessories, etc., of which the key parts are the transmission lines and pylons (also called towers). Based on the spatial stratification of the corridor and the features of PLs discussed above, PLs were segmented first. HV pylons were then recognized by their properties in vertical and horizontal distributions without considering PL points.
3.3.1. Power Line Extraction
According to the abovementioned features of the geometric spatial distribution of overhead PLs, they were extracted in two steps: local line segment extraction based on dimensional features, and global PL merging based on local collinearity and height approximation. The key was to search for linear and parallel structures exceeding the minimum height interval in clustered point sets.
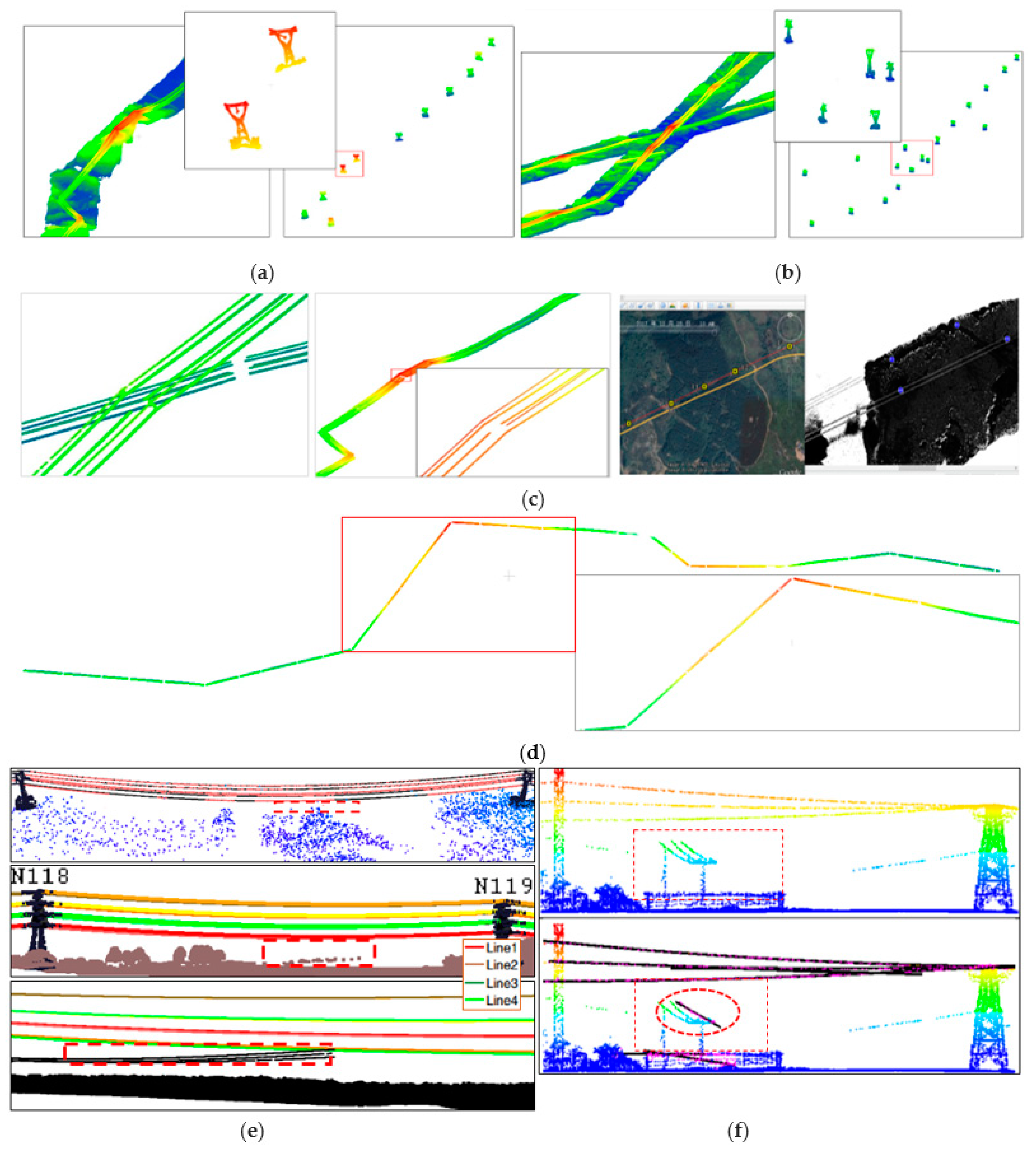
Local segmentation: The local segment extraction was carried out by judging the dimensionality of clustered point set—whether it had a linear feature. The next step was to search for linear structures among neighbors by eigenvalues, i.e., a neighborhood cluster search. The retained results, including linear structure, were seen as candidate PL segments. To visually demonstrate the effectiveness of the algorithm,
Figure 5 shows the segmentation result of part of the input data. The resulting linear segments were then pushed to the memory to extract PLs globally.
PL segments detected within a cluster of voxel blocks were recognized as parts of different PLs. As shown in
Figure 5, they did not overlap by local linearity analysis. By this property, a randomly selected seed segment was clustered with segments in neighbor blocks. Each segment was independent of the others, and the calculation in each span was independent. To improve the computation efficiency, this part can run in parallel.
Global extraction: After extracting the candidate PL segments, as shown in
Figure 5c, the local collinearity of the adjacent PL segments was analyzed to get complete lines. The whole PL extraction based on local collinearity was achieved by point cloud clustering in the horizontal domain, where the cluster unit was the PL segment, and the constraint was spatial continuity and local collinearity. Meanwhile, a CLF (compass line filter) [
1,
68] was applied to analyze the line direction using PL candidate points.
In the process of clustering, each 2D grid calculated above was set as the center unit, and the PL segments within its eight neighborhoods were searched to merge with seed PL segments located in the center grid. For linear segments aligned with the principle direction of the seed line segment, collinearity with the seed segment was assessed to eliminate those belonging to other, adjacent PLs.
Figure 5d shows the extraction results within a span.
Shown in
Figure 5e, the detected PLs may include low-voltage transmission wires that cross underneath. Cross-over or short-spanned low-voltage conductors were detectable, but were not the object of interest. Further optimization by combining with HV tower extraction is detailed in
Section 3.4.
3.3.2. Regional Segmentation of Candidate High-Voltage Towers Based on 2D Features
HV pylons, which support the transmission lines, sit on the ground, as shown in the point cloud data. Therefore, they show a continuous distribution in the vertical direction. Furthermore, according to the regulations governing overhead transmission lines, they must maintain a safe clearance to the surroundings or ground objects, so HV pylons are generally built more than 20 meters high.
Figure 6 illustrates the characteristic of large local height difference in the areas where the HV towers are located. In the horizontal direction, the wing length of the HV pylons is related to the corresponding voltage level of the PLs. Given the voltage level, the distribution range of pylon points on the horizontal projection plane should be finite, as in Equation (4).
where R
(m, n) is the radius of the pylon candidates in the projected ground plane and r is the wing length. These distribution features of HV pylons were utilized to divide the candidate pylon areas.
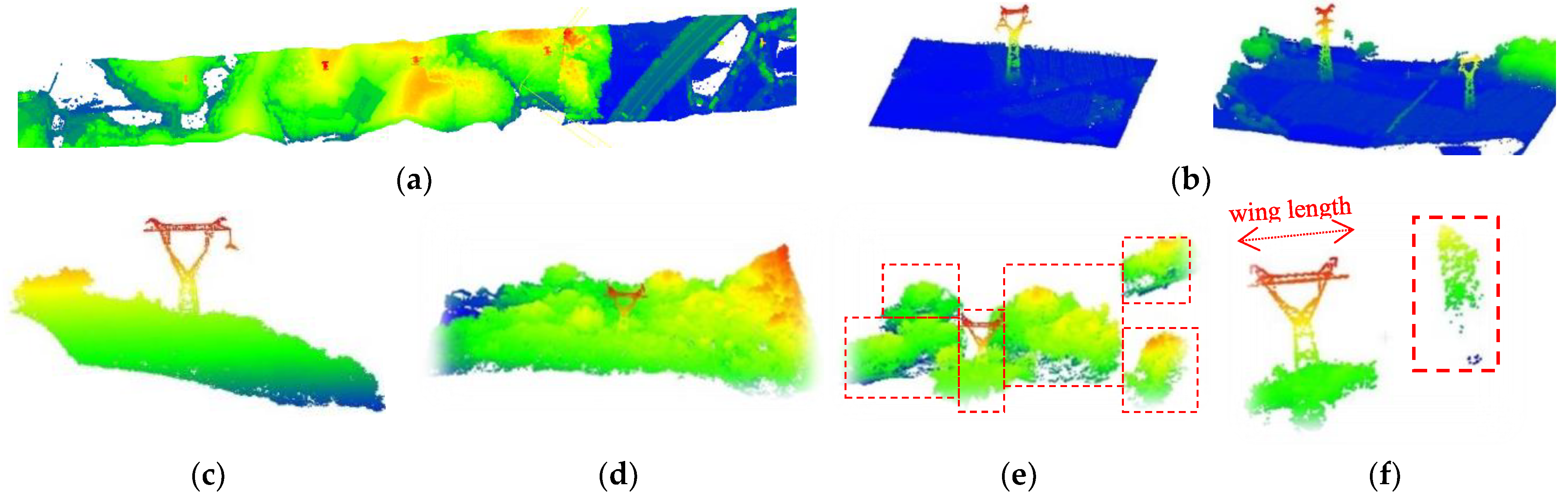
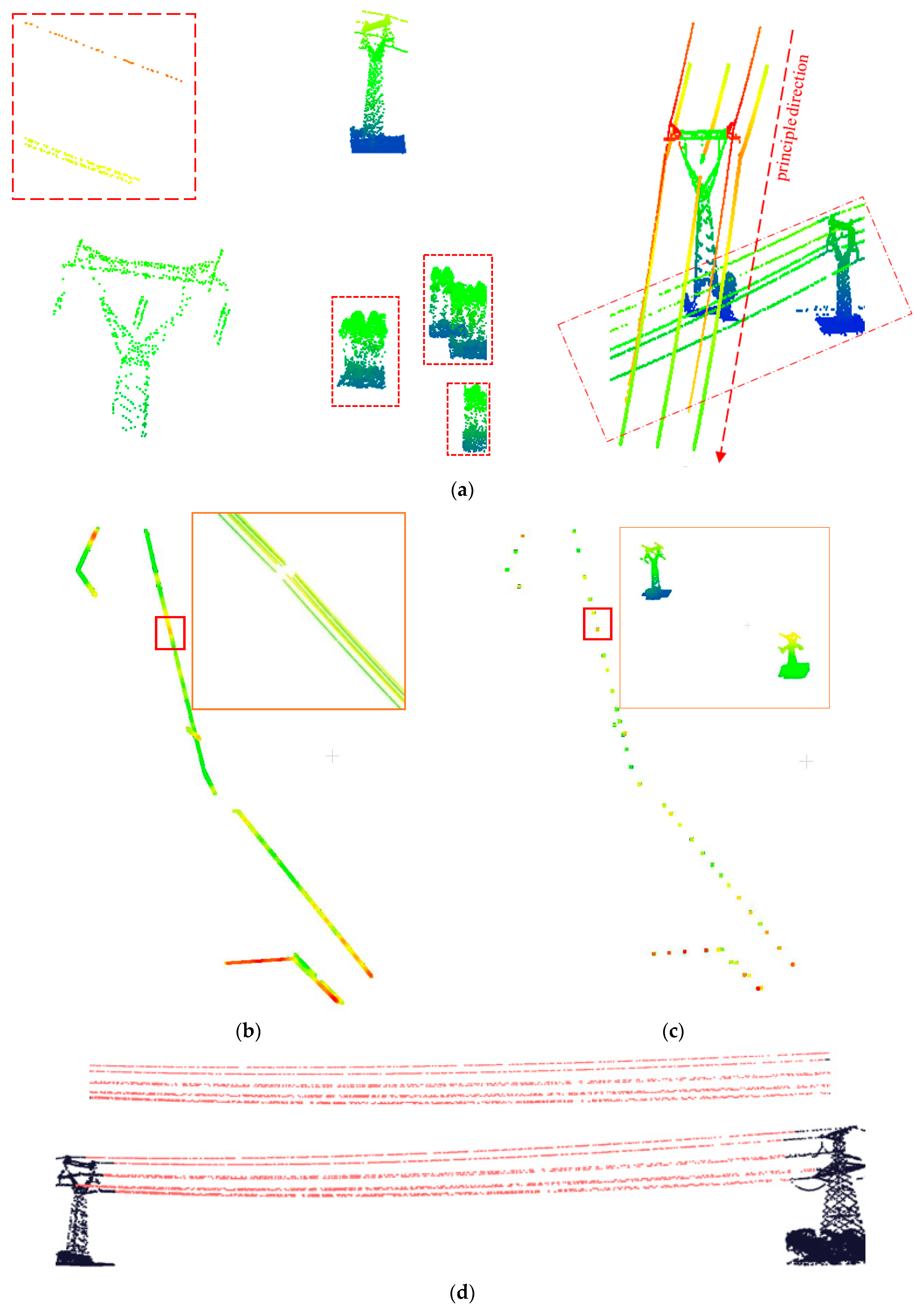
The segmentation was composed of five steps:
The 2D grids of large height difference in the input data were first identified according to the height difference feature. As seen in the red dashed boxes in
Figure 6e, these grids mainly consisted of towers, individual tall trees, or groups of clumped trees.
A 2 × 2m grid was created as a moving window to detect the finer characteristics of the grids with large height differences. The window was initialized with the same features as the grid. When it moved, its features were updated. The height difference value of the moving window that was greater than the pre-defined threshold (the minimum height difference between PLs and the ground from previous analysis) was retrieved and the corresponding grid was marked.
The vertical continuity of the points in each marked grid was checked. Given the maximum height gap threshold (usually set as the absolute height of the tower), grids containing a window of a higher gap than the threshold were removed to filter out outliers.
The remaining grids were clustered to group the grids belonging to the same tower. Neighboring grids were clustered when their height differences were greater than the pre-defined threshold.
The distribution range of HV pylons in the planar projection was utilized to differentiate them from other clustered objects. The principal direction of each cluster was calculated. The semi-major axis of a tower in the planar projection range in the principle direction was not greater than the length of HV tower’s wing. From the horizontal projection range described by Equation (4), blocks of clumped trees were filtered out because their distribution ranges in the planar projection failed to meet the equation in the horizontal plane. Small clusters (see the dashed box in
Figure 6f) were then excluded by judging whether each grid in the clustering blocks had an extremely local high value in the DSM feature map.
Figure 6a shows one dataset in which PL points were removed, and
Figure 6b–d shows the top view and side view of some pylon areas. As a result of the extraction of pylons, points on the majority of non-power transmission components and tall clumped trees and arbors were removed. As can be seen from the result in
Figure 6f, by extracting the grids with large height differences, most non-tower points were removed and the target tower was completely retained.
3.4. Optimization of the Extraction of Power Transmission Components
After PL and tower detection, a few single tall trees, signal poles (happened to be in the corridor) and low-voltage PLs were still present in the scene as interference factors. However, in the transmission corridor, any PL was hanging in midair in the 3D space and was connected with HV pylons. This constraint was used to refine the pylon and PL detections. As seen in
Figure 7, pylon and PL points were connected to each other, which is a unique feature that can be used to distinguish HV towers from interference elements. Note that HV transmission lines were different from other linear interference factors such as low voltage conductors or supporting wires. Additionally, as a basic criterion, the principal direction of the candidate PL points was approximately parallel to the line connecting their two adjacent towers [
69].
Thus, the extractions of those two transmission objects were optimized simultaneously, considering the physical connections between them. This included the following constraints: (a) the transmission tower and the PLs were connected to each other [
27], meaning the PLs in neighbor spans were connected through the HV towers; (b) the dominant orientation of the PLs was approximately parallel to the line connecting the towers at both ends; (c) the neighboring grid of the tower must contain PLs, and there should be a tower at the position of the derivative extremum of each adjacent line.
First, the extracted HV towers were taken as searching objects. For each HV tower, the neighboring grids were searched for PL points.
Secondly, the PL point set and the tower were confirmed to be connected to each other. If a tower was connected with a PL, it was determined as HV tower area, and the PL connected with it was labeled as transmission wires.
Lastly, the directions formed by every two adjacent pylons were taken as references to remove the linear segments with large angles from these directions.
The above steps eliminated tall trees, signal poles, and other remaining interferences of low-voltage transmission wires and other linear targets. Illustrated in
Figure 8b,c, tree points with a similar distribution of pylons, and most low-voltage transmission lines and cross-over transmission lines (see in
Figure 8a), were excluded. As depicted in
Figure 8d, the result was the clean and complete detection of PLs and pylons in a span.
3.5. Reconstruction of Power Transmission Components
3D reconstruction of PLs is the basis for the applications of transmission corridor safety inspection, 3D scene visualization, and condition monitoring. Generally, the PLs are divided into individual fixed-length lines according to the POAs, to facilitate the line fitting.
3.5.1. Modeling of Power Lines
Through spatial connectivity analysis of adjacent transmission lines, the integrity of lines was guaranteed and the relationship between lines and towers was determined [
51]. The PLs were split into spans formed by adjacent towers. The 3D PLs were reconstructed on the assumption that they were flexible free-hanging wires that could be expressed by a mathematical model [
70]. The 3D model was described by a straight line using least squares in the horizontal plane and a catenary in the vertical plane. The PLs in each span were modeled separately. They were then combined with the models of pylons. The mathematical model demonstrated by Jwa and Sohn [
30] was separated into a catenary (Equation (5)) and a line (Equation (6)). Equation (5) is solved by minimizing the difference between the observed Z value and the fitted Z value of points in each segment, as in Equation (7).
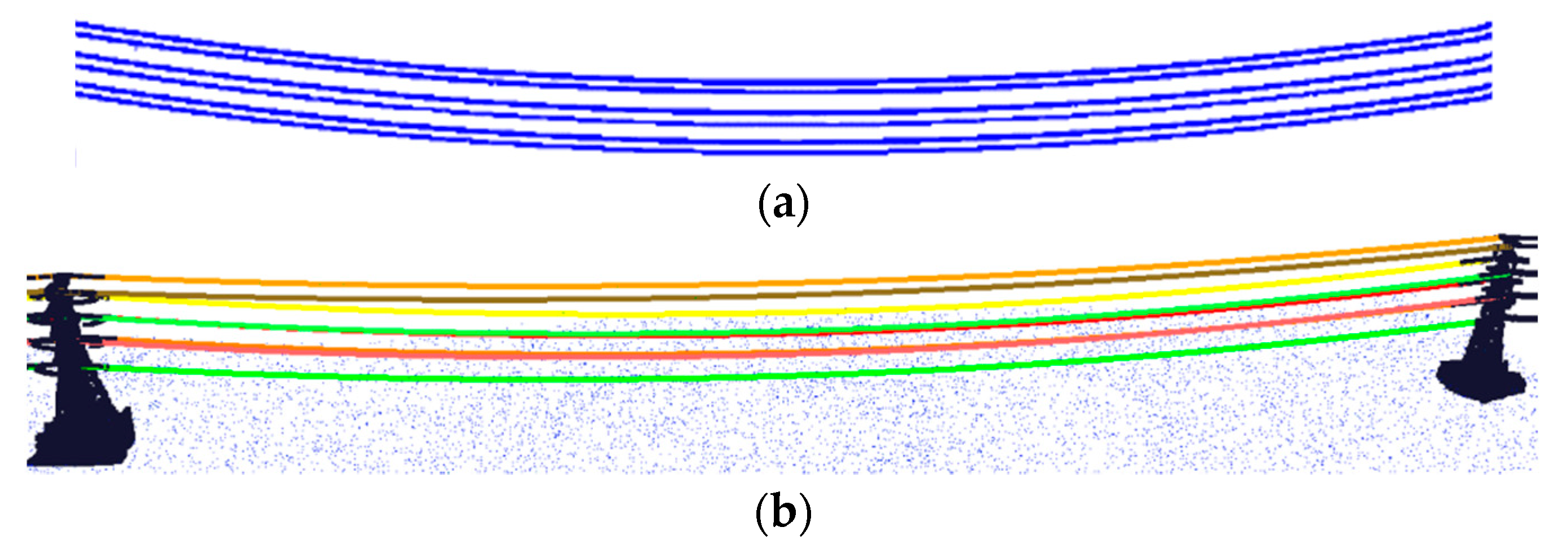
The Random Sample Consensus (RANSAC) algorithm was used to iterate each line point and rectify the fitted model using ever-increasing inner points to reconstruct each single PL.
Figure 9a shows some exemplary fitting results of PLs in a span. The PLs in each span were modeled and colored separately by their electrical phase (
Figure 9b). They were then combined with the models of pylons.
3.5.2. Modeling of Pylons Based on Tower Center Localization
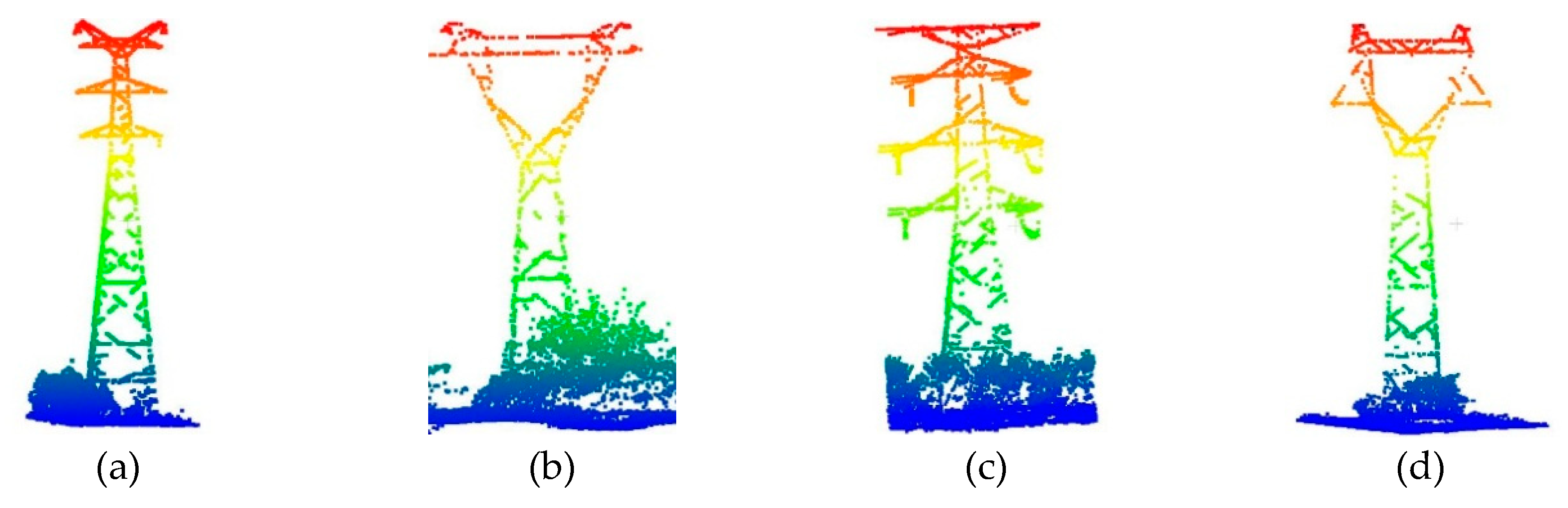
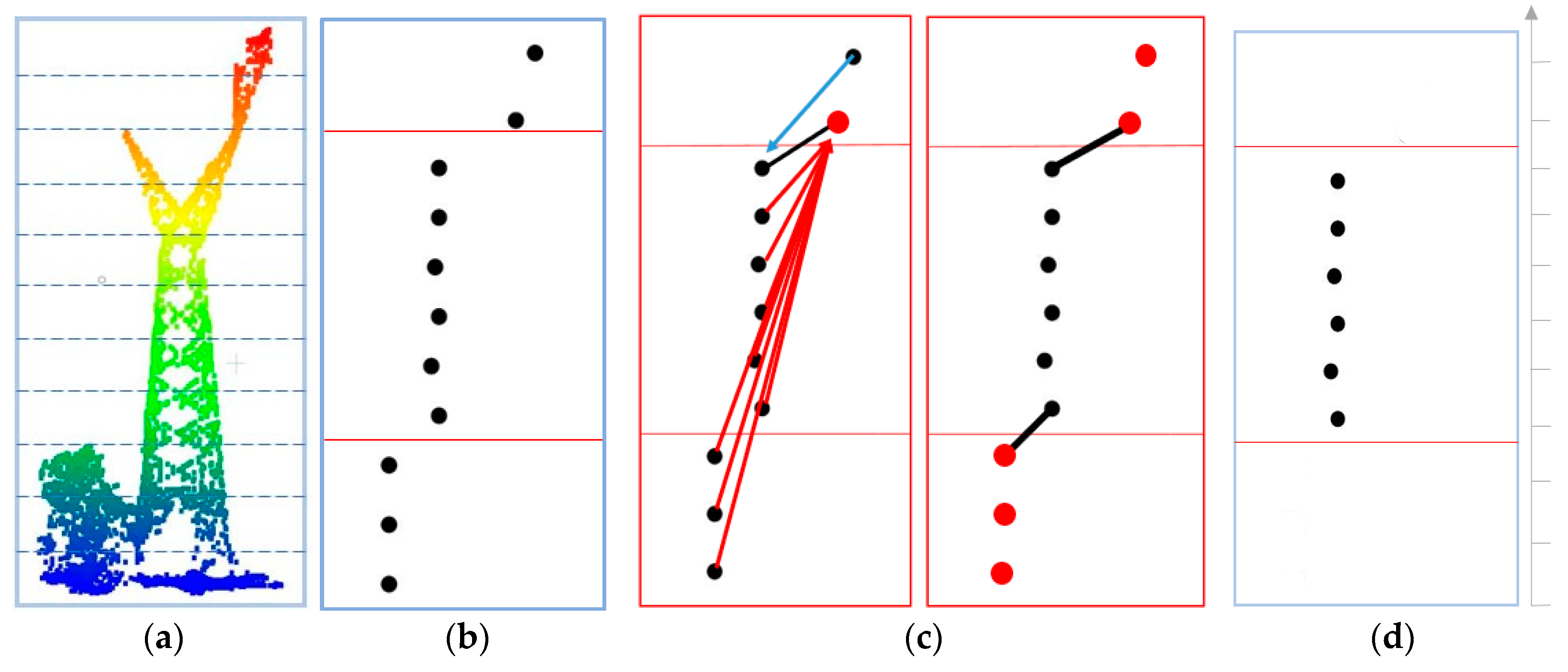
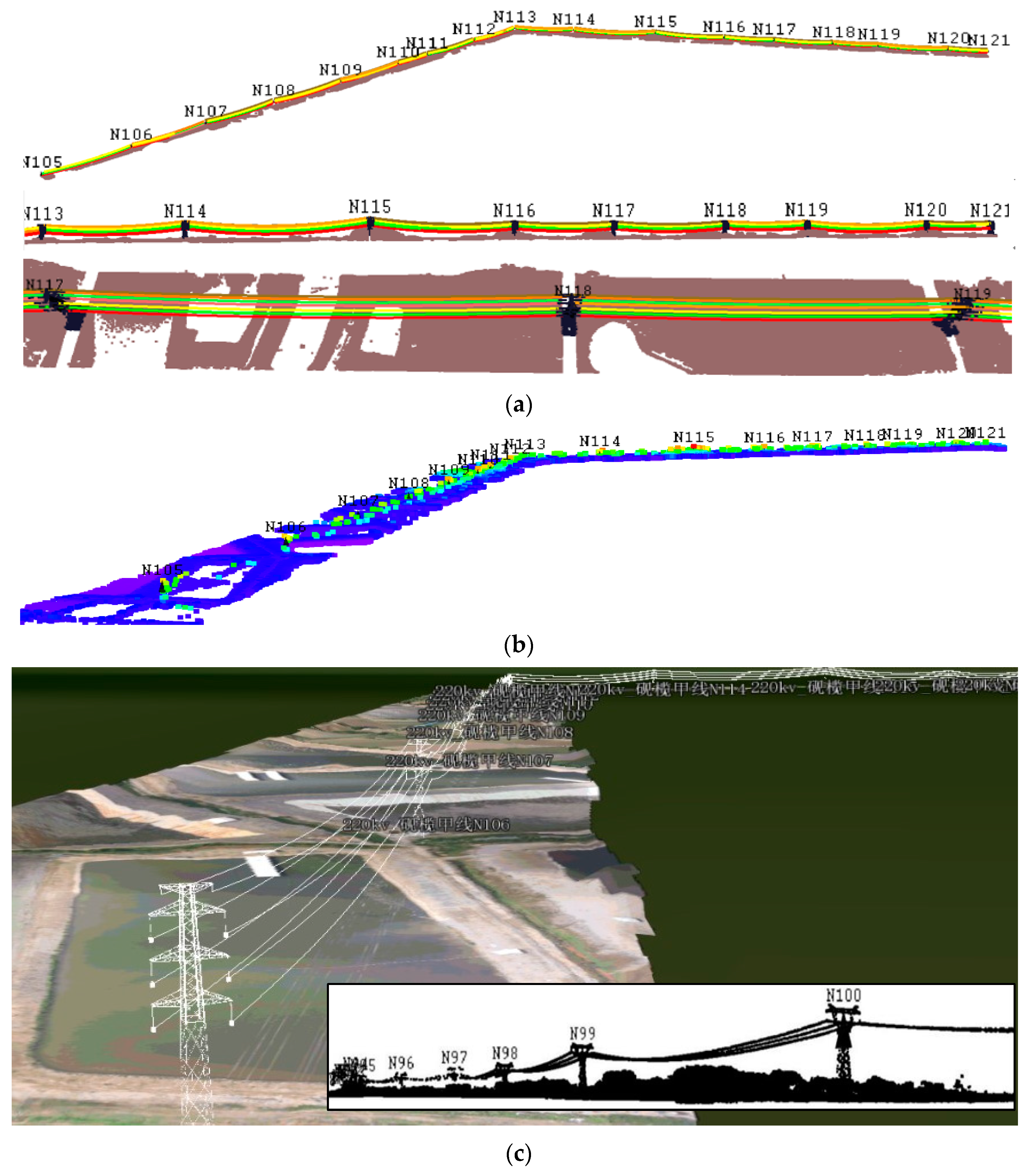
In the maintenance of power transmission, special attention should be paid to the stability of the HV pylons at a large scale and the accessories on them, i.e., the insulators and signs of tower number. Generally, the geographical coordinates of each pylon are required when dealing with the security of the transmission target. The main difference in this reconstruction approach is that we reconstructed not only the pylons, but also the insulators on them. First, the accurate planar coordinates of the pylons were calculated. Next, the library of tower templates was built according to the four basic types. Thus, the position error of the models built of each object in the corridor scene was smaller than others’ work. Moreover, the pylons were reconstructed as a whole model and were detailed by locating and modeling their insulators.
Planar Center Localization: Having identified the grids where the power towers are located, their structure and shape were abstracted to the four categories in
Figure 10. Their distribution varied, which had an obvious influence on the plain projection feature of density and feature of height distribution. When calculating their central points, multiple voting mechanisms were used to search for the most reliable point centers of the horizontal section in multiple iterations.
As HV towers are regular to some extent, a horizontally sliced layer at any height of a tower body has an in-plane symmetry, as long as the points on the tower are not largely missing. The centers of those sliced layers based on the stratification in vertical direction can be used to calculate the accurate planar coordinates of the HV tower.
As shown in
Figure 11a, there were still some vegetation points attached to the bottom of the tower, and the tower points were incomplete at the top. The central positions of the sliced layers shown in
Figure 11b were also affected by the missing points. According to the verticality of the HV tower, there should have been a small angle between the vertical direction and the vectors formed by the centers of the layers (
Figure 11c). The six points in the middle of
Figure 11d describe the identified candidate central points, analyzed statistically by the algorithm shown in
Table 1, in which
is a collection of tower grid, which is then divided in to several layers
2 meters in height;
is the horizontal distance of two center points;
is the angle between the z-axis and the line through the two central points determined by center point pairs, consecutively;
is the maximum of collection {
}; and
and
are center points of the two layers corresponding to
.
Pylon modeling: In this paper, the methodology proposed by Li et al. [
48] was applied to build the 3D pylon models, based on model fitting using a library of high-precision tower models built manually according to relevant specifications. The 3D model was initiated at the center of the detected tower, defined by the planar location and half of its height. The model size was determined by the voltage level when the power transmission was designed, as shown in
Figure 12a. The Gibbs energy model was established to estimate point cloud and model fitness during the reconstruction process. Since the optimization process of the energy model was non-convex, the towers were reconstructed by energy optimization using Markov chain Monte Carlo (MCMC) [
49].
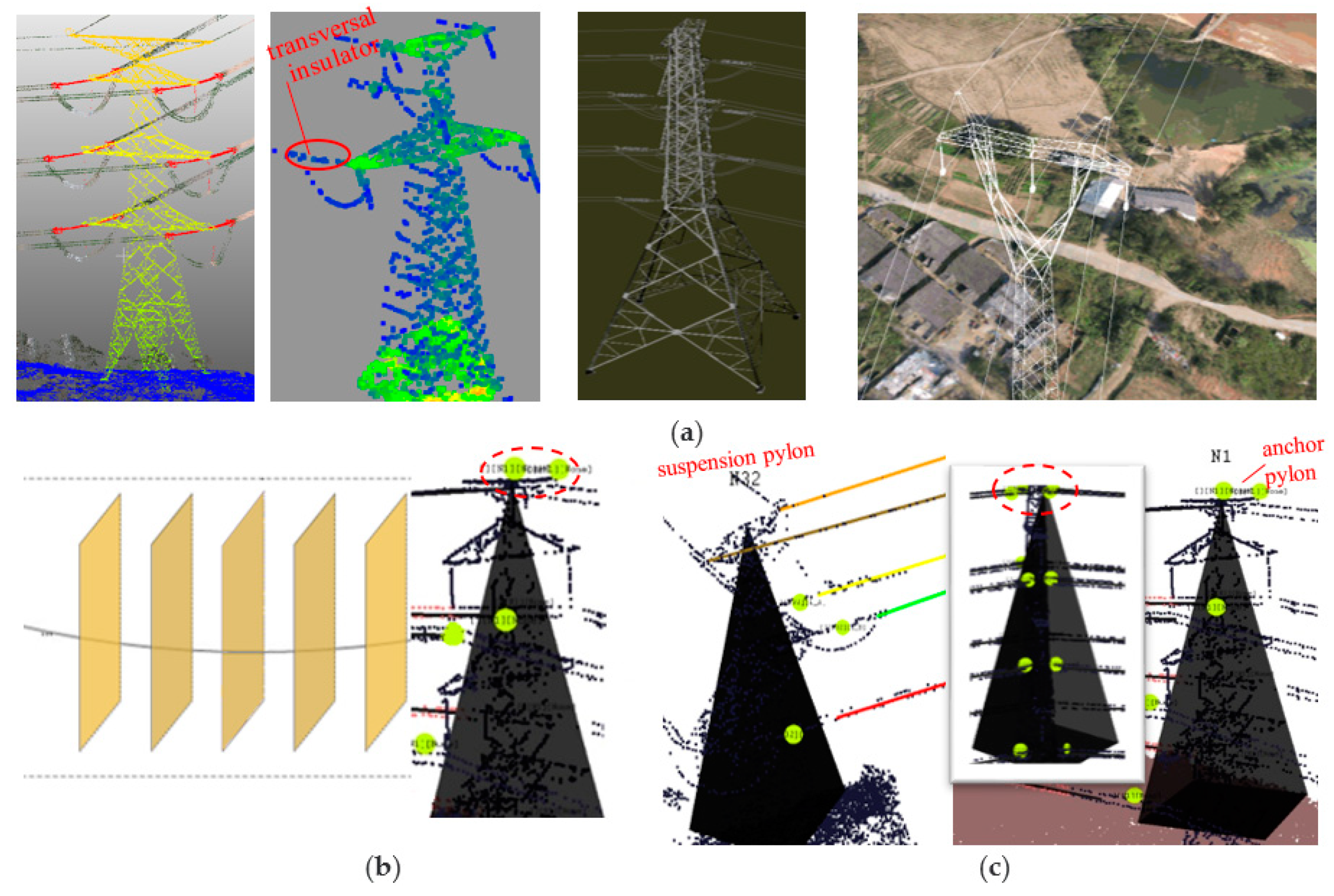
Insulator modeling: Insulator reconstruction was achieved by insulator matching based on a region growing method. In most cases, it was fixed to a tower model [
71]. Generally, insulator points were determined by contextual search and then clustered [
21]. The insulator candidate points were searched within several successive adjacent vertical profiles in the principle direction of the PL (
Figure 12b). In fact, insulator model construction was accompanied by the processes of line fitting and region growing along the vertical profile. The midpoint of the insulator point cloud was taken as the modeling center. For transversal insulators (points in the red ellipse in
Figure 12a), the points located along the PL from its end until the center of the nearest tower were marked as insulator points. When the growth and fitting of the whole PL was completed, the insulator points on the corresponding line were also searched out. The yellow dots in
Figure 12b were the centers of insulators. Note that the two (in the dashed ellipse) on the top were removed, as there was no insulator along the shielded wire. Finally, corresponding types of insulator models were added to the tower model.
6. Conclusions
This paper addressed the issue of automatic object detection and reconstruction from UAV airborne point cloud data in power transmission corridors, including the extraction of HV towers and overhead transmission lines. Additionally, accurate localization and reconstruction of pylons was explored.
An automatic method of power transmission object extraction was proposed, based on grid structures. The local collinearity of PLs in horizontal projection over their adjacent grid cells and parallel configuration among adjacent conductors were analyzed as features for segmentation. To roughly extract overhead PLs based on 2D gridding cells, the local line segments were clustered and merged. In addition, the features of large height difference, local maximum height, and continuous height distribution of HV tower were analyzed in order to detect and localize the pylons. The optimized extraction algorithm was then tested in the experiments. Results indicated that the proposed automatic power transmission object extraction method achieved high efficiency and nearly 97% accuracy in complex environments. The advantages of the proposed method are as follows:
The method utilizes a high volume of Lidar point cloud data with high density, and the spatial hashing matrix is utilized to store the grid data dynamically, which is beneficial for rapid access to the data.
The integrated analysis of PLs and pylons to refine the extraction results has been proven to produce a great improvement of accuracy.
Ground point filtering was not required, so the performance of the method does not depend on any ground point filtering algorithm. Additionally, it has a strong adaptability to ALS data with undulating terrain, and areas with clumped trees, single tall trees, and tall signal poles.
The coordinates of the HV towers are localized accurately and robustly by extracting reliable center points of the cross-section layers in the height direction.
The proposed method automatically extracted and reconstructed transmission corridor objects (PLs and pylons) in the studied area using UAV Lidar data. It was efficient in terms of speed, quality, and scalability. The algorithm has a few requirements for the data, such as a moderate gap between points. When the data gap in the main direction of the PLs is bigger than 4 m, the results will be affected. The processing efficiency of the algorithm can be further improved, and other surrounding objects (buildings, trees, railways, other poles, etc.) and small components (nests) may be also extracted in the future. In addition, physical analysis for structural health monitoring will be investigated [
74], taking the stability of the ground base into consideration, such as to detect the inclination or collapse of towers, etc. This could be further integrated via structure from motion (SfM) [
75].