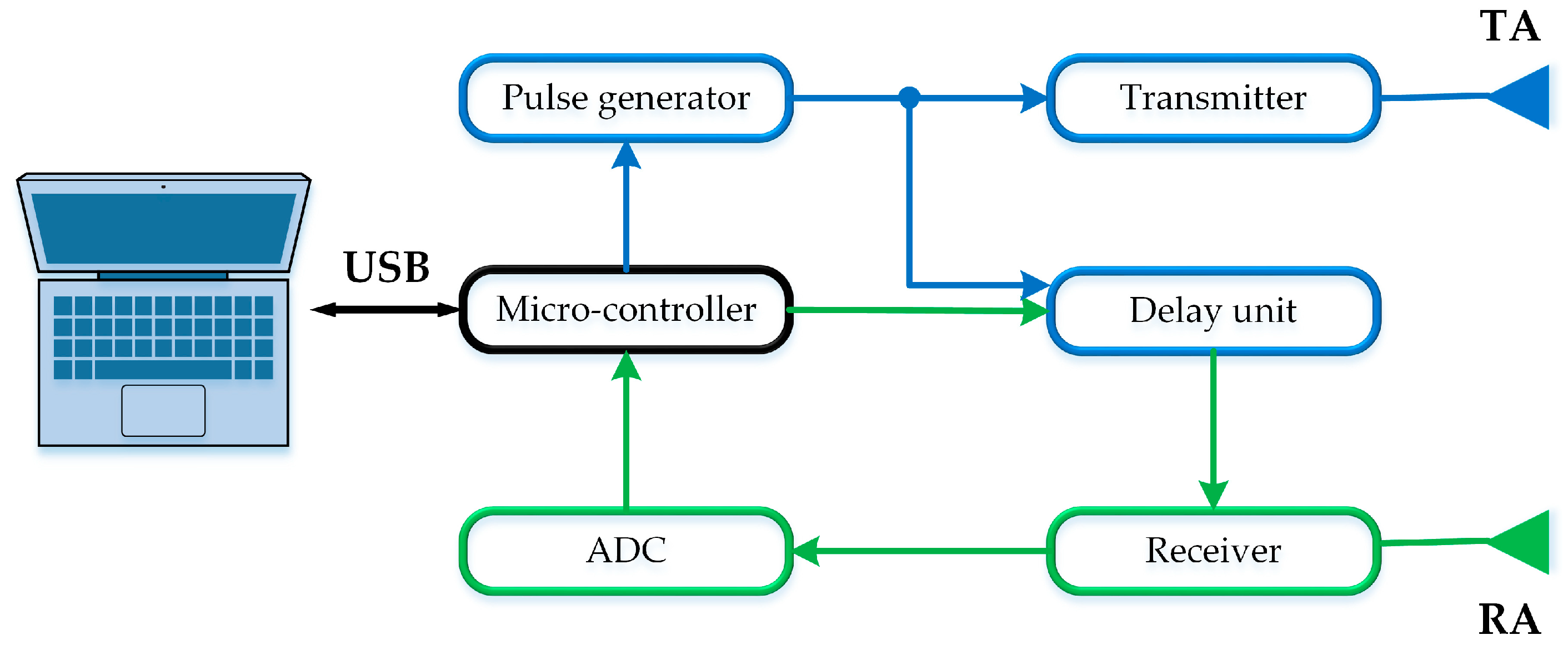
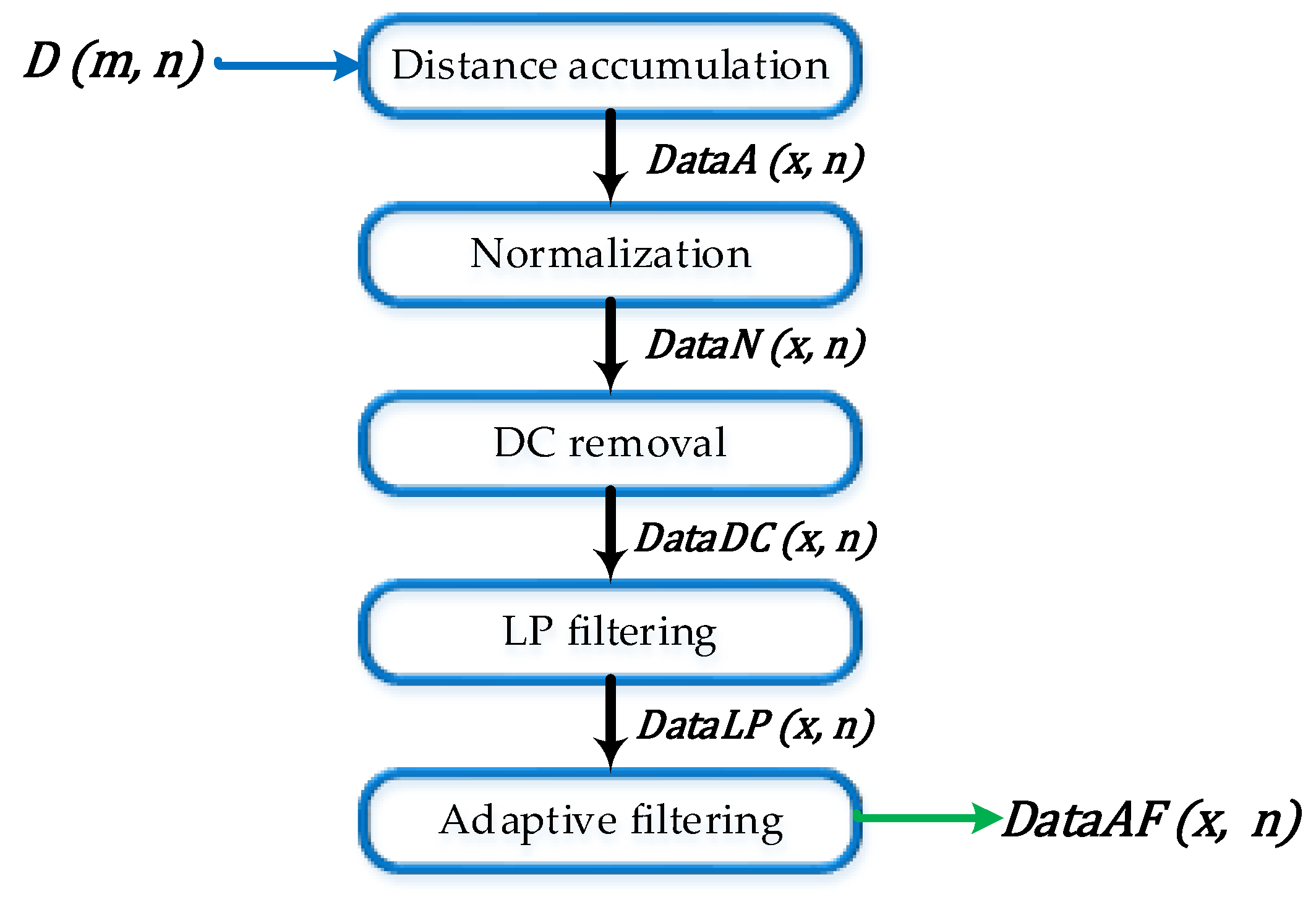
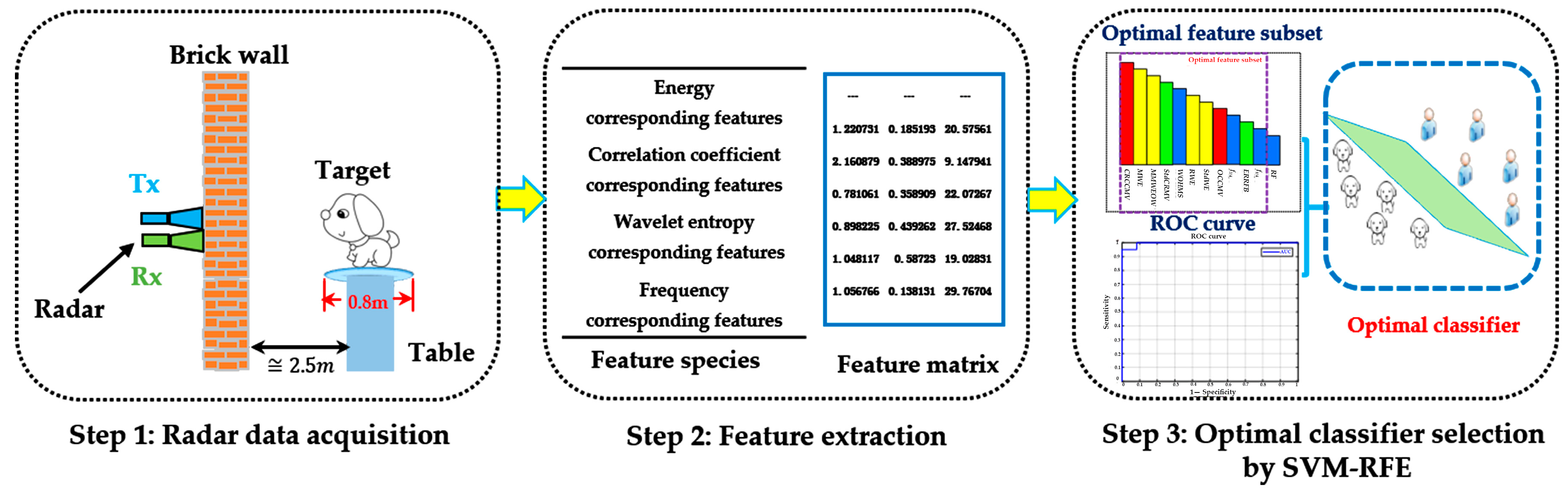
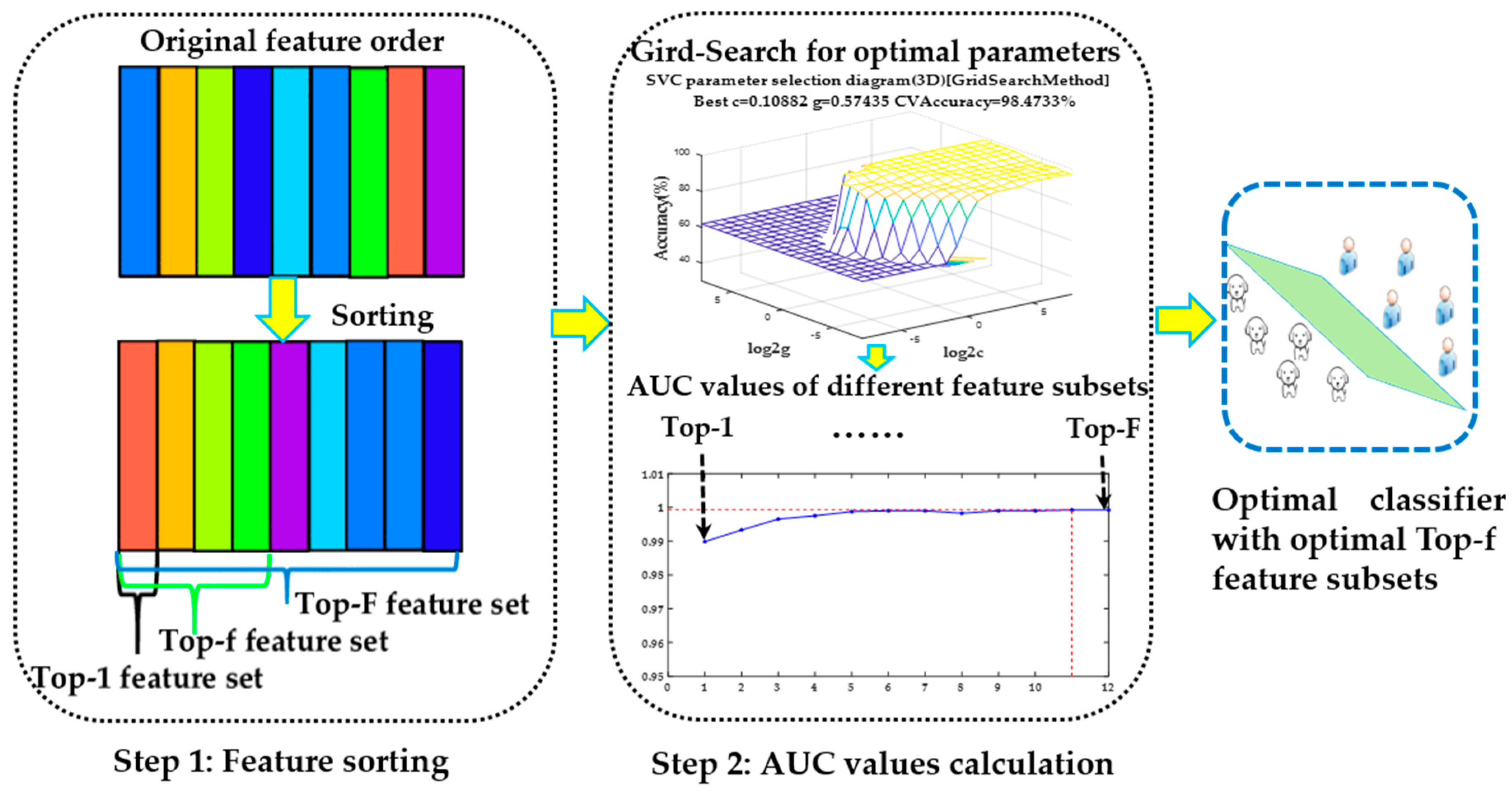
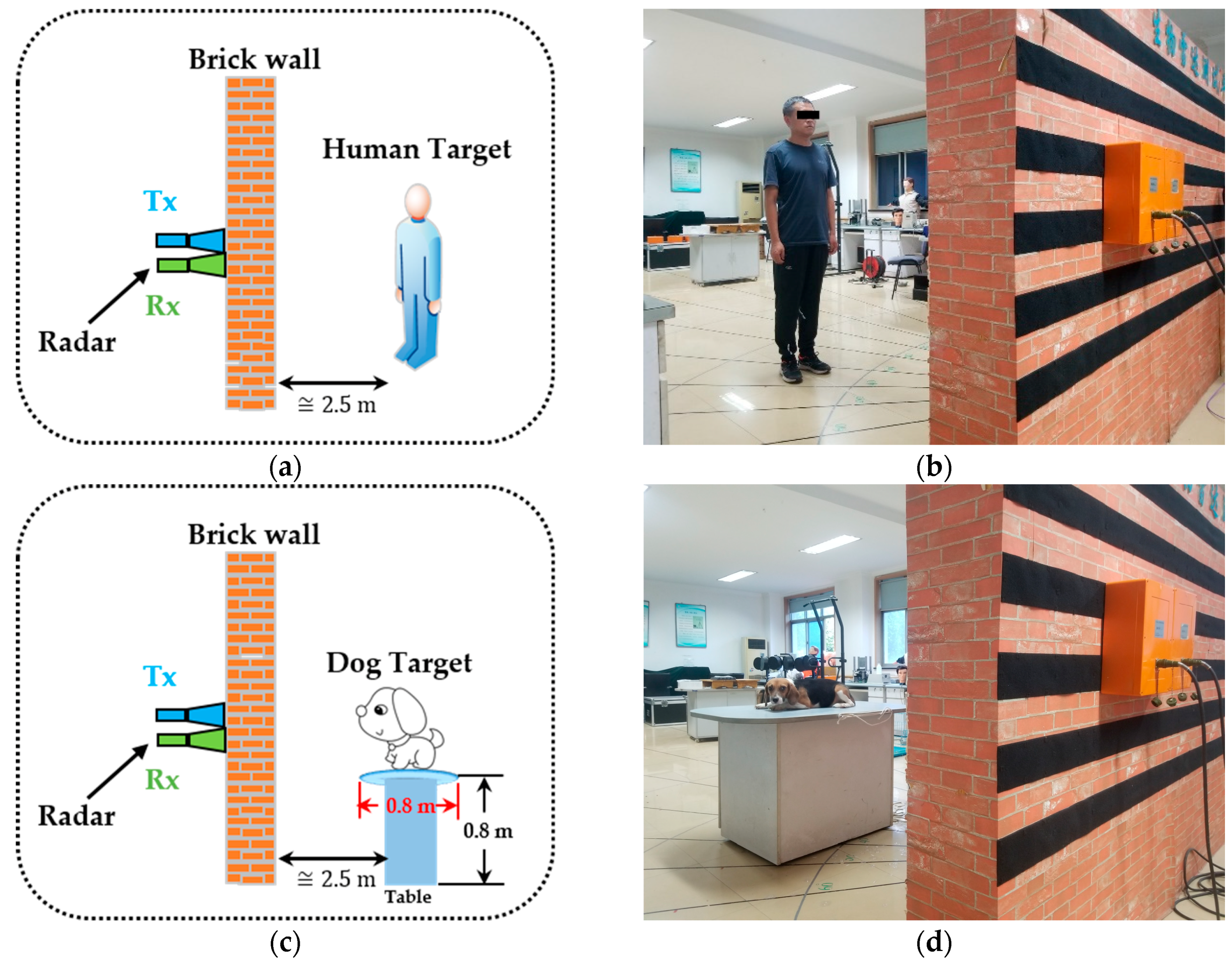
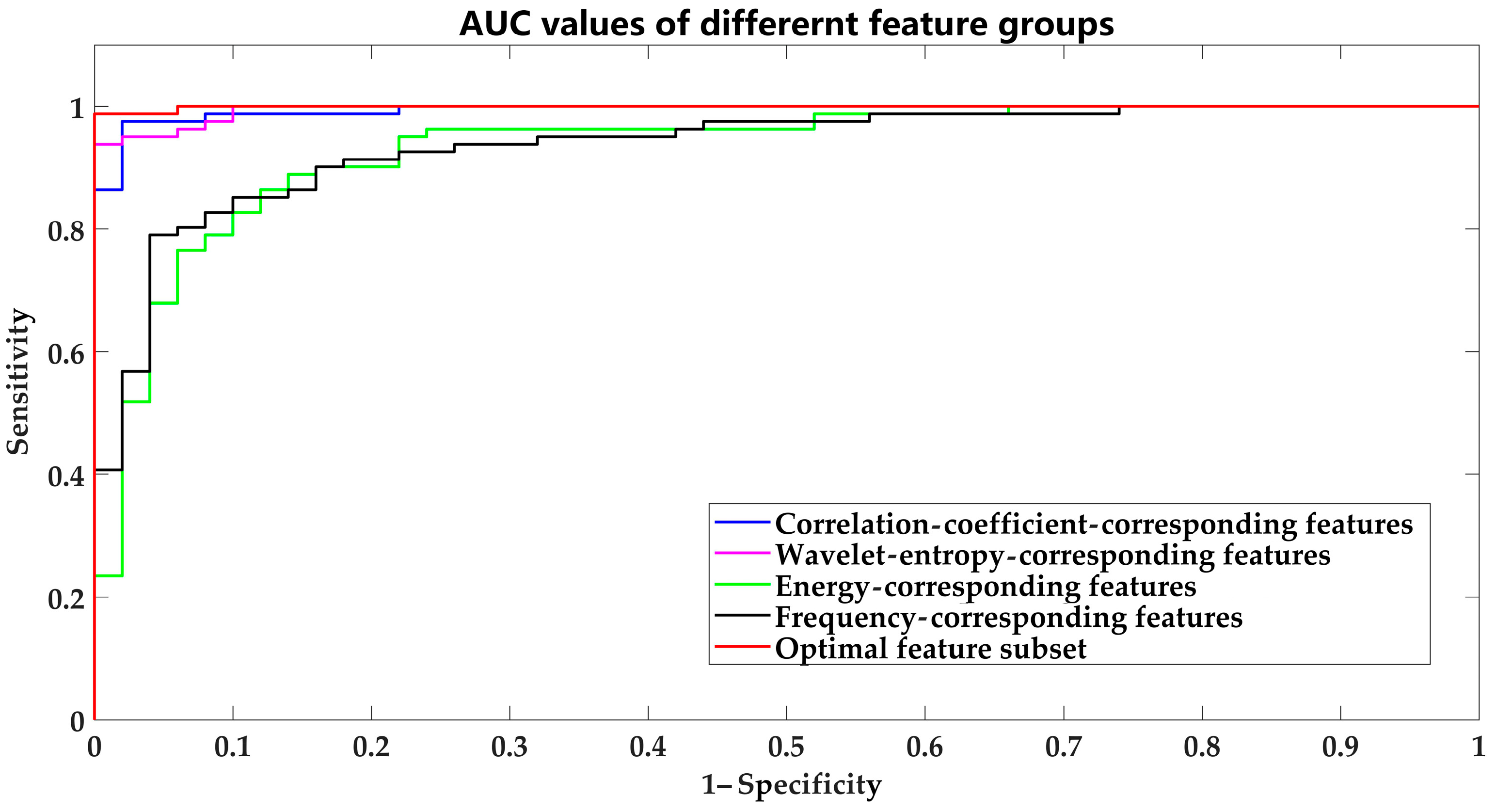
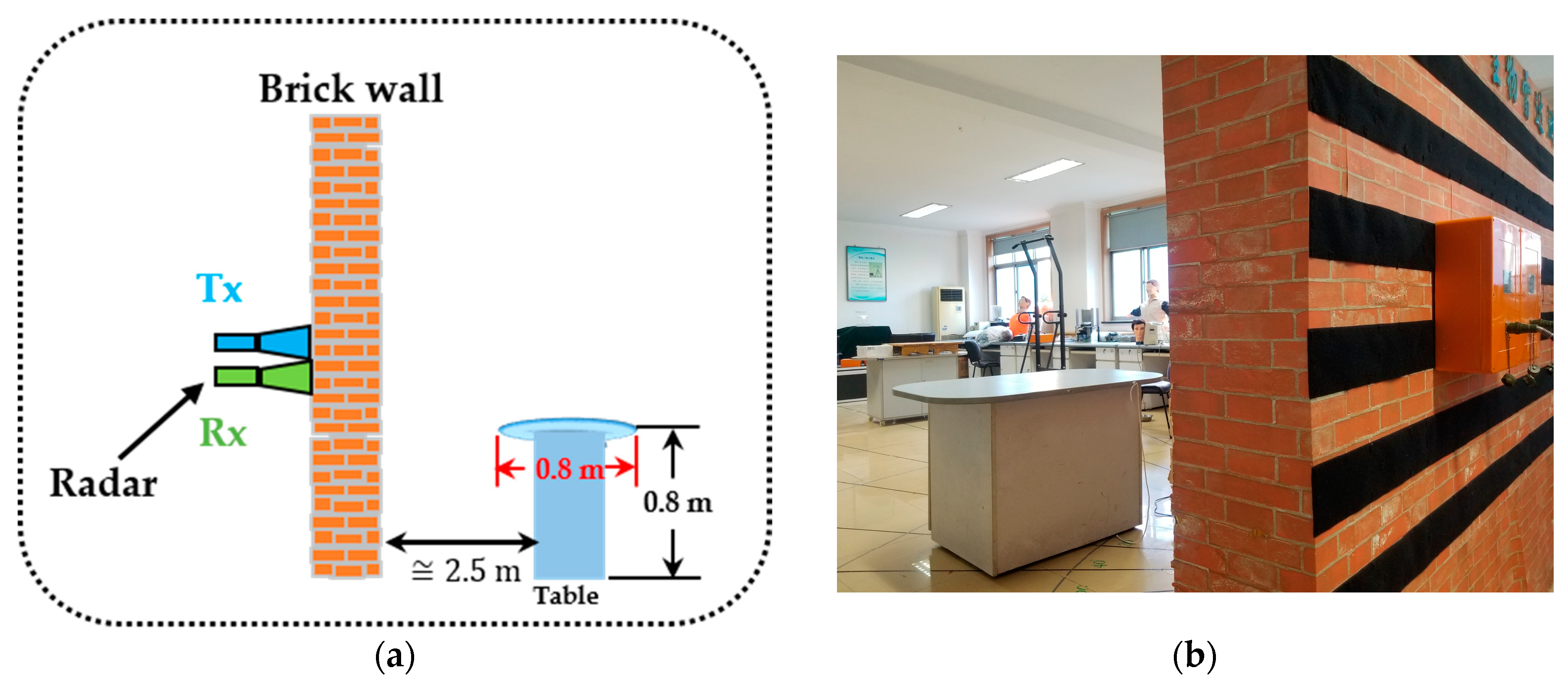
According to the accumulation of research results in recent years, 12 capable features belonging to four categories, consisting of two energy-corresponding features, two correlation coefficient-corresponding features, four wavelet entropy-corresponding features, and four frequency-corresponding features were utilized after signal preprocessing. The detailed feature descriptions are described below.
3.1. Energy-Corresponding Features
• Standard deviation change rate of micro vibration ()
When calculating
,
. Preliminary researches have shown that the deviations in the amplitude values in target position are the greatest in
, indicating that the standard deviation (
) of the target signal is the greatest. Target signal is defined as the specific point signal which is right at the target position. The calculation of
is expressed as:
where
is a scalar denoting amplitudes of the point signals. Then, an optimal window (OW), where the target signal is in the middle position, is chosen along the fast-time dimension with fixed width, and the
of every point signal in the OW is calculated. Accordingly, the
is expressed as:
where
is the max
value and
is the min
value within the OW. According to the work in [
18], it is better to choose the width of the OW as
, so that the difference between human targets and dog targets will be largest.
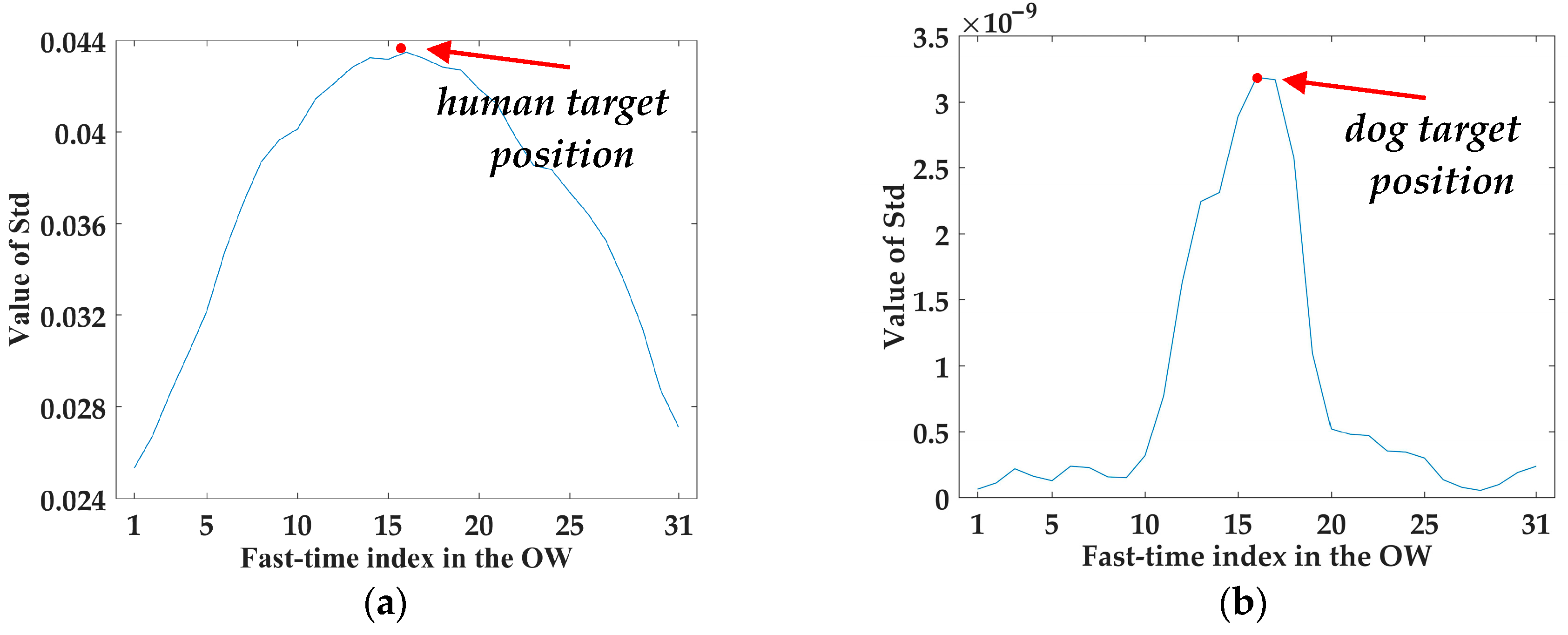
Figure 5 illustrates the value of
closer and further than the target’s position for 15 points of human and dog targets, respectively. Generally, the changing trend of
in the OW of human targets is much gentler than that of dog targets. Therefore, the
of human targets is much lower than that of dog targets.
• Energy ratio of the reference frequency band ()
In the calculation of
, the preprocessing steps are similar to that of
. The difference is that Q = 10 and the normalization is along the slow-time dimension, as illustrated in Equation (7). Thus, the 2048 points along the fast-time index associated to the range are compressed into 200 points [
18].
Then, ensemble empirical mode decomposition (EEMD) is performed on the target signal. EEMD is a noise-eliminating algorithm, and it can decompose the original target signal into a series of intrinsic mode function (IMF) components with different characteristic scales by adding multiple sets of different white noises [
19,
20,
21]. Its procedures are as follows:
After dividing the original target signal into V-order IMF components by EEMD, noise will be eliminated using the discriminant method as expressed in Equations (11) and (12):
where
is the energy concentration ratio and
is the discrete autocorrelation sequence of the
i-order (
i = 2,3, …,V) IMF components of the target signal, which is defined in Equation (10).
denotes the interval with length of three points wherein the symmetric point of
is in the middle and
denotes energy concentration ratio in the interval. When the decline rate of energy concentration ratio
satisfies the condition
, the
-order IMF component is considered as denoised signal. The reconstructed signal
is expressed in Equation (13).
is the energy proportion of the reconstructed signal in human respiratory frequency band (0.2–0.4 Hz), expressed in Equation (14).
where
is the total energy of the reconstructed signal in frequency domain, and
is the energy of reconstructed signal in the reference frequency band, i.e., the human respiratory frequency band. Generally,
of humans is approximately 40% and that of dogs is approximately 18% [
15,
19].
3.2. Correlation Coefficient-Corresponding Features
• Optimal Correlation Coefficient of Micro vibration ()
Because the details are particularly important in calculation with
, the distance window width here is
, and the width of OW here is
15. In this way,
is expressed as Equations (15) and (16):
where
TS represents the amplitudes of target signal, and
Y the amplitudes of other point signals within the OW. The horizontal bar above the
TS and
Y denotes the calculation of the average value.
is the correlation coefficient between target signal and another point signal in the OW.
is the mean value of the
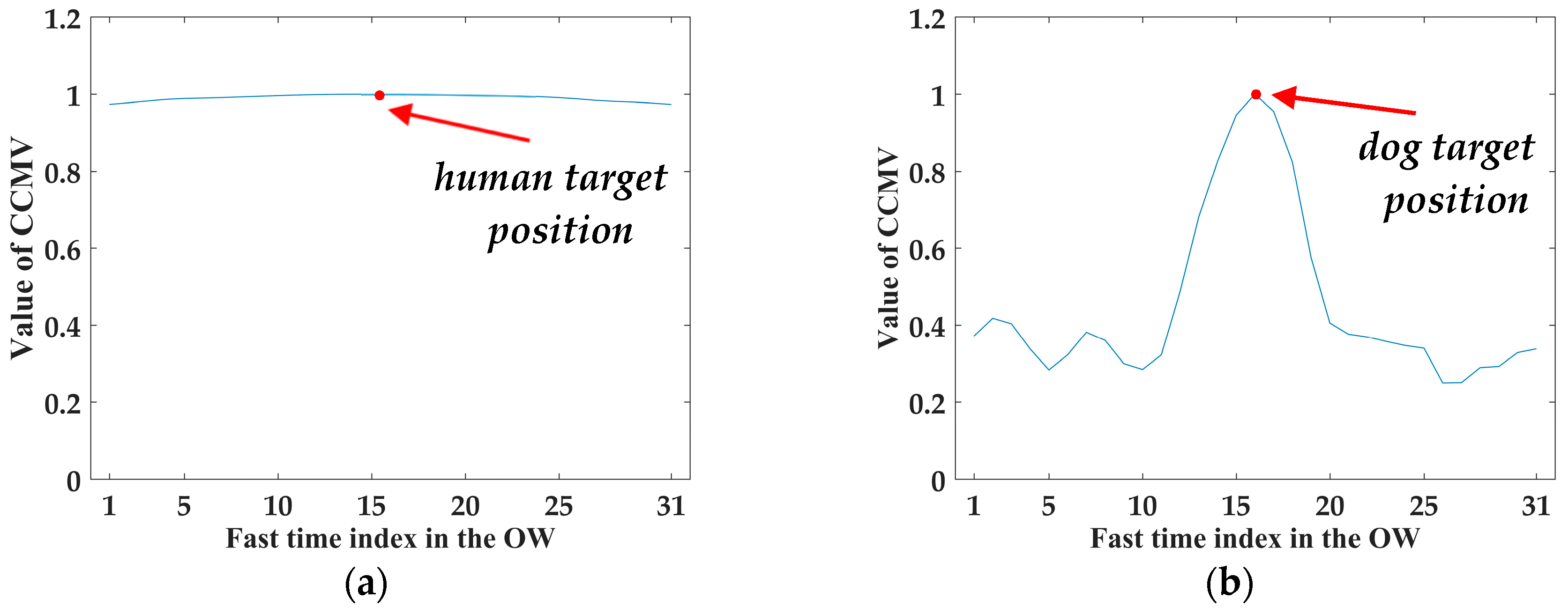
of each point signal in the OW. Generally, the
of human targets is very stable in the OW, close to one. Whereas the change of
of dog targets is greater. So the
of human targets is larger than that of dog targets. The comparison result of
of human targets and dog targets is expressed as in
Figure 6.
• Change rate of correlation coefficient of micro vibration ()
As illustrated in
Figure 6, the trend of change of human target is stable, whereas the trend of change of dog target is more intense. Therefore, the
of human targets is much smaller than that of dog targets. Equation (17) defines the calculation of
.
3.3. Wavelet Entropy-Corresponding Features
In the calculation of wavelet entropy-corresponding features, the parameter of Q in the preprocessing steps is chosen to be Q = 10 and the normalization is along slow-time dimension. Thus, the raw echo data are compressed into 200 points along the fast-time index, similar to the preprocessing of .
• Mean of wavelet entropy of target signal ()
Wavelet analysis can provide optimal time-frequency resolution of the signal and entropy can quantify the signal’s frequency patterns as a relevant measure of order or disorder in a dynamic system. Wavelet entropy (WE) combines the advantages of both. It can accurately characterize the dynamic change information of time-frequency variation of non-stationary signal complexity in time domain. More signal components indicate a more complex and irregular signal, and a larger value of wavelet entropy. Generally, dog signals are more complex than human signals [
12,
22]. Therefore, the
of human targets is much smaller than that of dog targets.
In the calculation of
, wavelet transform is first performed, followed by the calculation of relative wavelet energy. In Matsui, T. et al. [
23], Morlet first considered wavelets as a family of functions generated by translations and dilations of a unique function called the “mother wavelet”
. The family wavelet is expressed as:
where
is the scaling parameter which measures the degree of compression,
is the translation parameter which determines the time location of the wavelet, and
represents time. Let
be the real square integrable function space, the discrete wavelet transform of a signal
is defined as [
12,
13]:
where
is wavelet coefficient of wavelet sequence. For practical signal processing, the signal is assumed to be given by the sampled values
. Then, the signal reconstructed by wavelet transform is expressed as:
where
with
j,
k ∈ Z, and
is the mother wavelet.
is the number of resolution levels and its maximum value is
if the decomposition is performed over all resolution levels.
k is the time index and
is the residual at scale
j.In radar signal processing, the signal is divided among non-overlapping temporal windows of length
, and the length is chosen to be
empirically. Then, appropriate signal values are assigned to the central point of the time window for each interval
. Next, by considering the mean wavelet energy instead of the total wavelet energy, the mean energy at each resolution level
for the time window
using the wavelet coefficient is:
where
is the number of wavelet coefficients at resolution
involved in the time widow
. Then, the total energy of wavelet coefficient at interval
is expressed as:
Next, the relative wavelet energy that represents the energy’s probability distribution in scales is obtained by:
Finally, the average wavelet entropy of the whole time period is given by:
• Standard deviation of wavelet entropy of target signal ()
is a feature to quantitatively describe the fluctuation degree of wavelet entropy.
of human targets is much smaller than that of dog targets, since human target signals are more regular [
12,
13], generally speaking. It is given by:
• Mean of MWE in the OW window ()
In the calculation of
, an OW, where the target point signal is right in the middle, is also needed and the width is chosen to be
.
is the mean value of MWE of each point signal closer and further the target position for
point, i.e., the mean value of MWE in the OW. It is given by:
where
is the position of target point signal.
• Ratio of wavelet entropy ()
is the ratio of the mean value of
inside and outside the OW. It is expressed as:
3.4. Frequency-Corresponding Features
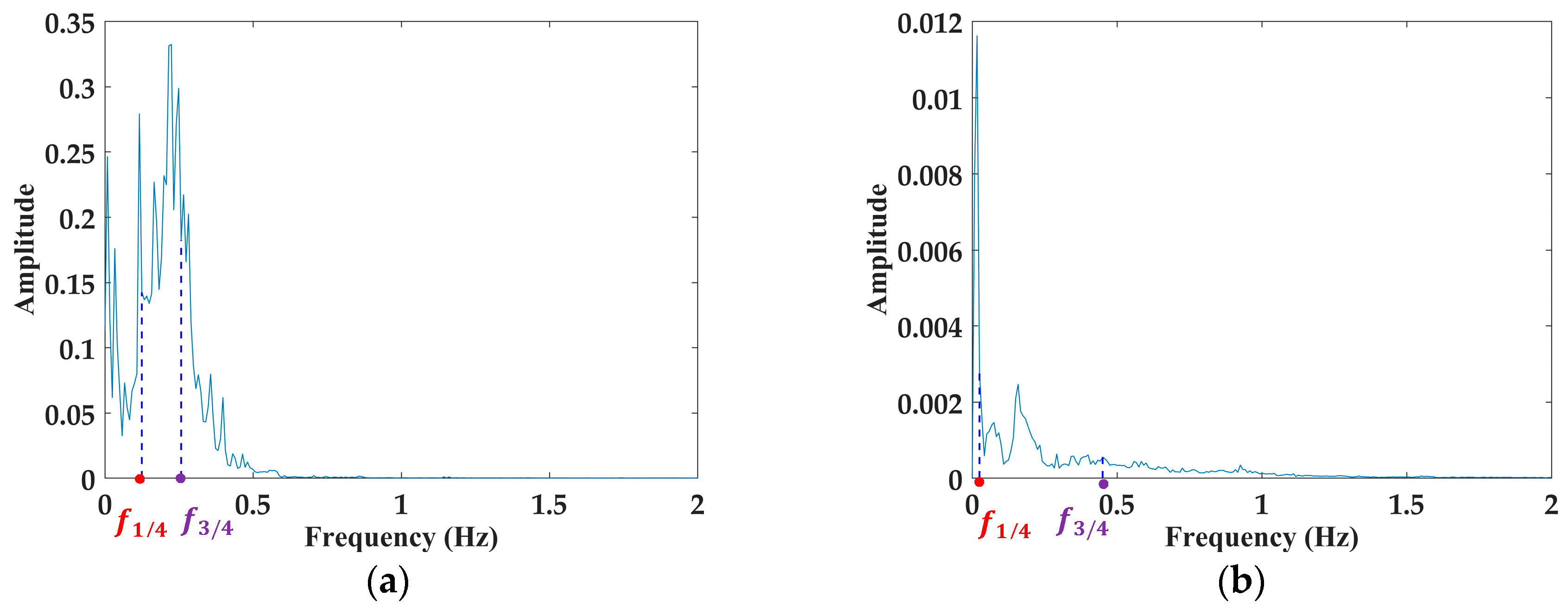
In this section, according to the research and accumulation of our group, it was found that the spectrum distribution of human targets in Hilbert marginal spectrum is different from that of dog targets. The curve of Hilbert marginal spectrum of human targets steeps slightly and the shape of the area under the curve is narrow and high. In contrast, the curve of dog targets is slightly gentle and the shape of the area under the curve is wide and low. Therefore, the frequency value corresponding to 1/4 total frequency band area, 3/4 total frequency band area under the Hilbert marginal spectrum curve, and the width between the above two are extracted.
• , and width between and ()
In this step, EEMD is performed first to process the target signal as Equations (8)–(13) illustrate. Then, Hilbert transformation is implemented in each IMF component of the reconstructed signal
.
Next, the analytical signals are constructed by:
The amplitude of the analytical signals is expressed by
and the instantaneous phase is expressed as
. Then, the Hilbert marginal spectrum can be given by:
where
is the total signal duration and
is the total IMF component number of the reconstructed signals.
is the instantaneous frequency which is defined as
[
24]. The comparison results of Hilbert marginal spectrum of human targets and dog targets are demonstrated in
Figure 7.
The
and
are the frequency values of the points corresponding to 1/4 total frequency band area and 3/4 total frequency band area, respectively, in
Figure 7. Accordingly,
is given by:
• Respiratory Frequency ()
After performing Fourier transform of the target signal, the of human targets and dog targets can be obtained.