An Empirical Assessment of Angular Dependency for RedEdge-M in Sloped Terrain Viticulture
Abstract
1. Introduction
2. Materials and Methods
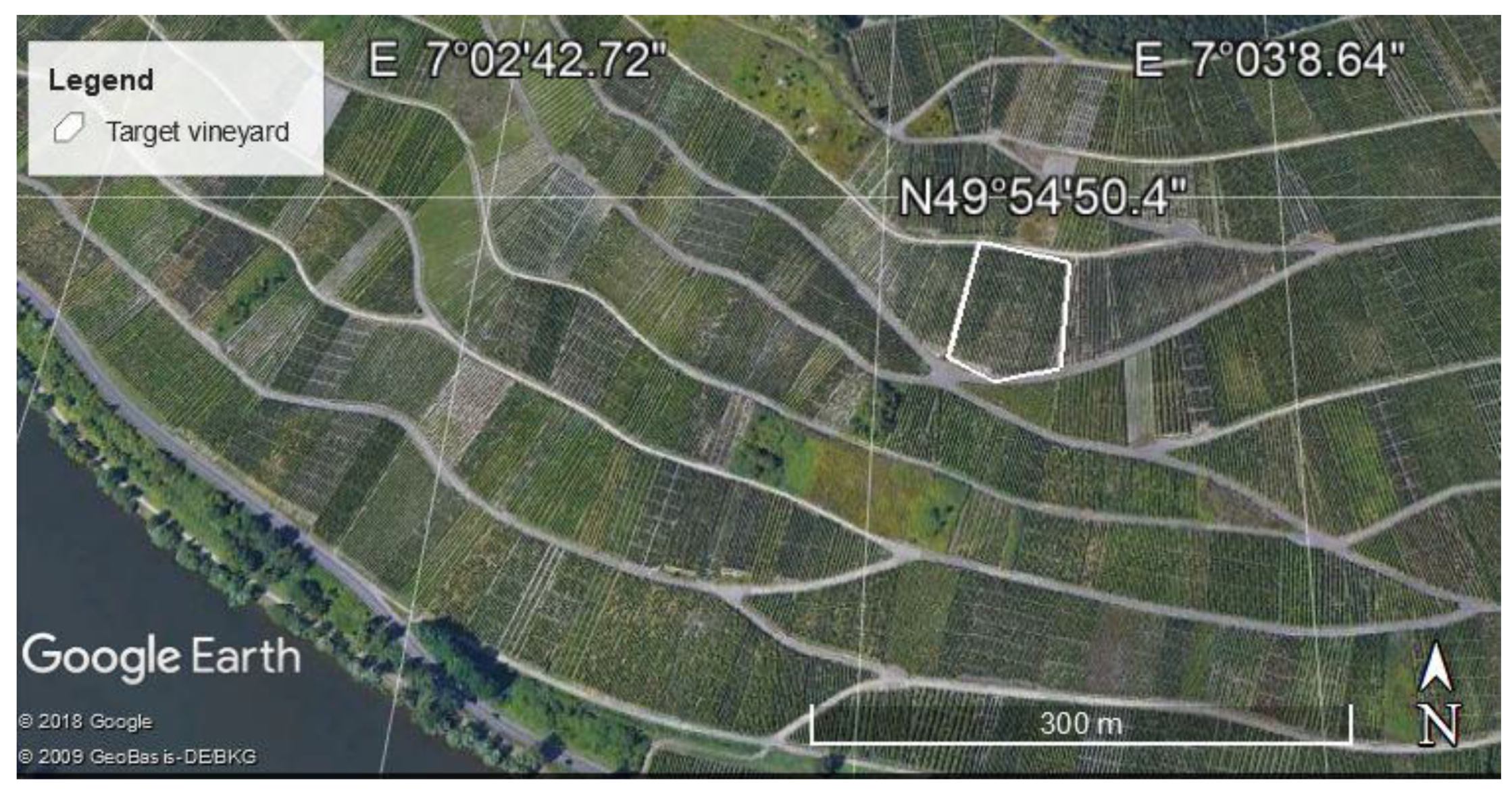
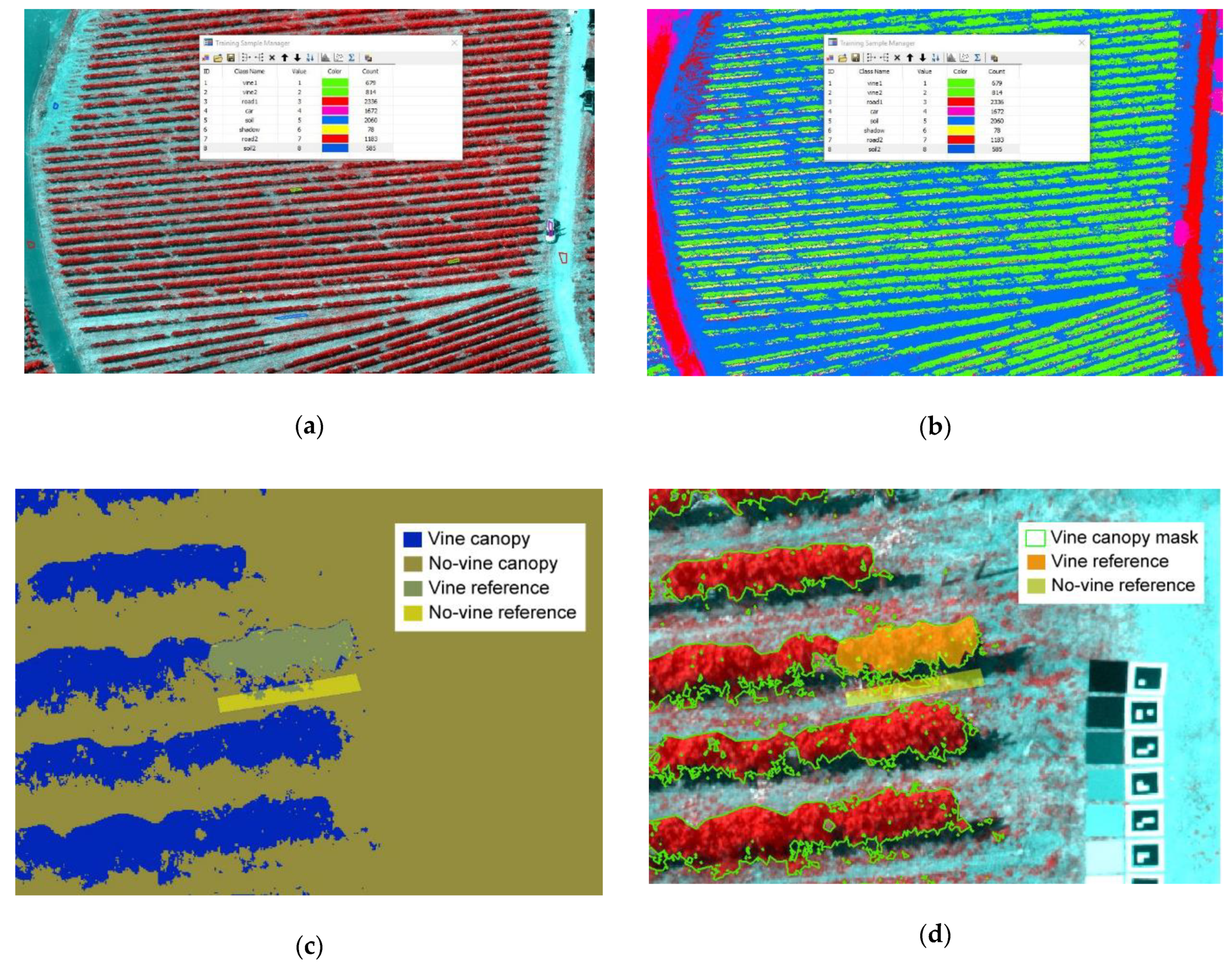
2.1. Study Area, UAV Trials, and Materials
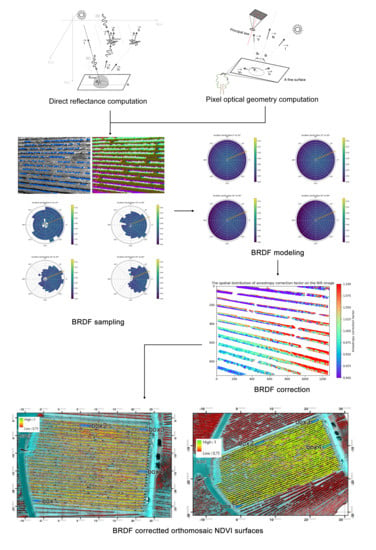
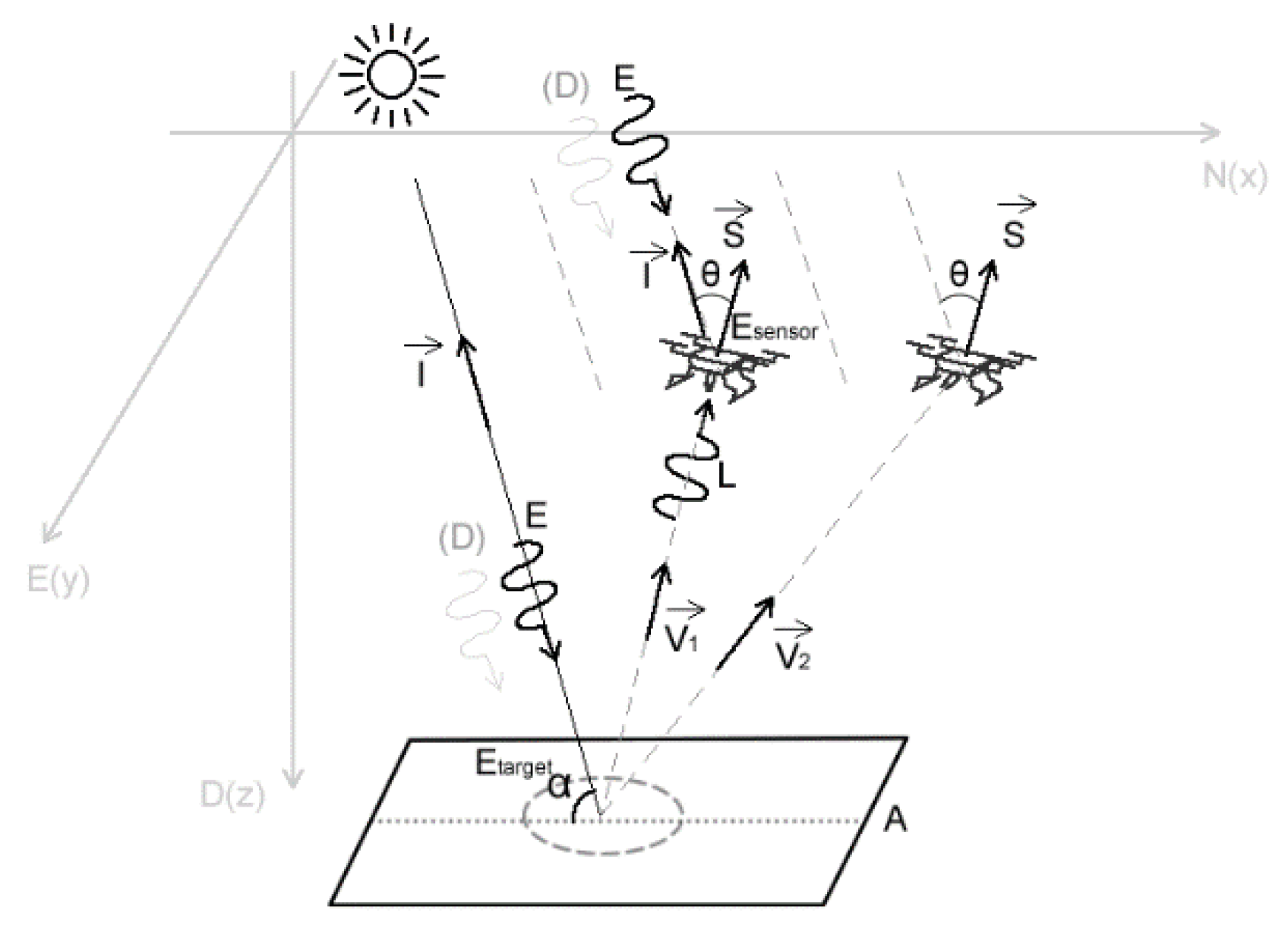
2.2. BRDF Sampling, Modeling, and Correction
- R—the observed directional reflectance factor;
- θi—the solar incident zenith;
- θv—the view zenith;
- φ—the relative azimuth;
- a, b, c, and d—coefficients to be empirically determined.
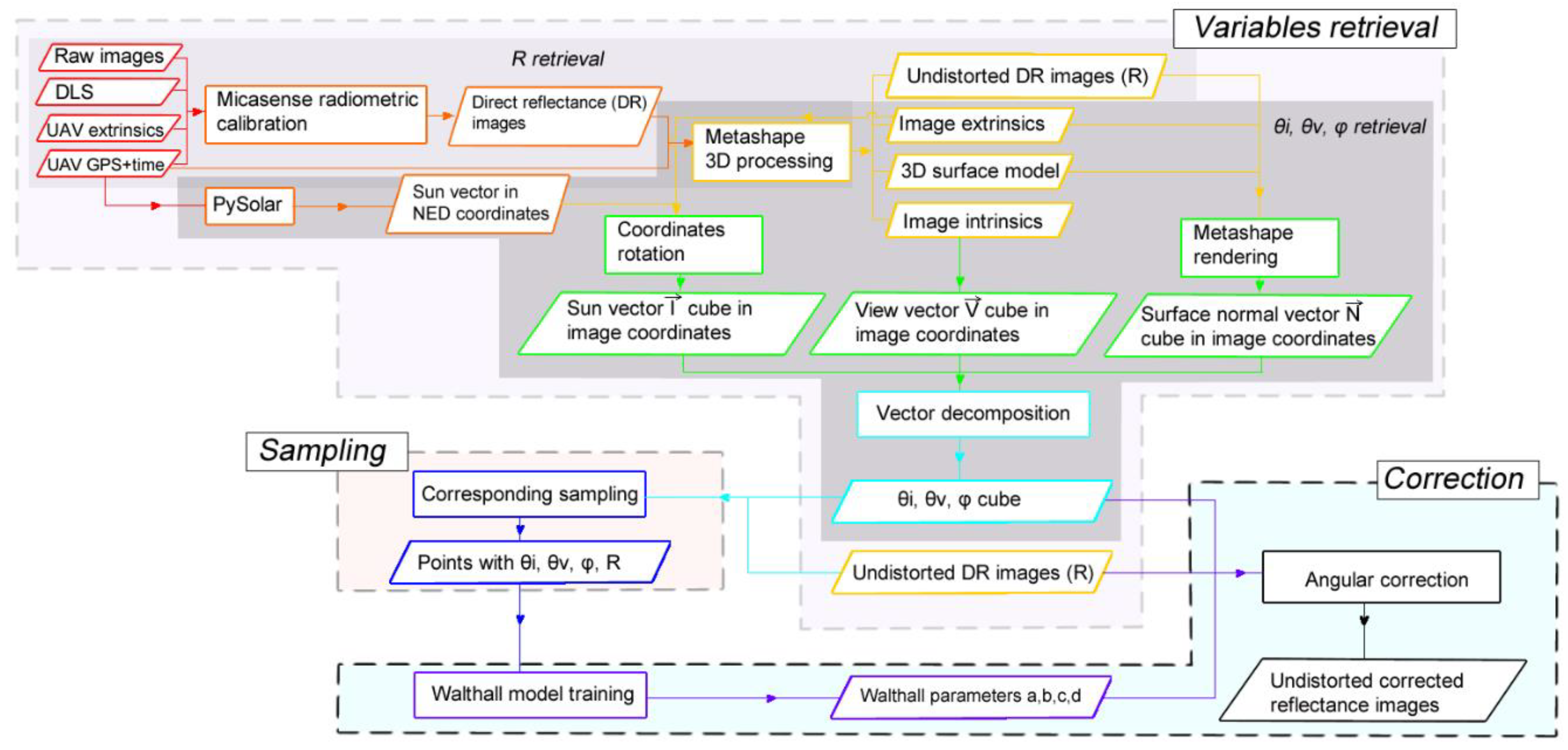
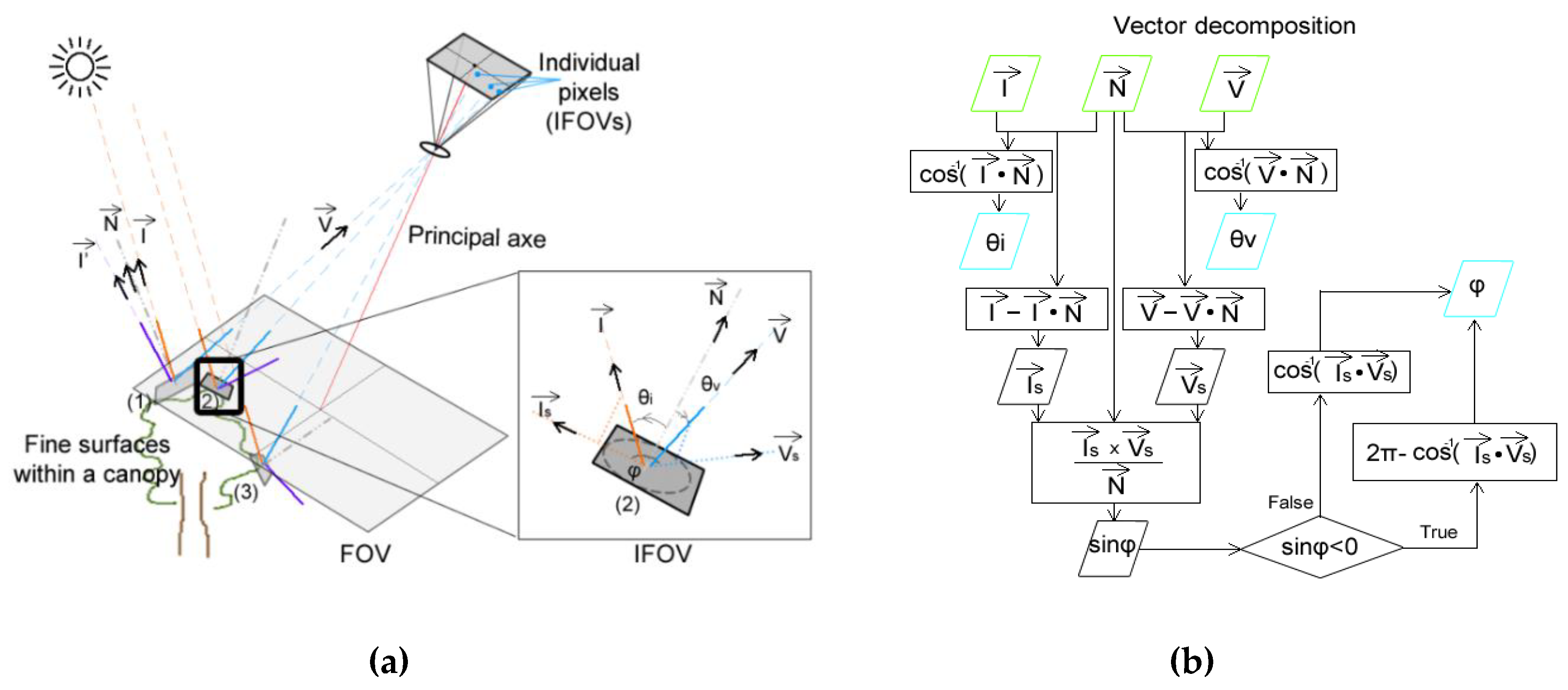
2.2.1. BRDF Variables Retrieval
- R—the observed reflectance factor;
- L—at-sensor-radiance (W/m2);
- Etarget—the irradiance (W/m2) at the target surface A;
- —the BRDF that takes the parameters of incoming zenith and azimuth θi, φi, and view zenith and azimuth θv, φv. To reduce one degree of freedom, the function is normally written as , where φ is the relative azimuth of φv counterclockwise rotated from φi. Here, this function is the Walthall model in Equation (1).
- A robust scale-invariant feature and match detection on image pairs. In this case, the direct reflectance images were used, and the RedEdge band was used as the master-band, due to its vegetation sensitivity.
- A sparse point cloud generation that computes the robust matching features in the 3D coordinates and aligns the camera extrinsic via structure from motion (SfM) methods.
- Depth maps generation on fine elements (on a downscaling of four pixels) by stereo pairs.
- A dense point cloud generation that computes the fine elements on the 3D coordinates based on their depth.
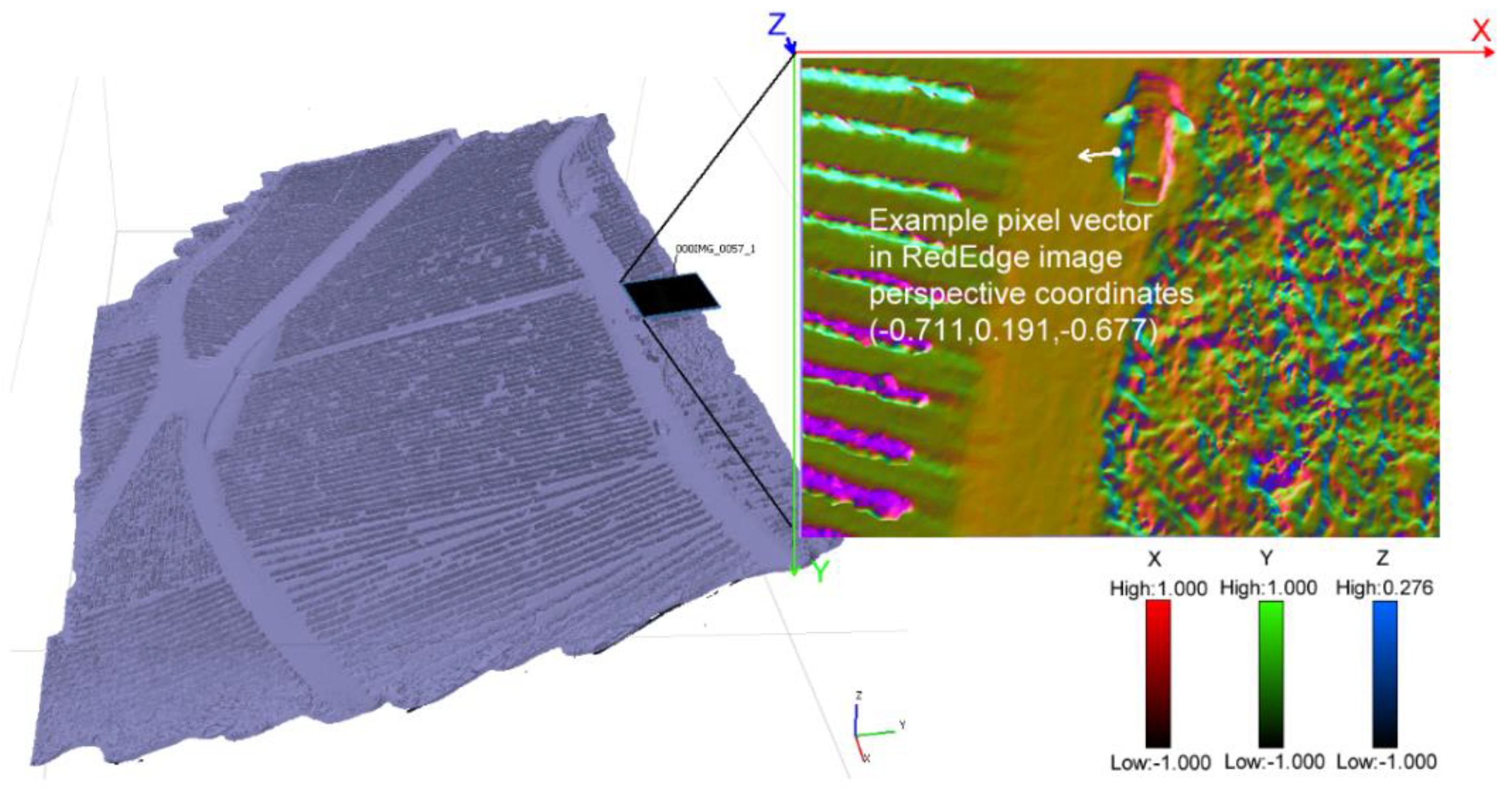
- Since the dense points do not have the image resolution, the mesh generation triangular irregular network (TIN) interpolates the dense points to the pixel level in the 3D coordinates to fill the gaps. In Figure 5, this mesh is visually described by the TIN faces (the violet 3D surface map on the left and the colorful micro triangle surfaces on the right) and numerically described by the unit surface normal vectors.
- Rendered by the FOVs from the mesh, the data cubes for all the images are thus reached.
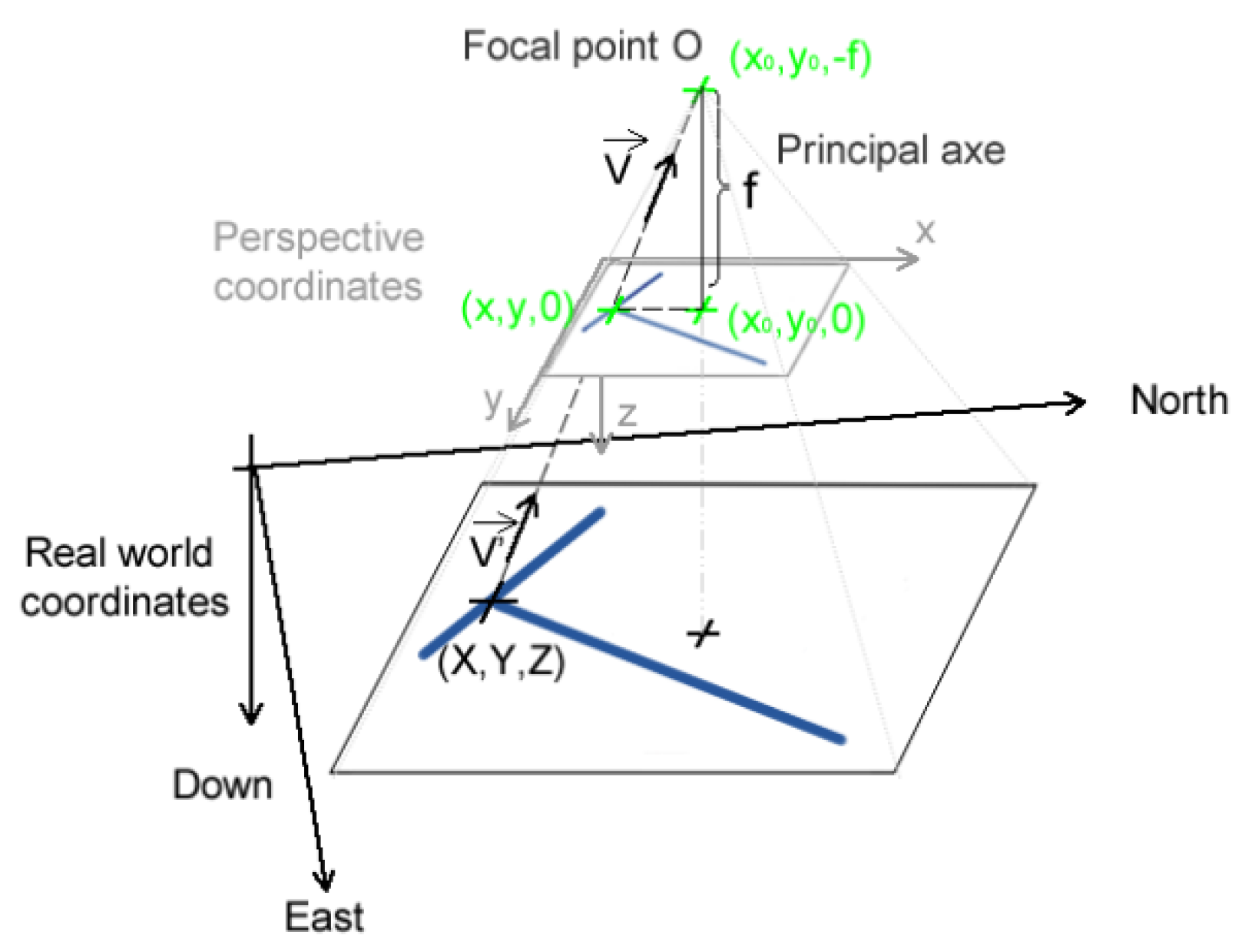
- (x, y)—the location of the pixel in RedEdge image perspective coordinates;
- (x0, y0)—the location of the principal point in RedEdge image perspective coordinates computed from Metashape;
- p—the pixel size;
- f—the focal length of each camera.
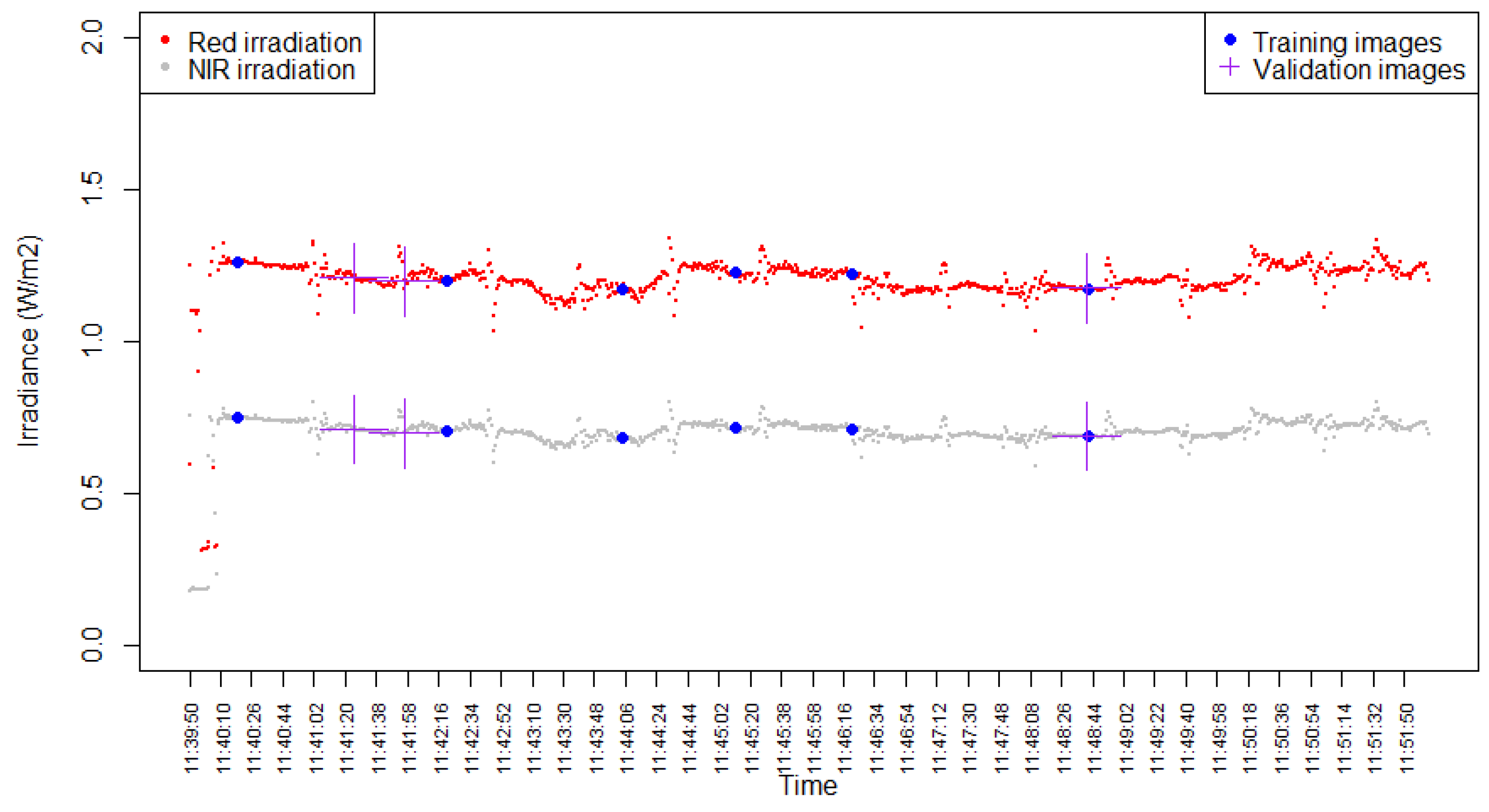
2.2.2. BRDF Sampling
2.2.3. BRDF Modeling and Correction
2.3. Result Analysis
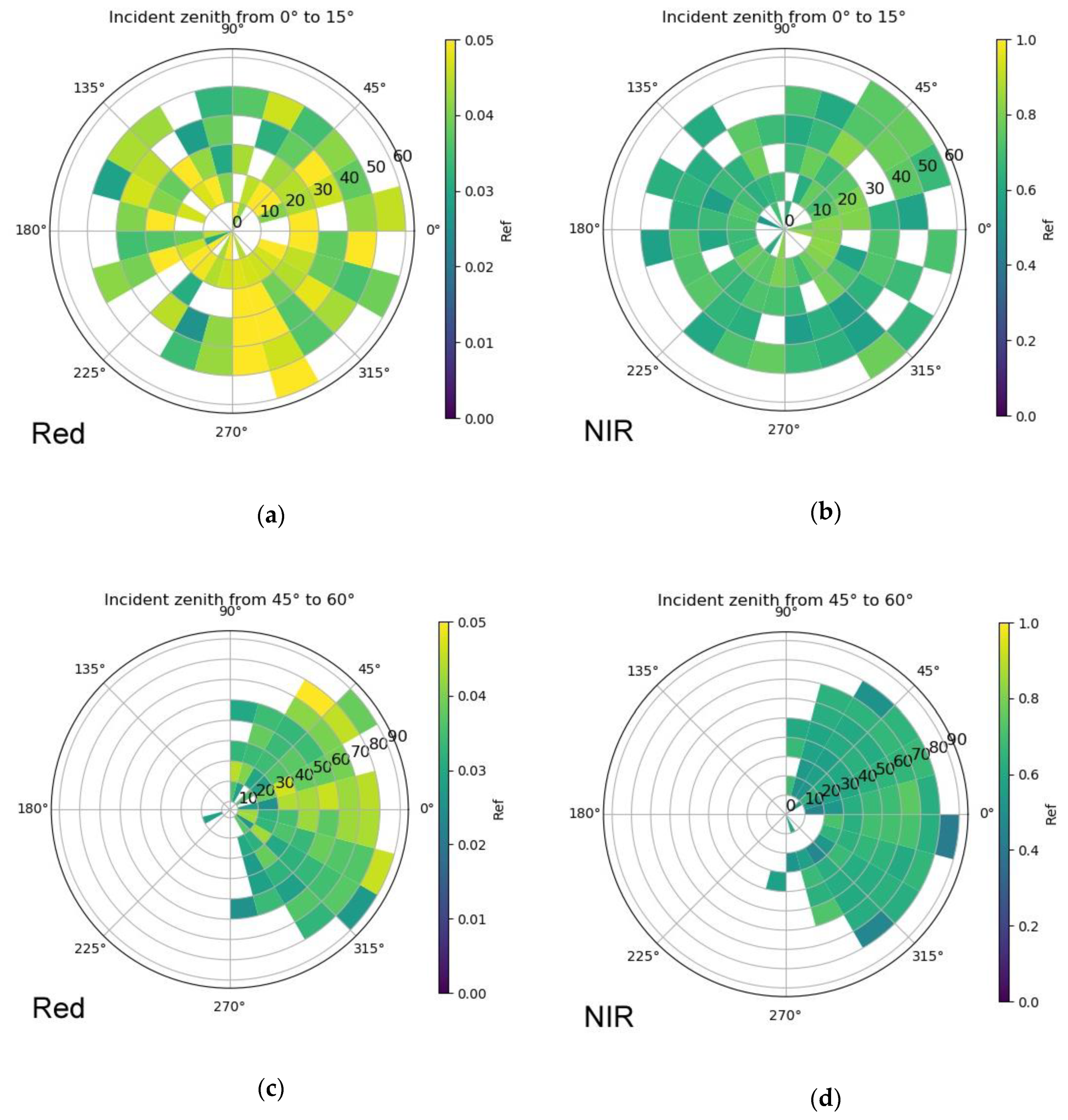
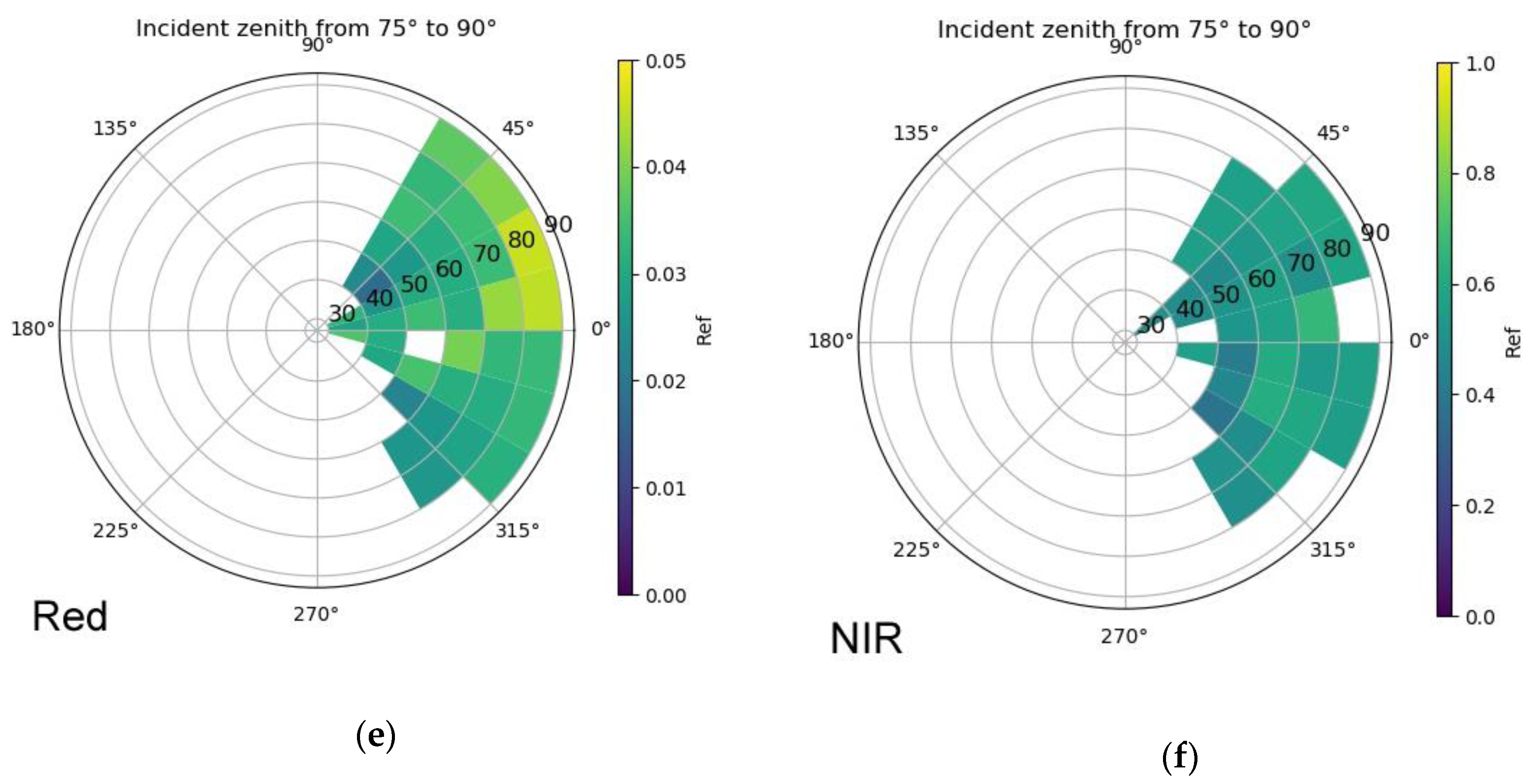
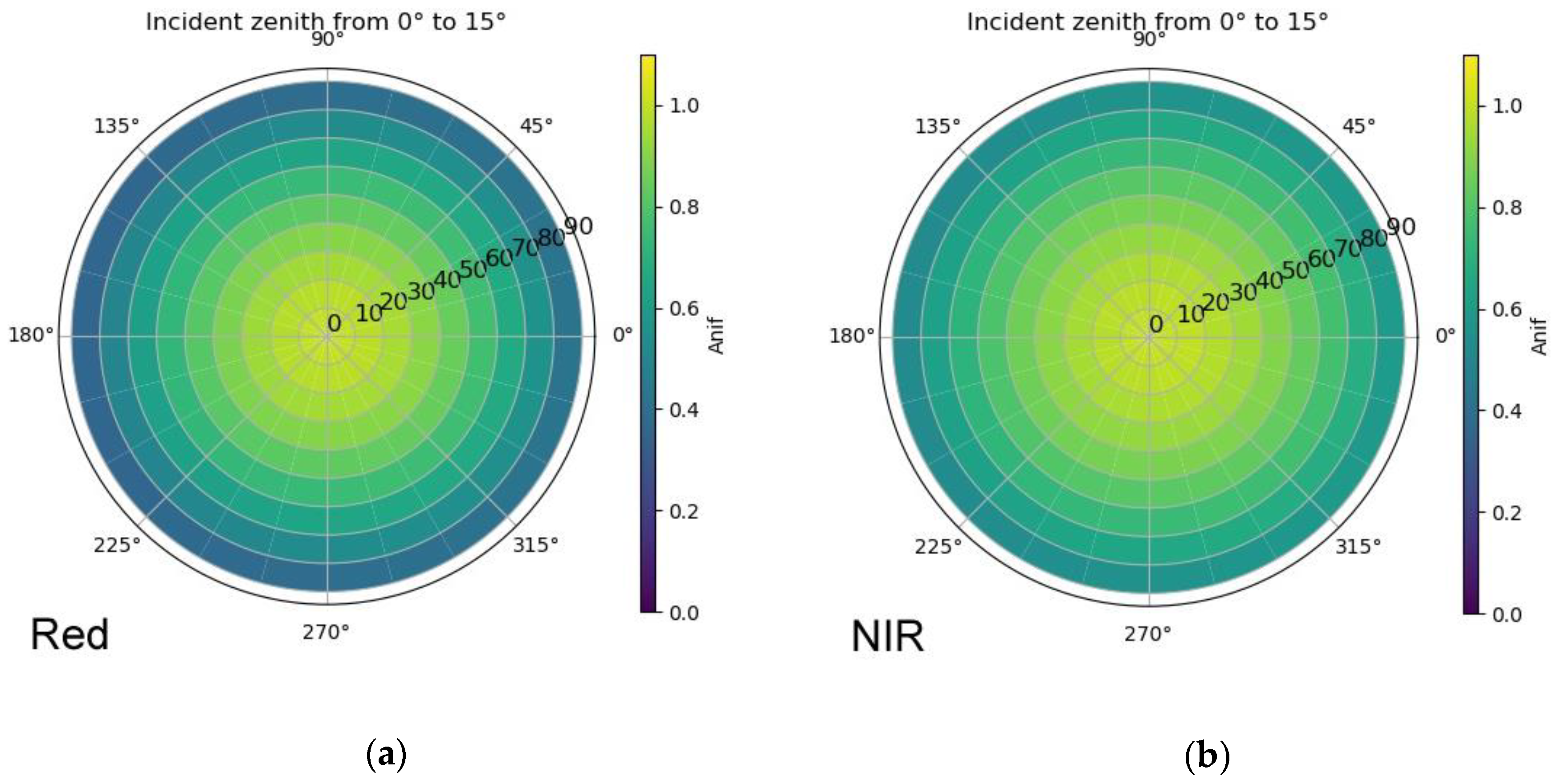
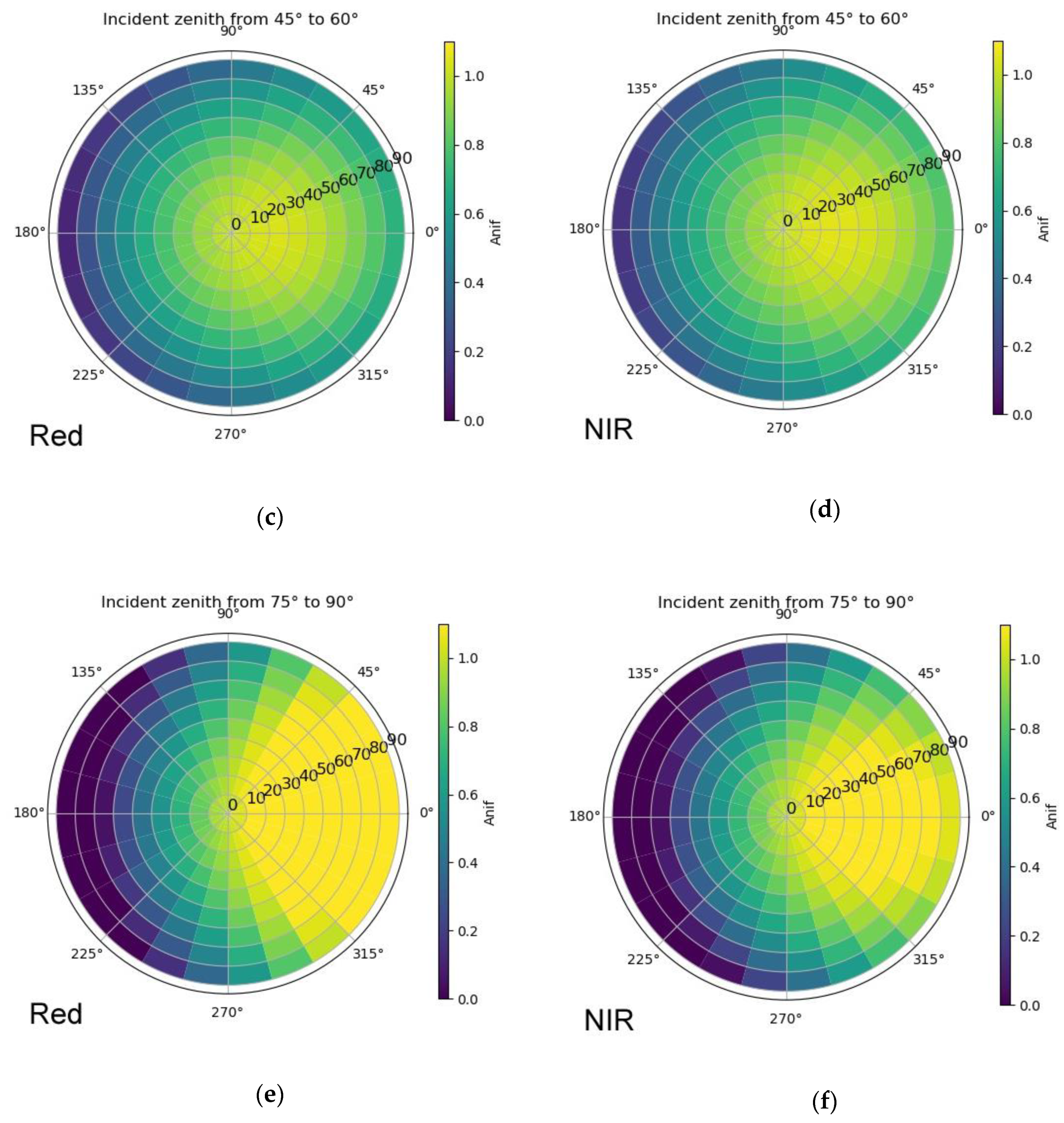
2.3.1. Sample and Model Visualization
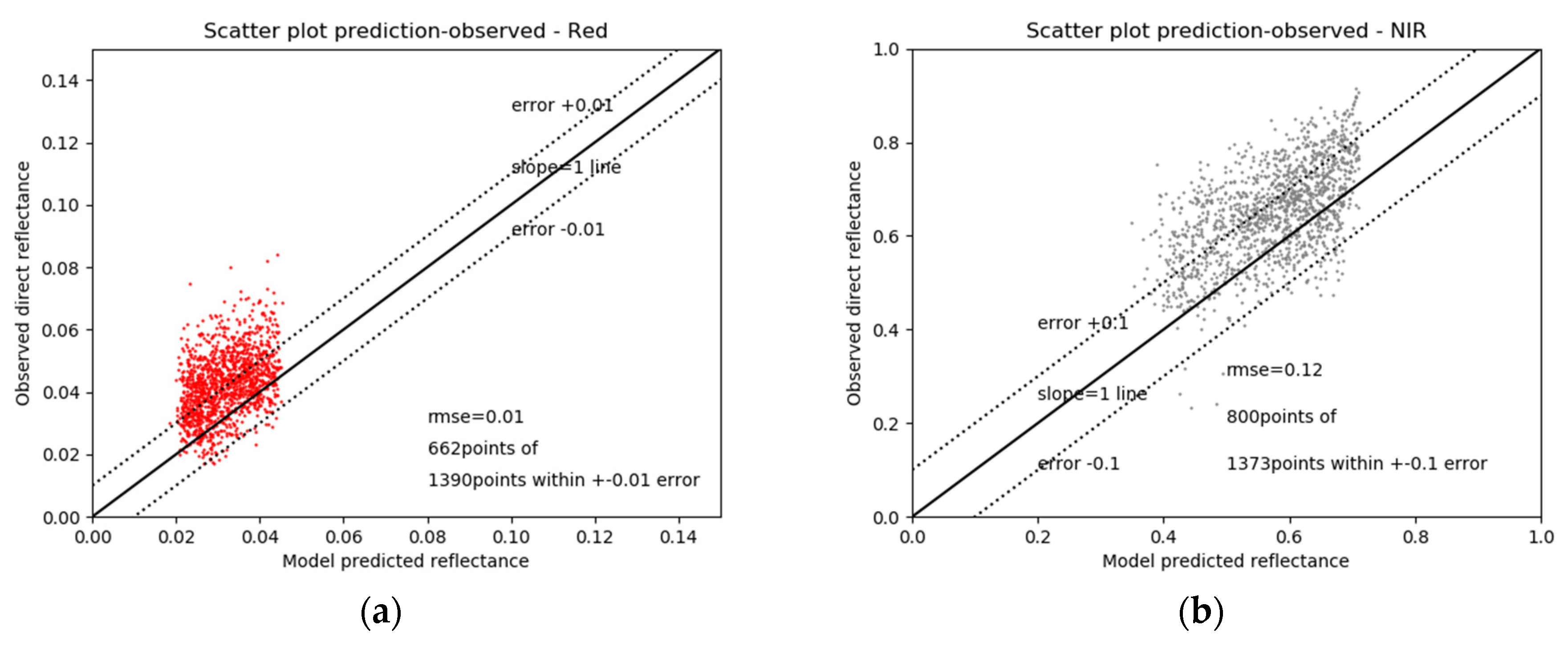
2.3.2. Prediction Assessment on Validation Points
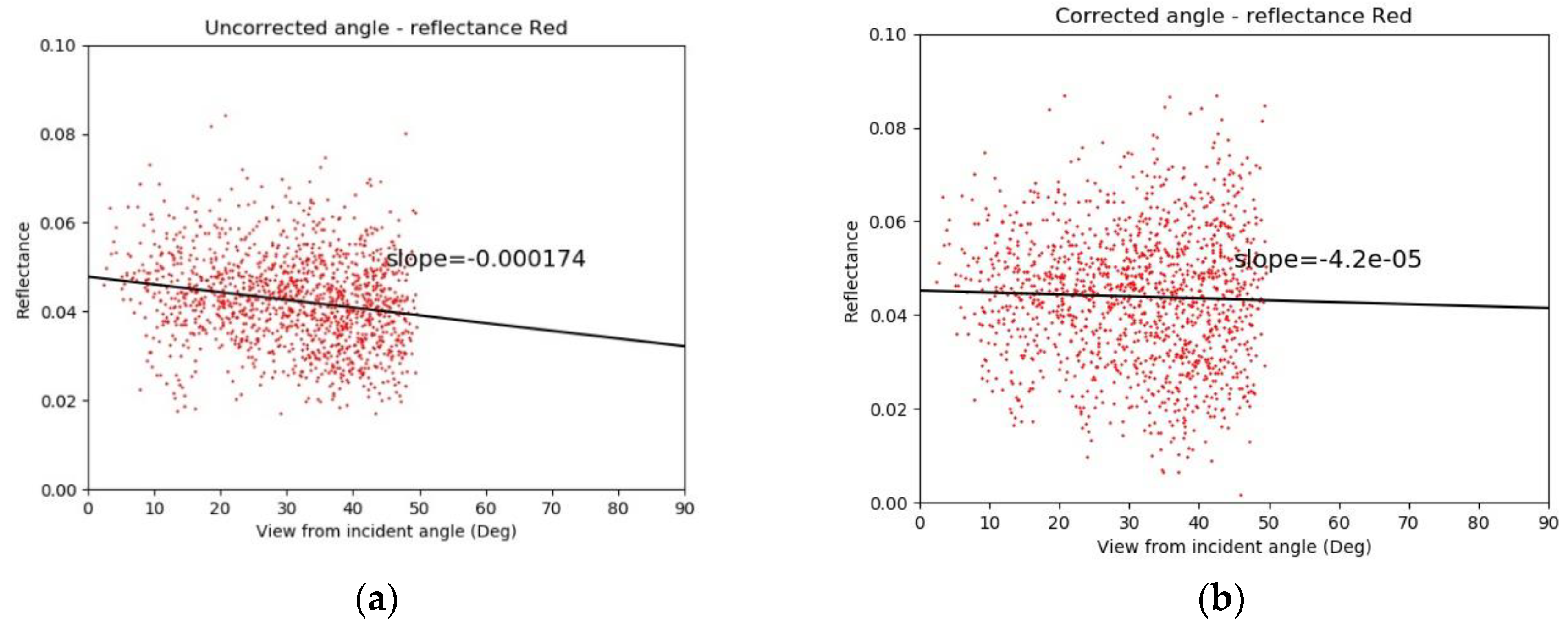
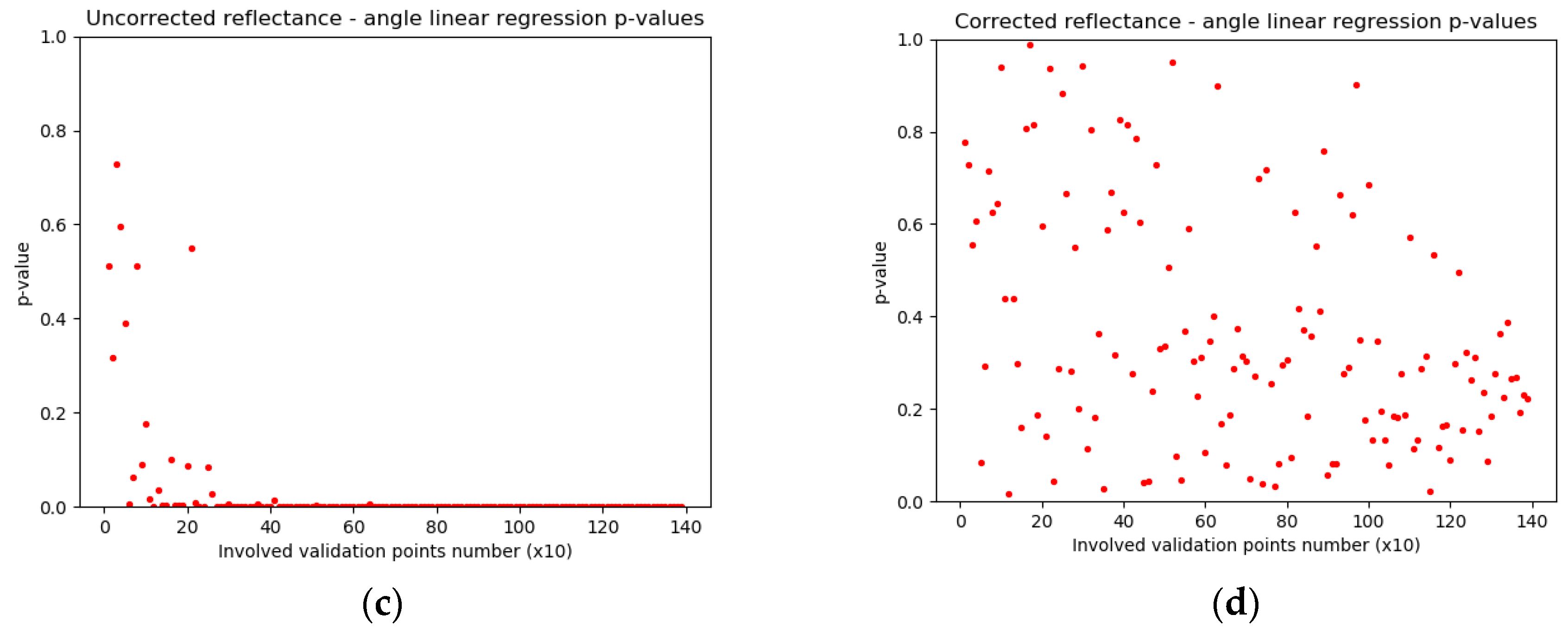
2.3.3. Correction Assessment on Validation Points
2.3.4. Correction Assessment on NDVI Orthomosaics
3. Results
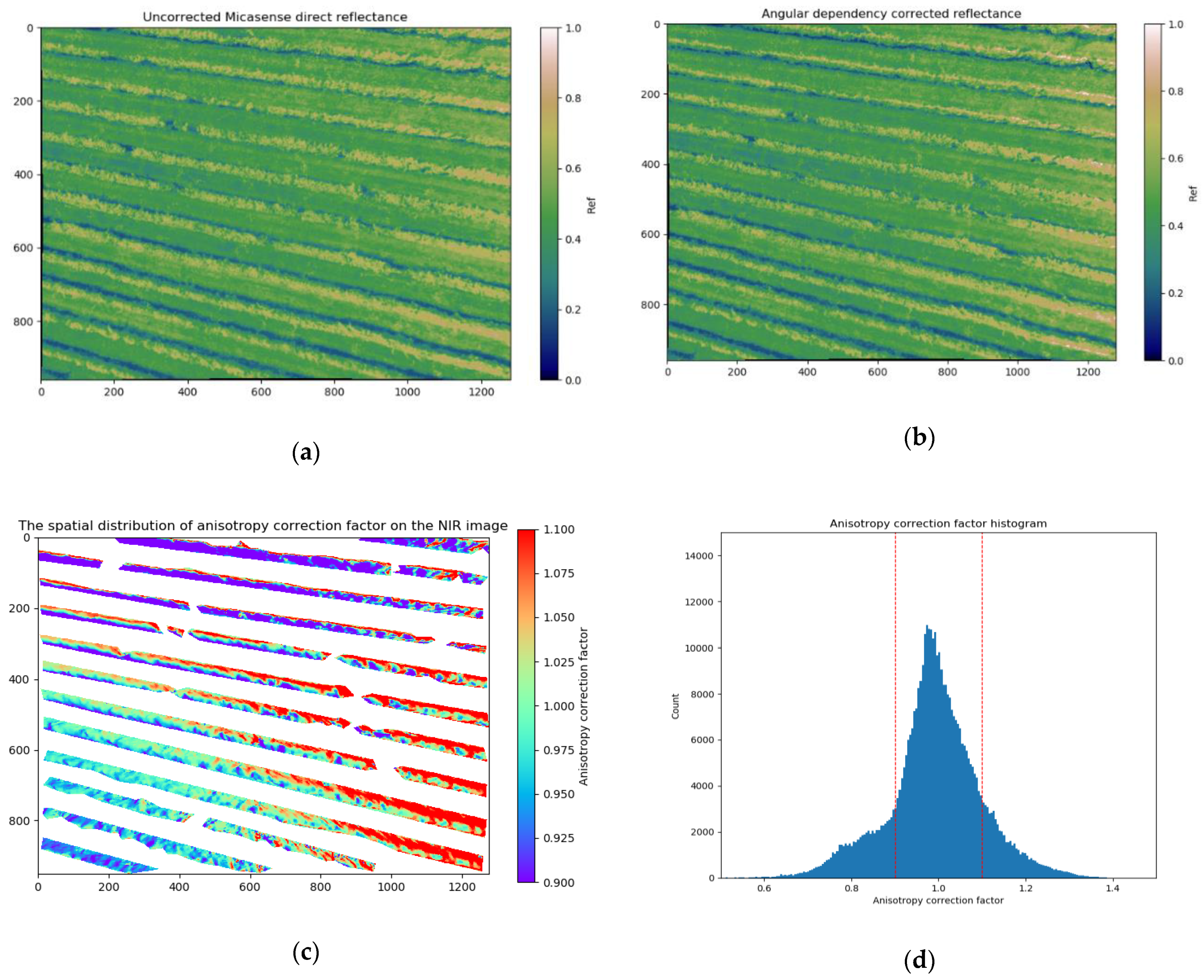
3.1. Sample and Model Visualization
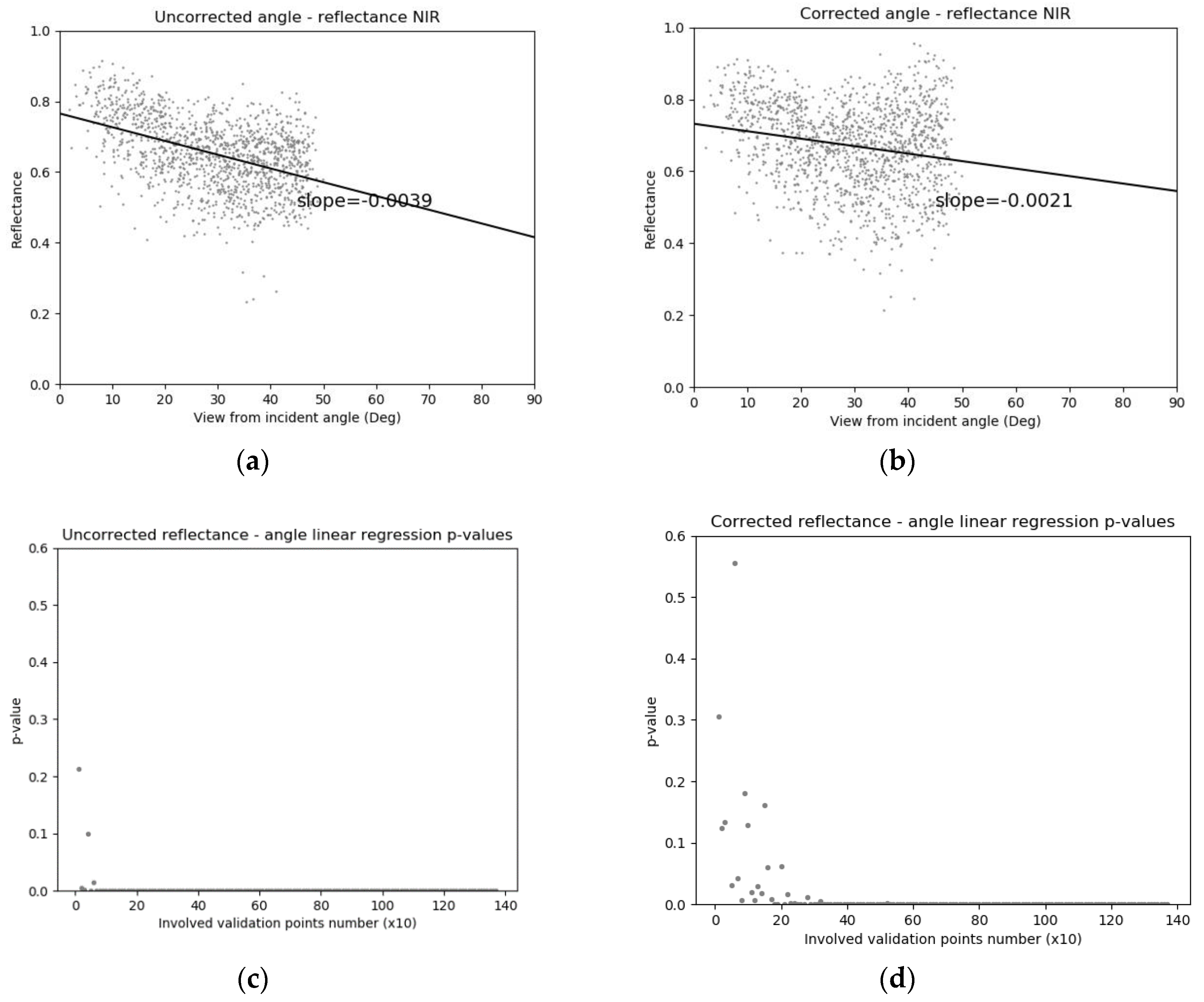
3.2. Prediction Assessment on Validation Points
3.3. Correction Assessment on Validation Points
3.4. Correction Assessment on NDVI Orthomosaics
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
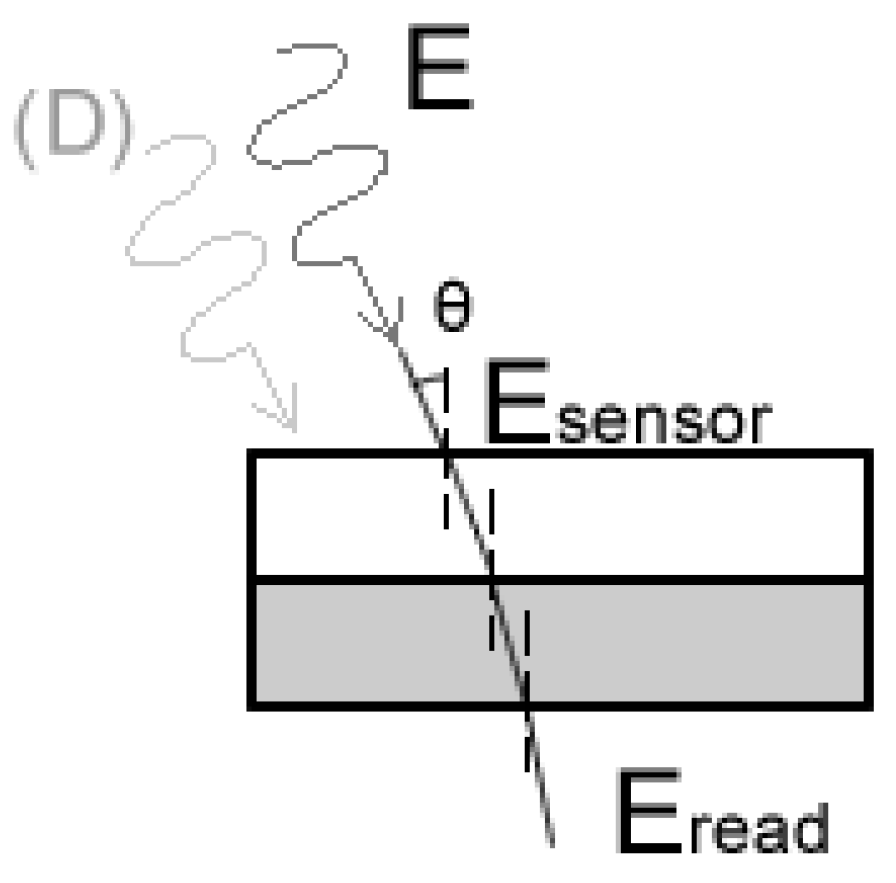
- L—absolute spectral radiance for the pixel (W/m2) at a given wavelength;
- V(x,y)—pixel-wise vignette correction function, see (Equation (A4));
- a1, a2, a3—RedEdge calibrated radiometric coefficients;
- te—image exposure time;
- g—sensor gain;
- x,y—the pixel column and row number;
- p—normalized raw pixel value;
- pBL—normalized black level value, attached in image metadata
- r—the distance of the pixel from the vignette center;
- cx,cy—vignette center location;
- k—a vignette polynomial function of 6 freedom degrees [36];
- k0, k1, k2, k3, k4, and k5—the MicaSense calibrated vignette coefficients.
- —a vector in real-world NED coordinates;
- —a vector in image perspective coordinates;
- α—the roll angle;
- β—the pitch angle;
- γ—the yaw angle;
- R—the overall rotation matrix.
- —the s-polarized reflectance of the media mi;
- —the p-polarized reflectance of the media mi;
- —the incident zenith on the media mi;
- —the refractive index of the media mi;
- —the transmissivity of media mi, when the fractions of reflectance are both assumed ½;
- —the overall transmissivity of the multilayer DLS receiver of 3 layers.
References
- Arnó, J.; Martínez-Casasnovas, J.A.; Ribes-Dasi, M.; Rosell, J.R. Review. Precision Viticulture. Research topics, challenges and opportunities in site-specific vineyard management. Span. J. Agric. Res. 2009, 7, 779–790. [Google Scholar]
- Weiss, M.; Baret, F. Using 3D Point Clouds Derived from UAV RGB Imagery to Describe Vineyard 3D Macro-Structure. Remote Sens. 2017, 9, 111. [Google Scholar] [CrossRef]
- De Castro, A.I.; Jiménez-Brenes, F.M.; Torres-Sánchez, J.; Peña, J.M.; Borra-Serrano, I.; López-Granados, F. 3-D Characterization of Vineyards Using a Novel UAV Imagery-Based OBIA Procedure for Precision Viticulture Applications. Remote Sens. 2018, 10, 584. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.R.; De Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Matese, A.; Di Gennaro, S.F. Practical Applications of a Multisensor UAV Platform Based on Multispectral, Thermal and RGB High Resolution Images in Precision Viticulture. Remote Sens. 2018, 8, 116. [Google Scholar] [CrossRef]
- Romero, M.; Luo, Y.; Su, B.; Fuentes, S. Vineyard water status estimation using multispectral imagery from an UAV platform and machine learning algorithms for irrigation scheduling management. Comput. Electron. Agric. 2018, 147, 109–117. [Google Scholar] [CrossRef]
- Burkart, A.; Aasen, H.; Fryskowska, A.; Alonso, L.; Menz, G.; Bareth, G.; Rascher, R. Angular Dependency of Hyperspectral Measurements over Wheat Characterized by a Novel UAV Based Goniometer. Remote Sens. 2015, 7, 725–746. [Google Scholar] [CrossRef]
- Aasen, H. Influence of the viewing geometry within hyperspectral images retrieved from UAV snapshot cameras. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 257. [Google Scholar] [CrossRef]
- Schapeman-Strub, G.; Schapeman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing-definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Walthall, C.L.; Norman, J.M.; Welles, J.M.; Campbell, G.; Blad, B.L. Simple equation to approximate the bidirectional reflectance from vegetative canopies and bare soil surfaces. Appl. Opt. 1985, 24, 383. [Google Scholar] [CrossRef]
- Nilson, T.; Kuusk, A. A reflectance model for the homogeneous plant canopy and its inversion. Remote Sens. Environ. 1989, 27, 157–167. [Google Scholar] [CrossRef]
- Beisl, U.; Woodhouse, N. Correction of atmospheric and bidirectional effects in multispectral ADS40 images for mapping purposes. Int. Arch. Photogramm. Remote Sens. 2004, B7, 1682–1750. [Google Scholar]
- Rahman, H.; Pinty, B.; Verstraete, M.M. Coupled surface-atmosphere reflectance (CSAR) model 2. Semiempirical surface model usable with NOAA advanced very high resolution radiometer data. J. Geophys. Res. 1993, 98, 20791–20801. [Google Scholar] [CrossRef]
- Baret, F.; Jacquemoud, S.; Guyot, G.; Leprieur, C. Modeled analysis of the biophysical nature of spectral shifts and comparison with information content of broad bands. Remote Sens. Environ. 1992, 41, 133–142. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, 56–66. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the PROSAIL Model Capabilities for Future Hyperspectral Model Environments: A Review Study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef]
- Deering, D.W.; Eck, T.; Otterman, J. Bidirectional reflectance of selected desert surfaces and their three-parameter soil characterization. Agric. For. Meteorol. 1990, 52, 71–93. [Google Scholar] [CrossRef]
- Jackson, R.D.; Teillet, P.M.; Slater, P.N.; Fedosejevs, G.; Jasinski, M.F.; Aase, J.K.; Moran, M.S. Bidirectional Measurements of Surface Reflectance for View Angle Corrections of Oblique Imagery. Remote Sens. Environ. 1990, 32, 189–202. [Google Scholar] [CrossRef]
- Hakala, T.; Suomalainen, J.; Peltoniemi, J.I. Acquisition of Bidirectional Reflectance Factor Dataset Using a Micro Unmanned Aerial Vehicle and a Consumer Camera. Remote Sens. 2010, 2, 819–832. [Google Scholar] [CrossRef]
- Honkavaara, E.; Markelin, L.; Hakala, T.; Peltoniemi, J.I. The Metrology of Directional, Spectral Reflectance Factor Measurements Based on Area Format Imaging by UAVs. Photogramm. Fernerkund. Geoinf. 2014, 3, 175–188. [Google Scholar] [CrossRef]
- Hakala, T.; Honkavaara, E.; Saari, H.; Mäkynen, J.; Kaivosoja, J.; Pesonen, L.; Pölönen, I. Spectral Imaging from UAVs under varying Illumination Conditions. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Rostock, Germany, 4–6 September 2013; pp. 189–194. [Google Scholar]
- Hakala, T.; Markelin, L.; Honkavaara, E.; Scott, B.; Theocharous, T.; Nevalainen, O.; Näsi, R.; Suomalainen, J.; Viljanen, N.; Greenwell, C.; et al. Direct Reflectance Measurements from Drones: Sensor Absolute Radiometric Calibration and System Tests for Forest Reflectance Characterization. Remote Sens. 2018, 18, 1417. [Google Scholar] [CrossRef] [PubMed]
- Schneider-Zapp, K.; Cubero-Castan, M.; Shi, D.; Strecha, C. A new method to determine multi-angular reflectance factor from lightweight multispectral cameras with sky sensor in a target-less workflow applicable to UAV. Remote Sens. Environ. 2019, 229, 60–68. [Google Scholar] [CrossRef]
- Roosjen, P.P.J.; Suomalainen, J.M.; Bartholomeus, H.M.; Clevers, J.G.P.W. Hyperspectral reflectance anisotropy measurements using a pushbroom spectrometer on an unmanned aerial vehicle-results for barley, winter wheat, and potato. Remote Sens. 2016, 8, 909. [Google Scholar] [CrossRef]
- Roosjen, P.P.J.; Suomalainen, J.M.; Bartholomeus, H.M.; Clevers, J.G.P.W. Mapping reflectance anisotropy of a potato canopy using aerial images acquired with an unmanned aerial vehicle. Remote Sens. 2016, 8, 909. [Google Scholar] [CrossRef]
- Honkavaara, E.; Khoramshahi, E. Radiometric Correction of Close-Range Spectral Image Blocks Captured Using an Unmanned Aerial Vehicle with a Radiometric Block Adjustment. Remote Sens. 2018, 10, 256. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Wierzbicki, D.; Kedzierski, M.; Fryskowska, A.; Jasinski, J. Quality Assessment of the Bidirectional Reflectance Distribution Function for NIR Imagery Sequences from UAV. Remote Sens. 2018, 10, 1348. [Google Scholar] [CrossRef]
- Micasense/imageprocessing on Github. Available online: https://github.com/micasense/imageprocessing (accessed on 16 April 2019).
- Agisoft Metashape. Available online: https://www.agisoft.com/ (accessed on 16 April 2019).
- Downwelling Light Sensor (DLS) Integration Guide (PDF Download). Available online: https://support.micasense.com/hc/en-us/articles/218233618-Downwelling-Light-Sensor-DLS-Integration-Guide-PDF-Download- (accessed on 16 April 2019).
- ArcMap. Available online: http://desktop.arcgis.com/en/arcmap/ (accessed on 16 April 2019).
- PySolar. Available online: https://pysolar.readthedocs.io/en/latest/ (accessed on 18 April 2019).
- Beisl, U. Reflectance Calibration Scheme for Airborne Frame Camera Images. In Proceedings of the 2012 XXII ISPRS Congress International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, Australia, 25 August–1 September 2012; pp. 1–5. [Google Scholar]
- RedEdge Camera Radiometric Calibration Model. Available online: https://support.micasense.com/hc/en-us/articles/115000351194-RedEdge-Camera-Radiometric-Calibration-Model (accessed on 17 April 2019).
- Kordecki, A.; Palus, H.; Ball, A. Practical Vignetting Correction Method for Digital Camera with Measurement of Surface Luminance Distribution. SIViP 2016, 10, 1417–1424. [Google Scholar] [CrossRef]




| Band Name | Center Wavelength (nm) | Bandwidth (nm) |
|---|---|---|
| Blue | 475 | 20 |
| Green | 560 | 20 |
| Red | 668 | 10 |
| RedEdge | 717 | 10 |
| NIR | 840 | 40 |
| Validation Image | Amount of Validation points | RMSE | RRSE |
|---|---|---|---|
| Red_vali img 1 | 303 | 0.0148 | 1.27 |
| Red_vali img 2 | 659 | 0.0159 | 1.74 |
| Red_vali img 3 | 428 | 0.0117 | 1.33 |
| All above | 1390 | 0.0145 | 1.42 |
| Validation Image | Amount of Validation points | RMSE | RRSE |
|---|---|---|---|
| NIR_vali img 1 | 317 | 0.1071 | 1.11 |
| NIR_vali img 2 | 687 | 0.1079 | 1.15 |
| NIR_vali img 3 | 602 | 0.1345 | 1.43 |
| All above | 1373 | 0.1155 | 1.17 |
| Box | Uncorrected Median NDVI Angular Differential | Corrected Median NDVI Angular Differential |
|---|---|---|
| Box1 | 0.019 | 0.016 |
| Box2 | 0.032 | 0.022 |
| Box3 | 0.026 | 0.035 |
| Box4 | 0.015 | 0.023 |
| All pixels | 0.018 | 0.019 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, C.; Buddenbaum, H.; Retzlaff, R.; Udelhoven, T. An Empirical Assessment of Angular Dependency for RedEdge-M in Sloped Terrain Viticulture. Remote Sens. 2019, 11, 2561. https://doi.org/10.3390/rs11212561
Gong C, Buddenbaum H, Retzlaff R, Udelhoven T. An Empirical Assessment of Angular Dependency for RedEdge-M in Sloped Terrain Viticulture. Remote Sensing. 2019; 11(21):2561. https://doi.org/10.3390/rs11212561
Chicago/Turabian StyleGong, Chizhang, Henning Buddenbaum, Rebecca Retzlaff, and Thomas Udelhoven. 2019. "An Empirical Assessment of Angular Dependency for RedEdge-M in Sloped Terrain Viticulture" Remote Sensing 11, no. 21: 2561. https://doi.org/10.3390/rs11212561
APA StyleGong, C., Buddenbaum, H., Retzlaff, R., & Udelhoven, T. (2019). An Empirical Assessment of Angular Dependency for RedEdge-M in Sloped Terrain Viticulture. Remote Sensing, 11(21), 2561. https://doi.org/10.3390/rs11212561