Dual Activation Function-Based Extreme Learning Machine (ELM) for Estimating Grapevine Berry Yield and Quality
Abstract
1. Introduction
- (i)
- we developed berry yield and quality prediction models with MLR, PLSR, RFR and WRELM using vegetation indices derived from canopy spectra;
- (ii)
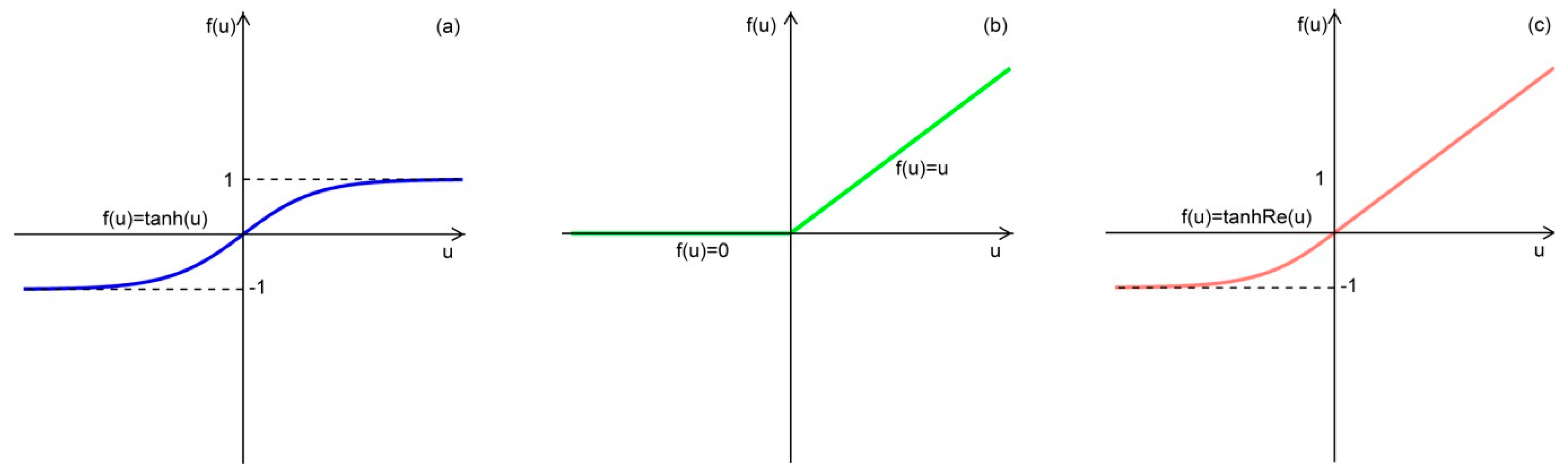
- we proposed a new activation function by fusing of hyperbolic tangent (Tanh) function and Rectified linear unit (ReLU) for Weighted Regularized ELM (WRELM-TanhRe);
- (iii)
- conducted comparative analysis between prediction models that were developed with existing methods and our newly proposed method;
- (iv)
- evaluated the relative importance of the vegetation indices to berry yield and quality estimation;
- (v)
- discussed the model scalability and transferability.
2. Study Site and Data
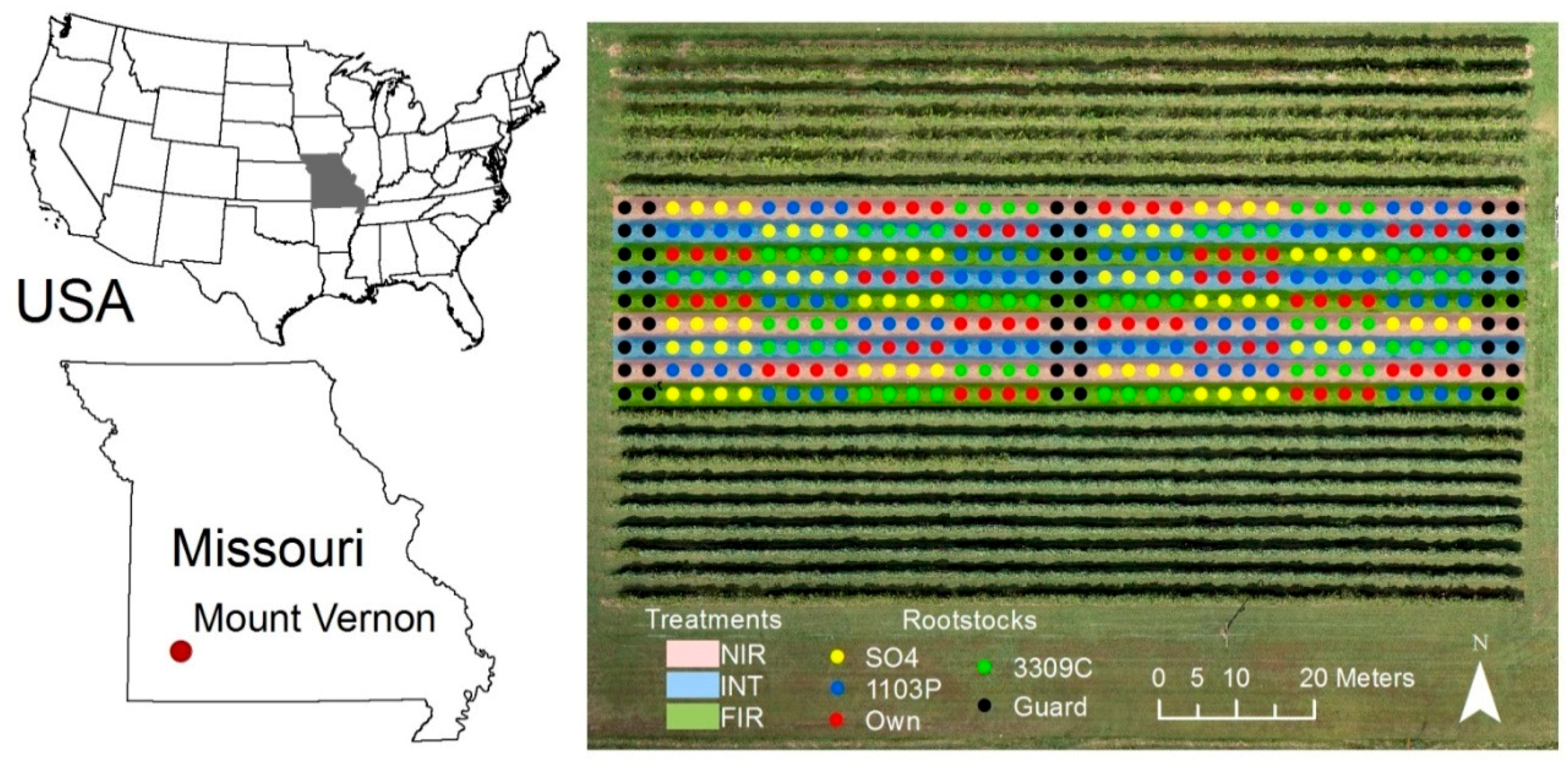
2.1. Study Site
2.2. Field Data Collection
2.2.1. Field Spectroscopy Measurements
2.2.2. Determination of Berry Yield and Quality
3. Methods
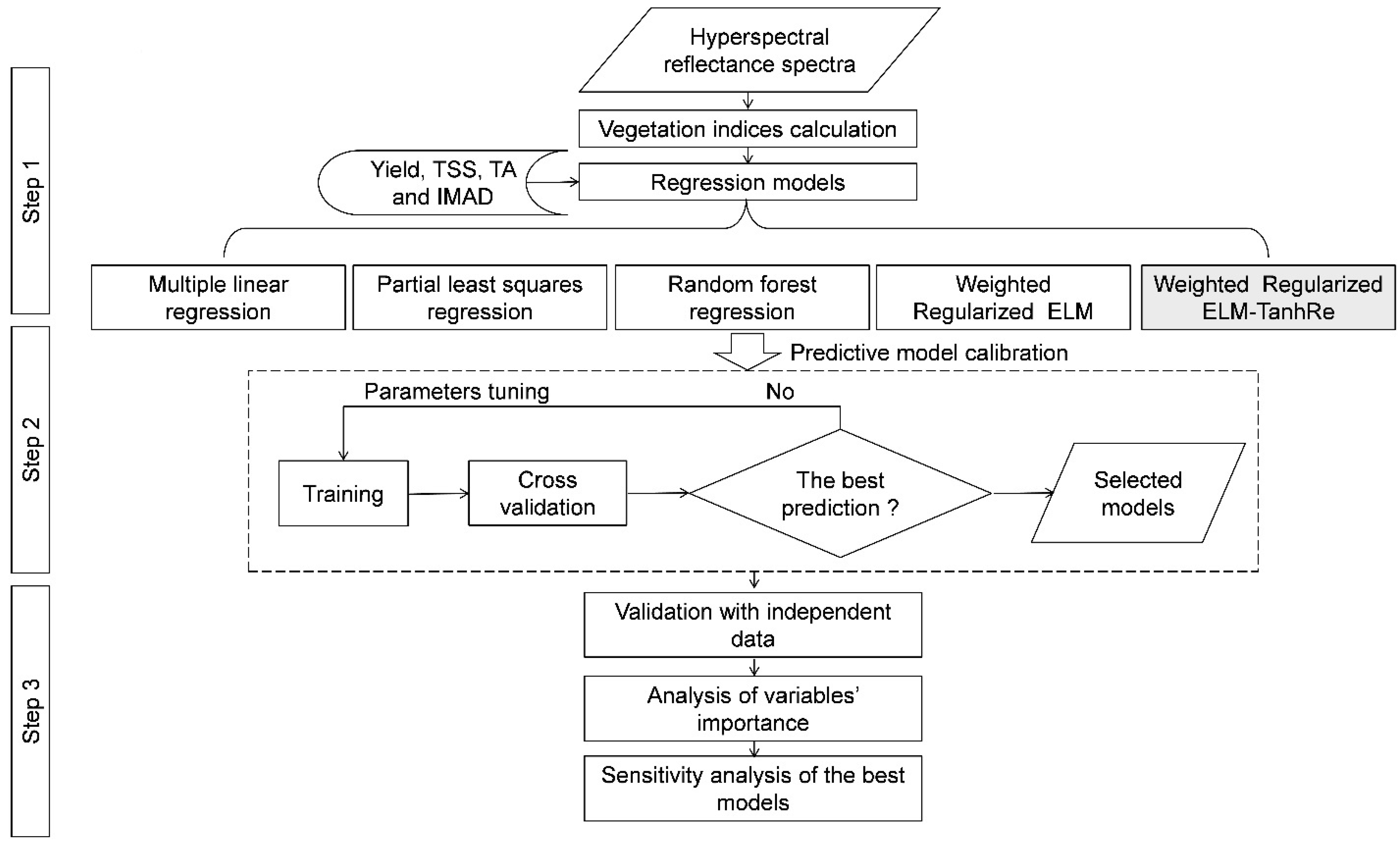
3.1. Workflow for the Model Development
3.2. Calculation of Vegetation Indices
3.3. Background on Extreme Learning Machines (ELMs) and the Developed Method
3.3.1. ELM
3.3.2. Regularized ELM (RELM)
3.3.3. WRELM
3.3.4. Proposed WRELM-TanhRe
3.4. Comparison to other Modeling Methods
3.5. Model Performance Analysis
3.6. Variable Importance
4. Results
4.1. Descriptive Analysis of Berry Yield and Quality
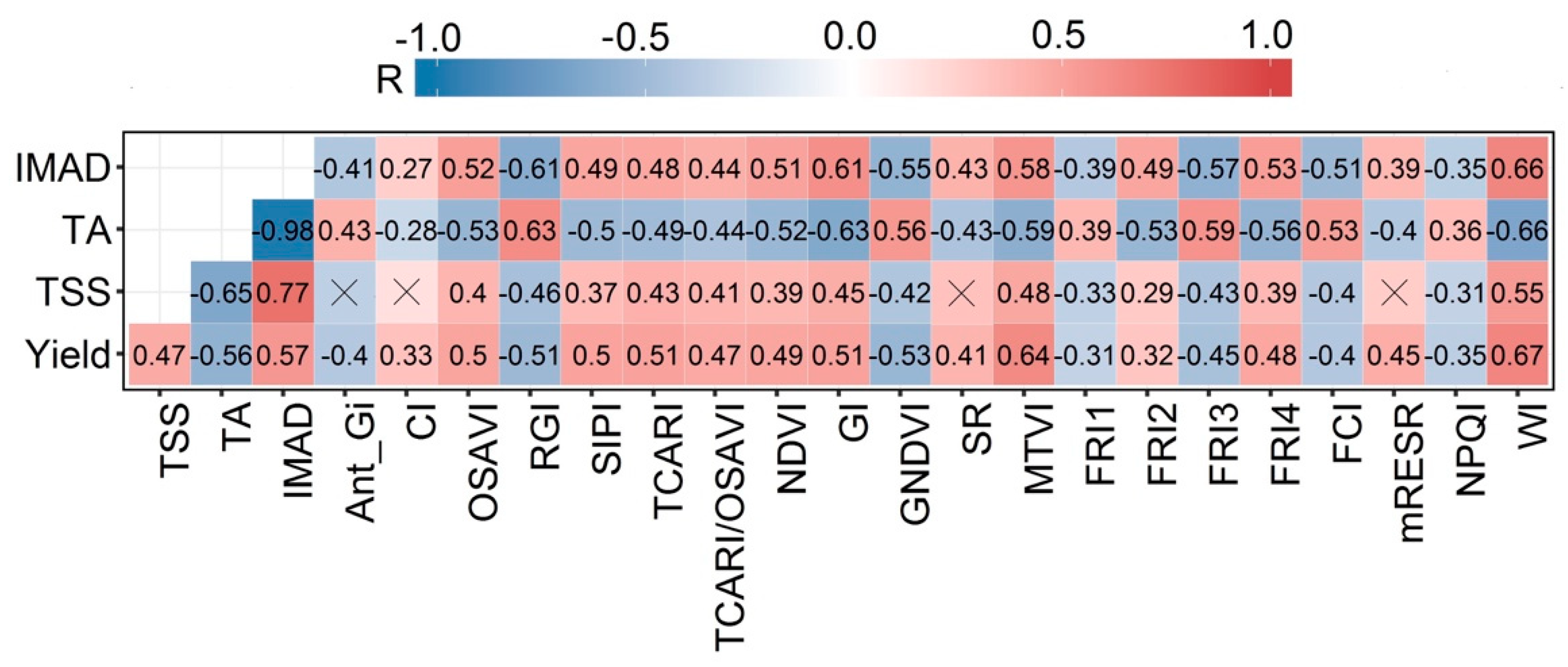
4.2. Relationship (in Absolute Terms) Between Grape Yield Parameters and Hyperspectral Vegetation Indices
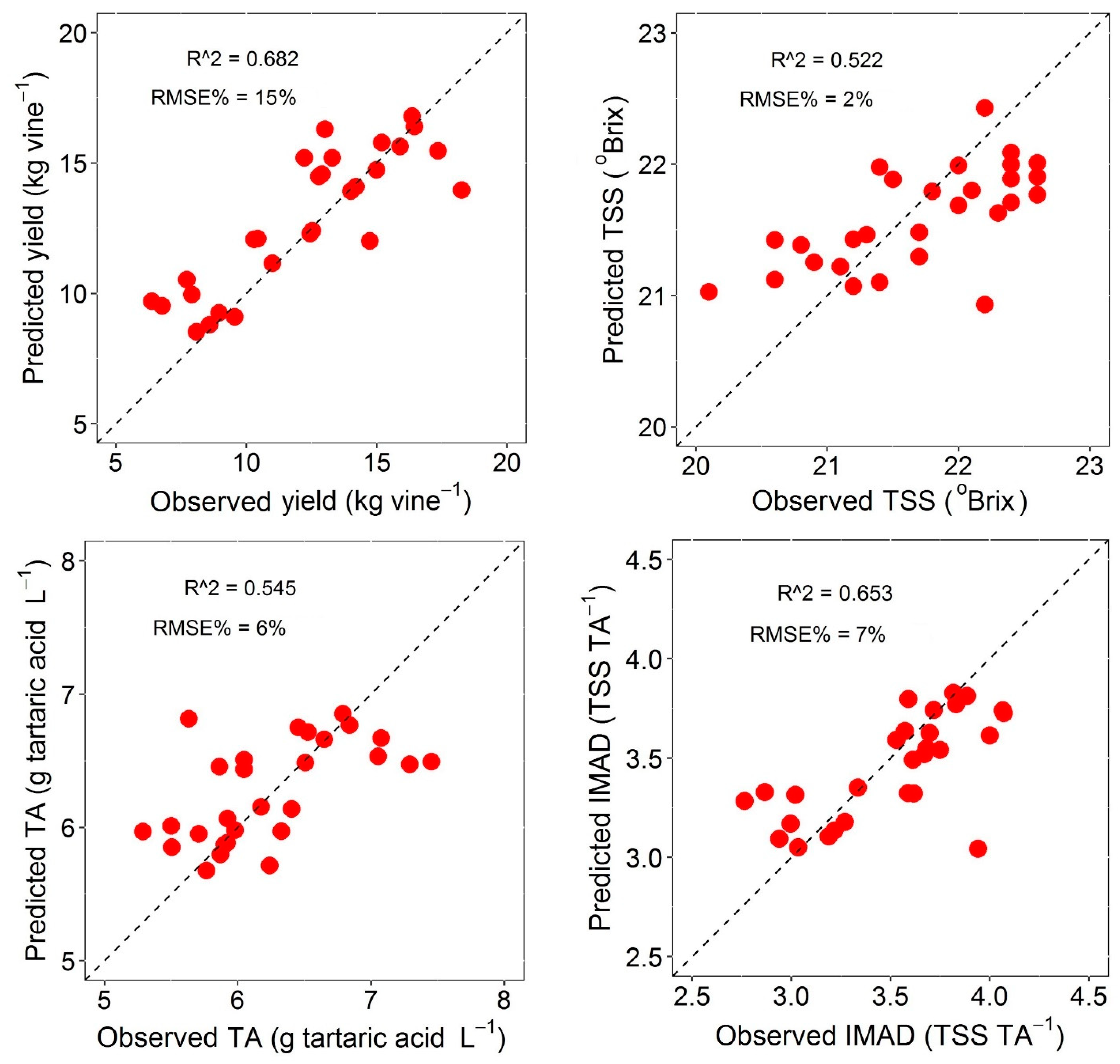
4.3. Model Performance and Accuracy Assessment
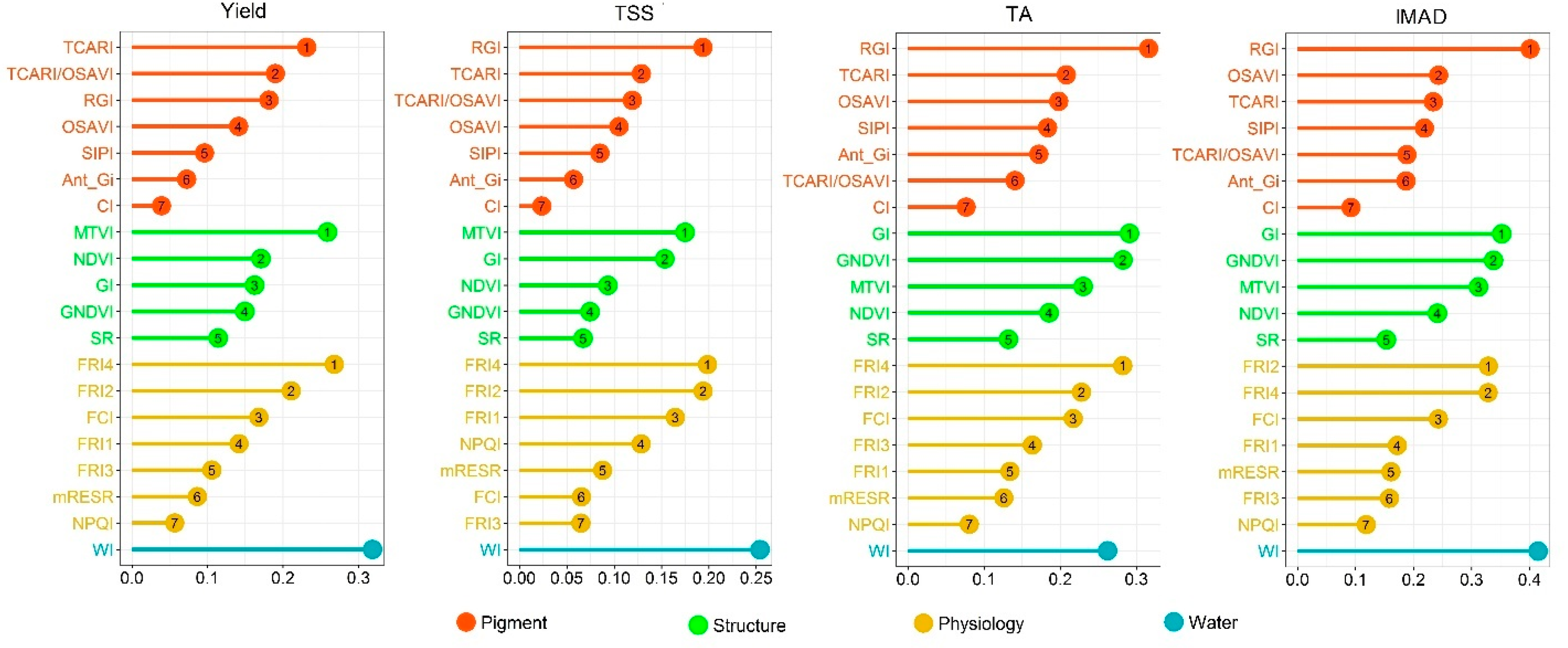
4.4. Variable Importance for Model Performance
5. Discussion
5.1. Overall Performance of the Berry Yield and Quality Models
5.2. Contribution of Vegetation Indices to Berry Yield and Quality Estimation
5.3. Model scalability and transferability
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bavaresco, L.; Lovisolo, C. Effect of grafting on grapevine chlorosis and hydraulic conductivity. VITIS J. Grapevine Res. 2015, 39, 89. [Google Scholar]
- Ferris, H.; Zheng, L.; Walker, M. Resistance of grape rootstocks to plant-parasitic nematodes. J. Nematol. 2012, 44, 377. [Google Scholar] [PubMed]
- Sohrabi, S.; Ebadi, A.; Jalali, S.; Salami, S.A. Enhanced values of various physiological traits and VvNAC1 gene expression showing better salinity stress tolerance in some grapevine cultivars as well as rootstocks. Sci. Hortic. 2017, 225, 317–326. [Google Scholar] [CrossRef]
- Corso, M.; Vannozzi, A.; Ziliotto, F.; Zouine, M.; Maza, E.; Nicolato, T.; Vitulo, N.; Meggio, F.; Valle, G.; Bouzayen, M.; et al. Grapevine Rootstocks Differentially Affect the Rate of Ripening and Modulate Auxin-Related Genes in Cabernet Sauvignon Berries. Front. Plant Sci. 2016, 7, 69. [Google Scholar] [CrossRef] [PubMed]
- Iacono, F.; Buccella, A.; Peterlunger, E. Water stress and rootstock influence on leaf gas exchange of grafted and ungrafted grapevines. Sci. Hortic. 1998, 75, 27–39. [Google Scholar] [CrossRef]
- Kliewer, W.M.; Dokoozlian, N.K. Leaf area/crop weight ratios of grapevines: Influence on fruit composition and wine quality. Am. J. Enol. Vitic. 2005, 56, 170–181. [Google Scholar]
- Martin, S.; Dunstone, R.; Dunn, G. How to forecast wine grape deliveries using grape forecaster excel workbook version 7. Gwrdcadelaideaustralia 2003, 100. [Google Scholar]
- Gamon, J.; Peñuelas, J.; Field, C. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, V.; Hernandez, P.; Solis, I.; Zarco-Tejada, P. Using High-Resolution Hyperspectral and Thermal Airborne Imagery to Assess Physiological Condition in the Context of Wheat Phenotyping. Remote Sens. 2015, 7, 13586–13605. [Google Scholar] [CrossRef]
- Panigada, C.; Rossini, M.; Meroni, M.; Cilia, C.; Busetto, L.; Amaducci, S.; Boschetti, M.; Cogliati, S.; Picchi, V.; Pinto, F. Fluorescence, PRI and canopy temperature for water stress detection in cereal crops. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 167–178. [Google Scholar] [CrossRef]
- Rischbeck, P.; Elsayed, S.; Mistele, B.; Barmeier, G.; Heil, K.; Schmidhalter, U. Data fusion of spectral, thermal and canopy height parameters for improved yield prediction of drought stressed spring barley. Eur. J. Agron. 2016, 78, 44–59. [Google Scholar] [CrossRef]
- Suárez, L.; Zarco-Tejada, P.J.; Berni, J.A.; González-Dugo, V.; Fereres, E. Modelling PRI for water stress detection using radiative transfer models. Remote Sens. Environ. 2009, 113, 730–744. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Teluguntla, P.; Gumma, M.K.; Dheeravath, V. Hyperspectral remote sensing for terrestrial applications. In Remote Sensing Handbook. Land Resources Monitoring, Modeling, and Mapping with Remote Sensing; Thenkabail, P.S., Ed.; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2016; pp. 201–233. [Google Scholar]
- Martín, P.; Zarco-Tejada, P.J.; González, M.; Berjón, A. Using hyperspectral remote sensing to map grape quality in Tempranillo vineyards affected by iron deficiency chlorosis. VITIS J. Grapevine Res. 2015, 46, 7. [Google Scholar]
- Meggio, F.; Zarco-Tejada, P.J.; Núñez, L.C.; Sepulcre-Cantó, G.; González, M.R.; Martín, P. Grape quality assessment in vineyards affected by iron deficiency chlorosis using narrow-band physiological remote sensing indices. Remote Sens. Environ. 2010, 114, 1968–1986. [Google Scholar] [CrossRef]
- Serrano, L.; González-Flor, C.; Gorchs, G. Assessment of grape yield and composition using the reflectance based Water Index in Mediterranean rainfed vineyards. Remote Sens. Environ. 2012, 118, 249–258. [Google Scholar] [CrossRef]
- Suárez, L.; Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A.J.; Sagardoy, R.; Morales, F.; Fereres, E. Detecting water stress effects on fruit quality in orchards with time-series PRI airborne imagery. Remote Sens. Environ. 2010, 114, 286–298. [Google Scholar] [CrossRef]
- Van Beek, J.; Tits, L.; Somers, B.; Deckers, T.; Verjans, W.; Bylemans, D.; Janssens, P.; Coppin, P. Temporal dependency of yield and quality estimation through spectral vegetation indices in pear orchards. Remote Sens. 2015, 7, 9886–9903. [Google Scholar] [CrossRef]
- Royo, C.; Aparicio, N.; Villegas, D.; Casadesus, J.; Monneveux, P.; Araus, J.L. Usefulness of spectral reflectance indices as durum wheat yield predictors under contrasting Mediterranean conditions. Int. J. Remote Sens. 2003, 24, 4403–4419. [Google Scholar] [CrossRef]
- Grossman, Y.; Ustin, S.; Jacquemoud, S.; Sanderson, E.; Schmuck, G.; Verdebout, J. Critique of stepwise multiple linear regression for the extraction of leaf biochemistry information from leaf reflectance data. Remote Sens. Environ. 1996, 56, 182–193. [Google Scholar] [CrossRef]
- Atzberger, C.; Guérif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric. 2010, 73, 165–173. [Google Scholar] [CrossRef]
- Mirzaie, M.; Darvishzadeh, R.; Shakiba, A.; Matkan, A.; Atzberger, C.; Skidmore, A. Comparative analysis of different uni-and multi-variate methods for estimation of vegetation water content using hyper-spectral measurements. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 1–11. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- González Vilas, L.; Spyrakos, E.; Torres Palenzuela, J.M. Neural network estimation of chlorophyll a from MERIS full resolution data for the coastal waters of Galician rias (NW Spain). Remote Sens. Environ. 2011, 115, 524–535. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A. Integrating imaging spectroscopy and neural networks to map grass quality in the Kruger National Park, South Africa. Remote Sens. Environ. 2004, 90, 104–115. [Google Scholar] [CrossRef]
- Ramoelo, A.; Cho, M.A.; Mathieu, R.; Madonsela, S.; van de Kerchove, R.; Kaszta, Z.; Wolff, E. Monitoring grass nutrients and biomass as indicators of rangeland quality and quantity using random forest modelling and WorldView-2 data. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 43–54. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, K.; Liu, L.; Myint, S.; Wang, S.; Liu, H.; He, Z. Exploring the Potential of WorldView-2 Red-Edge Band-Based Vegetation Indices for Estimation of Mangrove Leaf Area Index with Machine Learning Algorithms. Remote Sens. 2017, 9, 1060. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pôças, I.; Gonçalves, J.; Costa, P.M.; Gonçalves, I.; Pereira, L.S.; Cunha, M. Hyperspectral-based predictive modelling of grapevine water status in the Portuguese Douro wine region. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 177–190. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Alom, M.Z.; Sidike, P.; Taha, T.M.; Asari, V.K. State Preserving Extreme Learning Machine: A Monotonically Increasing Learning Approach. Neural Process. Lett. 2017, 45, 703–725. [Google Scholar] [CrossRef]
- Chen, Y.; Yao, E.; Basu, A. A 128-channel extreme learning machine-based neural decoder for brain machine interfaces. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 679–692. [Google Scholar] [CrossRef] [PubMed]
- Essa, A.; Sidike, P.; Asari, V. Volumetric Directional Pattern for Spatial Feature Extraction in Hyperspectral Imagery. IEEE Geosci. Remote Sens. 2017, 14, 1056–1060. [Google Scholar] [CrossRef]
- Moreno, R.; Corona, F.; Lendasse, A.; Graña, M.; Galvão, L.S. Extreme learning machines for soybean classification in remote sensing hyperspectral images. Neurocomputing 2014, 128, 207–216. [Google Scholar] [CrossRef]
- Sidike, P.; Krieger, E.; Alom, M.Z.; Asari, V.K.; Taha, T. A fast single-image super-resolution via directional edge-guided regularized extreme learning regression. Signalimage Video Process. 2017, 11, 961–968. [Google Scholar] [CrossRef]
- Tang, J.; Deng, C.; Huang, G.-B.; Zhao, B. Compressed-domain ship detection on spaceborne optical image using deep neural network and extreme learning machine. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1174–1185. [Google Scholar] [CrossRef]
- Hertz, J.A. Introduction to the Theory of Neural Computation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.-B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef] [PubMed]
- Maimaitijiang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitiyiming, M.; Peterson, K.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S. Unmanned Aerial System (UAS)-based phenotyping of soybean using multi-sensor data fusion and extreme learning machine. ISPRS J. Photogramm. Remote Sens. 2017, 134, 43–58. [Google Scholar] [CrossRef]
- Rocha Neto, O.; Teixeira, A.; Leão, R.; Moreira, L.; Galvão, L. Hyperspectral Remote Sensing for Detecting Soil Salinization Using ProSpecTIR-VS Aerial Imagery and Sensor Simulation. Remote Sens. 2017, 9, 42. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Bozzolo, A.; Wilkins, J.L.; Kwasniewski, M.T. Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy. Remote Sens. 2017, 9, 745. [Google Scholar] [CrossRef]
- Hall, A.; Lamb, D.W.; Holzapfel, B.P.; Louis, J.P. Within-season temporal variation in correlations between vineyard canopy and winegrape composition and yield. Precis. Agric. 2011, 12, 103–117. [Google Scholar] [CrossRef]
- Lamb, D.W.; Weedon, M.; Bramley, R. Using remote sensing to predict grape phenolics and colour at harvest in a Cabernet Sauvignon vineyard: Timing observations against vine phenology and optimising image resolution. Aust. J. Grape Wine Res. 2004, 10, 46–54. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Suárez, L.; González-Dugo, V. Spatial resolution effects on chlorophyll fluorescence retrieval in a heterogeneous canopy using hyperspectral imagery and radiative transfer simulation. IEEE Geosci. Remote Sens. 2013, 10, 937–941. [Google Scholar] [CrossRef]
- Fassnacht, F.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Sepulcre-Cantó, G.; Zarco-Tejada, P.; Jiménez-Muñoz, J.; Sobrino, J.; Soriano, M.; Fereres, E.; Vega, V.; Pastor, M. Monitoring yield and fruit quality parameters in open-canopy tree crops under water stress. Implications for ASTER. Remote Sens. Environ. 2007, 107, 455–470. [Google Scholar] [CrossRef]
- Somers, B.; Delalieux, S.; Verstraeten, W.W.; Eynde, A.V.; Barry, G.H.; Coppin, P. The contribution of the fruit component to the hyperspectral citrus canopy signal. Photogramm. Eng. Remote Sens. 2010, 76, 37–47. [Google Scholar] [CrossRef]
- Ye, X.; Sakai, K.; Manago, M.; Asada, S.-i.; Sasao, A. Prediction of citrus yield from airborne hyperspectral imagery. Precis. Agric. 2007, 8, 111–125. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Quantitative estimation of chlorophyll-a using reflectance spectra: Experiments with autumn chestnut and maple leaves. J. Photochem. Photobiol. B Biol. 1994, 22, 247–252. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.; De Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Peñuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Rouse Jr, J.W.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the Great Plains with ERTS. In Proceedings of the 3rd Erts Symposium, Washington, DC, USA, 10–14 December 1973; Volume 1, pp. 309–317. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L.; Sampson, P.H. Chlorophyll Fluorescence Effects on Vegetation Apparent Reflectance: II. Laboratory and Airborne Canopy-Level Measurements with Hyperspectral Data. Remote Sens. Environ. 2000, 74, 596–608. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L. Chlorophyll Fluorescence Effects on Vegetation Apparent Reflectance: I. Leaf-Level Measurements and Model Simulation. Remote Sens. Environ. 2000, 74, 582–595. [Google Scholar] [CrossRef]
- Dobrowski, S.; Pushnik, J.; Zarco-Tejada, P.J.; Ustin, S. Simple reflectance indices track heat and water stress-induced changes in steady-state chlorophyll fluorescence at the canopy scale. Remote Sens. Environ. 2005, 97, 403–414. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Barnes, J.; Balaguer, L.; Manrique, E.; Elvira, S.; Davison, A. A reappraisal of the use of DMSO for the extraction and determination of chlorophylls a and b in lichens and higher plants. Environ. Exp. Bot. 1992, 32, 85–100. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Biel, C.; Serrano, L.; Save, R. The reflectance at the 950–970 nm region as an indicator of plant water status. Int. J. Remote Sens. 1993, 14, 1887–1905. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, M. Outlier-robust extreme learning machine for regression problems. Neurocomputing 2015, 151, 1519–1527. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
- Huang, G.-B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Manand Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Deng, W.; Zheng, Q.; Chen, L. Regularized extreme learning machine. In Proceedings of the IEEE Symposium on Computational Intelligence and Data Mining (CIDM’09), Nashville, TN, USA, 30 March–2 April 2009; pp. 389–395. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 28, p. 6. [Google Scholar]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Martens, H.; Naes, T. Multivariate Calibration; John Wiley & Sons: Chichester, UK, 1992. [Google Scholar]
- Haaland, D.M.; Thomas, E.V. Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information. Anal. Chem. 1988, 60, 1193–1202. [Google Scholar] [CrossRef]
- Schapire, R.E.; Freund, Y.; Bartlett, P.; Lee, W.S. Boosting the margin: A new explanation for the effectiveness of voting methods. Ann. Stat. 1998, 26, 1651–1686. [Google Scholar] [CrossRef]
- Forkuor, G.; Hounkpatin, O.K.; Welp, G.; Thiel, M. High Resolution Mapping of Soil Properties Using Remote Sensing Variables in South-Western Burkina Faso: A Comparison of Machine Learning and Multiple Linear Regression Models. PLoS ONE 2017, 12, e0170478. [Google Scholar] [CrossRef] [PubMed]
- Statnikov, A.; Wang, L.; Aliferis, C.F. A comprehensive comparison of random forests and support vector machines for microarray-based cancer classification. BMC Bioinform. 2008, 9, 319. [Google Scholar] [CrossRef] [PubMed]
- Noi, P.T.; Degener, J.; Kappas, M. Comparison of Multiple Linear Regression, Cubist Regression, and Random Forest Algorithms to Estimate Daily Air Surface Temperature from Dynamic Combinations of MODIS LST Data. Remote Sens. 2017, 9, 398. [Google Scholar] [CrossRef]
- Xu, Y.; Knudby, A.; Ho, H.C. Estimating daily maximum air temperature from MODIS in British Columbia, Canada. Int. J. Remote Sens. 2014, 35, 8108–8121. [Google Scholar] [CrossRef]
- Chen, P.; Jing, Q. A comparison of two adaptive multivariate analysis methods (PLSR and ANN) for winter wheat yield forecasting using Landsat-8 OLI images. Adv. Space Res. 2017, 59, 987–995. [Google Scholar] [CrossRef]
- Reddy, T.A. Applied Data Analysis and Modeling for Energy Engineers and Scientists; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar] [CrossRef]
- Van Der Meij, B.; Kooistra, L.; Suomalainen, J.; Barel, J.M.; De Deyn, G.B. Remote sensing of plant trait responses to field-based plant-soil feedback using UAV-based optical sensors. Biogeosciences 2017, 14, 733. [Google Scholar] [CrossRef]
- Rey-Caramés, C.; Diago, M.; Martín, M.; Lobo, A.; Tardaguila, J. Using RPAS Multi-Spectral Imagery to Characterise Vigour, Leaf Development, Yield Components and Berry Composition Variability within a Vineyard. Remote Sens. 2015, 7, 14458–14481. [Google Scholar] [CrossRef]
- Anastasiou, E.; Balafoutis, A.; Darra, N.; Psiroukis, V.; Biniari, A.; Xanthopoulos, G.; Fountas, S. Satellite and Proximal Sensing to Estimate the Yield and Quality of Table Grapes. Agriculture 2018, 8, 94. [Google Scholar] [CrossRef]
- Asner, G.P.; Wessman, C.A.; Schimel, D.S.; Archer, S. Variability in Leaf and Litter Optical Properties: Implications for BRDF Model Inversions Using AVHRR, MODIS, and MISR. Remote Sens. Environ. 1998, 63, 243–257. [Google Scholar] [CrossRef]
- Pullanagari, R.R.; Kereszturi, G.; Yule, I.J. Mapping of macro and micro nutrients of mixed pastures using airborne AisaFENIX hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2016, 117, 1–10. [Google Scholar] [CrossRef]
- Ali, I.; Cawkwell, F.; Green, S.; Dwyer, N. Application of statistical and machine learning models for grassland yield estimation based on a hypertemporal satellite remote sensing time series. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 5060–5063. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using Landsat TM images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forest classification of multisource remote sensing and geographic data. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium (IGARSS’04), Anchorage, AK, USA, 20–24 September 2004; pp. 1049–1052. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Das, B.; Sahoo, R.N.; Pargal, S.; Krishna, G.; Verma, R.; Chinnusamy, V.; Sehgal, V.K.; Gupta, V.K. Comparison of different uni- and multi-variate techniques for monitoring leaf water status as an indicator of water-deficit stress in wheat through spectroscopy. Biosyst. Eng. 2017, 160, 69–83. [Google Scholar] [CrossRef]
- Das, B.; Sahoo, R.N.; Pargal, S.; Krishna, G.; Verma, R.; Chinnusamy, V.; Sehgal, V.K.; Gupta, V.K.; Dash, S.K.; Swain, P. Quantitative monitoring of sucrose, reducing sugar and total sugar dynamics for phenotyping of water-deficit stress tolerance in rice through spectroscopy and chemometrics. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 192, 41–51. [Google Scholar] [CrossRef]
- Deng, H.; Runger, G.; Tuv, E. Bias of importance measures for multi-valued attributes and solutions. In Proceedings of the 21st International Conference on Articial Neural Networks (ICANN 2011), Espoo, Finland, 14–17 June 2011; pp. 293–300. [Google Scholar]
- De Jong, S.M.; Addink, E.A.; Hoogenboom, P.; Nijland, W. The spectral response of Buxus sempervirens to different types of environmental stress—A laboratory experiment. ISPRS J. Photogramm. Remote Sens. 2012, 74, 56–65. [Google Scholar] [CrossRef]
- Pirie, A.J.; Mullins, M.G. Concentration of phenolics in the skin of grape berries during fruit development and ripening. Am. J. Enol. Vitic. 1980, 31, 34–36. [Google Scholar]
- Smart, R.; Robinson, M. Sunlight into Wine: A Handbook for Winegrape Canopy Management; Winetitles: Adelaida, SA, Australia, 1991. [Google Scholar]
- Stagakis, S.; González-Dugo, V.; Cid, P.; Guillén-Climent, M.; Zarco-Tejada, P.J. Monitoring water stress and fruit quality in an orange orchard under regulated deficit irrigation using narrow-band structural and physiological remote sensing indices. ISPRS J. Photogramm. Remote Sens. 2012, 71, 47–61. [Google Scholar] [CrossRef]
- García-Estévez, I.; Quijada-Morín, N.; Rivas-Gonzalo, J.C.; Martínez-Fernández, J.; Sánchez, N.; Herrero-Jiménez, C.M.; Escribano-Bailón, M.T. Relationship between hyperspectral indices, agronomic parameters and phenolic composition of Vitis vinifera cv Tempranillo grapes. J. Sci. Food Agric. 2017, 97, 4066–4074. [Google Scholar] [CrossRef]
- Gamon, J.; Field, C.; Bilger, W.; Björkman, O.; Fredeen, A.; Peñuelas, J. Remote sensing of the xanthophyll cycle and chlorophyll fluorescence in sunflower leaves and canopies. Oecologia 1990, 85, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Krause, G.H.; Weis, E. Chlorophyll fluorescence as a tool in plant physiology. Photosynth. Res. 1984, 5, 139–157. [Google Scholar] [CrossRef]
- Papageorgiou, G.C.; Govindjee, J. Chlorophyll a fluorescence, a signature of photosynthesis. In Advances in Photosynthesis and Respiration; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Gitelson, A.A.; Buschmann, C.; Lichtenthaler, H.K. Leaf chlorophyll fluorescence corrected for re-absorption by means of absorption and reflectance measurements. J. Plant Physiol. 1998, 152, 283–296. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef]
- Konings, A.G.; Williams, A.P.; Gentine, P. Sensitivity of grassland productivity to aridity controlled by stomatal and xylem regulation. Nat. Geosci. 2017, 10, 284. [Google Scholar] [CrossRef]
- Yang, P.; van der Tol, C.; Verhoef, W.; Damm, A.; Schickling, A.; Kraska, T.; Muller, O.; Rascher, U. Using reflectance to explain vegetation biochemical and structural effects on sun-induced chlorophyll fluorescence. Remote Sens. Environ. 2018. [Google Scholar] [CrossRef]
- De La Fuente Lloreda, M.; Linares Torres, R.; Baeza Trujillo, P.; Miranda, C.; Lissarrague Garcia-Gutierrez, J.R. Comparison of different methods of grapevine yield prediction in the time window between fruitset and veraison. OENO One 2015, 49, 27–35. [Google Scholar] [CrossRef]
- Parker, A.K.; De CortÁZar-Atauri, I.G.; Van Leeuwen, C.; Chuine, I. General phenological model to characterise the timing of flowering and veraison of Vitis vinifera L. Aust. J. Grape Wine Res. 2011, 17, 206–216. [Google Scholar] [CrossRef]
- Cola, G.; Mariani, L.; Salinari, F.; Civardi, S.; Bernizzoni, F.; Gatti, M.; Poni, S. Description and testing of a weather-based model for predicting phenology, canopy development and source–sink balance in Vitis vinifera L. cv. Barbera. Agric. For. Meteorol. 2014, 184, 117–136. [Google Scholar] [CrossRef]
- Santos, J.A.; Malheiro, A.C.; Karremann, M.K.; Pinto, J.G. Statistical modelling of grapevine yield in the Port Wine region under present and future climate conditions. Int. J. Biometeorol. 2011, 55, 119–131. [Google Scholar] [CrossRef]
- Suárez, L.; Zarco-Tejada, P.J.; Sepulcre-Cantó, G.; Pérez-Priego, O.; Miller, J.R.; Jiménez-Muñoz, J.; Sobrino, J. Assessing canopy PRI for water stress detection with diurnal airborne imagery. Remote Sens. Environ. 2008, 112, 560–575. [Google Scholar] [CrossRef]
- Rossini, M.; Fava, F.; Cogliati, S.; Meroni, M.; Marchesi, A.; Panigada, C.; Giardino, C.; Busetto, L.; Migliavacca, M.; Amaducci, S.; et al. Assessing canopy PRI from airborne imagery to map water stress in maize. ISPRS J. Photogramm. Remote Sens. 2013, 86, 168–177. [Google Scholar] [CrossRef]
- Santesteban, L.G.; Di Gennaro, S.F.; Herrero-Langreo, A.; Miranda, C.; Royo, J.B.; Matese, A. High-resolution UAV-based thermal imaging to estimate the instantaneous and seasonal variability of plant water status within a vineyard. Agric. Water Manag. 2017, 183, 49–59. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; North, P.R.; Hornero, A.; Zarco-Tejada, P.J. Assessing the effects of forest health on sun-induced chlorophyll fluorescence using the FluorFLIGHT 3-D radiative transfer model to account for forest structure. Remote Sens. Environ. 2017, 193, 165–179. [Google Scholar] [CrossRef]
- Camino, C.; Zarco-Tejada, P.J.; Gonzalez-Dugo, V. Effects of Heterogeneity within Tree Crowns on Airborne-Quantified SIF and the CWSI as Indicators of Water Stress in the Context of Precision Agriculture. Remote Sens. 2018, 10, 604. [Google Scholar] [CrossRef]
- Matese, A.; Di Gennaro, S. Practical Applications of a Multisensor UAV Platform Based on Multispectral, Thermal and RGB High Resolution Images in Precision Viticulture. Agriculture 2018, 8, 116. [Google Scholar] [CrossRef]
- Chapman, S.; Merz, T.; Chan, A.; Jackway, P.; Hrabar, S.; Dreccer, M.; Holland, E.; Zheng, B.; Ling, T.; Jimenez-Berni, J. Pheno-Copter: A Low-Altitude, Autonomous Remote-Sensing Robotic Helicopter for High-Throughput Field-Based Phenotyping. Agronomy 2014, 4, 279–301. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of Spectral–Temporal Response Surfaces by Combining Multispectral Satellite and Hyperspectral UAV Imagery for Precision Agriculture Applications. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Zaman-Allah, M.; Vergara, O.; Araus, J.L.; Tarekegne, A.; Magorokosho, C.; Zarco-Tejada, P.J.; Hornero, A.; Albà, A.H.; Das, B.; Craufurd, P.; et al. Unmanned aerial platform-based multi-spectral imaging for field phenotyping of maize. Plant Methods 2015, 11, 35. [Google Scholar] [CrossRef]
- Sagan, V.; Maimaitijiang, M.; Sidike, P.; Eblimit, K.; Peterson, K.T.; Hartling, S.; Esposito, F.; Khanal, K.; Newcomb, M.; Pauli, D.; et al. UAV-Based High Resolution Thermal Imaging for Vegetation Monitoring, and Plant Phenotyping Using ICI 8640 P, FLIR Vue Pro R 640, and thermoMap Cameras. Remote Sens. 2019, 11, 330. [Google Scholar] [CrossRef]
- Jay, S.; Baret, F.; Dutartre, D.; Malatesta, G.; Héno, S.; Comar, A.; Weiss, M.; Maupas, F. Exploiting the centimeter resolution of UAV multispectral imagery to improve remote-sensing estimates of canopy structure and biochemistry in sugar beet crops. Remote Sens. Environ. 2018. [Google Scholar] [CrossRef]
- Sankaran, S.; Khot, L.R.; Espinoza, C.Z.; Jarolmasjed, S.; Sathuvalli, V.R.; Vandemark, G.J.; Miklas, P.N.; Carter, A.H.; Pumphrey, M.O.; Knowles, N.R. Low-altitude, high-resolution aerial imaging systems for row and field crop phenotyping: A review. Eur. J. Agron. 2015, 70, 112–123. [Google Scholar] [CrossRef]
- Morellos, A.; Pantazi, X.-E.; Moshou, D.; Alexandridis, T.; Whetton, R.; Tziotzios, G.; Wiebensohn, J.; Bill, R.; Mouazen, A.M. Machine learning based prediction of soil total nitrogen, organic carbon and moisture content by using VIS-NIR spectroscopy. Biosyst. Eng. 2016, 152, 104–116. [Google Scholar] [CrossRef]
| Vegetation Index | Acronym | Equation | References |
|---|---|---|---|
| Pigment | |||
| Anthocyanin (Gitelson) | AntGitelson | AntGitelson = (1/R550 − 1/ R700) * R780 | [51] |
| Chlorophyll Index | CI | CI = (R750 − R705)/(R750 + R705) | [52] |
| Optimized Soil-Adjusted Vegetation Index | OSAVI | OSAVI = (1 + 0.16) * (R800 − R670)/(R800 + R670 + 0.16) | [53] |
| Red Green Index | RGI | RGI = R690/R550 | [54] |
| Structure Intensive Pigment Index | SIPI | SIPI = (R800 − R450)/(R800 + R650) | [55] |
| Transformed Chlorophyll Absorption in Reflectance Index | TCARI | TCARI = 3 * ((R700 − R670) − 0.2 * (R700 − R550) * (R700/R670)) | [56] |
| TCARI/OSAVI | TCARI/OSAVI | [56] | |
| Structure | |||
| Normalized Difference Vegetation Index | NDVI | NDVI = (R800 − R670)/(R800 + R670) | [57] |
| Greenness Index | GI | GI = R554/R677 | [54] |
| Green NDVI | GNDVI | GNDVI = (R750 − R540 + R570)/(R750 + R540 − R570) | [58] |
| Simple Ratio | SR | SR = R900/R680 | [59] |
| Modified Triangular Vegetation Index | MTVI | MTVI = 1.2*(1.2*(R800 − R550) − 2.5*(R670 − R550)) | [60] |
| Physiology | |||
| Fluorescence Ratio Index 1 | FRI1 | FRI1 = R690/R630 | [61] |
| Fluorescence Ratio Indices 2 | FRI2 | FRI2 = R750/R800 | [62] |
| Fluorescence Ratio Index3 | FRI3 | FRI3 = R690/R600 | [63] |
| Fluorescence Ratio Indices 4 | FRI4 | FRI4 = R740/R800 | [63] |
| Fluorescence Curvature Index | FCI | FCI = R2683/(R675*R691) | [61] |
| Modified Red Edge Simple Ratio Index | mRESR | mRESR = (R750 − R445)/(R705 + R445) | [64] |
| Normalized Phaeophytinization Index | NPQI | NPQI = (R415 − R435)/(R415 + R435) | [65] |
| Water content | |||
| Water Index | WI | WI = R900/R970 | [66] |
| Full Name | Acronym |
|---|---|
| Extreme Learning Machine | ELM |
| Regularized Extreme Learning Machine | RELM |
| Weighted Extreme Learning Machine | WRELM |
| Hyperbolic tangent function | Tanh |
| Rectified Linear Unit | ReLU |
| Combination of hyperbolic tangent and Rectified Linear Unit functions | TanhRe |
| TanhRe -based Weighted Regularized Extreme Learning Machine | WRELM-TanhRe |
| Berry Yield and Quality Parameters | Year | Number of Samples | Mean | Max. | Min. | SD | CV (%) |
|---|---|---|---|---|---|---|---|
| Yield (kg/vine) | 2014 | 72 | 14.51 | 21.49 | 8.48 | 2.58 | 18 |
| 2015 | 72 | 14.21 | 22.31 | 7.94 | 2.79 | 20 | |
| Total | 144 | 14.36 | 22.31 | 7.94 | 2.68 | 19 | |
| TSS (°Brix) | 2014 | 72 | 21.86 | 22.70 | 20.20 | 0.46 | 2 |
| 2015 | 72 | 21.14 | 22.60 | 20.00 | 0.53 | 3 | |
| Total | 144 | 21.50 | 22.70 | 20.00 | 0.62 | 3 | |
| TA (g tartaric acid L−1) | 2014 | 72 | 5.85 | 6.41 | 5.14 | 0.31 | 5 |
| 2015 | 72 | 6.83 | 9.35 | 5.63 | 0.60 | 9 | |
| Total | 144 | 6.34 | 9.35 | 5.14 | 0.68 | 11 | |
| IMAD (TSS/TA) | 2014 | 72 | 3.75 | 4.28 | 3.29 | 0.22 | 6 |
| 2015 | 72 | 3.12 | 3.94 | 2.29 | 0.28 | 9 | |
| Total | 144 | 3.43 | 4.28 | 2.29 | 0.40 | 12 |
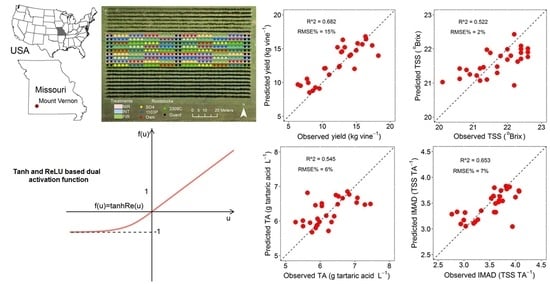
| Berry Yield and Quality Parameters | Evaluation Metrics | Calibration Dataset (n = 115) | Independent Validation Dataset (n = 29) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MLR | PLSR | RFR | WR ELM | WRELM-TanhRe | MLR | PLSR | RFR | WR ELM | WRELM-TanhRe | ||
| Yield (kg/vine) | R2 | 0.458 | 0.413 | 0.859 | 0.412 | 0.383 | 0.200 | 0.474 | 0.632 | 0.623 | 0.682 |
| RMSE | 3.008 | 3.130 | 1.535 | 3.132 | 3.209 | 2.943 | 2.386 | 1.995 | 2.019 | 1.856 | |
| RMSE% | 24 | 25 | 12 | 25 | 26 | 24 | 20 | 16 | 17 | 15 | |
| TSS (°Brix) | R2 | 0.328 | 0.279 | 0.845 | 0.283 | 0.257 | 0.421 | 0.435 | 0.449 | 0.352 | 0.522 |
| RMSE | 0.475 | 0.492 | 0.228 | 0.490 | 0.499 | 0.547 | 0.541 | 0.534 | 0.579 | 0.497 | |
| RMSE% | 2 | 2 | 1 | 2 | 2 | 3 | 3 | 2 | 3 | 2 | |
| TA (g tartaric acid L−1) | R2 | 0.510 | 0.348 | 0.873 | 0.426 | 0.371 | 0.320 | 0.407 | 0.522 | 0.545 | 0.535 |
| RMSE | 0.458 | 0.528 | 0.233 | 0.496 | 0.518 | 0.497 | 0.464 | 0.417 | 0.407 | 0.411 | |
| RMSE% | 7 | 8 | 4 | 8 | 8 | 8 | 7 | 7 | 6 | 6 | |
| IMAD (TSS/TA) | R2 | 0.551 | 0.512 | 0.884 | 0.459 | 0.453 | 0.548 | 0.643 | 0.631 | 0.647 | 0.653 |
| RMSE | 0.247 | 0.258 | 0.125 | 0.271 | 0.272 | 0.268 | 0.238 | 0.242 | 0.237 | 0.235 | |
| RMSE% | 7 | 7 | 4 | 8 | 8 | 8 | 7 | 7 | 7 | 7 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maimaitiyiming, M.; Sagan, V.; Sidike, P.; Kwasniewski, M.T. Dual Activation Function-Based Extreme Learning Machine (ELM) for Estimating Grapevine Berry Yield and Quality. Remote Sens. 2019, 11, 740. https://doi.org/10.3390/rs11070740
Maimaitiyiming M, Sagan V, Sidike P, Kwasniewski MT. Dual Activation Function-Based Extreme Learning Machine (ELM) for Estimating Grapevine Berry Yield and Quality. Remote Sensing. 2019; 11(7):740. https://doi.org/10.3390/rs11070740
Chicago/Turabian StyleMaimaitiyiming, Matthew, Vasit Sagan, Paheding Sidike, and Misha T. Kwasniewski. 2019. "Dual Activation Function-Based Extreme Learning Machine (ELM) for Estimating Grapevine Berry Yield and Quality" Remote Sensing 11, no. 7: 740. https://doi.org/10.3390/rs11070740
APA StyleMaimaitiyiming, M., Sagan, V., Sidike, P., & Kwasniewski, M. T. (2019). Dual Activation Function-Based Extreme Learning Machine (ELM) for Estimating Grapevine Berry Yield and Quality. Remote Sensing, 11(7), 740. https://doi.org/10.3390/rs11070740