Abstract
Sun-Induced fluorescence at 760 nm (F760) is increasingly being used to predict gross primary production (GPP) through light use efficiency (LUE) modeling, even though the mechanistic processes that link the two are not well understood. We analyzed the effect of nitrogen (N) and phosphorous (P) availability on the processes that link GPP and F760 in a Mediterranean grassland manipulated with nutrient addition. To do so, we used a combination of process-based modeling with Soil-Canopy Observation of Photosynthesis and Energy (SCOPE), and statistical analyses such as path modeling. With this study, we uncover the mechanisms that link the fertilization-driven changes in canopy nitrogen concentration (N%) to the observed changes in F760 and GPP. N addition changed plant community structure and increased canopy chlorophyll content, which jointly led to changes in photosynthetic active radiation (APAR), ultimately affecting both GPP and F760. Changes in the abundance of graminoids, (%graminoids) driven by N addition led to changes in structural properties of the canopy such as leaf angle distribution, that ultimately influenced observed F760 by controlling the escape probability of F760 (Fesc). In particular, we found a change in GPP–F760 relationship between the first and the second year of the experiment that was largely driven by the effect of plant type composition on Fesc, whose best predictor is %graminoids. The P addition led to a statistically significant increase on light use efficiency of fluorescence emission (LUEf), in particular in plots also with N addition, consistent with leaf level studies. The N addition induced changes in the biophysical properties of the canopy that led to a trade-off between surface temperature (Ts), which decreased, and F760 at leaf scale (F760leaf,fw), which increased. We found that Ts is an important predictor of the light use efficiency of photosynthesis, indicating the importance of Ts in LUE modeling approaches to predict GPP.
1. Introduction
An accurate estimation of gross primary production (GPP) by terrestrial ecosystems is crucial to understanding the variability of the global carbon (C) cycle [1]. One of the most common ways to estimate GPP relies on the use of light use efficiency (LUE) models (Equation (1)). In the LUE framework [2], estimates of GPP are based on three variables: (i) the fraction of photosynthetically active radiation (fAPAR) absorbed by the vegetation; (ii) the actual light use efficiency of photosynthesis (LUEp), i.e., the conversion efficiency of absorbed radiation to fixed carbon; and (iii) incident photosynthetically active radiation (PAR).
The development and retrieval methods in passive sensing of sun-induced chlorophyll fluorescence (SIF), i.e., the radiation emitted by plants upon sun exposure, opens new possibilities to estimate GPP using remotely sensed data [3,4,5]. In the last decade, several studies have shown that sun-induced fluorescence at 760 nm retrieved from top-of-canopy (TOC) measurements (F760) can track changes in APAR and LUEp, and therefore can be directly linked to GPP from leaves [6], ecosystem, [7,8,9,10] to regional and global scale [3,11,12,13].
Although the mechanistic link between GPP and F760 is not completely understood, recent advances in the field have contributed to explain the process under various conditions [14,15]. The reason F760 and GPP correlate is that both processes start with the absorption of light by a chlorophyll molecule. Once the photon is captured by the antenna and reaches the reaction center of the photosystem II, the chlorophyll molecule can return to the ground state through photochemical quenching (PQ), through the non-photochemical quenching of the excited state (NPQ), as the photon is dissipated non-radiatively as heat [16], or it can be re-emitted as a photon of fluorescence [17]. Fluorescence emission cannot be physiologically regulated, and its quantum yield depends on the efficiency of PQ and NPQ [17]. The mechanisms regulating the partitioning of absorbed photosynthetically active radiation (APAR) into the different pathways is therefore fundamental to grasping the GPP–F760 connection [18,19].
F760 is usually described with a similar approach to the Monteith’s LUE framework, as shown in Equation (2):
where F760 is equal to the product of fAPAR, PAR, the light use efficiency of fluorescence emission at 760 nm (LUEf), and the escape probability of chlorophyll fluorescence at 760 nm (Fesc) [20].
Equations (1) and (2) can be combined into Equation (3), which shows that the only variables that control the relationship between GPP and F760 are LUEp, LUEf and Fesc:
Multiple factors can influence the different terms in Equation (3), and eventually GPP–F760 relationship [5,8]. Among these, the ones that require more attention because they are not fully understood are: (i) leaf nutrient content, in particular nitrogen (N) and phosphorous (P); and (ii) canopy structural parameters such as leaf area index (LAI) and leaf angle distribution (LAD), which in grasslands are often related to the community structure of the canopy [8,21]. Quantifying the effect of nutrients and canopy structure on the partitioning of absorbed radiation and on LUEp, LUEf, and Fesc is the first step to shed light on GPP and F760 changes under different nutrient availability.
Canopy N concentration (hereafter N%, N mass per gram of leaves of the whole canopy) is often related to the nutritional condition where the plant grows. Nitrogen is a fundamental constituent of leaves that is typically associated with higher LAI, and positively correlated with the amount of chlorophyll a and b (Cab) [22]. Higher LAI and Cab increase APAR, but at the same time should reduce Fesc due to higher absorption and scattering of emitted fluorescence [14]. Nitrogen is also positively related to the amount of ribulose-l,5-bisphosphate carboxylase and oxygenase (Rubisco) protein content [23,24], and thus the maximum carboxylation rates (Vcmax), which is a key determinant of the maximum photosynthetic rates, and therefore GPP [25]. Therefore, nitrogen can influence the partitioning of APAR into PQ, NPQ, and fluorescence emission [15], but different studies, mainly at leaf level, showed contrasting results [14,26]. Moreover, there is a lack of studies that investigate at canopy scale how LUEp, LUEf, and Fesc are modulated under varying nitrogen availability [14]. Canopy phosphorous concentration (hereafter P%) is another critical element for photosynthesis, being involved in the synthesis of Adenosine triphosphate (ATP) [27]. Leaf-level studies with active fluorescence measurements showed that P% deficient plants have lower chlorophyll fluorescence emission efficiency [28]. However, we are not aware of canopy level studies showing the effect of P% on F760 and LUEf.
Canopy structural variables, such as LAI and LAD, influence the radiative transfer of incoming radiance and emitted SIF within the canopy [19]. LAD can vary on daily and seasonal bases and is strongly influenced by species composition and plant functional forms [29]. LAI and LAD can have a major influence on the sun/shaded leaf ratio through the canopy. This ratio has the potential to directly influence the level of NPQ in the canopy [30] (higher in sunlit, lower in shaded leaves) and therefore could indirectly influence the LUEf. Canopy structure, through absorption and scattering of the fluorescence emitted by the leaves, has a significant influence on observed F760, determining Fesc, the probability of F760 to escape the canopy [31]. Absorption by chlorophyll is higher in the red region, whereas multiple scattering in the far-red region increases the probability of absorption by soil and woody elements. It has been shown recently with modeling studies that TOC observed F760 (canopy scale) is only a fraction of the F760 emitted at leaf scale (F760leaf) [32]. The decoupling between F760leaf and F760, mainly mediated by Fesc, can have implications for the GPP–F760 relationships. Recently, new methods to estimate Fesc are being developed, potentially allowing to downscaling the F760 signal at the leaf level [31,33]. Finally, other variables such as soil moisture or surface temperature (Ts) also have the potential to impact the GPP–F760 relationship. Heat and water stress have been proven to affect photorespiration, but not the PQ in Mediterranean species [34], thus decoupling photochemistry from F760 [18]. Ts, in particular, contains information on both the activation of NPQ mechanisms and other processes related to stomatal closure and sensible heat losses [35]. Therefore, surface temperature might also help to better characterize the seasonal variations of LUEp and therefore to better predict GPP, in particular under stress conditions [35,36]. Figure 1 illustrates a theoretical framework that sums up current knowledge and our hypothesis regarding the interlinks between GPP and F760 and their relationship with canopy structural parameters and leaf traits of vegetation. In Figure 1, solid colored lines represent the energy partitioning at both leaf and canopy level and dotted lines represent the hypothesized relationships.
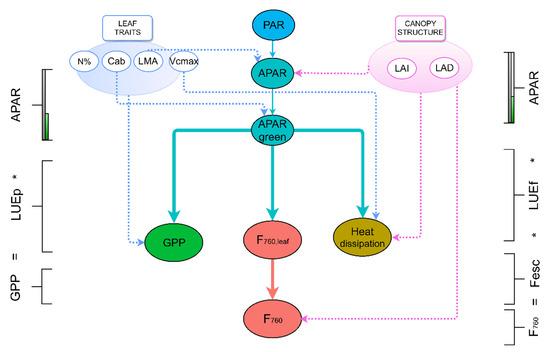
Figure 1.
Energy partitioning at the leaf and canopy level representing the processes involved in the photosynthetic light use efficiency model (GPP = APAR x LUEp) and fluorescence light use efficiency model (F760 = APAR *LUEf * Fesc) are represented with solid arrows. Dotted arrows represent the hypothesized relationship between leaf traits, canopy structure and the various processes related to the allocation of energy and transfer of SIF within the canopy. Photosynthetic active radiation (PAR); absorbed (by vegetation) photosynthetic active radiation (APAR); PAR absorbed by chlorophyll a and b molecules (APARgreen), represented as the green bar in the equations on both sides of the figure; gross primary production (GPP); sun-induced fluorescence emitted by all leaves at 760 nm (F760leaf); sun-induced fluorescence at 760 nm observed at top of canopy (F760); nitrogen concentration on a mass basis (N%); chlorophyll a and b on a mass basis (Cab); leaf mass per area (LMA); maximum carboxylation rate (Vcmax); leaf area index (LAI); leaf angle distribution (LAD).
All factors illustrated in Figure 1 play a role in determining GPP, F760, and their relationship. However, the strength of these influences, and whether leaf nutrient content and canopy structure influence the GPP–F760 relationship directly (through LUEp, LUEf and Fesc) or occur indirectly (mediated by APAR or by a third variable), is not clear. In this study, we aimed to fill the gap in understanding on how nutrients and canopy structure control LUEp, LUEf and Fesc, and we investigated the mechanisms that drive GPP and F760 in a nutrient manipulation experiment. We asked the following questions:
How do the treatments (N, NP, and P) influence LUEp, LUEf, and Fesc?
What are the drivers of the light use efficiency equations terms (LUEp, LUEf, Fesc) that relate GPP and F760?
What are the direct and indirect effects of nutrients (in particular N%) and canopy structure on GPP and F760?
To answer these questions, we used GPP, F760, and additional data on vegetation properties from a nutrient manipulation experiment in Mediterranean grassland with addition of N, P and N and P together (NP). The aim of the fertilization was to induce a changed in both plant nutrient content and structural traits (through changes in LAD mediated by plant community and LAI) within the ecosystem.
2. Materials and Methods
2.1. Experimental Site
The study was conducted in a Mediterranean savannah located in Spain (39°56'24.68"N, 5°45'50.27"W; Majadas de Tietar, Caceres) characterized by a continental Mediterranean climate, with temperate winters and warm dry summers: mean annual temperature of 16.7 °C and annual precipitation of ~650 mm distributed mainly between September and May [37].
The herbaceous layer is dominated by annual C3 species of the three main functional plant forms, namely grasses, forbs and legumes, which are green and active from October to end of May [38]. The site is managed as a typical wood pasture (Iberian Dehesa) with low intensity grazing by cows (~0.3 cows ha−1) [37].
2.2. Nutrient Manipulation Experiment, Gross Primary Production and Ancillary Data
A nutrient manipulation experiment focused on the herbaceous layer was established in early spring 2014 and 2015. The set-up consisted of four 20 m × 20 m width randomized blocks. Within each block we established four plots (9 m × 9 m) with 2 m of buffer between treatments (Figure S1). We established four treatments (for details, see [37]): control (C) with no fertilization, N addition with one application of 100 kg N ha−1 as potassium nitrate (KNO3) and ammonium nitrate (NH4NO3), P addition with 50 kg P ha−1 as monopotassium phosphate (KH2PO4), and nitrogen–phosphorous (NP) addition, with 100 kg N ha−1 and 50 kg P ha−1 as NH4NO3 and KH2PO4, respectively.
Carbon Dioxide (CO2) fluxes between the herbaceous layer and the atmosphere were measured in 32 collars of 60 cm × 60 cm for each field campaign around noon local solar time (Table 1). At each collar, GPP (μmol CO2m−2s−1) was estimated as the difference between net ecosystem CO2 exchange (NEE) measured with transparent chambers and ecosystem respiration (Reco) measured with opaque chambers. Measures CO2 and water vapor mole fractions (W) were collected at 1 Hz by means of an infrared gas analyzer (IRGA LI-840, Lincoln, NE, USA) connected to the chambers. The flux calculations and corrections were conducted using the self-developed R package “RespChamberProc” (https://github.com/bgctw/RespChamberProc). Air temperature (Ta,°C) was measured with a thermistor probe (Campbell Scientific, Logan, UT, USA). Soil moisture content (%) at 5 cm depth was determined with an impedance soil moisture probe (Theta Probe ML2x, Delta-T Devices, Cambridge, UK). Vapor pressure deficit (VPD, hPa) was computed using relative humidity and Ta. Incident PAR (µmol m−2 s−1) was measured with a quantum sensor (Li-190, Li-Cor, Lincoln, NE, USA) mounted outside of the chamber. Surface temperature (Ts, °C) was measured with infrared thermometer installed in the chambers (Tc, IRTS-P, Apogee, UT, USA).

Table 1.
Summary of the main meteorological data collected in each field campaign.
The meteorological conditions for each field campaign are reported in Table 1. Destructive sampling of the vegetation in four parcels (0.25 m × 0.25 m each) within each plot was conducted to estimate LAI and green to dry biomass ratio [37]. The abundance of each functional group such as fraction of graminoids (%graminoids), forbs (%forbs), and legumes (%legumes) was determined. The Shannon biodiversity index (H) among plant functional types was determined as in [39]. N% and P% in plant tissues were determined as described in [37]. Carbon isotopic signature (δ13C) for the vegetation was determined from dried samples using a DeltaPlus isotope ratio mass spectrometer (Thermo Fisher, Bremen, Germany) coupled via a ConFlowIII open-split to an elemental analyzer (Carlo Erba 1100 CE analyzer; Thermo Fisher Scientific, Rodano, Italy). δ13C was calculated using the measured ratio between 13C and 12C in the sample and in a calibrated in-house-standard (Acetanilide: −30.06 ± 0.05‰) as in [40,41] (Equation (4) and Figure S2):
where 13Rsample and 13Rstandard are 13C/12C ratio of the sample and of the standard, respectively.
2.3. Transpiration Estimates
Two independent estimates of transpiration (expresses as latent heat fluxes, LE) were obtained: one from upscaling the δ13C measurements (LEISO) and the other from the runs of SCOPE optimized at the experimental site [42] to obtain the LE of canopy component (LEcanopy,inv).
LEISO was calculated from δ13C, GPP and VPD according to Equation (5) [43], and then the units were converted from mmolH20 m−2 s-1 to W m−2.
where VPDmean is the mean daytime VPD computed over the period between the beginning of the growing season and the plant sampling dates for the isotope measurements, and intrinsic water use efficiency (WUEi) was calculated as following:
where Ca is the CO2 mole fraction in ambient air, b’ is the mean fractionation during carboxylation and internal transfer (−27‰), a is the fractionation during diffusion through stomata (4.4‰) and Δlin is the community weighted mean of δ13C.
Figure S3a,b displays LEISO and LEcanopy,inv, respectively, and Figure S3c shows the scatterplot of the two estimates. The two independent estimates have a good relationship, with Pearson correlation coefficient (r) of 0.701 and slope of 0.809. In Figure S3a there are no significant differences among treatments for each campaign in 2014 or 2015 in LEISO. According to the ANOVA test, the LEcanopy,inv shows significant differences in Campaign 2 in 2014 (F3,11 = 11.4, p = 0.01) and the Tukey HSD post hoc-test identifies the P treatment as significantly different from the C treatment (p = 0.012). In addition, in 2015, in Campaign 7, there is a significant difference (F3,10 = 5.47, p = 0.017) and the Tukey post-hoc identifies a significant decrease for N and P treatments in comparison with the control (p = 0.016, p = 0.042, respectively).
2.4. Field Spectroscopy, Retrieval of Sun-Induced Fluorescence and Biophysical Properties
TOC spectral radiances were collected under clear-sky conditions immediately before flux measurements at each collar [8,37]. The sampling strategy was designed to minimize the differences in solar zenith angle (SZA) between measurements, confirmed by the ANOVA test, which reports non-significant differences in SZA between treatments in each campaign (p = 0.43, p = 0.41, p = 0.33, p = 0.65, p = 0.99, p = 0.99, and p = 0.57 for Campaigns 1–7, respectively). The ranges of SZA for the spectral measurements are reported in Table 1. Two portable spectrometers (HR4000, OceanOptics, USA) were used to estimate chlorophyll fluorescence at the O2A band (i.e., F760,) and reflectance in the spectral range 400–1000 nm. The measurements protocol was the following: We first measured the incident solar irradiance by nadir observations of a leveled calibrated standard reflectance panel (Spectralon, LabSphere, USA). We then acquired five measurements of TOC spectral radiances from nadir at 110 cm above the targeted area using bare fiber optics of 25° of field of view (about 43 cm diameter at the ground, Figure S4). F760 was estimated by exploiting the spectral fitting method [6]. The spectral interval used for F760 was set to 759.00–767.76 nm. Albedo400–900 was calculated from TOC spectral radiances as shown in Equation (7), assuming a Lambertian behavior of the reflected radiance.
where Lr is the reflected radiance and E400–900 is the Irradiance. fAPAR was estimated in three different ways: (i) fAPARSCOPE was simulated by the process based SCOPE model [44]. (ii) fAPARRENDVI was based on the established relationship between measured fAPAR and the red edge NDVI (RENDVI) found in maize, soybean and grasslands [45] (Equation (8)).
where RENDVI is calculated as shown in Equation (9):
where RNIR and RRE are reflectance factors in spectral bands 770–800 nm and 700–710 nm, respectively. (iii) APARLi&Moreau1996 was based on subtracting the integral (between 400 and 700 nm) of the incoming PAR (PARinc) from the integral (between 400 and 700 nm) of the reflected PAR (PARrefl) measured by the spectrometers [7,46] and then multiplying by the proportion of canopy absorption (RAPAR) [47] (Equation (10)).
where RAPAR is calculated as:
The fAPAR formulations are quite consistent with each other (Figure S5), and therefore hereafter we use fAPARRENDVI.
2.5. SCOPE Model Simulations
Forward and inverse simulations with the SCOPE model were conducted to assess the robustness of fAPAR, Fesc, and LEISO derived from field observations.
The forward runs model was parameterized using the structural and functional traits derived from the field sampling as well as meteorological and chamber data. Vapor pressure deficit (VPD, hPa), air pressure (p, hPa), short wave downwelling radiation (Rin, W m−2), long wave downwelling radiation (Rli, W m−2), air temperature (Ta, °C), wind speed (u, m s−1), soil moisture content (SMC, %), leaf area index (LAI m2 m−2), canopy height (h, m), chlorophyll a and b content (Cab, μg cm−2), dry matter content (Cdm, g cm−2), maximum carboxylation rate (Vcmax, μmol m−2 s−1) and the parameters to characterize the leaf angle distribution (LAD), respectively, LIDFa and LIDFb, were used to parameterize the model run. SCOPE meteorological drivers were measured along with chamber measurements for the majority; in the case they were not available with the chambers, such as Rin, Rli, p, VPD, wind speed, atmospheric CO2 concentration (Ca, ppm), and atmospheric O2 concentration (Oa, ppm), they were derived by linearly interpolating two consecutive measurements around the chambers measurement time collected at the nearby eddy covariance flux tower at 10 min of temporal resolution. Canopy height was estimated in the field with a meter stick in five positions within the measurement collar. Additional parameters such as leaf equivalent water thickness, leaf width, Ball–Berry stomatal conductance parameter and dark respiration rate at 25 °C as fraction of Vcmax were obtained from the literature for C3 grasses [8]. The SZA at the time of the collection of the spectral measurements was used as model input. Soil reflectance spectra were collected in a dedicated field campaign in April 2015 and used for all the runs. Leaf angle distribution was parameterized in SCOPE as in [8] by assuming grasses to be erectophile, forbs spherical and legumes planophiles.
The accuracy of F760 and GPP simulated with SCOPE (F760FW and GPPFW, respectively) was evaluated by root mean-squared error (RMSE), slope, intercept, and the determination coefficient (R2) of the linear regression between observed and modeled data (Figure S6).
Inverse runs of SCOPE against reflectance, F760, GPP and thermal radiance, as described in [42], were carried out to obtain LEcanopy,inv and Fesc (Fescinv).
2.6. Calculation of the Light Use Efficiency of Photosynthesis (LUEp), Light use Efficiency of Fluorescence Emission (LUEf) and Escape Probability of F760 (Fesc)
For each plot and campaign, LUEp, LUEf and Fesc were computed. LUEp was calculated as in Equation (12):
where GPP is the one measured with the chambers and APAR was calculated as in Equation (13):
LUEf was computed as in Equation (14):
where F760 is the TOC fluorescence retrieved and Fescfw is the escape probability calculated from forward runs of SCOPE and APARradiance (mW m−2 nm−1 sr−1) is calculated from APAR (μmol m−2 s−1) as shown in Equation (15).
where 4.6 represent the conversion factor from μmol m−2 s−1 to W m-2 for radiation from 400 to 700 nm [48] and wl is the wavelength interval (300 nm), and π is used to transform irradiance to radiance.
We computed Fesc and F760leaf in three alternative ways to evaluate their consistency:
(i) Combination of forward runs of SCOPE and measured F760 (Fescfw) as shown in Equation (16):
where F760leaf,FW and F760leaf,fw are fluorescence emitted by all leaves at 760 nm as calculated by the forward SCOPE run (hemispherical and directional, respectively).
(ii) An empirical estimate of Fesc (Fescemp) computed according to Equation (17) [33]:
NIRV was calculated as in Equation (18), where NIRT is the reflectance at 858 nm.
Then, empirical Fleaf (F760leaf,emp) was calculated as in Equation (19).
(iii) An estimation of Fesc using data from a SCOPE inversion (Fescinv) (Equation (20)).
Fescinv was obtained from inversion of SCOPE against reflectance, F760, GPP and thermal radiance, as described in [42] and was calculated as in Equation (20).
where F760INV and F760leaf,INV are the top-of canopy sun-induced fluorescence at 760 nm and sun-induced fluorescence emitted by all leaves at 760 nm as obtained from SCOPE inversion.
Finally, F760leaf,inv was calculated as in Equation (21).
The three alternative Fesc and Fleaf computed (F760leaf,fw, F760leaf,emp, and F760leaf,inv) were compared against each other (Figure S7). The analysis presented below were conducted with all the different estimates of Fesc to evaluate the effect on the results presented. Hereafter, we report only the results obtained with Fescfw and F760leaf,fw.
2.7. Statistical Analysis
Our statistical analysis consisted of three parts. First, to answer Research Question (i), group differences among treatments were analyzed with Analysis of Variance (ANOVA) and differences among groups were tested with Tukey Honest Significant differences (HSD) post-hoc test. In the case of violation of the assumption of homoscedasticity of residuals, the ANOVA with the Welch’s correction [49] and post-hoc analysis with Games–Howell test [50] were used. In addition, an analysis of Covariance (ANCOVA) was used to test if the relationship between GPP and F760 (canopy scale) and F760leaf,fw (leaf level) is changing with the treatment and in time.
Second, we addressed Research Question (ii) with the relative importance analysis with “lmg” (Lindeman, Merenda and Gold), a popular approach for quantifying the individual contributions of multiple regressors, assuming linear relationships, as implemented in the R package “relaimpo” [51]. Standard errors were computed by means of bootstrapping (n = 1000 realizations). Independent variables (i.e., predictors) used in the relative importance analysis are N%, %graminoids, %legumes, Ts, LAI, Shannon Biodiversity Index (H) and soil moisture. Additional relative importance analyses were carried out with the surface-air temperature (Ts - Ta) in place of Ts (Figure S8), as Ts −Ta could be a good proxy for water stress [52].
Third, to answer Research Question (iii), a path analysis was used. The path analysis assumes linearity among variables and the effects are considered additive and not multiplicative. The structural model is based on expected relationships hypothesized and its model structure is shown in Figure S9. The user specifies the model structure, and the method outputs estimates of the path coefficients. The analysis was conducted with the R package “lavaan” [53]. The individual links among variables were evaluated by means of the p-value and standardized coefficient (β). It should be noted that in the analysis we used Ts in place of the reflectance based indexes because: (i) Ts contains information on NPQ [54]; and (ii) Ts is independent from the measurements used to estimate F760.
Chi-squared (χ2), comparative fit index (CFI), standardized root mean square of residual (SRMR) and Root Mean Square Error of Approximation (RMSEA) were computed to evaluate the overall accuracy of the models. The standard error of β and of the model fit indices were obtained from bootstrapping the dataset (n =100 realizations). Additionally, to assess the stability of the individual paths across treatments and the robustness of the original model, we made intervention on the dataset by removing from the dataset one treatment and evaluating the impact on the individual β coefficients (Figures S10–S13).
3. Results
3.1. Description of Fertilization Effects on Fluxes, Optical Data, and Vegetation Characteristics
The effect of the fertilization treatment on GPP, LUEp, F760, LUEf and Fescfw is shown in Figure 2. All these variables show a wide variation in time (campaign) and with treatment. GPP is higher in the N and NP treatments in 2014 and more substantially in 2015 during Campaigns 5 (F3,18= 15.6, p < 0.01) and 6 (F3,26= 13.1, p < 0.01). LUEp in the N treatment is significantly different from the C treatment only during Campaign 6 (F3,26= 2.7, p < 0.05).
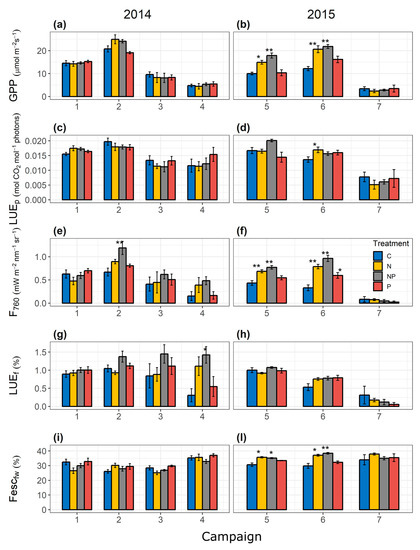
Figure 2.
Bar graphs representing differences among treatments (control treatment, C; nitrogen treatment, N; nitrogen and phosphorus treatment, NP; and control treatment, C) of Gross Primary Production (GPP) in 2014 (a) and 2015 (b); light use efficiency of photosynthesis (LUEp) in 2014 (c) and 2015 (d); Fluorescence at 760 nm (F760) in 2014 (e) and 2015 (f); light use efficiency of fluorescence emission at 760 nm (LUEf) in 2014 (g) and 2015 (h); and fraction of F760 that escapes the canopy (Fescfw) in 2014 (i) and 2015 (l). Data are divided among campaigns. Bar graphs represent means and error bars represent 1 standard error. Group differences in (a–h) were analyzed with ANOVA test and individual differences among groups were evaluated with Tukey HSD post hoc test. Group differences in (i,l) were analyzed with ANOVA with the Welch correction and individual differences among groups were evaluated with the Games–Howell post hoc test. “*” refers to a significant difference from the control treatment with p value < 0.05 and “**” refers to a significant difference from the control treatment with p value < 0.01.
F760 shows a significant increase during Campaign 2 for the NP treatment (F3,11= 5.9, p < 0.05) and during Campaigns 5 (for N and NP) (F3,18 = 13.2, p < 0.01) and 6 (for N,NP, and P) (F3,26= 19.7, p < 0.01) of 2015. LUEf is significantly higher for the NP treatment during Campaign 4 of 2014 (F3,12= 4.59, p < 0.05), while Fesc shows significant increases for the N and NP treatment of Campaigns 5 (F3,18= 11.32, p < 0.05 and p < 0.05, respectively ) and 6 (F3,26 = 15.91, p < 0.05 and p < 0.01, respectively) of 2015.
Figure 3 displays changes in N%, APAR, Albedo400–900, Ts and plant community (%graminoids) with the fertilization treatment. N% shows a quite consistent increase in the N and NP treatment in 2014 in comparison with the C treatment for Campaigns 2 (F3,11 = 26.8, p < 0.01), 3 (F3,12= 14.2, p < 0.01) and 4 (F3,11= 14.2, p < 0.01) and in 2015 in Campaigns 5 (F3,18= 56.2, p < 0.01) and 6 (F3,26= 18.5, p < 0.01). APAR presents significant differences for the N and NP treatment of Campaign 2 (F3,11= 24.98, p < 0.01) of 2014 and Campaigns 5 and 6 of 2015 (F3,18= 7.37, p < 0.01 and F3,26= 38.5, p < 0.01, respectively).
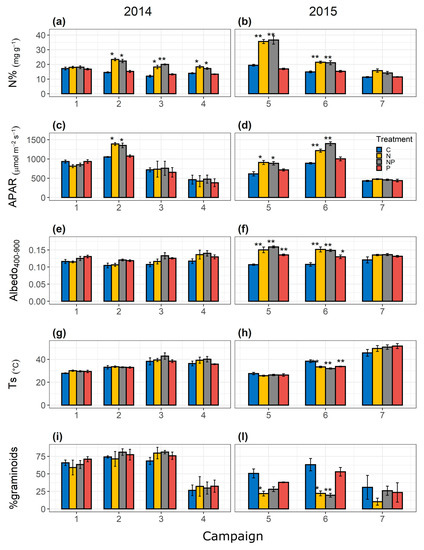
Figure 3.
Bar graph representing differences among treatments (control treatment, C; nitrogen treatment, N; nitrogen and phosphorus treatment, NP; and control treatment, C) of Canopy nitrogen content (N%) in 2014 (a) and 2015 (b); absorbed photosynthetic active radiation (APAR) in 2014 (c) and 2015 (d); Albedo400–900 in 2014 (e) and 2015 (f); Surface Temperature (Ts) in 2014 (g) and 2015 (h); and graminoids relative abundance (%graminoids) in 2014 (i) and 2015 (l). Data are divided among campaigns. Bar graphs represent means and error bars represent 1 standard error. Group differences in (e–h) were analyzed with ANOVA test and individual differences among groups were evaluated with Tukey HSD post hoc test. Group differences in (a,b,i,l) were analyzed with ANOVA with the Welch correction and individual differences among groups were evaluated with the Games–Howell post hoc test. “*” refers to a significant difference from the control treatment with p value < 0.05 and “**” refers to a significant difference from the control treatment with p value < 0.01.
All treatments show a significant increase in Albedo400–900 during Campaigns 5 (F3,18= 29.3, p < 0.01) and 6 (F3,26= 13.6, p < 0.01) in 2015, but no significant treatment-induced changes in Albedo400–900 are observed in 2014. Ts shows significant differences in Campaign 6 for the N, NP and P treatments (F3,26= 13.5, p < 0.01). LEISO follows the phenological cycle with lower values in 2015 (Figure S3a). There are differences in LEISO among treatments (such as the increase during Campaign 2 of 2014 for N and NP), but these appeared not significant according to the ANOVA. LEISO estimates are consistent also with independent simulations with SCOPE (Figure S3c).
Instead, significant differences in %graminoids among treatments occur mainly in 2015 in Campaigns 5 (F3,18= 9.4, p < 0.01) and 6 (F3,26= 13.3, p < 0.01) with lower %graminoids in N and NP treatments. %Forbs also present significant differences in 2015 by increasing in the N treatment (in comparison with the C treatment) (F3,18= 8.8, p < 0.01) and in Campaign 6 in the N and NP treatment (F3,26= 11.5, p < 0.01) (Figure S14d). %Legumes is marginal and does not change significantly among treatments (Figure S14e,f).
3.2. Temporal Variability of GPP–F760 and GPP–F760leaf.fw Relationship among Treatments
The results of the ANCOVA show that, in 2014, the intercept of the C treatment is significantly different from the other treatments for both F760 (as shown in previous studies [8,37] and F760leaf,fw (p < 0.05 and p < 0.05, respectively) (Figure 4 and Table S1).
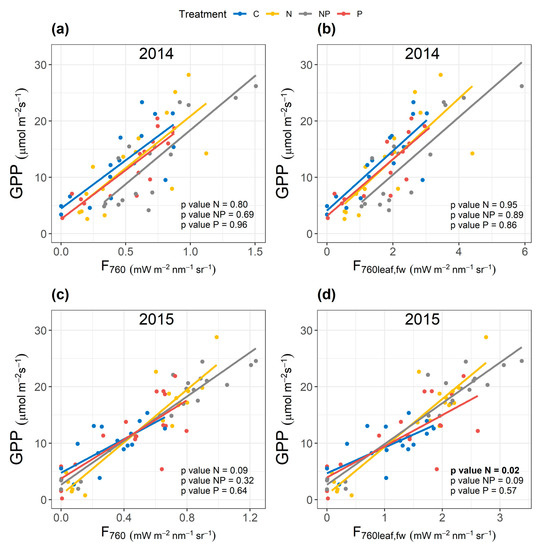
Figure 4.
Scatterplot of observed fluorescence at 760 nm from top of canopy (F760) vs. Gross Primary Production (GPP) for 2014 (a) and for 2015 (c); and directional fluorescence emitted by all leaves at 760 nm calculated from forward SCOPE runs (F760leaf,fw) vs. GPP for 2014 (b) and for 2015 (d). Data are divided for the four treatments; control (C), nitrogen addition (N), nitrogen and phosphorus addition (NP) and phosphorus addition (P). P values of the interaction treatment with independent variable (in comparison with the control treatment, C) from an analysis of covariance (ANCOVA) are reported in the bottom-right of each panel. Colored lines represent the regression from the ordinary least square regression.
In 2015, the intercept is different for the C treatment for both F760 and F760leaf,fw (p < 0.01 for both) and for the NP treatment with p < 0.05 for both F760 and F760leaf,fw. In 2015, for the N treatment, there is no significant interaction between F760 and treatment (Figure 4c), but there is a significant interaction between F760leaf,fw and the N treatment (p < 0.05) (Figure 4d), with significant differences of the GPP–F760leaf,fw relationship. There is no significant effect of the year on the GPP–F760 relationship. For each treatment, p = 0.706, p = 0.323, p = 0.927 and p = 0.992 for N, P and NP and C, respectively. Instead, when substituting F760 with F760leaf,fw, the effect of the year is not significant in the treatments C and P (p = 0.659 and p=0.742), but is significant for the NP treatment with p < 0.05, and barely not significant for the N treatment with p = 0.057.
3.3. Factors Controlling the Parameters of Light Use Efficiency Equation (LUEp, LUEf and Fesc)
The relative importance analysis with “lmg” method shows that LUEp is the variable with the highest explained variance (R2 = 0.67 ± 0.054), followed by Fesc (R2 = 0.62 ± 0.06) and LUEf (R2 = 0.46 + 0.06) (Figure 5). The variable that explains the most variance of LUEp is Ts (R2 = 0.36 ±0.06), followed by LAI (R2 = 0.13 ±0.05), Canopy N% (R2 = 0.06 ± 0.04) and H (R2 = 0.05 ± 0.04). The main predictor of LUEf is %graminoids (R2 = 0.15 ± 0.07), followed by Ts (R2 = 0.13 ± 0.08), LAI (R2 = 0.07 ± 0.05), and Canopy N% (R2 = 0.05 ± 0.03). The main predictor of Fesc is clearly %graminoids (R2 = 0.52 ± 0.03), followed by soil moisture (R2 = 0.03 ± 0.04) and Canopy N% (R2 = 0.02 ± 0.02), the latter contributing only marginally.
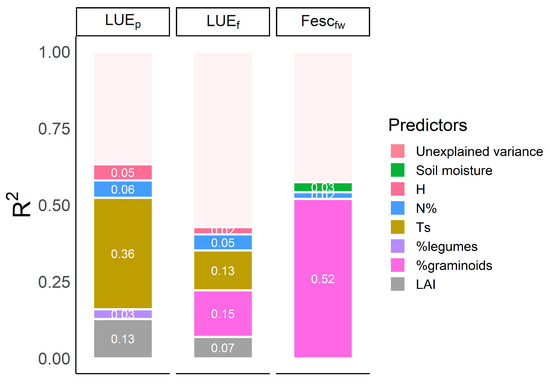
Figure 5.
Relative importance analysis with “lmg”(Lindeman, Merenda and Gold) method of Light use efficiency of photosynthesis (LUEp), Light use efficiency of fluorescence emission at 760 nm (LUEf) and escape probability of sun-induced fluorescence at 760 nm obtained from forward runs of SCOPE (Fescfw). Predictors included in the analysis are: soil moisture, Shannon biodiversity index (H), canopy nitrogen content (N%), surface temperature (Ts), relative abundance of legumes (%legumes), relative abundance of graminoids (%graminoids) and leaf area index (LAI). Error bars (1 SE) are calculated through bootstrapping (n = 1000), but are not shown in the figure. They are however reported in the result section.
The results of the relative importance analysis for GPP, F760, and F760leaf.fw show the importance of LAI that controls the seasonality of canopy structure and APAR (Figure S15).
When substituting as predictor Ts with Ts - Ta, we found slightly better results than Ts alone when predicting GPP, F760, and F760leaf,fw (Figure S8). However, including Ts - Ta does not improve the overall prediction, as the contribution to R2 of LAI decreases, but the total R2 remains similar. When predicting LUEp, LUEf, and Fesc, Ts - Ta is a worse predictor of LUEp than Ts (R2 = 0.28 ± 0.05).
3.4. Mechanisms behind the Treatment Effect on GPP and F760 at Leaf and Canopy Scale
Figure 6 shows the output of the path analysis. The results of the final models are displayed as graphs. The overall model fit is evaluated: χ2 = 129 ± 23, CFI = 0.901 ± 0.03, SRMR = 0.07 ± 0.02 and RMSEA= 0.19 ± 0.02. CFI and SRMR show excellent fit according to Hu & Bentler [55]. In contrast, the RMSEA is higher than expected. RMSEA is part of the parsimony-adjusted fit indexes, which reward low model complexity. Our goal is however to represent a holistic model that includes all the relevant processes and we do not use the path analysis a posteriori as a mean of model selection. Additionally, according to [56], “RMSEA over-rejects true models for ‘small’ n (n < 250)”, which might be the cause of our RMSEA value, as our sample size is 133.
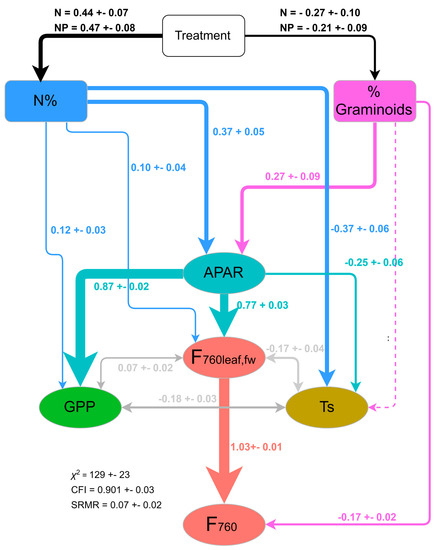
Figure 6.
Path analysis displays the role of canopy nitrogen content (Canopy N) and relative graminoids abundance (%graminoids) on the energy partitioning at the leaf and canopy level. Photosynthetic active radiation (PAR); absorbed by vegetation photosynthetic active radiation (APAR); fluorescence emission by all leaves at 760 nm calculated by forward runs of SCOPE (F760leaf,fw); gross primary production (GPP); surface temperature (Ts); and observed fluorescence at 760 nm (F760). The strength of the relationship among variables is expressed by the standardized coefficient (β) of the path analysis. Each standardized coefficient has a standard error obtained from bootstrapping (n = 100 times). The width of the arrows is proportional to their standardized coefficient (β). Colored lines (both solid or dotted) represent direct relationships between variables, whereas gray double-headed arrows represent the covariance among variables. Solid and dotted lines indicate significant (p < 0.05) and non-significant relationships, respectively. The width of the arrows is proportional to their standardized coefficient (β). The different colors are introduced to increase readability of the standardized path coefficients. The fit by the overall model is measured by means of Chi-squared (χ2), comparative fit index (CFI) and standardized root mean square of residual (SRMR).
Figure 6 shows the clear effect of the %graminoids on F760. The N and NP treatments significantly affect N% with β of 0.44 ± 0.07 and 0.47 ± 0.08, respectively. N and NP treatments also affect significantly %graminoids with β of −0.27 ± 0.1 and −0.21 ± 0.09, respectively. N% has a significant relationship with four variables: APAR, Ts, GPP, and F760leaf,fw with β of 0.37 ± 0.05, −0.37 ± 0.06, 0.12 ± 0.03 and 0.10 ± 0.04, respectively. %graminoids significantly affects APAR and F760 with β of 0.27 ± 0.09 and −0.17 ± 0.02, respectively. The path between %graminoids and Ts is however not significant. APAR significantly influences GPP, F760leaf,fw and Ts with β of 0.87 ± 0.02, 0.77 ± 0.03 and −0.25 ± 0.06. Finally, F760leaf,fw and Ts have a significant covariance with β of −0.17 ± 0.04. F760leaf,fw and GPP have a significant covariance with β of 0.07 ± 0.02 and so do GPP and Ts with β of −0.18 ± 0.03.
Alternative models using different estimates of F760leaf were tested and we found that the same paths are selected as significant, and the magnitude of the β coefficients are almost unchanged (Figure S16). This suggests that the path analysis model is not strongly dependent by the estimation type of the fluorescence emission. The results of the intervention removing treatments show that the vast majority of the paths remain constant and significant. The only difference can be seen when removing the NP treatment (Figure S11), where the links between canopy N and GPP and canopy N and F760leaf,fw become non-significant.
4. Discussion
In the following section, we first discuss the treatment effects (N, NP, and P) on the LUE equation terms, second the predictors of LUEp, LUEf and Fescfw, and third how the nutrient fertilization affects GPP and F760 through changes in N%, plant community and canopy structure.
4.1. Treatment Effect on LUEp, LUEf, Fescfw
The relative stability among treatments of LUEp, which is significantly different for the N treatment only in Campaign 6 and shows an increase of NP in Campaign 5 in 2015, suggests that our Mediterranean grasslands is quite constrained in its photosynthetic efficiency, and that any nutrient induced changes in GPP (Figure 2) are mostly modulated by changes in structural parameters such as fAPAR.
The increase in LUEf in the NP treatment compared to N alone suggests a co-limitation of nitrogen and phosphorus on fluorescence efficiency. The role of P on the functional modulation of fluorescence efficiency at canopy scale has not yet been shown in the literature. However, a series of studies at leaf level showed a positive relationship between photochemical quenching and P in leaves as well as an effect of P on active fluorescence measurements [57]; these support the differences in LUEf observed in our study. Our study suggests that P, and in particular the co-limitation N and P, might have an important role on determining F760 but is not conclusive on the mechanism, and more research is needed to understand the mechanism and also to support the current efforts to include P in terrestrial biosphere and photosynthesis models [27]. The fact that the magnitude of increase of Fescfw is very similar in N and NP treatments support the idea that N addition is the main factor regulating canopy structure (Fescfw and APAR). Other works show that N addition strongly impacts canopy structural parameters such as LAI and plant height in a short-grass prairie [58], although there are no studies focused on the effect of N and NP on Fesc.
Overall, the ecosystem responded in the first year to the fertilization, mainly in a functional way (higher LUEf), whereas, in the second year of fertilization, we observed structurally mediated increase in GPP and F760 (through higher APAR and Fescfw) (Figure 2l and Figure 3d). The structurally mediated changes in 2015, driven by a decrease in abundance of erectophiles plants as the graminoids in the N containing treatments, caused a change in slope in the GPP–F760 relationship for the N and NP treatment (Figure 4c), which is almost significantly different from the C for F760, but significantly different from the C for F760leaf,fw in the NP treatment (Figure 4d).
The N treatment has proven to affect plant functioning and canopy structure (APAR and Fescfw), while P has only a marginal role on the LUEf. For this reason, in the next paragraphs, more attention is paid to the role of N%, together with meteorology and canopy structure, as driver of in LUEp, LUEf and Fescfw, as well as GPP and F760.
4.2. Predictors of the Terms of the Light Use Efficiency Equation
Understanding the causes of variability of the parameters of LUE equations (LUEp, LUEf, and Fescfw is fundamental to exploit remote sensing information such as F760 for modeling spatio-temporal patterns of GPP [20]. We show that Ts is the main predictor of LUEp, and together with %graminoids is one of the two main predictors of LUEf. Ts is a good indicator of water stress and strongly related to phenology and green fraction of vegetation [59,60], which ultimately relates to temporal variability of LUEp. However, the fact that variables normalized by APAR such as LUEp and LUEf are driven by Ts indicates that it is not only a seasonal effect but rather physiological. In fact, Ts contains also information related to the activation of the xanthophyll cycle responsible for NPQ processes (Figure S17) that ultimately is related to LUEp and LUEf [18]. Finally, many variables that have the potential to influence LUEp, such as photorespiration and chlororespiration, are influenced by leaf temperature [61], potentially explaining why Ts is being selected. Our results reinforce the idea that Ts should be used as additional input of LUE models aimed at the prediction of GPP [62].
The %graminoids is by far the best predictor of Fescfw, independently by the method used for the calculation of Fesc. Graminoids are mainly erectophiles [29], because of this particular LAD, most of the fluorescence is emitted laterally and therefore scattered by the vegetation [8]. In this work, we tested different formulations of Fescfw with consistent results, in particular between the model-based (Fescfw) and the data-driven (Fescemp) estimates. The fact that %graminoids is a good proxy for the effect of structure on F760 and Fesc also opens interesting perspective to use F760 as well as Fesc to assess taxonomic diversity, when diversity is somehow represented by changes in canopy architecture [63].
N% is an additional predictor selected for LUEf and LUEp, although the additional explained variance seems marginal (Figure 5). N% is positively related to Vcmax [24,64], and under light saturated conditions a higher Vcmax leads to an increase of LUEp and, to less extent, to increase of LUEf [65]. As hypothesized, from this analysis, it appears that the effect of N% on F760 and LUE equation terms is not direct and, in Section 4.3, we discuss the relationships between N%, canopy structure, and the observed variables.
4.3. Mechanisms behind the Treatment Effect on GPP and F760 at Leaf and Canopy Scale
The effect of canopy structure on F760 manifests itself mainly through variation in APAR and Fescfw (Figure 6 and Figure 2i,l, respectively). With the path analysis, we conclude that %graminoids positively influences APAR that leads to an increase of F760leaf,fw indirectly. Moreover, %graminoids negatively influence Fescfw. The changes of canopy structure mediated by changes in plant community at plot level are the most important factors controlling the pathway between F760leaf,fw and F760, and ultimately GPP and F760.
By analyzing the relationships between different components measured in the manipulative experiment presented here, we were able to disentangle the pathways, mostly unknown [14,20], through which N% influence the different components of the LUE equations. Our results show that the largest effect of N% on fluorescence emission is not direct, but rather mediated by APAR and Ts (Figure 6), which in turn affect F760leaf,fw.
There are two indirect ways in which N% affects F760leaf,fw: (i) Higher N% in the green fraction of the vegetation is associated to an increase of photosynthetic pigments and in particular Cab in leaves [64] and in the canopy [22], which ultimately has a positive effect on APAR [15,66]. Increase in APAR causes higher fluorescence emission at leaf and canopy level (Figure 6) [67]. There are contrasting results in the literature regarding the effect of N% on fluorescence and all the studies conducted at the leaf level [14,15,26]. Our study at canopy level supports the findings in [15] that at varying levels of N available APAR modulates F760leaf,fw and F760, and its relationship with GPP. (ii) N% influences positively F760leaf,fw through Ts. N% has a negative effect on Ts and F760leaf,fw exhibits a negative relationship with Ts. The first hypothesized mechanism is related with the observed increased in Albedo400–900 (Figure 3e,f) associated with the higher N%. The effect of N% on albedo, despite being quite debated in the literature [68,69], has been demonstrated both at canopy scale [70,71] and at leaf level [72] and has to do with the increase in near infra-red (NIR) reflectance that is larger than the decrease of the reflectance in the visible region due to higher Cab and light absorption. Therefore, the increase of Albedo400–900 with increasing N% results in less available energy in the canopy, which eventually leads to a decrease of Ts if other conditions such as soil moisture and VPD are similar [69,72]. The second has to do with the modulation of transpiration due to the fertilization (Figure 3g,h), which cools down the canopy, as the leaf surfaces lose heat when water evaporates through the stomata. Our estimate of LEISO show an increase in N and NP treatments during the peak of the growing season, but it is not significant (Figure S3a,b) and lower than the changes in in Albedo400–900 for N, NP and P, in particular in 2015 (Figure 3c,d). Given the strong response of GPP in the N and NP treatments in 2015 (Figure 2b), the mild change in LEISO (Figure S3a,b) suggests an increase of water use efficiency, which is backed by δ13C measurements, which show a significant increase in the N and NP treatment of Campaign 6 (Figure S2) (where less negative values correspond to higher WUE [73]). Therefore, we can conclude that, although transpiration might be involved in the regulation of Ts at the peak of the season, biophysical variables such as Albedo400–900 are much more affected by N% and contribute to reduce Ts.
Given that a large amount of N is invested in Rubisco protein [23], N can impact directly the carboxylation rates. The direct link between carboxylation rates and F760leaf is not yet clear [74]. However, we found a direct, though weak, relationship between N% and F760leaf,fw (Figure 6) that is likely mediated by the ceiling effect mechanism described in the literature in an elevated CO2 manipulation experiment [19,65], but not yet observed in nutrient manipulation experiments.
5. Conclusions
This study analyzed and explained the underlying mechanism responsible for the changes in gross primary productivity (GPP) and sun-induced fluorescence at 760 nm (F760), and their relationship, due to a nutrient fertilization with nitrogen (N), phosphorous (P), and the combination of the two nutrients (NP). The nitrogen additions (N and NP) had an effect mainly through changes in absorbed photosynthetically active radiation (APAR) and escape probability of fluorescence (Fescfw). Changes in APAR are directly related to changes in GPP and F760 and are due to the combination of changes in canopy chlorophyll content and in species composition that modifies the canopy structure. Changes in Fescfw are mainly due to the changes in the abundance of erectophile vegetation with N addition. In the treatment with the addition of N, forbs (non-erectophile) increased while graminoids (erectophile) decreased, which ultimately led to changes in leaf angle distribution and modified the F760 observed in particular in 2015. This has an effect on GPP–F760 relationship both across treatments and from year to year. Phosphorous addition had a significant effect on the light use efficiency of fluorescence, in particular when combined with high nitrogen availability. This result points toward the need of better understanding the thus far neglected role of phosphorous on modulating sun-induced fluorescence.
With a path analysis, we also revealed that N% not only affects F760 indirectly through APAR and Fescfw, but also is tightly related with surface temperature (Ts). The negative relationship between N% and Ts is biophysically mediated by higher albedo observed after the fertilization, and only marginally physiological mediated by increase in transpiration. We also found a trade-off between F760 and Ts (likely mediated by the non-photochemical quenching mechanisms), indicating the importance of measuring simultaneously these two quantities. We finally found that Ts is also the main predictor of the light use efficiency of photosynthesis, which is a fundamental parameter to improve the predictability of GPP. In conclusion, our results show that both nutrient availability and their indirect effect on biodiversity are fundamental drivers of sun-induced fluorescence, and its relationship with gross primary productivity. Our results also reveal the interlink among fluorescence, surface temperature and GPP, and support the importance of tandem missions such as the FLuorescence EXplorer (FLEX) and Sentinel-3, providing concomitant estimates of sun-induced fluorescence, vegetation related spectral indices, and land surface temperature.
Supplementary Materials
The following are available online at https://www.mdpi.com/2072-4292/11/21/2562/s1, Figure S1: Aerial photograph of the experimental site (SMANIE). Figure S2: Group differences among treatment of carbon isotopic signature (δ13C). Figure S3: The two transpiration estimates and the albedo400–900 across treatments. Figure S4: Schematic of the radiometric and chamber footprint. Figure S5: Scatterplot of the two APAR estimations. Figure S6: Scatterplot of modeled vs. observed GPP and F760. Figure S6: Relationship between F760leaf from forward runs of SCOPE, inverse runs and empirical estimates. Figure S7: Scatterplot of GPP–F760 at leaf and canopy scale across treatments. Figure S8: Relative importance analysis of GPP, F760, F760leaf,fw, F760leaf,inv, LUEp, LUEf, and Fescfw with Ts −Ta instead of Ts. Figure S9: Set of equations that represent the model structure for the path analysis. Figure S10: Path analysis without the nitrogen treatment. Figure S11: Path analysis without the nitrogen and phosphorus treatment. Figure S12: Path analysis without the phosphorus treatment. Figure S13: Path analysis without the control treatment. Figure S14. Bar graph representing differences among treatments of %graminoids, %Forbs and %Legumes. Table S1: Evaluation of the relationship between GPP and F760 and between GPP and F760leaf,fw among different treatments. Figure S15: Relative importance analysis of GPP, F760, F760leaf,fw, F760leaf,inv, LUEp, LUEf, and Fescfw. Figure S16: Path analysis with fluorescence emission at 760 nm calculated from SCOPE inversion. Figure S17: Scatterplot of Ts and PRI . Table S1: Evaluation of the relationship between Gross Primary Production (GPP) and Fluorescence at 760 nm (F760) and between GPP and Fluorescence at emission level at 760 nm (F760leaf,fw) among different treatments.
Author Contributions
D.M. and M.M. designed the study and carried out the majority of the data-analysis. M.M. and M.R. (Markus Reichstein) designed the experiment. J.P.-L., O.P.-P., M.M., G.M., A.C., M.R. (Micol Rossini) and J.G. collected and processed the data and R.G.-C. and G.M. contributed with laboratory analysis. O.P.-P. carried out the analysis of flux data. J.P.-L. contributed with SCOPE inversion runs. T.J. and M.R. (Micol Rossini) contributed with the field calibration of the spectrometers and fluorescence retrieval. C.v.d.T contributed to discussion about SCOPE and the role of transpiration. T.S.E.-M. contributed with the discussion about the role of albedo. R.C. helped to structure the manuscript and provided discussion about the statistical methods used. M.R. (Micol Rossini), M.R. (Markus Reichstein), U.R., G.M., M.P.M., P.Y., A.C., D.M. and M.M. contributed to the discussion about the role of nutrients in influencing sun-induced fluorescence. All authors contributed to the discussion of the results and to the writing of the manuscript.
Funding
The project received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No. 721995. The authors acknowledge the Alexander von Humboldt Foundation for supporting this research with the Max-Planck Prize to Markus Reichstein, and the EUFAR TA project DEHESHyrE (EU FP7 Program), the EnMAP project “MoReDEHESHyReS” (Contract No. 50EE1621, German Aerospace Center (DLR) and German Federal Ministry of Economic Affairs and Energy), SynerTGE (CGL2015-69095-R, MINECO/FEDER, UE) and FLUχPEC (CGL2012-34383, Spanish Ministry of Economy and Competitiveness). This work was supported by a research grant (18968) from VILLUM FONDEN.
Acknowledgments
We acknowledge the Majadas de Tiétar city council for its support. We thank Anatoly Gitelson, Tiana Hammer, Kathrin Henkel and Thomas Wutzler for the support.
Conflicts of Interest
No conflict of interests.
References
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Monteith, J. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Guanter, L.; Zhang, Y.G.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.E.; et al. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proc. Natl. Acad. Sci. USA 2014, 111, E1327–E1333. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Tang, J.; Mustard, J.F.; Lee, J.E.; Rossini, M.; Joiner, J.; Munger, J.W.; Kornfeld, A.; Richardson, A.D. Solar--induced chlorophyll fluorescence that correlates with canopy photosynthesis on diurnal and seasonal scales in a temperate deciduous forest. Geophys. Res. Lett. 2015, 42, 2977–2987. [Google Scholar] [CrossRef]
- Zhang, Y.; Guanter, L.; Berry, J.A.; Joiner, J.; van der Tol, C.; Huete, A.; Gitelson, A.; Voigt, M.; Köhler, P. Estimation of vegetation photosynthetic capacity from space--based measurements of chlorophyll fluorescence for terrestrial biosphere models. Glob. Chang. Biol. 2014, 20, 3727–3742. [Google Scholar] [CrossRef]
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ. 2009, 113, 2037–2051. [Google Scholar] [CrossRef]
- Damm, A.; Elbers, J.; Erler, A.; Gioli, B.; Hamdi, K.; Hutjes, R.; Kosvancova, M.; Meroni, M.; Miglietta, F.; Moersch, A. Remote sensing of sun--induced fluorescence to improve modeling of diurnal courses of gross primary production (gpp). Glob. Chang. Biol. 2010, 16, 171–186. [Google Scholar] [CrossRef]
- Migliavacca, M.; Perez-Priego, O.; Rossini, M.; El-Madany, T.S.; Moreno, G.; van der Tol, C.; Rascher, U.; Berninger, A.; Bessenbacher, V.; Burkart, A.; et al. Plant functional traits and canopy structure control the relationship between photosynthetic co2 uptake and far-red sun-induced fluorescence in a mediterranean grassland under different nutrient availability. New Phytol. 2017, 214, 1078–1091. [Google Scholar] [CrossRef]
- Rossini, M.; Meroni, M.; Migliavacca, M.; Manca, G.; Cogliati, S.; Busetto, L.; Picchi, V.; Cescatti, A.; Seufert, G.; Colombo, R. High resolution field spectroscopy measurements for estimating gross ecosystem production in a rice field. Agr. For. Meteorol. 2010, 150, 1283–1296. [Google Scholar] [CrossRef]
- Wieneke, S.; Ahrends, H.; Damm, A.; Pinto, F.; Stadler, A.; Rossini, M.; Rascher, U. Airborne based spectroscopy of red and far-red sun-induced chlorophyll fluorescence: Implications for improved estimates of gross primary productivity. Remote Sens. Environ. 2016, 184, 654–667. [Google Scholar] [CrossRef]
- Guan, K.; Berry, J.A.; Zhang, Y.; Joiner, J.; Guanter, L.; Badgley, G.; Lobell, D.B. Improving the monitoring of crop productivity using spaceborne solar--induced fluorescence. Glob. Chang. Biol. 2016, 22, 716–726. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-E.; Frankenberg, C.; van der Tol, C.; Berry, J.A.; Guanter, L.; Boyce, C.K.; Fisher, J.B.; Morrow, E.; Worden, J.R.; Asefi, S. Forest productivity and water stress in amazonia: Observations from gosat chlorophyll fluorescence. Proc. R. Soc. B Biol. Sci. 2013, 280, 20130171. [Google Scholar] [CrossRef] [PubMed]
- Parazoo, N.C.; Bowman, K.; Fisher, J.B.; Frankenberg, C.; Jones, D.B.; Cescatti, A.; Pérez--Priego, Ó.; Wohlfahrt, G.; Montagnani, L. Terrestrial gross primary production inferred from satellite fluorescence and vegetation models. Glob. Chang. Biol. 2014, 20, 3103–3121. [Google Scholar] [CrossRef]
- Ač, A.; Malenovský, Z.; Olejníčková, J.; Gallé, A.; Rascher, U.; Mohammed, G. Meta-analysis assessing potential of steady-state chlorophyll fluorescence for remote sensing detection of plant water, temperature and nitrogen stress. Remote Sens. Environ. 2015, 168, 420–436. [Google Scholar] [CrossRef]
- Cendrero-Mateo, M.P.; Moran, M.S.; Papuga, S.A.; Thorp, K.; Alonso, L.; Moreno, J.; Ponce-Campos, G.; Rascher, U.; Wang, G. Plant chlorophyll fluorescence: Active and passive measurements at canopy and leaf scales with different nitrogen treatments. J. Exp. Bot. 2015, 67, 275–286. [Google Scholar] [CrossRef]
- Bilger, W.; Bjorkman, O. Temperature-dependence of violaxanthin deepoxidation and nonphotochemical fluorescence quenching in intact leaves of gossypium-hirsutum l and malva-parviflora l. Planta 1991, 184, 226–234. [Google Scholar] [CrossRef]
- Govindjee. 63 years since kautsky - chlorophyll-a fluorescence. Aust. J. Plant Physiol. 1995, 22, 131–160. [Google Scholar]
- Porcar-Castell, A.; Tyystjarvi, E.; Atherton, J.; van der Tol, C.; Flexas, J.; Pfundel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef]
- van der Tol, C.; Berry, J.A.; Campbell, P.K.E.; Rascher, U. Models of fluorescence and photosynthesis for interpreting measurements of solar-induced chlorophyll fluorescence. J. Geophys. Res. Biogeosci. 2014, 119, 2312–2327. [Google Scholar]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M.E. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- Grime, J.P. Trait convergence and trait divergence in herbaceous plant communities: Mechanisms and consequences. J. Veg. Sci. 2006, 17, 255–260. [Google Scholar] [CrossRef]
- Niinemets, Ü.; Kull, O.; Tenhunen, J.D. Variability in leaf morphology and chemical composition as a function of canopy light environment in coexisting deciduous trees. Int. J. Plant Sci. 1999, 160, 837–848. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.R. Photosynthesis and nitrogen relationships in leaves of c 3 plants. Oecologia 1989, 78, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Houborg, R.; Cescatti, A.; Migliavacca, M.; Kustas, W. Satellite retrievals of leaf chlorophyll and photosynthetic capacity for improved modeling of gpp. Agr. For. Meteorol. 2013, 177, 10–23. [Google Scholar] [CrossRef]
- Farquhar, G.D.; von Caemmerer, S.v.; Berry, J. A biochemical model of photosynthetic co 2 assimilation in leaves of c 3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Verhoeven, A.S.; Demmig-Adams, B.; Adams III, W.W. Enhanced employment of the xanthophyll cycle and thermal energy dissipation in spinach exposed to high light and n stress. Plant Physiol. 1997, 113, 817–824. [Google Scholar] [CrossRef]
- Jiang, M.; Caldararu, S.; Zaehle, S.; Ellsworth, D.S.; Medlyn, B.E. Towards a more physiological representation of vegetation phosphorus processes in land surface models. New Phytol. 2019, 222, 1223–1229. [Google Scholar] [CrossRef]
- Singh, S.; Reddy, V.; Fleisher, D.; Timlin, D. Relationship between photosynthetic pigments and chlorophyll fluorescence in soybean under varying phosphorus nutrition at ambient and elevated co 2. Photosynthetica 2017, 55, 421–433. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Bahn, M.; Tappeiner, U.; Cernusca, A. A multi-component, multi-species model of vegetation-atmosphere co2 and energy exchange for mountain grasslands. Agr. For. Meteorol. 2001, 106, 261–287. [Google Scholar] [CrossRef]
- Porcar-Castell, A.; Juurola, E.; Ensminger, I.; Berninger, F.; Hari, P.; Nikinmaa, E. Seasonal acclimation of photosystem ii in pinus sylvestris. Ii. Using the rate constants of sustained thermal energy dissipation and photochemistry to study the effect of the light environment. Tree Physiol. 2008, 28, 1483–1491. [Google Scholar] [CrossRef]
- Yang, P.Q.; van der Tol, C. Linking canopy scattering of far-red sun-induced chlorophyll fluorescence with reflectance. Remote Sens. Environ. 2018, 209, 456–467. [Google Scholar] [CrossRef]
- Liu, X.; Guanter, L.; Liu, L.; Damm, A.; Malenovský, Z.; Rascher, U.; Peng, D.; Du, S.; Gastellu-Etchegorry, J.-P. Downscaling of solar-induced chlorophyll fluorescence from canopy level to photosystem level using a random forest model. Remote Sens. Environ. 2018, 231, 110772. [Google Scholar] [CrossRef]
- Zeng, Y.; Badgley, G.; Dechant, B.; Ryu, Y.; Chen, M.; Berry, J.A. A practical approach for estimating the escape ratio of near-infrared solar-induced chlorophyll fluorescence. Remote Sens. Environ. 2019, 232, 111209. [Google Scholar] [CrossRef]
- Galmés, J.; Ribas-Carbó, M.; Medrano, H.; Flexas, J. Response of leaf respiration to water stress in mediterranean species with different growth forms. J. Arid Environ. 2007, 68, 206–222. [Google Scholar] [CrossRef]
- Alonso, L.; Van Wittenberghe, S.; Amorós-López, J.; Vila-Francés, J.; Gómez-Chova, L.; Moreno, J. Diurnal cycle relationships between passive fluorescence, pri and npq of vegetation in a controlled stress experiment. Remote Sens. 2017, 9, 770. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Hall, F.G.; Black, T.A.; Wulder, M.A.; Nesic, Z.; Krishnan, P. Separating physiologically and directionally induced changes in pri using brdf models. Remote Sens. Environ. 2008, 112, 2777–2788. [Google Scholar] [CrossRef]
- Perez-Priego, O.; Guan, J.; Rossini, M.; Fava, F.; Wutzler, T.; Moreno, G.; Carvalhais, N.; Carrara, A.; Kolle, O.; Julitta, T.; et al. Sun-induced chlorophyll fluorescence and photochemical reflectance index improve remote-sensing gross primary production estimates under varying nutrient availability in a typical mediterranean savanna ecosystem. Biogeosciences 2015, 12, 6351–6367. [Google Scholar] [CrossRef]
- Luo, Y.; El-Madany, T.; Filippa, G.; Ma, X.; Ahrens, B.; Carrara, A.; Gonzalez-Cascon, R.; Cremonese, E.; Galvagno, M.; Hammer, T. Using near-infrared-enabled digital repeat photography to track structural and physiological phenology in mediterranean tree–grass ecosystems. Remote Sens. 2018, 10, 1293. [Google Scholar] [CrossRef]
- Spellerberg, I.F.; Fedor, P.J. A tribute to claude shannon (1916-2001) and a plea for more rigorous use of species richness, species diversity and the ‘shannon-wiener’ index. Glob. Ecol. Biogeogr. 2003, 12, 177–179. [Google Scholar] [CrossRef]
- Brand, W.A.; Coplen, T.B. Stable isotope deltas: Tiny, yet robust signatures in nature. Isot. Environ. Health Stud. 2012, 48, 393–409. [Google Scholar] [CrossRef]
- Coplen, T.B. Guidelines and recommended terms for expression of stable-isotope-ratio and gas-ratio measurement results. Rapid Commun. Mass Spectrom. 2011, 25, 2538–2560. [Google Scholar] [CrossRef] [PubMed]
- Pacheco-Labrador, J.; Perez-Priego, O.; El-Madany, T.S.; Julitta, T.; Rossini, M.; Guan, J.; Moreno, G.; Carvalhais, N.; Martín, M.P.; Gonzalez-Cascon, R. Multiple-constraint inversion of scope. Evaluating the potential of gpp and sif for the retrieval of plant functional traits. Remote Sens. Environ. 2019, 234, 111362. [Google Scholar] [CrossRef]
- Seibt, U.; Rajabi, A.; Griffiths, H.; Berry, J.A. Carbon isotopes and water use efficiency: Sense and sensitivity. Oecologia 2008, 155, 441–454. [Google Scholar] [CrossRef] [PubMed]
- van der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An integrated model of soil-canopy spectral radiances, photosynthesis, fluorescence, temperature and energy balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef]
- Vina, A.; Gitelson, A.A. New developments in the remote estimation of the fraction of absorbed photosynthetically active radiation in crops. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Li, Z.; Moreau, L. A new approach for remote sensing of canopy-absorbed photosynthetically active radiation. I: Total surface absorption. Remote Sens. Environ. 1996, 55, 175–191. [Google Scholar] [CrossRef]
- Moreau, L.; Li, Z. A new approach for remote sensing of canopy absorbed photosynthetically active radiation. Ii: Proportion of canopy absorption. Remote Sens. Environ. 1996, 55, 192–204. [Google Scholar] [CrossRef]
- Sager, J.; McFarlane, J. Plant growth chamber handbook. Radiation 1997, 1–29. [Google Scholar]
- Moder, K. Alternatives to f-test in one way anova in case of heterogeneity of variances (a simulation study). Psychol. Test. Assess. Model. 2010, 52, 343–353. [Google Scholar]
- Games, P.A.; Howell, J.F. Pairwise multiple comparison procedures with unequal n’s and/or variances: A monte carlo study. J. Educ. Stat. 1976, 1, 113–125. [Google Scholar]
- Groemping, U.; Matthias, L. Relaimpo: Relative Importance of Regressors in Linear Models; R Package Version 1.1-1; Foundation for Open Access Statistics: Los Angeles, CA, USA, 2006. [Google Scholar]
- Sumayao, C.; Kanemasu, E.; Brakke, T. Using leaf temperature to assess evapotranspiration and advection. Agric. Meteorol. 1980, 22, 153–166. [Google Scholar] [CrossRef]
- Rosseel, Y. Lavaan: An r package for structural equation modeling and more. Version 0.5–12 (beta). J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Weis, E.; Berry, J.A. Plants and high temperature stress. Symp. Soc. Exp. Biol. 1988, 42, 329–346. [Google Scholar] [PubMed]
- Hu, L.t.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Model. A Multidiscip. J. 1999, 6, 1–55. [Google Scholar] [CrossRef]
- Iacobucci, D. Structural equations modeling: Fit indices, sample size, and advanced topics. J. Consum. Psychol. 2010, 20, 90–98. [Google Scholar] [CrossRef]
- Singh, S.K.; Reddy, V.R. Combined effects of phosphorus nutrition and elevated carbon dioxide concentration on chlorophyll fluorescence, photosynthesis, and nutrient efficiency of cotton. J. Plant Nutr. Soil Sci. 2014, 177, 892–902. [Google Scholar] [CrossRef]
- Tatarko, A.R.; Knops, J.M.H. Nitrogen addition and ecosystem functioning: Both species abundances and traits alter community structure and function. Ecosphere 2018, 9, e02087. [Google Scholar] [CrossRef]
- Jackson, R.D.; Idso, S.; Reginato, R.; Pinter, P. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- Boulet, G.; Chehbouni, A.; Gentine, P.; Duchemin, B.; Ezzahar, J.; Hadria, R. Monitoring water stress using time series of observed to unstressed surface temperature difference. Agr. For. Meteorol. 2007, 146, 159–172. [Google Scholar] [CrossRef]
- Diaz, M.; de Haro, V.; Munoz, R.; Quiles, M.J. Chlororespiration is involved in the adaptation of brassica plants to heat and high light intensity. Plant Cell Environ. 2007, 30, 1578–1585. [Google Scholar]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Bolstad, P.V.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L. A new model of gross primary productivity for north american ecosystems based solely on the enhanced vegetation index and land surface temperature from modis. Remote Sens. Environ. 2008, 112, 1633–1646. [Google Scholar] [CrossRef]
- Weisser, W.W.; Roscher, C.; Meyer, S.T.; Ebeling, A.; Luo, G.; Allan, E.; Beßler, H.; Barnard, R.L.; Buchmann, N.; Buscot, F. Biodiversity effects on ecosystem functioning in a 15-year grassland experiment: Patterns, mechanisms, and open questions. Basic Appl. Ecol. 2017, 23, 1–73. [Google Scholar] [CrossRef]
- Feng, X.H.; Dietze, M. Scale dependence in the effects of leaf ecophysiological traits on photosynthesis: Bayesian parameterization of photosynthesis models. New Phytol. 2013, 200, 1132–1144. [Google Scholar] [CrossRef] [PubMed]
- Frankenberg, C.; Berry, J. Solar induced chlorophyll fluorescence: Origins, relation to photosynthesis and retrieval. In Comprehensive Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Peng, Y.; Gitelson, A.A.; Keydan, G.; Rundquist, D.C.; Moses, W. Remote estimation of gross primary production in maize and support for a new paradigm based on total crop chlorophyll content. Remote Sens. Environ. 2011, 115, 978–989. [Google Scholar] [CrossRef]
- Buschmann, C. Variability and application of the chlorophyll fluorescence emission ratio red/far-red of leaves. Photosynth. Res. 2007, 92, 261–271. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Mõttus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Carmona, P.L.; Kaufmann, R.K.; Lewis, P. Hyperspectral remote sensing of foliar nitrogen content. Proc. Nat. Acad. Sci. USA 2013, 110, E185–E192. [Google Scholar] [CrossRef]
- Ollinger, S.V.; Richardson, A.D.; Martin, M.E.; Hollinger, D.Y.; Frolking, S.E.; Reich, P.B.; Plourde, L.C.; Katul, G.G.; Munger, J.W.; Oren, R. Canopy nitrogen, carbon assimilation, and albedo in temperate and boreal forests: Functional relations and potential climate feedbacks. Proc. Nat. Acad. Sci. USA 2008, 105, 19336–19341. [Google Scholar] [CrossRef]
- Migliavacca, M.; El-Madany, T.S.; Perez-Priego, O.; Carrara, A.; Gonzalez-Cascon, R.; Martin Isabel, M.P.; Moreno, G.; Guan, J.; Hammer, T.W.; Henkel, K.; et al. Effects of a large scale stoichiometric imbalance manipulation on the ecosystem functioning of a Mediterranean tree-grass ecosystem: The MANIP experiment. In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2018. [Google Scholar]
- Ollinger, S.; Frolking, S.; Richardson, A.; Martin, M.; Hollinger, D.; Reich, P.; Plourde, L. Reply to fisher: Nitrogen–albedo relationship in forests remains robust and thought-provoking. Proc. Nat. Acad. Sci. USA 2009, 106, E17. [Google Scholar] [CrossRef]
- Sullivan, F.B.; Ollinger, S.V.; Martin, M.E.; Ducey, M.J.; Lepine, L.C.; Wicklein, H.F. Foliar nitrogen in relation to plant traits and reflectance properties of new hampshire forests. Can. J. For. Res. 2012, 43, 18–27. [Google Scholar] [CrossRef]
- Sun, Z.; Livingston, N.; Guy, R.; Ethier, G. Stable carbon isotopes as indicators of increased water use efficiency and productivity in white spruce (picea glauca (moench) voss) seedlings. Plant Cell Environ. 1996, 19, 887–894. [Google Scholar]
- Vilfan, N.; van der Tol, C.; Verhoef, W. Estimating photosynthetic capacity from leaf reflectance and chlorophyll fluorescence by coupling radiative transfer to a model for photosynthesis. New Phytol. 2019, 223, 487–500. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).