Abstract
A systematic and precise understanding of urban socio-economic spatial inequalities in developing regions is needed to address global sustainability goals. At the intra-urban scale, access to detailed databases (i.e., a census) is often a difficult exercise. Geolocated surveys such as the Demographic and Health Surveys (DHS) are a rich alternative source of such information but can be challenging to interpolate at such a fine scale due to their spatial displacement, survey design and the lack of very high-resolution (VHR) predictor variables in these regions. In this paper, we employ satellite-derived VHR land-use/land-cover (LULC) datasets and couple them with the DHS Wealth Index (WI), a robust household wealth indicator, in order to provide city-scale wealth maps. We undertake several modelling approaches using a random forest regressor as the underlying algorithm and predict in several geographic administrative scales. We validate against an exhaustive census database available for the city of Dakar, Senegal. Our results show that the WI was modelled to a satisfactory degree when compared against census data even at very fine resolutions. These findings might assist local authorities and stakeholders in rigorous evidence-based decision making and facilitate the allocation of resources towards the most disadvantaged populations. Good practices for further developments are discussed with the aim of upscaling these findings at the global scale.
1. Introduction
The adequate monitoring of socio-economic indicators in the Global South is a crucial task in order to meet the United Nations Sustainable Development Goals (SDGs) [1]. In order to eliminate poverty and reduce inequalities [2], the most reliable and informative methods to make targeted assessments at the local, national and regional levels are through exhaustive census data combined with geospatial analyses [3,4,5]. Nonetheless, census information in several developing countries are outdated, unreliable or inaccessible for the most part, making such efforts challenging, particularly for fine-scale geographical estimations (i.e., at subnational or intra-urban level) [6,7]. An alternative way to investigate the local heterogeneities of socioeconomic indicators is through the coupling of geolocated surveys that contain socio-economic information with ancillary spatial variables. A rich source of consistent, standardized and geolocated surveys in numerous developing countries are the Demographic and Health Surveys (DHS) [8]. However, DHS surveys are designed mostly to summarize indicators at the national level, which forbids intra-national or urban variations to be shown. Recently, Bosco et al. [6] explored the potential of combining DHS surveys with geospatial features, for fine-scale mapping at the sub-national level. Their results were encouraging as they were able to model and map several DHS indicators (i.e., stunting in children) successfully at a high resolution (1 by 1-kilometer grids) for several countries such as Nigeria, Kenya and Tanzania. Nonetheless, due to the type of analysis undertaken, the mapping of intra-urban variations was poor. The authors concluded that with appropriate modelling efforts and inclusion of very high-resolution (VHR) covariates, intra-urban variation of DHS indicators could be made possible. Similar research has proposed the use of VHR variables to address the poor performance of DHS indicators in an intra-urban setting [9].
Recent work has highlighted the importance of remotely sensed (RS) features such as land use/land cover (LULC) for mapping demographic and socio-economic conditions at various geographic scales [5,10,11,12,13,14,15,16,17]. In [5], satellite image features such as the number and density of buildings, type of roads and number cars explained roughly 60% of the variation in poverty models derived from census household consumption per capita estimates in Sri Lanka. In [10], it was demonstrated that satellite images, in combination with census and survey data could reveal the distribution of spatial inequalities in health and well-being in the city of Accra, with the proportional abundance of vegetation being the most discriminative predictor. Similar research in Accra, has confirmed the merits of using satellite information for socio-economic mapping as in [13], where a set of image metrics describing the geometry, orientation and patterns of objects within an image exhibited moderate to strong degrees of correlation against several socio-economic census indicators. In the absence of census data, similar results have been reported when using ground surveys to train and validate models. In [11,12] satellite-derived metrics and LULC information were used to classify the city of Lima, Peru, in a set of socioeconomic classes. The satellite features were combined with reference data from ground surveys and a neural network was used to make predictions with satisfactory accuracy (R2 = 0.7). Nonetheless, the limiting factors of the above studies regard data availability, which is always time- and place-specific.
To address this shortcoming, this study aims to fill an important gap, and proposes the coupling of satellite VHR information with the standardized DHS surveys for accurate intra-urban socioeconomic mapping. We present a first attempt to model a widely used DHS survey indicator, the Wealth Index, with VHR LULC variables and machine-learning (ML) methods. Our results are validated against census data for the city of Dakar, Senegal.
2. Materials and Methods
2.1. Overview
In this section we describe the data and methods used in the study. First, we justify and present the choice of the case study (Dakar, Senegal). Second, we discuss in length the DHS Wealth Index (WI) data that were employed while we particularly emphasize describing the DHS survey spatial displacement issue which can negatively influence the prediction accuracy. Afterwards, we present the satellite-derived information that were used to model the WI. Finally, we present the modelling and optimization techniques as well as our efforts to validate the results against census information.
2.2. Study Area
We selected Dakar, the capital of Senegal, as a case study for two reasons: (i) the availability of georeferenced fine-scale census information, (ii) existing, high-quality VHR RS LULC products [18,19] and (iii) the relative abundance of DHS surveys across the city. The study area encompassed zones for which there is almost full overlap between the available LULC and census information (Figure 1).
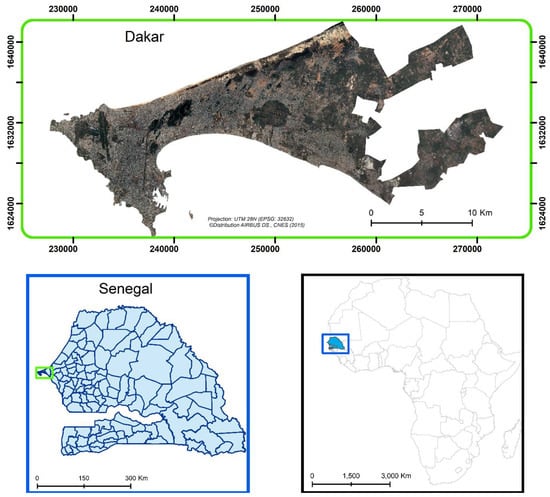
Figure 1.
Study area extent.
2.3. Demographic and Health Surveys (DHS)
The DHS program routinely collects geolocated socio-economic and health indicators in more than 90 developing countries. It aims to improve evidence-based policy making by authorities and related organizations. The DHS surveys follow a standardized, stratified and multi-stage sampling design where several census enumeration areas (EA) are selected as sampling clusters. Afterwards, a set of households within the selected EAs is interviewed and the Global Positioning System (GPS) coordinates of the centroid of the EA are recorded [20]. From the interviews undertaken, a vast amount of information is collected ranging from household indicators (e.g., construction material, water source and ways of garbage disposal) and socio-economic information (e.g., educational level) to health measurements such as malaria prevalence. In order to ensure privacy, before the coordinates of the urban clusters are publicly released, data points are randomly displaced up to 2 kilometers using a random direction/random distance approach [20]. The surveys are designed to be representative at the admin-1 level (regional level), but also have shown being useful for spatial extrapolation at finer scales [6,9,20]. The random displacement has been a factor of negative influence when undertaking spatial analyses as there can be strong spatial mismatches between the extracted spatial variables and the true location of the survey. The best way to mitigate this issue is to extract average/proportional values from the spatial predictors around the DHS surveys locations, using buffers. In DHS reports, buffers between 1 and 5 kilometers have been successfully employed to extract spatial information in rural and urban surveys [20,21].
DHS Wealth Index (WI)
The variable of interest in this study is the DHS Wealth Index that acts as a surrogate of a household’s economic status. At the national scale, it has a standard deviation of 1 and a mean value of 0, with higher values indicating wealthier households [22]. The WI is an ownership composite of household assets or services such as ownership of a television set, vehicle or land, type of water supply, access to electricity and persons sleeping per room, among others derived from a principal component analysis (PCA). It has been used for several spatial and non-spatial analyses, mainly as a potential indicator of health, mortality, socioeconomic status and wealth [23,24,25,26,27].
The WI can only be directly compared within a specific survey and country as it is a relative measure of wealth and not an absolute one, whereas construction of a comparative WI is recommended for trend analysis or inter-country comparisons [22]. In this study, we operated under the assumption that the WI is stationary over the time period examined as we only included urban surveys in Dakar and no trend analysis or inter-country comparisons were performed. Moreover, in recent work, it was demonstrated that comparative WI was stationary across a 5-year period in Senegal while both indexes demonstrated high and comparable explanatory power when used as predictive variables in regression models [22]. Therefore, here we solely used the WI for simplicity purposes. For analysis, we extracted the WI from available DHS surveys from 2008–2016 in Dakar. To create a WI suited for geographical modelling, we averaged the values from the household level to the cluster level [6], for which GPS coordinates, although displaced, exist and a total of 120 geolocated clusters were produced (Figure 2). There exists a clear gradient on the WI’s spatial distribution, with higher values being found in the central part of the city (south-east region) and decreasing values in peri-urban regions. The distribution of the WI from the selected surveys in Dakar followed a normal distribution as demonstrated in the histogram of Figure 3.
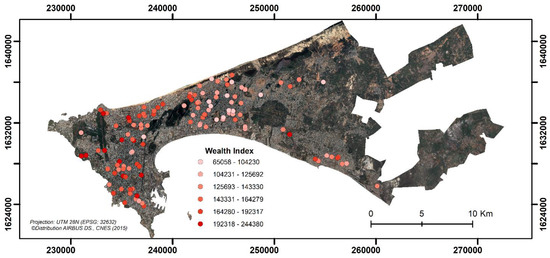
Figure 2.
Demographic and Health Surveys (DHS) Wealth Index across Dakar between 2008–2016.
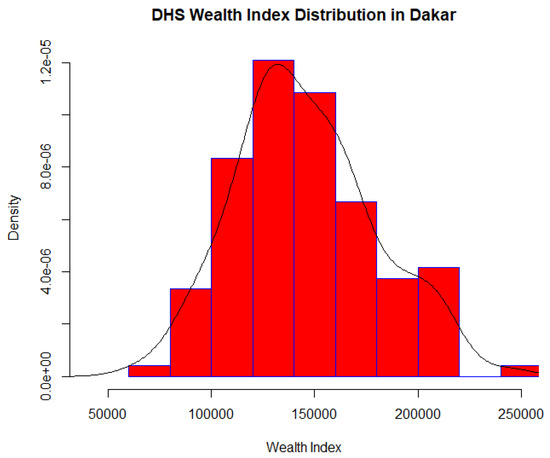
Figure 3.
Histogram with probability density curve of the DHS Wealth Index in Dakar, between 2008–2016.
2.4. Very High-Resolution (VHR) Satellite Data
As predictors of the DHS WI, we used two satellite derived VHR LULC maps. The LULC products are publicly available with a LC map at 0.5 resolution and a LU map at the street block level (Figure 4) [18,28]. These products have been successfully used for urban local climate zone validation [29] and population models at similar geographical scales [16,30]. The overall accuracy of the LC and LU maps was 89.5% and 79%, respectively [16]. Both were derived from Pleiades imagery collected in 2015. The variables are explicitly documented in Table 1. The categorization of built-up was made possible through the use of a normalized elevation surface model produced by stereophotogrammetry [31].
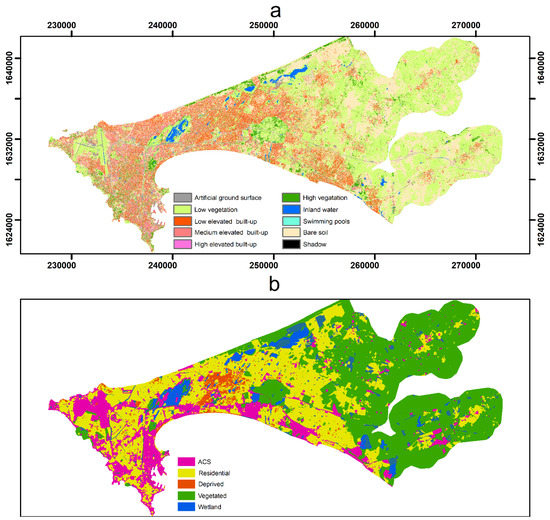
Figure 4.
(a) Very high-resolution land cover (LC) of Dakar derived from a 2015 Pleiades imagery and (b) land use at the street block level for the same date.

Table 1.
Satellite-derived land use/land cover (LULC) features used in the study [18,28].
According to the DHS guidelines, buffers between 1–5 kilometers can provide relatively unbiased coefficient estimates in generalized linear models (with the reference being an unbiased model of a 2 kilometer buffer), depending on the degree of smoothness of each variable [20]. Nonetheless, we use 1-kilometer buffers due to the complex and quite heterogeneous urban landscape. As such, we extracted LULC class proportions within a 1-kilometer buffer from each DHS survey point. Increasing the buffer would be an unsuitable practice leading to oversmoothed models and refrain intra-urban variation to manifest [6]. At the same time, we investigated some spatial optimization techniques to help mitigate the displacement issue.
2.5. Model Selection and Spatial Optimization Methods
As mentioned previously, the maximum geographical displacement for an urban DHS cluster is 2 kilometers, which may cause the creation of noisy or inappropriate spatial models. Thus, we investigated two simple and intuitive spatial optimization methods that might mitigate the effect of the displacement. The two procedures were based on refining or enriching the contextual spatial feature extraction.
The first method aimed to increase the amount of available training data in the models by extracting features from multiple 1-kilometer buffers around each survey point. In practice, for each DHS survey point, we created duplicates at 500 and 1000 meters along four main directions, East, West, North and South, as illustrated in Figure 5. Then, we extracted the LULC proportions for each newly created survey location and hence, more training data were created. In the end, we combined all initial and newly created training data in one model which comprised 1040 data points. Spatial duplicates falling in the sea were removed. We refer to this approach as P1, with the benchmark method being training a model where features are extracted only from buffers along the 120 initial survey locations (P0). The idea behind this method was based on the positive effect that spatial autocorrelation might have in the extracted features—aking as an assumption that at least 50% of the displaced surveys will fall within a 1-kilometre buffer [21].
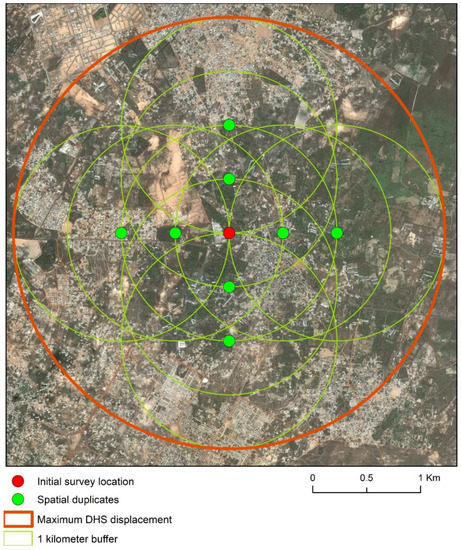
Figure 5.
Example of the spatial duplication in one DHS cluster in Dakar, Senegal.
The second optimization technique (P2) aimed to refine rather than enrich the feature extraction through spatial permutation. The general procedure is described as follows:
For each survey, randomly select one of the 9 potential locations that were created previously (Figure 5).
Extract the associated LULC features for the selected location, coming from the 1-kilometer buffer:
Compute a regression model between the selected features and the WI;
Assess model performance through the implementation of an evaluation metric;
Repeat steps 1 to 4 until a preset number of iterations is done;
Select the model that minimizes the evaluation metric.
Our rationale rested on the idea that there is an established relationship between the physical surface and household wealth, as several studies have shown [5,6,10,11,12,32]. Therefore, through the iterative random sampling, models with more appropriate feature extraction are expected to have a better performance than the standard approach of extracting features only for the original (i.e., DHS provided) location. Nonetheless, the proposed approach assumes an axiomatic, strong relationship between LULC variables and the WI that is better than random chance. The only way to ensure that the selected model after applying the optimization is indeed a better choice and not an artifact of a random combination or overfitting is through independent validation. In our case we preset 10 million iterations—an arbitrary but reasonable number to test enough combinations coming out of a random sampling process given the precise problem solution requires a substantial amount of computational resources. As an evaluation metric to select the best model we selected the root mean squared error (RMSE) coming from the out-of-bag (OOB) predictions of the random forest (RF) regressor. RF is a decision-tree ensemble machine learning algorithm that has been shown resilient to overfitting and robust to model the complex non-linear relationships among satellite derived features and socio-economic and demographic indicators [16,30,33]. For optimizing the parameters of the three final RF models (P0, P1, P2) we used the cross-validation functions of the “caret” package in R statistical software [34,35]. Finally, it should be noted that the objective of the proposed approaches (P1 and P2), is not to find the true locations of the DHS surveys or account for the displacement of each survey independently, but rather to create models that, on average, capture the relationship between LULC and WI in a more robust manner.
2.6. Validation Scheme
2.6.1. Validation at the DHS Survey Level
To assess the training performance for each modelling approach (P0, P1, P2), we derived the RMSE (Equation (1)) and mean absolute error (MAE; Equation (2)) from a 5-fold repeated cross validation (10 repeats) procedure.
where xi is the observed variable, yi is the predicted value and n is the sample size.
2.6.2. Validation at the Census Level
For independent validation, we employed the latest census of Dakar (2013) that contained information from all recorded households in the region, acquired from the National Agency for Statistics and Demography of Senegal [36]. The employed household indicators are summarized in Table 2 and consist of exhaustive information regarding household material and access to services, similarly to the DHS WI. First, we computed these variables as proportions (i.e., proportion of households that have a house tap) at each administrative unit. Then, we performed a PCA on these features and extracted the first principal component as a Census Wealth Index (CWI), similarly to other studies that develop wealth composite measures [37,38]. On average, and depending on the census administrative resolution, the CWI captured roughly 30% of the total variance which is comparable with existing values such as the International Wealth Index [37]. It has to be noted that the CWI is not the direct equivalent of DHS WI, but we assume they are very similar as i) both are PCA composites on household variables and ii) the survey/census information has been collected by the same statistical agency.

Table 2.
Available household indicators for Dakar, derived from the 2013 Census. The first component of a principal component analysis (PCA) was used as the Census Wealth Index.
To address scale effects in prediction, we computed and aggregated the CWI in multiple geographical resolutions (to reach a total of 300, 150, 75, 40 administrative units; Figure 6) using a procedure proposed in [16]. The aggregation method was based on k-means clustering on the geographical coordinates of each census unit. Afterwards, we used the three trained RF models to predict the DHS WI at each administrative level by using the LULC variables which are also aggregated at the same scale. We then computed Pearson’s correlation coefficient to assess the degree of similarity amongst the predicted DHS Wealth Index and the Census Wealth Index. Finally, we used the Getis–Ord Gi* index to visualize locations where high or low values cluster spatially (hot/cold spots) and see whether there is similarity between the census and predicted spatial clusters [39].
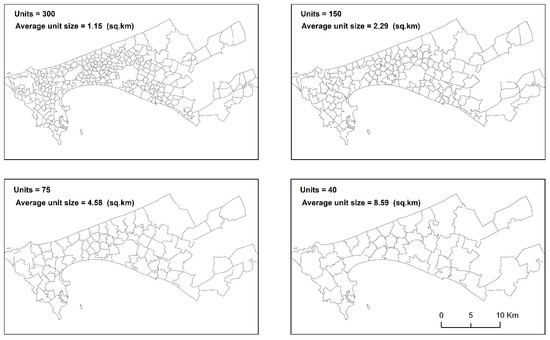
Figure 6.
Different geographical census aggregations that were used as validation to investigate prediction of the DHS WI in a multiscale setting.
3. Results
3.1. DHS WI Models
The evaluation of the various models is illustrated in Figure 7. Both RMSE and MAE are lower for the optimized approaches (P1 and P2). The P2 approach exhibited the best performance (RMSE = 26,358, MAE 20,770), followed by P1 (RMSE = 28,465, MAE = 22,786), whereas the naïve approach (P0) performed most poorly (RMSE = 30,219, MAE = 23,776). Apart from the error evaluation, it can be enlightening to visualize the feature importance and impact of each predictor on the WI. As an example, Figure 8 shows the feature importance of the P2 approach, which performed best, as derived by mean decrease in squared error (MDA %), i.e., the most common way to assess importance of an RF regressor. The most important variables are the proportions of the different building categories, followed by the proportion of ACS, deprived regions and swimming pools, while vegetation variables appear to be the least important.
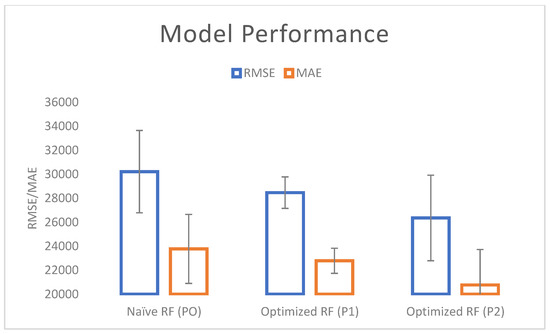
Figure 7.
Model evaluation from a k-fold cross validation (10 repetitions) for the different approaches.
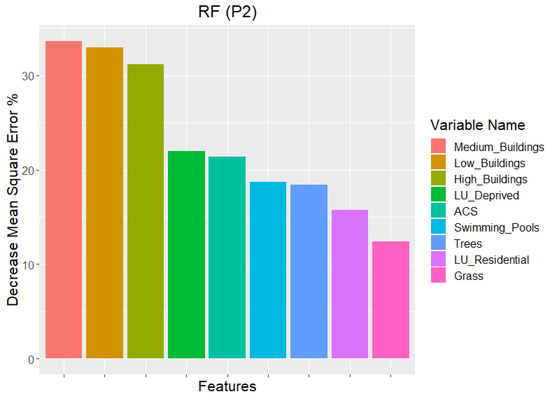
Figure 8.
Feature importance extracted from the P2 optimized random forest (RF) model.
Figure 9 illustrates the partial dependency plots for each predictor. Most of the predictors exhibit strong non-linear relationships with the WI and can be semantically explained. For example, an increase in the proportion of swimming pools is associated with a sharp increase in the WI as it likely represents the wealthier areas in Dakar. In a similar fashion, an increase of the proportion of neighborhoods classified as deprived is associated with sharp decreases of the WI. Interestingly, the density of the various building types plays an important role in explaining the WI. In particular, large proportions of high elevated buildings indicate regions with wealthier households, as they likely indicate central business or leisure districts. On the other hand, an increasing density of low-elevated buildings is associated with a steep decrease in the WI, which could be linked to the high-density poorer residential regions of Dakar, mainly prevalent in Pikine district. Notably, the nature of the relationships ranges from almost linear (i.e., proportion of swimming pools) to sharply non-linear (i.e., proportion of low elevated buildings) where there seemingly exists a threshold around the 20% margin that rapidly decreases the predicted WI. This can be explained by the built-up transition between one type of neighborhood to another, that could better be explained with thresholds rather than a linear progression.
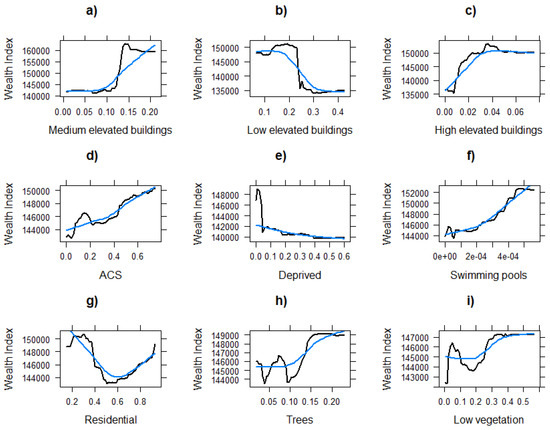
Figure 9.
Partial dependence plots for the RF (P3) predictors. The x-axis in each plot describes the proportion of that class extracted from the 1-km buffer. The blue line is the result of locally estimated scatterplot smoothing (LOESS) to help illustrate the overall trend in the relationship among each predictor and the wealth index.
3.2. Validation
We compare the performance of the DHS models against independent census data. The three RF models used to predict the WI at the various geographical scales are described in the methods section (Figure 6). Then, we compare the degree of similarity of the predicted WI against the reference CWI. The maps in Figure 10, Figure 11, Figure 12 and Figure 13 illustrate the predicted WI from the RF models and the CWI for the investigated census scales. Encouragingly, the overall spatial trends between the CWI and WI are similar in all cases. The households in the central regions of Dakar appear to be wealthier, with a peripheral decrease as we move into the peri-urban regions. Notably, all models have managed to highlight the less wealthy regions of the greater Pikine region. Nonetheless, there are also important differences between the predicted WI and CWI patterns particularly in the peri-urban regions of Dakar.
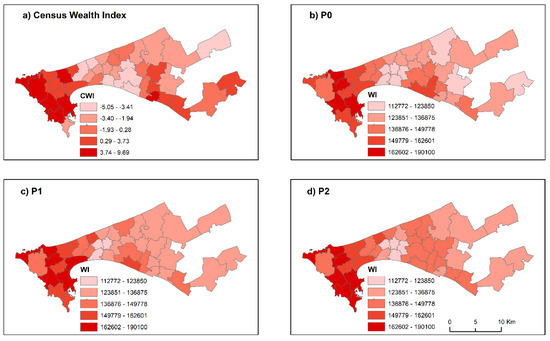
Figure 10.
Census data and model predictions at a scale of 40 admin units. (a) Census Wealth Index (CWI), (b) predicted DHS WI (PO), (c) predicted DHS WI (P1), (d) predicted DHS WI (P2).
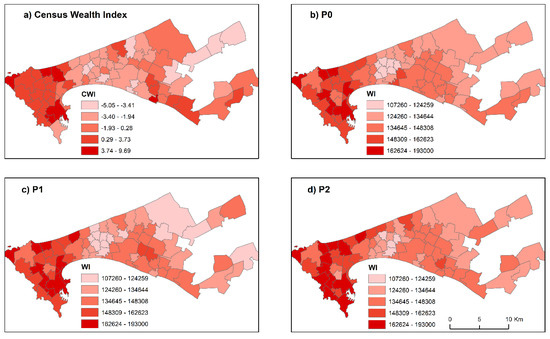
Figure 11.
Census data and model predictions at a scale of 75 admin units. (a) Census Wealth Index (CWI), (b) predicted DHS WI (PO), (c) predicted DHS WI (P1), (d) predicted DHS WI (P2).
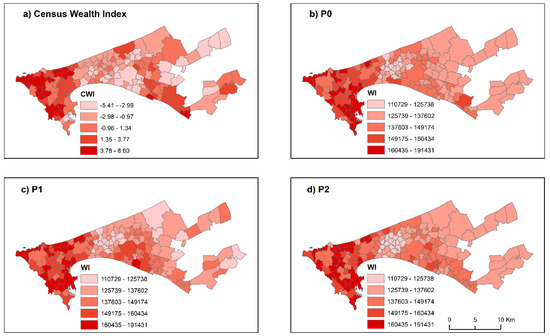
Figure 12.
Census data and model predictions at a scale of 150 admin units. (a) Census Wealth Index (CWI), (b) predicted DHS WI (PO), (c) predicted DHS WI (P1), (d) predicted DHS WI (P2).
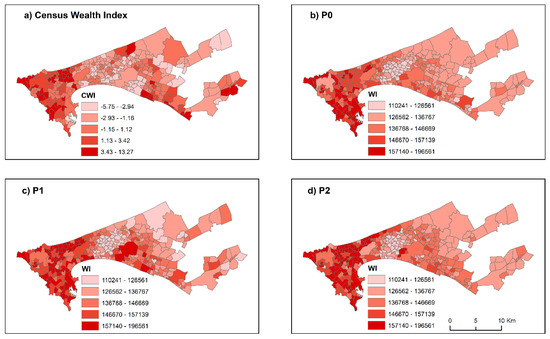
Figure 13.
Census data and model predictions at a scale of 300 admin units. (a) Census Wealth Index (CWI), (b) predicted DHS WI (PO), (c) predicted DHS WI (P1), (d) predicted DHS WI (P2).
Table 3 depicts the correlation coefficient values between the predicted WI and CWI for each geographical scale and method.

Table 3.
Correlation coefficient between the predicted DHS WI from each RF model (P0, P1, P2) and the CWI at different resolutions. All values are statistically significant at the 95% confidence level.
In general, the correlations are moderate (0.40–0.59) with the best results being found when the city is partitioned in 75 administrative units. Nonetheless, the correlations are almost as strong at finer resolutions, which is highly encouraging. As for the performance among the difference models, the optimized approaches (P1 and P2) always outperformed the naive approach (PO). Although the improvements were small, they are still important given that the CWI is derived from an exhaustive database that includes all documented households in Dakar. As such, even a minor improvement might indicate a better prediction over thousands of households in reality. Finally, the Getis–Ord hot/cold spot analysis for the CWI and best RF model for each resolution is illustrated in Figure 14. The patterns of the hot/cold spots were similar between the CWI and WI, with largest deviations being in the peri-urban transect of Dakar.
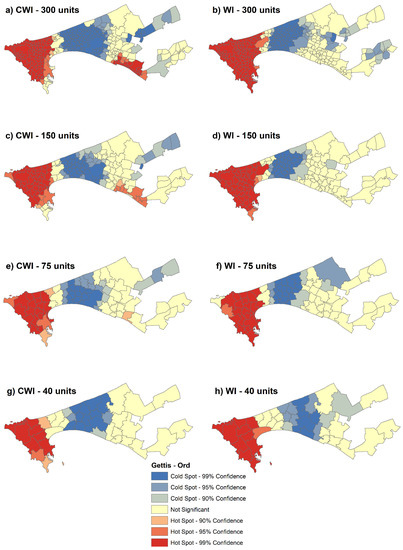
Figure 14.
Getis-Ord Gi* hot/cold spot analysis between the CWI and the best performing RF WI model.
4. Discussion
This research documented a first attempt to model DHS indicators using VHR Earth observation datasets for fine-scale intra-urban analysis. The results are encouraging and validated the recommendations of previous work [6], which indicated that RS VHR information may be adequate predictors of DHS survey indicators. However, one important limitation of using satellite VHR information is the increased cost, image-processing knowledge and computational resources that are required. Encouragingly, technological advances have allowed for large-scale computing using cloud systems and Earth observation data such as Google Earth Engine (GEE) [40] which can be of particular merit in upscaling the conclusions of this research in several cities. Currently, VHR data are still not available at a global extent in GEE, but other products could be investigated until the VHR imagery integration is realized. To reproduce this research, a few other RS VHR urban datasets are available and contain similar, openly accessible information in cities such as Ouagadougou, Kampala and Dar es Salaam [41,42].
Another important outcome of this research is the production of detailed and unique information in areas where minimum knowledge exists. In most Sub-Saharan African (SSA) cities, census data is hard to access or outdated. For regional or national assessments a lot of survey indicators have been produced at coarser resolutions [6,43,44,45,46,47,48,49,50,51] but this was the first DHS fine-scale indicator production derived from VHR earth observation information directed specifically for intra-urban policy making and decision support. An additional highlight of this work is that not only were VHR variables able to train robust models based on DHS surveys, but also their predictions were in relative agreement with exhaustive census data at various geographical resolutions. These outputs can transfer additional and unique information to scientists, local stakeholders and policy makers, particularly in an era where a part of the Earth observation community is focused on precise and accurate slum detection in the less economically developed regions of the world [52,53,54,55,56]. Indeed, it could allow for a systematic understanding of developing cities that will go beyond delineating slum regions and highlight intra-slum socio-economic and health inequalities. Consequently, future research should investigate the production of several other DHS indicators such as mortality, malnutrition, educational levels, among others for intra-urban mapping.
With respect to the modelling efforts, the thematic detail of the detailed LU/LC products explained a large part of the variation of the DHS Wealth Index. The most crucial features were the various types of buildings categorized by elevation, so that further attempts to model DHS cluster indicators in an urban context should strive to include similar information. For instance, if object elevation models are not available, the size of classified buildings might act as a similar proxy. Nonetheless, the predicted WI failed to match the census patterns in a few regions which indicates that relying solely on LULC information might not be enough. More discriminate variables should be investigated in future efforts such as the distance from the commercial center, vegetation indices, population density layers or image metrics (i.e., texture). Regarding the modelling algorithm, robust ML methods that are ideal when the relationship between dependent and independent variables is highly non-linear such as RF [33] performed satisfactorily in a multiscale setting. As ML techniques make no assumptions regarding data distribution, their use is more rewarding in cases where there is a lot of uncertainty-which is the case here, given the spatial displacement of DHS surveys. Although it is impossible to document the exact effect of the DHS displacement in the constructed models, a 1-kilometer buffer with or without further optimization was enough to model the WI successfully. In our case, the size of the buffer had to be a trade-off between constructing meaningful models and adequately addressing the displacement uncertainty. Larger buffers would be meaningless, at least in the case of Dakar, as they would incorporate exceedingly heterogeneous information that would lead to oversmoothed models with no explanatory power. On the other hand, similar buffers have been used in similar studies which attempt to model survey-based indicators through survey data [57]. Finally, better results could be expected if the various administrative aggregations were performed through expert knowledge, rather from an automated process [13].
Concerning the optimization procedures, the two feature-extraction methods we proposed produced i) better predictive performance when validated at the DHS cluster level and ii) higher correlations with the independent Census Wealth Index. However, the improvement of the optimized models (P1 and P2) was much higher when validated at the DHS level, rather than against the census. This can be interpreted as evidence of overfitting and, thus, caution should be taken when applying optimization methods in future studies. Hence, an important take away message for future work is to investigate more sophisticated spatial optimization and feature-extraction techniques in similar settings. It could be reasonable to assume the Bayesian optimization methods using spatial priors, or heuristic approaches will be able to find models that are more robust in less time, contrary to the random sampling simulations investigated here. Moreover, random spatial sampling rather than predetermined placement within the buffers, coupled with data augmentation techniques to increase robustness, might also provide viable approaches.
5. Conclusions
In this study we documented some first attempts in modelling the DHS WI through VHR satellite-derived variables for the purpose of fine scale intra-urban mapping. The results indicated that when appropriate variables are included, the predicted values are in moderate agreement with census data (r = 0.40–0.59) and display similar spatial patterns. In addition, we discuss some good practices and optimization approaches that mitigated the effect of the DHS displacement in the accuracy of the models. Moreover, the prediction performance remained satisfactory even at very fine resolutions (i.e., 300 administrative units) which is encouraging for the systematic production of gridded products on a larger scale. The importance of these findings can direct future research into mapping more DHS indicators in cities of the Global South, promoting international collaborations between institutions that have the necessary computational resources and stakeholders, in order to better address sustainable development goals in the developing regions of the world.
Author Contributions
Conceptualization, S.G.; methodology, S.G., M.L., S.V., T.G., S.D., N.M.; validation, S.G., A.N.G. and C.L.; data curation, S.G. and A.N.G.; writing—original draft preparation, S.G.; writing—review and editing, S.G.; supervision, M.L. and C.L.; project administration, M.L. and E.W.
Funding
This research was funded by BELSPO (Belgian Federal Science Policy Office) in the frame of the STEREO III program, as part of the REACT (SR/00/337) project (http://react.ulb.be/). The census data were provided by the ANSD (Agence Nationale de la Statistique et de la Démographie du Sénégal) in the framework of the ASSESS project, funded by the ARES-CDD.
Acknowledgments
We would like to thank the two anonymous reviewers whose comments and recommendations greatly improved the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Prashad, V. The Poorer Nations: A Possible History of the Global South; London Verso Trade: London, UK, 2013. [Google Scholar]
- Weiss, T.G. The United Nations and Changing World Politics; Routledge: Abingdon, UK, 2018. [Google Scholar]
- Stoler, J.; Daniels, D.; Weeks, J.R.; Stow, D.A.; Coulter, L.L.; Finch, B.K. Assessing the Utility of Satellite Imagery with Differing Spatial Resolutions for Deriving Proxy Measures of Slum Presence in Accra, Ghana. GISci. Remote Sens. 2012, 49, 31–52. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.R.; Hill, A.; Stow, D.; Getis, A.; Fugate, D. Can we spot a neighborhood from the air? {Defining} neighborhood structure in {Accra}, {Ghana}. GeoJournal 2007, 69, 9–22. [Google Scholar] [CrossRef] [PubMed]
- Engstrom, R.; Hersh, J.; Newhouse, D. Poverty in HD: What Does High Resolution Satellite Imagery Reveal about Economic Welfare? Available online: Pubdocs.worldbank.org/en/60741466181743796/Poverty-in-HD-draft-v2-75.pdf (accessed on 1 December 2016).
- Bosco, C.; Alegana, V.; Bird, T.; Pezzulo, C.; Bengtsson, L.; Sorichetta, A.; Steele, J.; Hornby, G.; Ruktanonchai, C.; Ruktanonchai, N.; et al. Exploring the high-resolution mapping of gender-disaggregated development indicators. J. R. Soc. Interface 2017, 14, 20160825. [Google Scholar] [CrossRef] [PubMed]
- Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating census data for population mapping using Random forests with remotely-sensed and ancillary data. PLoS ONE 2015, 10, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Corsi, D.J.; Neuman, M.; Finlay, J.E.; Subramanian, S.V. Demographic and health surveys: A profile. Int. J. Epidemiol. 2012, 41, 1602–1613. [Google Scholar] [CrossRef] [PubMed]
- Gething, P.W.; Tatem, A.J.; Bird, T.; Burgert, C. Creating Spatial Interpolation Surfaces with DHS Data; DHS Program: Rockville, MD, UDA, 2015. [Google Scholar]
- Weeks, J.R.; Getis, A.; Stow, D.A.; Hill, A.G.; Rain, D.; Engstrom, R.; Stoler, J.; Lippitt, C.; Jankowska, M.; Lopez-Carr, A.C.; et al. Connecting the Dots Between Health, Poverty and Place in Accra, Ghana. Ann. Assoc. Am. Geogr. 2012, 102, 932–941. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Avelar, S.; Tavares-corrêa, C.; Zah, R.; Tapiador, F.J.; Avelar, S.; Tavares-corrêa, C. Deriving fine-scale socioeconomic information of urban areas using very high-resolution satellite imagery. Int. J. Remote Sens. 2011, 32, 6437–6456. [Google Scholar] [CrossRef]
- Avelar, S.; Zah, R.; Tavares-Corrêa, C. Linking socioeconomic classes and land cover data in Lima, Peru: Assessment through the application of remote sensing and GIS. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 27–37. [Google Scholar] [CrossRef]
- Sandborn, A.; Engstrom, R.N. Determining the {Relationship} {Between} {Census} {Data} and {Spatial} {Features} {Derived} {From} {High}-{Resolution} {Imagery} in {Accra}, {Ghana}. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1970–1977. [Google Scholar] [CrossRef]
- Sliuzas, R.; Kuffer, M. Analysing the spatial heterogeneity of poverty using remote sensing: Typology of poverty areas using selected {RS} based indicators. Remote Sens. N. Chall. High Resolut. Bochum 2008, 5–7. [Google Scholar]
- Sedda, L.; Tatem, A.J.; Morley, D.W.; Atkinson, P.M.; Wardrop, N.A.; Pezzulo, C.; Sorichetta, A.; Kuleszo, J.; Rogers, D.J. Poverty, health and satellite-derived vegetation indices: Their inter-spatial relationship in {West} {Africa}. Int. Health 2015, 7, 99–106. [Google Scholar] [CrossRef] [PubMed]
- Grippa, T.; Linard, C.; Lennert, M.; Georganos, S.; Mboga, N.; Vanhuysse, S.; Gadiaga, A.; Wolff, E. Improving Urban Population Distribution Models with Very-High Resolution Satellite Information. Data 2019, 4, 13. [Google Scholar] [CrossRef]
- Liu, X.; Clarke, K.; Herold, M. Population density and image texture. Photogramm. Eng. Remote Sens. 2006, 72, 187–196. [Google Scholar] [CrossRef]
- Grippa, T.; Georganos, S. Dakar Very-High Resolution Land Cover Map. Available online: https://doi.org/10.5281/zenodo.1290800 (accessed on 15 June 2018).
- Grippa, T.; Georganos, S.; Zarougui, S.; Bognounou, P.; Diboulo, E.; Forget, Y.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E. Mapping Urban Land Use at Street Block Level Using OpenStreetMap, Remote Sensing Data, and Spatial Metrics. ISPRS Int. J. Geo-Inf. 2018, 7, 246. [Google Scholar] [CrossRef]
- Burgert, C.R.; Colston, J.; Roy, T.; Zachary, B. Geographic Displacement Procedure and Georeferenced Data Release Policy for the Demographic and Health Surveys; ICF International: Calverton, MD, USA, 2013. [Google Scholar]
- Warren, C.P.J.L.; Burgert, C.R.; Emch, M.E. Influence of Demographic and Health Survey Point Displacements on Raster-Based Analyses. Spat. Demogr. 2015, 4, 135–153. [Google Scholar] [CrossRef]
- Rutstein, S.O.; Staveteig, S. Making the Demographic and Health Surveys Wealth Index Comparable; ICF International: Calverton, MD, USA, 2014. [Google Scholar]
- Garenne, M.; Hohmann-Garenne, S. A wealth index to screen high-risk families: Application to Morocco. J. Heal. Popul. Nutr. 2003, 21, 235–242. [Google Scholar]
- Urke, H.B.; Bull, T.; Mittelmark, M.B. Socioeconomic status and chronic child malnutrition: Wealth and maternal education matter more in the Peruvian Andes than nationally. Nutr. Res. 2011, 31, 741–747. [Google Scholar] [CrossRef]
- Mishra, U.S.; Dilip, T.R. Reflections on wealth quintile distribution and health outcomes. Econ. Political Wkly. 2008, 43, 77–82. [Google Scholar]
- Fuchs, R.; Pamuk, E.; Lutz, W. Education or wealth: Which matters more for reducing child mortality in developing countries? Vienna Yearb. Popul. Res. 2010, 8, 175–199. [Google Scholar] [CrossRef]
- Mustafa, H.E.; Odimegwu, C. Socioeconomic determinants of infant mortality in Kenya: Analysis of Kenya DHS 2003. J. Humanit. Soc. Sci. 2008, 2, 1722–1934. [Google Scholar]
- Grippa, T.; Georganos, S. Dakar Land Use Map at Street Block Level. Available online: https://zenodo.org/record/1291389#.XbPgQ2YRVPY (accessed on 16 June 2018).
- Brousse, O.; Georganos, S.; Demuzere, M.; Vanhuysse, S.; Wouters, H.; Wolff, E.; Linard, C.; Nicole, P.-M.; Dujardin, S. Using Local Climate Zones in Sub-Saharan Africa to tackle urban health issues. Urban Clim. 2019, 27, 227–242. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Gadiaga, A.N.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.O.; Wolff, E.; Kalogirou, S. Geographical Random Forests: A Spatial Extension of the Random Forest Algorithm to Address Spatial Heterogeneity in Remote Sensing and Population Modelling. Geocarto Int. 2019, 1–12. [Google Scholar] [CrossRef]
- Vanhuysse, S.; Grippa, T.; Lennert, M.; Wolff, E.; Idrissa, M. Contribution of nDSM derived from VHR stereo imagery to urban land-cover mapping in Sub-Saharan Africa. In Proceedings of the 2017 Joint Urban Remote Sensing Event (JURSE), Dubai, UAE, 6–8 March 2017; pp. 1–4. [Google Scholar]
- Engstrom, R.; Copenhaver, A.; Qi, Y. Evaluating the use of multiple imagery-derived spatial features to predict census demographic variables in Accra, Ghana. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7318–7321. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Benesty, M.; et al. Caret: Classification and Regression Training; R Package Version 6.0-21; CRAN: Vienna, Austria, 2014. [Google Scholar]
- R Core Team: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008; ISBN 3-900051-07-0.
- Agence Nationale de la Statistique et de la Démographie (ANSD). Rapport Définitf du RGPHAE 2013; Agence Nationale de la Statistique et de la Démographie (ANSD): Dakar, Senegal, 2013. [Google Scholar]
- Smits, J.; Steendijk, R. The international wealth index (IWI). Soc. Indic. Res. 2015, 122, 65–85. [Google Scholar] [CrossRef]
- Rutstein, S.O. The DHS Wealth Index: Approaches for Rural and Urban Areas; Demographic and Health Research Division, Macro International Inc.: Calverton, NY, USA, 2008. [Google Scholar]
- Getis, A. Spatial statistics. Geogr. Inf. Syst. 1999, 1, 239–251. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Remote Sensing of Environment Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Grippa, T.; Georganos, S. Ouagadougou land use map at street block level. Zenodo 2019. [Google Scholar] [CrossRef]
- Grippa, T.; Georganos, S. Ouagadougou very-high resolution land cover map. Zenodo 2018. [Google Scholar] [CrossRef]
- Bosco, C.; de Rigo, D.; Tatem, A.; Pezzulo, C.; Wood, R.; Chamberlain, H.; Bird, T. Geostatistical Tools to Map the Interaction between Development Aid and Indices of Need; AidData: Washington, DC, USA, 2018. [Google Scholar]
- Pezzulo, C.; Utazi, E.; Sorichetta, T.B.A.; Tatem, A.; Yourkavitch, J.; Pullum, T.; Burgert-Brucker, C. Subnational Modelling of Child Mortality and Its Drivers Across 27 Countries in Sub-Saharan Africa. In Proceedings of the PAA Meeting, Chicago, IL, USA, 27–29 April 2017. [Google Scholar]
- Neal, S.; Ruktanonchai, C.W.; Chandra-Mouli, V.; Harvey, C.; Matthews, Z.; Raina, N.; Tatem, A. Using geospatial modelling to estimate the prevalence of adolescent first births in Nepal. BMJ Glob. Health 2019, 4, e000763. [Google Scholar] [CrossRef]
- Neal, S.; Ruktanonchai, C.; Chandra-Mouli, V.; Matthews, Z.; Tatem, A.J. Mapping adolescent first births within three east African countries using data from Demographic and Health Surveys: Exploring geospatial methods to inform policy. Reprod. Health 2016, 13, 98. [Google Scholar] [CrossRef]
- Utazi, C.E.; Thorley, J.; Alegana, V.A.; Ferrari, M.J.; Takahashi, S.; Metcalf, C.J.E.; Lessler, J.; Tatem, A.J. High resolution age-structured mapping of childhood vaccination coverage in low and middle income countries. Vaccine 2018, 36, 1583–1591. [Google Scholar] [CrossRef] [PubMed]
- Utazi, C.E.; Thorley, J.; Alegana, V.A.; Ferrari, M.J.; Nilsen, K.; Takahashi, S.; Metcalf, C.J.E.; Lessler, J.; Tatem, A.J. A spatial regression model for the disaggregation of areal unit based data to high-resolution grids with application to vaccination coverage mapping. Stat. Methods Med. Res. 2019, 28, 3226–3241. [Google Scholar] [CrossRef] [PubMed]
- Utazi, C.E.; Sahu, S.K.; Atkinson, P.M.; Tejedor-Garavito, N.; Lloyd, C.T.; Tatem, A.J. Geographic coverage of demographic surveillance systems for characterising the drivers of childhood mortality in sub-Saharan Africa. BMJ Glob. Heal. 2018, 3, e000611. [Google Scholar] [CrossRef] [PubMed]
- Ruktanonchai, C.W.; Nilsen, K.; Alegana, V.A.; Bosco, C.; Ayiko, R.; Kajeguka, A.C.S.; Matthews, Z.; Tatem, A.J. Temporal trends in spatial inequalities of maternal and newborn health services among four east African countries, 1999–2015. BMC Public Health 2018, 18, 1339. [Google Scholar] [CrossRef]
- Sinha, P.; Gaughan, A.E.; Stevens, F.R.; Nieves, J.J.; Sorichetta, A.; Tatem, A.J. Assessing the spatial sensitivity of a random forest model: Application in gridded population modeling. Comput. Environ. Urban Syst. 2019, 75, 132–145. [Google Scholar] [CrossRef]
- Kohli, D.; Warwadekar, P.; Kerle, N.; Sliuzas, R.; Stein, A. Transferability of Object-Oriented Image Analysis Methods for Slum Identification. Remote Sens. 2013, 5, 4209–4228. [Google Scholar] [CrossRef]
- Ezeh, A.; Oyebode, O.; Satterthwaite, D.; Chen, Y.; Ndugwa, R.; Sartori, J.; Mberu, B.; Haregu, T.; Watson, S.I.; Caiaff, W.; et al. The history, geography, and sociology of slums and the health problems of people who live in slums. Lancet 2017, 389, 547–558. [Google Scholar] [CrossRef]
- Kuffer, M.; Sliuzas, R.; Pfeffer, K.; Baud, I. The utility of the co-occurrence matrix to extract slum areas from {VHR} imagery. In Proceedings of the 2015 Joint Urban Remote Sensing Event (JURSE), Lausanne, Switzerland, 30 March–1 April 2015; pp. 1–4. [Google Scholar]
- Kit, O.; Lüdeke, M.; Reckien, D. Texture-based identification of urban slums in Hyderabad, India using remote sensing data. Appl. Geogr. 2012, 32, 660–667. [Google Scholar] [CrossRef]
- Kohli, D.; Sliuzas, R.; Kerle, N.; Stein, A. An ontology of slums for image-based classification. Comput. Environ. Urban Syst. 2012, 36, 154–163. [Google Scholar] [CrossRef]
- Kabaria, C.W.; Molteni, F.; Mandike, R.; Chacky, F.; Noor, A.M.; Snow, R.W.; Linard, C. Mapping intra-urban malaria risk using high resolution satellite imagery: A case study of Dar es Salaam. Int. J. Health Geogr. 2016, 15, 26. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).