Retrieval of the Fraction of Radiation Absorbed by Photosynthetic Components (FAPARgreen) for Forest Using a Triple-Source Leaf-Wood-Soil Layer Approach
Abstract
1. Introduction
2. Materials and Methods
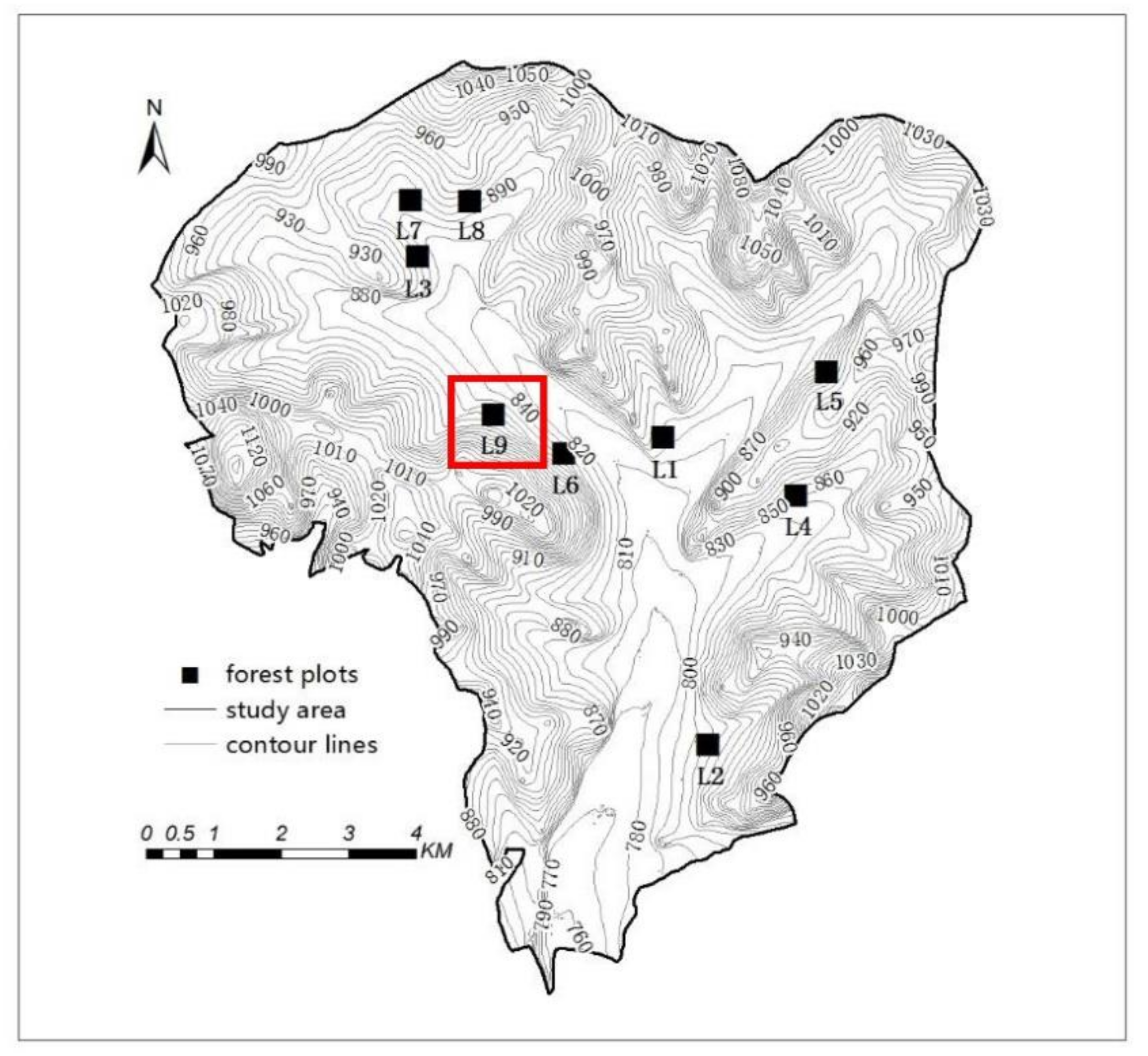
2.1. Satellite Datasets
2.1.1. MODIS LAI/FAPAR Products (MCD15A2H)
2.1.2. MODIS Land Cover Product (MCD12Q1)
2.1.3. Global Clumping Index (CI) Product
2.1.4. Global Soil Albedo Product
2.2. Data Simulated by the LESS Model
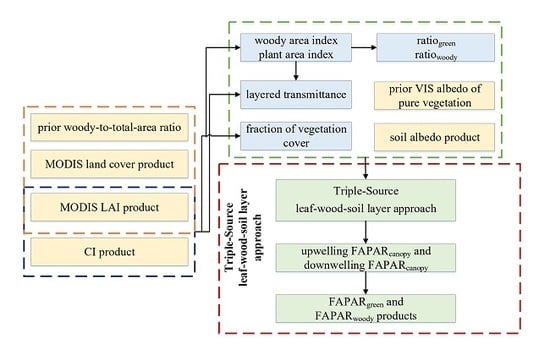
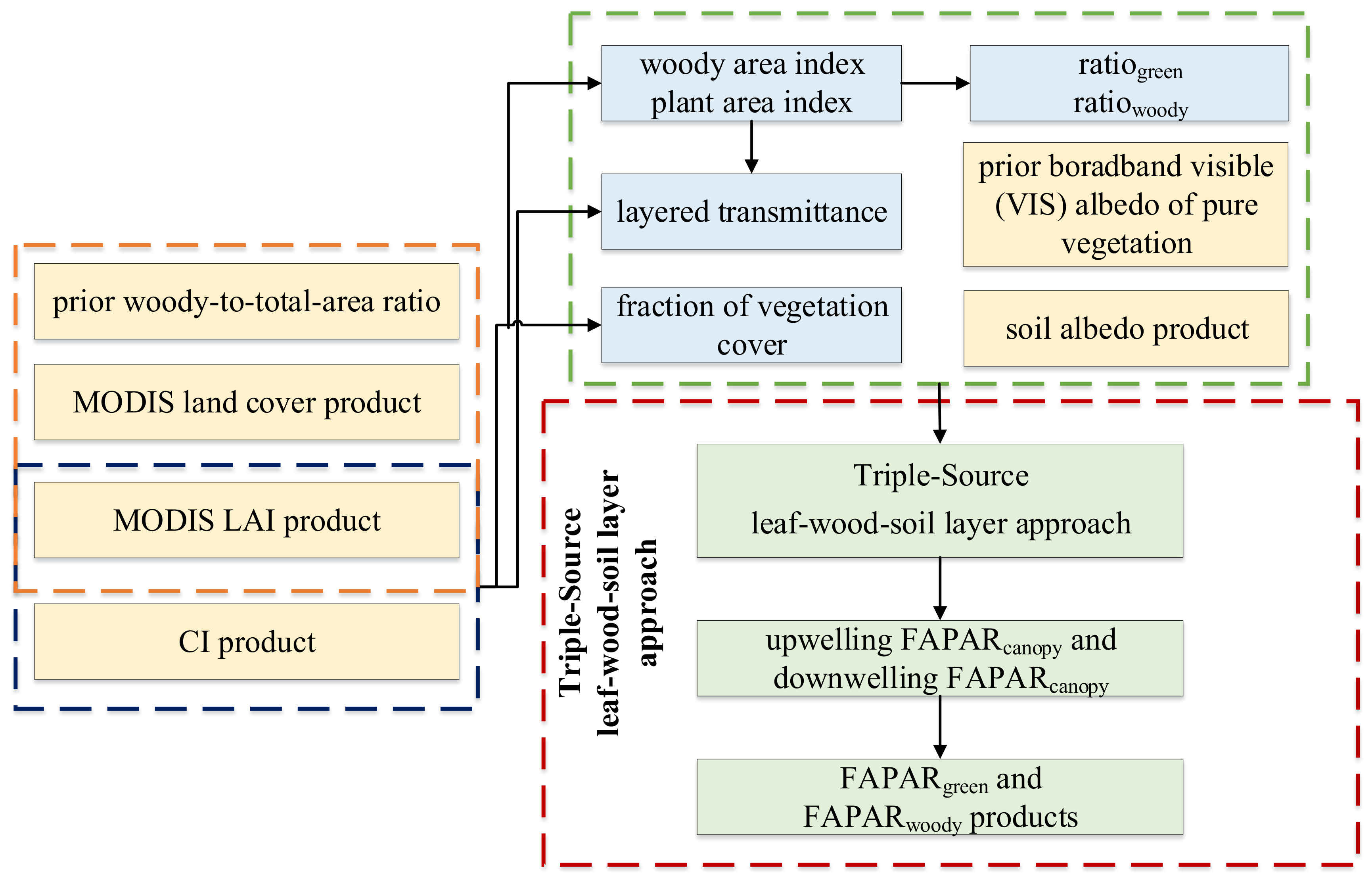
2.3. Algorithms for Estimating Global and Datasets
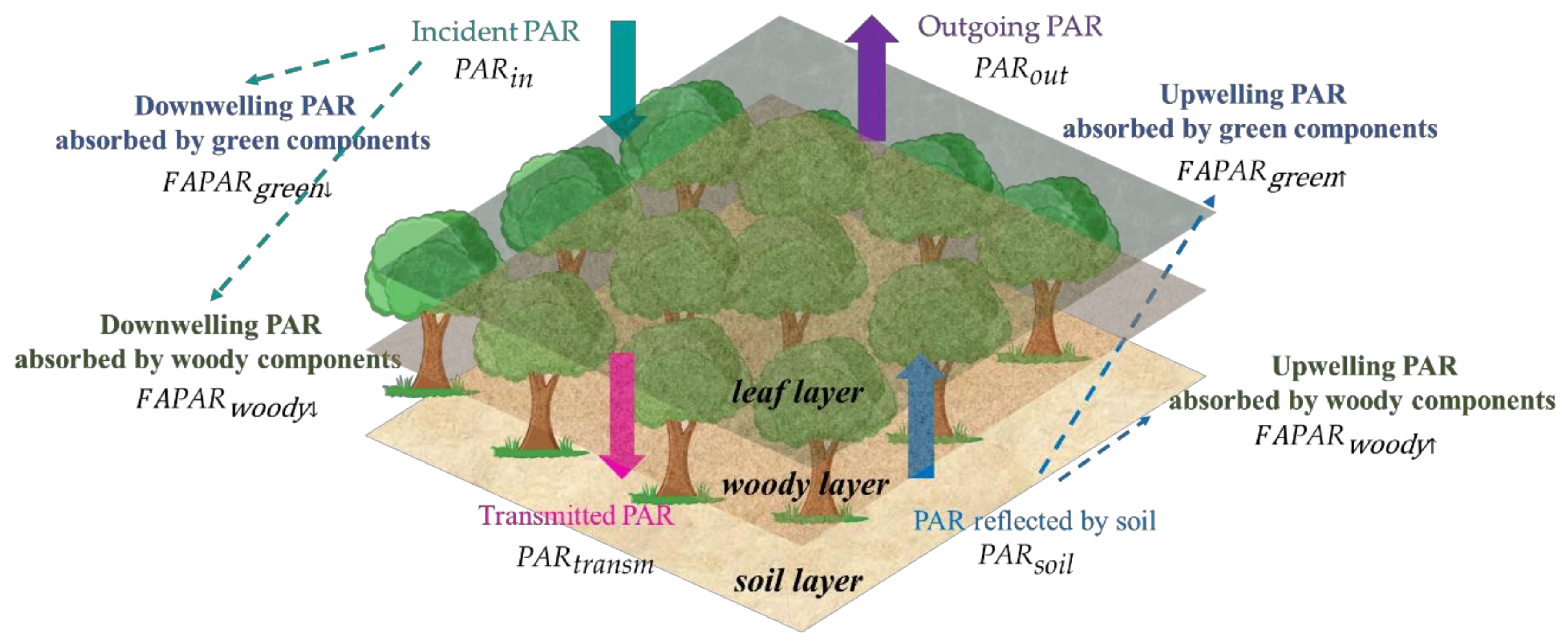
2.3.1. The Triple-Source Leaf–Wood–Soil Layer Model
2.3.2. Determination of Woody Area Index
2.3.3. Separating and from
3. Results
3.1. Validation of the TriLay Method using Simulations made by the LESS Model
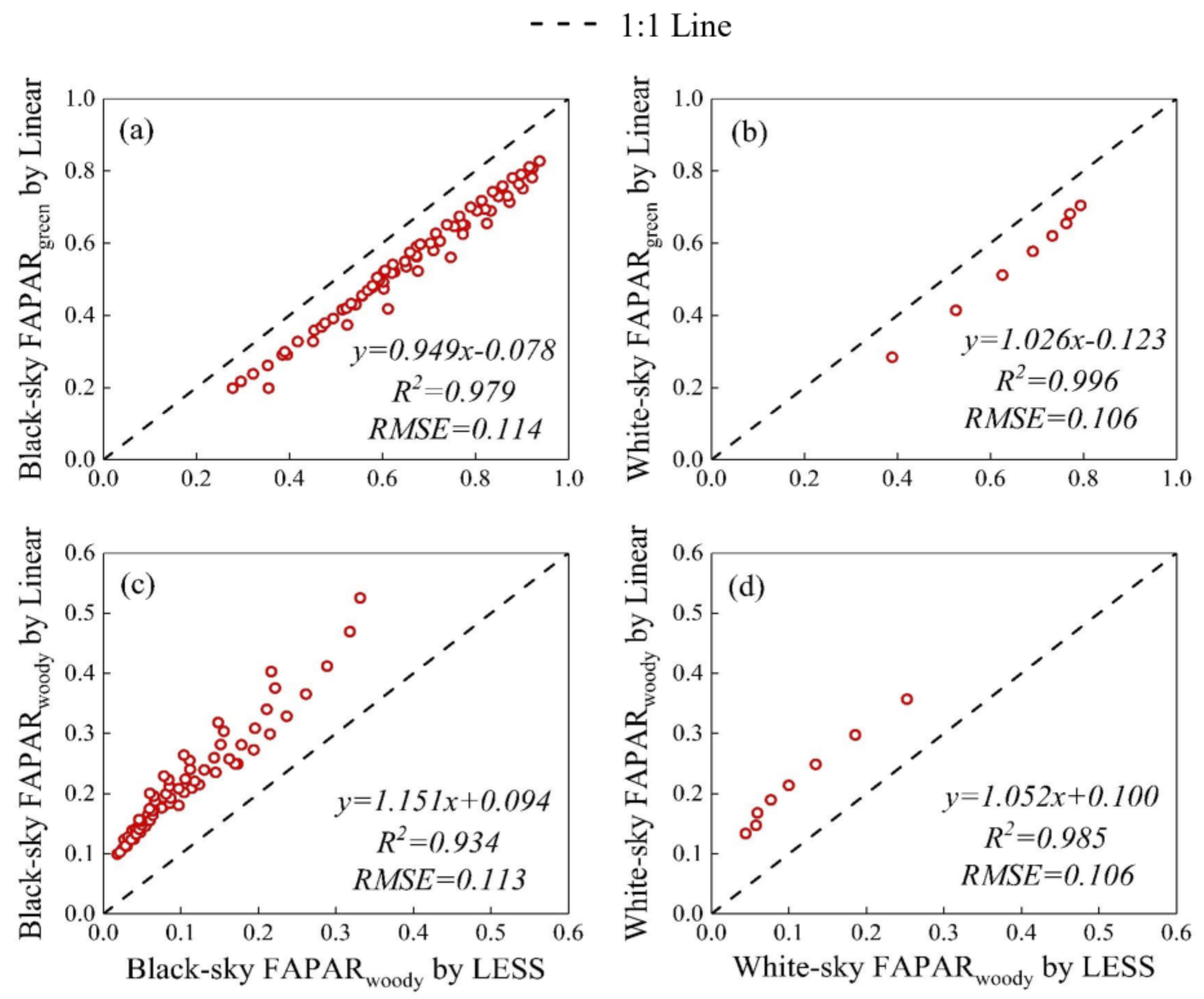
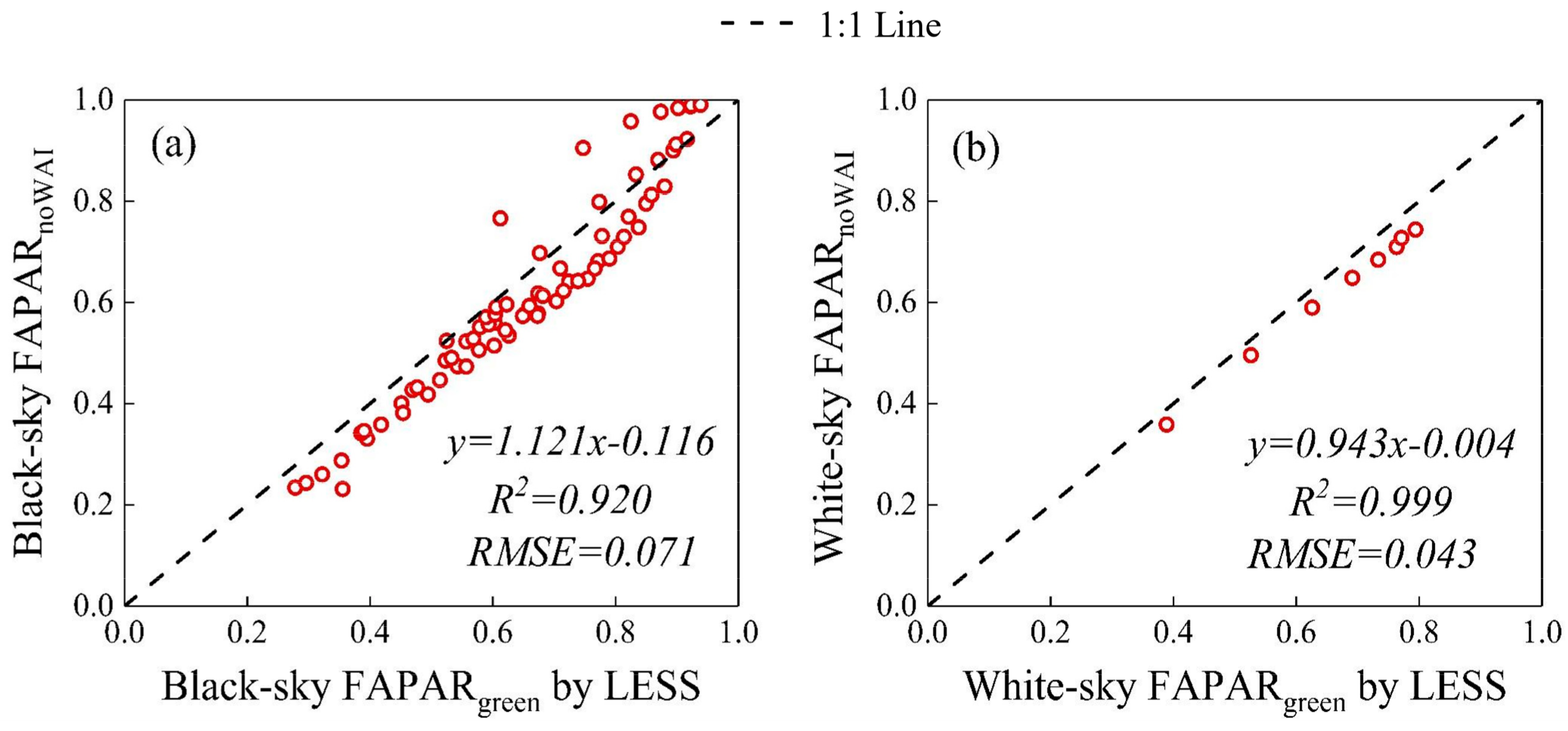
3.2. Comparison of Different Methods using the LESS Simulations
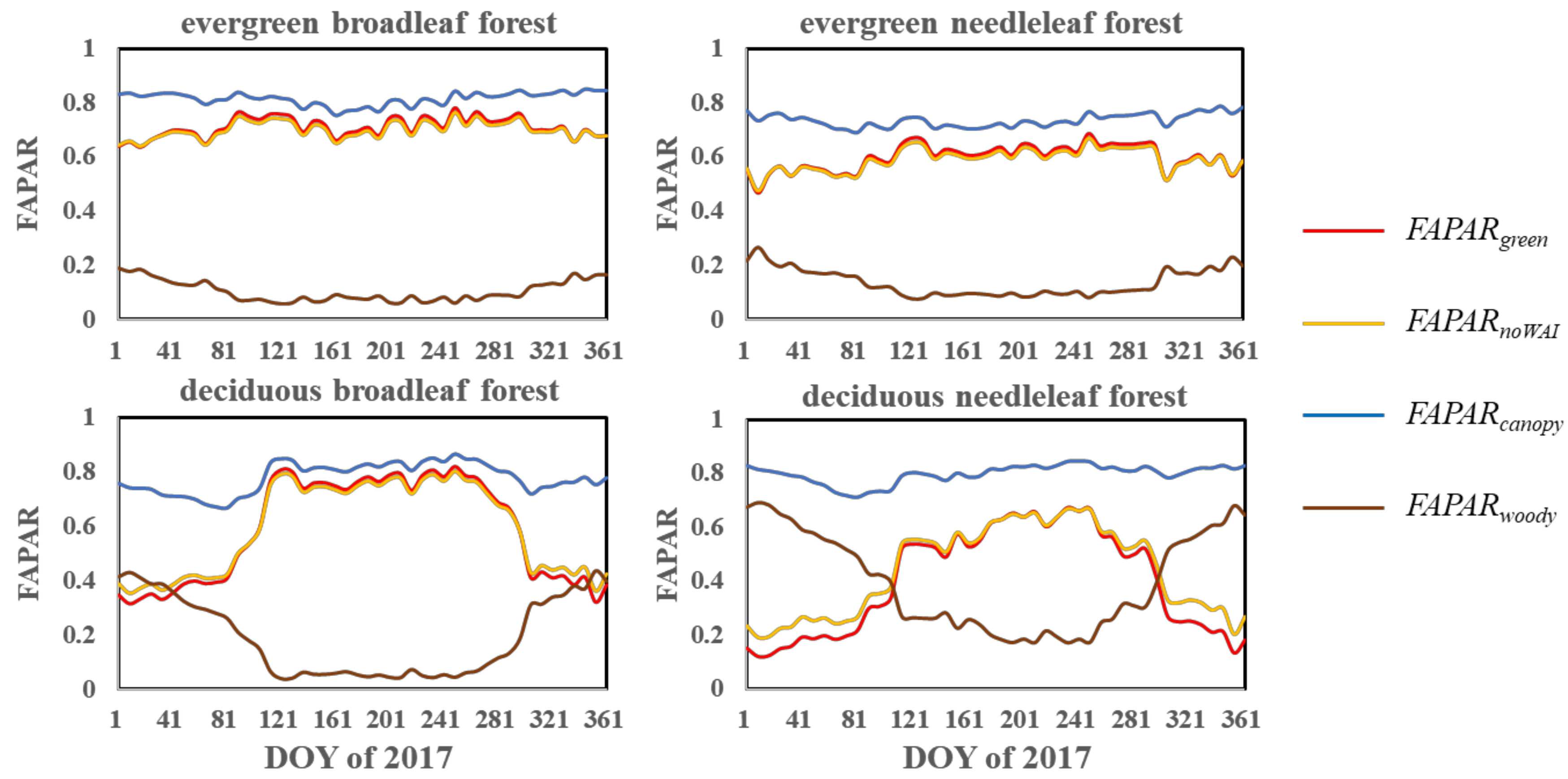
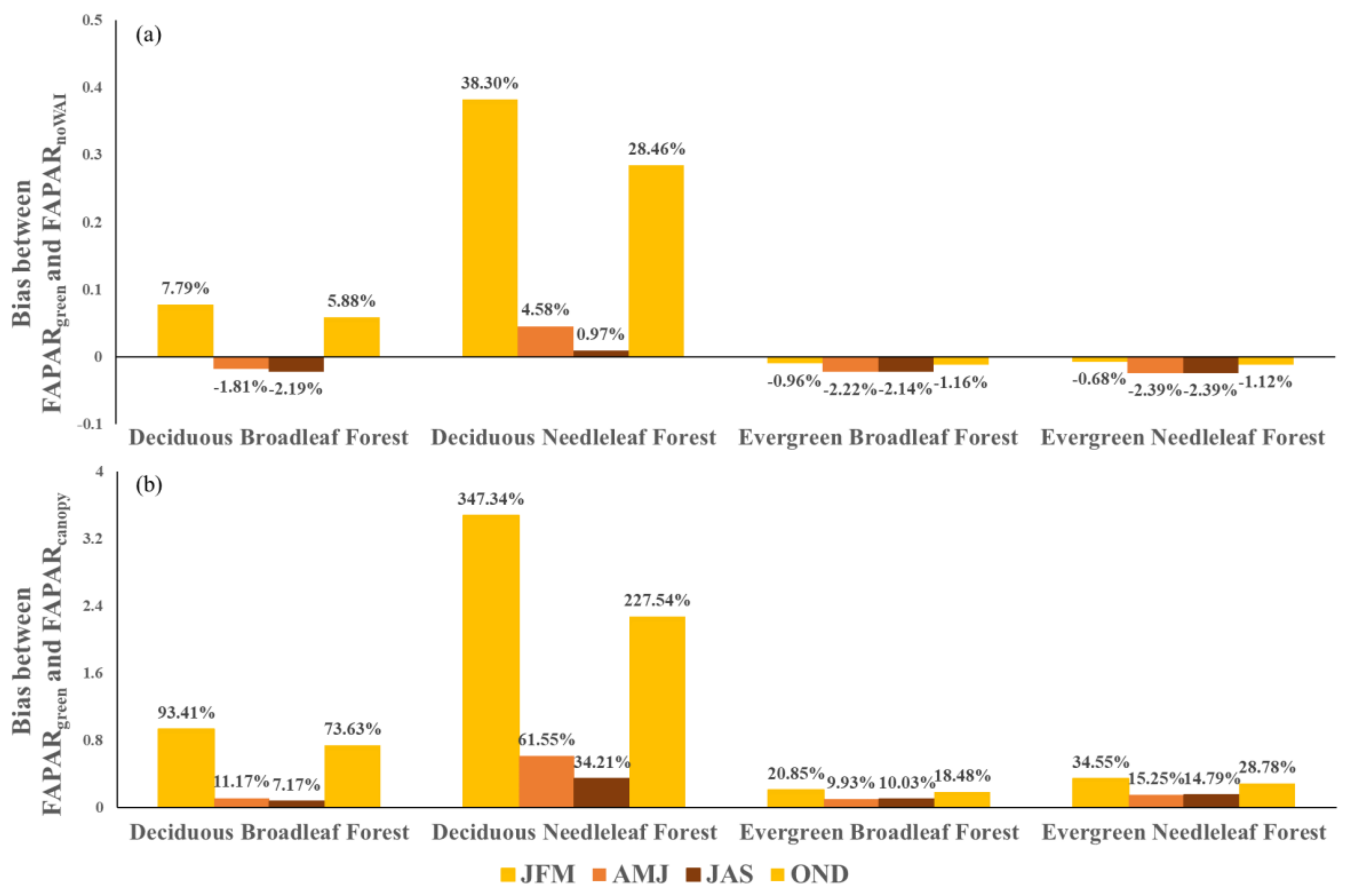
3.3. Temporal Variations in Different FAPAR Products
4. Discussion
4.1. Uncertainty in Determining WAI
4.2. Uncertainty Caused by the Use of Fixed Values of the Extinction Coefficients and
4.3. Setting the Clumping Index for Photosynthetic and Woody Components
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Monteith, J.L. Vegetation and the atmosphere. Volume 1. Principles. J. Appl. Ecol. 1977, 14, 655. [Google Scholar]
- Sellers, P.; Dickinson, R.; Randall, D.; Betts, A.; Hall, F.; Berry, J.; Collatz, G.; Denning, A.; Mooney, H.; Nobre, C. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Prince, S.D.; Goward, S.N. Global primary production: A remote sensing approach. J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- Ruimy, A.; Dedieu, G.; Saugier, B. Turc: A diagnostic model of continental gross primary productivity and net primary productivity. Glob. Biogeochem. Cycles 1996, 10, 269–285. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch FAZhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Coupled soil-leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and toa radiance data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
- Liu, R.; Huang, W.; Ren, H.; Yang, G.; Xie, D.; Wang, J. Photosynthetically active radiation vertical distribution model in maize canopy. Trans. Chin. Soc. Agric. Eng. 2011, 27, 115–121. [Google Scholar]
- Li, W.; Fang, H. Estimation of direct, diffuse, and total fpars from landsat surface reflectance data and ground-based estimates over six fluxnet sites. J. Geophys. Res. Biogeosci. 2015, 120, 96–112. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 2002, 35, 1380–1393. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Martonchik, J.V.; Diner, D.J.; Myneni, R.B.; Verstraete, M.; Pinty, B.; Gobron, N. Estimation of vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from atmosphere-corrected misr data. J. Geophys. Res. Space Phys. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y.; Knyazikhin, Y.; Myneni, R.B.; Glassy, J.M.; Dedieu, G.; Running, S.W. Prototyping of modis lai and fpar algorithm with lasur and landsat data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2387–2401. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.M.; Govaerts, Y. A semidiscrete model for the scattering of light by vegetation. J. Geophys. Res. Space Phys. 1997, 102, 9431–9446. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Rui, S.; Wang, J.; Bo, J. Estimating the fraction of absorbed photosynthetically active radiation from the modis data based glass leaf area index product. Remote Sens. Environ. 2015, 171, 105–117. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X.; Xie, S.; Liu, X.; Song, B.; Chen, S.; Peng, D. Global white-sky and black-sky fapar retrieval using the energy balance residual method: Algorithm and validation. Remote Sens. 2019, 11, 1004. [Google Scholar] [CrossRef]
- Chen, J.M. Canopy architecture and remote sensing of the fraction of photosynthetically active radiation absorbed by boreal conifer forests. IEEE IEEE Trans. Geosci. Remote Sens. 1996, 34, 1353–1368. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Q.; Fan, W.; Li, X.; Xiao, Q.; Yan, G.; Tian, G. A bi-directional gap model for simulating the directional thermal radiance of row crops. Sci. China 2002, 45, 1087–1098. [Google Scholar] [CrossRef]
- Fan, W.; Yuan, L.; Xu, X.; Chen, G.; Zhang, B. A new fapar analytical model based on the law of energy conservation: A case study in china. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3945–3955. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Mcclaran, M.P.; Leeuwen, W.J.D.V.; Drake, S.; Marsh, S.E.; Thomson, A.M.; Izaurralde, R.C.; Rosenberg, N.J. Biophysical characterization and management effects on semiarid rangeland observed from landsat etm+ data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 125–134. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed par from year one of modis data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Martonchik, J.; Myneni, R.B.; Diner, D.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from modis and misr data. J. Geophys. Res. Space Phys. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O. Lai, fapar and fcover cyclopes global products derived from vegetation: Part 1: Principles of the algorithm. Remote Sens. Environ. 2009, 110, 275–286. [Google Scholar] [CrossRef]
- Plummer, S.; Arino, O.; Simon, M.; Steffen, W. Establishing a earth observation product service for the terrestrial carbon community: The globcarbon initiative. Mitig. Adapt. Strat. Glob. Chang. 2006, 11, 97–111. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.; Govaerts, Y. The MERIS Global Vegetation Index (MGVI): Description and preliminary application. Int. J. Remote Sens. 1999, 20, 1917–1927. [Google Scholar] [CrossRef]
- Pinty, B.; Clerici, M.; Andredakis, I.; Kaminski, T.; Taberner, M.; Verstraete, M.M.; Gobron, N.; Plummer, S.; Widlowski, J.-L. Exploiting the MODIS albedos with the Two-stream Inversion Package (JRC-TIP): 2. Fractions of transmitted and absorbed fluxes in the vegetation and soil layers. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Disney, M.; Muller, J.-P.; Kharbouche, S.; Kaminski, T.; Voßbeck, M.; Lewis, P.; Pinty, B. A New Global fAPAR and LAI Dataset Derived from Optimal Albedo Estimates: Comparison with MODIS Products. Remote Sens. 2016, 8, 275. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, Y.; Zhang, Y.; Elsaleous, N.; Knyazikhin, Y.; Vermote, E.; Myneni, R.B. Investigation of product accuracy as a function of input and model uncertainties—Case study with seawifs and modis lai/fpar algorithm. Remote Sens. Environ. 2000, 78, 299–313. [Google Scholar] [CrossRef]
- Camacho, F.; Cernicharo, J.; Lacaze, R.; Baret, F.; Weiss, M. GEOV1: LAI, FAPAR essential climate variables and FCOVER global time series capitalizing over existing products. Part 2: Validation and intercomparison with reference products. Remote Sens. Environ. 2013, 137, 310–329. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Aussedat, O.; Taberner, M.; Faber, O.; Melin, F.; Lavergne, T.; Robustelli, M.; Snoeij, P. Uncertainty estimates for the FAPAR operational products derived from MERIS—Impact of top-of-atmosphere radiance uncertainties and validation with field data. Remote Sens. Environ. 2008, 112, 1871–1883. [Google Scholar] [CrossRef]
- Fritsch, S.; Machwitz, M.; Ehammer, A.; Conrad, C.; Dech, S. Validation of the collection 5 MODIS FPAR product in a heterogeneous agricultural landscape in arid Uzbekistan using multitemporal RapidEye imagery. Int. J. Remote Sens. 2012, 33, 6818–6837. [Google Scholar] [CrossRef]
- Pickett-Heaps, C.A.; Canadell, J.; Briggs, P.R.; Gobron, N.; Haverd, V.; Paget, M.J.; Pinty, B.; Raupach, M.R. Evaluation of six satellite-derived Fraction of Absorbed Photosynthetic Active Radiation (FAPAR) products across the Australian continent. Remote Sens. Environ. 2014, 140, 241–256. [Google Scholar] [CrossRef]
- Tao, X.; Liang, S.; Wang, D. Assessment of five global satellite products of fraction of absorbed photosynthetically active radiation: Intercomparison and direct validation against ground-based data. Remote Sens. Environ. 2015, 163, 270–285. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Suyker, A.E. Productivity, absorbed photosynthetically active radiation, and light use efficiency in crops: Implications for remote sensing of crop primary production. J. Plant Physiol. 2015, 177, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Tewes, A.; Schellberg, J. Towards remote estimation of radiation use efficiency in maize using uav-based low-cost camera imagery. Agronomy 2018, 8, 16. [Google Scholar] [CrossRef]
- Miao, G.; Guan, K.; Xi, Y.; Bernacchi, C.J.; Masters, M.D. Sun-induced chlorophyll fluorescence, photosynthesis, and light use efficiency of a soybean field. J. Geophys. Res. Biogeosci. 2018, 123, 610–623. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Arkebauer, T.J.; Suyker, A.E. Convergence of daily light use efficiency in irrigated and rainfed C3 and C4 crops. Remote Sens. Environ. 2018, 217, 30–37. [Google Scholar] [CrossRef]
- Asner, G.P.; Wessman, C.A.; Archer, S. Scale dependence of absorption of photosynthetically active radiation in terrestrial ecosystems. Ecol. Appl. 1998, 8, 1003–1021. [Google Scholar] [CrossRef]
- Hall, F.G.; Huemmrich, K.F.; Goetz, S.J.; Sellers, P.J.; Nickeson, J.E. Satellite remote sensing of surface energy balance: Success, failures, and unresolved issues in FIFE. J. Geophys. Res. Space Phys. 1992, 97, 19061–19089. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, X.; Braswell, B.; Linder, E.; Baret, F.; Moore, B. Estimating light absorption by chlorophyll, leaf and canopy in a deciduous broadleaf forest using MODIS data and a radiative transfer model. Remote Sens. Environ. 2005, 99, 357–371. [Google Scholar] [CrossRef]
- Gitelson, A.A. Remote estimation of fraction of radiation absorbed by photosynthetically active vegetation: Generic algorithm for maize and soybean. Remote Sens. Lett. 2019, 10, 283–291. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Schepers, J. Relationships between gross primary production, green LAI, and canopy chlorophyll content in maize: Implications for remote sensing of primary production. Remote Sens. Environ. 2014, 144, 65–72. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Huemmrich, K.F. Relationship between fraction of radiation absorbed by photosynthesizing maize and soybean canopies and NDVI from remotely sensed data taken at close range and from MODIS 250m resolution data. Remote Sens. Environ. 2014, 147, 108–120. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Guo, D.; Yan, G. A large-scale emulation system for realistic three-dimensional (3-d) forest simulation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4834–4843. [Google Scholar] [CrossRef]
- Myneni, R.; Knyazikhin, Y.; Park, T. MCD15A2H MODIS/Terra + Aqua leaf area index/FPAR 8-day L4 Global 500 m SIN Grid V006, NASA EOSDIS Land Processes DAAC. 2015. Available online: http://doi.org/10.5067/MODIS/MCD15A2H.006 (accessed on 12 September 2019).
- Vermote, E.; Vermeulen, A. Atmospheric correction algorithm: Spectral reflectances (mod09). ATBD Version 1999, 4, 1–107. [Google Scholar]
- Friedl, M.; McIver, D.; Hodges, J.; Zhang, X.; Muchoney, D.; Strahler, A.; Woodcock, C.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Chen, J.; Menges, C.; Leblanc, S. Global mapping of foliage clumping index using multi-angular satellite data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- Jiao, Z.; Dong, Y.; Schaaf, C.B.; Chen, J.M.; Roman, M.; Wang, Z.; Zhang, H.; Ding, A.; Erb, A.; Hill, M.J.; et al. An algorithm for the retrieval of the clumping index (CI) from the MODIS BRDF product using an adjusted version of the kernel-driven BRDF model. Remote Sens. Environ. 2018, 209, 594–611. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X. Dynamic Mapping of Broadband Visible Albedo of Soil Background at Global 500-m Scale from MODIS Satellite Products. In Land Surface and Cryosphere Remote Sensing IV; International Society for Optics and Photonics: Washington, DC, USA, 2018; p. 107770L. [Google Scholar]
- Irons, J.R.; Ranson, K.J.; Daughtry, C.S.T. Estimating big bluestem albedo from directional reflectance measurements. Remote Sens. Environ. 1988, 25, 185–199. [Google Scholar] [CrossRef]
- Carrer, D.; Meurey, C.; Ceamanos, X.; Roujean, J.L.; Calvet, J.C. Dynamic mapping of snow-free vegetation and bare soil albedos at global 1 km scale from 10-year analysis of modis satellite products. Remote Sens. Environ. 2014, 140, 420–432. [Google Scholar] [CrossRef]
- Widlowski, J.-L. On the bias of instantaneous FAPAR estimates in open-canopy forests. Agric. For. Meteorol. 2010, 150, 1501–1522. [Google Scholar] [CrossRef]
- Lhomme, J.-P.; Chehbouni, A. Comments on dual-source vegetation—Atmosphere transfer models. Agric. For. Meteorol. 1999, 94, 269–273. [Google Scholar] [CrossRef]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical Properties Experiment 93 (LOPEX93); Report EUR—16095-EN; Joint Research Centre, Institute for Remote Sensing Applications: Ispra, Italy; European Commission: Luxembourg, 1995. [Google Scholar]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Féret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.; Ustin, S.L.; Le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Chen, J.M. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agric. For. Meteorol. 1996, 80, 135–163. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Norman, J.M.; Gower, S.T. Measurements of branch area and adjusting leaf area index indirect measurements. Agric. For. Meteorol. 1998, 91, 69–88. [Google Scholar] [CrossRef]
- Sea, W.B.; Choler, P.; Beringer, J.; Weinmann, R.A.; Hutley, L.B.; Leuning, R. Documenting improvement in leaf area index estimates from MODIS using hemispherical photos for Australian savannas. Agric. For. Meteorol. 2011, 151, 1453–1461. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Jie, Z.; Yan, G.; Ling, C. Estimation of canopy and woody components clumping indices at three mature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1–10. [Google Scholar]
- Clark, D.B.; Olivas, P.C.; Oberbauer, S.F.; Clark, D.A.; Ryan, M.G. First direct landscape-scale measurement of tropical rain forest leaf area index, a key driver of global primary productivity. Ecol. Lett. 2008, 11, 163–172. [Google Scholar] [CrossRef]
- Zheng, G.; Ma, L.; Wei, H.; Eitel, J.U.H.; Moskal, L.M.; Zhang, Z. Assessing the contribution of woody materials to forest angular gap fraction and effective leaf area index using terrestrial laser scanning data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1475–1487. [Google Scholar] [CrossRef]
- Zou, J.; Zhuang, Y.; Chianucci, F.; Mai, C.; Lin, W.; Leng, P.; Luo, S.; Yan, B. Comparison of Seven Inversion Models for Estimating Plant and Woody Area Indices of Leaf-on and Leaf-off Forest Canopy Using Explicit 3D Forest Scenes. Remote Sens. 2018, 10, 1297. [Google Scholar] [CrossRef]
- Zou, J.; Yan, G.; Zhu, L.; Zhang, W. Woody-to-total area ratio determination with a multispectral canopy imager. Tree Physiol. 2009, 29, 1069–1080. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Zheng, G.; Eitel, J.U.; Magney, T.S.; Moskal, L.M. Determining woody-to-total area ratio using terrestrial laser scanning (TLS). Agric. For. Meteorol. 2016, 228, 217–228. [Google Scholar] [CrossRef]
- Suwa, R. Canopy photosynthesis in a mangrove considering vertical changes in light-extinction coefficients for leaves and woody organs. J. For. Res. 2011, 16, 26–34. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using landsat tm images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar] [CrossRef]
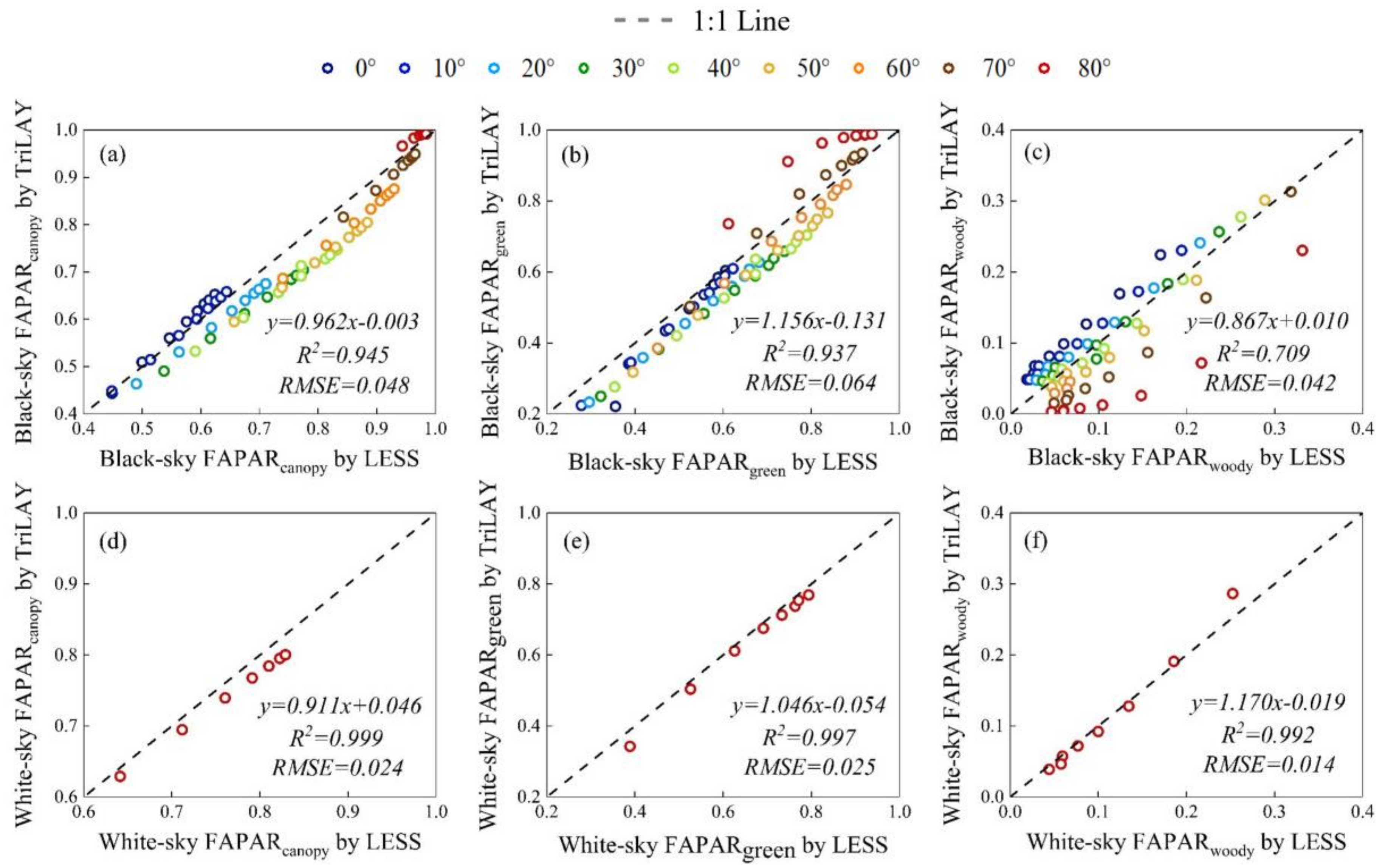
| Parameter | Definition | Units | Range or Values |
|---|---|---|---|
| Canopy | |||
| LAI | leaf area index | m2/m2 | 1.31–8.69 |
| WAI | woody area index | m2/m2 | 1.65 |
| Leaf layer | |||
| Reflectance | — | 0.041–0.205 | |
| Transmittance | — | 0.001–0.286 | |
| Soil layer | |||
| Reflectance | — | 0.001–0.134 | |
| Woody layer | |||
| Reflectance | — | 0.069–0.237 | |
| Imaging Geometry | |||
| SZA | sun zenith angle | degrees | 0, 10, 20, 30, 40, 50, 60, 70, 80 |
| ratio of diffuse light | — | 0, 1 | |
| (a) For Products | ||||||
| TriLay | Linear | noWAI | ||||
| Black-Sky | White-Sky | Black-Sky | White-Sky | Black-Sky | White-Sky | |
| R2 | 0.937 | 0.997 | 0.979 | 0.996 | 0.920 | 0.999 |
| RMSE | 0.064 | 0.025 | 0.114 | 0.106 | 0.071 | 0.043 |
| Bias | −6.02% | −4.04% | −18.04% | −16.93% | −7.14% | −6.41% |
| (b) For products | ||||||
| TriLay | Linear | |||||
| Black-Sky | White-Sky | Black-Sky | White-Sky | |||
| R2 | 0.709 | 0.992 | 0.934 | 0.985 | ||
| RMSE | 0.042 | 0.014 | 0.113 | 0.106 | ||
| Bias | 6.87% | −4.64% | 153.84% | 123.47% | ||
| Period of Year | DBF | DNF | EBF | ENF | ||||
|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (%) | (%) | |||||
| JFM | 52.59 | 93.14 | 23.86 | 73.90 | 82.94 | 101.01 | 74.55 | 100.72 |
| AMJ | 90.74 | 101.93 | 64.13 | 96.32 | 91.03 | 102.27 | 86.85 | 102.46 |
| JAS | 93.36 | 102.24 | 75.02 | 99.19 | 90.93 | 102.19 | 87.14 | 102.46 |
| OND | 60.60 | 95.50 | 35.75 | 81.65 | 84.54 | 101.20 | 78.00 | 101.19 |
| Forest Vegetation Type | ENF | EBF | DNF | DBF |
|---|---|---|---|---|
| number of samples | 35 | 8 | 3 | 4 |
| mean value | 0.185 | 0.18 | 0.3 | 0.158 |
| standard deviation | 0.062 | 0.148 | 0.03 | 0.101 |
| coefficient of variation | 33.51% | 82.22% | 10.00% | 63.92% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Liu, L.; Zhang, X.; Liu, X.; Chen, X.; Qian, X.; Xu, Y.; Xie, D. Retrieval of the Fraction of Radiation Absorbed by Photosynthetic Components (FAPARgreen) for Forest Using a Triple-Source Leaf-Wood-Soil Layer Approach. Remote Sens. 2019, 11, 2471. https://doi.org/10.3390/rs11212471
Chen S, Liu L, Zhang X, Liu X, Chen X, Qian X, Xu Y, Xie D. Retrieval of the Fraction of Radiation Absorbed by Photosynthetic Components (FAPARgreen) for Forest Using a Triple-Source Leaf-Wood-Soil Layer Approach. Remote Sensing. 2019; 11(21):2471. https://doi.org/10.3390/rs11212471
Chicago/Turabian StyleChen, Siyuan, Liangyun Liu, Xiao Zhang, Xinjie Liu, Xidong Chen, Xiaojin Qian, Yue Xu, and Donghui Xie. 2019. "Retrieval of the Fraction of Radiation Absorbed by Photosynthetic Components (FAPARgreen) for Forest Using a Triple-Source Leaf-Wood-Soil Layer Approach" Remote Sensing 11, no. 21: 2471. https://doi.org/10.3390/rs11212471
APA StyleChen, S., Liu, L., Zhang, X., Liu, X., Chen, X., Qian, X., Xu, Y., & Xie, D. (2019). Retrieval of the Fraction of Radiation Absorbed by Photosynthetic Components (FAPARgreen) for Forest Using a Triple-Source Leaf-Wood-Soil Layer Approach. Remote Sensing, 11(21), 2471. https://doi.org/10.3390/rs11212471