A New Processing Chain for Real-Time Ground-Based SAR (RT-GBSAR) Deformation Monitoring
Abstract
1. Introduction
2. Materials and Methods
3. Results
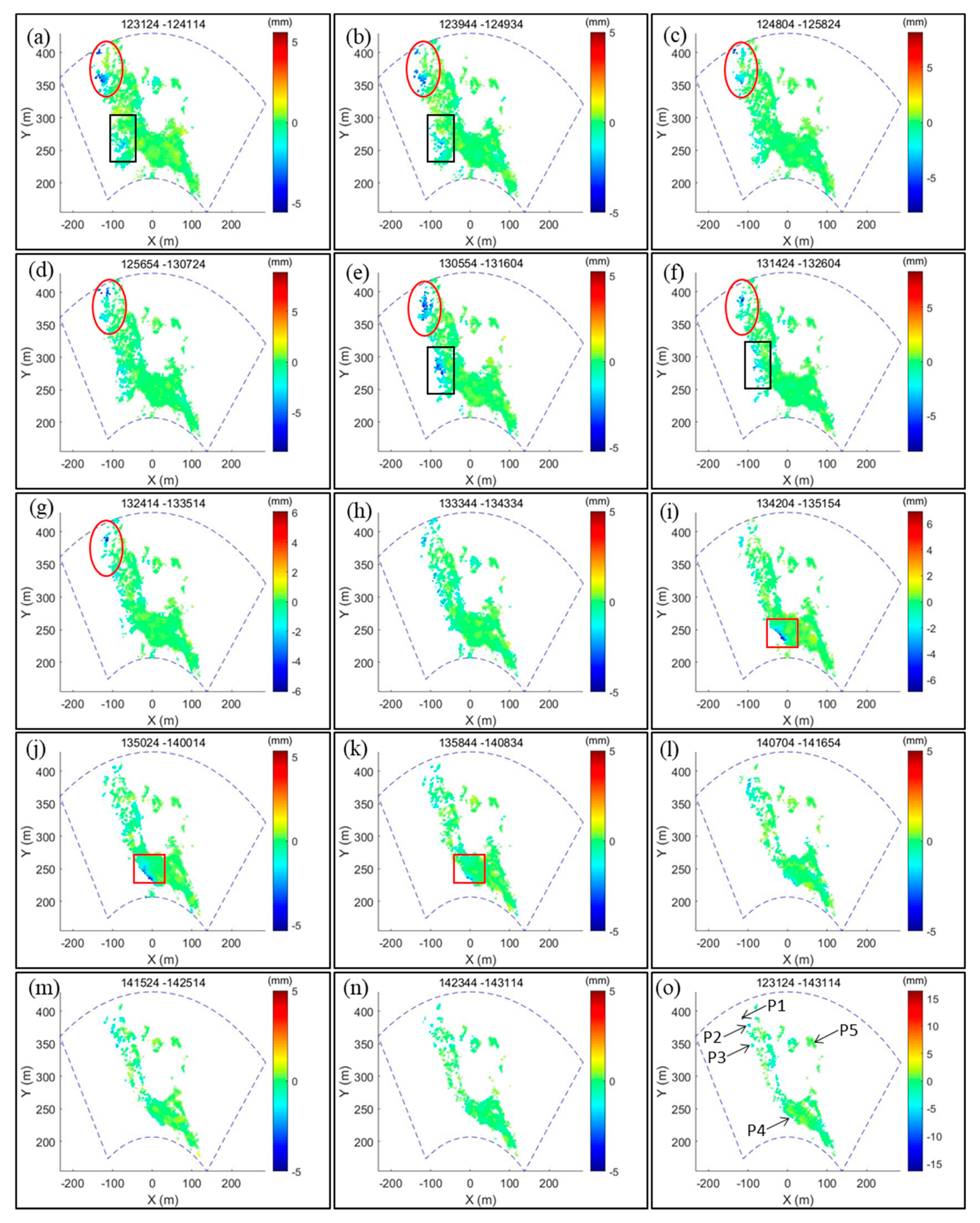
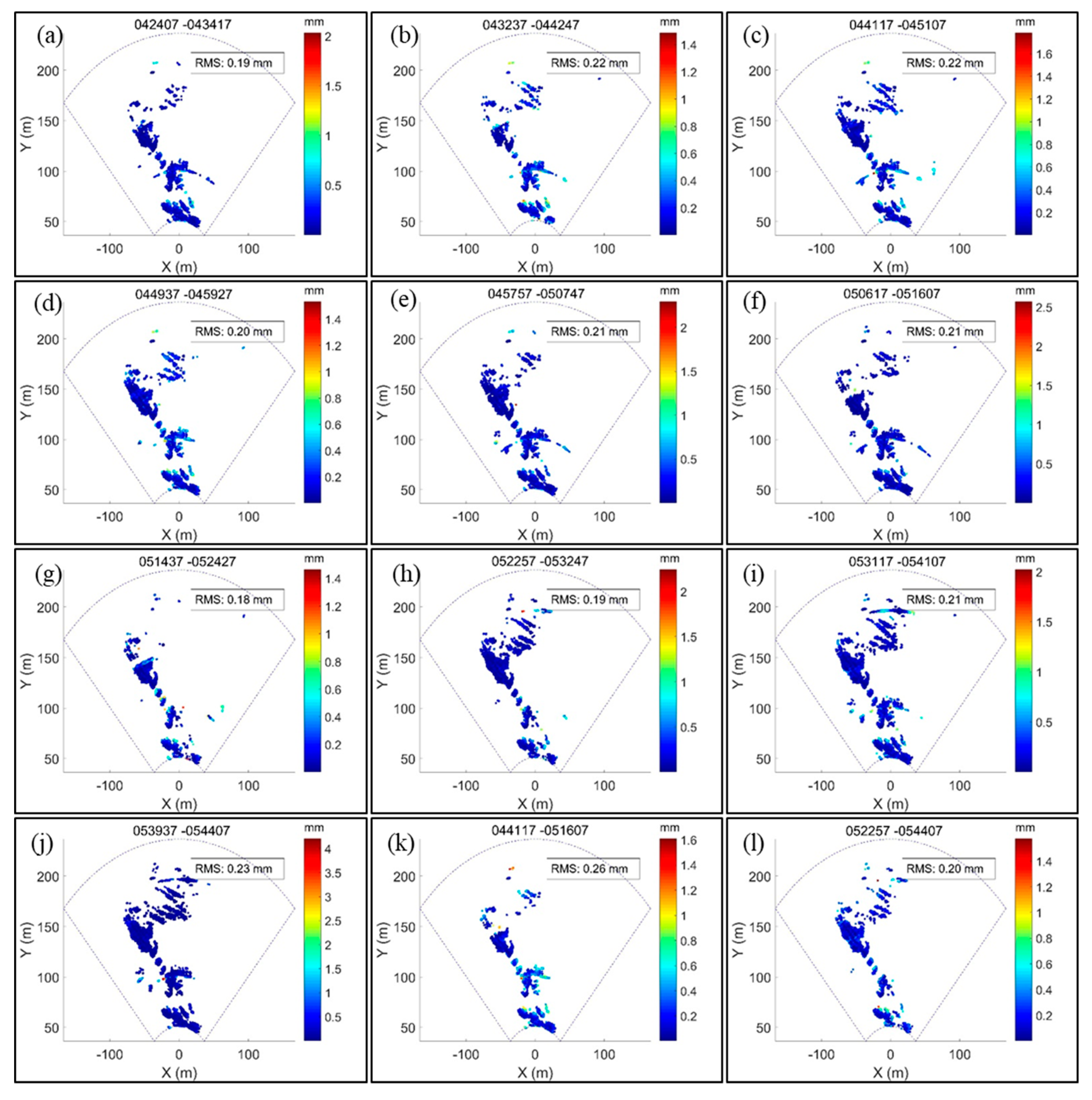
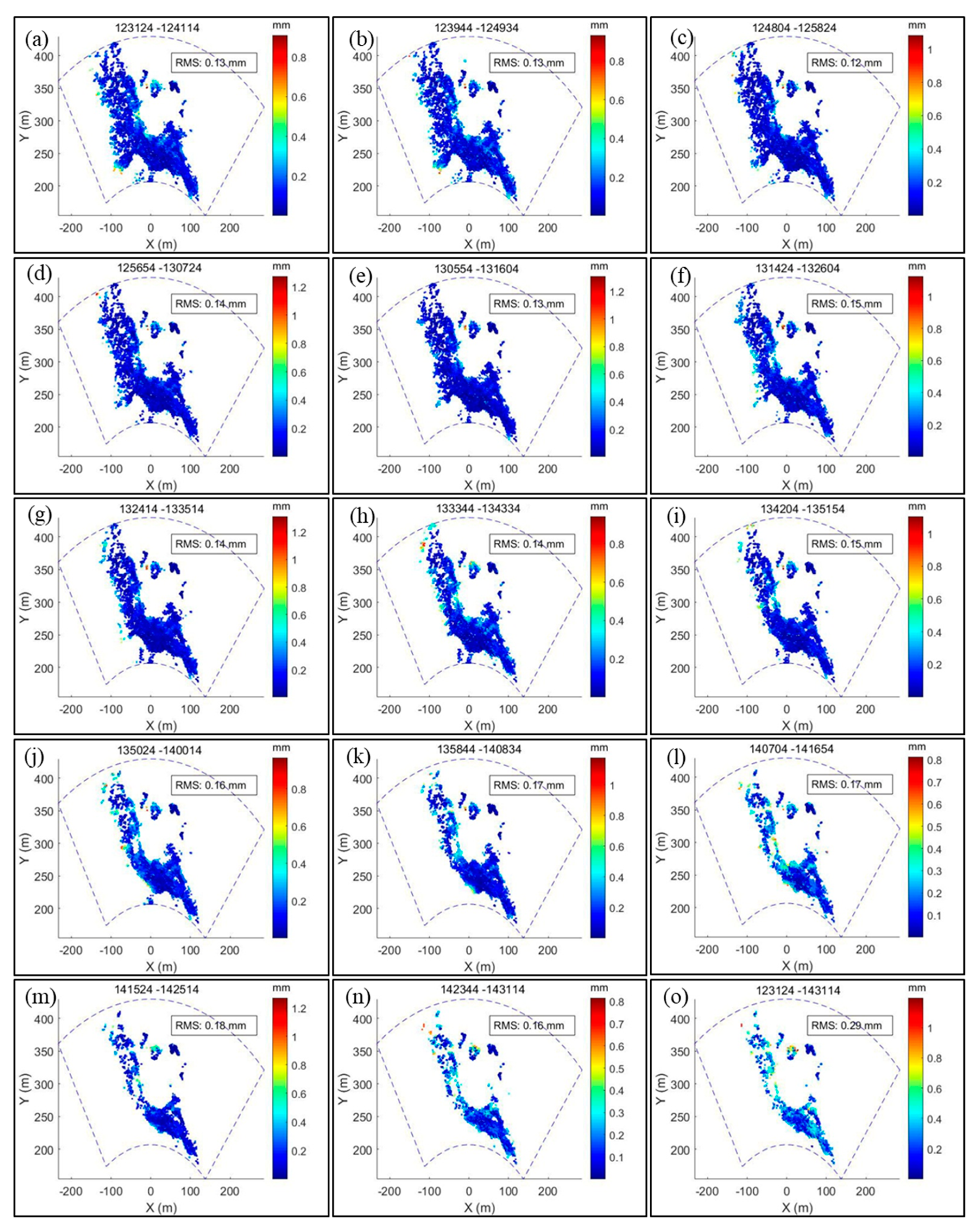
3.1. Sand Dune Case Study
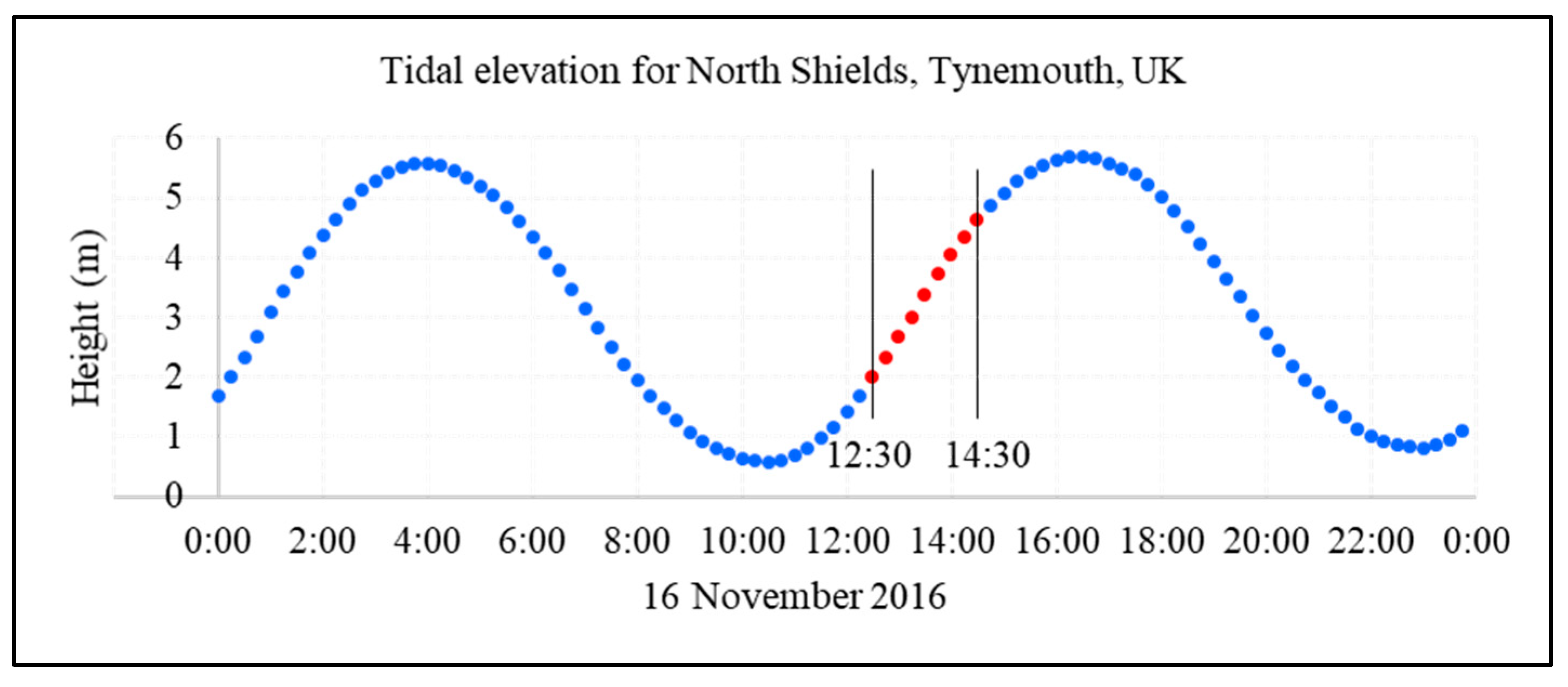
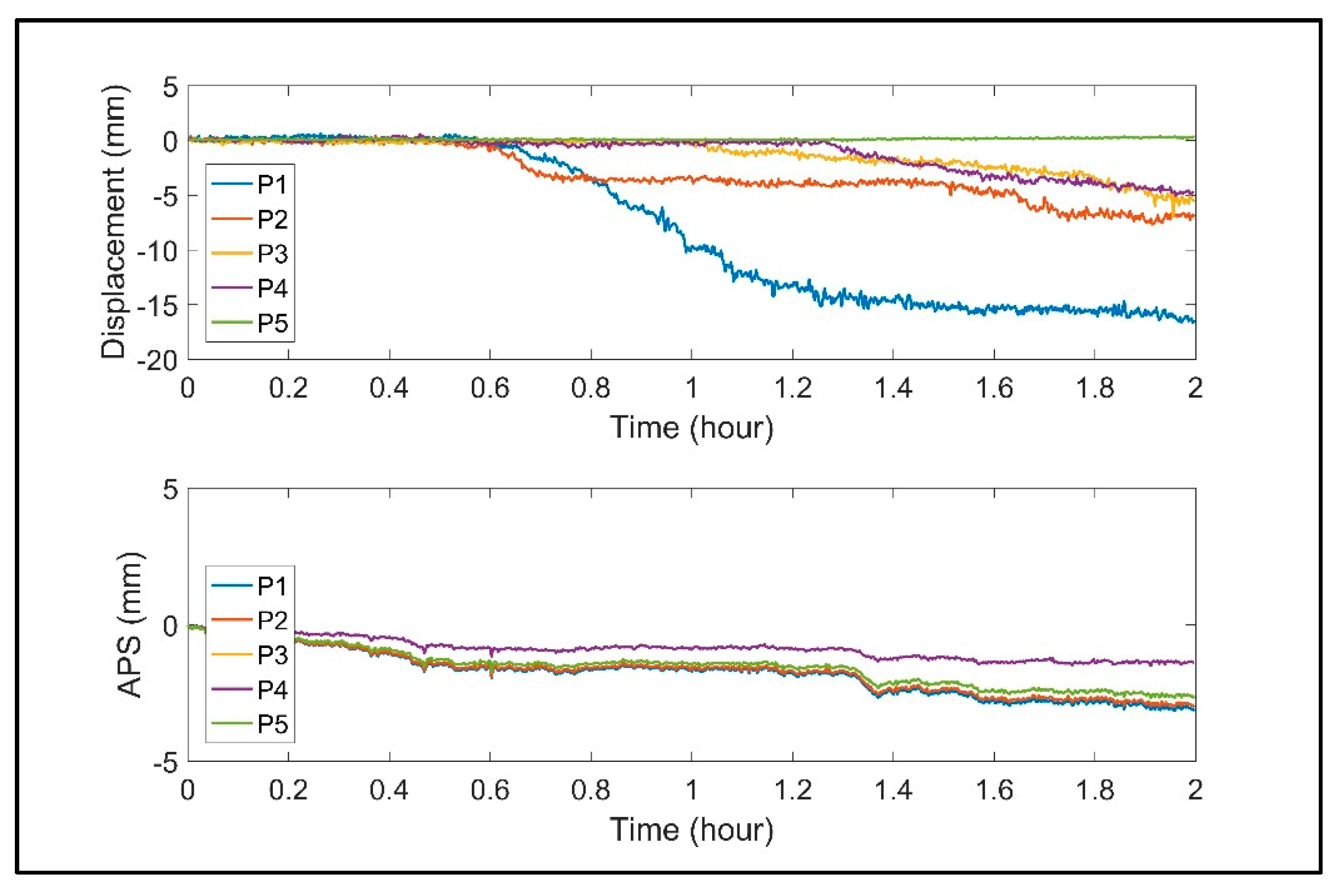
3.2. Coastal Cliff Case Study
4. Discussion
4.1. Identification of Unwrapping Errors
4.2. Precision of Time Series Analysis
4.3. Real-Time Capability of RT-GBSAR
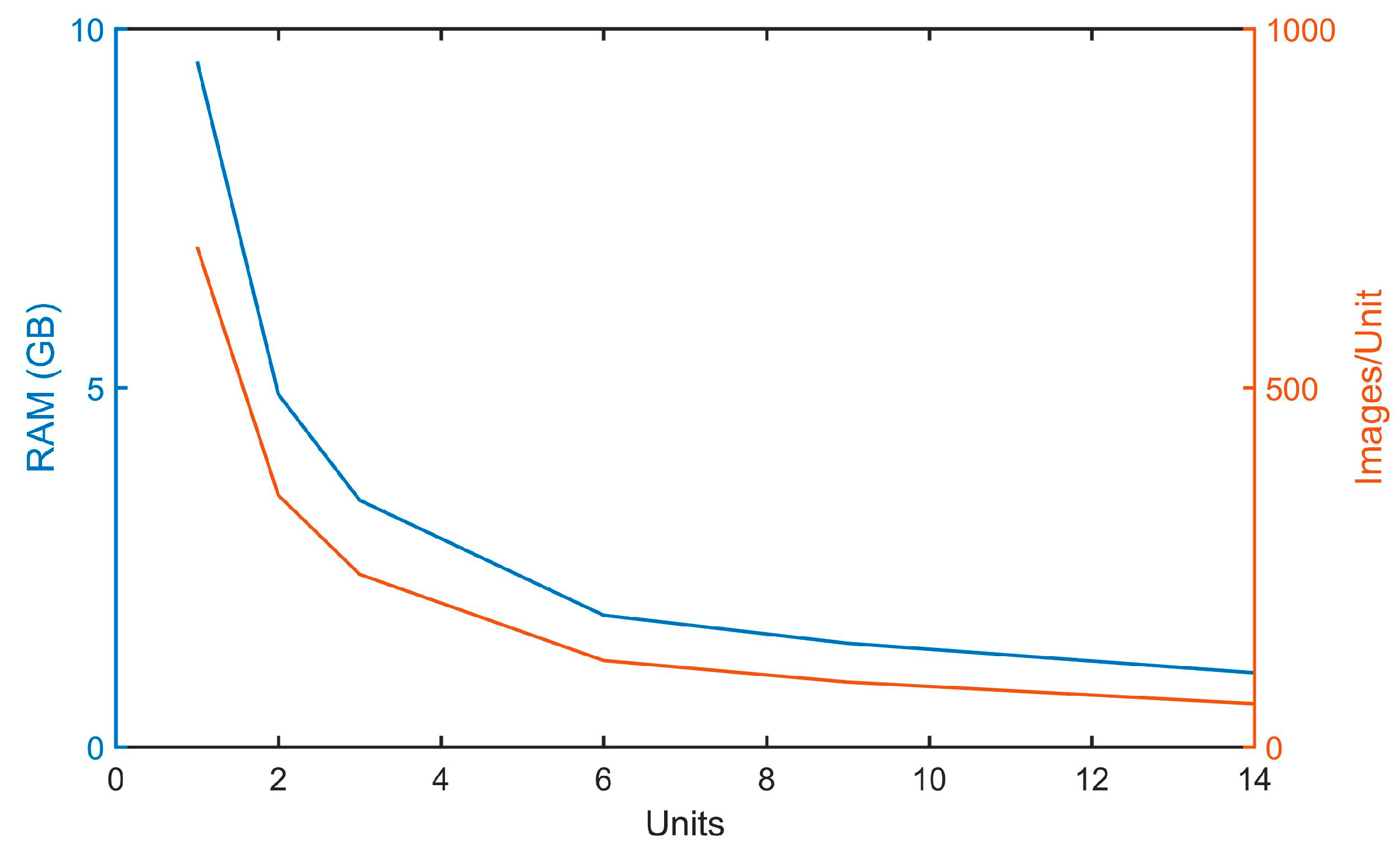
4.4. Computational RAM of RT-GBSAR
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Crosetto, M.; Monserrat, O.; Luzi, G.; Devanthéry, N.; Cuevas-González, M.; Barra, A. Data processing and analysis tools based on ground-based synthetic aperture radar imagery. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 593–596. [Google Scholar] [CrossRef]
- Monserrat, O.; Crosetto, M.; Luzi, G. A review of Ground-Based sar interferometry for deformation measurement. ISPRS J. Photogramm. Remote Sens. 2014, 93, 40–48. [Google Scholar] [CrossRef]
- Caduff, R.; Schlunegger, F.; Kos, A.; Wiesmann, A. A review of terrestrial radar interferometry for measuring surface change in the geosciences. Earth Surf. Process. Landf. 2015, 40, 208–228. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Mills, J. Modelling of instrument repositioning errors in discontinuous Multi-Campaign Ground-Based sar (mc-gbsar) deformation monitoring. ISPRS J. Photogramm. Remote Sens. 2019, 157, 26–40. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Luzi, G.; Cuevas-González, M.; Devanthéry, N. Discontinuous gbsar deformation monitoring. ISPRS J. Photogramm. Remote Sens. 2014, 93, 136–141. [Google Scholar] [CrossRef]
- Tarchi, D.; Antonello, G.; Casagli, N.; Farina, P.; Fortuny-Guasch, J.; Guerri, L.; Leva, D. On the use of ground-based sar interferometry for slope failure early warning: The cortenova rock slide (italy). In Landslides; Springer: Berlin/Heidelberg, Germany, 2005; pp. 337–342. [Google Scholar]
- Placidi, S.; Meta, A.; Testa, L.; Rödelsperger, S. Monitoring Structures with Fastgbsar. In Proceedings of the 2015 IEEE Radar Conference, Johannesburg, South Africa, 27–30 October 2015; IEEE: Arlington, VA, USA, 2015; pp. 435–439. [Google Scholar]
- Li, Z.; Fielding, E.J.; Cross, P. Integration of insar time-series analysis and water-vapor correction for mapping postseismic motion after the 2003 bam (Iran) earthquake. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3220–3230. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential sar interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Rödelsperger, S. Real-Time Processing of Ground Based Synthetic Aperture Radar (GB-SAR) Measurements. Ph.D. Thesis, Technische Universität Darmstadt, Fachbereich Bauingenieurwesen und Geodäsie, Darmstadt, Germany, 2011. [Google Scholar]
- Li, Y.; Jiao, Q.; Hu, X.; Li, Z.; Li, B.; Zhang, J.; Jiang, W.; Luo, Y.; Li, Q.; Ba, R. Detecting the slope movement after the 2018 baige landslides based on Ground-Based and Space-Borne radar observations. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101949. [Google Scholar] [CrossRef]
- Caduff, R.; Wiesmann, A.; Bühler, Y.; Pielmeier, C. Continuous monitoring of snowpack displacement at high spatial and temporal resolution with terrestrial radar interferometry. Geophys. Res. Lett. 2015, 42, 813–820. [Google Scholar] [CrossRef]
- Iglesias, R.; Aguasca, A.; Fabregas, X.; Mallorqui, J.J.; Monells, D.; López-Martínez, C.; Pipia, L. Ground-Based polarimetric sar interferometry for the monitoring of terrain displacement Phenomena–Part i: Theoretical description. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 980–993. [Google Scholar] [CrossRef]
- Roedelsperger, S.; Becker, M.; Gerstenecker, C.; Laeufer, G. Near Real-Time Monitoring of Displacements with the Ground Based Sar Ibis-L. In Proceedings of the International Workshop on ERS SAR Interferometry, Frascati, Italy, 30 November–4 December 2009. [Google Scholar]
- Wang, Z.; Li, Z.; Mills, J. A new approach to selecting coherent pixels for ground-based sar deformation monitoring. ISPRS J. Photogramm. Remote Sens. 2018, 144, 412–422. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Mills, J. A new nonlocal method for ground-based synthetic aperture radar deformation monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3769–3781. [Google Scholar] [CrossRef]
- Hooper, A. A Statistical-Cost Approach to Unwrapping the Phase of INSAR Time Series. In Proceedings of the International Workshop on ERS SAR Interferometry, Frascati, Italy, 30 November–4 December 2009. [Google Scholar]
- Iannini, L.; Guarnieri, A.M. Atmospheric phase screen in Ground-Based radar: Statistics and compensation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 537–541. [Google Scholar] [CrossRef]
- Pipia, L.; Fabregas, X.; Aguasca, A.; Lopez-Martinez, C. Atmospheric artifact compensation in Ground-Based dinsar applications. IEEE Geosci. Remote Sens. Lett. 2008, 5, 88–92. [Google Scholar] [CrossRef]
- Iglesias, R.; Fabregas, X.; Aguasca, A.; Mallorqui, J.J.; Lopez-Martinez, C.; Gili, J.; Corominas, J. Atmospheric phase screen compensation in Ground-Based sar with a Multiple-Regression model over mountainous regions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2436–2449. [Google Scholar] [CrossRef]
- Caduff, R.; Kos, A.; Schlunegger, F.; McArdell, B.W.; Wiesmann, A. Terrestrial radar interferometric measurement of hillslope deformation and atmospheric disturbances in the illgraben Debris-Flow catchment, switzerland. IEEE Geosci. Remote Sens. Lett. 2014, 11, 434–438. [Google Scholar] [CrossRef]
- Dong, Y.; Huang, D.; Du, J. Observations of coastal aeolian dune movements at feicuidao, on the changli gold coast in hebei province. Sci. Cold Arid Reg. 2013, 5, 0324–0330. [Google Scholar]
- NTSLF. The UK National Tidal Gauge Network. 2018. Available online: https://www.Ntslf.Org/data (accessed on 20 November 2018).
- Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-Interferogram method for measuring interseismic deformation: Denali fault, alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef]
- Usai, S. A least squares database approach for sar interferometric data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 753–760. [Google Scholar] [CrossRef]
- Samiei-Esfahany, S.; Martins, J.E.; van Leijen, F.; Hanssen, R.F. Phase estimation for distributed scatterers in insar stacks using integer least squares estimation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5671–5687. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric Data-Stacks: Squeesar. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
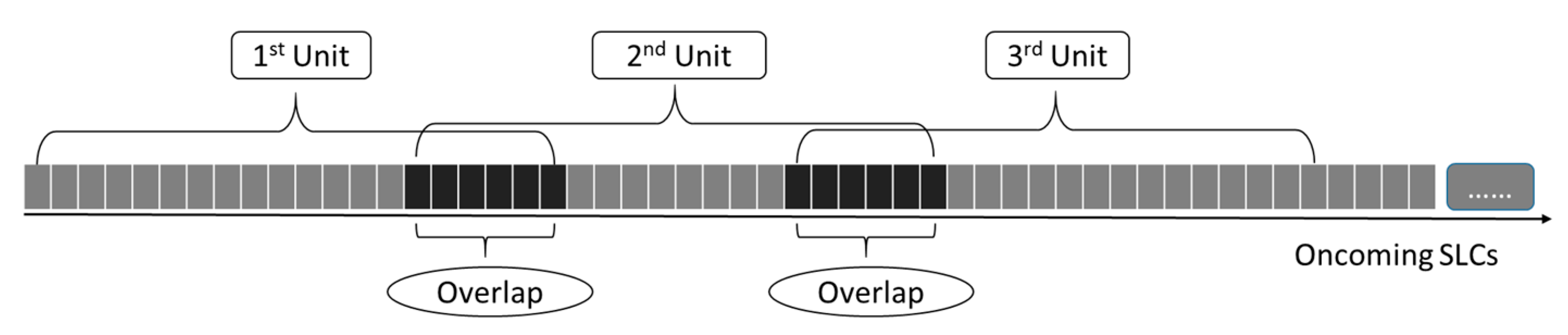
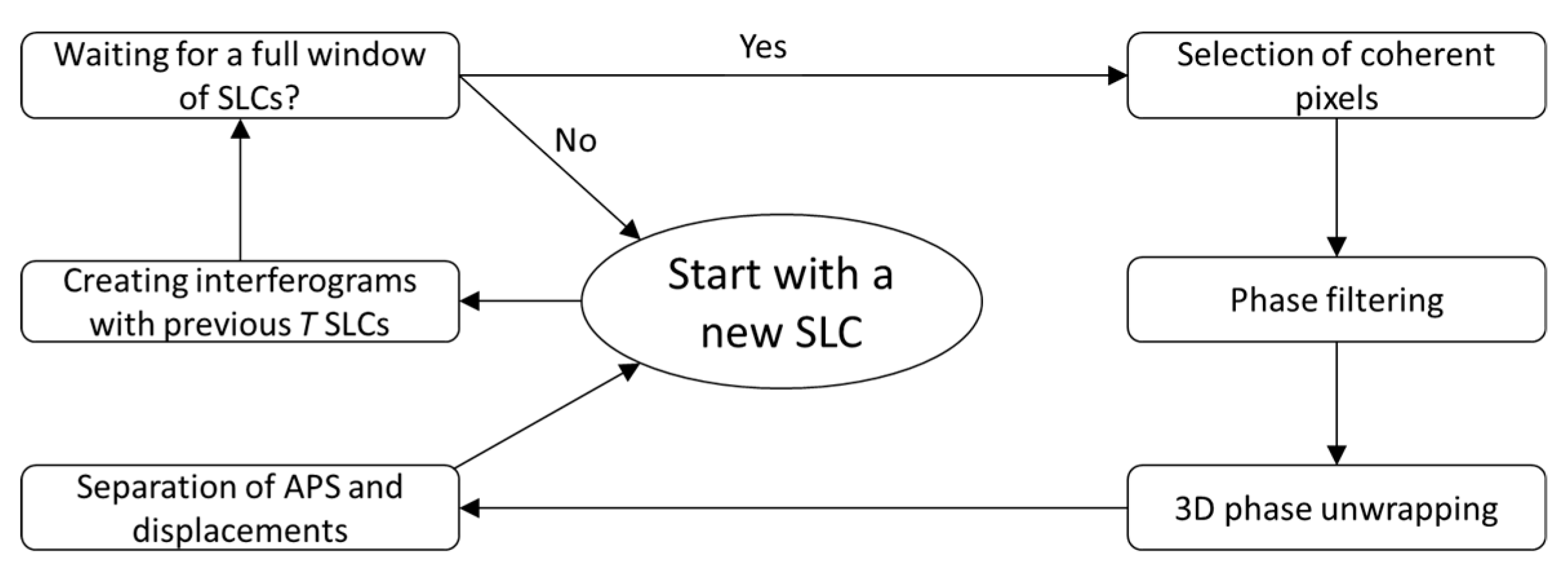
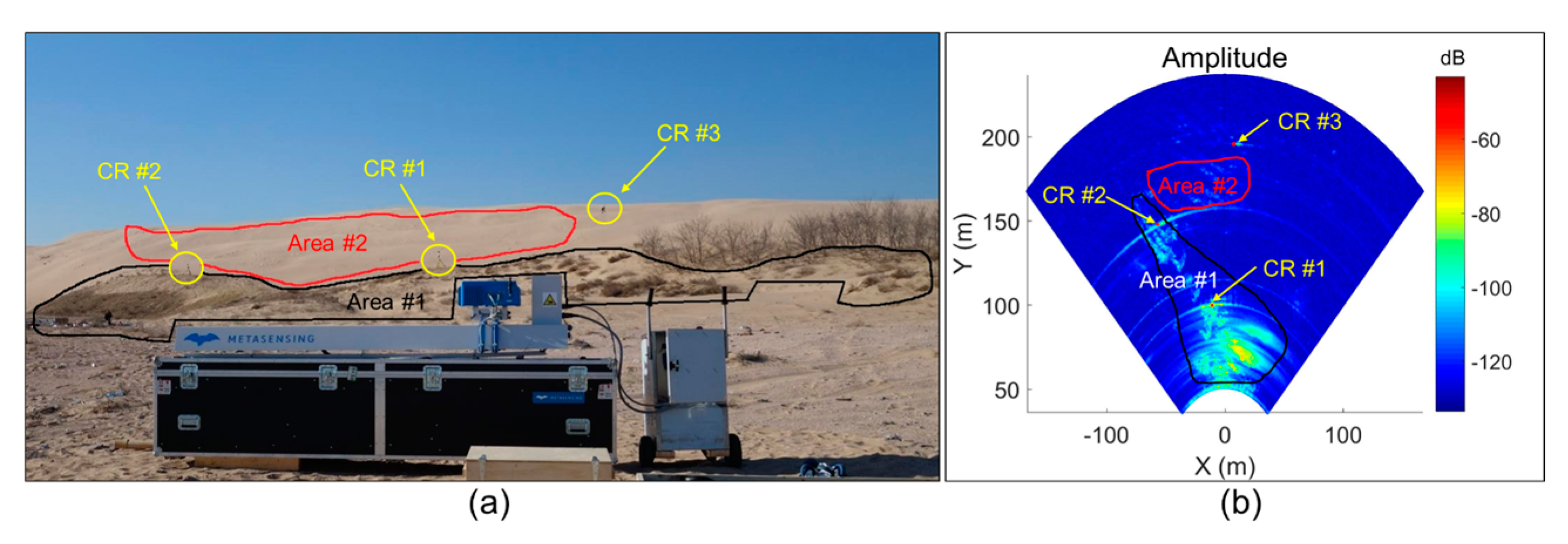

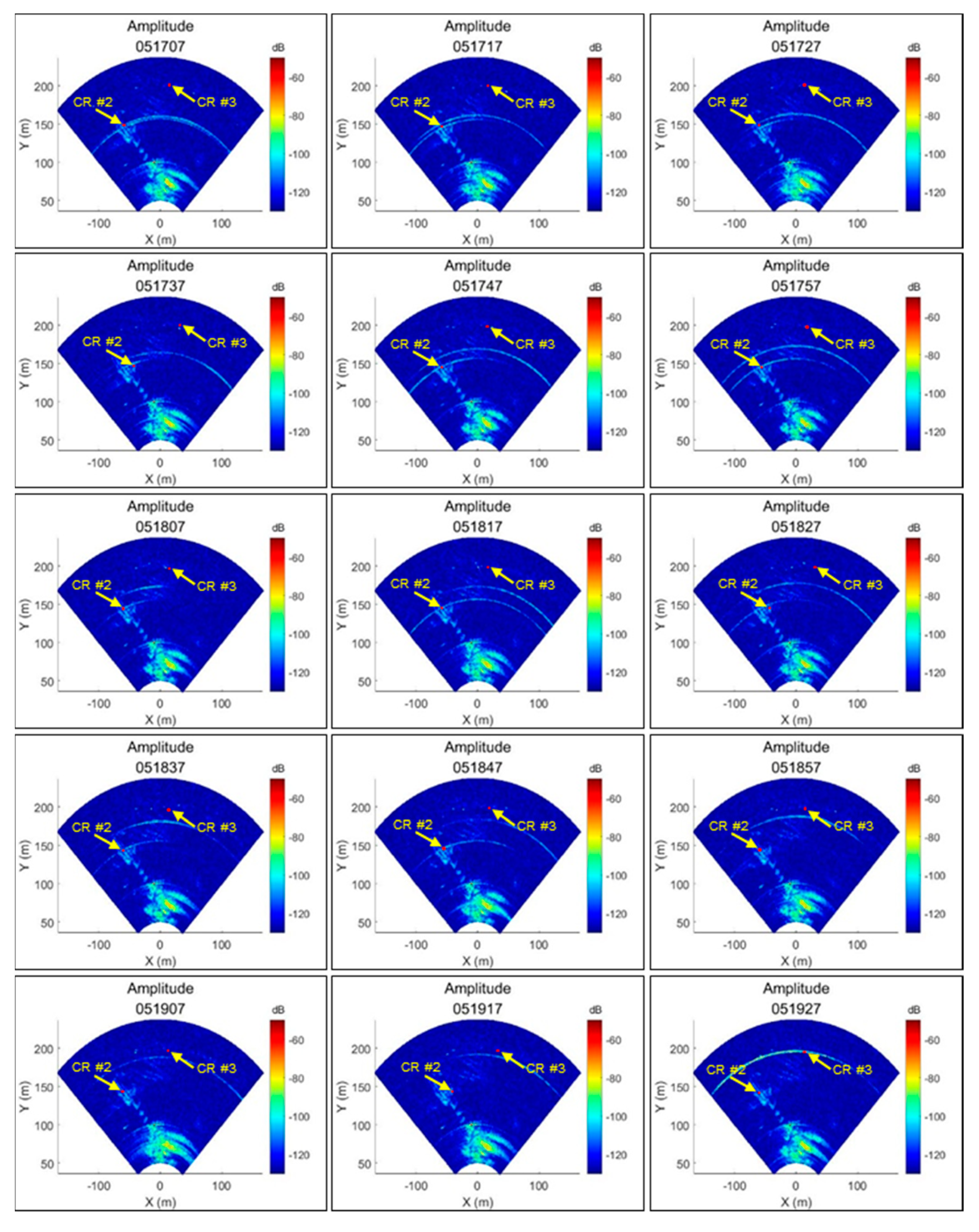

| Unit | Start | End | Coherent Pixels |
|---|---|---|---|
| 1 | 1 | 60 | 5085 |
| 2 | 51 | 110 | 3643 |
| 3 | 101 | 160 | 5222 |
| 4 | 151 | 210 | 5664 |
| 5 | 201 | 260 | 6128 |
| 6 | 251 | 310 | 6102 |
| 7 | 301 | 360 | 3298 |
| 8 | 351 | 410 | 4569 |
| 9 | 401 | 460 | 6887 |
| 10 | 451 | 478 | 6831 |
| Unit | Start | End | Coherent Pixels |
|---|---|---|---|
| 1 | 1 | 60 | 11,859 |
| 2 | 51 | 110 | 10,975 |
| 3 | 101 | 160 | 10,671 |
| 4 | 151 | 210 | 10,046 |
| 5 | 201 | 260 | 10,303 |
| 6 | 251 | 310 | 9273 |
| 7 | 301 | 360 | 9508 |
| 8 | 351 | 410 | 8887 |
| 9 | 401 | 460 | 8391 |
| 10 | 451 | 510 | 7503 |
| 11 | 501 | 560 | 6661 |
| 12 | 551 | 610 | 5691 |
| 13 | 601 | 660 | 4531 |
| 14 | 651 | 696 | 4331 |
| Unit | Coherent Pixels | Pixels without Unwrapping Errors (Percentage) | Pixels with Unwrapping Errors (Percentage) |
|---|---|---|---|
| 1 | 5085 | 5070 (99.71%) | 15 (0.29%) |
| 2 | 3643 | 3613 (99.18%) | 30 (0.82%) |
| 3 | 5222 | 5219 (99.94%) | 3 (0.06%) |
| 4 | 5664 | 5660 (99.93%) | 4 (0.07%) |
| 5 | 6128 | 6119 (99.85%) | 9 (0.15%) |
| 6 | 6102 | 6043 (99.03%) | 59 (0.97%) |
| 7 | 3298 | 3255 (98.70%) | 43 (1.30%) |
| 8 | 4569 | 4528 (99.10%) | 41 (0.90%) |
| 9 | 6887 | 6868 (99.72%) | 19 (0.28%) |
| 10 | 6831 | 6781 (99.27%) | 50 (0.73%) |
| 3–6 | 4030 | 4021 (99.78%) | 9 (0.22%) |
| 8–10 | 3712 | 3690 (99.41%) | 22 (0.59%) |
| Unit | Coherent Pixels | Pixels without Unwrapping Errors (Percentage) | Pixels with Unwrapping Errors (Percentage) |
|---|---|---|---|
| 1 | 11,859 | 11,857 (99.98%) | 2 (0.02%) |
| 2 | 10,975 | 10,973 (99.98%) | 2 (0.02%) |
| 3 | 10,671 | 10,668 (99.97%) | 3 (0.03%) |
| 4 | 10,046 | 10,032 (99.86%) | 14 (0.14%) |
| 5 | 10,303 | 10,297 (99.94%) | 6 (0.06%) |
| 6 | 9273 | 9272 (99.99%) | 1 (0.01%) |
| 7 | 9508 | 9506 (99.98%) | 2 (0.02%) |
| 8 | 8887 | 8868 (99.79%) | 19 (0.21%) |
| 9 | 8391 | 8388 (99.96%) | 3 (0.04%) |
| 10 | 7503 | 7502 (99.99%) | 1 (0.01%) |
| 11 | 6661 | 6659 (99.97%) | 2 (0.03%) |
| 12 | 5691 | 5691 (100.00%) | 0 (0.00%) |
| 13 | 4531 | 4531 (100.00%) | 0 (0.00%) |
| 14 | 4331 | 4331 (100.00%) | 0 (0.00%) |
| 1–14 | 3428 | 3421 (99.80%) | 7 (0.20%) |
| W | T (Δt) | Overlap: 2T (Δt) | Ifgs 1/Unit | Units | CPs 2 | L 3 | Errors 4 | RMS 5 (mm) | Total ifgs | TW (Δt) | TP (s) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1 | 2 | 4 | 33 | 1826 | 0 | NA | NA | 131 | 3 | 101 |
| 10 | 1 | 2 | 9 | 9 | 2122 | 0 | NA | NA | 111 | 8 | 56 |
| 15 | 1 | 2 | 14 | 8 | 2264 | 0 | NA | NA | 106 | 13 | 48 |
| 20 | 1 | 2 | 19 | 6 | 2319 | 0 | NA | NA | 104 | 18 | 41 |
| 5 | 2 | 4 | 7 | 94 | 2194 | 98 | 0 | 0.33 | 662 | 1 | 329 |
| 10 | 2 | 4 | 17 | 16 | 2997 | 98 | 0 | 0.38 | 272 | 6 | 77 |
| 15 | 2 | 4 | 27 | 9 | 3229 | 98 | 0 | 0.4 | 237 | 11 | 72 |
| 20 | 2 | 4 | 37 | 6 | 3410 | 98 | 0 | 0.44 | 222 | 16 | 62 |
| 5 | 3 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 10 | 3 | 6 | 24 | 23 | 3166 | 292 | 0 | 0.27 | 558 | 4 | 144 |
| 15 | 3 | 6 | 39 | 11 | 3673 | 292 | 1 | 0.3 | 414 | 9 | 110 |
| 20 | 3 | 6 | 54 | 7 | 3691 | 292 | 0 | 0.31 | 366 | 14 | 93 |
| 5 | 4 | NA | NA | NA | NA | NA | NA | NA | NA | NA | 386 |
| 10 | 4 | 8 | 30 | 44 | 3175 | 580 | 0 | 0.19 | 1336 | 2 | 163 |
| 15 | 4 | 8 | 50 | 13 | 3670 | 580 | 7 | 0.23 | 654 | 7 | 151 |
| 20 | 4 | 8 | 70 | 8 | 3972 | 580 | 6 | 0.26 | 544 | 12 | 101 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Li, Z.; Liu, Y.; Peng, J.; Long, S.; Mills, J. A New Processing Chain for Real-Time Ground-Based SAR (RT-GBSAR) Deformation Monitoring. Remote Sens. 2019, 11, 2437. https://doi.org/10.3390/rs11202437
Wang Z, Li Z, Liu Y, Peng J, Long S, Mills J. A New Processing Chain for Real-Time Ground-Based SAR (RT-GBSAR) Deformation Monitoring. Remote Sensing. 2019; 11(20):2437. https://doi.org/10.3390/rs11202437
Chicago/Turabian StyleWang, Zheng, Zhenhong Li, Yanxiong Liu, Junhuan Peng, Sichun Long, and Jon Mills. 2019. "A New Processing Chain for Real-Time Ground-Based SAR (RT-GBSAR) Deformation Monitoring" Remote Sensing 11, no. 20: 2437. https://doi.org/10.3390/rs11202437
APA StyleWang, Z., Li, Z., Liu, Y., Peng, J., Long, S., & Mills, J. (2019). A New Processing Chain for Real-Time Ground-Based SAR (RT-GBSAR) Deformation Monitoring. Remote Sensing, 11(20), 2437. https://doi.org/10.3390/rs11202437






