A Synergistic Use of a High-Resolution Numerical Weather Prediction Model and High-Resolution Earth Observation Products to Improve Precipitation Forecast
Abstract
1. Introduction
2. Material and Methods
2.1. Case Studies Description
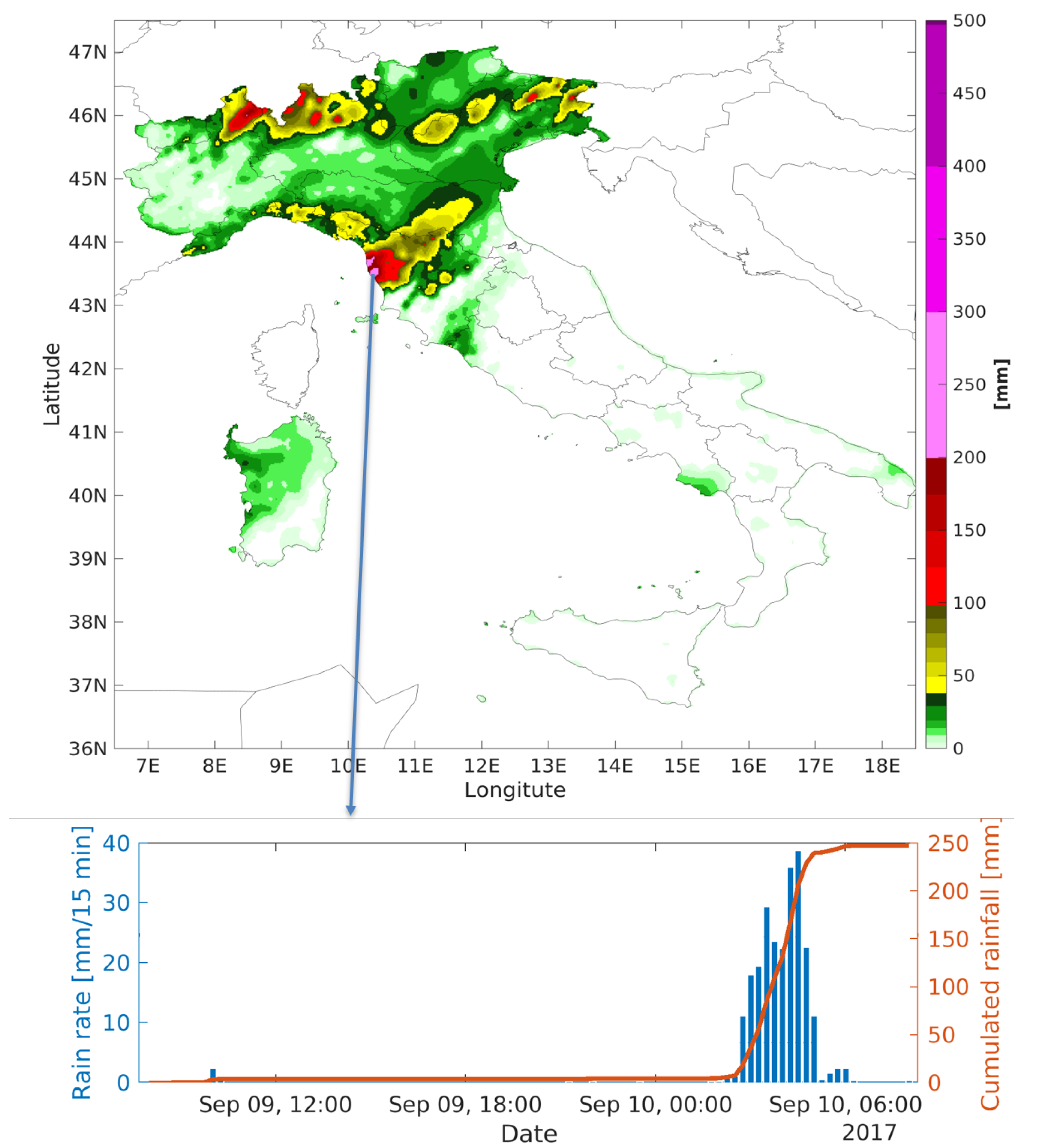
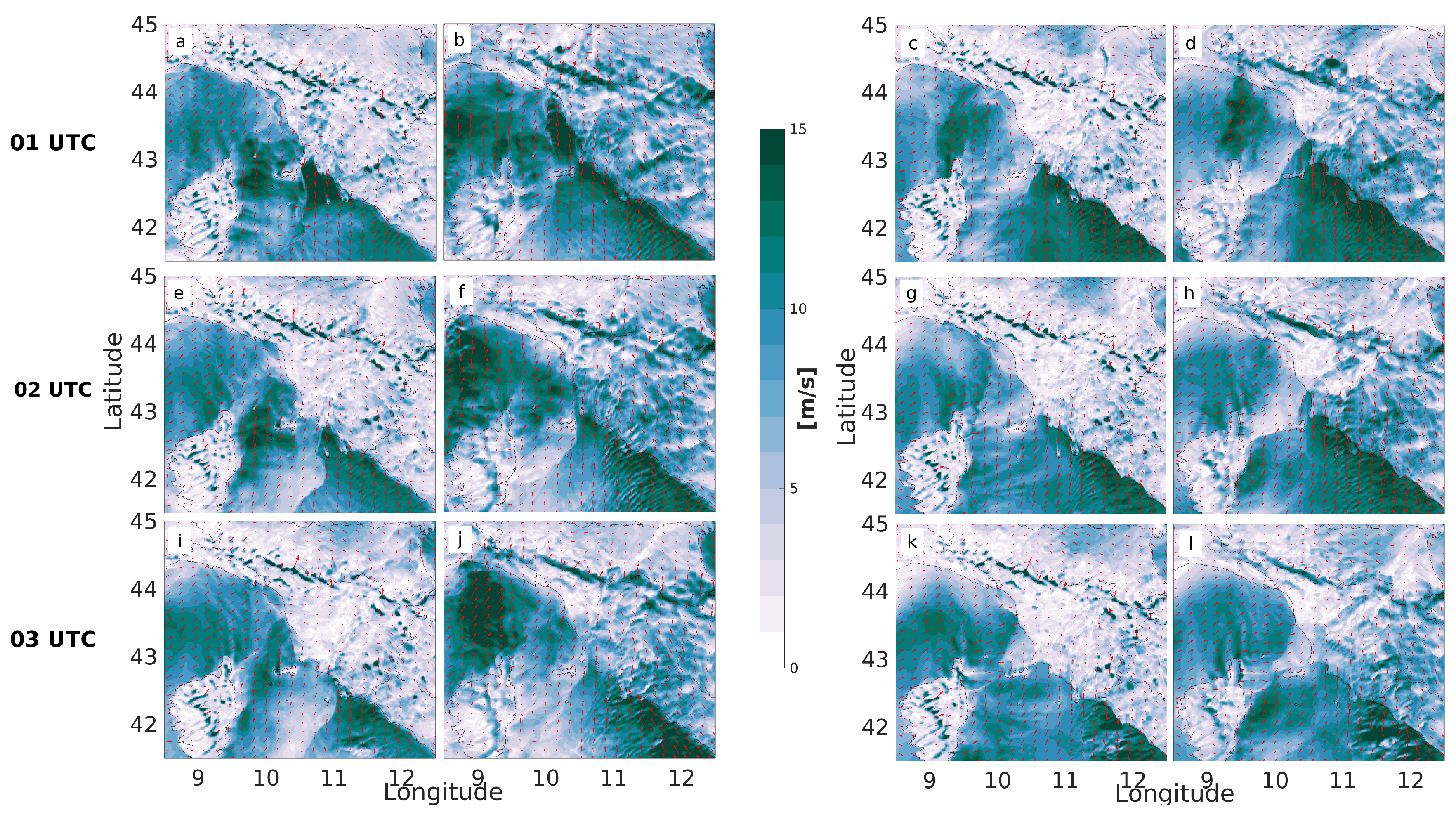
2.1.1. The Livorno Event
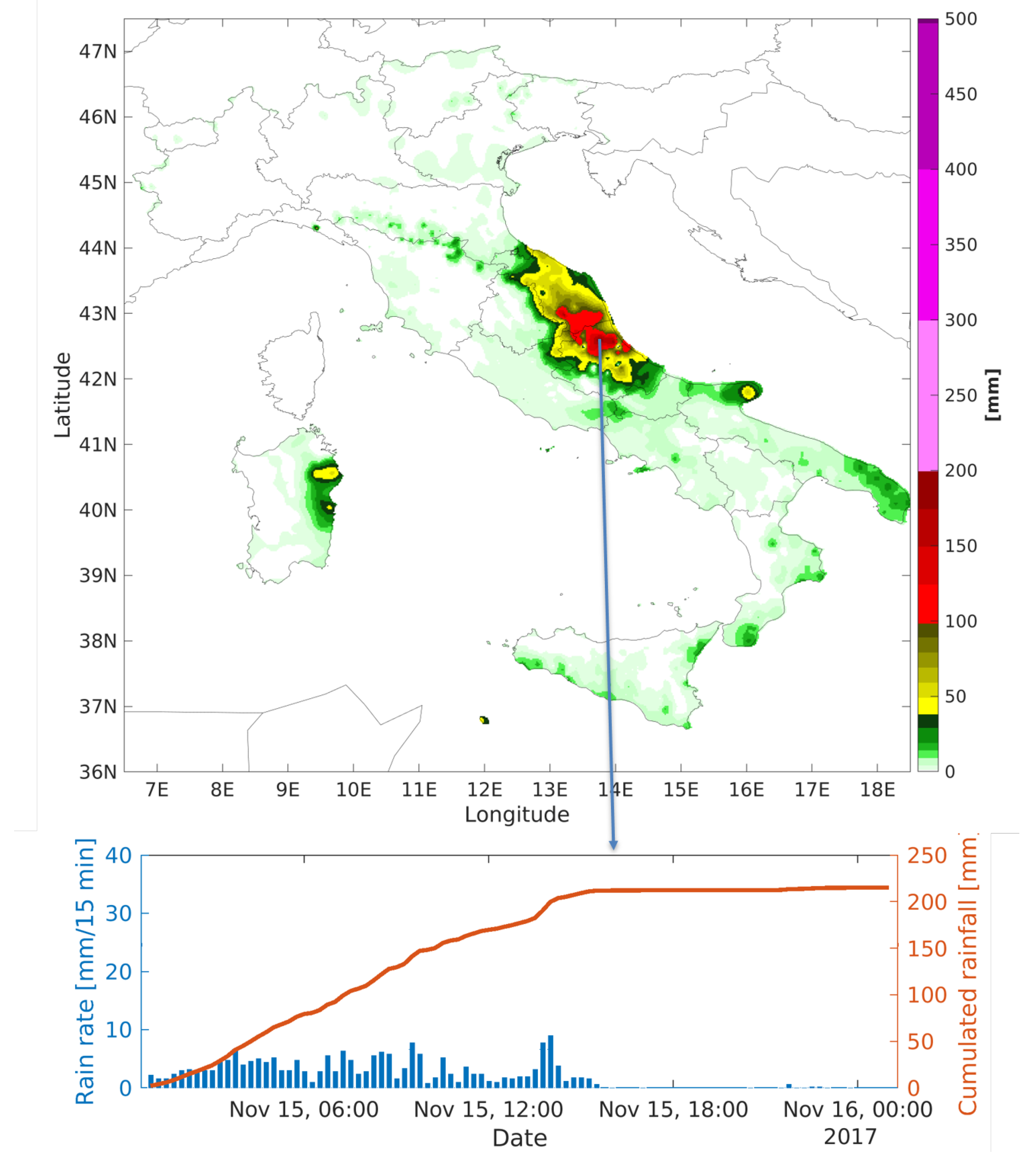
2.1.2. The Silvi Marina Event
2.2. WRF Model Setup
2.3. Data Assimilation Techniques
3. Observational Data Description, Assimilation and Experimental Design
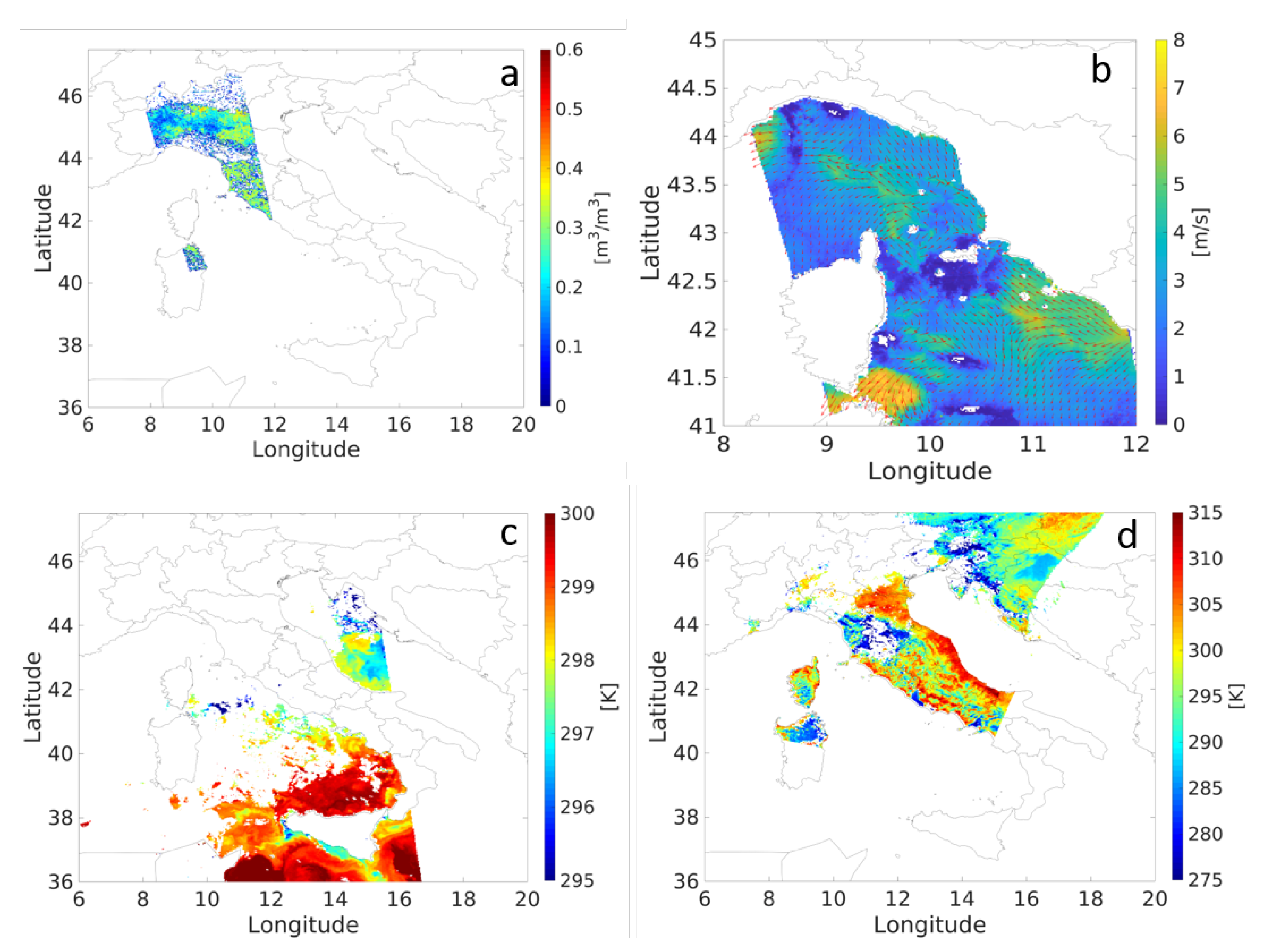
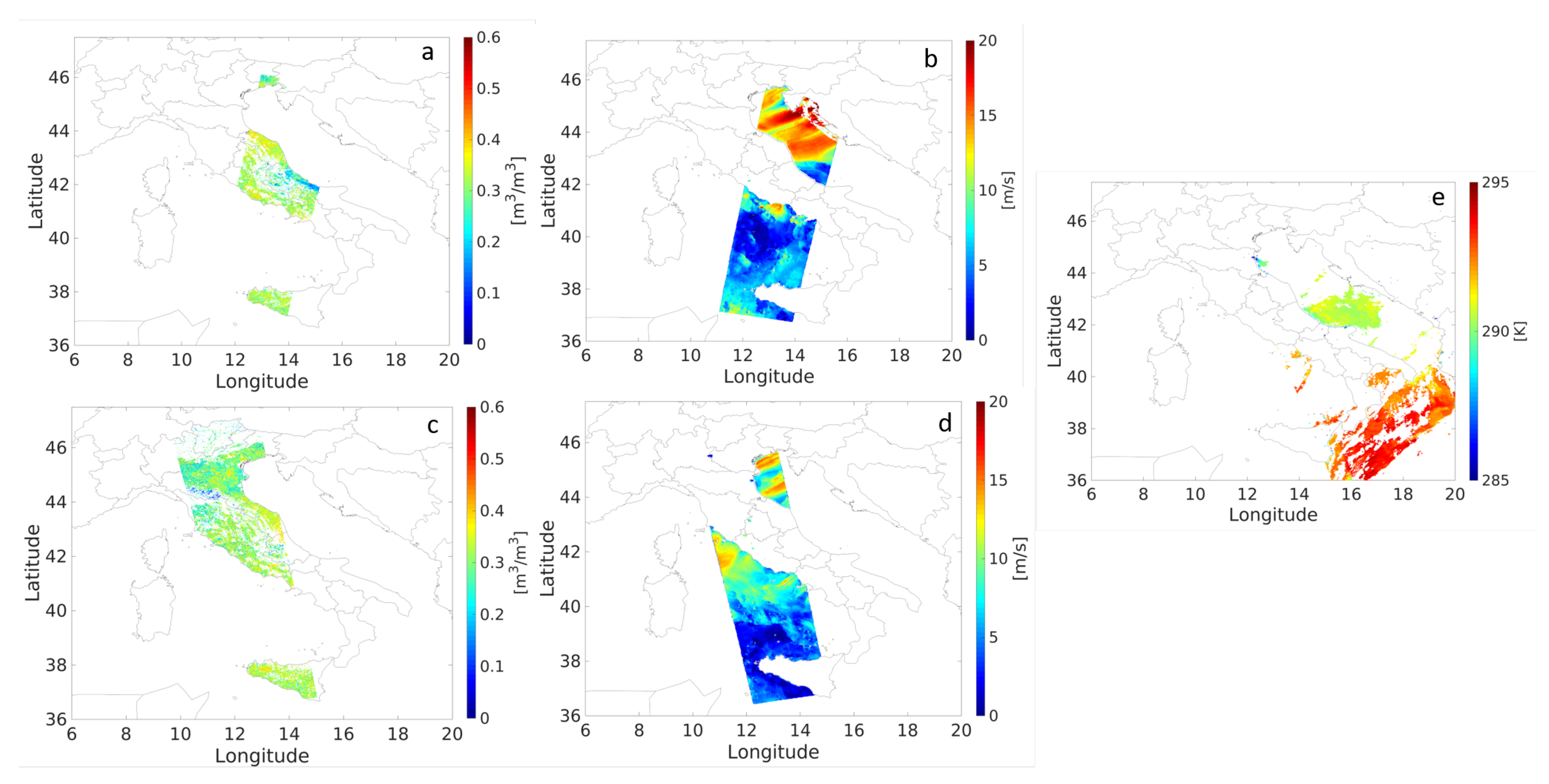
3.1. The EO Variables of Interest
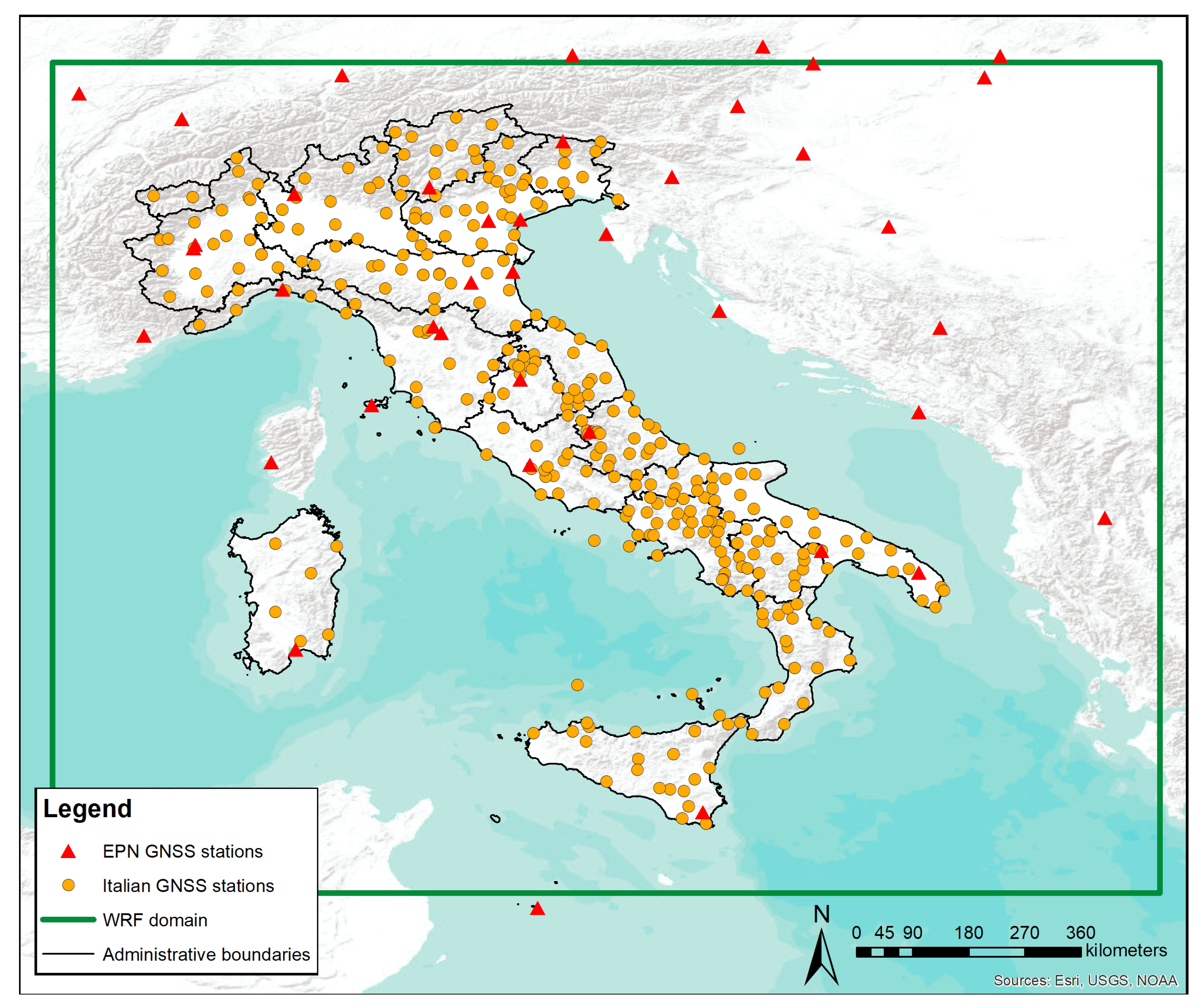
3.2. GNSS Observations for the Livorno and Silvi Marina Test Cases
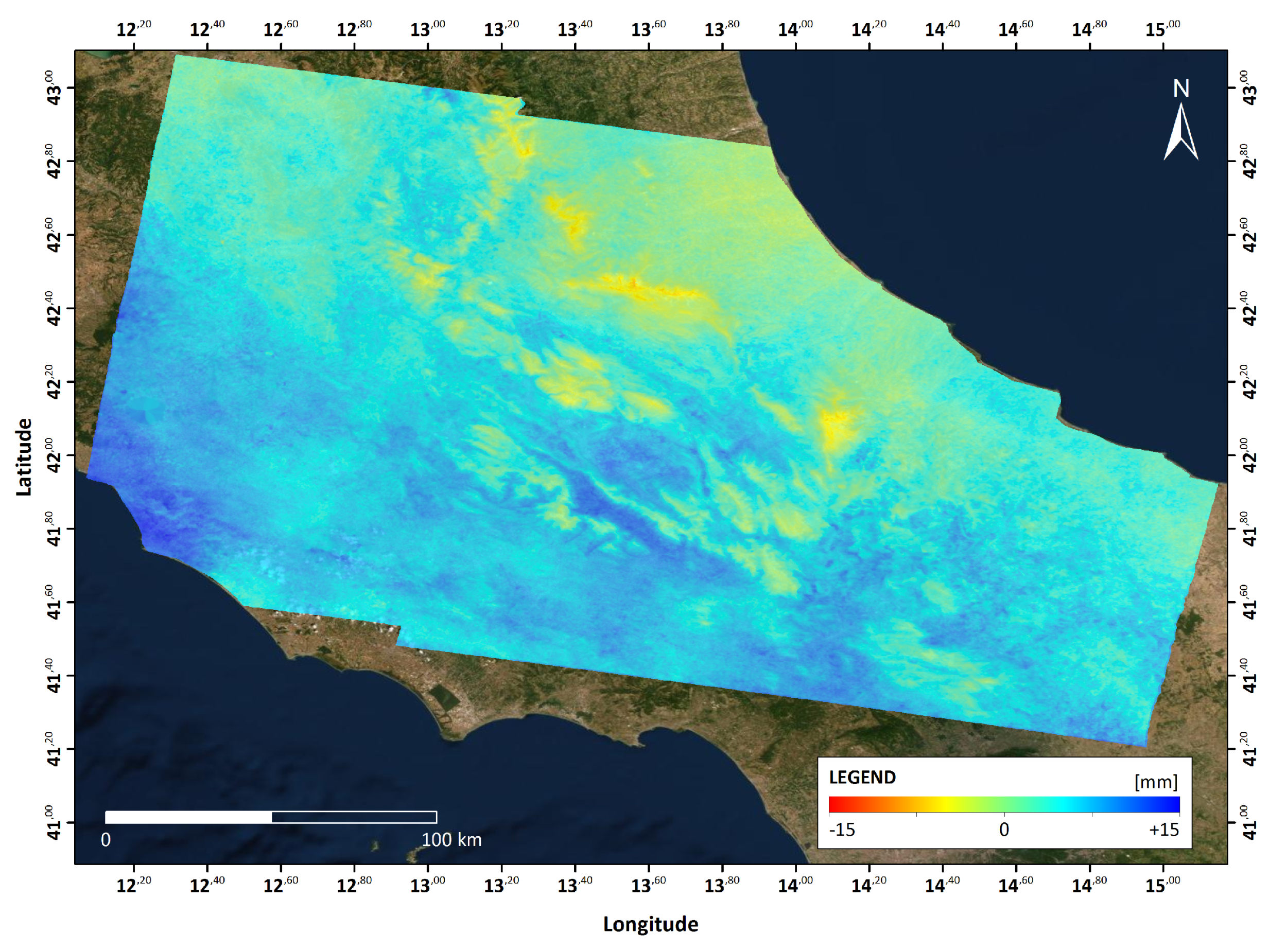
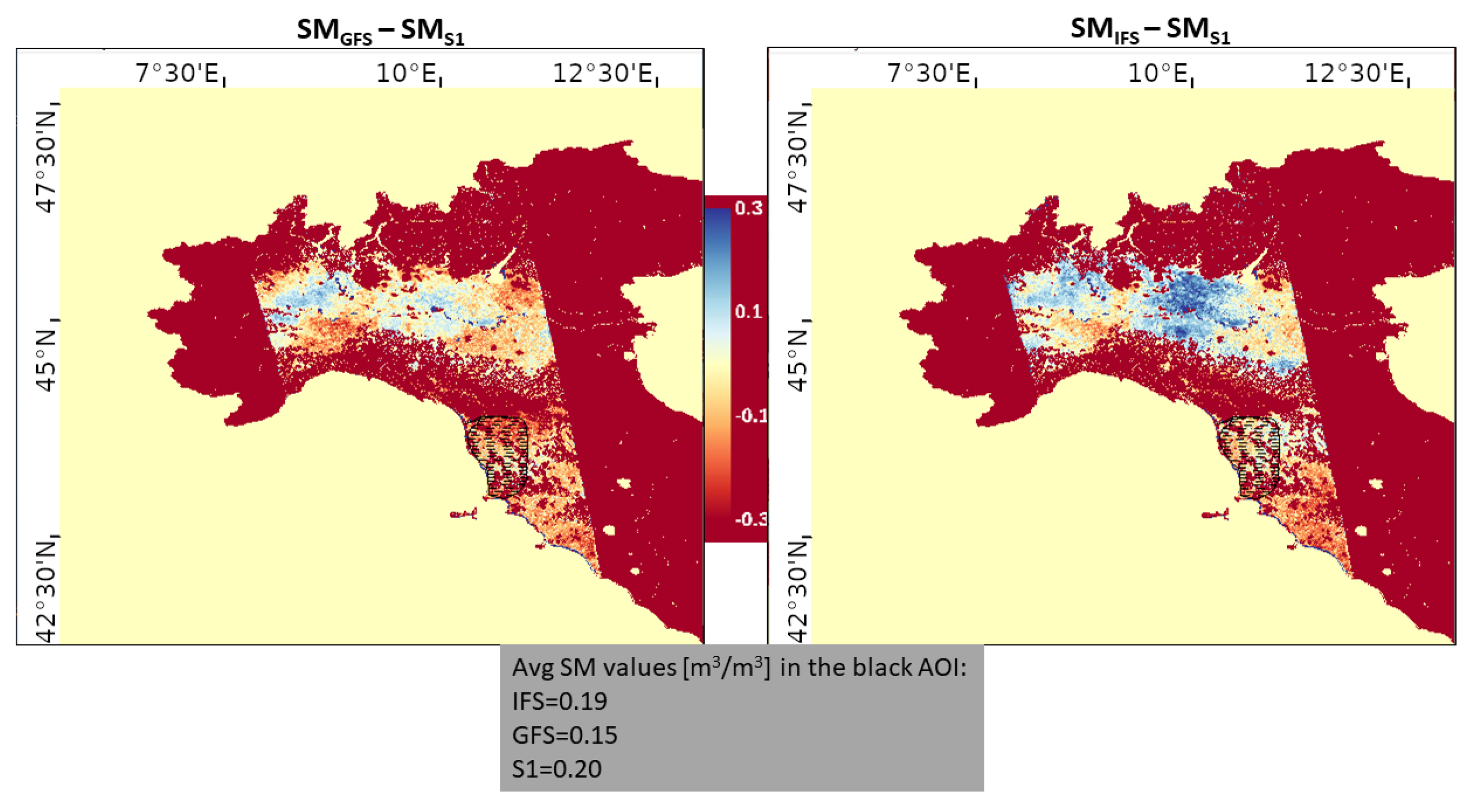
3.3. Sentinel Observations for the Livorno Test Case
3.4. Sentinel Observations for the Silvi Marina Test Case
3.5. Experimental Design
4. Validation and Results
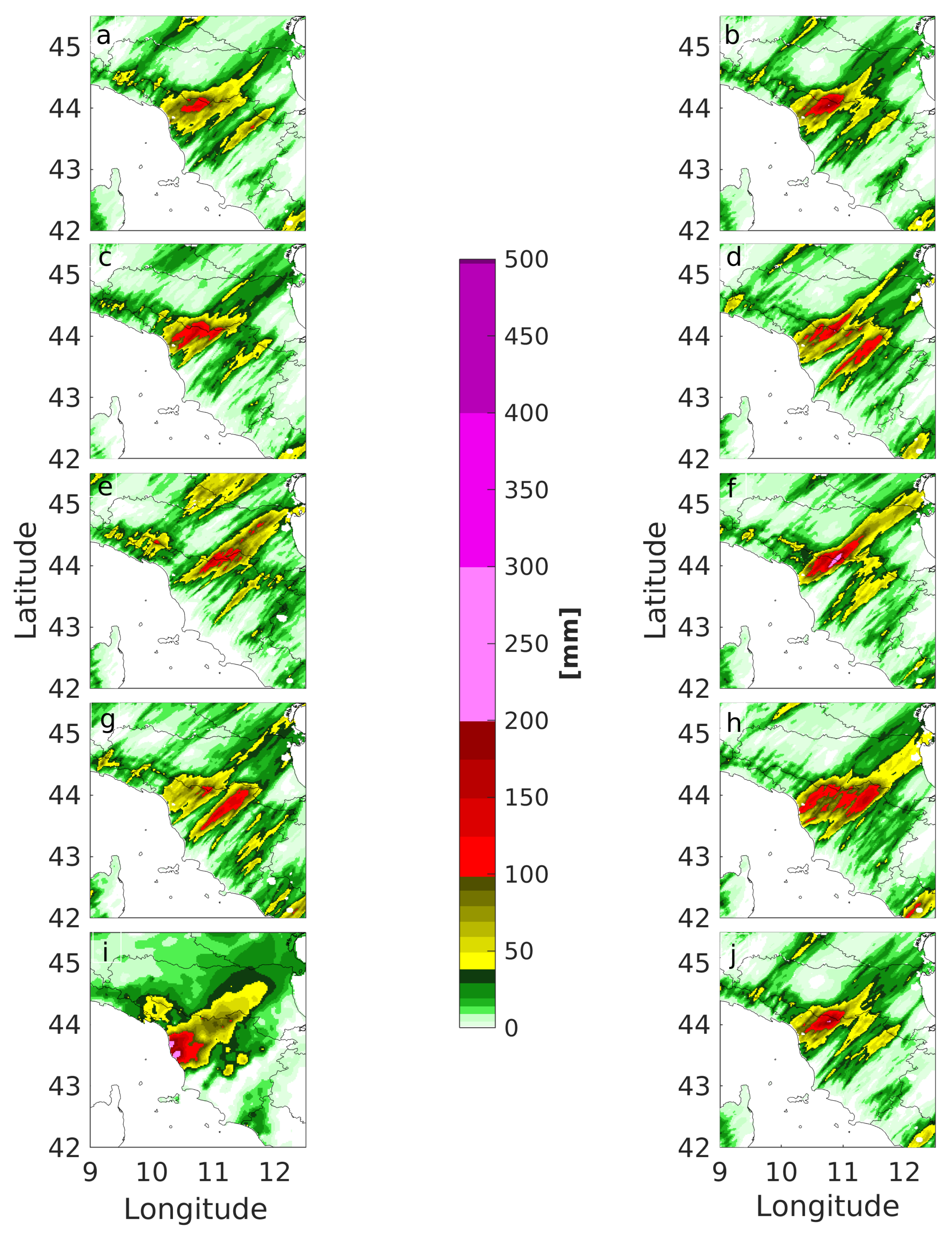
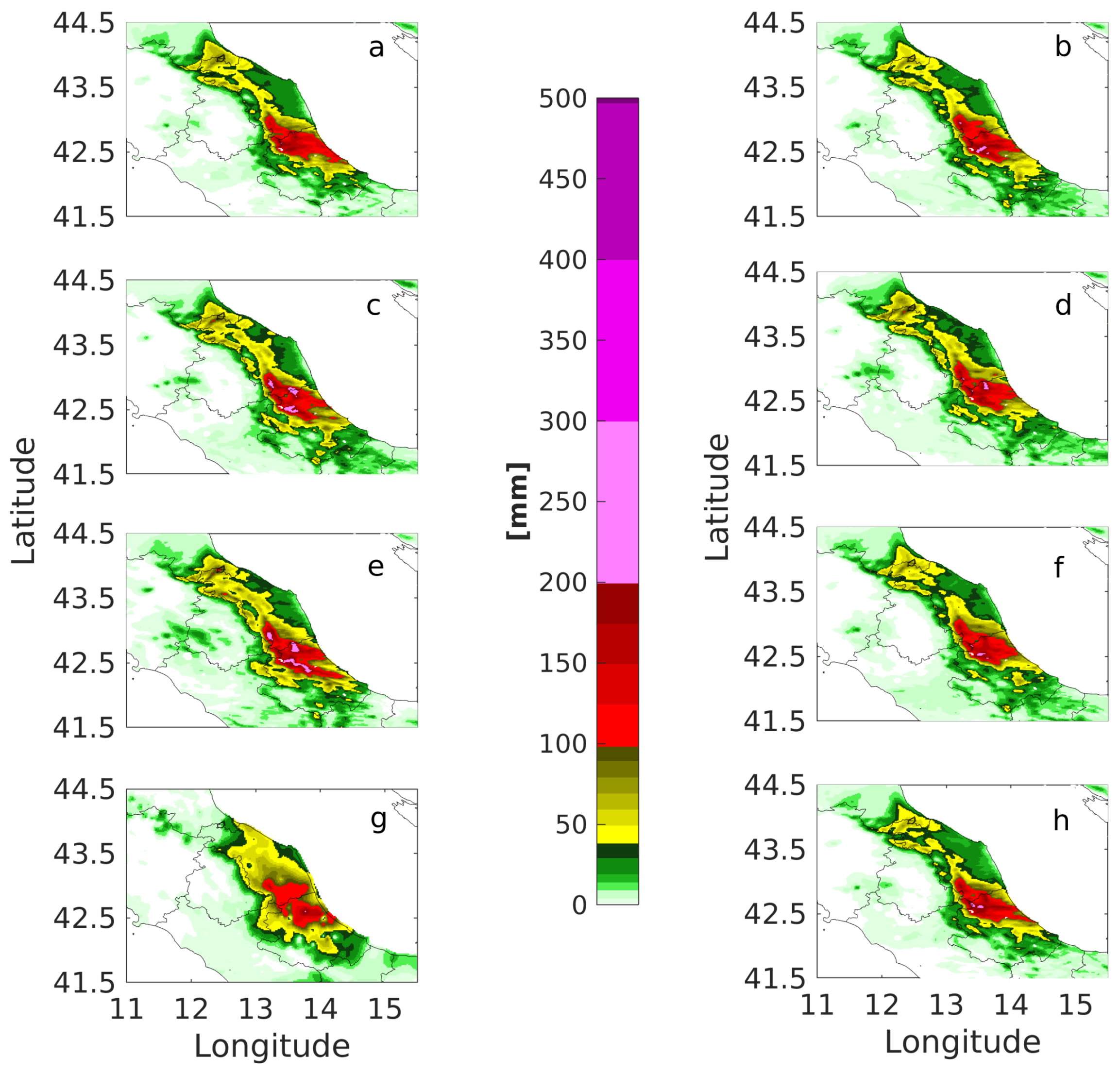
4.1. Livorno Test Case
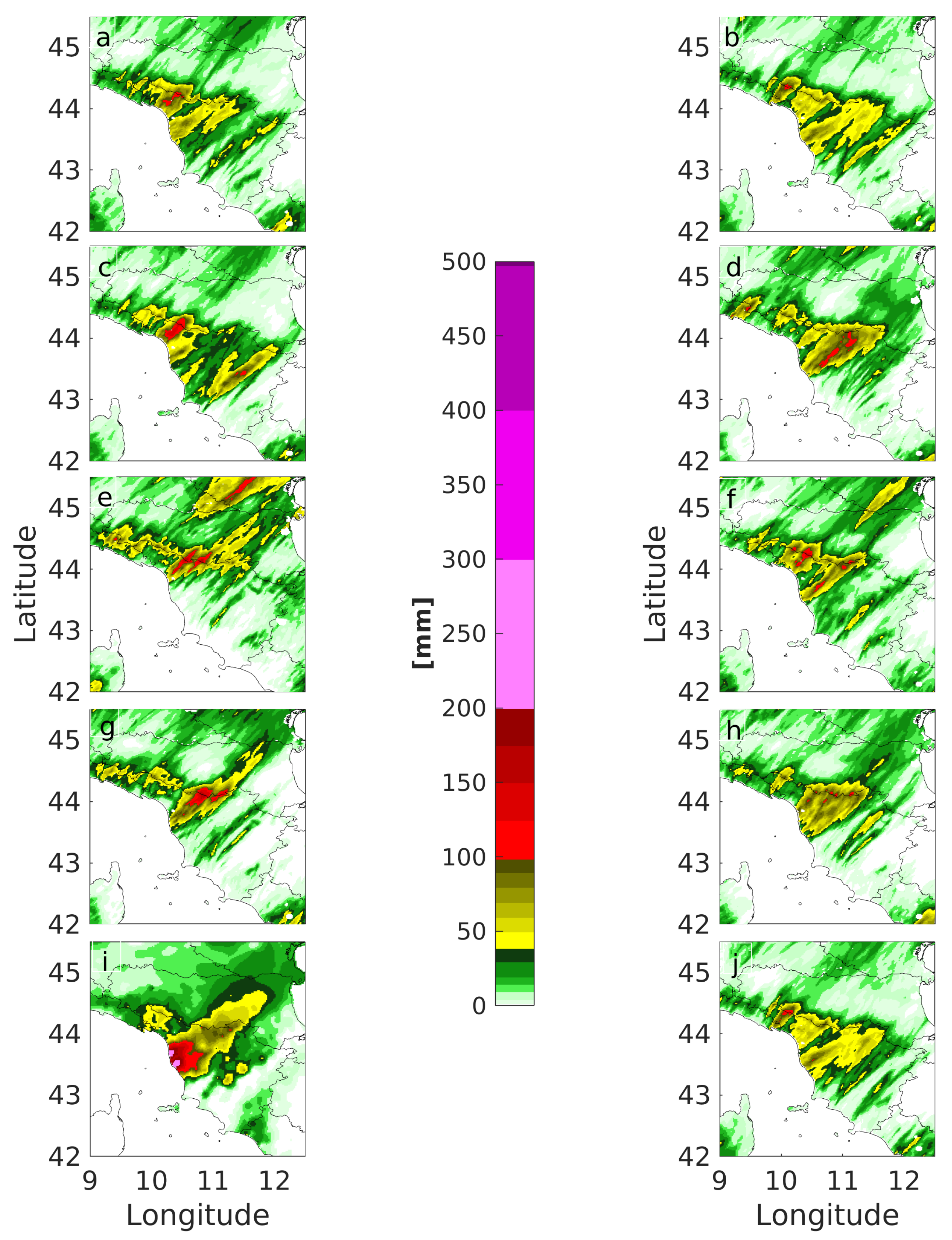
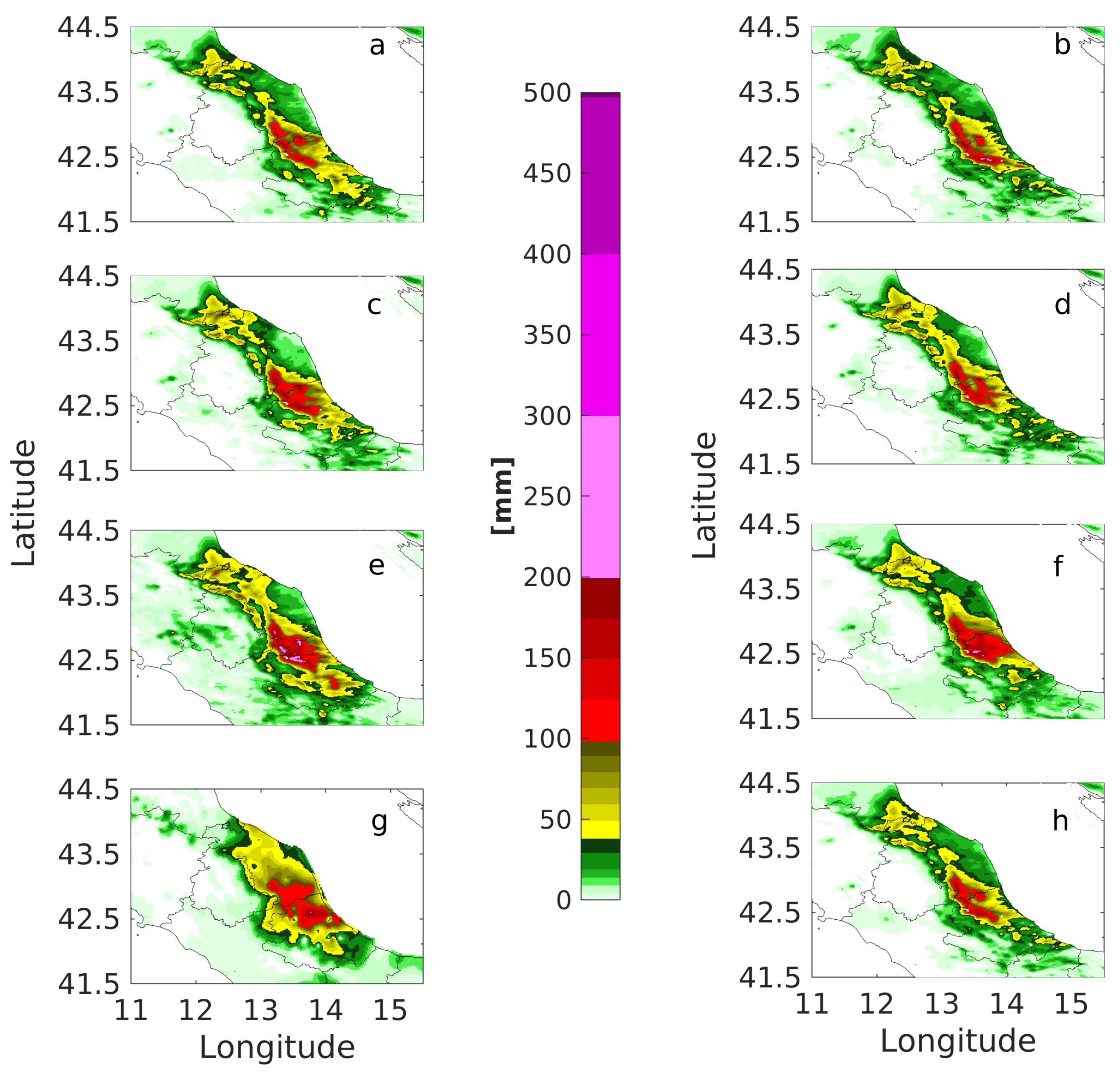
4.2. Silvi Marina Test Case
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Variable Retrieval
Appendix A.1. Soil Moisture Retrieval
Appendix A.1.1. Zenith Total Delay Retrieval from GNSS
Appendix A.1.2. Zenith Total Delay Retrieval from InSAR
| SAR APS Feature | SENTINEL-1 |
|---|---|
| Spatial Resolution | 100 × 100 [m] |
| Temporal Resolution | 6 days |
| Timeliness | 24 h from image delivery |
| Coverage | 250 × 210 [km] |
| Thematic Accuracy | Millimetric precision on LOS delay |
| Availability | TRE ALTAMIRA Data Center |
| Notes | None |
Appendix A.2. ZTD Maps Derivation
Appendix B. MODE Indices
| 24 mm (GFS) Livorno Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 5.34 | 4.15 | 0.73 | 3027.00 | 3395.00 | 6422.00 | 0.95 | 0.86 | 0.59 | 0.31 | 0.47 | 0.48 | 0.50 |
| LST | 5.88 | 23.10 | 0.70 | 3440.00 | 3202.00 | 6642.00 | 0.93 | 0.82 | 0.54 | 0.34 | 0.43 | 0.43 | 0.46 |
| SM | 4.73 | 12.86 | 0.72 | 3536.00 | 3209.00 | 6745.00 | 0.93 | 0.77 | 0.55 | 0.29 | 0.45 | 0.46 | 0.49 |
| SST | 4.97 | 5.64 | 0.73 | 2959.00 | 3450.00 | 6409.00 | 0.92 | 0.88 | 0.60 | 0.32 | 0.47 | 0.48 | 0.50 |
| WIND | 7.63 | 7.50 | 0.79 | 3902.00 | 3228.00 | 7130.00 | 0.88 | 0.92 | 0.55 | 0.40 | 0.41 | 0.40 | 0.41 |
| WIND+SM+ZTD_GNSS3h_1ist | 9.44 | 8.17 | 0.83 | 3683.00 | 3470.00 | 7153.00 | 0.98 | 0.93 | 0.59 | 0.37 | 0.44 | 0.45 | 0.46 |
| WIND+SM+ZTD_GNSS3h_1ist_18UTC | 14.09 | 12.80 | 0.78 | 3411.00 | 3429.00 | 6840.00 | 0.82 | 0.91 | 0.58 | 0.36 | 0.44 | 0.45 | 0.46 |
| ZTD_GNSS3h | 6.58 | 22.54 | 0.76 | 4019.00 | 3067.00 | 7086.00 | 0.95 | 1.07 | 0.52 | 0.51 | 0.34 | 0.30 | 0.29 |
| ZTD_GNSS3h_1ist | 7.70 | 2.89 | 0.80 | 3741.00 | 3329.00 | 7070.00 | 0.92 | 0.88 | 0.57 | 0.36 | 0.43 | 0.44 | 0.45 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 24 mm (IFS) Livorno Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 18.77 | 65.31 | 0.76 | 3323.00 | 3418.00 | 6741.00 | 0.96 | 0.77 | 0.59 | 0.24 | 0.50 | 0.51 | 0.55 |
| LST | 15.33 | 40.81 | 0.70 | 3484.00 | 3192.00 | 6676.00 | 0.96 | 0.80 | 0.54 | 0.32 | 0.43 | 0.44 | 0.47 |
| SM | 16.99 | 50.12 | 0.77 | 3474.00 | 3295.00 | 6769.00 | 0.97 | 0.82 | 0.57 | 0.31 | 0.46 | 0.47 | 0.50 |
| SST | 15.88 | 47.68 | 0.76 | 3152.00 | 3434.00 | 6586.00 | 0.94 | 0.80 | 0.59 | 0.26 | 0.49 | 0.51 | 0.54 |
| WIND | 11.28 | 40.31 | 0.56 | 3105.00 | 2875.00 | 5980.00 | 0.82 | 0.69 | 0.50 | 0.27 | 0.43 | 0.43 | 0.47 |
| WIND+SM+ZTD_GNSS3h_1ist | 16.52 | 10.32 | 0.66 | 3985.00 | 2875.00 | 6860.00 | 0.98 | 0.78 | 0.49 | 0.37 | 0.38 | 0.37 | 0.40 |
| WIND+SM+ZTD_GNSS3h_1ist_18UTC | 11.52 | 24.46 | 0.62 | 3234.00 | 3138.00 | 6372.00 | 0.91 | 0.66 | 0.53 | 0.19 | 0.48 | 0.48 | 0.54 |
| ZTD_GNSS3h | 24.91 | 2.59 | 0.95 | 5522.00 | 3271.00 | 8793.00 | 0.93 | 1.09 | 0.56 | 0.49 | 0.36 | 0.34 | 0.33 |
| ZTD_GNSS3h_1ist | 10.65 | 14.09 | 0.73 | 4058.00 | 2961.00 | 7019.00 | 0.98 | 0.75 | 0.50 | 0.32 | 0.41 | 0.40 | 0.44 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 48 mm (GFS) Livorno Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 6.93 | 12.37 | 0.58 | 1653.00 | 760.00 | 2413.00 | 0.97 | 0.68 | 0.37 | 0.46 | 0.28 | 0.33 | 0.39 |
| LST | 7.07 | 21.42 | 0.67 | 1225.00 | 987.00 | 2212.00 | 0.90 | 0.81 | 0.48 | 0.40 | 0.36 | 0.45 | 0.49 |
| SM | 9.95 | 21.70 | 0.61 | 1456.00 | 817.00 | 2273.00 | 0.96 | 0.62 | 0.41 | 0.35 | 0.33 | 0.38 | 0.46 |
| SST | 8.09 | 23.04 | 0.63 | 1623.00 | 750.00 | 2373.00 | 0.92 | 0.65 | 0.36 | 0.44 | 0.28 | 0.33 | 0.39 |
| WIND | 3.80 | 28.05 | 0.98 | 1833.00 | 1022.00 | 2855.00 | 0.99 | 1.08 | 0.50 | 0.54 | 0.31 | 0.43 | 0.42 |
| WIND+SM+ZTD_GNSS3h_1ist | 6.68 | 25.38 | 0.98 | 1325.00 | 1276.00 | 2601.00 | 0.98 | 1.06 | 0.62 | 0.41 | 0.43 | 0.57 | 0.56 |
| WIND+SM+ZTD_GNSS3h_1ist_18UTC | 5.78 | 13.95 | 0.89 | 1256.00 | 1410.00 | 2666.00 | 0.87 | 1.22 | 0.69 | 0.44 | 0.45 | 0.63 | 0.57 |
| ZTD_GNSS3h | 30.67 | 2.35 | 0.69 | 1629.00 | 809.00 | 2438.00 | 0.99 | 1.18 | 0.43 | 0.64 | 0.24 | 0.34 | 0.32 |
| ZTD_GNSS3h_1ist | 29.33 | 2.38 | 0.80 | 2042.00 | 700.00 | 2742.00 | 0.95 | 0.91 | 0.35 | 0.62 | 0.22 | 0.28 | 0.30 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 48 mm (IFS) Livorno Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 13.39 | 80.17 | 0.44 | 1731.00 | 537.00 | 2268.00 | 0.74 | 0.67 | 0.29 | 0.57 | 0.21 | 0.25 | 0.29 |
| LST | 7.06 | 13.13 | 0.30 | 1354.00 | 570.00 | 1924.00 | 0.75 | 0.59 | 0.32 | 0.46 | 0.25 | 0.29 | 0.35 |
| SM | 23.40 | 41.72 | 0.31 | 2147.00 | 186.00 | 2333.00 | 0.98 | 0.62 | 0.14 | 0.78 | 0.09 | 0.08 | 0.10 |
| SST | 8.41 | 48.21 | 0.53 | 1873.00 | 533.00 | 2406.00 | 0.73 | 0.67 | 0.30 | 0.56 | 0.21 | 0.25 | 0.30 |
| WIND | 1.19 | 18.00 | 0.76 | 1171.00 | 1105.00 | 2276.00 | 0.92 | 0.88 | 0.56 | 0.36 | 0.43 | 0.53 | 0.56 |
| WIND+SM+ZTD_GNSS3h_1ist | 6.78 | 8.92 | 0.47 | 1226.00 | 795.00 | 2021.00 | 0.98 | 0.56 | 0.41 | 0.27 | 0.36 | 0.39 | 0.49 |
| WIND+SM+ZTD_GNSS3h_1ist_18UTC | 6.99 | 16.59 | 0.72 | 1040.00 | 1130.00 | 2170.00 | 0.92 | 0.81 | 0.56 | 0.31 | 0.45 | 0.53 | 0.58 |
| ZTD_GNSS3h | 12.97 | 19.91 | 0.49 | 1757.00 | 550.00 | 2307.00 | 0.83 | 1.13 | 0.30 | 0.74 | 0.16 | 0.20 | 0.19 |
| ZTD_GNSS3h_1ist | 13.91 | 41.69 | 0.58 | 1812.00 | 685.00 | 2497.00 | 0.93 | 0.75 | 0.33 | 0.56 | 0.24 | 0.29 | 0.32 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 72 mm (GFS) Livorno Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 12.32 | 9.93 | 0.54 | 1201.00 | 227.00 | 1428.00 | 0.97 | 0.55 | 0.21 | 0.61 | 0.16 | 0.19 | 0.25 |
| LST | 11.47 | 20.60 | 0.53 | 1118.00 | 263.00 | 1381.00 | 0.92 | 0.61 | 0.25 | 0.59 | 0.18 | 0.23 | 0.28 |
| SM | 11.57 | 20.55 | 0.64 | 1115.00 | 322.00 | 1437.00 | 0.93 | 0.65 | 0.30 | 0.53 | 0.23 | 0.28 | 0.34 |
| SST | 12.52 | 10.44 | 0.54 | 1213.00 | 221.00 | 1434.00 | 0.96 | 0.55 | 0.21 | 0.62 | 0.15 | 0.19 | 0.24 |
| WIND | 11.49 | 15.39 | 0.66 | 1078.00 | 352.00 | 1430.00 | 0.97 | 1.06 | 0.33 | 0.69 | 0.19 | 0.29 | 0.28 |
| WIND+SM+ZTD_GNSS3h_1ist | 9.11 | 13.49 | 0.78 | 755.00 | 577.00 | 1332.00 | 0.95 | 1.06 | 0.54 | 0.49 | 0.36 | 0.51 | 0.50 |
| WIND+SM+ZTD_GNSS3h_1ist_18UTC | 11.50 | 22.88 | 0.71 | 1217.00 | 681.00 | 1898.00 | 0.97 | 1.53 | 0.64 | 0.58 | 0.34 | 0.59 | 0.47 |
| ZTD_GNSS3h | 38.14 | 2.82 | 0.70 | 1298.00 | 262.00 | 1560.00 | 0.95 | 0.84 | 0.25 | 0.71 | 0.15 | 0.21 | 0.23 |
| ZTD_GNSS3h_1ist | 20.16 | 0.06 | 0.68 | 1317.00 | 242.00 | 1559.00 | 0.90 | 0.71 | 0.23 | 0.68 | 0.15 | 0.20 | 0.23 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 72 mm (IFS) Livorno Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 14.53 | 0.84 | 0.09 | 973.00 | 99.00 | 1072.00 | 0.87 | 0.23 | 0.09 | 0.60 | 0.08 | 0.09 | 0.13 |
| LST | 12.49 | 13.28 | 0.05 | 1021.00 | 51.00 | 1072.00 | 0.82 | 0.29 | 0.05 | 0.83 | 0.04 | 0.03 | 0.05 |
| SM | 16.38 | 4.69 | 0.04 | 1031.00 | 41.00 | 1072.00 | 0.85 | 0.48 | 0.04 | 0.92 | 0.03 | 0.01 | 0.02 |
| SST | 15.03 | 1.67 | 0.08 | 989.00 | 84.00 | 1073.00 | 0.85 | 0.21 | 0.08 | 0.62 | 0.07 | 0.07 | 0.12 |
| WIND | 8.37 | 0.94 | 0.62 | 783.00 | 477.00 | 1260.00 | 0.93 | 0.73 | 0.45 | 0.38 | 0.35 | 0.43 | 0.50 |
| WIND+SM+ZTD_GNSS3h_1ist | 11.23 | 6.73 | 0.49 | 914.00 | 344.00 | 1258.00 | 0.98 | 0.51 | 0.32 | 0.36 | 0.27 | 0.31 | 0.41 |
| WIND+SM+ZTD_GNSS3h_1ist_18UTC | 9.82 | 21.93 | 0.58 | 996.00 | 348.00 | 1344.00 | 0.87 | 0.63 | 0.33 | 0.48 | 0.25 | 0.31 | 0.38 |
| ZTD_GNSS3h | 16.77 | 19.09 | 0.33 | 1371.00 | 30.00 | 1401.00 | 0.99 | 0.70 | 0.03 | 0.96 | 0.02 | -0.01 | -0.01 |
| ZTD_GNSS3h_1ist | 8.10 | 3.48 | 0.25 | 872.00 | 233.00 | 1105.00 | 0.91 | 0.48 | 0.22 | 0.54 | 0.17 | 0.21 | 0.27 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| Livorno Use Case | ||||
|---|---|---|---|---|
| 24 mm | 48 mm | 72 mm | TOT | GFS-driven CASES |
| 3 | 0 | 1 | 4 | OL |
| 0 | 2 | 0 | 2 | LST |
| 2 | 0 | 0 | 2 | SM |
| 5 | 0 | 0 | 5 | SST |
| 0 | 3 | 2 | 5 | WIND |
| 4 | 3 | 8 | 15 | WIND+SM+ZTD_GNSS3h_1ist |
| 0 | 5 | 4 | 9 | WIND+SM+ZTD_GNSS3h_1ist_18UTC |
| 1 | 1 | 0 | 2 | ZTD_GNSS3h |
| 1 | 0 | 1 | 2 | ZTD_GNSS3h_1ist |
| Livorno Use Case | ||||
|---|---|---|---|---|
| 24 mm | 48 mm | 72 mm | TOT | GFS-driven CASES |
| 4 | 0 | 2 | 6 | OL |
| 0 | 1 | 1 | 2 | LST |
| 0 | 1 | 1 | 2 | SM |
| 3 | 0 | 0 | 3 | SST |
| 3 | 5 | 8 | 16 | WIND |
| 1 | 3 | 1 | 5 | WIND+SM+ZTD_GNSS3h_1ist |
| 1 | 6 | 0 | 7 | WIND+SM+ZTD_GNSS3h_1ist_18UTC |
| 3 | 0 | 1 | 4 | ZTD_GNSS3h |
| 1 | 0 | 1 | 2 | ZTD_GNSS3h_1ist |
| 24 mm (GFS) Silvi Marina Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 10.55 | 5.70 | 0.87 | 2534.00 | 3533.00 | 6067.00 | 0.81 | 0.91 | 0.72 | 0.21 | 0.60 | 0.65 | 0.67 |
| SM | 8.78 | 4.12 | 0.95 | 2246.00 | 3891.00 | 6137.00 | 0.84 | 1.01 | 0.79 | 0.22 | 0.65 | 0.71 | 0.71 |
| SST | 12.29 | 5.04 | 0.95 | 2322.00 | 3833.00 | 6155.00 | 0.86 | 0.99 | 0.78 | 0.21 | 0.64 | 0.71 | 0.71 |
| WIND | 9.05 | 2.58 | 0.99 | 2333.00 | 3989.00 | 6322.00 | 0.89 | 1.06 | 0.81 | 0.24 | 0.65 | 0.72 | 0.71 |
| ZTD_GNSS3h_1ist | 11.03 | 4.70 | 0.95 | 1874.00 | 4342.00 | 6216.00 | 0.96 | 1.13 | 0.88 | 0.22 | 0.71 | 0.80 | 0.76 |
| ZTD_INSAR | 15.24 | 5.18 | 0.99 | 2143.00 | 4026.00 | 6169.00 | 0.86 | 1.04 | 0.82 | 0.21 | 0.67 | 0.74 | 0.73 |
| WIND+SM+ZTD_INSAR_GNSS3h_1ist | 12.44 | 5.25 | 0.91 | 2275.00 | 3758.00 | 6033.00 | 0.85 | 0.96 | 0.76 | 0.21 | 0.64 | 0.69 | 0.70 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 24mm (IFS) Silvi Marina Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 12.85 | 6.96 | 0.86 | 3068.00 | 3250.00 | 6318.00 | 0.77 | 0.90 | 0.66 | 0.27 | 0.53 | 0.58 | 0.59 |
| SM | 12.40 | 6.78 | 0.85 | 3051.00 | 3226.00 | 6277.00 | 0.74 | 0.90 | 0.65 | 0.27 | 0.53 | 0.57 | 0.59 |
| SST | 5.88 | 6.03 | 0.90 | 3326.00 | 3212.00 | 6538.00 | 0.80 | 0.95 | 0.65 | 0.31 | 0.50 | 0.55 | 0.56 |
| WIND | 12.22 | 5.44 | 0.89 | 2733.00 | 3488.00 | 6221.00 | 0.86 | 0.96 | 0.71 | 0.26 | 0.57 | 0.62 | 0.63 |
| ZTD_GNSS3h_1ist | 9.11 | 2.01 | 0.90 | 2857.00 | 3985.00 | 6842.00 | 0.89 | 1.17 | 0.81 | 0.31 | 0.60 | 0.68 | 0.65 |
| ZTD_INSAR | 7.03 | 7.30 | 0.93 | 3030.00 | 3449.00 | 6479.00 | 0.81 | 0.98 | 0.70 | 0.29 | 0.55 | 0.60 | 0.61 |
| WIND+SM+ZTD_INSAR_GNSS3h_1ist | 11.90 | 5.54 | 0.83 | 3171.00 | 3124.00 | 6295.00 | 0.74 | 0.88 | 0.63 | 0.28 | 0.51 | 0.55 | 0.57 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 48 mm (GFS) Silvi Marina Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 10.87 | 14.91 | 0.53 | 1775.00 | 1401.00 | 3176.00 | 0.75 | 0.60 | 0.48 | 0.20 | 0.43 | 0.46 | 0.55 |
| SM | 10.50 | 11.80 | 0.59 | 1649.00 | 1567.00 | 3216.00 | 0.82 | 0.70 | 0.54 | 0.23 | 0.47 | 0.51 | 0.58 |
| SST | 11.89 | 12.09 | 0.60 | 1790.00 | 1499.00 | 3289.00 | 0.82 | 0.74 | 0.52 | 0.31 | 0.42 | 0.47 | 0.53 |
| WIND | 8.33 | 9.53 | 0.65 | 1724.00 | 1613.00 | 3337.00 | 0.88 | 0.84 | 0.55 | 0.34 | 0.43 | 0.50 | 0.54 |
| ZTD_GNSS3h_1ist | 8.07 | 6.82 | 0.96 | 2213.00 | 1833.00 | 4046.00 | 0.97 | 0.99 | 0.63 | 0.37 | 0.46 | 0.57 | 0.57 |
| ZTD_INSAR | 7.82 | 9.47 | 0.59 | 1401.00 | 1683.00 | 3084.00 | 0.87 | 0.78 | 0.58 | 0.25 | 0.48 | 0.54 | 0.60 |
| WIND+SM+ZTD_INSAR_GNSS3h_1ist | 12.70 | 12.78 | 0.54 | 1560.00 | 1526.00 | 3086.00 | 0.78 | 0.69 | 0.52 | 0.24 | 0.45 | 0.50 | 0.57 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 48 mm (IFS) Silvi Marina Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 5.65 | 6.44 | 0.41 | 2008.00 | 1117.00 | 3125.00 | 0.95 | 0.51 | 0.38 | 0.25 | 0.34 | 0.36 | 0.45 |
| SM | 10.54 | 6.84 | 0.39 | 1971.00 | 1103.00 | 3074.00 | 0.94 | 0.48 | 0.38 | 0.21 | 0.34 | 0.36 | 0.46 |
| SST | 15.64 | 9.28 | 0.50 | 2036.00 | 1236.00 | 3272.00 | 0.99 | 0.59 | 0.43 | 0.29 | 0.36 | 0.39 | 0.47 |
| WIND | 9.61 | 9.37 | 0.53 | 1990.00 | 1303.00 | 3293.00 | 0.93 | 0.69 | 0.45 | 0.35 | 0.36 | 0.40 | 0.46 |
| ZTD_GNSS3h_1ist | 5.83 | 6.34 | 0.74 | 1843.00 | 1687.00 | 3530.00 | 0.97 | 0.91 | 0.58 | 0.36 | 0.44 | 0.52 | 0.54 |
| ZTD_INSAR | 5.32 | 7.76 | 0.47 | 1932.00 | 1243.00 | 3175.00 | 0.99 | 0.62 | 0.43 | 0.31 | 0.36 | 0.39 | 0.46 |
| WIND+SM+ZTD_INSAR_GNSS3h_1ist | 14.17 | 7.26 | 0.38 | 2081.00 | 1028.00 | 3109.00 | 0.89 | 0.46 | 0.35 | 0.24 | 0.32 | 0.33 | 0.43 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 72 mm (GFS) Silvi Marina Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 7.09 | 12.62 | 0.72 | 716.00 | 964.00 | 1680.00 | 0.84 | 0.74 | 0.64 | 0.13 | 0.58 | 0.63 | 0.72 |
| SM | 5.28 | 7.73 | 0.73 | 678.00 | 993.00 | 1671.00 | 0.82 | 0.77 | 0.66 | 0.14 | 0.60 | 0.65 | 0.73 |
| SST | 7.92 | 13.03 | 0.74 | 753.00 | 957.00 | 1710.00 | 0.83 | 0.79 | 0.64 | 0.19 | 0.55 | 0.62 | 0.69 |
| WIND | 7.20 | 9.17 | 0.74 | 783.00 | 943.00 | 1726.00 | 0.83 | 0.81 | 0.63 | 0.22 | 0.53 | 0.61 | 0.67 |
| ZTD_GNSS3h_1ist | 8.58 | 5.21 | 0.89 | 922.00 | 990.00 | 1912.00 | 0.81 | 1.01 | 0.66 | 0.35 | 0.49 | 0.63 | 0.62 |
| ZTD_INSAR | 4.50 | 8.48 | 0.70 | 730.00 | 937.00 | 1667.00 | 0.84 | 0.79 | 0.62 | 0.21 | 0.54 | 0.61 | 0.68 |
| WIND+SM+ZTD_INSAR_GNSS3h_1ist | 4.29 | 10.15 | 0.72 | 649.00 | 993.00 | 1642.00 | 0.85 | 0.75 | 0.66 | 0.12 | 0.61 | 0.65 | 0.74 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| 72 mm (IFS) Silvi Marina Use Case | |||||||||||||
| Run | CENTROID DIST | ANGLE DIFF | AREA RATIO | SYMMETRIC DIFF | INTERSECTION AREA | UNION AREA | P90 RATIO | FBIAS | PODY | FAR | CSI | HK | HSS |
| OL | 7.59 | 1.12 | 0.44 | 1035.00 | 587.00 | 1622.00 | 0.96 | 0.45 | 0.39 | 0.13 | 0.37 | 0.39 | 0.52 |
| SM | 7.42 | 3.47 | 0.44 | 1034.00 | 588.00 | 1622.00 | 0.98 | 0.45 | 0.39 | 0.13 | 0.37 | 0.39 | 0.52 |
| SST | 6.13 | 1.79 | 0.47 | 996.00 | 629.00 | 1625.00 | 0.95 | 0.50 | 0.42 | 0.16 | 0.39 | 0.41 | 0.54 |
| WIND | 6.30 | 7.20 | 0.57 | 893.00 | 758.00 | 1651.00 | 0.91 | 0.62 | 0.51 | 0.19 | 0.45 | 0.50 | 0.60 |
| ZTD_GNSS3h_1ist | 9.08 | 1.30 | 0.74 | 1009.00 | 832.00 | 1841.00 | 0.85 | 0.81 | 0.56 | 0.32 | 0.44 | 0.53 | 0.58 |
| ZTD_INSAR | 6.89 | 0.96 | 0.46 | 984.00 | 625.00 | 1609.00 | 0.96 | 0.51 | 0.42 | 0.18 | 0.38 | 0.41 | 0.53 |
| WIND+SM+ZTD_INSAR_GNSS3h_1ist | 7.40 | 2.67 | 0.44 | 1030.00 | 587.00 | 1617.00 | 0.96 | 0.44 | 0.39 | 0.12 | 0.37 | 0.39 | 0.52 |
| Best small | Best small | Best = 1 | Best small | Best big | Best small | Best = 1 | Best = 1 | Best = 1 | Best = 0 | Best = 1 | Best = 1 | Best = 1 | |
| Silvi Marina Use Case | ||||
|---|---|---|---|---|
| 24 mm | 48 mm | 72 mm | TOT | GFS-driven CASES |
| 1 | 1 | 0 | 2 | OL |
| 2 | 0 | 3 | 5 | SM |
| 2 | 0 | 0 | 2 | SST |
| 2 | 0 | 0 | 2 | WIND |
| 7 | 7 | 4 | 18 | ZTD_GNSS3h_1ist |
| 2 | 5 | 0 | 7 | ZTD_INSAR |
| 2 | 0 | 10 | 12 | WIND+SM+ZTD_INSAR_GNSS3h_1ist |
| Silvi Marina Use Case | ||||
|---|---|---|---|---|
| 24 mm | 48 mm | 72 mm | TOT | IFS-driven CASES |
| 0 | 0 | 0 | 0 | OL |
| 0 | 1 | 1 | 2 | SM |
| 1 | 1 | 1 | 3 | SST |
| 3 | 0 | 3 | 6 | WIND |
| 7 | 8 | 5 | 20 | ZTD_GNSS3h_1ist |
| 2 | 2 | 1 | 5 | ZTD_INSAR |
| 0 | 1 | 1 | 2 | WIND+SM+ZTD_INSAR_GNSS3h_1ist |
References
- Gatelli, F.; MontiGuamieri, A.M.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–865. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Multibaseline InSAR DEM reconstruction: The wavelet approach. IEEE Trans. Geosci. Remote Sens. 1999, 37, 705–715. [Google Scholar] [CrossRef]
- Randel, D.L.; Vonder Haar, T.H.; Ringerud, M.A.; Stephens, G.L.; Greenwald, T.J.; Combs, C.L. A new global water vapor dataset. Bull. Am. Meteorol. Soc. 1996, 77, 1233–1246. [Google Scholar] [CrossRef]
- Schneider, T.; O’Gorman, P.A.; Levine, X.J. Water vapor and the dynamics of climate changes. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Roca, R.; Weckwerth, T.M.; Andronova, N.G. Tropospheric water vapor, convection, and climate. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Schepanski, K.; Knippertz, P.; Fiedler, S.; Timouk, F.; Demarty, J. The sensitivity of nocturnal low-level jets and near-surface winds over the Sahel to model resolution, initial conditions and boundary-layer set-up. Q. J. R. Meteorol. Soc. 2015, 141, 1442–1456. [Google Scholar] [CrossRef]
- Muñoz Sabater, J.; Fouilloux, A.; De Rosnay, P. Technical implementation of SMOS data in the ECMWF integrated forecasting system. IEEE Geosci. Remote Sens. Lett. 2012, 9, 252–256. [Google Scholar] [CrossRef]
- Mateus, P.; Tomé, R.; Nico, G.; Member, S.; Catalão, J. Three-Dimensional Variational Assimilation of InSAR PWV Using the WRFDA Model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7323–7330. [Google Scholar] [CrossRef]
- Mateus, P.; Miranda, P.; Nico, G.; Catalão, J.; Pinto, P.; Tomé, R. Assimilating InSAR Maps of Water Vapor to Improve Heavy Rainfall Forecasts: A Case Study With Two Successive Storms. J. Geophys. Res. Atmos. 2018, 123, 3341–3355. [Google Scholar] [CrossRef]
- Pichelli, E.; Ferretti, R.; Cimini, D.; Panegrossi, G.; Perissin, D.; Pierdicca, N.; Rocca, F.; Rommen, B. InSAR water vapor data assimilation into mesoscale model MM5: Technique and pilot study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3859–3875. [Google Scholar] [CrossRef]
- Panegrossi, G.; Ferretti, R.; Pulvirenti, L.; Pierdicca, N. Impact of ASAR soil moisture data on the MM5 precipitation forecast for the Tanaro flood event of April 2009. Nat. Hazards Earth Syst. Sci. 2011, 11, 3135–3149. [Google Scholar] [CrossRef]
- Lagasio, M.; Pulvirenti, L.; Parodi, A.; Boni, G.; Pierdicca, N.; Venuti, G.; Realini, E.; Tagliaferro, G.; Barindelli, S.; Rommen, B. Effect of the ingestion in the WRF model of different Sentinel-derived and GNSS-derived products: Analysis of the forecasts of a high impact weather event. Eur. J. Remote Sens. 2019, 1–18. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.; Wang, X.Y.; Wang, W.; Power, J.G. A Description of the Advanced Research WRF Version 3. NCAR Tech. Note NCAR/TN-475+STR. 2008. Available online: https://opensky.ucar.edu/islandora/object/technotes:500 (accessed on 20 January 2019). [CrossRef]
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaskovicová, L.; Blöshl, G.; Borga, M.; Dumitrescu, A.; et al. A compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef]
- Llasat, M.C.; Llasat-Botija, M.; Petrucci, O.; Pasqua, A.A.; Rosselló, J.; Vinet, F.; Boissier, L. Towards a database on societal impact of Mediterranean floods within the framework of the HYMEX project. Nat. Hazards Earth Syst. Sci. 2013, 13, 1337–1350. [Google Scholar] [CrossRef]
- Dayan, U.; Nissen, K.; Ulbrich, U. Review article: Atmospheric conditions inducing extreme precipitation over the eastern and western Mediterranean. Nat. Hazards Earth Syst. Sci. 2015, 15, 2525–2544. [Google Scholar] [CrossRef]
- Ducrocq, V.; Nuissier, O.; Ricard, D.; Lebeaupin, C.; Thouvenin, T. A numerical study of three catastrophic precipitating events over southern France. II: Mesoscale triggering and stationarity factor. Q. J. R. Meteorol. Soc. 2008, 134, 131–145. [Google Scholar] [CrossRef]
- Nuissier, O.; Ducrocq, V.; Ricard, D.; Lebeaupin, C.; Anquetin, S. A numerical study of three catastrophic precipitating events over southern France. I: Numerical framework and synoptic ingredients. Q. J. R. Meteorol. Soc. 2008, 134, 111–130. [Google Scholar] [CrossRef]
- Fiori, E.; Ferraris, L.; Molini, L.; Siccardi, F.; Kranzlmueller, D.; Parodi, A. Triggering and evolution of a deep convective system in the Mediterranean sea: Modelling and observations at a very fine scale. Q. J. R. Meteorol. Soc. 2017, 143, 927–941. [Google Scholar] [CrossRef]
- Molini, L.; Parodi, A.; Rebora, N.; Craig, G.C. Classifying severe rainfall events over Italy by hydrometeorological and dynamical criteria. Q. J. R. Meteorol. Soc. 2011, 137, 148–154. [Google Scholar] [CrossRef]
- Pignone, F.; Rebora, N. GRISO: Rainfall Generator of Spatial Interpolation from Observation. EGU General Assembly Conference Abstracts. 2014, Volume 16. Available online: https://meetingorganizer.copernicus.org/EGU2014/EGU2014-13946.pdf (accessed on 20 January 2019).
- Barker, D.; Huang, X.Y.; Liu, Z.; Auligné, T.; Zhang, X.; Rugg, S.; Ajjaji, R.; Bourgeois, A.; Bray, J.; Chen, Y.; et al. The weather research and forecasting model’s community variational/ensemble data assimilation system: WRFDA. Bull. Am. Meteorol. Soc. 2012, 93, 831–843. [Google Scholar] [CrossRef]
- Lagasio, M.; Parodi, A.; Procopio, R.; Rachidi, F.; Fiori, E. Lightning potential index performances in multimicrophysical cloud-resolving simulations of a back-building mesoscale convective system: The Genoa 2014 event. J. Geophys. Res. Atmos. 2017, 122, 4238–4257. [Google Scholar] [CrossRef]
- Lagasio, M.; Silvestro, F.; Campo, L.; Parodi, A. Predictive capability of a high-resolution hydrometeorological forecasting framework coupling WRF cycling 3dvar and Continuum. J. Hydrol. 2019. [Google Scholar] [CrossRef]
- Paulson, C.A. The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteorol. 1970, 9, 857–860. [Google Scholar] [CrossRef]
- Dyer, A.J.; Hicks, B.B. Flux-gradient relationships in the constant flux layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Webb, E.K. Profile relationships: The log-linear range, and extension to strong stability. Q. J. R. Meteorol. Soc. 1970, 96, 67–90. [Google Scholar] [CrossRef]
- Beljaars, A.C. The parametrization of surface fluxes in large-scale models under free convection. Q. J. R. Meteorol. Soc. 1995, 121, 255–270. [Google Scholar] [CrossRef]
- Smirnova, T.G.; Brown, J.M.; Benjamin, S.G. Performance of different soil model configurations in simulating ground surface temperature and surface fluxes. Mon. Weather Rev. 1997, 125, 1870–1884. [Google Scholar] [CrossRef]
- Smirnova, T.G.; Brown, J.M.; Benjamin, S.G.; Kim, D. Parameterization of cold season processes in the MAPS land-surface scheme. J. Geophys. Res. 2000, 105, 4077–4086. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Hong, S.Y.; Lim, J.O.J. The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Bouttier, F.; Courtier, P. Data Assimilation Concepts and Methods. Meteorological Training Course Lecture Series; ECMWF: Reading, UK, 1999. [Google Scholar]
- Ide, K.; Courtier, P.; Ghil, M.; Lorenc, A.C. Unified notation for data assimilation: Operational, sequential and variational. J. Meteorol. Soc. Jpn. 1997, 75, 181–189. [Google Scholar] [CrossRef]
- Wang, H.; Huang, X.Y.; Sun, J.; Xu, D.; Zhang, M.; Fan, S.; Zhong, J. Inhomogeneous background error modeling for WRF-Var using the NMC method. J. Appl. Meteorol. Climatol. 2014, 53, 2287–2309. [Google Scholar] [CrossRef]
- Barindelli, S.; Realini, E.; Venuti, G.; Fermi, A.; Gatti, A. Detection of water vapor time variations associated with heavy rain in northern Italy by geodetic and low-cost GNSS receivers. Earth Planets Space 2018, 70, 28. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The constants in the equation for atmospheric refractive index at radio frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Mendes, V.B. Modeling the Neutral-Atmospheric Propagation Delay in Radiometric Space Techniques. Ph.D. Thesis, University of New Brunswick, Fredericton, NB, Canada, 1999. [Google Scholar]
- Davis, A.C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
- Davis, A.C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part II: Application to convective rain system. Mon. Weather Rev. 2006, 134, 1785–1795. [Google Scholar] [CrossRef]
- Ebert, E.E. Fuzzy verification of high-resolution gridded forecasts: A review and proposed framework. Meteorol. Appl. 2008, 15, 51–64. [Google Scholar] [CrossRef]
- Pastor, F.; Estrela, M.J.; Peñarrocha, D.; Millán, M.M. Torrential rains on the Spanish Mediterranean coast: Modeling the effects of the sea surface temperature. J. Appl. Meteorol. 2001, 40, 1180–1195. [Google Scholar] [CrossRef]
- Lebeaupin, C.; Ducrocq, V.; Giordani, H. Sensitivity of torrential rain events to the sea surface temperature based on high-resolution numerical forecasts. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Meroni, A.N.; Renault, L.; Parodi, A.; Pasquero, C. Role of the Oceanic Vertical Thermal Structure in the Modulation of Heavy Precipitations Over the Ligurian Sea. Pure Appl. Geophys. 2018, 175, 4111–4130. [Google Scholar] [CrossRef]
- Meroni, A.N.; Parodi, A.; Pasquero, C. Role of SST patterns on surface wind modulation of a heavy midlatitude precipitation event. J. Geophys. Res. Atmos. 2018, 123, 9081–9096. [Google Scholar] [CrossRef]
- Cassola, F.; Ferrari, F.; Mazzino, A.; Miglietta, M.M. The role of the sea in the flash floods events over Liguria (northwestern Italy). Geophys. Res. Lett. 2016, 43, 3534–3542. [Google Scholar] [CrossRef]
- Monti Guarnieri, A.; Rocca, F. Options for continuous radar Earth observations. Sci. China Inform. Sci. 2017, 60, 060301. [Google Scholar] [CrossRef]
- Balenzano, A.; Mattia, F.; Satalino, G.; Davidson, M.W.J. Dense temporal series of C- and L-band SAR data for soil moisture retrieval over agricultural crops. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 439–450. [Google Scholar] [CrossRef]
- Kim, S.B.; Tsang, L.; Johnson, J.T.; Huang, S.; Van Zyl, J.J.; Njoku, E.G. Soil moisture retrieval using time-series radar observations over bare surfaces. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1853–1863. [Google Scholar] [CrossRef]
- Pierdicca, N.; Pulvirenti, L.; Bignami, C. Soil moisture estimation over vegetated terrains using multitemporal remote sensing data. Remote Sens. Environ. 2010, 114, 440–448. [Google Scholar] [CrossRef]
- Oh, Y. Quantitative retrieval of soil moisture content and surface roughness from multipolarized radar observations of bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2014, 42, 596–601. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Squicciarino, G.; Cenci, L.; Boni, G.; Pierdicca, N.C.M.; Campanella, P. A surface soil moisture mapping service at national (Italian) scale based on Sentinel-1 data. Environ. Model. Softw. 2018, 102, 13–28. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Bindlish, R.; Barros, A.P. Parameterization of vegetation backscatter in radar-based, soil moisture estimation. Remote Sens. Environ. 2001, 76, 130–137. [Google Scholar] [CrossRef]
- Realini, E.; Reguzzoni, M. goGPS: Open source software for enhancing the accuracy of low-cost receivers by single-frequency relative kinematic positioning. Meas. Sci. Technol. 2013, 24. [Google Scholar] [CrossRef]
- Herrera, A.M.; Suhandri, H.F.; Realini, E.; Reguzzoni, M.; de Lacy, M.C. goGPS: Open-source MATLAB software. GPS Solut. 2016, 20, 595–603. [Google Scholar] [CrossRef]
- Héroux, P.; Kouba, J. GPS precise point positioning using IGS orbit products. Phys. Chem. Earth Part A 2001, 26, 573–578. [Google Scholar] [CrossRef]
- Porcello, L.J. Turbulence-Induced Phase Errors in Synthetic-Aperture Radars. IEEE Trans. Aerosp. Electron. Syst. 1970, AES-6, 636–644. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; Wiley: New York, NY, USA, 1998; Volume 4. [Google Scholar]
- Azcueta, M.; Tebaldini, S. SAOCOM-CS bistatic phase calibration and tomographic performance analysis. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 111–114. [Google Scholar] [CrossRef]
- Gomba, G.; González, F.R.; De Zan, F. Ionospheric phase screen compensation for the Sentinel-1 TOPS and ALOS-2 ScanSAR modes. IEEE Trans. Geosci. Remote Sens. 2016, 55, 223–235. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]


| before Orbital Error Removal | after Orbital Error Removal | |
|---|---|---|
| no. of data | 53 | 53 |
| mean [cm] | 1.24 | −0.14 |
| standard deviation [cm] | 4.87 | 2.42 |
| min [cm] | −9.54 | −5.19 |
| max [cm] | 9.89 | 4.46 |
| Number of Images | 49 |
|---|---|
| First Image | 18 May 2017 |
| Last Image | 14 March 2018 |
| Image Dimensions [pixels] | 67,395 × 12,141 |
| AOI [km] | 340 × 200 |
| Livorno Use Case | |||
| Experiment Name | Assimilated Variable | Assimilation Methodology | Timing (HH UTC DD/MM/YYYY) |
| OL | - | No assimilation | |
| LST | Land Surface Temperature | Direct insertion | 10 UTC 09/09/2017 |
| SST | Sea Surface Temperature | Direct insertion | 21 UTC 09/09/2017 |
| SM | Soil Moisture | Nudging-like | 18 UTC 08/09/2017 |
| ZTD_GNSS3h | Zenith Total Delay | 3DVAR of all obs. available in the time window (1/2 h) around the analysis time | 3 h cycling |
| ZTD_GNSS3h_1ist | Zenith Total Delay | 3DVAR only of obs. closest to the analysis time | 3 h cycling |
| WIND | Wind speed and direction | 3DVAR | 18 UTC 08/09/2017 |
| WIND+SM+ZTD_GNSS3h_1ist | Wind speed and direction, Soil Moisture, Zenith Total Delay | Nudging-like, 3DVAR | Refer to the single variable timing |
| WIND+SM+ZTD_GNSS3h_1ist_18UTC | Wind speed and direction, Soil Moisture, Zenith Total Delay | Nudging-like, 3DVAR only of obs. closest to the analysis time | 18 UTC 08/09/2017 |
| Silvi Marina Use Case | |||
| Experiment name | Assimilated Variable | Assimilation Methodology | Timing (HH UTC DD/MM/YYYY) |
| OL | - | No assimilation | |
| SST | Sea Surface Temperature | Direct insertion | 00 UTC 14/11/2017 |
| SM | Soil Moisture | Nudging-like | 05 UTC and 17UTC 14/11/2017 |
| ZTD_GNSS3h_1ist | Zenith Total Delay | 3DVAR only of obs. closest to the analysis time | 3-h cycling |
| ZTD_INSAR | Zenith Total Delay | 3DVAR | 05 UTC 14/11/2017 |
| WIND | Wind speed and direction | 3DVAR | 05 UTC and 17UTC UTC 14/11/2017 |
| WIND+SM+ZTD_INSAR_GNSS3h_1ist | Wind speed and direction, Soil Moisture, Zenith Total Delay | Nudging-like, 3DVAR | 05 UTC 14/11/2017 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lagasio, M.; Parodi, A.; Pulvirenti, L.; Meroni, A.N.; Boni, G.; Pierdicca, N.; Marzano, F.S.; Luini, L.; Venuti, G.; Realini, E.; et al. A Synergistic Use of a High-Resolution Numerical Weather Prediction Model and High-Resolution Earth Observation Products to Improve Precipitation Forecast. Remote Sens. 2019, 11, 2387. https://doi.org/10.3390/rs11202387
Lagasio M, Parodi A, Pulvirenti L, Meroni AN, Boni G, Pierdicca N, Marzano FS, Luini L, Venuti G, Realini E, et al. A Synergistic Use of a High-Resolution Numerical Weather Prediction Model and High-Resolution Earth Observation Products to Improve Precipitation Forecast. Remote Sensing. 2019; 11(20):2387. https://doi.org/10.3390/rs11202387
Chicago/Turabian StyleLagasio, Martina, Antonio Parodi, Luca Pulvirenti, Agostino N. Meroni, Giorgio Boni, Nazzareno Pierdicca, Frank S. Marzano, Lorenzo Luini, Giovanna Venuti, Eugenio Realini, and et al. 2019. "A Synergistic Use of a High-Resolution Numerical Weather Prediction Model and High-Resolution Earth Observation Products to Improve Precipitation Forecast" Remote Sensing 11, no. 20: 2387. https://doi.org/10.3390/rs11202387
APA StyleLagasio, M., Parodi, A., Pulvirenti, L., Meroni, A. N., Boni, G., Pierdicca, N., Marzano, F. S., Luini, L., Venuti, G., Realini, E., Gatti, A., Tagliaferro, G., Barindelli, S., Monti Guarnieri, A., Goga, K., Terzo, O., Rucci, A., Passera, E., Kranzlmueller, D., & Rommen, B. (2019). A Synergistic Use of a High-Resolution Numerical Weather Prediction Model and High-Resolution Earth Observation Products to Improve Precipitation Forecast. Remote Sensing, 11(20), 2387. https://doi.org/10.3390/rs11202387














