GPS-PWV Based Improved Long-Term Rainfall Prediction Algorithm for Tropical Regions
Abstract
:1. Introduction
2. Methodology
2.1. Derivation of GPS-PWV Values
2.2. Rainfall Prediction Algorithms
2.2.1. Rainfall Prediction Algorithm from the Temperate Region
2.2.2. Three-Factor Rainfall Prediction Algorithm from the Sub-Tropical Region
3. Database Description
3.1. GPS-PWV Data
3.2. Weather Station Data
4. Implementation of Existing Algorithms using Tropical Data
4.1. Time Series Analysis
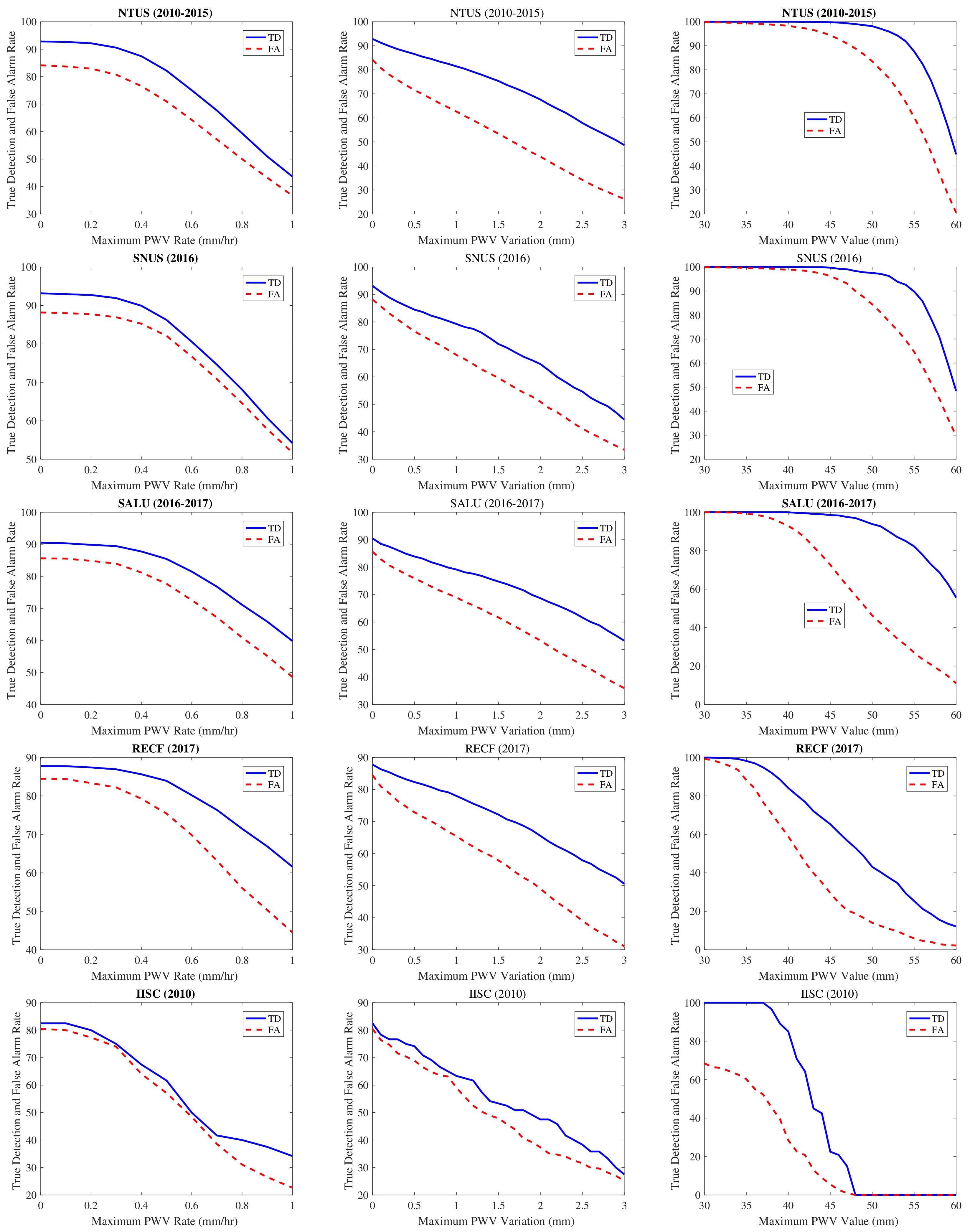
4.2. Results for Maximum Rate of Increment of PWV Values (mm/hr)
4.3. Results for the Three-Factor Method
5. Proposal of an Improved Long-Term Rainfall Prediction Algorithm for the Tropical Region
5.1. Determination of Optimum Threshold Criteria for the Tropical Region
5.2. Rainfall Detection Criteria for Tropical Region
6. Analysis of Effects of Different Lead Time and Historical Time Values on Rainfall Prediction
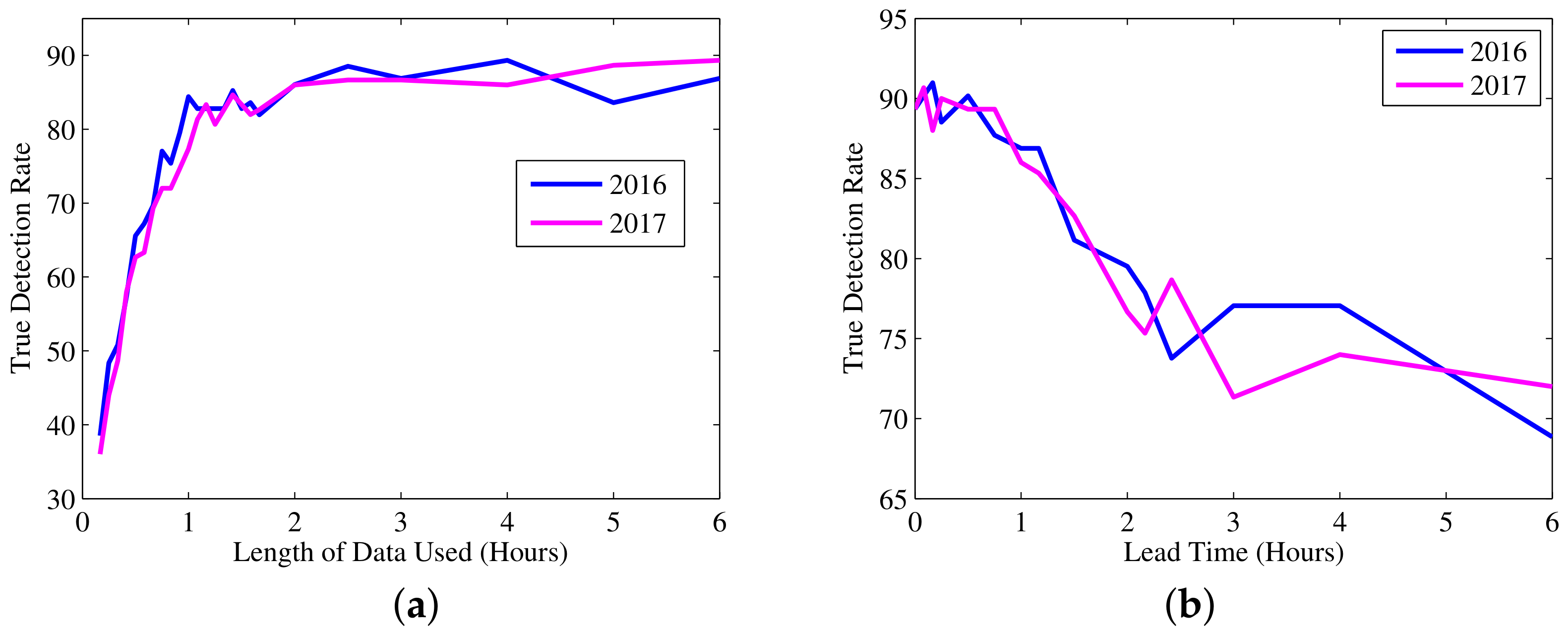
6.1. Varying Historical Length of Data
6.2. Varying Lead Time Length
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Jin, S.G.; Park, J.; Cho, J.; Park, P.H. Seasonal variability of GPS-derived Zenith Tropospheric Delay (1994-2006) and climate implications. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Dai, A.; Hove, T.V.; Baelen, J. A near-global, 2-hourly data set of atmospheric Precipitable water from ground-based GPS measurements. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, X.; Liu, Y.; Zhou, D.; Zhang, H.; Sun, W. Precipitable water vapor characterization in the coastal regions of China based on ground-based GPS. Adv. Space Res. 2017, 60, 2368–2378. [Google Scholar] [CrossRef]
- Yeh, T.; Shih, H.; Wang, C.; Choy, S.; Chen, C.; Hong, J. Determining the precipitable water vapor thresholds under different rainfall strengths in Taiwan. Adv. Space Res. 2018, 61, 941–950. [Google Scholar] [CrossRef]
- Hu, P.; Huang, G.; Zhang, Q.; Wang, X.; Mao, M. Algorithm and Performance of Precipitable Water Vapor Retrieval Using Multiple GNSS Precise Point Positioning Technology. China Satell. Navig. Conf. (CSNC) 2018, 497, 139–151. [Google Scholar]
- Ansari, K.; Corumluoglu, O.; Panda, S.K.; Verma, P. Spatiotemporal variability of water vapor over Turkey from GNSS observations during 2009-2017 and predictability of ERA-Interim and ARMA model. J. Glob. Position. Syst. 2018, 16, 8. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W. GPS-based PWV for precipitation forecasting and its application to a typhoon event. J. Atmospheric Sol.-Terr. Phys. 2018, 167, 124–133. [Google Scholar] [CrossRef]
- Prasad, A.K.; Singh, R.P. Validation of MODIS Terra, AIRS, NCEP/DOE AMIP-II Reanalysis-2, and AERONET Sun photometer derived integrated precipitable water vapor using ground-based GPS receivers over India. J. Geophy. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, A.K.; Prasad, A.K.; Singh, R.P. Variability of GPS derived water vapor and comparison with MODIS data over the Indo-Gangetic plains. Phy. Chem. Earth, Parts A/B/C 2013, 55, 11–18. [Google Scholar] [CrossRef]
- Gui, K.; Che, H.; Chen, Q.; Zeng, Z.; Liu, H.; Wang, Y.; Zhang, X. Evaluation of radiosonde, MODIS-NIR-Clear, and AERONET precipitable water vapor using IGS ground-based GPS measurements over China. Atmos. Res. 2017, 197, 461–473. [Google Scholar] [CrossRef]
- Singh, R.P.; Dey, S.; Sahoo, A.K.; Kafatos, M. Retrieval of water vapor using SSM/I and its relation with the onset of monsoon. Ann. Geophys. 2004, 22, 3079–3083. [Google Scholar] [CrossRef]
- Barindelli, S.; Realini, E.; Venuti, G.; Fermi, A.; Gatti, A. Detection of water vapor time variations associated with heavy rain in northern Italy by geodetic and low-cost GNSS receivers. Earth Planets Space 2018, 70. [Google Scholar] [CrossRef]
- Shi, J.; Xu, C.; Guo, J.; Gao, Y. Real-Time GPS precise point positioning-based precipitable water vapor estimation for rainfall monitoring and forecasting. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3452–3459. [Google Scholar]
- Benevides, P.; Catalao, J.; Miranda, P.M.A. On the inclusion of GPS Precipitable water vapour in the nowcasting of rainfall. Nat. Hazards Easrth Syst. Sci. 2015, 15, 2605–2616. [Google Scholar] [CrossRef]
- Yao, Y.; Shan, L.; Zhao, Q. Establishing a method of short term rainfall forecasting based on GNSS-derived PWV and its application. Sci. Rep. 2017, 7, 3452–3459. [Google Scholar] [CrossRef] [PubMed]
- Manning, T.; Zhang, K.; Rohm, W.; Choy, S.; Hurter, F. Detecting Severe Weather using GPS Tomography: An Australian Case Study. J. Glob. Pos. Sys. 2012, 11, 58–70. [Google Scholar] [CrossRef]
- Suparta, W.; Zulkeple, S.K.; Putro, W.S. Estimation of Thunderstorm Activity in Tawau, Sabah Using GPS Data. Adv. Sci. Lett. 2017, 23, 1370–1373. [Google Scholar] [CrossRef]
- Zhang, K.; Manning, T.; Wu, S.; Rohm, W.; Silcock, D.; Choy, S. Capturing the signature of severe weather events in Australia using GPS measurements. IEEE Trans. Geosci. Remote Sens. 2015, 8, 1839–1847. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S.; Yuan, F.; Ong, J.T. GPS Derived PWV for Rainfall Nowcasting in Tropical Region. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4835–4844. [Google Scholar] [CrossRef]
- Manandhar, S.; Dev, S.; Lee, Y.H.; Meng, Y.S.; Winkler, S. A Data-Driven Approach For Accurate Rainfall Prediction. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9323–9331. [Google Scholar] [CrossRef]
- Kumar, L.S.; Manandhar, S.; Lee, Y.H.; Meng, Y.S. GPS derived PWV for monitoring cloud evolution. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium—Fall (PIERS—FALL), Singapore, 19–22 November 2017; pp. 1421–1423. [Google Scholar] [CrossRef]
- Wang, Z.; French, J.; Vali, G.; Wechsler, P.; Haimov, S.; Rodi, A.; Deng, M.; Leon, D.; Snider, J.; Peng, L.; et al. Single aircraft integration of remote sensing and in situ sampling for the study of cloud microphysics and dynamics. Bull. Amer. Meteor. Soc. 2012, 93, 653–668. [Google Scholar] [CrossRef]
- Elgered, G.; Davis, J.L.; Herring, T.A.; Shapiro, I.I. Geodesy by radio interferometry: water vapor radiometry for estimation of the wet delay. J. Geophys. Res. 1991, 96, 6541–6555. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S.; Ong, J.T. A Simplified Model for the Retrieval of Precipitable Water Vapor from GPS Signal. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6245–6253. [Google Scholar] [CrossRef]
- Alshawaff, F.; Fuhrmann, T.; Knopfler, A.; Luo, X.; Mayer, M.; Hinz, S.; Heck, B. Accurate estimation of atmospheric water vapor using GNSS observations and surface meteorological data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3764–3771. [Google Scholar] [CrossRef]
- Crustal Dynamics Data Information System: NASA’s Archive of Space Geodesy Data. Available online: ftp://cddis.gsfc.nasa.gov/pub/gps/data/ (accessed on 30 June 2018).
- SiReNT Station Network. Available online: https://sirent.inlis.gov.sg/ (accessed on 30 June 2018).
- National University of Singapore, Singapore. Geography Weather Station. Available online: https://inetapps.nus.edu.sg/fas/geog/ (accessed on 30 June 2018).
- Cemaden’s Observational Network for Natural Disaster Risk Monitoring. Available online: http://www.cemaden.gov.br/mapainterativo/ (accessed on 30 June 2018).
- Yeo, J.X.; Lee, Y.H.; Ong, J.T. Performance of site diversity investigated through Radar derived results. IEEE Trans. Antennas Prop. 2000, 59, 3890–3898. [Google Scholar] [CrossRef]



| Country | GPS Station ID | location | Provider | Station Height (m) | Years |
|---|---|---|---|---|---|
| Singapore | NTUS | ( N, E) | IGS | 2010–2015 | |
| Singapore | SNUS | ( N, E) | SiReNT | 2016 | |
| Brazil | SALU | ( S, W) | IGS | 2016–2017 | |
| Brazil | RECF | ( S, W) | IGS | 2017 | |
| India | IISC | ( N, E) | IGS | 2010 |
| Region | Station | Year | Maximum PWV Rate (mm/hr) | TD (%) | FA (%) |
|---|---|---|---|---|---|
| Tropical | NTUS | 2010 | |||
| 2011 | |||||
| 2012 | |||||
| 2013 | |||||
| 2014 | |||||
| 2015 | |||||
| SNUS | 2016 | ||||
| SALU | 2016 | ||||
| 2017 | |||||
| RECF | 2017 | ||||
| IISC | 2010 | ||||
| Sub-Tropical [15] | LJSL | 2015 | |||
| ZHOS | 2015 | ||||
| ZJPH | 2015 | ||||
| ZJXC | 2015 | ||||
| ZJYH | 2015 | ||||
| Temperate [14] | Lisbon | 2012 | 75 |
| Region | Station | Year | TD (%) | FA (%) | |
|---|---|---|---|---|---|
| Major Factor Only (mm/hr) | Three-Factors | ||||
| Tropical | NTUS | 2010 | |||
| 2011 | |||||
| 2012 | |||||
| 2013 | |||||
| 2014 | |||||
| 2015 | |||||
| SNUS | 2016 | ||||
| SALU | 2016 | ||||
| 2017 | |||||
| RECF | 2017 | ||||
| IISC | 2010 | ||||
| Sub-Tropical [15] | LJSL | 2015 | |||
| ZHOS | 2015 | ||||
| ZJPH | 2015 | ||||
| ZJXC | 2015 | ||||
| ZJYH | 2015 | ||||
| Station | Year | Max PWV Value (mm) | TD (%) | FA (%) |
|---|---|---|---|---|
| NTUS | 2010–2015 | 55 | ||
| SNUS | 2016 | 56 | ||
| SALU | 2016–2017 | 50 | ||
| RECF | 2017 | 40 | ||
| IISC | 2010 | 39 |
| Station | Year | Three-factor Method | Proposed Method | ||||
|---|---|---|---|---|---|---|---|
| TD (%) | FA (%) | Max PWV (mm) | Max Rate (mm/hr) | TD (%) | FA (%) | ||
| NTUS | 2010 | 55 | |||||
| 2011 | 55 | ||||||
| 2012 | 55 | ||||||
| 2013 | 55 | ||||||
| 2014 | 55 | ||||||
| 2015 | 55 | ||||||
| SNUS | 2016 | 56 | |||||
| SALU | 2016 | 50 | |||||
| 2017 | 50 | ||||||
| RECF | 2017 | 40 | |||||
| IISC | 2010 | 39 | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manandhar, S.; Lee, Y.H.; Meng, Y.S. GPS-PWV Based Improved Long-Term Rainfall Prediction Algorithm for Tropical Regions. Remote Sens. 2019, 11, 2643. https://doi.org/10.3390/rs11222643
Manandhar S, Lee YH, Meng YS. GPS-PWV Based Improved Long-Term Rainfall Prediction Algorithm for Tropical Regions. Remote Sensing. 2019; 11(22):2643. https://doi.org/10.3390/rs11222643
Chicago/Turabian StyleManandhar, Shilpa, Yee Hui Lee, and Yu Song Meng. 2019. "GPS-PWV Based Improved Long-Term Rainfall Prediction Algorithm for Tropical Regions" Remote Sensing 11, no. 22: 2643. https://doi.org/10.3390/rs11222643
APA StyleManandhar, S., Lee, Y. H., & Meng, Y. S. (2019). GPS-PWV Based Improved Long-Term Rainfall Prediction Algorithm for Tropical Regions. Remote Sensing, 11(22), 2643. https://doi.org/10.3390/rs11222643






